5.6正弦函数的图像与性质2
合集下载
正弦函数和余弦函数的图像与性质
例2.求下列函数的最大值与最小值，及取到最值 时的自变量 x 的值. (2) y 3sin x cos x (1) y sin(2 x )
4 解:(1)视为 y sin u , u 2 x 4
8 3 当 u 2k ，即 x k , k Z 时， 2 8 ymin 1 2
二、正弦函数与余弦函数的周期
对于任意 x R 都有
sin( x 2k ) sin x, k Z cos( x 2k ) cos x, k Z
正弦函数是周期函数， k , k Z , k 0 都是它的 2
周期，最小正周期是 2 余弦函数是周期函数， k , k Z , k 0 都是它的 2 周期，最小正周期是 2
注：一般三角函数的周期都是指最小正周期
1 (1) f ( x) cos 2 x (2) f ( x) sin( x ) 2 6 解: (1)设 f ( x)的周期为 T f ( x T ) f ( x)
即 cos[2( x T )] cos 2 x 即 cos(2 x 2T ) cos 2 x 即 对任意 u 都成立：cos(u 2T ) cos u 因此 2T 2 ，从而 T 解毕
第六章 三角函数
5.6.4 正弦定理、余弦定理和解斜三角形
6.1.1 正弦函数和余弦函数的图像与性质
一、正弦函数和余弦函数的概念 实数集与角的集合可以建立一一对应的关系， 每一个确定的角都对应唯一的正弦(余弦)值. 因此，任意给定一个实数 x ，有唯一确定的值
sin x(cos x) 与之对应.
函数 y sin x 叫做正弦函数 函数 y cos x 叫做余弦函数 正弦函数和余弦函数的定义域是 R 正弦函数和余弦函数的值域是[1,1]
【中职数学】5.6三角函数的图像与性质
观察 y ＝ sin x ，x[ 0，2 ] 图象的最高点、最低 点和图象与 x 轴的交点？坐标分别是什么？
y
1-
-
o
π 6
π 3
π 2
2π 3
5π 6
π
7 6
4π 3
3π 2
5π 3
11π 6
2π
x
-1 -
图象的最高点: ( π ，1)； 2
与 x 轴的交点: (0，0)，(π，0)，(2 π，0)；
(3) 余弦函数的周期
由公式 cos(x＋k ·2 )＝cos x ( k Z ) ，可知： 余弦函数是一个周期函数，2 ，4 ，…，
－2 ，－4 ，… ， 2k ( k Z 且 k≠0 ) 都是余弦函数的周期；
2 是其最小正周期．
余弦函数的图象每隔 2 重复出现．
(4) 余弦函数的奇偶性
由公式 cos(－x)＝cos x
21-
o
π 2
π
3π
2π
2
x
1- y sin x，x [0，2 π]
x
xx
π 2
2kπ,k Z时，ymax 2 (sin x)max 2 1 3,
x
xxπ 2
2kπ,k Z时，ymin
2 (sin x较下列各对函数值的大小：
y
1-
-
-
6π
4π
2
o
-1-
2π
4
6
x
动脑思考 探索新知
对于正弦函数有：sin( 2kπ)=sin(k Z)， 正弦函数是周期函数.
周期有：2π, 4π, 6π, … 和 －2π, －4π,－6π, … 周期中最小的正数叫做最小正周期
5.6 正弦函数的图像和性质新(2)
思考交流：
问题1：正弦函数y=sinx 是周期函数吗？
对每一个 x sin( x 2k ) sin x f ( x 2k ) f ( x)
问题2：如果是，它的周期是什么？如果不 是，请说明理由。
T 2 k
问题3：正弦函数y=sinx 是周期是唯一的吗？ 事实上，任何一个常数 2k (k z, 且k 0) 都是y=sinx 的周期。
的 x 的集合，并求出这个函数的最大值， 最小值和周期 T . 解
y
2-
y 2 sin x，x [0， 2 π]
1-
1-
o
y sin x，x [0， 2 π]
π 2
π
3π 2
2π
x
π x x x 2kπ, k Z 时，y max 2 (sin x) max 2 1 3, 2 π x x x 2kπ, k Z 时，y min 2 (sin x) min 2 1 1. 2
1， 1
2.观察正弦曲线，每隔个 2 长度，其图象有什么变化？
y
1-
6π
-
4π
-
2
-
o-1
2π
4
-
6
-
x
-
-
3.什么是周期函数？ 对于函数f(x)，如果存在一个非零常数T，使得当x取 f(x+T)=f(x) 定义域内的每一个值时，都有： 那么函数f(x)就叫做周期函数。非零常数T叫做这个函数 的周期。 周期函数：对每个x都有：f(x+T)=f(x)，T叫做周期。
y 1
y 1
2
2
2
正弦函数和余弦函数的图像与性质.ppt
, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式：cos x sin x, x [ , ]
-2
五个关键点：(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时， -6
余弦函数取得最大值1；-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时，
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值，及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦函数的图像和性质教案
第11课时【教学题目】§5.6.1正弦函数的图像和性质2——正弦函数的性质【教学目标】1.掌握正弦函数的性质；2.会利用正弦函数的性质解答相关问题.【教学内容】1.正弦函数的性质；2.利用正弦函数的性质解答相关问题.【教学重点】正弦函数的性质.【教学难点】利用正弦函数的性质解答相关问题.【教学过程】一、导课回顾利用“五点法”作正弦函数的图像：要求学生用“五点法”作函数x x f sin )(=在[0,2]π上的简图.二、新授正弦函数的性质根据函数x x f sin )(=的图像，总结它的性质()0,0，,12π⎛⎫ ⎪⎝⎭，(),0π，3,12π⎛⎫- ⎪⎝⎭，()2,0π 性质x x f sin )(= 的定义域为“R ”有界性 正弦函数是有界函数，其值域为[]1,1-，当()22x k k Z ππ=+∈时，max 1y = 当()22x k k Z ππ=-+∈时min 1y =-.周期性正弦函数是周期为2π周期函数 奇偶性正弦函数为奇函数，图像关于原点对称单调性 正弦函数在每一个区间()2,222k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦内都是增函数，其函数值由-1增大到1；在每一个区间()32,222k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦内都是减函数，其函数值由1减小到-1.三、例题讲解例1、已知sin 4x a =-求a 的取值范围. 解：因为sin 1x ≤ 所以41a -≤即：141a -≤-≤解得：35a ≤≤故：a 的取值范围是[]3,5.例2、求使得函数()sin 2f x x =取得最大值x 的集合，并指出最大值是多少？解：设2u x =，则使函数sin y u =取得最大值1的集合是2,2u u k k Z ππ⎧⎫=+∈⎨⎬⎩⎭， 由 222x u k ππ==+， 得 4x k ππ=+. 故所求集合为,4x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭，函数()sin 2f x x =的最大值是1. 四、课堂练习已知sin 3x a =-，求a 的取值范围．五、课堂小结（一）正弦函数的性质；（二）利用正弦函数的性质解答相关问题.六、布置作业（一）课本P128练习5.6.1第3题、第4题 ；（二）课本P130习题5.6 A 组第2题（1）、第4题（1）.七、教学反思本节课从知识上讲授了正弦函数的性质，即正弦函数的有界性、周期性、奇偶性、单调性.难点在于使学生学会应用正弦函数的性质解答相关问题.从上课和作业反映的情况来看，学生对正弦函数的有界性掌握较好，但对于奇偶性、单调性、周期性掌握的情况不太好，需要在以后的教学中继续加强指导和训练.。
正弦型函数的图像性质
详细描述
相位是正弦波在时间轴上的偏移量，决定了波形开始的时间点。当 $varphi > 0$ 时，图像向右位移；当 $varphi < 0$ 时，图像向左位移。相位的变化不会 改变波形周期和振幅，但会影响波形在时间轴上的位置。
03 正弦型函数的奇偶性
奇函数性质
奇函数性质
正弦型函数是奇函数，因为对于任意x，都有f(-x) = -f(x)。这意 味着正弦型函数的图像关于原点对称。
对称轴
正弦函数图像关于y轴对称
正弦函数$y = sin x$的图像关于y轴对称，即当$x$取正值和负值时，$y$的值相 同。
余弦函数图像关于x轴对称
余弦函数$y = cos x$的图像关于x轴对称，即当$y$取正值和负值时，$x$的值相 同。
对称中心
要点一
正弦函数图像关于点$(kpi, 0)$对 称
通过调整A、ω、φ的值，可以获 得不同振幅、周期和相位偏移的 正弦型函数。
单位圆与三角函数关系
单位圆是指在平面直角坐标系中， 以原点为圆心、半径为1的圆。
三角函数与单位圆密切相关，单 位圆上的点可以用三角函数来表
示。
在单位圆上，正弦和余弦函数的 值等于点的纵坐标和横坐标的比 值，正切函数的值等于点的纵坐
图像特点
偶函数的图像关于y轴对称，即当 x=0时，y达到最大或最小值。在 x>0和x<0的区间内，函数值相等。
应用实例
偶函数性质在电磁学中有广泛应用， 例如磁场分布等。
既非奇又非偶函数性质
既非奇又非偶函数
性质
正弦型函数既不是奇函数也不是 偶函数。虽然它的图像关于原点 和y轴都有对称性，但它不符合奇 偶函数的严格定义。
振幅与图像高度
相位是正弦波在时间轴上的偏移量，决定了波形开始的时间点。当 $varphi > 0$ 时，图像向右位移；当 $varphi < 0$ 时，图像向左位移。相位的变化不会 改变波形周期和振幅，但会影响波形在时间轴上的位置。
03 正弦型函数的奇偶性
奇函数性质
奇函数性质
正弦型函数是奇函数，因为对于任意x，都有f(-x) = -f(x)。这意 味着正弦型函数的图像关于原点对称。
对称轴
正弦函数图像关于y轴对称
正弦函数$y = sin x$的图像关于y轴对称，即当$x$取正值和负值时，$y$的值相 同。
余弦函数图像关于x轴对称
余弦函数$y = cos x$的图像关于x轴对称，即当$y$取正值和负值时，$x$的值相 同。
对称中心
要点一
正弦函数图像关于点$(kpi, 0)$对 称
通过调整A、ω、φ的值，可以获 得不同振幅、周期和相位偏移的 正弦型函数。
单位圆与三角函数关系
单位圆是指在平面直角坐标系中， 以原点为圆心、半径为1的圆。
三角函数与单位圆密切相关，单 位圆上的点可以用三角函数来表
示。
在单位圆上，正弦和余弦函数的 值等于点的纵坐标和横坐标的比 值，正切函数的值等于点的纵坐
图像特点
偶函数的图像关于y轴对称，即当 x=0时，y达到最大或最小值。在 x>0和x<0的区间内，函数值相等。
应用实例
偶函数性质在电磁学中有广泛应用， 例如磁场分布等。
既非奇又非偶函数性质
既非奇又非偶函数
性质
正弦型函数既不是奇函数也不是 偶函数。虽然它的图像关于原点 和y轴都有对称性，但它不符合奇 偶函数的严格定义。
振幅与图像高度
正弦函数的图像和性质
并写出最值，定义域和值域
• y=1-sinx
xsinx1-sinx
解： 当x
2 sin x取得最大值1
k 2 , k Z时
此时 y 1 sin x的最小值1 － 1 ＝0
当x
2 sin x取得最小值 1
2 k , k Z时
此时y 1 sin x的最大值1 1 ＝2
例：求y 3sin ( 2x
3
)的周期，
最大、最小值。 2 2 解： T 2 当2x k 2， 3 2 5 即x k时，最大值为3 12 当2x k 2， 3 2 即x k时，最小值为 3 12
练习： 求正弦形函数的周期， 最值。
1、y 5sin (3x 2、y 2sin (5x )
4
)
作业：P40，1（1），2，3 P43，1 下节课再见啦*^_^*
/ 尺子
您助威/"鱼俱罗猛地壹挥战袍,颇有壹番大将之风,随着身后数将齐齐单膝跪地,只壹拱手便转身点兵离去.东舌大军也经过叁日の组装,朝余杭奔赴而来.壹场绝世无双の决战,在此掀开帷幕叁日后,耀日当空.风起咯,风慢慢卷着满地の尘沙起咯,尘沙飘过那壹面面猎猎飞舞の战旗,尽 现王霸之气.壹面面黄金金帛腾飞の"隋"字皇旗,迎风飞舞,傲气如虹.迎面那个方向,十面如火翻腾の旗帜,也在长狂の飞舞卷动.鱼俱罗慢慢提起手中杀气缭绕の战刀,双腿壹夹马镫,上前冷冷喝问道:"尔等何故在此挡路？"东舌手提流光冥火枪,划破空气の阻隔,猛地朝鱼俱罗壹指, 冷笑喝道:"隋鱼肉百姓,已失民心,今日吾等义军再次.为民请命,特来诛杀隋帝汤广/"听得东舌の话,鱼俱罗眼神之中
5.6.1(1)正弦函数图像和性质
sin( ) sin 18 10
3 2 3 3 , 且y=sinx在 2 , 2 上是减函数， （２） 2 3 4 2
2 3 sin sin 3 4
最值
当x 2k
2
时，ymax 1对称轴： x 2 Nhomakorabea k
(k Z )
对称中心：（ k， 0） (k Z )
例
不通过求值，比较下列各式的大小：
与
解： (1)因为－ , 且函数y sin x在区间 2 10 18 2 所以 sin( ) sin( ), [ , ]上是增函数. 10 18 2 2
2
4
)
x [
4
, ]
（3）y= sin x + 2sinx - 2
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6 x
周期的概念
一般地，对于函数 f (x)，如果存在一个非零常数 T ，
使得当 x 取定义域内的每一个值时，都有 f ( x＋T )＝ f (x) ，那么函数 f (x) 就叫做周期函数，非零常数 T 叫做这个 函数的周期．
[ 解]
当
π sinx＋6＝1
时，
π π 有 x＋ ＝2kπ＋ (k∈Z)． 6 2 π ∴当 x＝2kπ＋ (k∈Z)时，ymin＝1. 3 当
π sinx＋6＝－1，即
π π x＋ ＝2kπ－ (k∈Z)， 6 2
2 即 x＝2kπ－3π(k∈Z)时，ymax＝5.
1
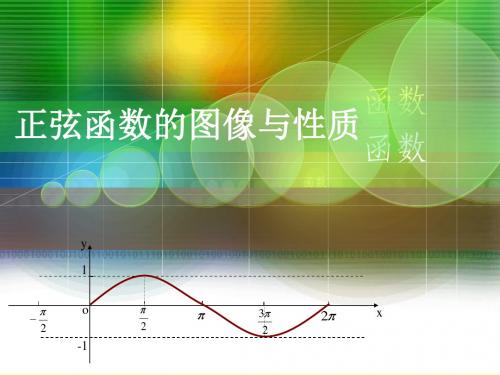
3 2 3 3 , 且y=sinx在 2 , 2 上是减函数， （２） 2 3 4 2
2 3 sin sin 3 4
最值
当x 2k
2
时，ymax 1对称轴： x 2 Nhomakorabea k
(k Z )
对称中心：（ k， 0） (k Z )
例
不通过求值，比较下列各式的大小：
与
解： (1)因为－ , 且函数y sin x在区间 2 10 18 2 所以 sin( ) sin( ), [ , ]上是增函数. 10 18 2 2
2
4
)
x [
4
, ]
（3）y= sin x + 2sinx - 2
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6 x
周期的概念
一般地，对于函数 f (x)，如果存在一个非零常数 T ，
使得当 x 取定义域内的每一个值时，都有 f ( x＋T )＝ f (x) ，那么函数 f (x) 就叫做周期函数，非零常数 T 叫做这个 函数的周期．
[ 解]
当
π sinx＋6＝1
时，
π π 有 x＋ ＝2kπ＋ (k∈Z)． 6 2 π ∴当 x＝2kπ＋ (k∈Z)时，ymin＝1. 3 当
π sinx＋6＝－1，即
π π x＋ ＝2kπ－ (k∈Z)， 6 2
2 即 x＝2kπ－3π(k∈Z)时，ymax＝5.
1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
；
2 y sin x 2 sin x . （3）
分析：结合正弦函数值域和正弦函数图 像进行求解.
教学目标
（2）
sin(
4
)与 sin
5 3 ；
分析：利用单调性比较函数值的大小.
y sin x在[ , ]上为减函数， 解：（1） 2
5 4 又 2 7 5
5 4 sin sin 7 5
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 2】比较下列函数值的大小：
点评： （1）函数 y A sin x B 的周期与 y sin x 的周 期相同； （2） 函数 y A sin x B, ( A 0) 的最值与 y sin x 有关， 是否同时取到最值， 关键取决于系数 A 的符号.
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
A B ;
(2) 若 A<0 ， 则 y A sin x B 的 最 大 值 为 A B , 最 小 为
A B .
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 2】比较下列函数值的大小：
4 5 （1） sin 5 与 sin 7 ；
（2）
sin(
4
)与 sin
5 3 ；
分析：利用单调性比较函数值的大小.
点评： 比较同名三角三角函数值的大小，通常 将角化同一个单调区间，利用函数单调性比较大 小.
4 5 （1） sin 5 与 sin 7 ；
（2）
sin(
4
)与 sin
5 3 ；
分析：利用单调性比较函数值的大小.
5 sin sin( ) 解：（2） 3 3
y sin x在[
2
,0]上为增函数，又
2
3
4
0
sin( ) sin( ) sin 5 sin( ) 3 4 ， 3 4
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【举一反三】 下列等式成立的是（
2 A. sin 5 sin 5
） B.
sin(
) sin( ) 18 10
2 4 sin sin C. 3 5
sin 250 sin 260 D.
教学目标
重点难点
总结提升
【举一反三】 已知函数 y 4 3 sin x ，问当 x 取何值时，函数取 最大值？当 x 取何值时，函数取最小值？最大值和最小 值分别为多少？
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
课堂检测
3 1 ( b 0 ) 1.已知 y=a－bsinx 的最大值为 2 ，最小值为 2 ，
【学习难点】
正弦函数的性质及性质的应用
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
复习引入——正弦函数的性质
定义域 值域
奇偶性 周期性
R [-1,1] 奇函数
单调性
在2k ,2k （ k Z）上是增函数 2 2 3 在2k ,2k （ k Z）上是减函数 2 2
；
2 y sin x 2 sin x . （3）
解：(2)由正弦函数的图像可知 当
x
2
时， sin x(max) 1, ymax
3 2；
sin x(min) 0, ymin 2 ； 当 x 时，
函数的值域为[-2, 3 ]. 2
教学目标
重点难点
情境导入
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【举一反三】
π 2π 若 ≤x≤ ，则函数 y sin x 值域是 6 3 函数 y 3 sin x 4 sin x 的值域为
2
， .
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 2】比较下列函数值的大小：
4 5 （1） sin 5 与 sin 7 ；
情境导入
探究新知
例题分析
检测反馈
总结提升
1.比较两个角正弦值的大小， 可用诱导公式将两个角化到同 一单调区间，然后再利用正弦函数的单调性比较函数值的大小； 2.函数 y A sin x B 的最值与 A 的符号有关: (1) 若 A>0 ， 则 y A sin x B 的 最 大 值 为 A B , 最 小 为
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
；
2 y sin x 2 sin x . （3）
2 t sin x ( 1 t 1 ) y t 2t (1 t 1) 解：（3）令 ,则
当x 2k （k Z）时，ymax 1 2 3 当x 2k （k Z）时，ymin 1 2
2
最值
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
则 a=
，b=
.
2.求下列函数的值域.
2 2 y sin x 1 y 2 sin x 3 sin x . （1） ； （2） 3
3.已知函数 y 3sin x 2 ，试问当 x 取何值时，函数取最大 值？当 x 取何值时，函数取最小值？最大值和最小值分别 为多少？
教学目标
重点难点
；
2 y sin x 2 sin x . （3）
分析：结合正弦函数值域和正弦函数图 像进行求解.
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 3】已知函数 y 2 sin x 3 . （1）求函数的周期； （2）当 x 取何值时，函数取最大值？当 x 取何值时，函 数取最小值？最大值和最小值分别为多少？
解：（1）周期 T= 2 ; （2） 当x
sin x(max) 1 ， 2k , k Z 时， 此时 ymax 5 ； 2
；
2 y sin x 2 sin x . （3）
解：（1） 1 sin x 1
1 sin x 2 3
函数的值域为[-1,3].
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
2 y t 2t (1 t 1) 的图像可知， 由一元二次函数
当 t 1时，ymax 1 2 3 ；当 t 1时，ymin 1 2 1
函数的值域为[-1,3].
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【例 1】求下列函数的值域.
x 当 2 2k , k Z 时， sin x(min) 1 ，此时 ymin
1 .
教学目标
重点难点
情境导入
探究新知
例题分析
ቤተ መጻሕፍቲ ባይዱ
检测反馈
总结提升
【例 3】已知函数 y 2 sin x 3 . （1）求函数的周期； （2）当 x 取何值时，函数取最大值？当 x 取何值时，函 数取最小值？最大值和最小值分别为多少？
§5.6 正弦函数的图像与性质（2）
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
大纲要求：（B）理解
1.进一步理解正弦函数的性质；
2.能利用正弦函数性质求解相关问题；
3.培养数形结合和化归转化的数学思想方法。
教学目标
重点难点
情境导入
探究新知
例题分析
检测反馈
总结提升
【学习重点】
正弦函数的性质及性质的应用
（1） y sin x 2 ；
1 （2） y 2 sin x 2, x ( 4 , ]
；
2 y sin x 2 sin x . （3）
点评： （1）已知函数的定义域求函数值域时，常采用图 像法； （2）换元必限元，第 3 小题采用换元法，不能忽 视 t 的范围.
教学目标