2007年高考数学试题(广东卷)与评析和教学启示
广东理科2007年普通高等学校招生全国统一考试(高考数学试卷)

2007年普通高等学校全国招生统一考试(广东卷)数学(理科) 参考答案及试题解析一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求的。
1. 已知函数xx f -=11)(的定义域为M ,)1ln()(x x g +=的定义域为N ,则=⋂N MA.{}1φx xB.{}1πx xC.{}11ππx x -D.φ【命题意图】考查函数的定义域和集合的基本运算 【参考答案】C 【原题解析】由解不等式1-x>0求得M=(-∞,1),由解不等式1+x>0求得N=(-1,+∞),因而M ⋂N=(-1,1),故选C 。
【备考锦囊】在备考中应把握好对基本概念的理解,尤其要把握好集合的交并补等基本运算。
2. 若复数)2)(1(i bi ++是纯虚数(i 是虚数单位,b 是实数)则b =A.2B.21C.21-D.-2【命题意图】考查复数的运算和相关基本概念的理解 【参考答案】A【原题解析】(1+bi)(2+i)=2-b+(1+2b)i ,而复数(1+bi)(2+i)是纯虚数,那么由2-b=0且1+2b ≠0得b=2,故选A 。
3. 若函数是则)(R),(21sin )(2x f x x x f ∈-=A.最小正周期为2π的奇函数 B.最小正周期为π的奇函数C.最小正周期为π2的偶函数D.最小正周期为π的偶函数 【命题意图】考查三角变换和三角函数的性质 【参考答案】D【原题解析】通过二倍角公式可将f(x)等价转化为f(x)=21cos2x ,有余弦函数的性质知f(x)为最小正周期为π的偶函数,选D 。
【备考锦囊】运用二倍角公式来降幂是常用的技巧,备考中学生应该熟练的掌握这种方法 4. 客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是【命题意图】考查分段函数 【参考答案】B【原题解析】由题意可知客车在整个过程中的路程函数S(t)的表达式为0≤t ≤1 S(t)= 1≤t ≤3/23/2≤t ≤5/2对比各选项的曲线知应选D 。
2007 广东高考真题 文科 解析版

要满足 5<ak<8,只须 5<2k-10<8,从而有
15 <k<9,而 k 为自然数。因而只能取 k=8。 2
14.(坐标系与参数方程选做题)在极坐标系中,直线 l 的方程为 sin 3 ,则点 (2, 为 .
6
பைடு நூலகம்
) 到直线 l 的距离
答案:2【解析】该直线对应的直角坐标系下的方程为 y-3=0,而点对应的直角坐标系下的坐标为( 3 , 1),进而求得点到直线的距离为 2。 15.(几何证明选讲选做题)如图4所示,圆 O 的直径AB=6,C 为圆周上一点, BC 3 .过 C 作圆的切线 l , 过A作 l 的垂线AD,垂足为D, 则∠DAC=
2
【解析】(1) AB (3, 4) , AC (c 3, 4) 由 AB AC 0 ,即 -3(c-3)+( -4) =0。 有c= (2)当 c=5 时, AC (2, 4) cos A cos AC , AB
6 16 5 2 5 1 5
3 /7
“硕士刘教育”——数学
调增区间为(
1 ,+ )。 e
;若它的第 k 项满足 5 ak 8 ,则
13.已知数列{ an }的前 n 项和 Sn n2 9n ,则其通项 an
k
. 答案:2n-10;8【解析】a1=S1= -8,而当 n≥2 时,由 an=Sn-Sn-1 求得 an=2n-10,此式对于 n=1 也成立。
.
答案:30 【解析】由 Rt ACB 的各边的长度关系知∠CAB= 30 , 而弦切角 ∠BC =∠CAB= 30 。那么在 Rt ADC 中∠ACD=60 ,故∠DAC=30 。
2007年高考数学试题(广东卷)与评析和教学启示

2007年高考数学试题(广东卷)与评析和教学启示广州市从化中学宋发奎自2004年广东省自主命题以来,广东高考数学试题从04、05年的探索期到06年的适应期,07年迎来了她的成熟期和创新期。
看完全卷,使人眼前一亮,改革步伐之快让人耳目一新,是近几年来难得的好卷。
这份试卷可用“试题新颖,难度略降,紧扣课标,考查能力”来概括,命题风格向上海高考题靠近。
以下谈谈试卷特点和对今后教学的启示。
一、试题特点1.试题新颖,考查能力全卷新颖题很多,如第4题是一道分段函数图像题,既考查了函数的图像也间接考查了分段函数的解析式,定义域、值域,同时还是一道实际应用题。
第6题是统计与算法相结合的好题,同时也是图表信息题,要求学生从图表中获取信息。
第7题是一个优化问题,是线性规划的变种题,线性规划已经考过多年,确实要变一变,今年的优化问题,课本中找不到同类型的练习题,此题考查学生分析问题解决问题的能力。
第8题是“新定义”问题,考查学生的阅读理解能力、自学能力、知识迁移能力,06年也有些题,但今年此题更好,只需运用一般与特殊的关系,不难选出正确答案。
第12题是填空题中的“爬坡题”,是一道立体几何中的计数问题,同时也是一个归纳推理问题,比06年的“垒球”问题难度稍小一些,这样更合理。
第一大题是三角求值题,为送分题。
已知条件为:在直角坐标系中,给定三点的坐标,求一个角的三角函数值问题,考查余弦定理。
既容易又不落俗套。
第二大为《统计》中的求线性回归方程问题,在全国首创,新课标增加了统计的内容,此题体现了新课标的要求,考查了新课标要求的运算能力和数据处理能力。
这种题型出乎许多老师的意外,试题并不难,只相当于课本例题,高三复习一般都很少把其作为重点来复习,正因为如此,这道题就考平时学习的基本功了。
第18题为解析几何题,难度比06年明显下降,这也体现了新课程的特点,在新课程中增加了许多学习内容,当然传统的重点内容如三角、解析几何的学习时间比以前减少,要求也有所降低。
2007年广东高考数学试卷分析

2007年广东高考数学试卷分析一、特点和评价1、平稳过渡,涛声依旧(1)不超大纲例如:(文科19题,理科18题)19.(本小题满分14分)在平面直角坐标系中,已知圆心在第二象限,半径为的圆与直线相切于坐标原点,椭圆与圆的一个交点到椭圆两焦点的距离之和为。
(1)求圆的方程;(2)试探究圆上是否存在异于原点的点,使到椭圆右焦点的距离等于线段的长.若存在,请求出点的坐标;若不存在,请说明理由.分析:本题属于解析几何问题,方法较多(详见评分细则),可以采用最常规的解法,设出方程,解二元二次方程组即可。
(2)不加题量文科:选择题10;填空4;解答题6;共20道题。
理科:选择题8;填空题6;解答题6;共20道题。
(3)不增加难度减少考生的记忆量和运算量(如:文18,理17,提供计算公式,只要代入计算即可)增加每道题的切入口;弱化试题的奥数味和高数味;基础分增加:06年基础分占84分;07年文科基础分达110分;理科基础分占86分。
2、锐意改革,理念更新(1)尝试用新形式:文理分科;增加选做题。
构建“新双基”:传统的双基仍然是考查的重点,07年增加了有应用背景的双基:如,文科17题“三视图”的考查。
(2)增加新的考点07年增加了用数学理论指导实践应用的试题:如文18,理17:18.(本小题满分12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出(参考数值:)分析:回归方程是数学知识的应用,也是近几年第一次高考涉及到。
数学究竟用来干什么?不是用来考试和竞赛,而是为应用服务的。
这也提示我们要注意数学知识的应用性考查。
07年还在文科5,7,题(理科4,6,题)出现。
另外出现非数学形式的考题:文科10(理科7)10.图3是某汽车维修公司的维修点环形分布图.公司在年初分配给四个维修点某种配件各50件.在使用前发现需将四个维修点的这批配件分别调整为,,,件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(件配件从一个维修点调整到相邻维修点的调动件次为)为()A.B.C.D.(4)强化新的理念第一、强化通性,淡化技巧。
2007年高考理科数学试题及参考答案(广东卷)

盘点歌坛最新动态,享受听觉饕餮盛宴。
哈喽大家好,我是小可,本期的榜样音乐为你带来时下最流行的最炫民族风。
五彩缤纷民族乐韵,尽显当代民族风情。
最炫民族风本是凤凰传奇的一张专辑大碟,随后被网友恶搞,成为时下最流行的音乐话题,新世纪元素,加上古典韵味,旋律如行云流水,朗朗上口,那本期节目小可就为你盘点那些民族风。
凤凰传奇---《最新民族风》
民族的就是世界的,本首歌以更多元的手法、更开阔的视觉全方位展示他们的民族风情。
旋律煽情,朗朗上口,极具流行性。
就连NBA的赛场上都响起了最炫民族风的旋律,民族风的流行程度可见一斑啊。
乌拉托亚--《套马杆》
乌兰图雅“来自草原最纯净的声音”把草原神曲《套马杆》演绎得富有草原的味道,将蒙古族的青春豪情、奔放热辣演绎得淋漓尽致,她独特的声音和因其纯正蒙古族血统而对草原音乐的心领神会,带着天籁般的声音,伴着青草的香气。
将本首歌演绎的精彩之极。
格格---《火苗》
一首轻巧热情而富有草原情调的歌曲在前段时间开始发热,各种拼盘都可见到。
格格豪情、洒脱、温柔、火辣,驾驭歌曲的声线和唱腔不断给广大歌迷们惊喜,这个蒙古姑娘通过声音来表现迷人的蒙古风情,她的音乐必定把大家带回一片繁荣的草原风光中来。
听完了如此有民族风情的情歌后,下面为大家带来另一种风格的民族风
南拳妈妈--《牡丹江》
这首歌是南拳妈妈的一首出色地民族民谣歌曲,轻缓的曲调,唯美的歌词,动人的旋律,吧歌的韵味唱的恰到好处。
墨明棋妙-《且试天下》
且试天下是知名音乐团队莫名其妙的一首民族风歌曲,男女的深情对唱,加上民族韵味的江湖气息,让整首歌在民族风的旋律中带着淡淡的侠义风范。
2007年高考试题评价(广东卷)

广东卷一、总体评价广东省试卷是实施《普通高中数学课程标准(实验)》后第一年的高考试卷。
试卷分为文、理科试卷,内容和结构符合课程标准版《考试大纲》和《考试说明》的要求,试卷体现了课标的理念,继承了历年的传统,着重考查数学基础知识、基本方法和基本能力,体现了不同层次的要求,较好地发挥了为高等学校选拔新生的功能,推动和促进了中学数学课程改革。
二、试卷特点1.试卷内容布局合理,主干知识重点考查与2006年试卷有所不同,试卷在题型结构和分值分布都有所调整:选择题文科10题,理科8题;填空题必考题文科3题,理科4题,选考题文科2选1,理科3选2;解答题文理科均为6题。
试卷涵盖了课程标准版《考试大纲》规定的集合、函数、导数、三角函数、数列、概率与统计、向量、解析几何和立体几何等方面的内容。
同时,对与大学数学学习相关的主干内容进行了重点考查,对选修内容按《考试说明》的规定命制了选考题。
2.重视基础知识、方法和技能的考查试卷考查基础知识的试题比例较大,选择题和填空题除文科第(10)题、理科第(8)、(12)题外,其余大部分试题都是基础题,着重考查基础知识、基本方法,突出考查通性通法。
解答题中文科第(16)、(17)、(18)题,理科第(16)、(17)题属于基础题。
文科第(19)、理科第(18)题是比较常规的、难度中等的解析几何试题。
理科第(19)题也是中等难度试题,将立体几何与函数最大值问题结合,有一定的综合性,对能力要求较高,但所用的方法也是教材中常见的方法。
如此试题设置,遵循了课标理念,对课标教材的教学实践有较好的指导意义。
3.注意考查课标新增内容试卷内容符合课标版《考试大纲》,对课标新增的内容有所反映,如理科第(6)题、文科第(7)题考查了算法。
理科第(17)题考查了回归方程。
文科第(18)题考查了三视图。
4.妥善处理选考内容《考试大纲》规定的选考内容理科有3个专题,文科有2个专题。
试卷依据《考试说明》的要求,在填空题考查选考内容:文科2选1,分值5分;理科3选2,分值10分;选考题难度基本平衡。
普通高考数学(广东卷)命题思路解读和试题分析

试题分析
二、填空题
第 9小题理科卷得分:4.49。 第10小题理科卷得分:4.32。 第11小题 理科卷得分:2.15,文科卷得分:2.40。 第12小题 理科卷得分:0.95,文科卷得分:1.15。 第13小题 理科卷得分:4.42,文科卷得分:3.41。 第14小题 理科卷得分:3.91,文科卷得分:3.88。 第15小题 理科卷得分:4.06,文科卷得分:4.43。
试题分析
三、解答题
第16小题 理科卷得分:9.33,文科卷得分:9.21。 文理科题均是解三角形问题,属基础题。 第17小题 文科卷得分:5.54。 试题是立体几何问题,利用三视图求立体体积和侧 面积,属基础题。
试题分析
第17小题 理科卷得分:6.31。 第18小题 文科卷得分:5.38。 文理科题是同一题,考查线性回归问题。 第18小题 理科卷得分:7.34。 第19小题 文科卷得分:4.34。 文理科题是同一题,考查解析几何问题。
(三)对试题情景的创设体现时代性
3.解析几何和三角函数内容的考查体现了课程改革发 展的趋势,避免了以往繁、难、偏的问题。 4.加大试题呈现采用图、表、文并举方式的尝试,文 科卷有6道、理科卷有7道试题配有图表,提高考查考生阅 读信息、获取信息、处理信息能力的力度。
(四)对考生的个性发展体现多样性
(二)对数学能力的考查体现全面性
4.通过解答的多样性考查数学创新意识。注重创设能 考查考生创新意识的情景,如文科卷第10题(理科卷第7 题)的物流配送问题,实质是函数的最值问题,但可通过对 图形的探究,运用合情推理和进行简单运算去解答,题目新 颖,较好地考查了创新意识。文科卷第21题(理科卷第20 题)的函数零点问题,有考生根据函数单调性性质,利用函 数导数的知识来解答,体现了创新意识。
2007广东高考数学(理科)考试及详解
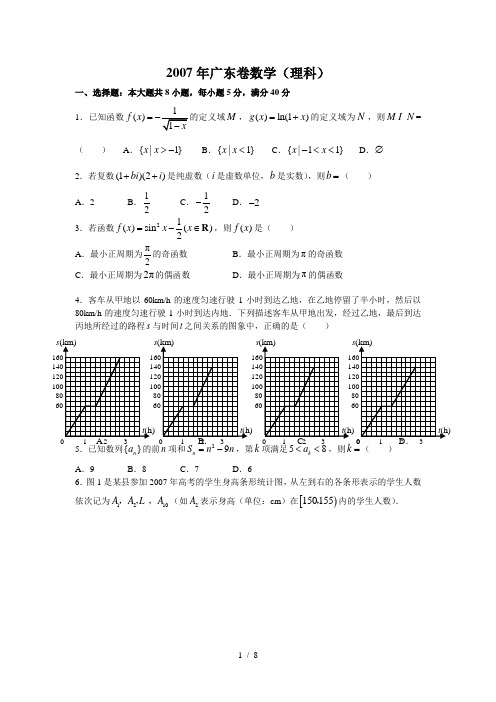
2007年广东卷数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分 1.已知函数()f x =M ,()ln(1)g x x =+的定义域为N ,则M N =( ) A .{|1}x x >-B .{|1}x x <C .{|11}x x -<<D .∅2.若复数(1)(2)bi i ++是纯虚数(i 是虚数单位,b 是实数),则b =( ) A .2B .12C .12-D .2-3.若函数21()sin ()2f x x x =-∈R ,则()f x 是( ) A .最小正周期为π2的奇函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数D .最小正周期为π的偶函数4.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( )5.已知数列{}n a 的前n 项和29n S n n =-,第k 项满足58k a <<,则k =( )A .9B .8C .7D .6 6.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为1210A A A ,,,(如2A 表示身高(单位:cm )在[)150155,内的学生人数).s s ss图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm (含160cm ,不含180cm )的学生人数,那么在流程图中的判断框内应填写的条件是( ) A.6i < B.7i < C.8i <7.图3是某汽车维修公司的维修点环形分布图.公司在年初分配给A B C D ,,,四个维修点某种配件各50件.在使用前发现需将A B C D ,,,四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为( ) A.15B.16C.17D.188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的a b S ∈,,对于有序元素对(a b ,),在S 中有唯一确定的元素*a b 与之对应).若对任意的a b S ∈,,有()**a b a b =,则对任意的a b S ∈,,下列等式中不恒成立的是( ) A .()**a b a a = B .[()]()****a b a a b a = C .()**b b b b =D .()[()]****a b b a b b =二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装图3 图1 图2身高/cm有4个红球,2个白球,乙袋装有1个红球,5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球是红球的概率为 .(答案用分数表示) 10.若向量,a b 满足1==a b ,a 与b 的夹角为120,则a a +a b = . 11.在平面直角坐标系xOy 中,有一定点(21)A ,,若线段OA 的垂直平分线过抛物线22(0)y px p =>的焦点,则该抛物线的准线方程是 .12.如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有()f n 对异面直线,则(4)f = ;()f n = .(答案用数字或n 的解析式表示) 13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为33x t y t=+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2sin 2x y θθ=⎧⎨=+⎩(参数[)02θ∈π,),则圆C 的圆心坐标为 ,圆心到直线l 的距离为 .14.(不等式选讲选做题)设函数()213f x x x =-++,则(2)f -= ;若()5f x ≤,则x 的取值范围是 .15.(几何证明选讲选做题)如图5所示,圆O 的直径6AB =,C 为圆周上一点,3BC =.过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D E ,,则DAC =∠ ,线段AE 的长为 .三、解答题:本大题共6小题,满分80分.16.(12分)已知ABC △顶点的直角坐标分别为(34)A ,,(00)B ,,(0)C c ,.(1)若5c =,求sin A ∠的值;(2)若A ∠是钝角,求c 的取值范围. 17.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa=+; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=)图5图418.(14分)在平面直角坐标系xOy ,已知圆心在第二象限、半径为C 与直线y x=相切于坐标原点O .椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10. (1)求圆C 的方程;(2)试探究圆C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点F 的距离等于线段OF 的长,若存在,请求出点Q 的坐标;若不存在,请说明理由.19.(14分)如图6所示,等腰ABC △的底边AB =高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF△的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P-(1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值?(3)当()V x 取得最大值时,求异面直线AC 与PF20.(14分)已知a 是实数,函数2()223f x ax x a =+--,如果函数()y f x =在区间[]11-,上有零点,求a 取值范围.21.(14分)已知函数2()1f x x x =+-,αβ,是方程()0f x =的两个根(αβ>),()f x '是()f x 的导数,设11a =,1()(12)()n n n n f a a a n f a +=-=',,. (1)求αβ,的值;(2)证明:对任意的正整数n ,都有n a α>; (3)记ln (12)n n n a b n a βα-==-,,,求数列{}n b 的前n 项和n S .图6AB2007年(广东卷)数学(理科B )参考答案一.选择题 CDDC BBCA 1.101110x x x ->⎧⇒-<<⎨+>⎩故选(C )2.(1)(2)(2)(21)bi i b b i ++=-++为纯虚数2b ⇒=,故选(D )3.22111()sin (12sin )cos 2222f x x x x =-=--=- 故选(D ) 4.60(01)60(1 1.5)80( 1.5)60(1.5 2.5)t t s t t t ≤≤⎧⎪=<≤⎨⎪-+<≤⎩,故选(C )5.182(5)6n n n a s s n a -=-=-⇒=,k=8,(或5<2k -10<8)故选(B ) 6.计算4567A A A A +++,由算法框图知,8i < 故选(B ) 7.A D →11件,B C →4件,B A →1件,共16件,故选(C ) 8.()a b a b **=∴当a b =时()b b b b **=,又[()]()()a b a a b b a b a ****=**=;()[()]()a b b a b a b a b ****=**=,故选(A ) 二.填空题9.411()()()669P AB P A P B ==⋅= 10.2cos12012⋅+⋅+=a ab a a a b = 11.线段OA 的垂直平分线方程为152(1)(,0)24y x F -=--⇒⇒准线方程54x =-12.21(1)2n n n C ++=;12;21(1)(2)2n n n n n C ---⋅=13.参数方程化普通方程得直线方程为60x y +-=,圆的方程为22(2)4x y +-= 因此圆心为(0,2),圆心到直线的距离为d ==14.41(2)236f ---=-+=;21()5211x f x x x -≤⇒≤-⇒-≤≤三.解答题16.(1)当5c =时,5,5,cos sin AB BC AC A A ===∠=⇒∠=(2)AC BC c ==,A 为钝角222AB AC AB +<⇒2225(3)16c c +-+<253c ∴>17.(1)(略)(2)97,22x y ==,4166.5i i i x y ==∑,42186i i x ==∑,414221466.5630.786814i ii i i x y x yb x x==--===--∑∑0.35a y bx =-=,故现线性回归方程为0.70.35y x =+(3)当100x =时,70.35y =,9070.3519.65-=,故预测生产100吨甲产品的生产能耗比技改前降低19.65吨标准煤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年高考数学试题(广东卷)与评析和教学启示广州市从化中学宋发奎自2004年广东省自主命题以来,广东高考数学试题从04、05年的探索期到06年的适应期,07年迎来了她的成熟期和创新期。
看完全卷,使人眼前一亮,改革步伐之快让人耳目一新,是近几年来难得的好卷。
这份试卷可用“试题新颖,难度略降,紧扣课标,考查能力”来概括,命题风格向上海高考题靠近。
以下谈谈试卷特点和对今后教学的启示。
一、试题特点1.试题新颖,考查能力全卷新颖题很多,如第4题是一道分段函数图像题,既考查了函数的图像也间接考查了分段函数的解析式,定义域、值域,同时还是一道实际应用题。
第6题是统计与算法相结合的好题,同时也是图表信息题,要求学生从图表中获取信息。
第7题是一个优化问题,是线性规划的变种题,线性规划已经考过多年,确实要变一变,今年的优化问题,课本中找不到同类型的练习题,此题考查学生分析问题解决问题的能力。
第8题是“新定义”问题,考查学生的阅读理解能力、自学能力、知识迁移能力,06年也有些题,但今年此题更好,只需运用一般与特殊的关系,不难选出正确答案。
第12题是填空题中的“爬坡题”,是一道立体几何中的计数问题,同时也是一个归纳推理问题,比06年的“垒球”问题难度稍小一些,这样更合理。
第一大题是三角求值题,为送分题。
已知条件为:在直角坐标系中,给定三点的坐标,求一个角的三角函数值问题,考查余弦定理。
既容易又不落俗套。
第二大为《统计》中的求线性回归方程问题,在全国首创,新课标增加了统计的内容,此题体现了新课标的要求,考查了新课标要求的运算能力和数据处理能力。
这种题型出乎许多老师的意外,试题并不难,只相当于课本例题,高三复习一般都很少把其作为重点来复习,正因为如此,这道题就考平时学习的基本功了。
第18题为解析几何题,难度比06年明显下降,这也体现了新课程的特点,在新课程中增加了许多学习内容,当然传统的重点内容如三角、解析几何的学习时间比以前减少,要求也有所降低。
第19题为立体几何题,为折叠问题中的最值问题,并用导数求解,第三问为用向量方法求异面直线所成的角。
这题集折叠问题、最值问题和导数为一体,体现了函数思想,淡化了推理论证,符合新课标对立体几何处理的思想。
第20题为含参二次方程的零点问题。
新标把二次函数、函数与方程作为函数的重点,这道题应运而生,此题考查了零点定理、数形结合思想和分类讨论思想。
第21题为递推数列问题,用到函数、导数等知识。
此题为压轴题,比去年的难度有所下降。
第一问为送分题,第二问是证明α<a,可用分析法或数学n归纳法证明,第三问转化为等比数列求和,但要发现并证明此数列为等比数列要有很高的数素养和变换技巧。
此题考查推理论证能力和化归思想。
2.紧扣新课标,全面考查各种数学能力和应用意识、创新意识今年是新课标实施后的第一次高考,人们都在猜测今年究竟是按新《课标》要求命题?还是按原《大纲》命题?或是过渡一年?07年试题明确地告诉我们,试题按新课标要求命题。
(1)在内容上,新课标中被删除或降低要求的内容也相应不再出现或降低了要求。
如降低要求的有:、三角函数、立体几何中的推理论证、解析几何等,不再出现的内容如:反函数、极限、坐标平移、定比分点等内容。
而新增内容如函数与方程,统计、算法等在大题和小题中,得到充分的体现。
(2)新课标要求的各种能力在试题中得到充分的体现。
如第19题,考查空间想象能力,第17题考查运算求解能力和数据处理能力,21题考查推理论证能力,第12、21题考查了抽象概括能力。
在注重数学应用方面,第4、6、7、17题,三道小题和一道大题为实际应用问题,改革力度之大让人惊讶。
第7、8、21题等新题型考查了学生的创新意识和创新能力。
第4、6、17题,考查了学生的画图、识图能力。
3.试题梯度明显,区分度高选择题可分为二个层次,前六题为第一层次,主要考查基础知识和基本技能,没有复杂的运算,前四题一看就能得出结果。
第7、8两题为第二层次,没有繁难运算,考查思维能力。
填空题也分两个层次,第12题为第二层次,其他题为第一层次,各层次试题的难度与选择题难度一样。
解答题可分为三个层次,前三题为基础题,只相当于课本难度,第19、20题为第二层次,属中档题,考查数学思想和方法和数学能力。
第21题为第三层次,属压轴题,考查推理论证能力和化归能力。
全卷梯度合理,区分度好。
4.试卷结构有所创新理科选择题由去年的10题变为今年的8题,填空题由去年的4题变为今年的6题,减少选择题,增加填空题有利于提高试卷的信度。
填空题的设问也作了调整,有三道题是一题两空,一道题为一题三空,这样增加了填空题的区分度,提高了得分率。
解答题的题数、分值没有变化,但高考从没考试过的新题型比较多,学生普遍感觉试题新。
5.文理试题有别,内容相差不大,小题有所区别,大题区别不大今年广东卷是首次文理分卷,人们普遍关注文理究竟有多大区别。
在试卷结构方面,文科选择题10题,填空题4题,在选择、填空共14道题中,文理共用题有8题(含一道选做题),文科与理科不同的题有7题,其中有4题是姊妹题,考同一内容,难度相差不大,还有一题是因为理科在选做题中有《不等式选讲》而文科没有,文科多了一道用导数求函数单调区间的小题,文理在小题上真正在难度上有区别的只有两题,文科将理科选择题中第8题(新定义题)和填空题中第12题(归纳推理题)变成了一道函数题和立几判断题,由第二层次降为第一层次,所以文科小题中基本上都是基础题。
在大题中,第一题是三角题,文理为姊妹题,理科题本来就很容易,文科更容易。
唯一有区别的是立体几何题,文科是已知几何体的三视图,求体积和侧面积。
位于第二题,属于容易题,理科是折叠问题中的最值问题,位于倒数第三题,属中难度题。
统计大题、解析几何大题和函数大题则完全一样,理科的压轴题共有三问,去掉第二问,保留第一问和最难的一问后作为文科倒数第二题,所以在大题中,除立体几何外,其他题难度下降不大。
其实文科题应将理科压轴题改为常规等差、等比数列题也许效果会更好。
二、对今后的教学启示1.学习新《课标》、钻研新《课标》、落实新《课标》。
新《课标》不仅是高一、高二上新课时的行动指南,更是高三复习的行动指南。
2.抓基础,精讲精练,培养能力。
应对这种试题,题海战术显然不能奏效,只有精讲精练,让学生扎实打好基础,把时间还给学生,让学生多思考,在日常教学中注重培养数学的运算能力、数据处理能力、空间想象能力和推理论证能力。
只有把培养学生的思维能力放在首位,才能以不变应万变。
平时的训练要控制好难度和比例,选择、填空题以基础题为主,大题以基础题和中难度题为主。
3.重视数学思想方法的渗透,注重培养学生的应用意识和创新意识。
在教学中注重渗透函数与方程思想、数形结思想、分类讨论思想和化归思想等数学思想方法。
数学的精华在于数学思想方法,思考问题的支撑点也是数学思想方法,只有理解了数学思想方法,才算真正学明白了数学。
三、高考揭榜后的反思本文是在高考成绩没有放榜时写成,现结合高考结果,谈谈有关问题。
据了解,今年广州省全省理科平均分为79分,文科平均分是86分,文科均分比理科高,除试题难度不同外,还有题型不同的原因,选择的得分率比填空题的得分高。
广州市A 组理科104分,文科108分,B 组理科94分,文科99分。
附:2007年普通高等学校招生全国统一考试(广东卷)数学(理科)参考公式:锥体的体积公式sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+.如果事件A 、B 相互独立,那么)()()(B P A P B A P ∙=∙.用最小二乘法求线性同归方程系数公式1221ˆˆˆ,ni ii ni i x y nx ybay bx x nx==-==--∑∑. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求的. 1.已知函数xx f -=11)(的定义域为M ,)1ln()(x x g +=的定义域为N ,则M N =A .{}1x x >-B .{}1x x <C .{}11x x -<<D .∅2.若复数)2)(1(i bi ++是纯虚数(i 是虚数单位,b 是实数)则b =A .2B .21C .21-D .-23.若函数21()sin (),()2f x x x f x =-∈R 则是 A .最小正周期为2π的奇函数 B .最小正周期为π的奇函数C .最小正周期为π2的偶函数D .最小正周期为π的偶函数4.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是A .B .C .D . 5.已知数{}n a 的前n 项和29n S n n =-,第k 项满足58k a <<,则k= A .9 B .8 C .7 D .66.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A 1、A 2、…、A 10(如A 2表示身高(单位:cm )(150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是A .i<6B . i<7C . i<8D . i<97.图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为A .15B .16C .17D .188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的a,b ∈S ,对于有序元素对(a,b ),在S 中有唯一确定的元素a*b 与之对应),若对任意的a,b ∈S,有a*(b*a)=b,则对任意的a,b ∈S,下列等式中不恒成立的是A .(a*b )*a=aB .[a*(b*a)]*(a*b)=aC .b*(b*b)=bD .(a*b)* [b*(a*b)]=b二、填空题:本大题共7小题,每小题5分,满分30分,其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中均装有红、白两种颜色的小球,这些小球除颜色外完全相同.其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球. 现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为 .(答案用分数表示) 10. 若向量a 、b 满足|a |=|b |=1,a 与b 的夹角为120,则a a +=a b .11.在平面直角坐标系xOy 中,有一定点A (2,1),若线段OA 的垂直平分线过抛物线22(0)y px p =>的焦点,则该抛物线的准线方程是 .12.如果一个凸多面体n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有)(n f 对异面直线,则)4(f = 图4 ; )(n f = .(答案用数字或n 的解析式表示)13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为3()3x t t y t =+⎧∈⎨=-⎩R 参数,圆C 的参数方程为[])20(2sin 2cos 2πθθθ,参数∈⎩⎨⎧+==y x ,则圆C 的圆心坐标为 ,圆心到直线l 的距离为 . 14.(不等式选讲选做题)设函数)2(,312)(-++-=f x x x f 则= ;若2)(≤x f ,则x 的取值范围是 . 15.(几何证明选讲选做题)如图5所法,圆O 的直径6=AB ,C为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = ,线段AE 的长为 .图5 三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知△ABC 顶点的直角坐标分别为)0,()0,0()4,3(c C B A 、、. (1)若5=c ,求sin ∠A 的值; (2)若∠A 是钝角,求c 的取值范围.17.(本题满分12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生 产能耗y (吨标准煤)的几组对照数据(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bx a =+;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性 同归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=)18.(本小题满分14分)在平面直角坐标系xOy 中,已知圆心在第二象限,半径为22的圆C 与直线y=x 相切于坐标原点O .椭圆9222y ax +=1与圆C 的一个交点到椭圆两点的距离之和为10.(1)求圆C 的方程.(2)试探求C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点P 的距离等于线段OF 的长.若存在,请求出点Q 的坐标;若不存在,请说明理由.19.(本小题满分14分)如图6所示,等腰△ABC 的底边AB =66,高CD =3,点B 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置,使PE ⊥AE .记BE =x ,V (x )表示四棱锥P-ACFE 的体积.(1)求V (x )的表达式;(2)当x 为何值时,V (x )取得最大值?(3)当V (x )取得最大值时,求异面直线AC 与PF 所成角的余弦值20.(本小题满分14分)已知a 是实数,函数2()223f x ax x a =+--.如果函数()y f x =在区间[1,1]-上有零点,求a 的取值范围.21.(本小题满分14分)已知函数2()1f x x x =+-,α、β是方程()0f x =的两个根(αβ>),()f x '是()f x 的导数,设11a =,1()()n n n n f a a a f a +=-',(1,2,)n =. (1)求α、β的值;(2)证明:任意的正整数n ,都有n a α>; (3)记ln n n n a b a βα-=-,(1,2,)n =,求数列{n b }的前n 项和n S .2007年普通高等学校全国招生统一考试 (广东卷)数学(理科)参考答案一、选择题二、填空题9.19 10.12 11.54x =- 12.()12n n +,()()122n n n --13.(0,2), 14.6,[]1,1- 15.30 ,3三、解答题16.解:(1)∵()3,4A ,()0,0B ,∴5AB =,4sin 5B =. 当5c =时,5BC =,AC ==根据正弦定理,得sin sin BC ACA B=, ∴sin A =(2)∵()3,4A ,()0,0B ,(),0C c , ∴5AB =,AC =BC c =.根据余弦定理,得222cos 2AB AC BCA AB AC+-=.若A ∠为钝角,则cos 0A <,即2220AB AC BC +-<,即()22225340c c ⎡⎤+-+-<⎣⎦,解得253c >.17.解:(1)如下图(2)y x i ni i ∑=1=3⨯2.5+4⨯3+5⨯4+6⨯4.5=66.5,x =46543+++=4.5,y =2.534 4.54+++=3.5,222221345686ni ix ==+++=∑,b =266.54 4.5 3.50.7864 4.5-⨯⨯=-⨯, a =3.5-0.7⨯4.5=0.35.故线性回归方程为y =0.7x +0.35.(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为 0.7⨯100+0.35=70.35,故耗能减少了90-70.35=19.65(吨)18.解:(1)设圆心坐标为(m ,n )(m <0,n >0),则该圆的方程为()()228x m y n -+-=,已知该圆与直线y =x 相切,那么圆心到该直线的距离等于圆的半径,则2n m -=22.即n m -=4 ① 又圆与直线切于原点,将点(0,0)代入,得m 2+n 2=8. ② 联立方程①和②组成方程组解得⎩⎨⎧=-=22n m ,故圆的方程为()()22228x y ++-=. (2)a =5,∴a 2=25,则椭圆的方程为221259x y +=. 其焦距c =925-=4,右焦点为(4,0),那么OF =4.要探求是否存在异于原点的点Q ,使得该点到右焦点F 的距离等于OF 的长度4,我们可以转化为探求以右焦点F 为顶点,半径为4的圆()2248x y -+=与(1)所求的圆的交点数.通过联立两圆的方程解得x =54,y =512. 即存在异于原点的点Q (54,512),使得该点到右焦点F 的距离等于OF 的长. 19.解:(1)∵EF AB ⊥,∴EF PE ⊥.又∵PE AE ⊥,EF AE E =,且PE 在平面ACFE 外, ∴PE ⊥平面ACFE .∵EF AB ⊥,CD AB ⊥,∴EF CD .∴6EF x CD EF x x CD BD BD =⇒==. 所以四边形ACFE 的面积2211322ACFE ABC BEF S S S x x ∆∆=-=⨯-=.∴四棱锥P ACFE -的体积31363P ACFE ACFE V S PE x -==.即()336V x x =-(0x <<.(2)由(1)知()212V x x '=. 令()0V x '=,解得6x =.∵当06x <<时,()0V x '>,当6x <<()0V x '<,∴当6BE x ==时,()V x 有最大值,最大值为()6V =(3)(解法1)过点F 作FGAC 交AE 于点G ,连接PG ,则PFG ∠为异面直线AC 与PF 所成的角.∵ABC ∆是等腰三角形,∴GBF ∆也是等腰三角形.于是FG BF PF ====从而PG ==在GPF ∆中,根据余弦定理,得2221cos 27PF FG PG PFG PF FG +-∠==⋅. 故异面直线AC 与PF 所成的角的余弦值为17. (解法2)以点E 为坐标原点,向量EA ,EF ,EP 分别为x ,y ,z 轴的正向建立空间直角坐标系,则()0,0,0E ,()0,0,6P ,()F ,()6,0,0A ,()6,3,0C .于是()AC =-,()6PF =-. 异面直线AC 与PF 所成角θ的余弦为1cos 73AC PFAC PF θ===,故异面直线AC 与PF 所成的角的余弦值为17. 20.解:当a =0时,函数为()23f x x =-,其零点x =32不在区间[-1,1]上. 当a ≠0时,函数()f x 在区间[-1,1]分为两种情况:①方程()0f x =在区间[]1,1-上有重根.此时()4830a a ∆=++=,解得a =.当32a --=时,()0f x =的重根[]31,12x =∈-. ②函数在区间[─1,1]上只有一个零点,但不是()0f x =的重根.此时()()110f f -≤,即()()510a a --≤,解得15a ≤≤.③函数在区间[─1,1]上有两个零点,此时()()0,111,2110.a f f ⎧∆>⎪⎪-<-<⎨⎪⎪-≥⎩解得32a --<或5a ≥. 综上所述,如果函数在区间[─1,1]上有零点,那么实数a 的取值范围为[)1,⎛-∞+∞ ⎝⎦.21.解:(1)解方程x 2+x -1=0得x =251±-, 由αβ>,知α=β=. (2)∵()21f x x '=+,∴1()()n n n n f a a a f a +=-'2121n n a a +=+. ()()2222212121212121n n n n n n n n n a a a a a a a a a αααααααα+-+-+---+--===+++. 下面用数学归纳法证明,当1n ≥时,0n a α->成立.①当1n =时,110a αα-=-=>,命题成立.②假设n k =(1k ≥)时命题成立,即0k a α->,此时0k a α>>. 则当1n k =+时,()21021kk k a a a αα+--=>+,命题成立.根据数学归纳法可知,对任意的正整数n ,有0n a α->.(3)根据(2),同理可得()2121n n n a a a ββ+--=+. ∵n a αβ>>(1,2,3,n =),且11a =,∴11b ==14ln 2. ln nn n a b a βα-=-()()2111211ln 2ln 2n n n n n a a b a a ββαα-------===--, 即数列{}n b 为首项为1b ,公比为2的等比数列. 故数列{}n b 前n 项和()()()1212212412n n n n b S +-==-⋅=--.。
