spss练习作业具体步骤
spss数据分析结果（作业）
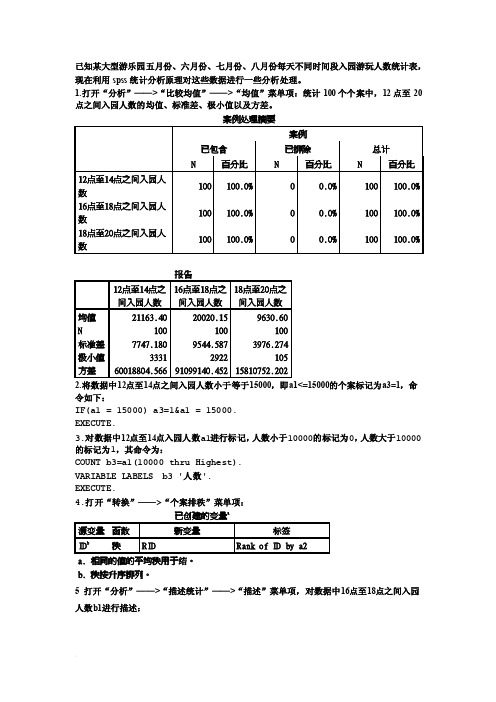
已知某大型游乐园五月份、六月份、七月份、八月份每天不同时间段入园游玩人数统计表，现在利用spss统计分析原理对这些数据进行一些分析处理。
1.打开“分析”——>“比较均值”——>“均值”菜单项：统计100个个案中，12点至20点之间入园人数的均值、标准差、极小值以及方差。
2.将数据中12点至14点之间入园人数小于等于15000，即a1<=15000的个案标记为a3=1，命令如下：IF(a1 = 15000) a3=1&a1 = 15000.EXECUTE.3.对数据中12点至14点入园人数a1进行标记，人数小于10000的标记为0，人数大于10000的标记为1，其命令为：COUNT b3=a1(10000 thru Highest).VARIABLE LABELS b3 '人数'.EXECUTE.5 打开“分析”——>“描述统计”——>“描述”菜单项，对数据中16点至18点之间入园人数b1进行描述：6.对数据中14点至16点之间入园人数a2进行“标识重复个案”：可以看出重复个案有19个，8.在100个个案（即5、6、7、8月份）中，对12点至14点之间入园人数a1绘制“直方图”进行分析：从上述直方图可以看出：在100个个案中，即从5月份到8月份，每天12点至14点之间入园人数大部分集中在10000人~40000人之间，人数小于10000、大于40000的较少。
9. 在100个个案（即5、6、7、8月份）中，对14点至16点之间入园人数a2绘制“箱图”进行分析：从箱图可以看出：在100个个案中，即从5月份到8月份，每天14点至16点之间入园人数大部分集中在10000人~20000人之间，人数小于5000、大于20000的较少。
10.对数据中12点至14点之间入园人数a1绘制“散点图”进行分析：从图上可以看出：在100个个案中，即从5月份到8月份，每天12点至14点之间入园人数大部分集中在10000人~40000人之间，人数小于10000、大于40000的较少，而且这组数据的整体离散程度很小。
北语21春《SPSS统计分析进阶》离线作业满分答案
北语21春《SPSS统计分析进阶》离线作业满分答案第一题：描述性统计分析数据准备操作步骤1. 打开SPSS，导入数据集。
2. 在菜单栏中选择“分析”→“描述性统计”→“频率”。
3. 将年龄、性别、收入和受教育程度变量拖动到“变量”框中。
4. 点击“确定”执行分析。
满分答案根据分析结果，我们可以得到以下描述性统计结果：- 年龄的平均值为35岁，标准差为10岁。
- 性别的分布中，男性占60%，女性占40%。
- 收入的平均值为5000元，标准差为2000元。
- 受教育程度的分布中，初中及以下占30%，高中/中专占40%，大专占20%，本科及以上占10%。
第二题：t检验数据准备我们需要准备一份数据集，数据集中包含两个变量：治疗前得分（pre_score）和治疗后得分（post_score）。
操作步骤1. 打开SPSS，导入数据集。
2. 在菜单栏中选择“分析”→“比较平均值”→“独立样本t检验”。
3. 将治疗前得分和治疗后得分变量拖动到“变量”框中。
4. 点击“确定”执行分析。
满分答案根据分析结果，我们可以得到以下t检验结果：- t值为2.56，p值为0.01。
- 治疗后的得分显著高于治疗前的得分（p<0.05）。
第三题：方差分析数据准备我们需要准备一份数据集，数据集中包含两个变量：组别（group）和得分（score）。
操作步骤1. 打开SPSS，导入数据集。
2. 在菜单栏中选择“分析”→“比较平均值”→“单因素方差分析”。
3. 将组别变量拖动到“因子”框中，将得分变量拖动到“变量”框中。
4. 点击“确定”执行分析。
满分答案根据分析结果，我们可以得到以下方差分析结果：- F值为3.34，p值为0.03。
- 组别对得分有显著影响（p<0.05）。
第四题：回归分析数据准备操作步骤1. 打开SPSS，导入数据集。
2. 在菜单栏中选择“分析”→“回归”→“线性”。
3. 将年龄、性别、收入和受教育程度变量拖动到“自变量”框中，将目标变量拖动到“因变量”框中。
SPSS作业综合
实验一一、实验目的：掌握用EXCEL进行数据的搜集整理和显示二、实验步骤：（一）用Excel搜集数据1、数据：先对数据进行编号，编号后，将编号输入工作表：2、抽样第一步：单击工具菜单，选择数据分析选项第二步：单击抽样选项，弹出抽样对话框第四步：指定输出区域，单击确定后，即可得到抽样结果，如图（二）、用Excel进行统计分组第一步：在工具菜单中单击数据分析选项，从其对话框的分析工具列表中选择直方图，打开直方图对话框：得到调整后的直方图如下：（三）、用Excel作统计图第一步：选中某一单元格，单击插入菜单，选择图表选项，弹出图表向导对话框。
如图：第二步：在图表类型中选择折线图，然后在子图表类型中选择一种类型，这里我们选用系统默认的方式。
然后单击下一步按钮，打开源数据对话框第三步：在源数据对话框中填入数据所在区域，单击完成按钮，即可得三、实验结论：由直方图和折线图可以看出，各地区的房价大多在2600~4000之间波动，其中，深圳市房价最高6164，南通市房价最低1700，结合其他地区房价，由此可知经济越发达的地区房价越高。
实验二描述统计分析过程一、实验目的：用EXCEL计算某班30人数学成绩相关统计量二、实验步骤：EXCEL中用于计算描述统计量的方法有两种，函数方法和描述统计工具的方法。
1、用函数计算描述统计量（一）众数单击任一空单元格，输入“=MODE（A2：A31）”，回车后即可得众数为85(二)中位数仍采用上面的例子，单击任一空单元格，输入“=MEDIAN（A2：A31）”，回车后得中位数为82(三)算术平均数单击任一单元格，输入“=AVERAGE（A2：A31）”，回车后得算术平均数为80.23333333。
(四)标准差单击任一单元格，输入“=STDEV（A2：A31）”，回车后得标准差为8.7678225712、描述统计工具量的使用第一步：在工具菜单中选择数据分析选项，从其对话框中选择描述统计，按确定后打开描述统计对话框，如图第二步：在输入区域中输入$A$2:$A$31，在输出区域中选择$B$1，其他复选框可根据需要选定，选择汇总统计，可给出一系列描述统计量；选择平均数置信度，会给出用样本平均数估计总体平均数的置信区间；第K大值和第K小值会给出样本中第K个大值和第K个小值。
SPSS详细解题步骤---2（1）
SPSS详细解题步骤---2（1）
Campare means ------Paired –Samples（配对样本）
然后点击“OK”就⾏了。
抄写：M、SD 、T、P 的值即可。
Campare means ------independent
点击“定义组”
点击“OK”
抄写P、T 值即可。
07-03
这个题实在有点⿇烦，⾃⼰去⽐较⼀下，得出的结果是A种最好。
不清楚的就问⼀下公⼦哈。
08--04
此题属于偏相关，解题⽅法和上次群邮件中发送的“详细解题步骤1”中的“数据：08-03”
⽅法⼀样，⾃⼰参考⼀下即可。
09--01
MPG=45.492 -- 0.007 × lbs
第9题（这个题⽐较⿇烦，⼤家耐⼼点哈）1、新建数据
2、输⼊数据
将⼩数点去掉
由“2”变为“0”
变量2为男⼥性别
变量3为3种不同的态度
点击“Data”中的“Weight Cases”
点击Analyze---Descriptive---Statistics-----Crosstabs
点击“Statistics”，勾选“Chi-square”（卡⽅）
然后点击“OK”
抄写第⼀个P值即可。
17--07
然后点击“OK”就ok了。
独联体的作图参照“详细步骤1”的作图步骤即可。
spss第六章作业
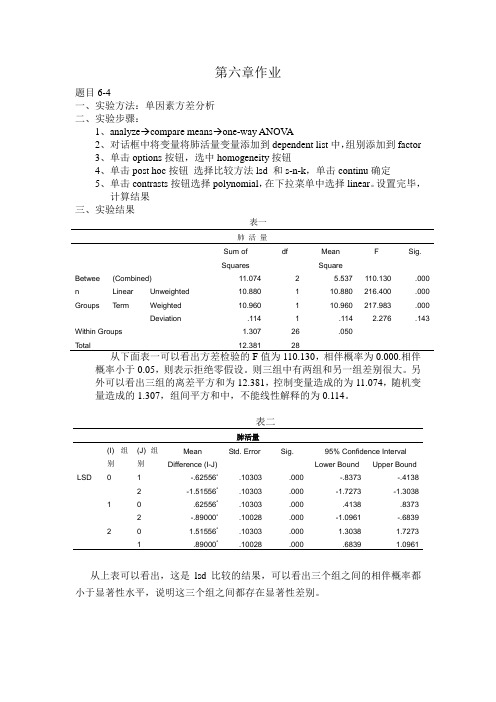
第六章作业题目6-4一、实验方法：单因素方差分析二、实验步骤：1、analyze→compare means→one-way ANOV A2、对话框中将变量将肺活量变量添加到dependent list中，组别添加到factor3、单击options按钮，选中homogeneity按钮4、单击post hoc按钮选择比较方法lsd 和s-n-k，单击continu确定5、单击contrasts按钮选择polynomial，在下拉菜单中选择linear。
设置完毕，计算结果三、实验结果表一肺活量Sum of Squares df MeanSquareF Sig.Betwee n Groups (Combined) 11.074 2 5.537 110.130 .000 LinearTermUnweighted 10.880 1 10.880 216.400 .000Weighted 10.960 1 10.960 217.983 .000Deviation .114 1 .114 2.276 .143Within Groups 1.307 26 .050Total 12.381 28从下面表一可以看出方差检验的F值为110.130，相伴概率为0.000.相伴概率小于0.05，则表示拒绝零假设。
则三组中有两组和另一组差别很大。
另外可以看出三组的离差平方和为12.381，控制变量造成的为11.074，随机变量造成的1.307，组间平方和中，不能线性解释的为0.114。
表二肺活量(I) 组别(J) 组别MeanDifference (I-J)Std. Error Sig. 95% Confidence IntervalLower Bound Upper BoundLSD 0 1 -.62556*.10303 .000 -.8373 -.41382 -1.51556*.10303 .000 -1.7273 -1.30381 0 .62556*.10303 .000 .4138 .83732 -.89000*.10028 .000 -1.0961 -.68392 0 1.51556*.10303 .000 1.3038 1.72731 .89000*.10028 .000 .6839 1.0961从上表可以看出，这是lsd比较的结果，可以看出三个组之间的相伴概率都小于显著性水平，说明这三个组之间都存在显著性差别。
spss实验四、实验步骤
实验四：SPSS一元线性相关回归分析预测为了了解某地母亲身高x与女儿身高Y的相关关系，随机测得10对母女的身高如下表所示：1.画出x、Y散点图，观察因变量与自变量之间关系是否有线性特点；2.试对x与Y进行一元线性回归分析，列出一元线性回归预测模型；3.预测当母亲身高为161cm时女儿的身高？1.画出x、Y散点图，观察因变量与自变量之间关系是否有线性特点；[实验步骤]（1）在数据编辑窗口中打开“母女身高.sav”。
（2）选择菜单：【图形】→【旧对话框】→【散点/点状】（3）出现下面的对话框。
（4）点击【简单分布】按钮，出现下面对话框。
（5）将变量“女儿身高”、“母亲身高”依次选入Y轴与X轴，单击【确定】按钮即可。
2.试对x与Y进行一元线性回归分析，列出一元线性回归预测模型；[实验步骤]（1）在数据编辑窗口中打开“母女身高.sav”。
（2）选择菜单：【分析】→【回归】→【线性】（3）这时将出现以下对话框，在左侧变量框中选择“女儿身高”，单击右向按钮，选入右侧上方的“因变量”框中，作为模型的被解释变量。
再选择“母亲身高”，单击右向按钮，选入右侧下方的“自变量”框中，作为模型的解释变量。
（4）单击【统计量】按钮，弹出“线性回归：统计量”对话框，如下图所示。
在“回归系数”框中选择“估计”。
（5）单击【继续】按钮回到线性回归分析对话框。
单击【绘制】按钮，打开“线性回归分析：图形”对话框，如下图所示。
从左边变量框中选择变量决定绘制何种散点图，这里分别把因变量（DEPENDNT）和标准化残差（ZRESID）选为Y和X轴来进行绘图，通过观察残差图我们可以验证回归模型是否符合经典回归模型的基本假设。
（6）单击【继续】按钮，回到线性回归分析对话框。
单击【保存】按钮，打开“线性回归分析：保存”对话框，如下图所示。
选择此对话框的选项，可决定将预测值、残差或其他诊断结果值作为新变量保存于当前工作文件或是保存到新文件。
在“预测值”框中选择“标准化”和“未标准化”的预测值。
spss作业完整版
均值比较与样本T检验1、（1）执行Transform—>Replace Missing Varies,将“机械化程度”移入NewVariables中，在Method中选择Mean of nearby points，单击change，单击OK提交系统。
（2）执行analyze->compare means->mean，将“户主年龄”、“文化程度”、“家庭人口”和“家庭总收入”移入 indenpendent List,将“机械化程度”移入dependent list（3）单击options,选择statistics for first layer 下的 anova table and eta, 单击 continue（4）单击ok数据分析：缺失值由3.8代替，所以用无任何机械代替。
年龄：显著性水平Sig.=0.572>0.05，说明不同户主年龄的机械化程度没有显著的差异。
文化程度：显著性水平Sig.=0.453，说明不同文化程度的机械化程度没有显著性差异；家庭人口：Sig.=0.625，说明不同家庭人口数的机械化程度没有显著性差异；家庭总收入：Sig.=0.139，说明不同家庭收入的农户的机械化程度没有显著性差异。
2、（1）执行analyze->compare means->independent-sample T Test（2）将“效果”移入test variables 框内（3）将“方法”移入grouping variables框内，单击define groups按钮，并在group1和group2框中分别输入有效值，单击continue （4）单击ok数据分析：显著性Sig.=0.128,所以在0.05的显著性水平上，两种激励方法的效果没有有显著差异。
3、（1）执行analyze->compare means->paird sample T Test，将“方案1”“方案3”移入paired variables（2）单击ok（3）以同样的方法比较“方案2”“方案3”数据分析：方案1与方案3的检验中,Sig.=0.044，说明方案1与方案3有显著性差异，所以均值相等的0假设不成立。
数据分析spss作业..
数据分析方法及软件应用（作业）题目：4、8、13、16题指导教师：学院：交通运输学院姓名：学号：4、在某化工生产中为了提高收率，选了三种不同浓度，四种不同温度做试验。
在同一浓度与温度组合下各做两次试验，其收率数据如下面计算表所列。
试在α=0.05显著性水平下分析(1)给出SPSS数据集的格式(列举前3个样本即可)；(2)分析浓度对收率有无显著影响；(3)分析浓度、温度以及它们间的交互作用对收率有无显著影响。
解答：（1）分别定义分组变量浓度、温度、收率，在变量视图与数据视图中输入表格数据，具体如下图。
(2)思路：本问是研究一个控制变量即浓度的不同水平是否对观测变量收率产生了显著影响，因而应用单因素方差分析。
假设：浓度对收率无显著影响。
步骤：【分析-比较均值-单因素】，将收率选入到因变量列表中，将浓度选入到因子框中，确定。
输出：變異數分析收率平方和df 平均值平方 F 顯著性群組之間39.083 2 19.542 5.074 .016在群組內80.875 21 3.851總計119.958 23显著性水平α为0.05，由于概率p值小于显著性水平α，则应拒绝原假设，认为浓度对收率有显著影响。
（3）思路：本问首先是研究两个控制变量浓度及温度的不同水平对观测变量收率的独立影响，然后分析两个这控制变量的交互作用能否对收率产生显著影响，因而应该采用多因素方差分析。
假设，H01：浓度对收率无显著影响；H02：温度对收率无显著影响；H03：浓度与温度的交互作用对收率无显著影响。
步骤：【分析-一般线性模型-单变量】，把收率制定到因变量中，把浓度与温度制定到固定因子框中，确定。
输出：主旨間效果檢定因變數: 收率來源第 III 類平方和df 平均值平方 F 顯著性修正的模型70.458a11 6.405 1.553 .230截距2667.042 1 2667.042 646.556 .000浓度39.083 2 19.542 4.737 .030温度13.792 3 4.597 1.114 .382浓度 * 温度17.583 6 2.931 .710 .648錯誤49.500 12 4.125總計2787.000 24校正後總數119.958 23a. R 平方 = .587（調整的 R 平方 = .209）第一列是对观测变量总变差分解的说明；第二列是观测变量变差分解的结果；第三列是自由度；第四列是均方；第五列是Ｆ检验统计量的观测值；第六列是检验统计量的概率ｐ值。
SPSS操作步骤汇总
SPSS操作步骤汇总SPSS学习第⼀章数据⽂件的建⽴数据编码Type：Numeric：数值型 string：字符串型Missing：Measure：scale定量变量 nominal定性变量根据已有的变量建⽴新变量1、对于数据进⾏重新编码Transform—recode into different variables—选择input variable output variable –定义新变量的名称—change—开始定义新旧变量—continue2、通过SPSS函数建⽴新变量Transform—compute variable –从function group中选择公式范围下⾯选择具体的公式—if中设置要改变—continue—OK(可以对变量进⾏各种计算)第⼆章清除数据与基本统计分析1、对不合理的数据检查并清理检查：analysis-description statistic-frequencies—选⼊要检查的数据—OK结果：频数统计表—看是否有错误—missing system清理：1.对系统缺失值的清理Data—select case—if condition is satisfied—if—function group（missing）--下⾯选（missing）--continue—output（delete unselected cases）--OK—对num为哪⼀位的进⾏修改2.对sex=3的清理（直接就清除了）Data—select case—if condition is satisfied—if—sex调⼊再输⼊=3—continue-- output（delete unselected cases）--OK—对num为哪⼀位的进⾏修改2. 对相关变量间逻辑性检查和清理Data—select case—if condition is satisfied—if—输⼊表达式（前后逻辑不相符合的表达式）-- continue-- output（delete unselected cases）--OK—对num为哪⼀位的进⾏修改3.统计描述正态分布统计描述1、正态性检验：Analysis—nonparametric tests—legacy dialogs—1-sample K-S—one-sample Kolomogorov Smirnov test –normal—ok/2、统计描述：Analysis—descriptives--time选⼊—options—ok3、按照男⼥统计描述：data—split file –compare group –sex 调⼊—okAnalysis-descriptive statistic –descriptive—time 调⼊—options选择—OK⾮正态分布资料统计描述1、正态性检验nonparametric2、Analysis—descriptive statistics—frequencies 选⼊--statistics选择—OK第三章T检验1、单样本t检验正态性检验—analyze—compare means—one-sample t test—test value选择要对⽐的数值—OK2、配对样本t检验建⽴数据⽂档—两列（前和后）--正态性检验—analysis- compare means—paired sample t test –调⼊—ok3、两独⽴样本t检验（正态性检验的时候采⽤分开组，其他都要合并在⼀起）建⽴数据库—第⼀列（group）第⼆列（数值）-- data—split file –compare group—调⼊group—ok-正态性检验—OK-- data—split file—选择analysis all—analyze—compare means—independent sample t test—选⼊，分组—OK结果分⽅差齐与否第四章⽅差分析（前提正态）1、单因素⽅差分析（就是平常的三个组⽐较）建⽴数据库—第⼀列（group）第⼆列（数值）- data—split file –compare group—调⼊group—ok-正态性检验—OK-- data—splitfile—选择analysis all--analyze—compare means—one-way-anova—数据调⼊dependent list—分组调⼊factor------options—descriptive基本统计描述—homogeneity of variance做⽅差齐性分析—OK2、⽅差分析两两⽐较analyze—compare means—one-way-anova---数据调⼊dependent list—分组调⼊factor—点post hoc—选择SNK LSD3、随机区组设计⽅差分析建⽴数据库—第⼀列（group）第⼆列（block）第三列（数值）--按照group split开，进⾏正态性检验—OK—general liner model—univairate—数值调⼊dependent variable—group和block 调⼊fixed factor—model—custom—build terms（main effects）再把group和block调⼊model下的矩形框---continue—OK如果区组间⽆差别，组间进⾏两两⽐较。
spss练习作业具体步骤
一、调查问卷二、用SPSS Statistics软件进行描述统计分析1、某地区经济增长率的时间序列图形。
解：第一步:数据来源，如图1图 1 某地区经济增长率xls截图图2 Spss软件制作过程截图第二步：将数据输入SPSS软件之中,如图2,制作某地区经济增长率的时间序列图形，如图3.图3某地区1990-2012年经济增长率的时间序列图第三步，从图中可以看出,某地区随时间的变化经济增长率变化趋势较大.2、用SPSS Statistics进行描述统计分析解：第一步，按照题目中的要求，随机选取了148个数据,如图4部分数据：图4 Spss随机数据截图第二步，根据要求，对上月工资进行描述统计分析,主要包括描述数据的集中趋势、离散程度（见表1），绘制直方图（见图5）。
表1 上月工资描述统计表(单位：元）集中趋势离散趋势均值2925 极小值1500中值2900 极大值4800众数2900 全距3300和432900 标准差496.364偏度0。
165 峰度1。
238数据总计148图5 上月工资直方图第三步，分析数据的统计分布状况。
首先，从集中趋势来，上个月平均工资2925元，其中众数和中数也都在2900元，这说明大部分工资水平在2900左右。
其次，从离散趋势来看，最高工资4800元，最低工资1500元，最高工资和最低工资相差3300元，标准差为496。
364，相差较大。
最后，从直方图来看和评述统计表来看，工资在2900元以上的占多数。
可以的该地区整体工资水平大于平均值的占多数，该地区工资水平相对较高。
峰度为1。
238，偏度为0.165符合正态分布。
三、用SPSS Statistics 软件进行参数估计和假设检验及回归分析1、计算总体中上月平均工资95%的置信区间（见表3)。
解：总体中上月平均工资分布未知，但是样本容量大于30,且已知标准误，所以通过SPSS 分析得出总体中上月平均工资95％的置信区间，见表3， 假设;H0：总体中上月平均工资95％的不在此在此区间H1：总体中上月平均工资95％的在此区间答，总体中上月平均工资095的置信区间为［2844.37，3005。
SPSS统计软件课程作业
SPSS统计软件课程作业《SPSS统计软件》课程作业信计111 刘晓蕾1. 某单位对100名⼥⽣测定⾎清总蛋⽩含量，数据如下：74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.579.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.075.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.073.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.575.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.070.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.373.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.767.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.775.8 73.5 75.0 73.5 73.5 73.5 72.7 81.6 70.3 74.373.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4计算样本均值、中位数、⽅差、标准差、最⼤值、最⼩值、极差、偏度和峰度，并给出均值的置信⽔平为95%的置信区间。
第1步数据组织：定义1个变量为：“⾎清总蛋⽩含量”，其度量标准为“度量”。
第2步探索分析设置：选择菜单“分析→描述统计→探索”，打开“探索”对话框，，将“⾎清总蛋⽩含量”字段移⼊“因变量列表”。
打开“统计量”对话框，选中“描述性”选项；打开“探索：图”对话框，选中“按因⼦⽔平分组”、“茎叶图”、“带检验的正态图”、“直⽅图”等选项。
打开“探索：选项”，选中“按列表排除个案”选项。
第3步运⾏结果及分析：表中显⽰“⾎清总蛋⽩含量”的描述性统计量，左表中只显⽰的是均值、均值的95%置信区间的上下限、中值、⽅差、标准差、极⼤/⼩值、偏度、峰度等2. 绘出习题1所给数据的直⽅图、盒形图和QQ图，并判断该数据是否服从正态分布。
spss的操作流程
spss的操作流程下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。
文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!SPSS（Statistical Product and Service Solutions）是一款广泛使用的统计分析软件，以下是一般的 SPSS 操作流程：1. 数据准备打开 SPSS 软件。
spss使用
作业2：要求：用SPSS绘制简单条形图、分组条形图、分段条形图、饼图、环形图。
1.简单条形图（数据1）（1）首先打开SPSS，点击“文件”>“新建”>“数据”。
然后点击“变量视图”对数据中的变量进行定义。
定义好后点击“数据视图”进行输入数据。
最后保存数据为“数据1”。
（2）数据录入完成后，点击菜单栏中得“图形”>“旧对话框”>“条形图”淡出对话框。
选择“简单箱图”以及“个案组摘要”复选框，点击“定义”按钮。
将左边框中得“政治面貌”添加为“类别轴”，“条的表征”选择为“累计个数”，然后点击“确定”。
在输出窗口就会看到生成的条形图（如下图1：），然后双击图表，进行颜色，标题，刻度等的设置。
结果解释：从上图中，我们可以看到这个班级中，团员占多数，其次是群众，而党员占少数。
2.分组条形图（数据1）（1）数据的输入过程如第1中简单条形图的数据录入一样。
（2）数据录入完成后，点击菜单栏中得“图形”>“旧对话框”>“条形图”淡出对话框。
选择“复式条形图”以及“个案组摘要”复选框，点击“定义”按钮。
然后淡出定义对话框，将左边的“政治面貌”添加到“类别轴”，接着将“性别”添加到“定义聚类”然后点击确定按钮。
在输出窗口就会看到生成的分组条形图（如下图2：），然后双击图表激活，进行颜色，标题，刻度等的设置。
结果解释：这个班中政治面貌为党员的女生比男生多，群众人数也是女生比男生多，同样政治面貌是团员的也是女生比男生多。
3.分段条形图（数据1）（1）数据录入。
“文件”>“新建”>“数据”，点击左下方的“变量视图”对变量进行定义，然后点击“数据视图”进行数据输入。
最后点击“保存”，选择指定路劲，保存为“数据1”（2）数据录入完成后，点击菜单栏中得“图形”>“旧对话框”>“条形图”淡出对话框。
选择“复式条形图”以及“个案组摘要”复选框，点击“定义”按钮。
弹出“定义对话框”，将左边的“政治面貌”添加为“类别轴”，将性别添加为“定义堆栈”，点击“确定”。
SPSS案例练习一步一步教你操作
字段
设置
可选择： 1.自动选择检验 2.2组以上样本用-Kruskal Wallis
5.答案
Sig值0.001 < 0.05 拒绝原假设 四种病人痰液中嗜酸性白细胞数有差别。
练习题-7
1.题目为两组独立样本 输入资料
2.先检验是否正态 Sig值 0.014,0.292 < 0.05 有数值为非正态
7.答案
检验结果： 方差Sig值 0.759 > 0.05 方差齐 两药降压效果无差异。
练习题-4
1.题目为多组独立样本 输入资料
2.设定变量视图内容
P.S.两组的话：独立样本T检验
3. 因“随机”分配 故选-单因素ANOVA
4. 导入 因子（分组） 因变量（量）
5.检验不同组的方差齐
6.单因素方差分析 显著性（P）0.000 < 0.05 有显著差异，故进一步两两分析
练习题-3
1.题目为2组独立样本 输入资料
2.设定变量视图内容
3.判断差值非正态或正态-探索
4.Sig值0.978，0.533 > 0.05
因正态分布，故选择独立样本T检验 P.S.如果不是正态，用非参-独立样本
左：>100组样本 右：<100组样本
5. 正态分布， 故选择独立样本T检验
6.导入先，后-确定
2.加权个案
计数资料 无论是列联表 或四格表 都要先加权个案
行
4.交叉表设定
列
5.结果-- Pearson卡方统计量
n>=40 且 n'>=5
合计（计数） 所有（期望计数）
6.答案 n’= 26.84 >5 必须使用Pearson卡方 卡方值4.13 Sig值0.042<0.05 有差异 愈合率有差异
SPSS详细步骤
SPSS详细步骤一、多选题1.录入数据（1）桌面新建记事本，名字随意。
（2）ABCDE各选项有则输入1，无则输入0（3）每一行录入一个人第一题和第二题的数据，如例题，第一行为1110001101(ABC,BCE) （4）保存。
2.SPSS软件中打开（1）文件--打开--数据（2）找到桌面（Destop)（3）文件类型--文本格式（4）打开所保存文件（5）下一步，第二步--固定宽度，下一步，鼠标点击每列一条变量终止线，下一步，下一步，完成。
（6）变量视图，修改变量名。
（可以省略，自己知道前五个为一组，后五个为一组即可）3.求个案数，响应比率，个案比率。
（1）分析--多重响应--定义变量集（2）选定前五个变量，点击箭头转入集合中的变量（3）二分法--计数值：1（即1表示有，0表示无）（4）名称：第一题。
--点击添加至多重响应集（5）选定后五个变量，点击箭头转入集合中的变量（6）二分法--计数值：1（7）名称：第二题。
--点击添加至多重响应集--关闭（8）分析--多重响应--频率（9）选定第一题第二题点击箭头转入表格--确定（10）N值为个案数，N值右侧百分比为响应比率，个案百分比为个案比例--填入自制手绘表格。
4.求期望数，卡方，P（P，渐进显著性，Sig，一个意思）（1）做第一题的卡方（2）在第一题频率表中找到N值（个案数）（3）复制或者记录N 值（4）文件--新建--数据（5）第一列变量粘贴或者竖着输入N值(变量名默认为V AR00001,可以自己修改) （6）第二列变量依次输入1,2,3,4,5（代表ABCDE第一列个案数相对应,变量名默认V AR00002)（7）数据--加权个案--频率变量V AR00001--确定（8）分析--非参数检验--旧对话框--卡方（9）选定V AR00002--点击箭头转入检验变量列表（10）期望值--值--从左至右输入题目所给选项比（例如1:2:2:3:2，则1添加，2添加，2添加，3添加，2添加）--确定（11）将V AR00002中期望数填入自制手写表格。
SPSS作业2
Zα/2=1.96
u - 总体均值的置信区间为（
2
n
u ，
2
n
)
计算可得置信区间为（115.8,124.2）
第二题：
某大学为了解学生每天上网的时间，在全校7500名学生中采取不重复抽样方法 随机抽取36人，调查他们每天上网的时间，得到的数据如下（单位：h）。
3.3 上网 时间 4.2 5.1 4.4 2.4 2.9 2.1 5.4 2.3 4.7 3.5 6.4 3.1 3.6 4.3 2 0.5 3.5 1.9 4.5 4.1 1.4 5.7 1.8 6.2 0.8 5.8 5.4 3.6 2.6 1.2 3.2 1.5 1.2 2.3 2.5
解： （1）由题意可知：（总体标准差） =15
n=49
由样本均值的抽样标准误差公式 (2)由1-α=0.95 允许误差公式 得 α=0.05
n
则：
15 49
2.1429
查表可知Zα/2=1.96 =1.96*2.1429=4.2
2
n
(3)由题意知 u=120
3.30
3.05
3.33
3.27
3.28
3.25
构造两个总体方差比 12
2 的95%的置信区间。 2
步骤一：SPSS工具—打开—数据——录入数据 步骤二：分析—描述统计——描述——选择两个变量—在选项中勾选“均值”、“ 方差”—— 点击确定
解：由SPSS求解可得：机器1： 1 3.3295 机器2： 自由度n1=21-1=20
1、置信水平α=90%
1-α=90% α=0.1 z/2 =1.64
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、调查问卷二、用SPSS Statistics软件进行描述统计分析1、某地区经济增长率的时间序列图形。
解：第一步：数据来源，如图1图 1 某地区经济增长率xls截图图2 Spss软件制作过程截图第二步：将数据输入SPSS软件之中，如图2，制作某地区经济增长率的时间序列图形，如图3。
图3某地区1990—2012年经济增长率的时间序列图第三步，从图中可以看出，某地区随时间的变化经济增长率变化趋势较大。
2、用SPSS Statistics进行描述统计分析解：第一步，按照题目中的要求，随机选取了148个数据，如图4部分数据：图4 Spss随机数据截图第二步，根据要求，对上月工资进行描述统计分析，主要包括描述数据的集中趋势、离散程度（见表1），绘制直方图（见图5）。
表1 上月工资描述统计表（单位：元）集中趋势离散趋势均值2925 极小值1500中值2900 极大值4800众数2900 全距3300和432900 标准差496.364偏度0.165 峰度 1.238数据总计148图5 上月工资直方图第三步，分析数据的统计分布状况。
首先，从集中趋势来，上个月平均工资2925元，其中众数和中数也都在2900元，这说明大部分工资水平在2900左右。
其次，从离散趋势来看，最高工资4800元，最低工资1500元，最高工资和最低工资相差3300元，标准差为496.364，相差较大。
最后，从直方图来看和评述统计表来看，工资在2900元以上的占多数。
可以的该地区整体工资水平大于平均值的占多数，该地区工资水平相对较高。
峰度为1.238，偏度为0.165符合正态分布。
三、用SPSS Statistics 软件进行参数估计和假设检验及回归分析1、计算总体中上月平均工资95%的置信区间（见表3）。
解：总体中上月平均工资分布未知，但是样本容量大于30，且已知标准误，所以通过SPSS 分析得出总体中上月平均工资95%的置信区间，见表3, 假设；H0：总体中上月平均工资95%的不在此在此区间H1：总体中上月平均工资95%的在此区间答，总体中上月平均工资095的置信区间为[2844.37，3005.63]，p=0.000<0.01,作出这样的推论正确的概率为0.95，错误的概率为0.05。
2、检验能否认为总体中上月平均工资等于2000元。
解：在本案例中，要检验样本中上月平均工资与总体中上月平均工资（为已知值：2000元）是否存在差异，即某一样本数据与某一确定均值进行比较。
虽然不知道总体分布是否正态，但样本较大（N>30），可以运用单样本T 检验.通过SPSS 检验结果见（表4 、表5） 设; H o:2000=μH 1:2000≠μ 其中，μ表示总体中上月平均工资表4 单个样本统计量表5 单个样本检验t df Sig.(双侧) 均值差值 检验值 上月工资22.6711470.000925.0002000答:作出结论，均值差值为925，t=22.671,p=0.000<0.01，所以拒绝原假设，接受备择假设，即否认总体中上月的平均工资等于2000元。
3、检验能否认为男生的平均工资大于女生解：两个样本均来自于正态分布的总体且男女上月工资独立，可以进行独立样本T 检验，（见表6、表7）假设1：H 0：2221δδ=H 1：2221δδ≠ 其中，代表女生总体方差代表男生总体方差，2221δδ从表7中方差方程的 Levene 检验可以看出，F=0.101,P=0.751>0.05,所以不能拒绝原假设，可以认为两组数据无显著差异，所以应该选择方差相等下的T 检验。
表7独立样本检验假设2： H 0：21μμ≤H 1：21μμ 其中μ1代表男生总体平均数，μ2代表女生总体平均数，下同作出结论：从表6、表7中可以看出，男生有73人，平均工资3156.16元，女生75人，平均工资2700.00元。
t=6.277,且p=0.000<0.001 所以拒绝原假设，接受备择假设，差异极显著。
根据表6，可以最后得出结论，男生平均工资大于女生的结论。
4、一些学者认为，由于经济不景气，学生的平均工资今年和去年相比没有显著提高。
检验这一假说。
解： 根据题意可知，需要进行相关样本T 检验,设：H 0：μ1≤μ2 H 1；μ1＞μ2 同上表8 相关样本T 检验均值标准差均值标准误 T df 相关系数 sig 上月工资 2925 496.364 40.801 去年同月工资 2721.62 447.296 36.767 上月工资&去年同月工资 203.378 183.10115.50113.5311470.930.000通过表8可知，t=13.531,P=0.000<0.01，所以拒绝原假设，接受备择假设，即学生的平均工资今年和去年相比有显著提高。
方差方程的 Levene 检验 T 检验FSig. t df Sig.(双侧) 均值差值 标准误差值 上月工资 假设方差相等 0.101 0.7516.2771460.000456.16472.667假设方差不相等6.277 145.859 0.000 456.164 72.6705、方差分析。
（1）使用单因素方差分析的方法检验：能否认为不同学科的上月平均工资相等。
如果不能认为全相等，请做多重比较。
解：第一步，提出假设，H0：不同学科上月的平均工资是相同的H1：至少有两门学科上个月的平局工资是相同的经过SPSS软件计算，见表9，第二步，决策，F=0.754，P=0.472>0.05，接受H0，拒绝H1，三者之间没有显著性差异。
可以认为不同学科上月工资水平相同。
第三步，多重比较，经过Levene检验（见表10），p=0.724，方差没有显著性差异，方差齐性，经过LSD检验（见表11），P值均大于0.05，所以可以得出同样的结论，三门学科的上月工资水平没有差异。
表10 方差齐性检验（2）在方差分析中同时考虑学科和性别因素，用双因素方差分析模型分析学科和性别对上月平均工资的影响。
解：第一步，提出假设，H0：性别和学科对上月工资水平没有影响H1：性别和学科同时对上月工资水平有影响第二步，经过SPSS计算，见表12，表12主体间效应的检验第三步，作出决策性别因素P=0.000<0.01,在0.01水平上差异显著，所以拒绝原假设，接受备择假设，即性别因素对工资水平有显著性影响，和前面结果一致。
学科因素P=0.465>0.05,在0.05水平上差异不显著，所以接受原假设，拒绝备择假设，即学科因素对上月工资水平没有影响，和前面结果一致。
性别* 学科p=0.962>0.05,在0.05水平上差异不显著，所以接受原假设，拒绝备择假设，即学科和性别因素同时对上月工资水平没有影响。
6、非参数检验。
（1）用非参数检验方法检验能否认为男生和女生上月工资的中位数相等。
解：第一步，采用wilcoxon符号秩检验中位数，选择的原设与备择假设如下：H0：男生与女生上月工资的中位数相等；H1：男生与女生上月工资的中位数不相等。
第二步，通过SPSS软件计算，见表13、14表表14 wilcoxon秩和检验的检验统计量和p值第三步，男生上月工资的平均秩为41.33，女生上月工资的平均秩是19.84，说明从样本看男生上月工资的中位数要高于女生。
用正态分布计算时的M=1265.000,W=4115.000,Z=-5.663,p=0.000<0.01，可以拒绝原假设，认为男生与女生上月工资中位数不相等。
若进行单侧检验：H0：男生月收入中位数小于女生月收入的中位数；H1：男生月收入中位数大于于女生月收入的中位数。
P值为0.000，可以拒绝原假设。
H0：男生月收入中位数大于女生月收入的中位数；H1：男生月收入中位数小于女生月收入的中位数。
P值为1-0.000/2 =1，接受原假设。
因此可以认为男生上月工资中位数大于女生上月工资中位数。
（2）用非参数检验方法检验学生上月工资和去年同月工资的中位数是否有显著变化。
解：第一步，采用非参数检验中的两个相关样本样本，选择的原假设与备择假设如下：H0：上月工资与去年同月工资差值为0H1：上月工资与去年同月工资差值不为0第二步，通过SPSS软件计算，结果如表15、16第三步，作出结论，由于此样本为大样本，应该采用渐近显著性的p值（0.000）,小于0.01，拒绝原假设，接受备择假设，则可以认为上月工资与去年同月工资有显著差别。
（3）用非参数检验方法不同学科学生平均学分绩点的中位数是否相等。
解：第一步，采用Kruskal-Wallis检验不同学科学生平均学分绩点的中位数是否相等，原假设和备择假设设置如下：H0：不同学科学生平均学分绩点的中位数相等；H1：不同学科学生平均学分绩点的中位数不相等第二步，通过SPSS软件计算结果如表17、18；表17 Kruskal-Wallis检验中计算的各组平均秩表18 Kruskal-Wallis检验的检验统计量和p值第三步，作出结论，因为p=0.653>0.05，不可拒绝原假设，认为三个学科平均学分绩点的中位数没有显著差异.。
（4）检验学生的上月工资是否服从正态分布。
解：第一步，样本是否来自正态分布，可用单样本K-S检验，原假设和备择假设设置如下H0：学生的上月工资服从正态分布H1：学生的上月工资不服从正态分布第二步，通过SPSS软件计算结果如表19表19 单样本Kolmogorov-Smirnov 检验第三步，作出结论，p=0.291，大于0.05，不能拒绝原假设，也就是说能认为此样本来自正态分布。
（5）检验学生对专业的满意程度是否为离散的均匀分布第一步，采用卡方分布进行检验，H0：学生对专业的满意程度服从离散的均匀分布H1：学生对专业的满意程度不服从离散的均匀分布第二步，通过SPSS软件计算结果表20、21表21 卡方分布检验计算结果和相应的p 值第三步，作出结论，因为p=0.000，小于0.01，可以拒绝原假设，接受备择假设认为学生对专业的满意程度不服从离散的均匀分布。
7、回归分析。
（1）计算上月工资与平均学分绩点的相关系数并作假设检验。
解：第一步，假设如下：H 0：0=ρ H 1：0≠ρ第二步，通过SPSS 计算，见表22第三步，根据计算相关系数为0.763，P=0.000<0.01,所以可以拒绝原假设，在0.01水平上二者显著相关。
（2）以上月工资为因变量，平均学分绩点为自变量做回归分析，分析模型的拟合效果和假设检验的结果。
（第一次抽样无法做回归分析，需要重新抽样）解：第一步，假设1，H0：回归模型无意义，H1:回归模型有意义 假设2，Ho ；常量为 H1：常量不等于0假设3，Ho ：平均学分绩点的系数为0，H1:平均学分绩点的系数不等于0 第二步，通过SPSS 分析，见表23、24、25表24 回归模型模型平方和df 均方 F Sig.1 回归 2.273E7 1 2.273E7 189.216 .000a残差 1.622E7 135 120118.458总计 3.894E7 136表25模型回归系数表模型 B t Sig.1 (常量) -661.720 269.159 -2.458 .015平均学分绩点1177.971 85.636 13.756 .000图6图7图8说明：图6为残差的直方图，图中残差的分布基本均匀图7为残差的正态P-P概率图，图中散点基本呈直线趋势，且并未发现异常点图8残差是否有随标准化预测值增大而改变的趋势。