14-7 基尔霍夫定律
《电路理论基础》学习指导(李晓滨) 第1章

电荷由a点移动到b点所发生的能量的变化称为两点间的电压。
电压的正极性:高电位指向低电位,即电位降落的方向。 电压的参考极性:人为假定的电压正极性。 功率:某二端电路的电功率(简称功率)是该二端电路吸 收或产生电能的速率。
第1章 电路模型和基尔霍夫定律 3. 基尔霍夫定律
第1章 电路模型和基尔霍夫定律
图 1-4
第1章 电路模型和基尔霍夫定律
1.2 重点、难点
1. 吸收功率、产生功率
根据关联参考方向计算功率的公式为
P(t)=u(t)i(t) 若P(t)>0 则真正吸收功率; 若 P(t)<0 则实际放出(产生)功率。 根据非关联参考方向计算功率的公式为 P(t)=u(t)i(t)
可见,P发出=P吸收,满足功率平衡。
第1章 电路模型和基尔霍夫定律 (2) 在图1-7(b)中,设各支路电流分别为i1,i2,i3,其参
考方向如图1-8(b)所示。由元件约束关系有
2 1 1 i1 0.5A, i2 1A 2 1
节点A的KCL方程: i3=i2-i1=1-0.5=0.5 A
的元件。它是集总(集中)参数元件。
常用理想元件:电阻、电感、电容、电压源、电流源、 受控源等。
第1章 电路模型和基尔霍夫定律 2. 电路变量 电流:带电粒子的定向移动形成电流。电流的大小用电 流强度来衡量。 电流强度:单位时间内通过导体横截面的电荷量。 电流方向:正电荷移动的方向。
电流参考方向:人为假定的电流正方向。只有数值而无
图 1-10
第1章 电路模型和基尔霍夫定律 【解题指南与点评】 在图1-9(a)中,i1的值只与10 V电
传感器原理及其应用-第10章-红外传感器重点

第10章 红外传感器
10.2 红外传感器
红外传感器是将红外辐射能量的变化转换为电量变化的一种传 感器,也常称为红外探测器。它是红外探测系统的核心,它的 性能好坏,将直接影响系统性能的优劣。选择合适的、性能良 好的红外传感器,对于红外探测系统是十分重要的。
按探测机理的不同,红外传感器分为热传感器和光子传感器两
维恩公式比普朗克公式简单,但仅适用于不超过3000 K的温 度范围,辐射波长在0.4~0.75m 之间。当温度超过3000 K时, 与实验结果就有较大偏差。
从维恩公式可以看出,黑体的辐射本领是波长和温度的函数, 当波长一定时,黑体的辐射本领就仅仅是温度的函数,这就是 单色辐射式测温和比色测温的理论依据。
武汉理工大学机电工程学院
第10章 红外传感器
近年来,红外技术在军事领域和民用工程上,都得到了广泛 应用。军事领域的应用主要包括: (1) 侦查、搜索和预警; (2) 探测和跟踪; (3) 全天候前视和夜视; (4) 武器瞄准; (5) 红外制导导弹; (6) 红外成像相机; (7) 水下探潜、探雷技术。
10.2.1 红外光子传感器
红外光子传感器是利用某些半导体材料在红外辐射的照射下, 产生光电效应,使材料的电学性质发生变化。通过测量电学性 质的变化,就可以确定红外辐射的强弱。
武汉理工大学机电工程学院
第10章 红外传感器
按照红外光子传感器的工作原理,一般分为外光电效应和内 光电效应传感器两种。内光电效应传感器又分为光电导传感器、 光生伏特(简称光伏)传感器和光磁电传感器3种。 (1) 大部分外光电传感器只对可见光有响应。可用于红外辐射 的光电阴极很少。S-1(Ag-O-Cs)是一种。它的峰值响应波长 是0.8 m,光谱响应扩展到1.2 m。目前外光电效应探测器只用 于可见光和近红外波长范围。
_基尔霍夫定律

§10-4 含源电路欧姆定律 *基尔霍夫定律1. 一段含源电路的欧姆定律如果研究的电路中包含电源,则在欧姆定律中应包含非静电场强,即将欧姆定律的微分形式推广为)(k E E ���+=γδA BCRi R ,εI即kE E ���−=γδA BCRi R ,εI 电源放电电源充电积分得∫⋅B A l E ��d l E l B Ak B A ����d d ⋅−⋅=∫∫γδ欧 姆A BC RiR ,εI A BCRi R ,εI 电源放电电源充电∫⋅BA l E ��d lE l l B A k B C C A ������∫∫∫⋅−⋅+⋅=d d d γδγδ 电源放电时,电流密度与积分方向相反;电源充电时,电流密度与积分方向相同,且BA BA V V l E −=⋅∫��d ε−=⋅=⋅∫∫l E l E C A k B A k ����d d SI =δ代入上式,则一段含源电路的欧姆定律εγγ++=−∫∫)d d (B C C A B A SlI S l I V V ∓∫⋅BA l E ��d l E l lB A kB C C A ������∫∫∫⋅−⋅+⋅=d d d γδγδε++=−)(i B A IR IR V V ∓A BCRi R ,εI A BCRi R ,εI 电源放电电源充电电流与电动势方向相同时,取负号,反之取正号。
上式称为一段含源电路的欧姆定律。
一段含源电路的欧姆定律•若I =0,则i B A IR V V −=−ε电源放电,端电压低于电动势。
iB A IR V V +=−ε电源充电,端电压高于电动势。
•若R =0,则ε=−B A V V 电路断开,端电压等于电动势。
•若AB 接在一起,形成闭合电路,则ABRiR ,εIiR R I +=εiR R +总电阻 闭合电路中的电流等于电源的电动势与总电阻之比。
一段含源电路的欧姆定律•一段含多个电源的电路的欧姆定律ABC 2R 22,i R ε1I 1R 3R 2I 3I 11,i R ε33,i R ε∑∑−=−εIR V V B A 正负号选取规则:任意选取线积分路径方向,写出初末两端点的电势差;电流的方向与积分路径方向相同,电流取正号,反之为负;电动势指向与积分路径同向,电动势取正号,反之为负。
第14章线性动态电路的复频域分析

18
(3) 电容C
时域形式:u(t)
=
1 C
t
i(t) dt + u(0-)
0-
取拉氏变换并应用线性和积分性质
得运算形式:U(s)
=
1
sC
I(s)
+
u(0-)
s
或者写为: I(s) = sCU(s) - Cu(0-)
1/sC称为C的运算阻抗。 I(s)
sC为C的运算导纳。 + 1
u(0-)为C的初始电压。 U(s)
0-
0-
(3)指数函数 f(t) = eat (a为实数)
ℒ [d(t)]=1
F(s) =
∞
eat e-st dt =
0-
∞
e-(s-a)t dt =
0-
1 -(s-a)
e-
(s-a)t
∞ 0-
ℒ [eat]=
1 s-a
2024年1月27日星期六
6
§14-3 拉氏反变换的部分分式展开
用拉氏变换求解线性电路的时域响应时,需要把 求得的响应的拉氏变换式反变换为时间函数。由 象函数求原函数的方法有
得运算形式:U(s) = sLI(s)-Li(0-)
或者写为:
I(s)
=
1
sL
U(s)
+
i(0-)
s
sL称为L的运算阻抗
I(s)
1/sL称为运算导纳 +
I(s)
i(0-) 为L的初始电流 U(s) 由上式得电感L的
运算电路如图。
-
sL
+
- U(s)
Li(0-) +
-
1
sL i(0-)
(电机学)第十四章 拉普拉斯变换-091216

线性动态电路的复频域分析
2014-12-29
浙江工业大学信息学院
1
主 要 内 容
拉 普 拉 斯 变 换
拉氏 变换 基本 性质
拉氏 反变 换的 部分 分式 展开
运 算 电 路
应用 拉氏 变换 分析 线性 电路
2014-12-29
浙江工业大学信息学院
14- 2
§14-1 拉氏变换的定义
例: 求下列函数的原函数
F (s)
F (s)
s 1 s 3 2s 2 2s
解:
s 1 s 1 A B C s 3 2s 2 2s s ( s 1 j )( s 1 j ) s s 1 j s 1 j
其中系数:A s F (s)
t2 tn
A/ s
1 e
t
A s A s(s )
e
t
sin(t )
et cos(t )
tet
sin(t )
s2 2
s s2 2 1 s2
(s )2 2 s (s )2 2
1 (s )2 s (s )2
若时间函数f (t) 的拉氏变换为F (s) ,则f (t) 的导数 f (1) (t)的拉氏变换为: £ £
如果f(t)代表电容电压或电感电流,则它们导数的象函数 中的第二项便是uc(0-)或iL(0-),即动态元件的初始状态。 二阶导数f (2) (t)的拉氏变换为:
£
n 阶导数f (n) (t)的拉氏变换为:
浙江工业大学信息学院
14- 14
五、复频域平移性质
若时间函数f (t) 的拉氏变换为F (s) ,则将f (t) 乘以eat后得拉氏变换为的拉氏变换为: £
电工基础题库-复杂直流电路

第三章复杂直流电路[知识点]1.支路节点回路网孔的概念2.基尔霍夫定律3.支路电流法4.叠加定理5.戴维南定理6.两种电源模型及等效变换[题库]一、是非题1.基尔霍夫电流定律是指沿任意回路绕行一周,各段电压的代数和一定等于零。
2 .任意的闭合电路都是回路。
3 .理想电压源和理想的电流源是可以进行等效变换的。
4 .电压源和电流源等效变换前后电源内部是不等效的。
5 .电压源和电流源等效变换前后电源外部是不等效的。
6.在支路电流法中用基尔霍夫电流定律列节点电流方程时。
若电路有m个节点,那么一定要列出m个方程来。
7 .回路电流和支路电流是同一电流。
8.在电路中任意一个节点上,流入节点的电流之和,一定等于流出该节点的电流之和。
9.在计算有源二端网络的等效电阻时,网络内电源的电动势可去掉,电源的内阻也可不考虑。
10 .由若干个电阻组成的无源二端网络,一定可以把它等效成一个电阻。
11 .任意一个有源二端网络都可以用一个电压源来等效替代。
12.用支路电流法求解各支路电流时,若电路有 n条支路,则需要列出n-1个方程式来联立求解。
13 .电路中的电压、电流和功率的计算都可以应用叠加定理。
14.如果网络具有两个引出端与外电路相连,不管其内部结构如何,这样的网络就叫做二端网络。
15 .在任一电路的任一节点上,电流的代数和永远等于零。
二、选择题1.某电路有3个节点和7条支路,采用支路电流法求解各支路电流时,应列出电流方程和电压方程的个数分别为A 、3, 4B 、4, 3C 、2, 5D 、4, 72.如图所示,可调变阻器 R获得最大功率的条件是A、1.2ΩB、2ΩC 、3 ΩD、5Ω3.实验测得某有源二端线性网络的开路电压为 6V,短路电流为2A,当外接电阻为3Ω,其端电压为A 、2VB 、3VC、4VD、6V4.在上题中,该线性网络的开路电压为 6V,短路电流为2A,当外接电阻为( )时,可获得最大功率。
A 、1 ΩB 、2ΩC、3 ΩD、4Ω5.上题中,该有源二端线性网络等效为一个电压源的电压为A 、2VB 、3VC、4VD、6V6.把图示电路用电流源等效替代,则该电流源的参数为A 、3A,3 ΩB 、3A,4ΩC、1A,1 ΩD、1.5A,4Ω7.上题电路用电压源等效替代,则电压源的参数为A 、9V,3 ΩB 、1V,1 ΩC、3V,4ΩD、6V,4Ω8.如图所示网络N1 、N2,已知I1=5A, I2=6A,则I3为A 、11AB 、-11AC、1AD、-1A9.如图所示,电流I的值为A 、1AB 、-2AC、2AD、-1A10 .上图中, Us的值为A 、3VB 、-3VC、2VD、-2V11.下面的叙述正确的是A、电压源和电流源是不能等效变换的B、电压源和电流源等效变换后,内部是不等效的C、电压源和电流源等效变换后,外部是不等效的D、以上说法都不正确12.电路如图,所示该电路的节点数和支路数分别为A 、3, 5B 、3, 6C、4, 6D、4, 513 .如图所示, A、B两点间的等效电压是A 、-18VB 、18VC、-6VD、6V14 .上题中, A、B两点间的等效电阻是A 、0 ΩB 、3 ΩC、6ΩD、不能确定15.电路如图所示,电流I为A 、0AB 、2AC、-2AD、4A三、填空题1.基尔霍夫电流定律指出流过任一节点的为零,其数学表达式为;基尔霍夫电压定律指出从电路上的任一点出发绕任意回路一周回到该点时为零,其数学表达式为。
《电路》第五版邱关源第十四章

sp1 sp2
spn
f( t) K 1 e p 1 t K 2 e p 2 t K n e p n t
返回 上页 下页
待定常数的确定: 方法1
K i F ( s ) ( s p i)s p i i 1 、 2 、 3 、 、 n
(s 令 s p =1 p)1F (s) K 1 (s p 1 ) s K 2 p 2 s K n p n
F(s) ∞ f (t)estdt
0
f (t)
1
c
j∞
F
(s)est
ds
2πj c j∞
正变换 反变换
简写 F ( s ) L f ( t ) , f ( t ) L - 1 F ( s )
s 复频率 sj
返回 上页 下页
注意
① 积分域
0
0 0
积分下限从0 开始,称为0 拉氏变换 。 积分下限从0 + 开始,称为0 + 拉氏变换 。
返回 上页 下页
F (s)N D ( (s s) )a b 0 0 s s m n a b 1 1 s sm n 1 1 b a n m(n m )
讨论
象函数的一般形式
(1)若D(s)=0有n个单根分别为p1、 、 pn
利用部分分式可将F(s)分解为
待定常数
F(s)K 1 K 2 K n
∞
t0
f(tt0)estdt
令tt0
∞
f(
)es(t0)d
0
est0
∞
f(
)esd
0
est0F(s)
延迟因子
返回 上页 下页
例2-5 求矩形脉冲的象函数。 解 f(t) ε (t) ε (t T )
§1—7基尔霍夫定律(1)
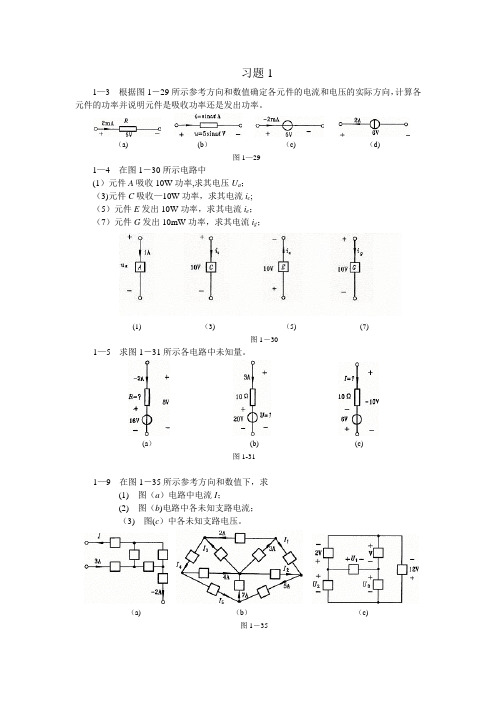
习题11—3 根据图1-29所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是吸收功率还是发出功率。
(a) (b)(c) (d)图1—291—4 在图1-30所示电路中(1)元件A吸收10W功率,求其电压U a;(3)元件C吸收—10W功率,求其电流i c;(5)元件E发出10W功率,求其电流i e;(7)元件G发出10mW功率,求其电流i g;(1) (3) (5) (7)图1-301—5 求图1-31所示各电路中未知量。
(a)(b) (c)图1-311—9 在图1-35所示参考方向和数值下,求(1) 图(a)电路中电流I;(2) 图(b)电路中各未知支路电流;(3) 图(c)中各未知支路电压。
(a) (b)(c)图1-351—11 求图1-37所示电路中电压U1、U ab、U cb。
图1-371—13 求图1-39所示电路中电压U1和电流I2。
图1-391—14 求图1-40所示电路中电压U s和电流I。
图1-40习题22—l 电路如图2-22所示,已知R1=1Ω,R2=2Ω,R3=4Ω,求各电路的等效电阻R ab.(c)(d) (e)(f)图2-222—3 电路如图2-24所示,已知R=2Ω,求开关打开和闭合时等效电阻R ab。
图2-242—9 电路如图2-30所示:(1)开关K打开时,求电压U ab;(2)开关K闭合时,求流过开关电流I ab。
(a)图2-302-13 求图2-34所示各电路的最简单的等效电路.(a)(b) (c)图2-342—14 求图2-35所示各电路的最简单的等效电路。
(b)(d)(f)图2-352-18 求图2-39所示各含受控源电路的输入电阻R i。
(b)图2-392-19 求图2-40所示各电路中的电压比Uσ/ U s。
(b)图2-402-23 电路如图2-44所示,求:(1)如果电阻R=4Ω,计算电压U和电流I。
(2)如果电压U=− 4V,计算电阻R。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
漫灰体
吸收比不受外界辐射影响 仅取决于物体本身特性
基尔霍夫定律升级版:
对于漫射灰体,吸收比恒等于同温度下的发射率。
3
不同层的表达式
基尔霍夫定律在不同层次的表达式:
层次
单色,定向 单色,半球 全波段,半球
数学表达式
λ (,,T)= λ(,,T) λ (T)= λ (T) (T)= (T)
基尔霍夫定律
发射率和吸收比的关系
发射率
黑体 Eb ,T1
基尔霍夫定律(1859) 绝对黑体(1862)
关系?
2
吸收比
任意物体 E , T2
,
热平衡:T1 T2 热量收支平衡:
E Eb
E
Eb
基尔霍夫定律
基尔霍夫定律:
热平衡时,任意物体对黑体投入辐射的吸收比等于 同温度下该物体的发射率。
成立条件
无条件 漫射表面 与黑体热平衡或漫灰表面
工程计算:
绝大多数工程材料可以近似为漫射灰体,同温度下发射率等于吸收比。
有缘学习交流+V:ygd3076或关注桃报:奉献教育(店铺)
Thank You!
5
