备战(湖北版)高考数学分项汇编专题16选考部分(含解析)理【含答案】
备战(湖北版)高考数学分项汇编专题16选考部分(含解析)理

专题16 选考部分一.选择题1. 【2012年普通高等学校招生全国统一考试湖北卷6】设,,,,,a b c x y z 是正数,且22210a b c ++=,22240x y z ++=,20ax by cz ++=,则a b c x y z++=++ ( ) A .14 B .13C .12D .34 【答案】C2.【2014年普通高等学校招生全国统一考试湖北卷10】已知函数)(x f 是定义在R 上的奇函数,当0≥x 时,)3|2||(|21)(222a a x a x x f --+-=,若R ∈∀x ,)()1(x f x f ≤-,则实数a 的取值范围为( ) A.]61,61[- B.]66,66[- C. ]31,31[- D. ]33,33[- 【答案】B考点:函数的奇函数的性质、分段函数、最值及恒成立,难度中等.二.填空题1.【2008年普通高等学校招生全国统一考试湖北卷15】圆34cos ,()24sin x C y θθθ=+⎧⎨=-+⎩为参数的圆心坐标为 ,和圆C 关于直线0x y -=对称的圆C ′的普通方程是 .【答案】15.(3,-2),(x +2)2+(y -3)2=16(或x 2+y 2+4x -6y -3=0)2.【2012年普通高等学校招生全国统一考试湖北卷15】(选修4-1:几何证明选讲)如图,点D 在O 的弦AB 上移动,4AB =,连接OD ,过点D 作OD 的垂线交O 于点C ,则CD 的最大值为 .【答案】23.【2012年普通高等学校招生全国统一考试湖北卷16】(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系. 已知射线π4θ=与曲线21,(1)x t y t =+⎧⎨=-⎩(t 为参数)相交于A ,B 两点,则线段AB 的中点的直角坐标为 .4.【2013年普通高等学校招生全国统一考试湖北卷13】设,,x y z R ∈,且满足:2221x y z ++=,2314x y z ++=,则x y z ++= 。
【备战2016】(湖北版)高考数学分项汇编 专题03 导数(含解析)理

专题3 导数一.选择题1.【2008年普通高等学校招生全国统一考试湖北卷7】若f(x)=21ln(2)2x b x -++∞在(-1,+)上是减函数,则b 的取值范围是 ( )A.[-1,+∞]B.(-1,+∞)C.(-∞,-1)D.(-∞,-1)2. 【2009年普通高等学校招生全国统一考试湖北卷9】设球的半径为时间t 的函数()R t 。
若球的体积以均匀速度c 增长,则球的表面积的增长速度与球半径( )A.成正比,比例系数为CB. 成正比,比例系数为2CC.成反比,比例系数为CD. 成反比,比例系数为2C3.【2011年普通高等学校招生全国统一考试湖北卷10】放射性元素由于不断有原子放射出微粒子而变成其它元素,其含量不断减少,这种现象称为衰变。
假设在放射性同位素铯137衰变过程中,其含量M(太贝克/年)与时间t(单位:年)满足函数关系:()3002t M t M -=,其中M 0为t=0时铯137的含量,已知t=30时,铯137含量的变化率为-10ln2(太贝克/年),则M (60)=( ) A. 5太贝克 B. 75ln2太贝克 C. 150ln2太贝克 D. 150太贝克 【答案】A 【解析】试题分析:()30012ln 230t M t M -'=-,因为t=30时,铯137含量的变化率为-10ln2, 所以()30300013010ln 22ln 260030M M M -'=-=-⇒=,故()2606002150M -=⨯=.4.【2012年普通高等学校招生全国统一考试湖北卷3】已知二次函数()y f x =的图象如图所示,则它与x 轴所围图形的面积为( )A .2π5B .43 C .32D .π25. 【2013年普通高等学校招生全国统一考试湖北卷7】一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度()25731v t t t=-++(t 的单位:s ,v 的单位:/m s )行驶至停止。
【精品】湖北数学高考选择填空部分及答案

一、选择题:1.若i 为虚数单位,图中复平面内点Z 表示复数z ,则表示复数iz+1的点是 A .EB .FC .GD .H2.设集合}3|),{(},1164|),{(22x y y x B y x y x A ===+=,则 B A 的子集的个数是A .4B .3C .2D .13.在ABC ∆中,a=15,b=10,A=︒60,则B cos =A .322-B .322 C .36-D .36 4.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A ,“骰子向上的点数是3”为事件B ,则事件A 、B 中至少有一件发生的概率是A .125 B .21 C .127 D .43 5.已知ABC ∆和点M 满足0=++MC MB MA ,若存在实数m 使得AM m AC AB =+成立,则m= A .2 B .3 C .4 D .56.将参加夏令营的600名学生编号为:001,002,…,600。
采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第1营区,从301到495在第II 营区,从496到600在第III 营区,三个营区被抽中的人数依次为 A .26,16,8 B .25,17,8 C .25,16,9 D .24,17,9 7.如图,在半径为r 的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设n S 为前n 个圆的面积之和,则n n S ∞→lim =A .22r πB .238r πC .24r πD .26r π8.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是 A .152 B .126 C .90 D .54 9.若直线b x y +=与曲线243x x y --=有公共点,则b 的取值范围是 A .]221,1[+- B .]221,221[+-C .]3,321[-D .]3,21[-10.记实数n x x x ,,,21 中的最大数为},,,max {21n x x x ,最小数为}.,,m in{21n x x x 已知ABC ∆的三边边长为a ,b ,c (c b a ≤≤),定义它的倾斜度为}.,,min{},,max{acc b b a a c c b b a l ⋅=则"1"2=l 是“ABC ∆为等边三角”的A .必要而不充分的条件B .充分而不必要的条件C .充要条件D .既不充分也不必要的条件二、填空题:11.在204)3(y x +的展开式中,系数为有理数的项共有项。
【备战2019】(湖北版)高考数学分项汇编 专题16 选考部分(含解析)理

专题16 选考部分一.选择题1. 【2019年普通高等学校招生全国统一考试湖北卷6】设,,,,,a b c x y z 是正数,且22210a b c ++=,22240x y z ++=,20ax by cz ++=,则a b cx y z++=++ ( )A .14 B .13C .12D .34【答案】C2.【2019年普通高等学校招生全国统一考试湖北卷10】已知函数)(x f 是定义在R 上的奇函数,当0≥x 时,)3|2||(|21)(222a a x a x x f --+-=,若R ∈∀x ,)()1(x f x f ≤-,则实数a 的取值范围为( ) A.]61,61[- B.]66,66[- C. ]31,31[- D. ]33,33[- 【答案】B考点:函数的奇函数的性质、分段函数、最值及恒成立,难度中等. 二.填空题1.【2008年普通高等学校招生全国统一考试湖北卷15】圆34cos ,()24sin x C y θθθ=+⎧⎨=-+⎩为参数的圆心坐标为 ,和圆C 关于直线0x y -=对称的圆C ′的普通方程是 . 【答案】15.(3,-2),(x +2)2+(y -3)2=16(或x 2+y 2+4x -6y -3=0)2.【2019年普通高等学校招生全国统一考试湖北卷15】(选修4-1:几何证明选讲)如图,点D 在O 的弦AB 上移动,4AB =,连接OD ,过点D 作OD 的垂线交O 于点C ,则CD 的最大值为 .【答案】23.【2019年普通高等学校招生全国统一考试湖北卷16】(选修4-4:坐标系与参数方程)在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系. 已知射线π4θ=与曲线21,(1)x t y t =+⎧⎨=-⎩(t 为参数)相交于A ,B 两点,则线段AB 的中点的直角坐标为 .4.【2019年普通高等学校招生全国统一考试湖北卷13】设,,x y z R ∈,且满足:2221x y z ++=,2314x y z ++=,则x y z ++= 。
(湖北版)高考数学分项汇编 专题02 函数(含解析)理

f x ax ax , g x 2 ,又 g 2 a ,故 a 2 ,于是 f x 2x 2x ,故 f 2 15 .
4
8. 【2011 年普通高等学校招生全国统一考试湖北卷 10】放射性元素由于不断有原子放射出微粒子而变成
其它元素,其含量不断减少,这种现象称为衰变。假设在放射性同位素铯 137 衰变过程中,其含量 M(太
足 f x g x ax ax 2a 0,且a 1,若 g 2 a ,则 f 2 ( )
A. a2
B.2
【答案】C
15
C.
4
17
D.
4
【解析】
试题分析: f x g x ax ax 2 f x g x,代入 f x g x ax ax 2 ,得:
a
;b
.
【答案】 a 6,b 1 2
【解析】
试题分析:由互反函数点之间的对称关系,取特殊点求解。在 y bx 3 上取点 0,3,得点 3, 0 在
y 2x a 上,故得 a 6 ;又 y 2x 6 上有点 0, 6,则点 6, 0在 y bx 3 .
千米时,车流 速度为 60 千米/小时。研究表明:当 20 x 200 时,车流速度 v 是车流密度 x 的一次函数。
(Ⅰ)当 0 x 200 ,求函数 v x的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
f x xAv x可以达到最大,并求出最大值。(精确到 1 辆/小时) 【解析】(Ⅰ)由题意:当 0 x 20 时, v x=60,当 20 x 200 时,设 v x ax b 。再由已知得:
高考理数试题参考答案(湖北卷)

教案示例教案要求1、了解翠鸟的外形和活动的特点,进而理解这些特点和翠鸟捉鱼本领的关系,初步知道翠鸟的特点是为了适应环境而渐渐形成的,教育学生懂得爱鸟、护鸟。
2、学习作者观察的顺序和抓住特点进行观察的方法。
3、能联系上下文理解课文中的一些词语。
4、利用多媒体技术激发学生学习兴趣,优化课堂结构。
5、学会本课生字新词,朗读课文,背诵课文第 1 —3自然段。
教案重点抓住描写翠鸟的外形和活动特点的词句,引导学生理解课文内容。
学习作者的观察顺序和观察方法。
教案用具媒体资源:教案课件《翠鸟》。
教案时间3课时教案过程第一课时一、形象感知,导入新课。
播放《翠鸟》课件中“拓展”部分内容,直观形象地认识翠鸟,进而导入新课,板书课题。
二、初读课文,自学字词1、学生自读课文,自学生字新词。
可利用《翠鸟》课件中“认一认”部分内容结合教案。
2、学生互相交流难点字词。
3、分组分段朗读课文(结合《翠鸟》课件中“课文朗读”部分内容进行教案)三、学习第一自然段1学生自读,思考:这段写翠鸟的什么?(外形)2、提示:课文从三个方面描写了翠鸟的外形,是哪三个方面呢?3、四人小组自学。
4、交流讨论,教师适时点拨。
(1第一句:写了翠鸟爱停在苇秆上。
突岀外形特点:“红色的小爪子”(2)第二一一五句:写翠鸟的颜色。
用一个词概括(“鲜艳”)。
重点理解:作者是怎样把翠鸟的颜色鲜艳写具体的?头上:橄榄色头巾,翠绿色花纹。
背上:浅绿色的外衣腹部:赤褐色的衬衫联系上文,理解“鲜艳”的意思(形容颜色又鲜明又美丽)。
思考:为什么作者用“头巾”“外衣”“衬衫”来打比方?体现了作者怎样的一种感情?对翠鸟的喜爱之情)(3)第六句学生自读句子,找出能概括本句的词语(小巧玲珑)。
“小巧玲珑”是什么意思?哪些地方能看出它小巧玲珑?眼:透亮灵活嘴:又尖又长联系上文理解“小巧玲珑”(形容又小又灵巧精致)。
5、结合板书,小结本段6、指导训练朗读。
第二课时一、试背第一自然段二、学习第二、三自然段1、齐读课文,思考:主要写了什么?(翠鸟的活动特点)2、学习第二自然段自读,理解每句话写了翠鸟活动的特点。
2022年湖北高考数学数学规划题及解析

2022年湖北高考数学数学规划题及解析2022年湖北高考数学科目一直是考生关注的焦点,而数学的规划题往往是难点之一。
本文将为大家介绍2022年湖北高考数学考试中的数学规划题,并提供详尽的解析。
一、选择题选择题是数学考试的常见题型,湖北高考数学科目中也不例外。
在2022年数学考试中,选择题占据了较大比重。
为了帮助考生更好地备考,以下是几个典型的数学规划题,以及其解析过程。
1. 在平面直角坐标系中,点A坐标为(2, 3),点B坐标为(4, 5)。
点P满足|PA| + |PB| = 10,设点P的坐标为(x, y),则点P的坐标为:A. (1, 2)B. (3, 4)C. (5, 6)D. (7, 8)解析:根据题意,点P到点A的距离加上点P到点B的距离等于10。
也就是说,点P到点A距离的绝对值加上点P到点B距离的绝对值等于10。
根据坐标距离的计算方式,可得到以下等式:|2-x|+|3-y| + |4-x| + |5-y| = 10。
解方程,最终可以得出(x, y)的值为(3, 4)。
因此答案选B。
2. 在某市一次地震中,一栋建筑物倾斜25°。
测量发现,地面上离建筑物10米处,与建筑物的连线与地面的夹角为45°。
此时,从这个角度观察建筑物的高度为多少米?A. 10B. 15C. 20D. 25解析:根据题意,建筑物与地面的夹角为25°,与地面连线的夹角为45°。
根据三角函数的相关原理,可以得到:tan(25°) = h/10,其中h 为建筑物的高度。
解方程,可以得到h的值为10 * tan(25°) ≈ 4.51米。
因此答案选A。
二、解析题解析题在湖北高考数学科目中占比较大,更加注重考生的综合能力和解题思路。
以下是一些2022年湖北高考数学科目中的典型解析题,以及解答过程。
1. 在平面直角坐标系中,曲线y = √x与抛物线y = -x² + 4x交于两个不同的点P和Q。
概率与统计(解答题)(文科专用)(原卷版)五年(2018-2022)高考数学真题分项汇编(全国通用)
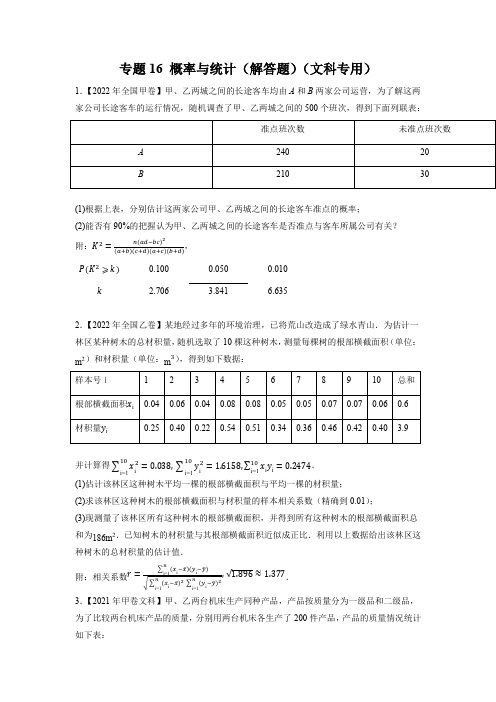
专题16 概率与统计(解答题)(文科专用)1.【2022年全国甲卷】甲、乙两城之间的长途客车均由A 和B 两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关? 附:K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d), P (K 2⩾k )0.100 0.050 0.010 k 2.7063.8416.6352.【2022年全国乙卷】某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m 2)和材积量(单位:m 3),得到如下数据:并计算得∑x i 210i=1=0.038,∑y i 210i=1=1.6158,∑x i y i10i=1=0.2474. (1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量; (2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186m 2.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值. 附:相关系数r =i n i=1i √∑(x i −x̅)2ni=1∑(y i−y ̅)2ni=1√1.896≈1.377.3.【2021年甲卷文科】甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:22()()()()()n ad bcKa b c d a c b d-=++++4.【2021年乙卷文科】某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:旧设备和新设备生产产品的该项指标的样本平均数分别记为x和y,样本方差分别记为21s和22s.(1)求x,y,21s,22s;(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果y x-≥认为有显著提高).5.【2020年新课标1卷文科】某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:甲分厂产品等级的频数分布表乙分厂产品等级的频数分布表(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务6.【2019年新课标1卷文科】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:(1)分别估计男、女顾客对该商场服务满意的概率;(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?附:22()()()()()n ad bcKa b c d a c b d-=++++.7.【2019年新课标2卷文科】某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)8.602.8.【2018年新课标1卷文科】某家庭记录了未使用节水龙头50天的日用水量数据(单位:3m)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:未使用节水龙头50天的日用水量频数分布表使用了节水龙头50天的日用水量频数分布表(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:(2)估计该家庭使用节水龙头后,日用水量小于30.35m的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题16 选考部分
一.选择题
1. 【2012年普通高等学校招生全国统一考试湖北卷6】设,,,,,a b c x y z 是正数,且22210a b c ++=,22240x y z ++=,20ax by cz ++=,则a b c x y z
++=++ ( ) A .14 B .13
C .12
D .34 【答案】C
2.【2014年普通高等学校招生全国统一考试湖北卷10】已知函数)(x f 是定义在R 上的奇函数,当0≥x 时,)3|2||(|2
1)(222a a x a x x f --+-=,若R ∈∀x ,)()1(x f x f ≤-,则实数a 的取值范围为( ) A.]61,61[- B.]66,66[- C. ]3
1,31[- D. ]33,33[- 【答案】B
考点:函数的奇函数的性质、分段函数、最值及恒成立,难度中等.
二.填空题
1.【2008年普通高等学校招生全国统一考试湖北卷15】圆34cos ,()24sin x C y θθθ
=+⎧⎨=-+⎩为参数的圆心坐标
为 ,和圆C 关于直线0x y -=对称的圆C ′的普通方程是 .
【答案】15.(3,-2),(x +2)2+(y -3)2=16(或x 2+y 2
+4x -6y -3=0)
2.【2012年普通高等学校招生全国统一考试湖北卷15】(选修4-1:几何证明选讲)如图,点D 在O 的弦AB 上移动,4AB =,连接OD ,过点D 作OD 的垂线交O 于点C ,则CD 的最大值为 .
【答案】2
3.【2012年普通高等学校招生全国统一考试湖北卷16】(选修4-4:坐标系与参数方程)
在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系. 已知射线π4
θ=
与曲线21,(1)x t y t =+⎧⎨=-⎩(t 为参数)相交于A ,B 两点,则线段AB 的中点的直角坐标为 .
4.
【2013年普通高等学校招生全国统一考试湖北卷13】设,,x y z R ∈,且满足:2221x y z ++=,2314x y z ++=,则x y z ++= 。
【答案】3147
x y z ++=
【相关知识点】柯西不等式及其等号成立的条件)
5.【2013年普通高等学校招生全国统一考试湖北卷15】如图,圆O 上一点C 在直线AB 上的射影为D ,点D 在半径OC 上的射影为E 。
若3AB AD =,则
CE EO
的值为 。
【答案】8
【解析】 O D E
B
A 第15题图
C
试题分析:由射影定理知()()2222812AD AB AD CE CD AD BD EO OD OA AD AB AD -====-⎛⎫- ⎪⎝⎭
. 6.【2013年普通高等学校招生全国统一考试湖北卷16】在直角坐标系xOy 中,椭圆C 的参数方程为cos sin x a y b θθ=⎧⎨=⎩
()0a b ϕ>>为参数,。
在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 与圆O 的极坐标方程分别为2sin 42
m πρθ⎛
⎫+= ⎪⎝⎭()m 为非零常数与b ρ=。
若直线l 经过椭圆C 的焦点,且与圆O 相切,则椭圆C 的离心率为。
7.【2014年普通高等学校招生全国统一考试湖北卷15】(选修4-1:几何证明选讲)
如图,P 为⊙O 的两条切线,切点分别为B A ,,过PA 的中点Q 作割线交⊙O 于D C ,两点,若,3,1==CD QC 则
=PB .
【答案】4
【解析】
试题分析:由切割线定理得4)31(12=+⨯=⋅=QD QC QA ,所以2=QA ,所以4==PA PB .
考点:圆的切线长定理,切割线定理,容易题.几何证明选讲一般考查圆的性质等简单的知识,主要以填空
题的形式出现,难度一般较小.
8.【2014年普通高等学校招生全国统一考试湖北卷16】(选修4-4:坐标系与参数方程)
已知曲线1C 的参数方程是⎪⎩
⎪⎨⎧==33t y t x ()为参数t ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,
曲线2C 的极坐标方程是2=ρ,则1C 与2C 交点的直角坐标为 . 【答案】)1,3(
9. 【2015高考湖北,理15】(选修4-1:几何证明选讲)
如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则AB AC
= . 【答案】2
1 【解析】因为PA 是圆的切线,A 为切点,PBC 是圆的割线,
由切割线定理知,)(2
BC PB PB PC PB PA +=⋅=,因为3BC PB =,
所以224PB PA =,即PB PA 2=, 由PAB ∆∽PCA ∆,所以2
1==PA PB AC AB . 【考点定位】圆的切线、割线,切割线定理,三角形相似.
第15题图 A
P B C
10. 【2015高考湖北,理16】在直角坐标系xoy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系. 已
知直线l 的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为1,1
x t t y t t
⎧=-⎪⎪⎨⎪=+⎪⎩ ( t 为参数) ,l
与C 相交于A ,B 两点,则||AB = . 【答案】52
【考点定位】极坐标方程、参数方程与普通方程的转化,两点间的距离.。
