南州中学中学课堂教学导学案.数列7doc
简单句

南州中学课堂教学导学案(grammar)设计者:杨丽审核人:审批人:学时:第2学时课题:lesson1 简单句基本句型学习目标:掌握了解简单句基本句型:主谓、主系表教学重难点:简单陈述句的语序及基本句型:主谓、主系表教学与学法:例析法、习题法教学用具:黑板、彩色粉笔教学过程:一.揭示目标、学法指导:1.掌握了解简单陈述句的语序及基本句型:主谓、主系表2.在学习过程中运用二.学生自学、教师巡导:学生结合资料,查阅并讨论简单陈述句的语序及基本句型:主谓、主系表三.学生展示,教师精导:1.句子成分(主语、谓语、宾语、表语、定语、状语、补语)1)什么叫主语?谓语讲述的对象,表示句子所说的是“什么人”或“什么事物”2)哪些可充当主语?The sun rises in the east.He likes dancing.Twenty years is a short time in history.Smoking does harm to the health.To learn English well is not easy.What we need is a book..3)谓语谓语是用来描述主语的行为动作或所处的状态。
在句子中谓语通常由()词充当。
①简单谓语:由一个动词或动词短语构成He practices running every morning.The plane took off at ten o’clock.②复合谓语:由情态动词加动词原形或者由其他助动词加实意动词构成You may keep the book for two weeks.He has caught a bad cold.注意:1.I am reading. We/you are reading. He/she is reading2.It snowed heavily. I like music3.He is talking loudly. He is talking with my sister loudly.2.简单句的基本句型(1)S()+ Vi()The sports meeting begins.She is singing.The students are listening.The pain has gone.The sun has risen.They won’t come.注意:(1)不及物动词不能直接加宾语。
七年级数学上册导学案(全集)
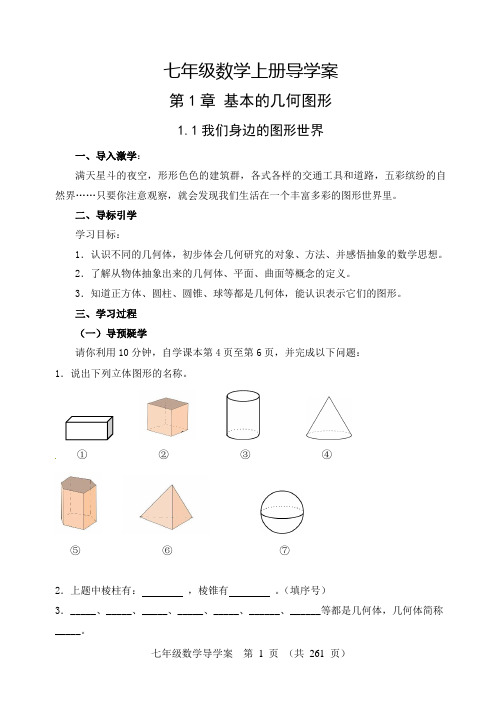
七年级数学上册导学案第1章基本的几何图形1.1我们身边的图形世界一、导入激学:满天星斗的夜空,形形色色的建筑群,各式各样的交通工具和道路,五彩缤纷的自然界……只要你注意观察,就会发现我们生活在一个丰富多彩的图形世界里。
二、导标引学学习目标:1.认识不同的几何体,初步体会几何研究的对象、方法、并感悟抽象的数学思想。
2.了解从物体抽象出来的几何体、平面、曲面等概念的定义。
3.知道正方体、圆柱、圆锥、球等都是几何体,能认识表示它们的图形。
三、学习过程(一)导预疑学请你利用10分钟,自学课本第4页至第6页,并完成以下问题:1.说出下列立体图形的名称。
①②③④⑤⑥⑦2.上题中棱柱有:,棱锥有。
(填序号)3._____、_____、_____、_____、_____、______、______等都是几何体,几何体简称_____。
4.观察下列实物图片,它们的形状分别类似于哪种几何体?①②③④⑤(二)导问互学问题:棱柱与圆柱、棱锥与圆锥的区别与联系:顶点棱侧面底面棱柱圆柱棱锥圆锥解决问题评价:(三)导根典学在下图中的三幅图案中,你分别看到了哪些图形?它们是怎样组合而成的?(四)导标达学1.下列几何体,是由一个曲面和两个平面围成的是_____。
A B C D2. 一个以下说法中正确的是。
A.正方体是棱柱。
B.电视机的形状类似于球体。
C.生活中应用的六角螺母的形状类似于圆柱。
D.鸡蛋的形状类似于圆锥。
3.一个七棱柱共有个面,条棱,个顶点,形状和面积完全相同的只有个面.4.图中的的几何体由几个面围成,面与面相交成几条线?它们是直的还是曲的?5.下列几何体中不是多面体的是( )A、立方体B、长方体C、三棱锥D、圆柱6.下列几何体没有曲面的是()A、圆柱B、圆锥C、球D、棱柱7.下列图案是由哪些简单的几何图形组成的?8.请你用两个圆、两个三角形和两条线段组合几幅新奇、有趣的图形,并给出文字说明。
反馈评价:四、导法慧学1.将所学知识纳入知识体系.2.本节解决问题的具体方法是怎样的?据此请总结此类问题的解题思路.3.还有没有更好的解法?你还有疑问吗?设计人:王望中学王志海1.2 几何图形一、导入激学:我们学过的长方体有几个面?几个顶点?几条棱?二、导标引学学习目标:1.认识点、线、面、体,初步感受“点动成线、线动成面、面动成体”的生活实例。
南州中学中学课堂教学导学案.数列5doc

南州中学高一B 组中学课堂教学导学案主备教师:李家海 审批人:田仁文 年 月 日 课 题:§2.3 等差数列的前n 项和(1)教学目的:1. 掌握等差数列前n 项和公式及其获取思路;2. 会用等差数列的前n 项和公式解决一些简单的与前n 项和有关的问题 教学重点:等差数列的前n 项和公式的理解、推导及应用.教学难点:灵活应用等差数列前n 项和公式解决一些简单的有关问题.4244找出疑惑之处) 复习1:什么是等差数列?等差数列的通项公式是什么?复习2:等差数列有哪些性质?二、新课导学 ※ 学习探究 探究:等差数列的前n 项和公式 问题: 1. 计算1+2+…+100=?2. 如何求1+2+…+n =?新知:数列{}n a 的前n 项的和:一般地,称 为数列{}n a 的前n 项的和,用n S 表示,即n S =反思:① 如何求首项为1a ,第n 项为n a 的等差数列{}n a 的前n 项的和?② 如何求首项为1a ,公差为d 的等差数列{}n a 的前n 项的和?试试:根据下列各题中的条件,求相应的等差数列{}n a 的前n 项和n S .⑴184188a a n =-=-=,,;⑵114.50.715a d n ===,,.小结:1. 用1()2n n n a a S +=,必须具备三个条件: .2. 用1(1)2n n n d S na -=+,必须已知三个条件: .※ 典型例题例1 2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的统治》. 某市据此提出了实施“校校通”工程的总目标:从2001年起用10年时间,在全市中小学建成不同标准的校园网.据测算,2001年该市用于“校校通”工程的经费为500万元. 为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元. 那么从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?小结:解实际问题的注意:① 从问题中提取有用的信息,构建等差数列模型;② 写这个等差数列的首项和公差,并根据首项和公差选择前n 项和公式进行求解. 例2 已知一个等差数列{}n a 前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的前n 项和的公式吗?变式:等差数列{}n a 中,已知1030a =,2050a =,242n S =,求n .小结:等差数列前n 项和公式就是一个关于11n a a n a n d 、、或者、、的方程,已知几个量,通过解方程,得出其余的未知量.※ 动手试试练1.一个凸多边形内角成等差数列,其中最小的内角为120°,公差为5°,那么这个多边形的边数n 为( ).A. 12B. 16C. 9D. 16或9三、总结提升 ※ 学习小结1. 等差数列前n 项和公式的两种形式;2. 两个公式适用条件,并能灵活运用;3. 等差数列中的“知三求二”问题,即:已知等差数列之1,,,,n n a a q n S 五个量中任意的三个,列方程组可以求出其余的两个.※ 知识拓展1. 若数列{}n a 的前n 项的和2n S An Bn =+(A 0≠,A 、B 是与n 无关的常数),则数列{}n a 是等差数列.2. 已知数列{},n a 是公差为d 的等差数列,S n 是其前n 项和,设232,,,k k k k k k N S S S S S +∈--也成等2.※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 在等差数列{}n a 中,10120S =,那么110a a +=( ). A. 12 B. 24 C. 36 D. 482. 在50和350之间,所有末位数字是1的整数之和是( ). A .5880 B .5684 C .4877 D .45663. 已知等差数列的前4项和为21,末4项和为67,前n 项和为286,则项数n 为( ) A. 24 B. 26 C. 27 D. 284. 在等差数列{}n a 中,12a =,1d =-,则8S = .5. 在等差数列{}n a 中,125a =,533a =,则6S =. 1. 数列{n a }是等差数列,公差为3,n a =11,前n 和n S =14,求n 和3a .2. 在小于100的正整数中共有多少个数被3除余2? 这些数的和是多少?。
人教版七年级下册数学全册导学案

人教版七年级下册数学全册导学案[标题] 人教版七年级下册数学全册导学案[正文]在中学生的学习生涯中,数学作为一门重要的学科,对于培养学生的逻辑思维和问题解决能力起着重要的作用。
为了帮助同学们更好地掌握人教版七年级下册数学全册的内容,本文将结合实际情况,从每个单元的重点知识和考点出发,为同学们制定导学案,以便他们能够更好地学习数学知识。
一、第一单元导数列、表示数列的一般写法【导学目标】1.了解数列的概念和基本符号。
2.掌握用一般法表示数列的方法。
3.能够求解与数列有关的问题。
【学习重点】1.数列的概念和基本符号。
2.一般法表示数列的方法。
3.与数列相关的问题求解。
【学习难点】数列的一般法表示。
【学习方法】1.阅读教材内容,掌握数列的定义和基本概念。
2.通过练习题,熟练掌握数列的一般法表示。
【课前预习】1.预习P1-P4的内容,了解数列的概念、基本符号以及一般法表示的方法。
2.预习人教版七年级下册数学全册P3的例题和习题。
【课堂探究】1.请同学们复述数列的定义和基本概念。
2.引导同学们用一般法表示数列。
例如:“写出数列1,3,5,7的一般法表示方法。
”【课后拓展】1.通过完成人教版七年级下册数学全册P6的练习题,进一步巩固数列的一般法表示。
2.找寻生活中的数列现象,并用一般法表示。
3.了解更多与数列相关的问题,并尝试解决。
二、第二单元一元一次方程与实际问题【导学目标】1.掌握一元一次方程的解集。
2.能够将实际问题转化为一元一次方程,并求解。
3.能够利用一元一次方程解决实际问题。
【学习重点】1.一元一次方程的解集。
2.将实际问题转化为一元一次方程。
3.利用一元一次方程解决实际问题。
【学习难点】如何将实际问题转化为一元一次方程。
【学习方法】1.阅读教材内容,了解一元一次方程的定义和基本概念。
2.通过解题方法的讲解,学会如何将实际问题转化为一元一次方程。
【课前预习】1.预习P11-P14的内容,了解一元一次方程的解集和实际问题的转化方法。
高中数学导学教案模板

高中数学导学教案模板
一、教学目标
1. 知识目标:学生能够掌握本节课所涉及的数学知识点。
2. 能力目标:通过练习和讨论,提高学生解决问题的能力。
3. 情感目标:培养学生对数学的兴趣,激发学生学习数学的热情。
二、教学重点和难点
1. 重点:本节课的重点是概念的讲解和相关例题的讲解。
2. 难点:难点在于一些抽象概念的理解和应用。
三、教学内容
本节课主要讲解【填写具体内容,如一次函数的性质】。
四、教学过程
1. 导入:通过简单的问题或案例引入本节课的主题。
2. 讲解:对本节课的重点知识点进行讲解,注意引导学生理解概念和方法。
3. 练习:组织学生进行相关练习,巩固所学知识。
4. 讨论:带领学生分组进行讨论或展示,促进学生之间的交流和学习。
5. 总结:对本节课的重点进行总结,梳理所学内容。
五、教学评价
本节课主要通过学生练习和讨论的表现来进行评价,关注学生对知识的理解和运用能力。
六、教学反馈
对学生在本节课中的表现进行适时的反馈,鼓励他们在数学学习中不断进步。
同时,也可以对教学过程进行总结和反思,为下一堂课的教学做好准备。
以上是本节课的教学设计模板,希望能够为您的教学工作提供一些帮助。
祝您教学顺利!。
1.3.1柱体、椎体、台体的表面积及体积

南州中学高一年级数学组学科导学案(累计25课时)设计者:张小兵审核人 :田仁文审批人: 时间:2011年9月25日班级姓名第组号上课时间:第周星期______课题§1.3。
1柱体、椎体、台体的表面积与体积课型新授课教学目标1.了解柱体、椎体、台体的表面积及体积公式2.能用所学的知识解决生产生活中的实际问题3.以这些公式为载体,增强学生的直观感知,加深类比思想、转化思想、整体思想的认识教学重点了解并会利用柱体、椎体、台体的表面积及体积公式教学难点利用柱体、椎体、台体的表面积及体积公式来解决实际生活中的问题教法与学法启发引导法,自主探究和共同探究相结合教学过程一、引入新课、揭示目标:1.回忆初中是如何求正方体和长方体的表面积的?2.几何体的展开图与它的表面积有着什么样的关系?画出下列几何体的展开图3.揭示课题、目标,引入新课。
一般地,我们可以把几何体展成平面图形,利用求平面图形的面积的方法来求几何体的面积二、学生自学、教师巡导:1.探究活动:棱柱、棱台、棱锥也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?2.已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积3. 如何根据圆柱、圆锥的结构特征,求它们的表面积圆柱表面积S=圆锥表面积S=4.参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 ?圆台的表面积=5.圆柱、圆锥、圆台三者之间的表面积公式有什么样的关系?6.柱体、椎体、台体的体积公式分别是什么?三者之间有着什么样的关系?B CASl三、学生展示、教师精导:1.如图,一个圆台形花盆盆口直径20 cm ,盆底直径为15cm ,底部渗水圆孔直径为1.5 cm ,盆壁长15cm .那么花盆的表面积约是多少平方厘米( 取3.14,结果精确到1 )?2.有一堆规格相同的铁制(铁的密度是3/8.7cm g )六角螺帽共重5.8kg ,已知底面是正六边形,边长为12mm ,内孔直径为10mm ,高为10mm ,问这堆螺帽大约有多少个( 取3.14)?四、边练边清、巩固提升:1.已知圆锥的表面积为a 2m ,且它的侧面展开图是一个半圆,求这个圆锥的底面直径?2.中心角为43π,面积为B 的扇形围成一个圆锥,若圆锥的全面积为A ,则A ∶B 等于( ) A .11∶8 B .3∶8 C .8∶3 D .13∶83.若正方体的全面积增为原来的2倍,那么它的体积增为原来的( ) A .2倍 B .4倍 C .2倍 D .22倍4.五棱台的上下底面均是正五边形,边长分别是8cm 和18cm ,侧面是全等的等腰梯形,侧棱长是13cm ,求它的侧面面积?5.如图所示,三棱锥D -ABC 一条侧棱AD =8cm ,底面一边长BC =18cm ,其余四条棱长都是17cm ,求三棱锥D -ABC 的体积.课堂小结课后反思①学习收获:②思想方法:③疑难困惑:cm15cm20cm15 ABCD。
南州中学七年级数学学科导学案4

南州中学七年级数学学科导学案4第七章三角形7.2.1 三角形的内角设计者:陈大文审核人:审批人:时间课型:新授课教学目标:1、会用平行线的性质与平角的定义证明三角形的内角和等于180°。
2、能应用三角形内角和定理解决一些简单的实际问题。
教学重点:1、三角形内角和定理教学难点:1、三角形内角和定理的推理过程。
教学过程一、揭示目标、学法指导通过本课的学习掌握以下目标:1、会用平行线的性质与平角的定义证明三角形的内角和等于180°2、能应用三角形内角和定理解决实际问题。
学法指导:学生自学尝试交流讨论二、学生自学、教师巡导1、学生看书P72页第一、二两段,理解通过度量只能验证一些具体的三角形的内角和等于180°,由于形状不同的三角形有无数个,不可能都用度量的方法,于是怎样用推理方法证明任意一个三角形内角和等于180°呢?2、看书P72页探究思考,在拼合的过程中,直线L与BC边有什么关系。
图(2)中的直线L与AB边有什么关系?由操作过程你能想出证明“三角形内角和等于180°吗?3、看书P73页思考怎样证明的三角形内角和定理。
4、看书P73页例1思考是如何应用内角和定理解决该问题的。
三、学生展示、教师精导1、任意一个三角形的三个内角和等于____________.2、经过剪、拼,书上P72页图1中直线L与BC_________,书上图2中直线L与AB边_________。
3、三角形内角和定理是_________________________________。
运用了平行线的性质和平角的定义证明的。
你还有其它方法吗?4、所作辅助线用___________线表示,辅助线在推理中当作___________使用,辅助线的作用:帮助我们解决问题的桥梁。
5、等量代换的意义。
6、证明一个问题的思路:由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程。
7、例1中分析,A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角,如果能求出∠CAB,∠ABC,根据内角和定理就能求出∠ACB,学生讨论后展示思路,你还能想出其他解法吗?并展示推理过程。
完整新人教版初中七年级数学下册导学案全册文档

2021年新人教版七年级数学下册导学案目录第五章相交线与平行线 1课题:5.1.1 相交线 1课题:5.1.2 垂线3课题:5.1.3 同位角、内错角、同旁内角 6课题:5.2.1 平行线8课题:5.2.2 平行线的判定10课题:5.3.1 平行线的性质13课题:平行线的判定及性质习题课15课题:5.3.2 命题、定理17课题:5.4平移20课题:相交线与平行线全章复习22第六章实数24课题:6.1平方根〔第1课时〕24课题:6.1平方根〔第2课时〕27课题:6.1平方根〔第3课时〕29课题:6.2立方根〔第1课时〕31课题:6.2立方根〔第2课时〕34课题:6.3 实数〔第1课时〕37课题:6.3 实数〔第2课时〕39课题:实数复习〔一〕41课题:实数复习〔二〕44第七章平面直角坐标系46课题:7.1.1 有序数对 46课题:7.1.2 平面直角坐标系48课题:7.1平面直角坐标系习题课51课题:7.2.1 用坐标表示地理位置 (53)课题:7.2.2 用坐标表示平移55课题:平面直角坐标系全章复习57第八章二元一次方程组60课题:8.1 二元一次方程组60课题:8.2.1 消元——解二元一次方程组〔代入法〕63课题:8.2.2 消元——解二元一次方程组〔代入法2〕65课题:8.2.3 消元——解二元一次方程组〔加减法1〕67课题:8.2.4 消元——解二元一次方程组〔加减法2〕70课题:8.3.1 实际问题与二元一次方程组〔 1〕72课题:8.3.2 实际问题与二元一次方程组〔 2〕74课题:8.3.3 实际问题与二元一次方程组〔 3〕76课题:8.4.1 三元一次方程组78第九章不等式与不等式组81课题:9.1.1 不等式及其解集81课题:9.1.2 不等式的性质83课题:9.2实际问题与一元一次不等式86课题:9.3一元一次不等式组〔1〕88课题:9.3一元一次不等式组〔2〕91章末复习 93第十章数据的收集、整理与描述99课题:10.1 统计调查〔第1课时〕99课题:10.1 统计调查〔第2课时〕100课题:10.2 ........................................................ 直方图〔第1课时〕102课题:10.2 直方图〔第2课时〕 (104)第五章相交线与平行线课题:5.1.1 相交线【学习目标】了解邻补角、对顶角,能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.【学习重点】邻补角、对顶角的概念,对顶角性质与应用 .【学习难点】理解对顶角相等的性质.【学习过程】一、学前准备各小组对七年级上学过的直线、射线、线段、角做总结.每人写一个总结小报告,并编写两道与它们相关的题目,在小组交流,并推出小组最好的两道题在班级汇报.二、探索思考探索一:完成课本P2页的探究,填在课本上.你能归纳出“邻补角〞的定义吗?.“对顶角〞的定义呢?.练习一:1.如图1所示,直线AB和CD相交于点O,OE是一条射线.〔1〕写出∠AOC的邻补角:_____ _____ ;〔2〕写出∠COE的邻补角:__ ;图1〔3〕写出∠BOC的邻补角:_____ _____ ;〔4〕写出∠BOD的对顶角:____ _ .2.如下图,∠1与∠2是对顶角的是〔〕1班级:姓名:探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.请归纳“对顶角的性质〞: .练习二: 1.如图,直线 a ,b 相交,∠1=40°,那么∠2=_______∠3=_______∠4=_______2.如图直线 AB 、CD 、EF 相交于点O ,∠BOE 的对顶角是______,∠COF 的邻补角是____,假设∠AOE=30°,那么∠BOE= ,∠BOF=_______3.如图,直线AB 、CD 相交于点O ,∠COE=90°,∠AOC=30°,∠FOB=90°,那么∠EOF=_____.aEDEB23AB1C4 bOO D第 1题CFF第2题A三、当堂反应第3题如下图,∠1和∠2是对顶角的图形有()1211222 1A.1个B.2个C.3个D.4个2.如图(1),三条直线 AB,CD,EF 相交于一点 O,∠AOD 的对顶角是_____,∠AOC的邻补角是_______,假设∠AOC=50°,那么∠BOD=______∠,COB=,∠AOE+∠DOB+∠COF=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南州中学高一B 组中学课堂教学导学案
主备教师:李家海 审批人:田仁文 年 月 日 课 题:§2.4等比数列(1)
教学目的:
1理解等比数列的概念;探索并掌握等比数列的通项公式、性质;
2. 能在具体的问题情境中,发现数列的等比关系,提高数学建模能力;
3. 体会等比数列与指数函数的关系. 教学重点:1.等比数列的概念; 2.等比数列的通项公式.
教学难点:1.在具体问题中抽象出数列的模型和数列的等比关系; 2..
4851找出疑惑之处) 复习1:等差数列的定义?
复习2:等差数列的通项公式n a = , 等差数列的性质有:
二、新课导学 ※ 学习探究
观察:①1,2,4,8,16,…
②1,12,14,1
8,116
,…
③1,20,220,320,420,…
思考以上四个数列有什么共同特征?
新知:
1. 等比数列定义:一般地,如果一个数列从第 项起, 一项与它的 一项的 等于 常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的 ,通常用字母 表示(q ≠0),
即:
1
n
n a a -= (q ≠0) 2. 等比数列的通项公式:
21a a = ; 3211()a a q a q q a === ; 24311()a a q a q q a === ; … …
∴ 11n n a a q a -==⋅ 等式成立的条件
3. 等比数列中任意两项n a 与m a 的关系是:
※ 典型例题
例1 (1) 一个等比数列的第9项是
49,公比是-1
3
,求它的第1项; (2)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项.
小结:关于等比数列的问题首先应想到它的通项公式11n n a a q -=.
例2 已知数列{n a }中,lg 35n a n =+ ,试用定义证明数列{n a }是等比数列.
小结:要证明一个数列是等比数列,只需证明对于任意正整数n ,
1
n n
a a +是一个不为0的常数就行了. ※ 动手试试
练1. 某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84%. 这种物质
的半衰期为多长(精确到1年)?
练2. 一个各项均正的等比数列,其每一项都等于它后面的相邻两项之和,则公比q =( ).
A.
B.
C.
D.
三、总结提升 ※ 学习小结
1. 等比数列定义;
2. 等比数列的通项公式和任意两项n a 与m a 的关系.
※ 知识拓展
在等比数列{}n a 中,
⑴ 当10a >,q >1时,数列{}n a 是递增数列; ⑵ 当10a <,01q <<,数列{}n a 是递增数列; ⑶ 当10a >,01q <<时,数列{}n a 是递减数列; ⑷ 当10a <,q >1时,数列{}n a 是递减数列; ⑸ 当0q <时,数列{}n a 是摆动数列; ⑹ 当1q =时,数列{}n a 是常数列.
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
※ 当堂检测(时量:5分钟 满分:10分)计分:
1. 在{}n a 为等比数列,112a =,224a =,则3a =( ). A. 36 B. 48 C. 60 D. 72
2. 等比数列的首项为98,末项为1
3
,公比为23,这个数列的项数n =( ).
A. 3
B. 4
C. 5
D. 6
3. 已知数列a ,a (1-a ),2(1)a
a -,…是等比数列,则实数a 的取值范围是( ). A. a ≠1 B. a ≠0且a ≠1
C. a ≠0
D. a ≠0或a ≠1
4. 设1a ,2a ,3a ,4a 成等比数列,公比为2,则
12
34
22a a a a ++= .
5. 在等比数列{}n a 中,4652a a a =-,则公比q = .
在等比数列{}n a 中,
⑴ 427a =,q =-3,求7a ;
⑵ 218a =,48a =,求1a 和q ;
⑶ 44a =,76a =,求9a ;
⑷ 514215,6a a a a -=-=,求3a .。
