答案~信息论与编码练习
信息论与编码理论习题答案

信息论与编码理论习题答案LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】第二章 信息量和熵八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率。
解:同步信息均相同,不含信息,因此 每个码字的信息量为 2⨯8log =2⨯3=6 bit因此,信息速率为 6⨯1000=6000 bit/s掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。
问各得到多少信息量。
解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1})(a p =366=61得到的信息量 =)(1loga p =6log = bit (2) 可能的唯一,为 {6,6})(b p =361得到的信息量=)(1logb p =36log = bit 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a) )(a p =!521信息量=)(1loga p =!52log = bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C = bit 随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。
解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立,则1x X =,21x x Y +=,321x x x Z ++=)|(Y Z H =)(3x H =log 6= bit )|(X Z H =)(32x x H +=)(Y H=2⨯(361log 36+362log 18+363log 12+364log 9+365log 536)+366log 6= bit )|(Y X H =)(X H -);(Y X I =)(X H -[)(Y H -)|(X Y H ]而)|(X Y H =)(X H ,所以)|(Y X H = 2)(X H -)(Y H = bit或)|(Y X H =)(XY H -)(Y H =)(X H +)|(X Y H -)(Y H 而)|(X Y H =)(X H ,所以)|(Y X H =2)(X H -)(Y H = bit),|(Y X Z H =)|(Y Z H =)(X H = bit )|,(Y Z X H =)|(Y X H +)|(XY Z H =+= bit设一个系统传送10个数字,0,1,…,9。
信息论与编码试题与答案

1、平均自信息为表示信源的平均不确定度,也表示平均每个信源消息所提供的信息量。
平均互信息表示从Y获得的关于每个X的平均信息量,也表示发X前后Y的平均不确定性减少的量,还表示通信前后整个系统不确定性减少的量。
2、最大离散熵定理为:离散无记忆信源,等概率分布时熵最大。
3、最大熵值为。
4、通信系统模型如下:5、香农公式为为保证足够大的信道容量,可采用(1)用频带换信噪比;(2)用信噪比换频带。
6、只要,当N足够长时,一定存在一种无失真编码。
7、当R<C时,只要码长足够长,一定能找到一种编码方法和译码规则,使译码错误概率无穷小。
8、在认识论层次上研究信息的时候,必须同时考虑到形式、含义和效用三个方面的因素。
9、1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
按照信息的性质,可以把信息分成语法信息、语义信息和语用信息。
按照信息的地位,可以把信息分成客观信息和主观信息。
人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。
信息的可度量性是建立信息论的基础。
统计度量是信息度量最常用的方法。
熵是香农信息论最基本最重要的概念。
事物的不确定度是用时间统计发生概率的对数来描述的。
10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用随机矢量描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为其发生概率对数的负值。
12、自信息量的单位一般有 比特、奈特和哈特 。
13、必然事件的自信息是 0 。
14、不可能事件的自信息量是 ∞ 。
15、两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。
16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量 趋于变小 。
17、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。
18、离散平稳有记忆信源的极限熵,=∞H )/(lim 121-∞→N N N X X X X H 。
信息论与编码试题集与答案

一填空题(本题20分,每小题2分)1、平均自信息为表示信源的平均不确定度,也表示平均每个信源消息所提供的信息量。
平均互信息表示从Y获得的关于每个X的平均信息量,也表示发X前后Y的平均不确定性减少的量,还表示通信前后整个系统不确定性减少的量。
2、最大离散熵定理为:离散无记忆信源,等概率分布时熵最大。
3、最大熵值为。
4、通信系统模型如下:5、香农公式为为保证足够大的信道容量,可采用(1)用频带换信噪比;(2)用信噪比换频带。
6、只要,当N足够长时,一定存在一种无失真编码。
7、当R<C时,只要码长足够长,一定能找到一种编码方法和译码规则,使译码错误概率无穷小。
8、在认识论层次上研究信息的时候,必须同时考虑到形式、含义和效用三个方面的因素。
9、1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
按照信息的性质,可以把信息分成语法信息、语义信息和语用信息。
按照信息的地位,可以把信息分成客观信息和主观信息。
人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。
信息的可度量性是建立信息论的基础。
统计度量是信息度量最常用的方法。
熵是香农信息论最基本最重要的概念。
事物的不确定度是用时间统计发生概率的对数来描述的。
10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用随机矢量描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为其发生概率对数的负值。
12、自信息量的单位一般有比特、奈特和哈特。
13、必然事件的自信息是 0 。
14、不可能事件的自信息量是∞。
15、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。
16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量趋于变小。
17、离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的 N倍。
18、离散平稳有记忆信源的极限熵,。
19、对于n元m阶马尔可夫信源,其状态空间共有 nm 个不同的状态。
信息论与编码习题答案

信息论与编码习题答案1.在无失真的信源中,信源输出由H(X) 来度量;在有失真的信源中,信源输出由R(D) 来度量。
2.要使通信系统做到传输信息有效、可靠和保密,必须首先信源编码,然后_____加密____编码,再______信道_____编码,最后送入信道。
3.带限AWGN波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)=+;当归一化信道容量C/W趋C W SNR近于零时,也即信道完全丧失了通信能力,此时E b/N0为-1.6 dB,我们将它称作香农限,是一切编码方式所能达到的理论极限。
4.保密系统的密钥量越小,密钥熵H(K)就越小,其密文中含有的关于明文的信息量I(M;C)就越大。
5.已知n=7的循环码42=+++,则信息位长g x x x x()1度k为 3 ,校验多项式《信息论与编码A》试卷第 2 页共 10 页《信息论与编码A 》试卷 第 3 页 共 10 页h(x)=31x x ++ 。
6. 设输入符号表为X ={0,1},输出符号表为Y ={0,1}。
输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )= 1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=1001⎡⎤⎢⎥⎣⎦;D max = 0.5 ,R (D max )= 0 ,相应的编码器转移概率矩阵[p(y/x )]=1010⎡⎤⎢⎥⎣⎦。
7. 已知用户A 的RSA 公开密钥(e,n )=(3,55),5,11p q ==,则()φn = 40 ,他的秘密密钥(d,n )=(27,55) 。
若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 。
二、判断题1. 可以用克劳夫特不等式作为唯一可译码存在的判据。
(√ )2. 线性码一定包含全零码。
信息论与编码理论习题答案

第二章 信息量和熵2.2八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率.解:同步信息均相同,不含信息,因此 每个码字的信息量为 2⨯8log =2⨯3=6 bit因此,信息速率为 6⨯1000=6000 bit/s2。
3 掷一对无偏骰子,告诉你得到的总的点数为:(a ) 7; (b) 12。
问各得到多少信息量.解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1})(a p =366=61得到的信息量 =)(1loga p =6log =2。
585 bit (2) 可能的唯一,为 {6,6})(b p =361得到的信息量=)(1logb p =36log =5。
17 bit2.4 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a ) )(a p =!521信息量=)(1loga p =!52log =225.58 bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C =13。
208 bit2.9随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。
解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立,则1x X =,21x x Y +=,321x x x Z ++=)|(Y Z H =)(3x H =log 6=2.585 bit )|(X Z H =)(32x x H +=)(Y H=2⨯(361log 36+362log 18+363log 12+364log 9+365log 536)+366log 6 =3。
信息论与编码考试题(附答案版)

1.按发出符号之间的关系来分,信源可以分为(有记忆信源)和(无记忆信源)2.连续信源的熵是(无穷大),不再具有熵的物理含义。
3.对于有记忆离散序列信源,需引入(条件熵)描述信源发出的符号序列内各个符号之间的统计关联特性3.连续信源X,平均功率被限定为P时,符合(正态)分布才具有最大熵,最大熵是(1/2ln(2 ⅇ 2))。
4.数据处理过程中信息具有(不增性)。
5.信源冗余度产生的原因包括(信源符号之间的相关性)和(信源符号分布的不均匀性)。
6.单符号连续信道的信道容量取决于(信噪比)。
7.香农信息极限的含义是(当带宽不受限制时,传送1bit信息,信噪比最低只需-1.6ch3)。
8.对于无失真信源编码,平均码长越小,说明压缩效率(越高)。
9.对于限失真信源编码,保证D的前提下,尽量减少(R(D))。
10.立即码指的是(接收端收到一个完整的码字后可立即译码)。
11.算术编码是(非)分组码。
12.游程编码是(无)失真信源编码。
13.线性分组码的(校验矩阵)就是该码空间的对偶空间的生成矩阵。
14.若(n,k)线性分组码为MDC码,那么它的最小码距为(n-k+1)。
15.完备码的特点是(围绕2k个码字、汉明矩d=[(d min-1)/2]的球都是不相交的每一个接受吗字都落在这些球中之一,因此接收码离发码的距离至多为t,这时所有重量≤t的差错图案都能用最佳译码器得到纠正,而所有重量≤t+1的差错图案都不能纠正)。
16.卷积码的自由距离决定了其(检错和纠错能力)。
(对)1、信息是指各个事物运动的状态及状态变化的方式。
(对)2、信息就是信息,既不是物质也不是能量。
(错)3、马尔可夫信源是离散无记忆信源。
(错)4、不可约的马尔可夫链一定是遍历的。
(对)5、单符号连续信源的绝对熵为无穷大。
(错)6、序列信源的极限熵是这样定义的:H(X)=H(XL|X1,X2,…,XL-1)。
(对)7、平均互信息量I(X;Y)是接收端所获取的关于发送端信源X的信息量。
信息论与编码习题参考答案(全)
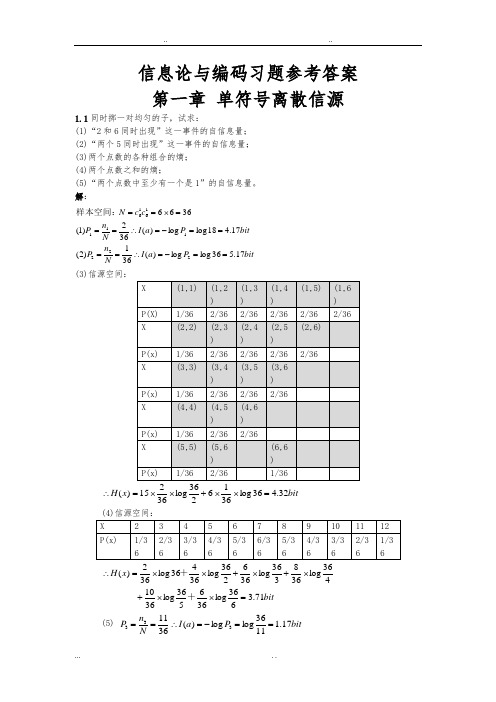
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ (4)信源空间: bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
(完整word版)答案~信息论与编码练习(word文档良心出品)

1、有一个二元对称信道,其信道矩阵如下图所示。
设该信道以1500个二元符号/秒的速度传输输入符号。
现有一消息序列共有14000个二元符号,并设在这消息中P(0)=P(1)=1/2。
问从信息传输的角度来考虑,10秒钟内能否将这消息序列无失真地传送完?解答:消息是一个二元序列,且为等概率分布,即P(0)=P(1)=1/2,故信源的熵为H(X)=1(bit/symbol)。
则该消息序列含有的信息量=14000(bit/symbol)。
下面计算该二元对称信道能传输的最大的信息传输速率: 信道传递矩阵为:信道容量(最大信息传输率)为:C=1-H(P)=1-H(0.98)≈0.8586bit/symbol得最大信息传输速率为:Rt ≈1500符号/秒× 0.8586比特/符号 ≈1287.9比特/秒 ≈1.288×103比特/秒此信道10秒钟内能无失真传输得最大信息量=10× Rt ≈ 1.288×104比特 可见,此信道10秒内能无失真传输得最大信息量小于这消息序列所含有的信息量,故从信息传输的角度来考虑,不可能在10秒钟内将这消息无失真的传送完。
2、若已知信道输入分布为等概率分布,且有如下两个信道,其转移概率矩阵分别为:试求这两个信道的信道容量,并问这两个信道是否有噪声?3 、已知随即变量X 和Y 的联合分布如下所示:01100.980.020.020.98P ⎡⎤=⎢⎥⎣⎦111122221111222212111122221111222200000000000000000000000000000000P P ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11222211122222log 4(00)1/()log 42/log 8(000000)2/(),H bit symbol H X bit symbol C C H bit symbol H X C =-===>=-==1解答:(1)由信道1的信道矩阵可知为对称信道故C 有熵损失,有噪声。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、有一个二元对称信道,其信道矩阵如下图所示。
设该信道以1500个二元符号/秒的速度传输输入符号。
现有一消息序列共有14000个二元符号,并设在这消息中P(0)=P(1)=1/2。
问从信息传输的角度来考虑,10秒钟内能否将这消息序列无失真地传送完?解答:消息是一个二元序列,且为等概率分布,即P(0)=P(1)=1/2,故信源的熵为H(X)=1(bit/symbol)。
则该消息序列含有的信息量=14000(bit/symbol)。
下面计算该二元对称信道能传输的最大的信息传输速率: 信道传递矩阵为:信道容量(最大信息传输率)为:C=1-H(P)=1-H(0.98)≈0.8586bit/symbol得最大信息传输速率为:Rt ≈1500符号/秒× 0.8586比特/符号 ≈1287.9比特/秒 ≈1.288×103比特/秒此信道10秒钟内能无失真传输得最大信息量=10× Rt ≈ 1.288×104比特 可见,此信道10秒内能无失真传输得最大信息量小于这消息序列所含有的信息量,故从信息传输的角度来考虑,不可能在10秒钟内将这消息无失真的传送完。
2、若已知信道输入分布为等概率分布,且有如下两个信道,其转移概率矩阵分别为:试求这两个信道的信道容量,并问这两个信道是否有噪声?3 、已知随即变量X 和Y 的联合分布如下所示:01100.980.020.020.98P ⎡⎤=⎢⎥⎣⎦111122221111222212111122221111222200000000000000000000000000000000P P ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11222211122222log 4(00)1/()log 42/log 8(000000)2/(),H bit symbol H X bit symbol C C H bit symbol H X C =-===>=-==1解答:(1)由信道1的信道矩阵可知为对称信道故C 有熵损失,有噪声。
(2)为对称信道,输入为等概率分布时达到信道容量无噪声0 1 01/83/81 3/8 1/8试计算:H (X )、H (Y )、H (XY )、H (X/Y )、H (Y/X )、I (X ;Y ) 解:(1) H X ()1:= H Y ()1:= (2)(3) H (X/Y )= H (XY )-- H (Y )=1.811-1=0.811 (4) H (Y/X )= H (XY )-- H (X )=1.811-1=0.811 (5)4、 有一个可以旋转的圆盘,盘面上被均匀的分成38份,用1,2,3,……,38数字标示,其中有2份涂绿色,18份涂黑色,圆盘停转后,盘面上指针指向某一数字和颜色。
(1)若仅对颜色感兴趣,计算平均不确定度;(2)若对颜色和数字都感兴趣,计算平均不确定度; (3)如果颜色已知,计算条件熵。
解:(1) H(色)=(2) P(色数)=H(色数)=(3) H(数/色)= H(色数)- H(色)=5、 在一个二进制信道中,信源消息集X={0,1},且P(0)=P(1),信宿的消息集Y={0,1},信道传输概率P (1/2)=1/4, P(0/1)=1/8。
求:(1)在接收端收到y=0后,所提供的关于传输消息X 的平均条件互信息量I(X ;y=0). (2) 该情况所能提供的平均互信息量I(X;Y). 解:(1)P(ij)= P(i/j)=(2) 方法1:=6 某一无记忆信源的符号集为{0,1},已知p0=1/4, p1=3/4 (1)求符号的平均熵(2)由100个符号构成的序列,求某一特定序列(例如有m 个“0”和(100-m )个“1”))的自信息量的表达式。
(3)计算(2)中的序列的熵。
YX解:(1) H(X)=(2) =(3)7、 一阶马氏链信源有三个符号{u1,u2,u3},转移概率为:P(u1/u2)=1/2, P(u2/u2)=1/2, P(u3/u1)=0, P(u1/u2)=1/3, P(u2/u2)=0, P(u3/u2)=2/3,P(u1/u3)=1/3, P(u2/u3)=2/3, P(u3/u3)=0, 画出状态图并求出各符号稳定概率。
解:P(j/i)= 解方程组 求得W=8、 设有一信源,它在开始时以p(a)=0.6,p(b)=0.3,p(c)=0.1的概率发出X1,如果X1为a 时则X2为a,b,c 的概率为1/3;如果X1为b 时则X2为a,b,c 的概率为1/3;如果X1为c 时则X2为a,b 的概率为1/2,而为c 的概率是0;而且后面发出X i 的概率只与 X i-1有关。
又p(X i / X i-1)=p(X2/ X1),i ≥3。
试利用马儿可夫信源的图示法画出状态转移图,并求出状态转移矩阵和信源熵H ∞S1 S2 S3 1/3 1/2 1/2 2/31/3 2/3P(j/i)=解方程组得到W1= , W2= , W3=9 某信源符号有8个符号{u1,…u8},概率分别是1/2,1/4,1/8.,1/16,1/32,1/64,1/128,1/128,编成这样的码:000,001,010,011,100,101,110,111。
求(1)信源的符号熵H(U)(2)出现一个“1”或一个“0”的概率;(3)这样码的编码效率;(4)相应的香农码和费诺玛;(5)该码的编码效率?解:(1) 12141811613216411281128H(U)=1 2Log2()14Log4()+18Log8()+116Log16()+132Log32()+164Log64()+1128Log128()+1128Log128()+ 1.984=(2) 每个信源使用3个二进制符号,出现0的次数为出现1的次数为P(0)=P(1)=(3)(4) 相应的香农编码信源符号xi 符号概率pi累加概率Pi-Logp(xi) 码长Ki 码字x1 1/2 0 1 1 0x2 1/4 0.5 2 2 10x3 1/8 0.75 3 3 110x4 1/16 0.875 4 4 1110x5 1/32 0.938 5 5 11110x6 1/64 0.969 6 6 111110 x7 1/128 0.984 7 7 1111110 x8 1/128 0.992 7 7 11111110 相应的费诺码信源符号xi 符号概率pi第一次分组第二次分组第三次分组第四次分组第五次分组第六次分组第七次分组二元码x1 1/2 0 0x2 1/41 0 10x3 1/81 0 110x4 1/161 0 1110x5 1/321 0 11110x6 1/641 0 111110x7 1/1281 0 1111110x8 1/128 1 11111110 (5)香农码和费诺码相同平均码长为编码效率为:10 已知符号集{x1,x2,x3,…}为无限离散集合,他们出现的概率分别是p(x1)=1/2,p(x2)=1/4,p(x3)=1/8,p(xi)=1/2i ,…。
(1)用香农编码方法写出各个符号的码字;(2)计算码字的平均信息传输率。
(3)计算信源编码效率。
3 解:(1) p i=累加概率为 P i=累加概率分别为符号x1 x1 x2 x3 x4 x5 x6 x7 …概率1/2 1/4 1/8 1/16 1/32 1/64 1/128 1/256 …累加概率0 0.5 0.75 0.875 0.938 0.969 0.984 0.992 …码长 1 2 3 4 5 6 7 8二元码0 10 110 1110 11110 111110 1111110 11111110 …(2)信源的信息量为平均码长为:码字的平均信息传输率为 R =bit/码(3)编码效率R =100% 11该二进制对称信道的概率转移矩阵为⎪⎪⎭⎫⎝⎛3/23/13/13/2,(1)若p(x0)=3/4,p(x1)=1/4,求H(X),H(X/Y),H(Y/X)和I(X;Y)。
(2)求该信道的信道容量及其达到信道容量时的输入概率分布。
12、某信源发送端有2个符号,xi,i=1,2,p(xi)=a,每秒发出一个符号。
接收端有3种符号yj,j=1,2,3,转移概率矩阵如下:⎪⎪⎭⎫ ⎝⎛=4/14/12/102/12/1p(1)计算接收端的平均不确定度;(2)计算由于噪声产生的不确定度H(Y/X);(3) 计算信道容量解:(1)接收端的不确定度为:(2)H(Y/X)==(3)=0得到得13 发送端有3种等概率符号(x1,x2,x3),p(xi)=1/3,接收端收到3种符号(y1,y2,y3),信道转移概率矩阵如下:(1)求接收端收到一个符号后得到的信息量H(Y);(2)计算噪声熵H(Y/X);(3)计算当接收到端收到一个符号y2的错误率;(4)计算从接收端看的平均错误率;(5)计算从发送端看的平均错误率;(6)从转移矩阵中你能看出信道的好坏吗:(7)计算发送端的H(X)和H(X/Y)。
解:(1)条件概率,联合概率,后验概率p y0 ()13:=,p y1()12:=,p y2()16:=(2)H(Y/X)=(3)当接收为y2,发为x1时正确,如果发的是x1和x3为错误,各自的概率为:P(x1/y2)=15,P(x2/y2)=15,P(x3/y2)=35其中错误概率为:Pe=P(x1/y2)+P(x3/y2)=1535+0.8=(4)平均错误概率为(5)仍为0.733(6)此信道不好原因是信源等概率分布,从转移信道来看正确发送的概率x1-y1的概率0.5有一半失真 x2-y2的概率0.3有失真严重 x3-y3的概率0 完全失真(7)H(X/Y)=1 6Log2()110Log5()+115Log52⎛⎝⎫⎪⎭+215Log52⎛⎝⎫⎪⎭+110Log5()+110Log53⎛⎝⎫⎪⎭+130Log10()+310Log53⎛⎝⎫⎪⎭+ 1.301=14、设离散无记忆信道的输入符号集X:{0,1},输出符号集Y:{0,1,2},信道矩阵为P=若某信源输出两个等该消息x1,x2,现在用信道输入符号集对x1,x2进行编码,W1=00,W2=11代表x1,x2。
按最大似然准则写出译码函数,并求出最小平均错误译码概率P emin。
解:(1) 选择译码函数 F(b1)=F(b2)=F(b3)=F(b4)=F(b7)=x1F(b5)=F(b6)=F(b8)=F(b9)=x2(1)。
