关于油藏的相渗曲线的以及含水饱和度曲线交点求法
计算相渗曲线的新方法_甲型水驱曲线法

的, 在此表示感谢。
参考文献
1 蒋明 利用水驱特征曲线计算相对渗透率曲线 新疆石油地
质, 1999, 20( 5) 2 秦同洛等 实用油藏工程方法 北京: 石油工业出版社, 1992 3 陈元千 实用油气藏工程方法 东营: 石油大学出版社, 1998 4 胡建国等 应用典型曲线拟合方法进行水驱曲线分析 石油
Q w 和累积产油量 Q o 与之对应, 所以对应数个时
间段, 就有数组 Q w 和 Q o 与之对应。将这数组 Q w 和 Q o 代入式( 1) , 应用最小二乘法, 可以求出 a1、 b1 的值, 然后将其代入式( 3) 、( 4) 求出 a、b 值。
38
1. 2
求
A
、B
、C
、KK
ro rw
、S
1 公式推导
1 1 求 a、b 值
甲型水驱特征曲线为:
lg Qw = a 1 + b1 Q o
( 1)
乙型水驱特征曲线为:
lg R wo = a + bQo
( 2)
据文献[ 2] :
a = a1 + lg ( 2. 303b1)
( 3)
因甲、乙型水驱特征曲线斜率相等, 故
b = b1
( 4)
对于每一 个时 间段, 都 有一 组累 积产 水量
断
块
油
气
田
第 8 卷第 1 期
3 结论
a) 应用甲型特征曲线时, 要依据直线段出现 后的数据计算 a、b 值, 且甲、乙型曲线斜率相对 平行时结果才可靠, 否则波动较大。
b) 对实验室测过油水相对渗透率曲线的油 田来说, 可以用本方法计算实际油水相对渗透率 曲线, 从而与实验室结果对比, 相互验证。
计算油藏相渗曲线的新方法及应用

对 于一 个特定 的油 藏 , A、 B为 常数 , 故 y、 X 呈
1 相渗 曲线 的公 式 推 导
1 . 1 确定油水相对渗透率比值与含水饱和度的关 系
线 性关 系 , 根 据生 产动 态数 据对其 进行 线性拟 合 , 可 确定 出 A、 B 的值 , 最终可求解出 口 、 b ; 将a 、 b代 人 ( 3 ) 式 可 以确定 与不 同含水 饱 和 度 下 油水 两 相 相 对 渗透率 比值 。
收 稿 日期 : 2 0 1 2—0 9—2 0
作者简介 : 黄祥 峰 , 1 9 8 5年 生 , 在读研 究生 , 主 要 从 事 油 藏 开 发 方 面 的 学 习 和研 究 。
・5 4・
石
油
地
质
与
工
程
2 0 1 3年
第1 期
K r o — K r o ( S ( } 三
2 0 1 3年 1月
石 油 地 质 与 工 程 P E T R O L E UM G E O L O GY A N D E N G I NE E R I N G
第2 7卷
第 1 期
文 章编 号 : 1 6 7 3 —8 2 1 7 ( 2 0 1 3 ) 0 1 —0 0 5 3 —0 3
R 一 妾
由( 4 ) 、 ( 5 ) 推导 出 :
w
㈣
( 6 )
相 对 渗透率 资料 无法 真实 代表 油藏 的平 均相对 渗透 率 。 目前研 究相 对渗 透率 比较 常用 的方法 主要 有利 用 测 井资料 估 算 、 毛管压力 曲线计算 、 水 驱 曲线 计
i n ( 旦 ) +l n ( 一1 ) 一一b ( 1 一S i ) R+l n 口 一b S
油藏综合相渗曲线拟合方法

中 图 分 类 号 :E 1 T 32 文献标识码 : A
油 气 藏评 价 与开 发
第1 第3 卷 期
R S R I V L A I N ND DE E OP NT E E VO R E A U T O A V L ME 2 年 6 0 1 1 月
油藏综合相渗 曲线拟合方法
戴胜群 , 付波 , 洪秀娥 , 尹太举 , 包勤永 。
(. 1 长江大学地球科学学院 3 G研究组 , R 湖北 荆州 4 4 2 ; 3 0 3 2长江大学油气资源与勘探技术教育部重点实验室 , . 湖北 荆州 44 2) 3 0 3
摘 要: 多孔介质 中存在、 岩石结构、 流体饱和 顺序等 因素影响。岩心 室内试验得到
f. mann 1Re iigRe o reRe erh G op, olg fGe sin e ,Y n teU iest, iz o , b i 3 0 3 C ia 2 M O Ke s uc s ac r u C le eo oce e s a gz n vri Jn h u Hu e 4 4 2 , hn ; . E y y
L brtyo Ol G s eore n E poa o eh iu, a g eU i ri , izo. bi 3 0 3 C ia a oa r f i& a sucs d x l tnT cnq e Yn t nv st J h u Hu e 44 2 , hn) o R a ri z e y n
由相渗曲线推导含水与含水上升率关系公式

由相渗曲线推导含水与含水上升率关系公式1.根据油水两相渗流的达西定律,在不考虑毛管力和重力的情况下,含水率的公式为rwroo w w k k f •+=μμ11(1)得到:wow w rw ro f f k k μμ•-=1 (2)根据:w bs rwroae k k -= (3)那么: wow w bs rw ro f f ae k k w μμ•-==-1 从而:⎪⎪⎭⎫ ⎝⎛-•-=ww w ow f f a b s 1ln 1μμ (4)求导得:()w w w w f f b df ds -=111 (5) 所以: ()w w ww f bf ds df -=1 (6)2.由 ()()wc o w oi s B s B R ---=111 (7)求导:owc o oiw s B B ds dR -=11(8) 所以:()wc oio w s B BdR ds -=1 (9) 3.由式(6)和式(9)()()oiwc o w w w w w w B s B f bf dR ds ds df dR df -•-=•=11 所以,得出含水上升率与含水率的关系为()()w w oiwc o w f f B s B b dR df --=11 (10) 注水开发油田B oi ≈B o 则式(10)可化简为:()()w w wc wf f s b dRdf --=11 (11) 含水率与采出程度关系式推导由(7)式()()()()()()wc wc w wc w wc o w oi s s s s s s B s B R --=---≈---=1111111 (12) 得出()wc wc w s R s s +-=1 (13)则由(4)知 ()wc wc w w w o w s R s f f a b s +-=⎪⎪⎭⎫⎝⎛-•-=11ln 1μμ (14) 所以 ()[]wc wc s R s b oww e a f +--+=111μμ (15)式中:B oi 、B o ---------分别为原始和任一压力下的原油体积系数; K ro 、k rw ---------油、水的相对渗透率; f w ----------------含水率,小数或百分数; s wc --------------束缚水饱和度,小数或百分数; s w --------------含水饱和度,小数或百分数;μo 、μw -------地下油、水粘度,MP a ·s ; R ----------------采出程度,小数或百分数;备注:按《油藏工程基础》(郎兆新主编)第243页内容定义定义无因次采油指数和无因次采液指数为有因次的采油采液指数除以油藏初始时刻无水采油期的采油指数,其值应该等于产油量或产液量除以初始时刻的产油量。
关于油藏的相渗曲线的以及含水饱和度曲线交点求法
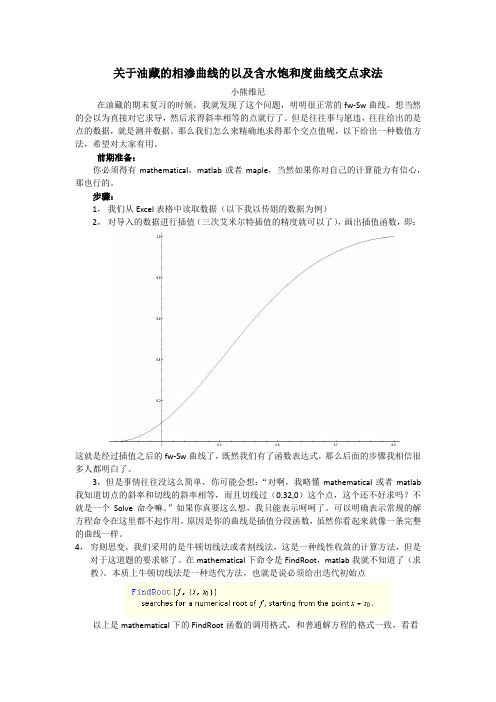
关于油藏的相渗曲线的以及含水饱和度曲线交点求法小熊维尼在油藏的期末复习的时候,我就发现了这个问题,明明很正常的fw-Sw曲线,想当然的会以为直接对它求导,然后求得斜率相等的点就行了。
但是往往事与愿违,往往给出的是点的数据,就是测井数据。
那么我们怎么来精确地求得那个交点值呢,以下给出一种数值方法,希望对大家有用。
前期准备:你必须得有mathematical,matlab或者maple,当然如果你对自己的计算能力有信心,那也行的。
步骤:1,我们从Excel表格中读取数据(以下我以传姐的数据为例)2,对导入的数据进行插值(三次艾米尔特插值的精度就可以了),画出插值函数,即:这就是经过插值之后的fw-Sw曲线了,既然我们有了函数表达式,那么后面的步骤我相信很多人都明白了。
3,但是事情往往没这么简单,你可能会想:“对啊,我略懂mathematical或者matlab 我知道切点的斜率和切线的斜率相等,而且切线过(0.32,0)这个点,这个还不好求吗?不就是一个Solve命令嘛。
”如果你真要这么想,我只能表示呵呵了。
可以明确表示常规的解方程命令在这里都不起作用。
原因是你的曲线是插值分段函数,虽然你看起来就像一条完整的曲线一样。
4,穷则思变,我们采用的是牛顿切线法或者割线法,这是一种线性收敛的计算方法,但是对于这道题的要求够了。
在mathematical下命令是FindRoot,matlab我就不知道了(求教)。
本质上牛顿切线法是一种迭代方法,也就是说必须给出迭代初始点以上是mathematical下的FindRoot函数的调用格式,和普通解方程的格式一致,看看下面的例子就明白了5,通过这样的方法我们就可以得到交点的x数值了带入插值函数(就是上面的函数可以求得y值了。
这样就可以把切线完美的表达出来了(两个点了)。
如下图:以下是传姐同学的数据,大家可以先仿照做一遍,看看自己做对没有:。
油藏工程常用计算方法

油藏工程常用计算方法油藏工程是石油工程中的一个重要领域,涉及到油藏的勘探、开发和生产等方面。
在油藏工程中,常常需要进行一系列的计算来评估和分析油藏的性质和行为。
下面将介绍一些油藏工程常用的计算方法。
1.计算原油储量原油储量是评估一个油藏的重要参数,常用的计算方法有静态法和动态法。
静态法通过测井数据和油藏地质模型,计算储量的地质体积。
动态法则通过考虑地层渗流和流体流动的动态特性,计算储量的产油体积。
2.计算油藏含水饱和度油藏的含水饱和度是指油藏中含有的水的比例。
常用的计算方法有电测井测井曲线分析法和测井资料解释法。
通过分析不同测井曲线(如电阻率曲线、自然伽玛曲线等)的变化规律,可以计算油藏的含水饱和度。
3.计算油藏渗透率油藏渗透率是衡量油藏储层导流能力的重要指标。
常用的计算方法有试油法和渗透率曲线法。
试油法通过实验室试验或现场试油,测量岩心样品或井中液体在单位时间内通过单位面积的流量,计算渗透率。
渗透率曲线法则通过测井曲线分析,利用渗透率曲线的特征,计算渗透率。
4.计算油藏压力与产量关系油藏的压力与产量关系是研究和预测油藏开发效果的重要依据。
常用的计算方法有压力-产量分析和产能预测法。
压力-产量分析通过分析油藏生产数据和压力变化,建立压力与产量的关系。
产能预测法则通过考虑岩石物性和流体性质等因素,结合油藏地质特征和开发方案,预测不同开发阶段的产能。
5.计算水驱油效果水驱是油藏开发中常用的一种增产方法。
计算水驱油效果是评估水驱效果的重要手段。
常用的计算方法有位移效率法和水驱指数法。
位移效率法通过考虑水驱后的产量与无水驱时的产量之比,计算水驱效果。
水驱指数法则通过测量水驱前后的注水压力和油井生产的工况参数,计算水驱指数。
以上介绍了一些油藏工程中常用的计算方法,涉及到油藏储量、含水饱和度、渗透率、压力与产量关系和水驱油效果等方面。
这些计算方法在油藏工程的勘探、开发和生产中具有重要的应用价值,能够帮助工程师和研究人员更好地了解和评估油藏的性质和行为。
低渗透油藏相渗曲线特征规律研究

低渗透油藏相渗曲线特征规律研究作者:孙永杰来源:《中国化工贸易·中旬刊》2018年第08期摘要:低渗特低渗油田的开发在我国石油生产中占有举足轻重的地位。
研究了太53区块储层的润湿性,对相对渗透率曲线进行了归一化处理,分析相渗曲线特征;认为低渗透储层受储层、流体特征的影响,两相共渗区较窄;随含水饱和度的上升,油相相对渗透率急剧下降,水相相对渗透率上升较快;同时水驱油效率较高。
关键词:低渗透油藏;相对渗透率曲线;归一化;渗流规律相对渗透率曲线是油藏工程研究中的一项重要的基础资料,它反映了油层内天然或人工水驱采油时,油水通过岩石孔隙的流动能力及其渗流阻力的变化规律,是反映一个油藏内部流体渗流特性的基本参数,储层岩石润湿性与相渗曲线的特征值具有一定相关性,油藏相对渗透率曲线等渗点处的含水饱和度大于50%,表现出亲水储层的特征,反之则表现出亲油的特征。
低渗透储层的油水相对渗透率曲线的特征及影响因素,与常规渗透率油藏的相渗曲线存在一定差异,是认识、分析低渗透储層油、水两相渗流机理的重要方法,可以为有效地开发油田提供理论基础。
本文通过室内试验测定了低渗透油藏岩心相对渗透率,分析了其相渗特征。
1 实验基本情况实验岩心取自太29、太43、太47三口井,共3个样本。
实验温度为70℃,采用非稳态法,按SY5345-1999《油水相对渗透率测定方法》测试标准进行。
实验岩芯样品长度为5.82~5.98cm,直径约2.5cm,孔隙度8.04%~12.6%,空气渗透率1.6~13.6×10-3μm2,物性差别不大。
分析3个样品实验数据可以看出,随着岩心渗透率增大,驱油效率、共渗区呈上升趋势,而束缚水、残余油饱和度呈下降趋势,说明试验结果的一致性较好。
2 相渗曲线归一化处理对油水两相相对渗透率的计算,国内水驱砂岩油田广泛采用相关经验公式。
根据测试的油水两相的相对渗透率曲线数据,由线性回归法,得到油田的相渗曲线和含水与饱和度关系曲线。
相渗曲线及其应用..

Sw
S
* w
Krw Sw
1 Swi Sor S wi
K
* rw
S
* w
K rw
S or
Kro Sw
K
* ro
S
* w
K ro
S wi
(8)根据上式的计算结果,绘制油藏的平均油水相对渗 透率曲线。
3、利用公式拟合相对渗透率方法
K
* ro
S
* w
K ro S w K ro S wi
K ro
Sw
(4)根据下列公式求取回归系数a、b。
K
* rw
S
* w
a
K
* ro
1
S
* w
b
lg
K
* rw
a lg
S
* w
lg
S
* w
Sw S wi 1 S wi Sor
S w S wi S w max S wi
K
* ro
S
* w
K ro S w K ro max
K
* rw
S
* w
K rw S w K rw max
(3)在标准化曲线上,将横坐标从0到1划分为n等分, 求取各分点处Sw*、各样品的Kro*(Sw*)和Krw*(Sw*),从而 作出平均的标准化相对渗透率曲线。
n
Swi i
n
Swmax i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于油藏的相渗曲线的以及含水饱和度曲线交点求法
小熊维尼
在油藏的期末复习的时候,我就发现了这个问题,明明很正常的fw-Sw曲线,想当然的会以为直接对它求导,然后求得斜率相等的点就行了。
但是往往事与愿违,往往给出的是点的数据,就是测井数据。
那么我们怎么来精确地求得那个交点值呢,以下给出一种数值方法,希望对大家有用。
前期准备:
你必须得有mathematical,matlab或者maple,当然如果你对自己的计算能力有信心,那也行的。
步骤:
1,我们从Excel表格中读取数据(以下我以传姐的数据为例)
2,对导入的数据进行插值(三次艾米尔特插值的精度就可以了),画出插值函数,即:
这就是经过插值之后的fw-Sw曲线了,既然我们有了函数表达式,那么后面的步骤我相信很多人都明白了。
3,但是事情往往没这么简单,你可能会想:“对啊,我略懂mathematical或者matlab 我知道切点的斜率和切线的斜率相等,而且切线过(0.32,0)这个点,这个还不好求吗?不就是一个Solve命令嘛。
”如果你真要这么想,我只能表示呵呵了。
可以明确表示常规的解方程命令在这里都不起作用。
原因是你的曲线是插值分段函数,虽然你看起来就像一条完整的曲线一样。
4,穷则思变,我们采用的是牛顿切线法或者割线法,这是一种线性收敛的计算方法,但是对于这道题的要求够了。
在mathematical下命令是FindRoot,matlab我就不知道了(求教)。
本质上牛顿切线法是一种迭代方法,也就是说必须给出迭代初始点
以上是mathematical下的FindRoot函数的调用格式,和普通解方程的格式一致,看看
下面的例子就明白了
5,通过这样的方法我们就可以得到交点的x数值了带入插值函数(就是上面的函数可以求得y值了。
这样就可以把切线完美的表达出来了(两个点了)。
如下图:
以下是传姐同学的数据,大家可以先仿照做一遍,看看自己做对没有:。
