八年级数学上册1421平方差公式导学案新版新人教版.doc
新人教版八年级数学上册《平方差公式》导学案2
ab新人教版八年级数学上册《平方差公式》导学案科目 数学 课题 14.2.1平方差公式授课时间 主备人课型新授课班级学生姓名学习目标 1、理解平方差公式，能运用公式进行计算；2、经历探索平方差公式的过程，进而感受特殊到一般、数形结合思想，发展学生的符号意识和几何直观观念。
学习重点 平方差公式学习难点平方差公式的灵活运用一、知识回顾多项式与多项式的乘法法则是什么？二、自主探究1、 计算下列多项式的积2、观察算式结构，你发现了什么规律？计算结果后，你又发现了什么规律？ ①算式中每个因式都是 项.②算式都是两个数的 与 的 . 即两个因式中，有一项 ，另一项 。
计算结果后，你又发现了什么规律？计算结果都是前项的 减去后项的 差。
3、我们再计算： （a+b ）（a －b ）= =4、得出：()()=-+b a b a 。
其中a 、b 表示任意数，也可以表示任意的单项 式、多项式，这个公式叫做整式乘法的 公式，用语言叙述为 。
5、做一做：如图，边长为a 的大正方形中有一个边长为b 的小正方形。
（1）请表示图中阴影部分的面积：S =（2）小颖将阴影部分拼成了一个长方形，这个长方形的长和宽分别是多少？ 你能表示出它的面积吗？长＝ 宽＝ S = （3）比较1，2的结果，你能验证平方差公式吗?∴ ＝ 三、例题精析1、判断下列式子是否可用平方差公式 ：(1) (-a+b)(a+b) (2) (-2a+b)(-2a-b) (3) (-a+b)(a-b) (4) (a+b)(a-c) 2、下面各式的计算对不对？如不对，应怎样改正？3、参照平方差公式“（a+b ）（a －b ）= a 2－b 2”填空：(1)(t+s)(t-s)= (2)(3m+2n)(3m-2n)=ab(3)(1+n)(1-n)= (4)(10+5)(10-5)＝ 总结：（1）平方差公式的特征：①公式左边是两个二项式相乘，并且两个二项式中有一项完全 相同，另一项互为相反数。
人教版八年级数学上册14.2.1平方差公式导学案
人教版义务教育课程标准实验教科书八年级上册14.2.1《平方差公式》导学案一、学习目标1.会推导平方差公式，并能运用公式进行简单的运算．2.培养学生观察、归纳、概括的能力．3.在探索平方差公式的过程中，培养符号感和推理能力．4.在计算过程中发现规律，并能用符号表示，从而体会数学的简捷美二、预习内容阅读课本P107 ～108 页，思考下列问题：1、平方差公式的内容是什么？2、 计算下列多项式的积，你能发现什么规律？（1）、（a+5）(b-2)= （2）、(x-3)(x+5)=（3）、(x+2)(x-2)= （4）、(2x+y)(2x-y)=3、课本P108页例1例2你能独立解答吗？三、探究学习1、趣味思考：有一个边长为a(a ﹥1)米的正方形，现在将其中一组对边增加5米，另一组对边减少5米，形成一个长方形。
请想一想：这时面积是增大，减小，还是不变。
2、几何验证：（1）请表示图(1)中阴影部分的面积.（2）将阴影部分拼成了一个长方形（图2），这个长方形的长和宽分别是多少？你能表示出它的面积吗？（3）比较前两问的结果，你有什么发现? ab bb a b -a b a b -ab四、巩固测评1、口答下列各题：(l)(-a+b)(a+b)=_________(2)(a-b)(b+a)= __________(3)(-a-b)(-a+b)=________(4)(a-b)(-a-b)=2、应用平方差公式计算。
1、(a＋3b) (a－3b)2、(3+2a) (-3+2a)3、(-2＋x) (-2－x)4、51×495、(－2x2－y)(－2x2+y)6、(3x+4)(3x-4)-(2x+3)(3x-2)3、[想一想]下列两个多项式相乘，哪些可以用平方差公式？哪些不能用？(1)(2x-3y)(3y-2x)(2)(-2x+3y)(2x+3y)(3)(2x-3y)(2x-3y)(4)(4)(2x+3y)(2x-3y)五、学习心得。
新人教版八年级数学上册《平方差公式》导学案
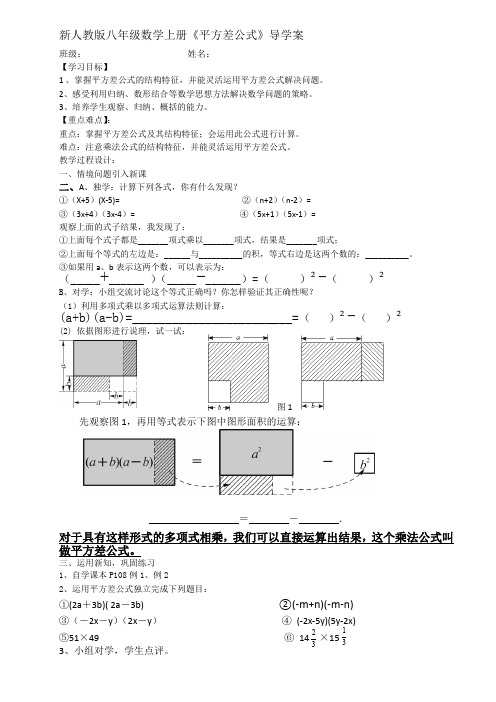
新人教版八年级数学上册《平方差公式》导学案班级： 姓名：【学习目标】1 、掌握平方差公式的结构特征，并能灵活运用平方差公式解决问题。
2、感受利用归纳、数形结合等数学思想方法解决数学问题的策略。
3、培养学生观察、归纳、概括的能力。
【重点难点】：重点：掌握平方差公式及其结构特征；会运用此公式进行计算。
难点：注意乘法公式的结构特征，并能灵活运用平方差公式。
教学过程设计：一、情境问题引入新课二、A 、独学：计算下列各式，你有什么发现？①（X+5）(X-5)= ②（n+2）（n-2）=③（3x+4）（3x-4）= ④（5x+1）（5x-1）=观察上面的式子结果，我发现了：①上面每个式子都是_______项式乘以_______项式，结果是_______项式；②上面每个等式的左边是：______与__________的积，等式右边是这两个数的：__________。
③如果用a 、b 表示这两个数，可以表示为：（_____+______ ）（_____-______）=（ ）²-（ ）²B 、对学：小组交流讨论这个等式正确吗？你怎样验证其正确性呢？（1）利用多项式乘以多项式运算法则计算：(a+b)(a-b)=________________________=（ ）²-（ ）²(2) 依据图形进行说理，试一试：先观察图1，再用等式表示下图中图形面积的运算：_________________ ＝ － ．对于具有这样形式的多项式相乘，我们可以直接运算出结果，这个乘法公式叫做平方差公式。
三、运用新知，巩固练习1、自学课本P108例1、例22、运用平方差公式独立完成下列题目：①(2a ＋3b)( 2a －3b) ②(-m+n)(-m-n)③（－2x －y ）（2x －y ） ④ (-2x-5y)(5y-2x)⑤51×49 ⑥ 14 ×15 3、小组对学，学生点评。
八年级数学上册-人教版八年级上册数学14.2.1平方差公式《平方差公式》参考学案
《平方差公式》导教案一、温故知新：（我最棒！）1．多项式乘以多项式的法例是什么？请用公式表示出来. 2．请利用多项式乘以多项式的法例计算以下各题：(1) x 1 x 2；；( 2 ) x2 y x 2y(3) x 1 x 1；；( 4 )x 3y x 3y(5) 3c d 3c d；(6) x 5y x 5 y .二、研究新知：（我能行！）察看上边 2 题中（ 3） ~（ 6）题的特点和计算结果，你有什么发现？勇敢猜想： a b a b ＝即：两个数的与这两个数的的积，等于这两个数的.这个公式叫做（乘法的）.三、思虑议论 :图 1 中长方形的面积与图 2 空白部分的面积有什么关系，经过对两个图形面积的计算能考证平方差公式吗 ?四、拓展延长：以下各式能利用平方差公式计算吗？若能，请说出哪一项相当于公式中的 a 和b ？若不可以，请说明原因 .（ 1）32a 3 2a ；（2） 3 2a 3 2a ；（3） 3 2a 3 2a .总结规律：能利用平方差公式计算的式子：符号同样的部分相当于公式中的，符号不一样的部分相当于公式中的.五、试试应用：1.下边各式的计算对不对 ?假如不对 ,请更正 .(1) x 2 x2x 22( 2 ) a322 a32 a 342．计算：（1） a3b a3b ；（2）(2 x 3 y)(2 x3y) ；（3） 100 4 100 4 ；（4）102 98.六、拓展提高：1．以下能利用平方差公式计算的是（）．A.(2m n)(2m n)B.( x3)( x2)C. (2m n)(n2m)D.( 2m n)(2 m n)2．利用平方差公式计算：(1) 34m 3 4m ；(2) 2x32x 3 ；(3)( x y)( x y) ( y 1)( y 2)3．计算：201122010 2012七、达标测试：（每题 20 分，共 120 分）1.计算（ 2a+5）（ 2a-5）的结果是（）A．4a2 -25 B ．4a2 -5C．2a2-25D．2a2-5 2.以下计算正确的选项是（）A．（x+5 ）（x-5） =x2-10B．（x+6）（x-5）=x2-30C．（3x+2）（ 3x-2）=3x2 -4D．（-5xy-2 ）（ -5xy+2） =25x2y2-43.计算（ 1-m）（-m-1）＝.4.（原创题）察看图 3 中图形的变化过程，计算此中空白图形的面积能考证的公式是.5.计算：(4 a3b)(3b 4a).6.先化简，再求值：(2 x)(2 x) x(x 4) ，此中x 2 .。
八年级数学上册《14.2.1 平方差公式》 精品导学案 新人教版
【学习目标】1．经历探索平方差公式的过程，会运用平方差公式。
2．在探索平方差公式的过程中，发展学生的符号感和推理能力。
学习重点：会运用平方差公式。
学习难点：会运用平方差公式。
【知识准备】1．单乘单法则：2．单乘多法则：3．多乘多法则：【自习自疑文】一、预习与新知（阅读教材P107-P108内容，并思考回答下列问题）1．计算下面各式（1）（x+3）(x-3) (2)(-2a-2)(2a-2)平方差公式：二、预习评估1．计算下列各题。
（1）（x+1）(x-1) (2)(a+2)(a-2)我想问：请你将预习中遇见的问题和疑问写下来，等待课堂上与同学、老师共同探究解决。
等级 组长（或家长）签字【自主探究文】【探究一】 验证平方差公式请用剪刀从边长为a 的正方形纸板上，剪下一个边长为b 的小正方形（如图1），然后拼成如图2的长方形，你能根据图中的面积说明平方差公式吗？【探究二】平方差公式的直接应用： ①（a-2b 2）(a+2b 2)② (3x+2y)(2y-3x)③(m-3n)(-m-3n)【探究三】灵活运用平方差公式2111(1)()()()242y y y -++ 2(2)201120092010⨯- (3)911101⨯⨯【探究四】a-b=10b-c=15c+a=20.a-c)(a+c)已知，，求(的值。
【自测自结文】1. 下列各式哪些可用平方差公式计算？能用的请在括号内写出结果，不能的化×. (1)(2)(2)a b b a -+ （ ）(2)(1)(2)x x ++（ ） (3)()()x y x y ---+ （ ） (4)(5)(5)a a --+（ ） (5)(23)(32)x y x y +- （ ） (6)()()a b b a --（ ）2. 直接写出结果：（1）(23)(23)x y x y +-= （2）22(51)(51)xx -+=（3）22(34)(34)b ab a +-= （4）=+-+)2)(2(b a a b（5）)(221(y x +-)22441y x -=3.利用平方差公式计算：（1）(ab+1)(-ab+1) （2）(-2xy+z)(-2xy-z)4.如果（2a+2b+1）(2a+2b-1)=63,那么a+b 的值等于多少？【自我小结】通过本节课的学习，你有哪些收获？还有哪些困惑呢？教师个人研修总结在新课改的形式下，如何激发教师的教研热情，提升教师的教研能力和学校整体的教研实效，是摆在每一个学校面前的一项重要的“校本工程”。
2019年八年级数学上册 14.2.1 平方差公式导学案(新版)新人教版.doc
2019年八年级数学上册 14.2.1 平方差公式导学案（新版）新人教版14.2.1 平方差公式1．探索平方差公式2.会推导平方差公式，并能运用公式进行简单的运算.3.在计算过程中发现规律，并能用符号表示，从而体会数学的简洁美. 学习重点：平方差公式的应用 学习难点：灵活应用平方差公式 【学前准备】 1.计算：（1）()()213x x ++ （2）()()23x x ++（3）()()23m n m n +- （4）()()x y x y -+ 【导入】【自主学习，合作交流】1.算算下面的题，写出步骤及结果，看看结果有什么规律？ （1）()()11x x +- （2）()()22m m +-（3）()()2121x x +- （4）()()55x y x y +-（5）（a –b ）（a+b ） （6）（a+b ）（a –b ）2.()()a b a b +-看看结果是什么？运用平方差公式计算：（通过自学你能学会吗？）（1）()()3232x x +-； （2）()()22b a a b +-；（3）()()22x y x y -+--.计算（注意：只有符合公式要求的乘法，才能运用公式简化运算） （1）102×98 （2）()()()()2215y y y y +----【精讲点拔】这个公式叫做（乘法的）平方差公式. （其实a 、b 可以表示任意数，也可以表示任意单项式、多项式）.（x+2y - 3）（x+2y + 3） 、（xy -1）（xy+1）思考？：你能根据图中的面积说明平方差公式吗？【本节小结】 【当堂测试】1.下面各式的计算对不对？如果不对，应怎样改正？ （1）()()2222x x x -+=- ( )（2）()()2323294a a a ---=-.( ) 2.运用平方差公式计算:（1）()()33a b a b +- （2）5149⨯（3）()()3232a a +-+ （4）()()()()34342332x x x x +--+-【课后作业】Ⅰ必做题1．计算：（1） 2001×1999 （2）（a 2+1）(a-1)(a+1)(3) (x-3)(x 2+9)(x+3) (4) (-2b-5)（2b-5）(5) (xy+1)(xy-1) (6) 998×1002Ⅱ选做题1.若()()293xx ++（ ）=481x-，则括号内应填入的代数式是（ ）A. 3x -B. 3x -C.3x +D. 9x -2．计算：（1）2233x y x y ⎛⎫⎛⎫-+ ⎪⎪⎝⎭⎝⎭（2）()()11xy xy +-【评价】【课后反思】优。
最新人教版八年级数学上册 第十四章《平方差公式》导学案
15.2.1 平方差公式学前温故多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加．新课早知1．平方差公式：(a ＋b )(a －b )＝a 2－b 2，即两数和与这两数差的积等于这两个数的平方差．2．(2x －y )(__________)＝4x 2－y 2.答案：2x ＋y3．下列各式中，不能用平方差公式的是（ ）．A ．(m －n )(－m －n )B ．(x 3－y 3)(y 3＋x 3)C ．(－m ＋n )(m －n )D ．⎝⎛⎭⎫2x －13⎝⎛⎭⎫13＋2x 答案：C1．利用平方差公式计算【例1】 计算：(1)(3x ＋2y )(2y －3x )；(2)(－2a ＋3b )(－2a －3b )．解：(1)原式＝(2y ＋3x )(2y －3x )＝4y 2－9x 2；(2)原式＝[(－2a )＋3b ][(－2a )－3b ]＝(－2a )2－(3b )2＝4a 2－9b 2.点拨：平方差公式(a ＋b )(a －b )＝a 2－b 2，是特殊形式的多项式乘法公式，它是最基本、用途最广泛的公式之一，有时题目中公式的特征并不明显，但只要给它进行适当的变形，特征就变得明显而直观．2．平方差公式的应用【例2】 计算：89×91.分析：看似无法用平方差公式，但89可写成90－1,91可写成90＋1，这样便符合公式特征．解：原式＝(90－1)(90＋1)＝902－1＝8 099.点拨：用构造平方差公式计算是快速计算某些有理数乘法的好方法．构造时，可利用两数的平均数．在解与两式(或两数)的乘积有关的问题时，只要先求出两式(或两数)的平均值，把原式写成两数和与两数差相乘的形式，便可以顺利地利用平方差公式来解决了．1．计算(x －y )(－y －x )的结果是（ ）．A ．－x 2－y 2B ．－x 2＋y 2C ．x 2－y 2D ．x 2＋y 2解析：(x －y )(－y －x )＝(－y ＋x )(－y －x )＝(－y )2－x 2＝y 2－x 2.答案：B2．能用平方差公式进行计算的是（ ）．A ．(2a －b )(b －2a )B ．(a －2b )(2a ＋b )C ．(－2a －b )(2a ＋b )D ．(－2a －b )(－2a ＋b )答案：D3．计算：(x ＋1)(x －1)＝________.答案：x 2－14．计算：111133x x ⎛⎫⎛⎫-+ ⎪⎪⎝⎭⎝⎭＝________.答案：1－1 9 x25．若m2－n2＝6，且m－n＝3，则m＋n＝________.答案：26．如图，在边长为a的正方形中剪去一个边长为b的小正方形(a＞b)，把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，以上验证了公式__________．解析：题中左图的阴影部分的面积为a2－b2，因为题中右图为梯形，梯形的高为(a－b)，所以阴影部分的面积为(2a＋2b)(a－b)÷2＝(a＋b)(a－b)．答案：(a＋b)(a－b)＝a2－b27．计算：(1)(x＋1)(x－1)＋1；(2)a(a－3)－(－a＋7)(－a－7)；(3)1122a b a b⎛⎫⎛⎫+-⎪⎪⎝⎭⎝⎭－(3a－2b)(2b＋3a)；(4)2 0122－2 011×2 013.解：(1)(x＋1)(x－1)＋1＝x2－1＋1＝x2.(2)a(a－3)－(－a＋7)(－a－7)＝a2－3a－(a2－72)＝49－3A．(3)1122a b a b⎛⎫⎛⎫+-⎪⎪⎝⎭⎝⎭－(3a－2b)(2b＋3a)＝a2－14b2－(9a2－4b2)＝－8a2＋154b2.(4)2 0122－2 011×2 013＝2 0122－(2 012－1)(2 012＋1)＝2 0122－(2 0122－12)＝2 0122－2 0122＋1＝1.。
人教版数学八年级上导学案14.2.1平方差公式
人教版数学八年级上导教案乘法公式平方差公式学目：1．能出平方差公式的特色，并会用式子表示.2．能正确地利用平方差公式行多式的乘法运算.3．通平方差公式得出的程，领会数形合的思想.学要点：掌握两数和乘以它的差的构特色.学点：正确理解两数和乘以它的差的公式的意 .学程：一、系生活,境激趣一：王林到小部去干,售告他:共千克，每千克.正当售在用算器算，王林上出了共元，售很诧异地：“你怎么比算器算的快呢？”王林很喜悦的告她：是一个奥密.同学,你能帮售揭开小林迅速口算出×的奥密?二.察归纳,探究二：1．本的学,我就能揭开一奥密了.同学算下边三道:(1)(x＋3)(x－3)；(2)(m＋5n)(m－5n)；(3)(4＋y)(4－y).2．你察思虑:以上几个多式与多式相乘的式子有什么特色?有什么特色?你能用字母表示？察：两数和乘以两数的等于两数的用一个数学等式表示:（a＋b）（a－b）＝⋯⋯平方差公式.3.个等式正确?你怎其正确性呢?⑴利用多式乘以多式算:⑵你能再用以下的形平方差公式？一.先察看图，再用等式表示以下图中图形面积的运算：＝－．拥有简短美的乘法公式:（a＋b）（a－b）＝a2－b2．三、理解运用，稳固提升问题三：1.填一填:①2x+1）（2x-1）=（）2-（）2=22②(3x+6y)(3x-6y)=()2-（）2=③(m3+5)(m3-5)=()2-（）2=2.辨一辨:(2x＋3)(2x－3)=2x2－9②(x＋y2)(x－y2)=x2－y2③(a＋b)(a－2b)=a2－b23.说一说：以下各式都能用平方差公式计算吗?①(2a－3b)(3b－2a) ②(－2a+3b)(2a+3b) ③(－2a－3b)(2a－3b)④(2a－3b)(2a+3b) ⑤(2a+3b)(－2a－3b) ⑥(2a－3b)(－3b+2a)4．做一做：（1）(a＋3)(a－3) （2）(2a＋3b)(2a－3b) （3）(1＋2c)(1－2c)（4）变式拓展:①（－2x－y）（2x－y）②(-m+n)(-m-n) ③(-2x-5y)(5y-2x)5．生活实践⑴计算：1998×2002⑵此刻你能揭开小林迅速口算出×的奥密吗?⑶街心花园有一块边长为 a米的正方形草坪，经一致规划后，南北向要加长2米，而东西向要缩短2米.问改造后的长方形草坪的面积是多少?四、实践应用，提升技术问题四：(用4分钟独立达成，看谁又快又准.)1.以下能够用两数和乘以这两数差公式计算的是（）A.（x-y）（x+y）B.（x-y）（y-x）C.（x-y）（-y+x）D.（x-y）（-x+y）2.比一比：①（5+6x）(5-6x）②（3m-2n）(3m+2n）③（ab+8）(ab-8）④（2x＋y）(－2x＋y) ⑤（－4a－）(4a＋）⑥(m+n)(m-n)+3n2⑦（-x+2）(-x－2) ⑧（－a+b）（a+b）3.请你独立达成课本P30练习，在经历训练中娴熟运用公式运算．五、总结反省________________________________________________________________.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品教案
14.2.1 平方差公式
【学习目标】： 1.会推导平方差公式，并能运用公式进行简单的运算．
2.培养学生观察、归纳、概括的能力．
3.在探索平方差公式的过程中，培养符号感和推理能力．
【学习重点】掌握平方差公式的推导和应用．
【学习难点】理解平方差公式的结构特征，灵活应用平方差公式
一 .自主学习
1.多项式与多项式相乘:多项式与多项式相乘，先用一个多项式的________乘另一个多项式的
，再把所得的积________。
符号表示：（m+b )(n+a )=-------------
2.计算⑴ (5+2)(5-2)=【__×__+__×__】+【__×__+__×〔__〕】= __- __=__
⑵(a+3) ×(a-3 )=
二.合作交流探究与展示：
1.计算下列多项式的积．
（ 1 ）（ x+1 ）（ x-1）（2）（m+2）（m-2）（3）（2x+1）（2x-1）从刚才的运算我发现：
等号的一边：
两个数的和与差的积，
等号的另一边：
是这两个数的平方差
2．提出问题：
观察上述算式，你发现什么规律？运算出结果后，你又发现什么规律？
等号的一边：两个数的和与差的积，等号的另一边：是这两个数的平方差
可编辑
得到结论：。
（文字叙述）
（ a+b ）（ a-b ）=a 2-ab+ab-b 2 =a2-b2．即（a+ b）（a-b）=a2-b 2 运用平方差公式计算
1.（ 1 ）（ 3x+2 ）（ 3x — 2）（2）（b+2a）（2a—b）（3）（—x+2y）（—x—2y）
2.用简便方法计算
（ 1 ） 102 ×98（2）（y+2）（y—2）—（y—1）（y+5）
三、当堂检测：（ 1 、2 、 3 题为必做题； 4 、5 、题为选做题）
1 、参照平方差公式“（a+b ）（ a － b） = a 2－ b 2”填空
（ 1 ） (t+s)(t-s)=(2) (3m+2n)(3m-2n)=
2 、 . ．下列哪些多项式相乘可以用平方差公式？
( 2a 3b)(2a 3b)( 2a 3b)( 2a 3b)( 2a 3b)( 2a3b)
( 2a 3b)(2a 3b)( a b c)( a b c)(a b c)( a b c)
3、用平方差公式计算：
（1 ）. (m n)(m n)（2）.( x 2 y)( x 2 y )（3）.( x 5)( x5)
（4 ） . (1
m 3n)(
1
m 3n) （5 ） . (7 x2
1
y)(7 x2
1
y) 3 3 2 2
可编辑
4 、计算2001 2 -199 9 2
5 、已知x2y28, x y 4，求x-y的值
可编辑。