定积分的应用面积,体积

合集下载

定积分的应用面积体积-2022年学习资料

例1.求由抛物线y2=2x及直线2x+y-2=0所围图形的面积。-→X-y+d---2,-2
y-=2x-2x+y-2=0-X-12-2,-2-求平面因形面积的基本步骤：-1作曲线图形、确定积分变量积分区间；-2求面积微元；-3计算定积分。
当曲边梯形的曲边由参数方程-北=pt-y=feG1ss2）,-给出时，曲边梯形的面积为-A-fudioif g&aw-其中t1,t2分别是曲边的起点与终点对应的参数值。
2.设fx、gx是[a,b]上的连续函数，且fx2gx,-求由直线x=a,r=b,和曲线y=fx、y=gx 围-成的平面图形的面积A。-dA=[f x-gxx-1y=8x-A=∫[fcx-gexr-xx+dx
3.py、yy是[c,d]上的连续函数，且py2wy,-求由直线y=C,y=d和曲线x=py、x=yy所围成的平面图形的面积A。-dA=[py-Ψ y]Wy-x=0y-x=Wy-A-ftoy-Wyldy-X
3.4.5一些物理量的计算-一、质量-例1.设半圆形线材的方程为y=VR2-x2-R<x<R,线-材上点的 x,y处的线密度为P=k-yk为常数，且k>R,-求该线材的质量。-ds-Ox x+dx R-X
二、功-例2.设一锥形贮水池，深15米，口径20米，盛满水，-试问将水全部吸出需作多少功？-10-X-Ax-B
例：求密度均匀（设为p,厚度为H,内外径为-r和R的飞轮绕中心轴转动的转动惯量J以及角速度-为o时的转动动 E.
3.4.6函数的平均值-一、函数的平均值-如何定义连续函数fx在[α ，b]上的平均值呢？-将[a,b]n等。当n很大时，小区间[；-1，x]的长-度Ax=b-u-i=1,2,Λ ，n很小，由于fxeC[a,b],在小区间[x-1,x]上函数值变化很小，可把fx在-该区间上的取值看作常数∫x,于是∫x在[a,b]上-的

考研数学定积分的应用

考研数学定积分的应用一、引言数学定积分是高等数学中的重要概念之一，它在实际生活中有着广泛的应用。

本文将从几个具体的应用案例入手，探讨考研数学定积分的应用。

二、面积计算数学定积分最基本的应用之一就是计算曲线与坐标轴所围成的面积。

例如，在工程测量中，我们经常需要计算某个区域的面积，如果该区域的边界曲线可以用函数表示，那么可以通过定积分来求解。

通过将曲线分割成无穷多个微小的矩形，计算每个矩形的面积并进行累加，最终得到所需的面积。

三、物体体积计算除了计算面积，数学定积分还可以用于计算物体的体积。

在工程设计中，经常需要计算复杂形状物体的体积，例如水库的容量、建筑物的体积等。

如果物体的截面可以用函数表示，那么可以通过定积分来求解。

同样地，将截面分割成无穷多个微小的面元，计算每个面元的体积并进行累加，最终得到所需的体积。

四、质心计算质心是物体在空间中的重心，对于复杂形状的物体，质心的计算可以通过数学定积分来实现。

首先，将物体分割成无穷多个微小的体积元，计算每个体积元的质量并与其质心坐标乘积，然后进行累加，最后将总质量除以总体积，即可得到质心的坐标。

五、弯曲杆件的弯矩计算在工程力学中，常常需要计算弯曲杆件的弯矩分布，以确定结构的稳定性和安全性。

通过数学定积分，可以将杆件分割成无穷多个微小的弯曲段，计算每个弯曲段的弯矩，并进行累加，最终得到整个杆件的弯矩分布。

六、概率密度函数计算概率密度函数是概率论与数理统计中的重要概念，用于描述随机变量的概率分布。

数学定积分可以用于计算概率密度函数的各种性质，例如求解期望值、方差以及其他统计指标。

通过对概率密度函数进行定积分，可以得到具体的数值，从而进行概率分析和决策。

七、总结本文简要介绍了考研数学定积分的几个应用，包括面积计算、物体体积计算、质心计算、弯曲杆件的弯矩计算以及概率密度函数的计算。

这些应用充分展示了数学定积分在实际生活和工程领域中的重要性和广泛应用。

通过学习和掌握数学定积分的应用技巧，可以更好地理解和应用数学知识，提高问题解决能力。

试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用1. 引言1.1 定积分的基本概念定积分是微积分的一个重要概念，它在数学中有着广泛的应用。

定积分的基本概念可以简单地理解为一个函数在一定区间内的累积效果。

在几何学中，定积分可以用来计算曲线下面积，图形的面积和体积等问题。

在数学上，定积分可以看作是不定积分的反运算，通过定积分我们可以求解函数的定积分值。

在实际应用中，定积分被广泛运用于物理、工程、经济等领域。

它的应用使得复杂问题的计算变得简单清晰。

通过定积分，我们可以计算出物体的质量、力的大小、功的大小等物理量。

在力学中，定积分可以用来描述物体的运动规律，计算出物体的位置、速度和加速度等。

在电磁学中，定积分常常用来计算电场强度、磁场强度等问题。

在热力学中，定积分可以用来计算热量、熵等热力学量。

在工程学中，定积分可以帮助工程师计算出工程设计中的各种参数。

在经济学中，定积分在求解供求关系、成本、收益等问题上起着重要作用。

定积分在各个领域中都有着重要的应用价值。

它的基本概念对于理解定积分的应用具有重要意义。

通过深入研究定积分的基本概念，可以更好地理解其在不同领域中的具体应用。

1.2 定积分在物理领域的重要性定积分在物理领域的重要性体现在多个方面，首先在力学中，定积分可以用来描述物体的质量、速度、加速度、力和能量等物理量随时间的变化，从而帮助解决力学中的各种问题。

在电磁学中，定积分可以用来描述电流、电荷、电场、磁场等物理量在空间中的分布和变化规律，从而帮助解决电磁学中的各种问题。

在热力学中，定积分可以用来描述热量、温度、熵等热力学量在空间中的分布和变化规律，从而帮助解决热力学中的各种问题。

在工程学和经济学中，定积分也有着重要的应用，可以用来描述工程和经济系统中的各种物理量的变化规律，从而帮助解决工程和经济学中的各种问题。

定积分在物理领域中的重要性不可忽视，它为我们理解和应用物理定律提供了重要的数学工具和方法。

2. 正文2.1 定积分在力学中的应用在力学中，定积分是一个非常重要的数学工具，它可以用来描述物体在运动过程中的各种性质和运动规律。

定积分的应用

定积分的应用定积分是微积分中的重要内容之一，经常被应用于实际问题的解决中。

本文将从三个方面来论述定积分的应用。

一、定积分在几何中的应用首先，定积分可以用于求曲线下面的面积。

以 y=f(x) 为例，若f(x)>0，则曲线 y=f(x) 与 x 轴的两点 a、b 组成的图形的面积为S=∫baf(x)dx这时，可以将曲线 y=f(x) 分成许多小块，每块宽度为Δx，高度为 f(xi)，从而可以得到其面积为ΔS=f(xi)Δx因此，当Δx 趋于 0 时，所有小块的面积之和就等于图形的面积，即∑ΔS→S因此，用定积分就可以求出图形的面积。

其次，定积分还可以用于求旋转体的体积。

以曲线 y=f(x) 在 x 轴上旋转360°为例，其体积为V=π∫baf(x)^2dx这里，π为圆周率。

最后，定积分还可以用于求某些奇特图形的长、面积等等。

二、定积分在物理中的应用物理中也有许多问题可以通过定积分来解决。

比如，运动问题中的速度、加速度，可以通过位移的变化来求得。

若某运动物体的速度为 v(t)，则其位移 s(t) 为s(t)=∫v(t)dt同样，若某运动物体的加速度为 a(t)，速度为 v(t)，则其位移为s(t)=∫v(t)dt=∫a(t)dt最后，定积分还可以用于求密度、质量等物理量。

三、定积分在工程中的应用定积分在工程中的应用也非常广泛。

比如，在流体力学中，对于一条管道中的液体，可以通过惯性和重力等因素，求出其中液体的流量和压力。

而这些流量和压力可以通过定积分计算得出。

在电学中，电量、电荷、电流和电势等都可以通过定积分来求解。

在结构设计中，定积分也常常被用来计算约束力、杠杆比例等。

总之，定积分在几何、物理和工程等领域中都有着广泛应用。

熟练地掌握定积分的方法和应用，对于科学研究和实际问题的解决都有着非常积极的帮助。

定积分求法

定积分求法一、定积分求法定积分是指把一段区间内的一种函数值相加以求出总和的方法。

它是微积分中的一种重要运算，可以用来解决一些微分方程的问题，也应用于电力学、力学、热学等领域。

1.求面积定积分的一个重要应用就是求一维函数在一段区间上的积分值，假定函数y=f (x)的定积分表示为∫a bf (x)dx，a、b是两个定义域，f (x)为一个定义域上的函数，这个函数的积分值可以用来表示其定义域内的面积。

2.求曲线的长度定积分也可以用来求出曲线的长度。

假设曲线由一个自变量x描绘出，那么曲线长度就等于∫a b(1+y' )^ dx，其中y'=dy/dx，同样可以利用定积分求出。

3.求体积定积分也可以用来求函数描绘的物体的体积。

假设物体的高度为z=f (x,y)，那么物体的体积就等于∫a b∫a bf (x, y) dx dy，这也是定积分的应用。

4.求重心定积分也可以用来求函数描绘的物体的重心坐标。

假设物体的重量为w=f (x,y,z)，那么物体的重心坐标就是(∫a b∫a b∫a bxf (x, y, z) dx dy dz / ∫a b∫a b∫a bw (x, y, z) dx dy dz, ∫a b∫a b∫a byf (x, y, z) dx dy dz/ ∫a b∫a b∫a bw (x, y, z) dx dy dz,∫a b∫a b∫a bzf (x, y, z) dx dy dz/ ∫a b∫a b∫a bw (x, y, z) dx dy dz)，同样也是定积分的应用之一。

二、定积分求法的两种类型定积分求法一般分为两类，一类是区间定积分，一类是积分形式定积分。

1.区间定积分所谓区间定积分，是指在一个定义域上，由两个端点定义的定义域内的函数求积分。

比如，假定函数y=f (x)在[a, b]上是定义的，求函数f (x)在[a, b]上的定积分，称为区间定积分。

2.积分形式定积分积分形式定积分是指在一个定义域上，由函数f (x)和定义域上的函数值g (x)求函数f (x)在定义域内的定积分。

定积分求体积的四个公式

定积分求体积的四个公式定积分是微积分的一个重要概念，可以用来计算曲线与坐标轴之间的面积、质量、重心等各种物理量。

在三维空间中，定积分也可以用来计算体积。

以下是四个常用的定积分求体积的公式：1. 平面图形的旋转体体积公式：假设有一个平面图形，它绕着某个轴旋转一周形成一个立体图形，那么它的体积可以通过定积分计算得到。

设平面图形为函数 y=f(x)，则旋转体的体积 V 可以表示为：V = π∫[a, b] f(x)^2 dx其中，a和b是平面图形上的两个点，π是圆周率。

这个公式可以推广到三维空间中的任意轴。

2. 用截面积求体积公式：对于一个平面图形，若其在垂直于某个轴的截面上的面积为 A(x)，则体积可以通过定积分计算得到。

设截面积函数为 A(x)，则体积 V 可以表示为：V = ∫[a, b] A(x) dx这个公式适用于任意形状的截面。

3. 用截面面积与高度的乘积求体积公式：对于一个平面图形，若其在垂直于某个轴的截面上的面积为 A(x)，且高度为 h(x)，则体积可以通过定积分计算得到。

设截面面积函数为 A(x)，高度函数为 h(x)，则体积 V 可以表示为：V = ∫[a, b] A(x)h(x) dx这个公式适用于各种不规则形状的图形。

4. 旋转体绕轴的体积壳公式：对于一个平面图形，若其在垂直于某个轴的截面上的面积为 A(x)，且旋转轴到截面的距离为 r(x)，则体积可以通过定积分计算得到。

设截面面积函数为 A(x)，旋转轴到截面的距离函数为 r(x)，则体积 V 可以表示为：V = 2π∫[a, b] A(x)r(x) dx这个公式适用于各种不规则形状的图形。

以上四个公式是定积分求体积常用的方法，可以根据具体问题选择适合的公式进行计算。

定积分在数学中的应用

定积分在数学中有广泛的应用，涵盖了多个领域，包括几何、物理、经济学和工程学等。

以下是一些常见的应用领域：
1. 几何学：定积分可用于计算曲线的弧长、曲线与坐标轴所围成的面积、空间曲面的面积和体积等。

通过将几何问题转化为定积分的计算，可以准确求解各种形状的几何量。

2. 物理学：定积分在物理学中的应用非常广泛。

例如，可以用定积分计算物体的质心、转动惯量、流体的压力和力矩等。

还可以通过定积分计算曲线下的面积来求解物体的位移、速度和加速度等运动学问题。

3. 经济学：定积分在经济学中的应用主要用于计算累积量。

例如，可以使用定积分计算总收益、总成本、总利润等经济指标。

还可以通过定积分计算边际收益和边际成本，从而进行经济决策和优化问题的分析。

4. 工程学：定积分在工程学中也具有重要的应用价值。

例如，可以使用定积分计算电路中的电流、电压和功率等物理量。

在结构工程中，可以通过定积分计算材料的体积、质量和重心位置等。

此外，定积分还在概率论、信号处理、图像处理等领域有各种应用。

总之，定积分作为微积分的重要工具，广泛应用于数学及其他学科的建模、计算和问题求解中，提供了丰富的数学工具和方法，有助于深入理解各个学科中的现象和问题。

经济学微积分定积分的应用求面积体积

(3) 生产多少单位产品才能获得最大利润；
(4) 最大利润是多少?
解：(1)
C( x) C(0)
x
C(t)dt 200
x
(16 0.002t)dt
0
0
16x 0.001x2 200
(2) L( x) R( x) C( x) px C( x) (20 0.001x)x (16x 0.001x2 200) 0.002x2 4x 200
S
2

y

4

2
dy
18.
选x为积分变量
2
8
S 0 2x ( 2x ) dx 2 ( 2x ( x 4))dx 18.
例：求由曲线 y 1 与y x, x 2 所围面积。
x
解：画草图，
y y 1
x
2
1
S

1
(x

)dx x
c
d
b
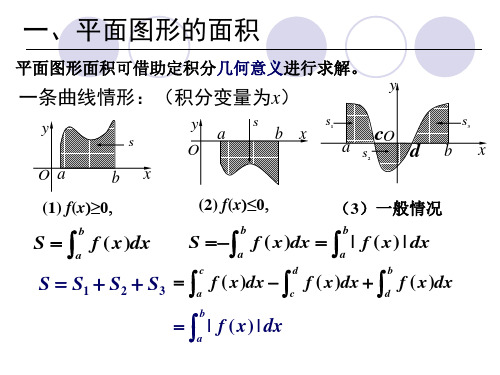
S S1 S2 S3
f ( x)dx
a
c
f ( x)dx
d
f ( x)dx
b
a | f ( x) | dx
由y f ( x), x a, x b及x轴所围图形的面积为
b
S a | f ( x) | dx
一条曲线（积分变量为y）
y
d
x (y)
y
d
y
d
x (y) e
c
c
c
O
x
O
x
O
x
(1) ( y) 0 (2) ( y) 0

第十章定积分的应用(一)

0
π
= abπ .
a x
1 1 2 = x 、y 例2 与直线 x = 3 、 2 2 1+ x x = 3 所围成的图形的面积。解：由对称性，图形面积是第一象限部分的两倍。 2 1 3 x 1 x2 1 S =2[ ∫ ( )dx + ∫ ( )dx ] 2 2 0 1+ x 1 2 2 1+ x 求曲线 y=
例9 连接坐标原点O及点P(h，r)的直线、直线x=h 及x轴围成一个直角三角形。将它绕x轴旋转构成一个底半径为r、高为h的圆锥体。计算这圆锥体的体积。 r 解：过原点 O 及点 P(h，r)的直线方程为 y = x 。 h P ( r , h) r y 所求圆锥体的体积为 y= x h h r 2 r V= ∫ π ( x ) dx 0 h O 2 x h h πr 1 = 2 ∫ x2dx = πhr 2 。 0 3 h
y
Vx = ∫
2π a
0
0
π y dx
2
2 2
y
o
= π ∫ a (1 cos t) a(1 cost) dt
3 π = 2π a (1 cos t)3 dt 0
2π
πa
2πa x
利用对称性
∫
3 2 6 3 5 = 32π a sin u du= 32π a 0 6 2 3
∫
π
3 π 6t =16π a sin dt 0 2
方法2 方法利用椭圆参数方程
则
V = 2∫ π y2 dx = 2π ∫ ab2 sin3t dt
0
a
2 = 2π ab 3 4 = π ab2 3
2
4 3 特别当b = a 时, 就得半径为a 的球体的体积 π a . 3

(完整版)定积分的简单应用——求体积

4.2定积分的简单应用(二)复习：（1）求曲边梯形面积的方法是什么？（2）定积分的几何意义是什么？（3）微积分基本定理是什么？引入：我们前面学习了定积分的简单应用——求面积。

求体积问题也是定积分的一个重要应用。

下面我们介绍一些简单旋转几何体体积的求法。

1. 简单几何体的体积计算问题：设由连续曲线()y f x =和直线x a =，x b =及x 轴围成的平面图形（如图甲）绕x 轴旋转一周所得旋转体的体积为V ，如何求V ？分析：在区间[,]a b 内插入1n -个分点，使0121n n a x x x x x b -=<<<<<=L ，把曲线()y f x =（a x b ≤≤）分割成n 个垂直于x 轴的“小长条”，如图甲所示。

设第i 个“小长条”的宽是1i i i x x x -∆=-，1,2,,i n =L 。

这个“小长条”绕x 轴旋转一周就得到一个厚度是i x ∆的小圆片，如图乙所示。

当i x ∆很小时，第i 个小圆片近似于底面半径为()i i y f x =的小圆柱。

因此，第i 个小圆台的体积i V 近似为2()i i i V f x x π=∆该几何体的体积V 等于所有小圆柱的体积和：2221122[()()()]n n V f x x f x x f x x π≈∆+∆++∆L这个问题就是积分问题，则有：22()()b b a a V f x dx f x dx ππ==⎰⎰归纳：设旋转体是由连续曲线()y f x =和直线x a =，x b =及x 轴围成的曲边梯形绕x 轴旋转而成，则所得到的几何体的体积为2()b a V f x dx π=⎰ 2. 利用定积分求旋转体的体积（1）找准被旋转的平面图形，它的边界曲线直接决定被积函数（2）分清端点（3）确定几何体的构造（4）利用定积分进行体积计算3. 一个以y 轴为中心轴的旋转体的体积若求绕y 轴旋转得到的旋转体的体积，则积分变量变为y ，其公式为2()b a V g y dy π=⎰类型一：求简单几何体的体积例1：给定一个边长为a 的正方形，绕其一边旋转一周，得到一个几何体，求它的体积思路：由旋转体体积的求法知，先建立平面直角坐标系，写出正方形旋转轴对边的方程，确定积分上、下限，确定被积函数即可求出体积。

定积分的应用计算面积和体积

定积分的应用计算面积和体积定积分是微积分中的一个重要概念，它在数学和物理学等领域中有着广泛的应用。

其中，一项常见的应用就是用定积分来计算图形的面积和物体的体积。

本文将从定积分的基本概念入手，介绍如何利用定积分来计算面积和体积。

一、定积分的基本概念定积分是积分学中的一种，它可以将函数与坐标轴之间的面积联系起来。

对于一个函数f(x)，我们可以通过定积分来计算其在某个区间[a, b]上的面积。

定积分的公式如下：∫[a,b]f(x)dx其中，∫表示积分符号，a和b是积分的下界和上界，f(x)是被积函数，dx表示积分变量。

二、使用定积分计算面积使用定积分计算面积时，我们需要确定被积函数和积分区间。

一般来说，面积可以通过将函数所在的曲线图形与坐标轴所夹的区域进行分割，将其近似看作多个矩形或梯形，再对这些矩形或梯形的面积进行求和来逼近真实的面积。

例如，我们要计算函数y = f(x)在区间[a, b]上的面积，可以先将该区间分割成n个小区间，每个小区间的长度为Δx。

然后，在每个小区间上选择一个点(xi, yi)，用这些点构成的矩形或梯形的面积之和来近似曲线与坐标轴之间的面积。

将小区间个数无限增加，使Δx趋近于0，此时逼近的面积将趋向于真实的面积，即可利用定积分公式求得准确的面积值。

三、使用定积分计算体积定积分在计算物体的体积时同样具有重要的作用。

当一个平面图形绕某条直线旋转一周，形成一个立体图形时，我们可以使用定积分来计算该立体图形的体积。

对于一个平面图形，假设其边界可以由函数y = f(x)和y = g(x)所描述，其中f(x)表示上曲线，g(x)表示下曲线。

图形绕x轴旋转一周后，所形成的立体体积可以通过定积分进行计算。

首先，我们将x轴上的区间[a, b]进行分割，并在每个小区间上选择一个点(xi, yi)。

然后，计算曲线与x轴所形成的圆柱的体积，并对所有小区间的体积求和，即可逼近真实的体积。

当小区间数量趋近于无穷大时，利用定积分公式可以得到准确的体积值。

定积分的应用公式总结

定积分的应用公式总结定积分是微积分中的重要概念，具有广泛的应用范围。

在实际问题中，定积分可以用于求解曲线下的面积、求解容积、质量、中心矩等问题。

接下来，我们将总结定积分的应用公式，包括面积、体积、质量、中心矩等几个重要应用。

1. 曲线下的面积定积分最常见的应用是求解曲线下的面积。

对于一个函数f(x)，在区间[a, b]上，曲线y=f(x)与x轴所围成的面积可以通过定积分来计算。

公式为：S = ∫(a到b)f(x)dx其中S表示曲线下的面积，∫表示定积分，f(x)是函数曲线在x轴上的对应值。

2. 旋转体的体积定积分还可以用于计算旋转体的体积。

考虑一个曲线y=f(x)，在[a, b]区间上绕x轴旋转一周，所形成的旋转体体积可以通过定积分来计算。

公式为：V = π∫(a到b)f(x)^2dx其中V表示旋转体的体积，π表示圆周率。

3. 弧长定积分可以用于计算曲线的弧长。

设有曲线y=f(x)，在区间[a,b]上的弧长可以通过定积分来计算。

公式为：L = ∫(a到b)√(1+(f'(x))^2)dx其中L表示曲线的弧长，f'(x)表示f(x)的导数。

4. 质量和质心对于一条位于直角坐标系中的线密度分布曲线，其质量可以通过定积分来计算。

设密度函数为ρ(x)，曲线上的质量可以表示为：m = ∫(a到b)ρ(x)dx其中m表示曲线上的质量，ρ(x)表示密度函数。

同时，还可以通过定积分来计算曲线的质心。

曲线的质心可以通过以下公式来计算：x_c = (1/m)∫(a到b)xρ(x)dxy_c = (1/m)∫(a到b)yρ(x)dx其中x_c和y_c表示曲线的质心的坐标。

以上的公式总结了定积分的一些重要应用，包括面积、体积、弧长、质量和质心等。

在实际问题中，我们可以根据具体的问题情况，选择适当的公式来计算所需的结果。

这些公式可以帮助我们更好地理解和应用定积分的概念，解决实际问题。

微积分第六章第四节定积分的应用

4ab
1
ab .
0
22
2 0
sinn
xdx
n
n
n
n
1 1
n n n n
3 2 3 2
3 4 4 5
1 2 2 3
, n为正偶数
2
, n为大于1的奇数
19
例4 计算由曲线 y2 2x 和直线 y x 4所围成
的图形的面积. 解两曲线的交点
y
y2 2x
(8, 4)
2
Vy 2
1 x 2x2dx .
0
o 1x
35
例12 求由曲线 y ( x 1)( x 2) 和 x 轴所围平面图
形绕 y 轴旋转一周而成的旋转体体积.
解
Vy 2
2
x( x 1)( x 2)dx
.
1
2
y
y
a
b
12
o
xo
x
y f (x)
“套筒法”推广：
由平面图形 0 a x b, f ( x) y 0 绕 y 轴
t (t 2 x2 )dx
1
(
x2
t
2
)
dx
0
t
y
1
y = x2
[t 2 x
x3 3
]
t 0
x3 [
3
t
2
x]
1 t
4t 3 t 2 1 ， 0 t 1
3
3
t2
S2
S1
o
t1 x
S 4t 2 2t
令
2t(2t 1)
0 ，得驻点:
t
0, t
1，
2
经比较，当t 1 时两面积和最小.

定积分的应用面积-文档资料

选y为积分变量,
1 2
(0,0) (1,1)
y [0 ,1 ]
3 2
2 y 1 1 A ( yy )d y ( y ) 0 . 0 3 3 3
3
13
y x 4 y 2 x 算由曲线和直线所围成例2 计
2
的图形的面积 .
解
两曲线的交点
y 2x
14
x ( x 4 )] d x A x ( 2 x )] d x [ 2 [ 2
0
2
8
2
此题选y为积分变量比较好,
2y4
y A (y 4 )d y 2 2
4
2
x y 4 y x 4
y y ( 4y ) 2 6 2
2
3
4
2 y y x2 2x 2
( x ) d x A A A A 1 2 3 4 f
a
b
2
1.以x轴为底边的曲边梯形的面积
y
f ( x)
y
a
b
0
f ( x)
x
0
a
b
b a
x
f( x ) 0 ,A ) d x ； f(x
a b
f( x ) 0 ,A ) d x ； f(x

A f(x )d x.
18 .
选择积分变量的原则： (1)尽量少分块； (2)积分容易。
15
2 1 x x 3所 y ,y 曲线直线例3 求 2 与 2 1 x
围成的平面图形的面积.
y
1 y 1 x2
1, 解交点 x

定积分的计算与应用于面积与体积的计算

定积分的计算与应用于面积与体积的计算定积分是微积分中的重要概念之一，它不仅可以用于计算函数的面积，还可以应用于计算物体的体积。

在本文中，我们将介绍定积分的计算方法，并探讨其在面积与体积计算中的应用。

一、定积分的计算方法定积分的计算方法可以通过数学积分公式进行求解。

它是对函数曲线下方某一区间的面积进行求和的过程。

计算定积分需要确定被积函数的上下限范围，并通过适当的数值方法进行近似求解。

以计算函数y=f(x)在区间[a, b]上的定积分为例，可以使用不同方法进行计算。

其中，常用的方法包括积分定义法、几何法和数字积分法。

积分定义法是定积分计算的基本方法，它通过将函数曲线下方的面积拆分为无穷多个小矩形的面积之和来进行求解。

具体求解过程可以通过Riemann和黎曼和来进行，这里不再赘述。

几何法是一种直观的计算方法，它通过将函数曲线下方的面积分割为几个几何形状（如矩形、三角形等）的面积之和来进行计算。

对于简单的几何形状，可以使用基本几何公式进行计算，对于复杂的几何形状，则需要进行适当的近似。

数字积分法是一种数值计算方法，它通过将区间[a, b]分成若干小区间，并在每个小区间内取函数值的平均来进行计算。

其中，较为常用的数值积分法有矩形法、梯形法和辛普森法等。

二、定积分在面积计算中的应用定积分在计算函数曲线下方的面积时发挥着重要作用。

它可以用于求解曲线与坐标轴所围成的面积，并可以通过变量变换等方法应用于不同形状的曲线。

例如，我们可以通过定积分计算圆的面积。

设函数y=f(x)为圆的上半部分，区间[a, b]为圆弧的长度，根据定积分的定义，圆的面积可表示为：S = ∫[a, b]f(x)dx其中，函数f(x)可以表示为圆的方程。

通过适当的变量变换和曲线的参数化，我们可以求解出圆的面积。

同样地，定积分可以用于计算其他几何形状的面积，如正方形、三角形、椭圆等。

只要能够将几何形状表示为函数曲线的形式，就可以利用定积分进行计算。

8定积分应用(求极限,变上限求导,面积,体积,不等式)

y
o
x
4.设 y ax与 y x 2 围成图形的面积为s1 , 它们与x 1 围成图形的面积为s2 , 且 0 a 1 (1) 求 a , 使 s1 s2 最小
(2) 求此最小值对应的平面图形绕 x 轴旋转而得的旋转体体积. 解 (1) 0 a 1 时, s s1 s2
例
x sin( xt ) f ( x) . lim 2 ，其中 f ( x) 2 dt x x 0 x t
例 : 设f ( x )连续, 且f ( 0 ) 0
求 lim
x0
x
0
( x t ) f (t )dt
x 0
x f ( x t )dt
1 ( ) 2
例.
例
3
设隐函数y y( x )由
o
x
1 3 1 2 （） (1 y 2 y) dy ( y y y ) . 1 S 0 3 3 0 2 2 1 2 2 （2） V ( x) dx ( x 1) dx 0 1 6 2
1 2
1
(3)绕直线 x 2 旋转所得旋转体的体积.
例
.设f ( x)为奇函数，且当 0时，f ( x) 0 x
sin( xt ) f ( x) 0, 其中 f ( x) 2 dt，令 x t
x
F ( x) f ( xt)dt tf (t 2 x 2 )dt,
1 0
1
x
判别F (x)在，上的凹凸性
3 2 2
2 f ( ) f ( ) 0
(2).设f ( x)在2,4上可导, 且
f (2) ( x 1) f ( x)dx 。