简谐振动旋转矢量法
大学物理-11第十一讲简谐振动、振动能量、旋转矢量法

14
例:边长l的立方体木块浮于静水中,浸入水中部分 的高度为b。今用手将木块压下去,放手让其开始运 动。忽略水的阻力,证明木块作谐振动。 解:以水面为原点建立坐标OX。
任意时刻 F浮水(bx)l2g mgF浮ma
水 b l2g水 l2(bx)gm a
力使 减小.
mgsinmldd2t2
很小,sin mg
ml
d2
dt2
l m
f mg
d 2
dt 2
g
l
0
角谐振动
解为 0cos(t)
g T 2 l
l
g
12
例:如图所示装置,轻弹簧k =50N/m,滑轮 M =1kg,
半径 R =0.2m,物体 m =1.5kg。若将物体由平衡位置
X
P
xAcos(t)
◆可用该旋转矢量末端的投影点 P 的运动来表示简 谐振动。
16
旋转矢量法的应用
1.确定初位相 ●由初始位置 x0 确定旋转矢量两个可能的位置。 (特殊情况下只有一个位置) ●根据初始速度方向,由旋转矢量两个可能的位 置中确定初始位置,从而找出初相.。
A
Ox
17
例:确定下列情况的初位相 (a) 已知 t = 0 时,x = -A。 (b) 已知 t = 0时,x = 0,且向 x 轴正方向运动。 (c) 已知 t = 0,x = -A/2,且向 x 轴负方向运动。 (d) 已知 t = 0,x = -A/2,且向 x 轴正方向运动。
13
d2x dt2
k x0 m(1/2)m
d2x dt 2
简谐振动的旋转矢量法

简谐振动的旋转矢量法
简谐振动的旋转矢量法(also known as the rotational vector method)是一种描述简谐振动运动的方法。
这种方法将简谐振动的位移表示为一个旋转矢量,该旋转矢量的大小和方向都随时间变化。
在这种方法中,假设物体在振动过程中绕一个固定轴旋转。
这个固定轴被称为挠度轴,它垂直于振动平面。
振动的位移被表示为从挠度轴指向物体的矢量。
根据简谐振动的性质,位移矢量旋转的角度随时间变化,而角度的变化速率与振动频率相关。
通过将位置矢量的旋转速率与振动频率相关联,可以得到简谐振动的动态方程。
旋转矢量法可以应用于各种简谐振动问题,包括简谐振子、摆线振动等。
通过使用该方法,可以更轻松地分析和计算简谐振动的运动特性,例如位移、速度和加速度等。
此外,该方法还可以用于解决相关问题,如相位差和共振等。
总的来说,简谐振动的旋转矢量法是一种较为直观和简便的分析简谐振动运动的方法,它通过描述位移矢量的旋转来描述振动过程,并可以得到简谐振动的动态方程。
旋转矢量表示法振动合成

方法二:
(t2t1)326 5
t
t2
t1
5 6
65
5s 6
2 3
-A
AX
旋转矢量表示法振动合成
§4--4谐振动的合成
解:(1)设物体谐振动方程为
xA co ts
由题意知 A0.12 m
22S1
T2
旋转矢量表示法振动合成
4 – 3 谐振动的旋转矢量表示法
第四章 机械振动
〈方法一〉用数学公式求
x0 Acos A0.12 m x0 0.06m
cos 1
2
3
v0Asin0
3
x0.12costm
3
旋转矢量表示法振动合成
动为简谐运
动.
4 – 3 谐振动的旋转 矢量表示法 一、旋转矢量 A
第四章 机械振动
其模为简谐振动的振幅A,绕o点逆时针转动,角速度
大小 ,为谐振动角频率。
x旋 转矢A 量c 表示法o 振动合t成s ()
4 – 3 谐振动的旋转矢量表示法
第四章 机械振动
二、表示法 xA cots()
1. t=0时,矢量与x轴夹角为谐振动的初相 ,
t时刻与x轴夹角为t时刻谐振动的位相 t
当t 0
A
时
o
x0 x
x0Acos
A
t t 时 t
o
x
xAcots()
旋转矢量表示法振动合成
4 – 3 谐振动的旋转矢量表示法
第四章 机械振动
2.矢量的矢端在x轴上投影点做谐振动.
3.旋转一周,投影点在x轴上作一次全振动,所用时间与 谐振动的周期相同 T 2。
xA co ts ()
旋转矢量表示法振动合成
大学物理B(Ⅱ)旋转矢量

t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
简谐振动-旋转矢量法
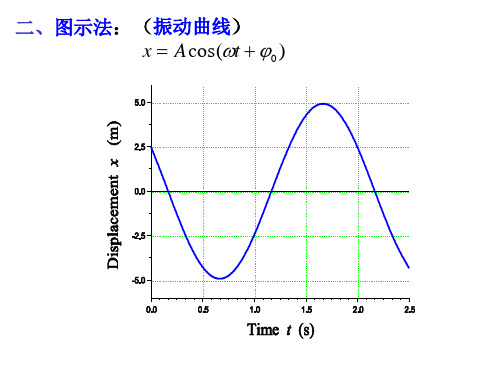
sin2 (2 1)
y
2) 2 1 π
y A2 x A1
3)2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位:
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量,问题就解决了。
旋转矢量和振动合成
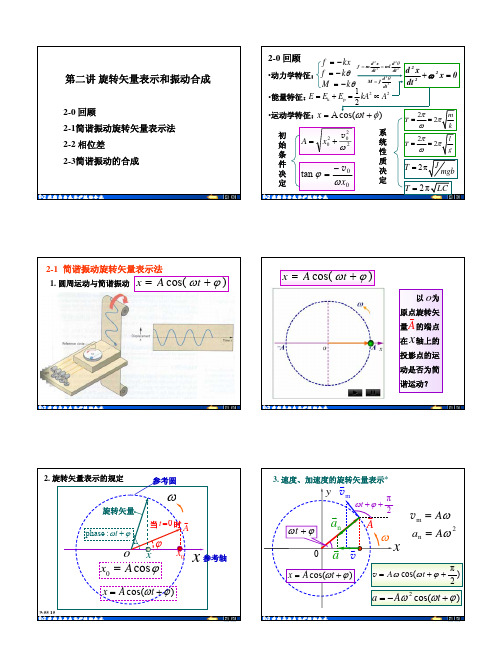
如:位相ωt2 +φ = 3π 2,问状态? x =0 ,且向 x 正向运动。
ω
Aπ
3
o
x
例2. 已知状态求位相(特别是初位相)
如:t =0,x0 = A 2,v0>0,求φ ?
φ = 5π 3 或 φ = −π 3
A2
如:t = 0 ,x0 = − A 2 ,v0 <0,求 φ ? −A 2 o
x/m
x/m
v A2 Δϕ
v A1
0.2
21
0.1
o
1234
56
t/s
解: A = 0.2m
ϕ1
=
−
π 2
T = 4s ω = 2π = π (1/s)
T2
x1
=
π 0.2 cos(
2
t
−
π 2
)
(SI)
Δt
=
Δϕ ω
φ2
=
−
π 3
x2
=
பைடு நூலகம்
π 0.2 cos(
2
t
−
π )
3
(SI)
(
=
π π
6 2
=
1 3
ω
Av
v A3
vϕ3
x ϕ
v
ϕ
A2
2
ϕ1 A1
多个同方向同频率简谐运动合成仍为简谐运动
11:00 10 9-2 旋转矢量表示和振动合成
x1 = A0 cos ω t
x2 = A0 cos( ω t + Δϕ )
xxNL3 ==LAA00ccooss[(ωωt
t +
第三节 旋转矢量法

§ 8.3 旋转矢量法一、旋转矢量1 矢量的模等于简谐振动的振幅A长度 = A ;2 矢量绕O 点作逆时针方向匀速转动,其角速度的大小等于简谐振动的角频率以ω为角速度绕o 点逆时针旋转;3 在t = 0时,矢量A 和x 轴的夹角为ϕ ,在任意时刻t ,它与x 轴的夹角为ωt +ϕ ,矢量A 的矢端M 在x 轴上的投影点P 的坐标为 矢量端点在x 轴上的投影做简谐振动例 已知简谐振动,A =4 cm ,ν = 0.5 Hz ,t =1s 时x =-2cm 且向x 正向运动。
写出此简谐振动的表达式。
解:由题意,T = 2 s由图, ϕ = π/3,当旋转矢量A 旋转一周,投影点P 作一次完全的振动 ,旋转矢量A 的端点在x轴上的投影点P 的运动为简谐振动例8-4 一物体沿x 轴作简谐振动,振幅为0.24m ,周期为2s 。
当t = 0时,x 0= 0.12m ,且向x 轴正方向运动。
试求(1)振动方程(2)从且向x 轴负方向运动这一状态,回到平衡位置所需的时间。
已知:0.24m =A s 2=T 0.12m 0=x 00>v ∴x = 4cos(πt + ) cmπ 3t = 1s x()ϕω+=t A x cos求:解:(1)简谐振动的角频率t = 0时旋转矢量的位置如图所示振动方程为(2)令φ < 0这一状态对应的时刻为 t 1;回到平衡位置的时刻为 t 2。
t 1和t 2时刻的旋转矢量位置,如图所示例8-5 两个同方向(沿x 轴方向)、同频率的简谐振动,其频率都是2s-1。
当第一个振子从平衡位置向正方向运动0.05s 后,第二个振子正处于正方向的端点。
求这两个简谐振动的相位差。
已知:求:当第一个振子从平衡位置向正方向运动时,其旋转矢量A 1的位置如图所示经过0.05s 后,旋转矢量A 1转过一角度?)( =t x (1) ?=∆t (2) 2π2πrad πrad 2ω T ===π3ϕ=-π0.24cos(π )m 3x t =- ()21ππ5π326t t ω-=+=215π6Δs 0.833s πt t t =-==-1212s ==νν10100,0x υ=>0.05s =∆t A x =2?=∆ϕ解: 简谐振动的角频率4π0.050.2πω t =⨯=此时,第二个振子刚好处在正方向端点,其旋转矢量A 2由图可见,两振子的相位差为第二个振子比第一个振子的相位超前二、相位差1 相位差和初相差相位差(phase difference)---相位之差。
第四章振动下
结论: 结论:
振子在振动过程中, (1) 振子在振动过程中,动能和势能分别随时间 变化,但任一时刻总机械能保持不变。 变化,但任一时刻总机械能保持不变。 (2) 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时, (3)频率一定时,谐振动的总能量与振幅的平方 成正比。(适合于任何谐振系统) 。(适合于任何谐振系统 成正比。(适合于任何谐振系统) 弹性势能
小结:
描述简谐振动的三种方法: 描述简谐振动的三种方法: 运动方程,振动曲线,旋转矢量。 运动方程,振动曲线,旋转矢量。
的简谐振动, 例1:一物体沿 轴作振 幅为 A 的简谐振动,若初始时该球的 :一物体沿x轴作振 状态为( ) ;(2)在平衡位置且向X轴正方向运动 轴正方向运动; 状态为(1)X0= -A;( )在平衡位置且向 轴正方向运动; ;( 处向X轴负方向运动;(4) 轴负方向运动;( (3)在 X0=1/2 A 处向 轴负方向运动;( )在 ) / 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求: ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解:
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0
