二次曲线、指数曲线、季节指数
统计学重点整理
参数(parameter)：描述总体特征的概括性数字度量，是研究者想要了解的总体的某种特征值。
所关心的参数主要有总体均值、标准差、总体比例等。
总体参数通常用希腊字母表示统计量(statistic)：用来描述样本特征的概括性数字度量，它是根据样本数据计算出来的一些量，是样本的函数。
所关心的样本统计量有样本均值(x)、样本标准差(s)、样本比例(p)等。
样本统计量通常用小写英文字母表示1、概率抽样：简单随机抽样（SRS）、系统抽样（SYS）、分层抽样（STS）、整群抽样（STS）、多阶段抽（MSS）简单随机抽样（SRS）特点：总体中每一个样本点均有相同机率被抽中、抽出某个样本后不影响另一个样本抽出的机率（独立性）、经常先列样本名册后用计算机产生随机数或随机表抽选放回和不放回：放回（重复）抽样；无放回（不重复）抽样系统抽样（SYS）等距抽样：将所有样本列册以序号排列，先随机抽取第一个样本，接着每隔Ｋ个样本抽取下一个样本；间隔K 的求法：Population size/ Sample size；常用于电话抽样（类似于简单随机抽样）分层抽样（STS）将总体区分为数个层（strata）：层之间互斥且周延、层内性质相近、层与层之间差异明显从每一层中简单随机抽取若干样本作为该层的代表，再将所有层总结集合整群抽样（STS）将总体区分为多个群集clusters：群集间互斥且周延、群集与群集间差异小、群集内类似总体随机抽取数个clusters将抽中的群集内每个样本均调查多阶段抽样（MSS）第一阶段：分群——整群抽样第二阶段：分层——分层抽样第三阶段……整群抽样的优点是实施方便、节省经费；整群抽样的缺点是往往由于不同群之间的差异较大，由此而引起的抽样误差往往大于简单随机抽样。
抽样方法优点缺点简单随机抽样操作简便易行，总体个数多时，工作量太大系统抽样操作便简易行，可以提高效率如不了解样本总体，抽出的样本有偏差分层抽样充分保证样本结构与总体的一致整体差异不明显时不适用，在使用时提高样本的代表性需要与其他抽样方法综合使用。
时间序列分析
时期序列
计算公式：
n
YY1Y2Yn
Yi i1
n
n
【例8.1】 根据表8.1中的国内生产总值序 列，计算各年度的平均国内生产总值
n
Yi
Yi1
4288.585 476.95（ 43 亿元）
n
9
绝对数序列的序时平均数
（计算方法）
时点序列— 间隔不相等
Y1 Y2
Y3 Y4
T1
T2
T3
Yn-1
发展速度与增长速度的计算（实例）
【例8.5】 根据表8-3中第三产业国内生产总值序列， 计算各年的环比发展速度和增长速度，及以1994年 为基期的定基发展速度和增长速度
表8- 4 第三产业国内生产总值速度计算表
年份
1994 1995 1996 1997 1998
国内生产总值(亿元)
发展速度 (%)
第8章 时间序列分析
第一节 时间序列的对比分析 第二节 时间序列及其构成因素 第三节 长期趋势分析 第四节 季节变动分析 第五节 循环波动分析
第一节 时间序列的对比分析
一. 时间序列及其分类 二. 时间序列的水平分析 三. 时间序列的速度分析
时间序列及其分类
1. 同一现象在不同时间上的相继观察值排 列而成的数列
803 896 1070 1331 1781 2311 2726 2944 3094
时间序列的分类
时间序列
绝对数序列 相对数序列 平均数序列
时期序列 时点序列
时间序列的分类
1. 绝对数时间序列 一系列绝对数按时间顺序排列而成 时间序列中最基本的表现形式 反映现象在不同时间上所达到的绝对水平 分为时期序列和时点序列
6种销售预测方法来更好地预测收入
6种销售预测方法来更好地预测收入销售预测是通过分析历史销售数据和市场趋势来预测未来销售收入的过程。
准确的销售预测对于企业制定合理的生产计划和市场战略至关重要。
下面将介绍六种常用的销售预测方法，以帮助企业更好地预测其收入。
1.回归分析法：回归分析法通过建立销售量与一系列相关因素的数学关系，来预测销售收入。
这些相关因素可以是市场规模、经济指标、竞争对手销售数据等，通过收集和分析这些数据，通过回归模型来预测销售收入。
2.移动平均法：移动平均法是通过计算历史销售数据的平均值来进行预测的。
它适用于需求波动相对平稳的产品。
通过计算过去几个时期的销售数据的平均值，可以得到一个趋势值，用来预测未来的销售收入。
3.季节性指数法：季节性指数法是通过分析产品在不同季节或时间段的销售数据，来确定季节性因素对销售量的影响程度，从而进行预测的方法。
通过计算季节性指数，可以根据历史销售数据和季节性变动，推测未来销售收入的趋势。
4.成熟度曲线法：成熟度曲线法是基于产品生命周期理论，通过分析产品销售量和时间的关系，来预测销售收入。
根据产品从引入到成熟的不同阶段，销售量呈现出不同的增长速度和趋势，通过曲线拟合来预测未来销售收入。
5.主观预测法：主观预测法是基于专家判断和经验的预测方法。
通过邀请销售人员、市场专家等关键人士参与，根据市场趋势、竞争情况和公司发展计划等因素，进行主观的预测分析，以确定未来销售收入的预测。
6.市场调研法：市场调研法是通过定期进行市场调研，收集顾客需求、竞争对手情况、市场趋势等信息，并结合历史销售数据，来预测销售收入。
通过市场调研的数据和分析，可以更准确地预测未来的销售收入。
以上是一些常用的销售预测方法，每种方法都有其适用的场景和优缺点。
企业可以根据自身情况选择合适的方法，通过数据分析和市场调研来提高销售预测的准确性，从而为制定合理的生产和市场策略提供依据。
指数曲线趋势法与季节变动法预测医院门诊量比较
５ ８・
中 国医 院 统 计
２０ ０ ９年 ３月 第 ｌ ６卷 第 １ 期
指 数 曲线 趋 势 法 与 季 节 变 动 法 预 测 医 院 门诊 量 比 较
朱 灼新 梁丽 萍
【 摘要】 目的 比较指数曲线趋势法和季节变动法预测门诊量的效果， 以便选择更合适的方法预测 门诊量。方法
（３ ｌｇ ６ ） ／ ） ／ ） ）７ ） ０ ｃ ）＋ ｏ（＇ ）３ ） ３ ） ，） ，） ４
＝ ｔｍ（Ｐ Ｗ ｔ １， （ 也０ ２ ＋ ０ （３ ＋ Ｏ ｃ ） ， ） ｏ ｔ ｅ （Ｏ ｍ （ Ｏ （ Ｇ ｃ ） Ｌ Ｇ ｃ ） Ｌ Ｇ（４ ） ３ ＋ Ｏ ｃ ） ， ） ／ ） ） （明崃 （Ｐ 昧 （ （ （Ｏ （５ Ｌ Ｇ（４ ） ３） ３ ） ） Ｐ （删 １ ＿（ （Ｌ Ｇ Ｃ ｏ
以指数 曲线趋势作 为理论依据 ， 并将其整合成 易于复制 移植 的 Ｅ ｃｌ ｘｅ 数据模 型， 其结果 与季 节变动法进行 效果对 比。 用 结果 指数 曲线趋势 法预测 结果优 于季节变动法。结论 医院门诊量增 长趋势为 逐期 等比 时， 用指数 曲线趋势 预测法 效果更佳 。
【 关键词 】 指数 曲线趋势法
～
登 一
图 １ 指 数 曲线 趋 势预 测 法 过 程 图
２ １ １ 将 时间数列分 为时期相 等的 ２段 （ ２０ － ２０ ． ． 即 ０ １ ０ ３为一 段 ，０ ４ ２ ０ ２０ － ０６为第 ２段 ） 计算 ２段 的简单 算术 平均数 ， 根 ， 并 据指数 曲线方程 ＝ ｂ 列 出二元联立 方程 ： ａ
１ 资 料 来 源 及 方 法
ｖ ＿一
一
（ 兰 一ｇ４ ｌ ５＋ｌｙ 卮 生２ — ＋ｇ ｇ ￣ ｌ ｙ ｙ
应用Excel进行时间序列分析
1
重点
❖ 1 Excel进行移动平均分析的操作步骤 ❖ 2 Excel进行指数平滑分析的操作步骤 ❖ 3 Excel进行趋势外推预测法的操作步骤 ❖ 4 Excel进行时间序列分解法的操作步骤
zf
zf
移动平均法是一种简单平滑预测技术;它的基 本思想是：根据时间序列资料 逐项推移;依次 计算包含一定项数的序时平均值;以反映长期 趋势的方法 因此;当时间序列的数值由于受周 期变动和随机波动的影响;起伏较大;不易显示 出事件的发展趋势时;使用移动平均法可以消 除这些因素的影响;显示出事件的发展方向与 趋势即趋势线;然后依趋势线分析预测序列的 长期趋势
16
在输入框中指定输入参数 在输入区域指定数据所在 的单元格区域B1:B22；因指定的输入区域包含标志 行;所以选中标志复选框；在阻尼系数指定加权系数 03
注:阻尼系数不是平滑常数 阻尼系数=1平滑常数
在输出选项框中指定输出选项 本例选择输出区域; 并指定输出到当前工作表以C2为左上角的单元格区 域；选中图表输出复选框 单击确定按钮 这时;Excel给出一次指数平滑值;如下图所示
适用于有长期趋势的时间序列 选择工具菜单中的数据分析命令;弹出数据分析对话框
在分析工具列表框中;选回归工具 这时;将弹出回归对话框;如图所示
20
21
指定输入参数 在输入Y区域原始的时间序列数据y 输入X区域y对应的时间t指定相应数据所在的单元 格区域
并选定标志复选框;在置信水平框内键入95% 对于 一些特殊的回归模型;可以根据需要指定常数为0即 指定输出选项 这里选择输出到新工作表组;并指 定工作表名称为回归模型;选定残差即随机误差项和 正态分布中的所有输出选项;以观察相应的结果 单击确定按钮 最后得到回归分析的计算结果
时间序列分析基于R——习题答案
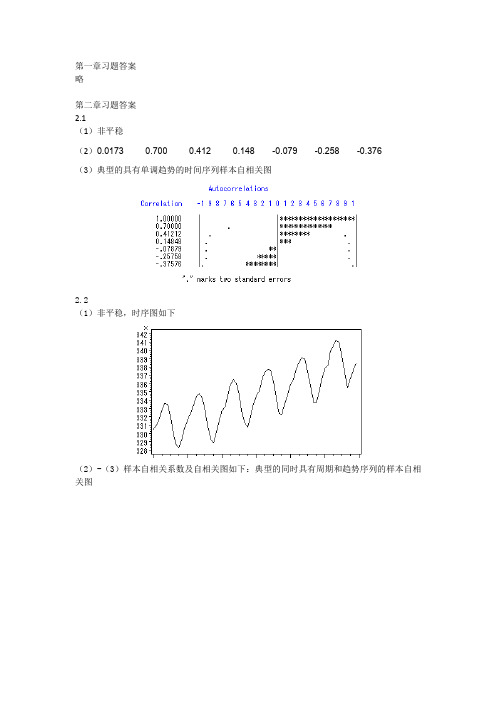
第一章习题答案略第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5（1）时序图与样本自相关图如下（2） 非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为：32--c 0c λλλ+=，解该特征方程得三个特征根：11λ=，2c λ=3c λ=-无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。
时间序列分析试题
第九章 时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。
这种模型将时间序列按构成分解为（ ） 等四种成分，各种成分之间( )，要测定某种成分的变动，只须从原时间序列中（ ）。
A. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案：C2、加法模型是分析时间序列的一种理论模型。
这种模型将时间序列按构成分解为（ ）等四种成分，各种成分之间( )，要测定某种成分的变动，只须从原时间序列中（ ）。
A. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D.. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案：B3、利用最小二乘法求解趋势方程最基本的数学要求是（ ）。
A.∑=-任意值2)ˆ(t Y Y B. ∑=-min )ˆ(2t Y Y C. ∑=-max )ˆ(2t Y Y D. 0)ˆ(2∑=-t Y Y 答案：B4、从下列趋势方程t Y t86.0125ˆ-=可以得出（ ）。
A. 时间每增加一个单位，Y 增加0.86个单位B. 时间每增加一个单位，Y 减少0.86个单位C. 时间每增加一个单位，Y 平均增加0.86个单位D. 时间每增加一个单位，Y 平均减少0.86个单位答案：D.5、时间序列中的发展水平（ ）。
时间序列分析的主要方法有哪些
时间序列分析的主要方法有哪些时间序列分析是一种用于研究随时间变化的数据的统计方法，它在经济学、金融学、气象学、工程学等众多领域都有着广泛的应用。
通过对时间序列数据的分析，我们可以揭示数据中的隐藏模式、趋势和周期性，从而进行预测和决策。
那么，时间序列分析的主要方法有哪些呢？移动平均法是时间序列分析中较为简单和常用的一种方法。
它通过计算一定时期内数据的平均值来平滑数据，从而消除短期波动和噪声。
移动平均法可以分为简单移动平均和加权移动平均。
简单移动平均是对过去若干个数据取相同的权重进行平均，而加权移动平均则根据数据的重要性给予不同的权重。
移动平均法的优点是计算简单，容易理解，但其缺点是对数据的适应性较差，可能会丢失一些重要的信息。
指数平滑法是另一种常见的平滑方法。
它通过对历史数据进行加权平均来预测未来值，权重随着时间的推移呈指数衰减。
指数平滑法有一次指数平滑、二次指数平滑和三次指数平滑等不同形式。
一次指数平滑适用于没有明显趋势和季节性的时间序列，二次指数平滑适用于具有线性趋势的时间序列，三次指数平滑则适用于具有二次曲线趋势或季节性的时间序列。
指数平滑法的优点是能够较好地适应数据的变化，对近期数据赋予较高的权重，更能反映数据的最新趋势。
自回归模型（AR）是时间序列分析中的一种重要方法。
它假设当前值是过去若干个值的线性组合加上一个随机误差项。
自回归模型的阶数决定了考虑过去值的个数，阶数越高，模型对历史数据的依赖程度越大。
自回归模型适用于具有平稳性的数据，如果数据不平稳，需要进行差分处理使其平稳后再应用模型。
移动平均自回归模型（ARMA）结合了自回归模型和移动平均模型的特点。
它不仅考虑了历史值的影响，还考虑了随机误差项的影响。
ARMA 模型的应用需要数据满足一定的条件，如平稳性和零均值等。
如果数据存在季节性，还可以使用季节性 ARMA 模型（SARMA）。
自回归整合移动平均模型（ARIMA）则是在ARMA 模型的基础上，考虑了数据的非平稳性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（三）季节变动预测法
季节变动预测法是根据历史数据中所 包含的季节变动规律性，对预测目标的 未来状况作出预测的方法。
1、季节变动的特点和衡量指标
（1）季节变动及其特点
季节变动的循环周期为一年，而且在 一年中随着季节的更替呈现有规律的变 动。
（2）衡量指标
季节指数（%）=历年同季平均数/全时期总 平均数×100%
合计 1849.87 2058.17 1302.25 2008.20 7218.49 1804.62
全年比率平均法：
例：某商店2000-2004年分季销售资料, 用全年比率平均法测算季节指数。
历年各季的比率（%）=各季的数值 / 相应 度 年份
一季 度
二季 度
年度
1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
合计
某企业近年营业额不同α值的指数平滑法对照表
α=0.3
α=0.5
营业额 指数平滑值 绝对误差 指数平滑值 绝对误差
(260)
262
260.60
257
259.52
252
季度 一季度 二季度 三季度 四季度 合计
年份
（1） （2） （3） （4） （5） （6）
2000 25.55 26.64 22.46 25.35 100.00
2001 22.48 30.35 17.86 29.31 100.00
2002 26.78 24.65 19.66 28.91 100.00
1992
(262)
1993 262 262.00
1994 257 258.50
1995 252 253.95
1996 247 249.09
1997 250 249.73
1998 258 255.52
1999 267 263.56
2000 278 273.67
2001 280 278.10
2002 297 291.33
对数曲线趋势法计算表
时序 实 际 销 售 逐 年 增 长 Y’i
t
额 Yi( 万 率（%） lgYi
元)
-5
100
2.00
= t Y’i -10.00
1995 -4
120
20
2.08
-8.32
1996 -3
146
21.7
2.16
-6.49
1997 -2
180
23.3
2.26
-4.51
1998 -1
210
2.1
249.72
0.3
255.52
2.5
263.55
3.4
273.67
4.3
278.10
1.9
291.33
5.7
297.40
2.6
302.72
2.3
28.9
某企业近年营业额不同 X0值的指数平滑法对照表
α=0.7
α=0.7
α=0.7
年度 营业额
指数平滑值 绝对误差 指数平滑值 绝对误差 指数平滑值 绝对误差
（二）长期趋势预测法
1、预测依据
连续性原理
2、直线模型预测法
Yt = a + bt
b ntY tY nt 2 (t)2
a Y b t
n
n
为了简化计算，使 t 0 的方法是：当时间序列中数据点数目 n 为奇数，如 n=7，则 t
取-3，-2，-1，0，1，2，3 为序号；若 n 为偶数，如 n=8，则 t 取-7，-5，-3，-1，1，3，5，
2004 107.98 126.66 56.83 108.53 100.00
合计 513.14 572.84 358.99 555.03 500.00
季节
指数 102.63 114.57 71.80 111.01 100.00
(%)
（2）季节变差预测法 （3）季节比重预测法 是历年同季季节比例的平均数。
7 为序号。此时，a，b 的计算公式可简化为：
a Y
n
b
tY t2
例：设某产品在 1994-2004 年的市场销售量如下表。用直线趋势预测法预测 2005 年的销售量。
观察期 实际销售量 Yi(万吨) t
t2
tY
预测值 Yt
1994
41
1995
30
1996
38
1997
46
1998
56
确定预测对象。
确定自变量
进行相关分析
确定预测模式和计算参数：
Yi = a + bX
进行相关分析、方差分析与显著性检
验
进行预测
2003 26.49 29.91 15.55 28.05 100.00
2004 27.00 31.66 14.21 27.13 100.00 合计 128.30 143.21 89.74 138.75 500.00
季节指 25.66
数(%)
28.64
17.95
27.75 100.00
（五）回归分析预测法
2825 0 28
t4
ty
t2y
81 -1125 3375
16 -650 1300
1
-275 275
0
0
0
1
425 425
16 950 1900
81 1725 5175
196 1050 12450
a=348.81;b=37.5,c=13.69
Y=348.81+37.5t+13.69t2 Y22007 =348.81+37.5×4+13.69×16 =717.85(万元）
5、指数平滑预测法
一次指数平滑法
是计算时间序列的一次指数平滑值，以当前 观察期的指数平滑值和观察值为基础，确定下 期预测值。
Y =αXt+(1-α)Yt-1 式中：α为平滑系数，且0≤α≤1
例：某企业1993-2004年的营业额资料如下 表 。 试 确 定 α 的 值 ， 设 X0=260，α 值 分 别 为 0.3、0.5、0.7等，然后分别求出指数平滑值， 与原来的观察值时间序列进行比较。α=0.7的 指数平滑值时间序列值与观察值时间序列比较 接近。
16.7
2.32
-2.32
1999 0
250
19.0
2.40
0.00
2000 1
300
20.0
2.48
2.48
2001 2
350
16.7
2.54
5.09
2002 3
430
22.9
2.63
7.90
2003 4
530
23.3
2.72
10.90
2004 5 合计 0
640 3256
20.8
2.81 26.40
（2）指数曲线模型预测法
Yi=abt 对公式两边取对数，则得：
lgYi = lga + t lgb 令Y’i = lgYi ，A = lga ，B = lgb ，故有： Y’I = A + Bt 例某企业的高科技产品近年来的销售额如下表：
请用对数曲线趋势法进行预测。
年份 1994
三季 度
四季 度
全年 平均
（1） （2） （3） （4） （5） （7）
2000 102.19 106.58 89.85 101.39 100.00
2001 89.91 121.38 71.43 117.28 100.00
2002 107.12 98.59 78.64 115.65 100.00
2003 105.94 119.63 62.24 112.18 100.00
2001 338.96 457.59 269.26 442.12 1507.93 376.98
2002 432.97 398.50 317.83 467.42 1616.72 404.18
2003 368.58 416.18 216.55 390.29 1391.60 347.90
2004 354.42 415.72 186.53 356.21 1312.88 328.22
1999
51
2000
48
2001
53
2002
50
2003
60
2004
61
n=11
534
-5
25
-205
36.64
-4
16
-120
39.02
-3
9
-114
41.40
-2
4
-92
43.78
-1
1
-56
46.16
0
0
0
48.55
1
1
48
50.93
2
4
106
53.31
3
9
150
55.69
4
16
240
58.07
2003 300 297.40
2004 305 302.72
合计
(257) 0.0 260.50 1.5 1.5 258.05 1.0 1.9 253.82 1.8 2.1 249.04 2.0 0.3 249.71 0.3 2.5 255.51 2.5 3.4 263.55 3.4 4.3 273.67 4.3 1.9 278.10 1.9 5.7 291.33 5.7 2.6 297.40 2.6 2.3 302.72 2.3