二次平滑曲线Matlab
matlab 点之间平滑曲线

matlab 点之间平滑曲线(原创实用版)目录1.MATLAB 简介2.平滑曲线的绘制方法3.应用实例正文【1.MATLAB 简介】MATLAB 是一种广泛使用的数学软件,它主要用于数据分析、可视化以及算法开发等方面。
在 MATLAB 中,用户可以利用各种函数和工具箱轻松地完成复杂的数学计算和工程任务。
【2.平滑曲线的绘制方法】在 MATLAB 中,我们可以使用曲线拟合工具箱来实现点之间平滑曲线的绘制。
以下是具体的操作步骤:1) 首先,打开 MATLAB 软件,并创建一个新的脚本文件。
2) 在脚本中,输入以下命令来加载曲线拟合工具箱:```matlabclc;clear;load curvefit;```3) 接下来,定义需要绘制平滑曲线的点。
例如,假设我们有以下五个点:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 2];```4) 使用`cftool`函数创建一个曲线拟合对象,并指定拟合类型。
例如,我们可以使用线性拟合(`lin`)或者二次拟合(`quad`):```matlabf = cftool(@(x) lin(x, y), x, y);```5) 使用`fit`函数进行曲线拟合:```matlab[fit_result, fit_obj] = fit(f, x, y);```6) 最后,使用`plot`函数绘制平滑曲线:```matlabplot(x, y, "o", x, fit_result(1:length(x)), "-");xlabel("x");ylabel("y");title("平滑曲线示例");grid on;```【3.应用实例】假设我们有以下一组数据,需要绘制点之间的平滑曲线:```matlabx = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];```我们可以按照上述步骤,使用 MATLAB 绘制平滑曲线。
MATLAB绘制平滑曲线
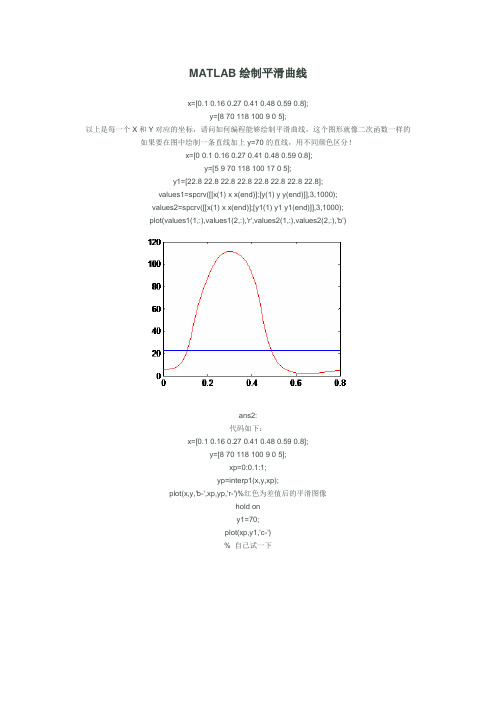
MATLAB绘制平滑曲线x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];以上是每一个X和Y对应的坐标,请问如何编程能够绘制平滑曲线,这个图形就像二次函数一样的如果要在图中绘制一条直线加上y=70的直线,用不同颜色区分!x=[0 0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[5 9 70 118 100 17 0 5];y1=[22.8 22.8 22.8 22.8 22.8 22.8 22.8 22.8];values1=spcrv([[x(1) x x(end)];[y(1) y y(end)]],3,1000);values2=spcrv([[x(1) x x(end)];[y1(1) y1 y1(end)]],3,1000);plot(values1(1,:),values1(2,:),'r',values2(1,:),values2(2,:),'b')ans2:代码如下:x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];xp=0:0.1:1;yp=interp1(x,y,xp);plot(x,y,'b-',xp,yp,'r-')%红色为差值后的平滑图像hold ony1=70;plot(xp,y1,'c-')% 自己试一下ans3:x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];X=linspace(0,.9);Y=spline(x,y,X);plot(x,y,'ro',X,Y,X,70+0*X)another file:>help smooth自己查一下帮助another question:x有90个值,Y也有90个值,一一对应,用PLOT(x,y)后是折线,请问怎样把它改为平滑曲线,谢谢!ans:平滑曲线的话,建议你用样条插值。
matlab二次指数平滑法预测

matlab二次指数平滑法预测二次指数平滑法是一种常用的时间序列预测方法,它基于指数平滑法的基础上,进一步考虑了二次趋势的影响,从而提高了预测的准确性和稳定性。
本文将介绍二次指数平滑法的原理和应用,并通过一个实例来演示该方法的预测效果。
二次指数平滑法是对指数平滑法的改进,指数平滑法是一种基于加权平均的时间序列预测方法。
在指数平滑法中,对于每个观测值,都赋予一个权重,权重随着观测值的远近而递减。
而二次指数平滑法在此基础上,考虑了时间序列的二次趋势,通过引入二次趋势的权重,能更好地捕捉时间序列的变化规律。
具体而言,在二次指数平滑法中,每个观测值的权重由三部分组成:一次趋势权重、二次趋势权重和平滑权重。
一次趋势权重用于计算一次趋势的预测值,二次趋势权重用于计算二次趋势的预测值,而平滑权重用于平衡一次趋势和二次趋势的影响。
通过不断迭代计算,可以得到最终的预测值。
为了更好地理解二次指数平滑法的原理,下面以某商品的销售数据为例进行演示。
假设某商品的销售数据如下表所示:时间销售量1 102 123 144 165 186 20我们需要确定一次趋势的初始预测值和二次趋势的初始预测值。
一次趋势的初始预测值可以通过一次指数平滑法来计算,而二次趋势的初始预测值可以通过一次趋势的差分来计算。
假设一次趋势的初始预测值为a1,二次趋势的初始预测值为b1,则有:a1 = 10b1 = (a1 - a0) = (10 - 0) = 10其中,a0为上一个时间点的一次趋势预测值,初始值为0。
接下来,我们需要确定一次趋势权重、二次趋势权重和平滑权重的值。
这些权重可以根据实际情况进行调整,一般情况下,一次趋势权重和二次趋势权重的和应该小于1,平滑权重的值应该在0到1之间。
假设一次趋势权重为α,二次趋势权重为β,平滑权重为γ,则有:α = 0.3β = 0.2γ = 0.5根据以上参数,我们可以开始进行二次指数平滑法的迭代计算。
首先,根据一次趋势的初始预测值和二次趋势的初始预测值,计算第一个时间点的一次趋势预测值和二次趋势预测值:a2 = α * 销售量2 + (1 - α) * (a1 + b1)b2 = β * (a2 - a1) + (1 - β) * b1接着,根据平滑权重,计算第一个时间点的最终预测值:y2 = γ * 销售量2 + (1 - γ) * (a2 + b2)重复以上步骤,可以得到每个时间点的一次趋势预测值、二次趋势预测值和最终预测值。
卡尔曼滤波二维轨迹平滑 matlab

卡尔曼滤波二维轨迹平滑 matlab卡尔曼滤波是一种常用的信号处理技术,可用于对二维轨迹进行平滑处理。
在Matlab中,我们可以使用卡尔曼滤波算法对二维轨迹数据进行处理,以减少噪声和不确定性,提高轨迹的精确度和平滑度。
卡尔曼滤波的基本原理是通过对系统的状态进行估计和修正来减小误差。
对于二维轨迹平滑问题,我们可以将轨迹的位置和速度作为系统的状态,并通过观测数据对其进行修正。
具体而言,卡尔曼滤波算法包括两个主要步骤:预测和更新。
在预测步骤中,我们使用系统的动态模型来预测下一个时刻的状态。
对于二维轨迹平滑问题,常用的动态模型是匀速模型,即假设轨迹在每个时刻以相同的速度进行运动。
通过预测过程,我们可以得到下一个时刻的位置和速度的估计值。
在更新步骤中,我们利用观测数据对预测的状态进行修正。
观测数据是指我们通过传感器或其他手段获得的实际测量值。
对于二维轨迹平滑问题,观测数据通常包括轨迹的位置信息。
通过与预测的状态进行比较,我们可以计算出修正量,并将其应用于预测的状态,得到更新后的状态估计值。
在Matlab中,我们可以使用卡尔曼滤波函数`kalman`来实现对二维轨迹的平滑处理。
该函数需要输入预测的状态、系统的动态模型、观测数据以及系统的协方差矩阵等参数。
具体的使用方法可以参考Matlab的帮助文档。
值得注意的是,在实际应用中,我们可能需要根据具体的需求对卡尔曼滤波算法进行调优。
例如,可以通过调整协方差矩阵的参数来权衡预测和观测的精确度。
此外,对于一些特殊情况,如轨迹存在突变或非线性运动等,可能需要采用其他的滤波算法来处理。
卡尔曼滤波是一种常用的信号处理技术,可用于对二维轨迹进行平滑处理。
在Matlab中,我们可以使用`kalman`函数来实现该算法。
通过对系统的状态进行预测和更新,可以减小误差,提高轨迹的精确度和平滑度。
然而,在实际应用中,我们需要根据具体情况进行调优,并注意特殊情况的处理。
希望本文对读者在二维轨迹平滑处理方面有所帮助。
matlab 点之间平滑曲线

matlab 点之间平滑曲线摘要:1.MATLAB 简介2.平滑曲线的绘制方法3.点之间平滑曲线的应用4.总结正文:一、MATLAB 简介MATLAB(Matrix Laboratory)是一款广泛应用于科学计算、数据分析、可视化等领域的编程软件。
它以矩阵运算为基础,提供了丰富的函数库和工具箱,使得用户可以方便地处理和分析数据。
在MATLAB 中,用户可以通过绘制点之间平滑曲线来实现数据的可视化,从而更直观地理解数据之间的关系。
二、平滑曲线的绘制方法在MATLAB 中,有多种方法可以绘制点之间平滑曲线。
这里介绍两种常用的方法:polyfit 和spline。
1.polyfitpolyfit 函数可以用于拟合一组数据点,生成多项式系数。
通过这些系数,可以绘制出平滑的曲线。
其基本语法如下:```matlabp = polyfit(x, y, n)```其中,x 和y 分别为数据点的横纵坐标,n 为多项式的阶数。
通过调整n 的值,可以控制曲线的平滑程度。
2.splinespline 函数可以用于生成样条曲线,通过指定控制点来控制曲线的形状。
其基本语法如下:```matlabs = spline(x, y, z, t)```其中,x、y 和z 分别为控制点的横纵坐标和样条值,t 为控制点的权重。
通过调整控制点的数量和权重,可以绘制出各种形状的平滑曲线。
三、点之间平滑曲线的应用点之间平滑曲线在数据可视化中具有广泛的应用。
例如,在数据拟合、信号处理、图像处理等领域,平滑曲线可以帮助我们更好地理解数据的内在规律,从而为后续的分析和处理提供有力支持。
四、总结MATLAB 作为一款强大的科学计算软件,提供了丰富的工具和方法来绘制点之间平滑曲线。
matlab计算曲线平滑度的函数

matlab计算曲线平滑度的函数曲线平滑度是研究曲线光滑程度的重要指标。
在曲线分析与处理中,我们常常需要对曲线进行平滑处理,以去除噪声、消除不必要的震荡或变化过快的部分。
在MATLAB中,有多种方法可以用于计算曲线的平滑度,下面将介绍几种常用的方法。
1. 曲线平滑度的定义曲线平滑度是指曲线在各点上具有的光滑程度。
一般来说,平滑度越高,曲线越光滑;平滑度越低,曲线越具有明显的起伏和变化。
常用的曲线平滑度指标包括曲率和弯曲度。
2. 曲线平滑度的计算方法2.1 曲率计算方法曲率是曲线在某一点上的弯曲程度。
计算曲线的曲率可以通过求取曲线的二阶导数来实现。
在MATLAB中,可以使用diff函数计算曲线点的一阶导数,再通过计算导数的导数来获得曲线的二阶导数,从而求取曲率。
2.2 弯曲度计算方法弯曲度是曲线在某一点上的弯曲角度。
计算曲线的弯曲度可以通过计算曲线的切线与法线之间的夹角来实现。
在MATLAB中,可以使用polyfit函数对曲线进行多项式拟合,从而获得曲线的切线和法线方程,进而计算弯曲度。
3. MATLAB中计算曲线平滑度的函数3.1 计算曲率的函数在MATLAB中,可以编写一个名为"compute_curvature"的函数来计算曲线的曲率。
该函数输入曲线的坐标点,并根据上述方法计算曲率并输出。
以下是该函数的示例代码:```matlabfunction curvature = compute_curvature(x, y)dx = diff(x);dy = diff(y);ddx = diff(dx);ddy = diff(dy);curvature = abs(ddx.*dy(2:end) - ddy.*dx(2:end)) ./ ...(dx(2:end).^2 + dy(2:end).^2).^1.5;end```3.2 计算弯曲度的函数在MATLAB中,可以编写一个名为"compute_torsion"的函数来计算曲线的弯曲度。
matlab 点之间平滑曲线

matlab 点之间平滑曲线在MATLAB中,要绘制点之间平滑的曲线,可以使用曲线拟合或插值的技术。
这些技术可以通过使用内置函数或自定义函数来实现。
一种常用的方法是使用插值技术。
插值是通过在给定的数据点之间拟合曲线来创建平滑曲线的过程。
MATLAB中的`interp1`函数可以用于一维插值。
它可以根据给定的数据点创建平滑的曲线。
例如,以下代码演示了如何使用`interp1`进行一维插值:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 6, 7];xi = linspace(1, 5, 100); % 在1到5之间创建100个等间距的点yi = interp1(x, y, xi, 'spline'); % 使用样条插值方法生成平滑曲线plot(x, y, 'o', xi, yi); % 绘制原始数据点和平滑曲线```另一种常用的方法是使用曲线拟合技术。
曲线拟合是通过在给定的数据点上拟合一个连续的曲线来创建平滑曲线的过程。
MATLAB中的`fit`函数可以用于曲线拟合。
以下代码演示了如何使用`fit`函数进行曲线拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 6, 7];f = fit(x', y', 'smoothingspline'); % 使用平滑样条拟合方法生成平滑曲线plot(f, x, y); % 绘制原始数据点和平滑曲线```除了`smoothingspline`之外,`fit`函数还可以使用其他拟合方法,如`polyfit`(多项式拟合)和`lowess`(局部加权回归拟合)。
这些方法可以根据数据性质的不同选择最合适的曲线拟合方法。
此外,MATLAB还提供了其他一些函数和工具箱来实现点之间平滑曲线的绘制。
例如,`smoothdata`函数可以用于平滑数据,`cscvn`函数可以用于创建二维曲线,`spline`函数可以用于一维样条插值等。
matlab二次指数平滑法预测

matlab二次指数平滑法预测二次指数平滑法是一种常用的时间序列预测方法,它可以有效地预测未来一段时间内的数据变化趋势。
本文将详细介绍二次指数平滑法的原理、计算方法以及在MATLAB中的应用。
一、原理介绍二次指数平滑法是指根据时间序列数据的特点,通过对原始数据进行加权平均来预测未来的趋势。
它的基本思想是将时间序列数据分解为趋势项、季节项和随机项三个部分,通过对趋势项和季节项进行平滑处理,得到预测结果。
二、计算方法1. 计算趋势项需要计算出原始数据的趋势项。
可以使用最小二乘法来拟合数据的趋势线,得到拟合的趋势项。
2. 计算季节项在计算季节项之前,需要先计算出原始数据的季节指数。
季节指数是指某一时间点上的数据相对于整个周期的平均值的比例。
3. 计算预测值根据计算得到的趋势项和季节项,可以计算出预测值。
预测值等于趋势项乘以季节项。
4. 更新参数在每次计算预测值之后,需要更新趋势项和季节项的参数。
可以使用加权平均法来更新参数。
三、MATLAB中的应用在MATLAB中,可以使用expsmooth函数来实现二次指数平滑法。
该函数可以通过设置参数来控制平滑法的具体计算方法。
具体步骤如下:1. 导入数据需要将需要预测的时间序列数据导入MATLAB中。
2. 设置参数设置二次指数平滑法的参数,包括平滑因子和季节周期等。
可以根据实际情况来调整这些参数的值。
3. 运行二次指数平滑法使用expsmooth函数来运行二次指数平滑法,得到预测结果。
4. 绘制预测图可以使用plot函数将原始数据和预测结果绘制在同一张图上,以便比较和分析。
四、总结二次指数平滑法是一种常用的时间序列预测方法,它可以通过对原始数据进行平滑处理,得到未来一段时间内的趋势预测。
在MATLAB中,可以使用expsmooth函数来实现二次指数平滑法,并根据实际情况来调整参数的值。
通过对预测结果的分析和比较,可以得出有关未来数据变化趋势的结论。
