数学:6.3《正弦函数y=sinx的性质》课件(沪教高一)
合集下载
高一数学 正弦函数的图象和性质课件
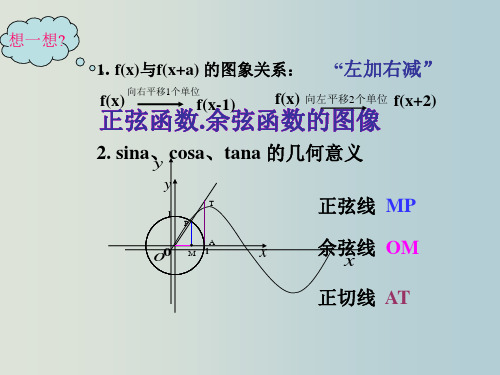
(0,0) ( ,0) (2 ,0)
简图作法 ( 五点作图法 )
图像的最低点(
3
2
,1)
(1) 列表(列出对图像形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连线(用光滑的曲线顺次连结五个点)
图像的最高点
(0,1) (2 ,1)
与x轴的交点
(
2
,0)
(
3 2
,0)
图像的最低点 ( ,1)
描点
(
3
,0.8660
)
y 1-
利做 用三 三角 角函 函数 数图 线象
-
0
2
1 -
3 2
2
x
y P
几何法: 做三角函数线得三角函数值
3
O M 1x
函数 y sin x, x 0,2 图像的几何作法 作法: (1) 等分
(2) 作正弦线
y
(3) 平移
(4) 连线
1-
P1
p1/
6
o1
M-1 1A
y 1
-6 -5 -4 -3 -2 - -1 0
2 3
fx = sinx
y
1
4 5
6 x
本节课小结 -6 -5 -4 -3 -2 - -1 0 2 3 fx = cosx
4 5
6 x
2¸ “五点法”
y
y
-
-
1-
1-
-1
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-1
o
6
3
2
正弦函数图像与性质.ppt

C.轮船招商局的轮船
D.福州船政局的军舰
[解析]
由材料信息“19世纪七十年代,由江苏沿江居民
到上海”可判断最有可能是轮船招商局的轮船。 [答案] C
[题组冲关] 1.中国近代史上首次打破列强垄断局面的交通行业是 ( )
A.公路运输
C.轮船运输
B.铁路运输
D.航空运输
解析:根据所学1872年李鸿章创办轮船招商局,这是洋务 运动中由军工企业转向兼办民用企业、由官办转向官督商 办的第一个企业。具有打破外轮垄断中国航运业的积极意 义,这在一定程度上保护了中国的权利。据此本题选C项。 答案:C
台湾 架设第一条电报线,成为中国自
出行 (1)新式交通促进了经济发展,改变了人们的通讯手段和 , 方式 转变了人们的思想观念。
(2)交通近代化使中国同世界的联系大大增强,使异地传输更为便 捷。 (3)促进了中国的经济与社会发展,也使人们的生活
多姿多彩 。
[合作探究· 提认知]
电视剧《闯关东》讲述了济南章丘朱家峪人朱开山一家, 从清末到九一八事变爆发闯关东的前尘往事。下图是朱开山 一家从山东辗转逃亡到东北途中可能用到的四种交通工具。
依据材料概括晚清中国交通方式的特点,并分析其成因。
提示:特点:新旧交通工具并存(或:传统的帆船、独轮车, 近代的小火轮、火车同时使用)。 原因:近代西方列强的侵略加剧了中国的贫困,阻碍社会发 展;西方工业文明的冲击与示范;中国民族工业的兴起与发展;
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
A
[题组冲关] 3.假如某爱国实业家在20世纪初需要了解全国各地商业信
息,可采用的最快捷的方式是
(
)
A.乘坐飞机赴各地了解 B.通过无线电报输送讯息 C.通过互联网 D.乘坐火车赴各地了解
正弦函数、余弦函数的性质 课件

3、函数y 2sin( x), x R的最小正周期是4,
3
求的值。
课堂小结
1、周期函数的定义
注:①注意定义中“每一个值”的要求
② 周期函数的周期不唯一
③周期函数不一定存在最小正周期
④如果不作特别说明,教科书中提到的周 期,一般是指最小正周期。
2、正弦、余弦函数的最小正周期为2 3、求函数周期常用的方法是(1)公式法:
余弦函数y=cosx(x∈R)是周期函数,2kπ(k∈Z且
k≠0)都是它的周期。最小正周期是2π。
今后提到的三角函数的周期,如果不加特别 说明,一般是指它的最小正周期。
(1)对于函数y sin x, x R是否有sin( ) sin 成立?
42
4
如果成立,能否说 是y sin x的周期?
正弦函数、余弦函数的性质
今天星期几? 7天后星期几? 14天后呢? 100天后呢?
世界上有许多事物都呈现“周而复始”的 变化规律,如年有四季更替,月有阴晴圆. 这种现象在数学上称为周期性,在函数领域 里,周期性是函数的一个重要性质.
y
1、三角函数线的“周而复始”变化
P
1
2、三角函数图像的“周而复始”变化 o M1 x
f(x+T) =f(x)
Sin(x+2kπ)=sinx (k z)
对于一个周期函数f(x),如果在它所有的周期中 存在一个最小的正数,那么这个最小的正数就
叫做f(x)的最小正周期。
正弦函数、余弦函数的周期性
正弦函数y=sinx(x∈R)是周期函数,2kπ(k∈Z且k≠0) 都是它的周期。最小正周期是2π。
函数
y y
Asin(x ), x R
的周期
3
求的值。
课堂小结
1、周期函数的定义
注:①注意定义中“每一个值”的要求
② 周期函数的周期不唯一
③周期函数不一定存在最小正周期
④如果不作特别说明,教科书中提到的周 期,一般是指最小正周期。
2、正弦、余弦函数的最小正周期为2 3、求函数周期常用的方法是(1)公式法:
余弦函数y=cosx(x∈R)是周期函数,2kπ(k∈Z且
k≠0)都是它的周期。最小正周期是2π。
今后提到的三角函数的周期,如果不加特别 说明,一般是指它的最小正周期。
(1)对于函数y sin x, x R是否有sin( ) sin 成立?
42
4
如果成立,能否说 是y sin x的周期?
正弦函数、余弦函数的性质
今天星期几? 7天后星期几? 14天后呢? 100天后呢?
世界上有许多事物都呈现“周而复始”的 变化规律,如年有四季更替,月有阴晴圆. 这种现象在数学上称为周期性,在函数领域 里,周期性是函数的一个重要性质.
y
1、三角函数线的“周而复始”变化
P
1
2、三角函数图像的“周而复始”变化 o M1 x
f(x+T) =f(x)
Sin(x+2kπ)=sinx (k z)
对于一个周期函数f(x),如果在它所有的周期中 存在一个最小的正数,那么这个最小的正数就
叫做f(x)的最小正周期。
正弦函数、余弦函数的周期性
正弦函数y=sinx(x∈R)是周期函数,2kπ(k∈Z且k≠0) 都是它的周期。最小正周期是2π。
函数
y y
Asin(x ), x R
的周期
沪教版高中数学高一下册-6.1.1 正弦函数、余弦函数的图像 课件 (共12张PPT)

最高点
(
3 2
,0)
零点
3 2
o
2
零点 2
x
-1
最低点
(
2
,0)
(,1)
(0,1)
( ,0) ( ,-1) 2
(3 0 )
2
( 2 ,1)
“五点作图法”
例1 画出函数y=1+sinx,x[0, 2]的简图:
x
0
2
3
2
2
sinx
0
1
0
-1
0
y=1+sinx 1
2
1
0
1
步骤:
1.列表 2.描点 3.连线
6.1 正弦、余弦 函数的图象
正弦函数的定义
实 一 一对应 数
唯一确定
正
角
弦
一对多 值
任意给定的一个实数x,有唯一确定的值sinx 与之对应。由这个法则所建立的函数 y=sinx 叫做正弦函数,其定义域为R。
函数 y sin x, x 0,2图 象的几何作法
2
2
3
5 6
o1
7
6
4
3
3
2
y
3
6
1
o
3
2
x
2
2
-1
y cx ox s0 ,2
练习:
P83 1.2.3 练习册:P35 A组 1.2
P37 B组1
我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。自我激 组成部分,主要表现在对于在压力或者困境中,个体自我安慰、自我积极暗示、自我调节的能力,在个体克服困难、顶住压力、勇对挑战等情况下,都发挥着关键性的 有弹性,经常表现出反败为胜、后来居上、东山再起的倾向,而缺乏这种能力的人,在逆境中的表现就大打折扣,表现为过分依赖外界的鼓励和支持。一个小男孩在自 对自己大喊:“我是世界上最棒的棒球手!”然后扔出棒球,挥动……但是没有击中。接着,他又对自己喊:“我是世界上最棒的棒球手!”扔出棒球,挥动依旧没有 和球,然后用更大的力气对自己喊:“我是世界上最棒的棒球手!”可是接下来的结果,并未如愿。男孩子似乎有些气馁,可是转念一想:我抛球这么刁,一定是个很 喊:“我是世界上最棒的挥球手!”其实,大多数情况下,很多人做不到这看似荒谬的自我鼓励,可是,这故事却深深反映了这个男孩子自我鼓励下的执著,而这执著
(
3 2
,0)
零点
3 2
o
2
零点 2
x
-1
最低点
(
2
,0)
(,1)
(0,1)
( ,0) ( ,-1) 2
(3 0 )
2
( 2 ,1)
“五点作图法”
例1 画出函数y=1+sinx,x[0, 2]的简图:
x
0
2
3
2
2
sinx
0
1
0
-1
0
y=1+sinx 1
2
1
0
1
步骤:
1.列表 2.描点 3.连线
6.1 正弦、余弦 函数的图象
正弦函数的定义
实 一 一对应 数
唯一确定
正
角
弦
一对多 值
任意给定的一个实数x,有唯一确定的值sinx 与之对应。由这个法则所建立的函数 y=sinx 叫做正弦函数,其定义域为R。
函数 y sin x, x 0,2图 象的几何作法
2
2
3
5 6
o1
7
6
4
3
3
2
y
3
6
1
o
3
2
x
2
2
-1
y cx ox s0 ,2
练习:
P83 1.2.3 练习册:P35 A组 1.2
P37 B组1
我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。自我激 组成部分,主要表现在对于在压力或者困境中,个体自我安慰、自我积极暗示、自我调节的能力,在个体克服困难、顶住压力、勇对挑战等情况下,都发挥着关键性的 有弹性,经常表现出反败为胜、后来居上、东山再起的倾向,而缺乏这种能力的人,在逆境中的表现就大打折扣,表现为过分依赖外界的鼓励和支持。一个小男孩在自 对自己大喊:“我是世界上最棒的棒球手!”然后扔出棒球,挥动……但是没有击中。接着,他又对自己喊:“我是世界上最棒的棒球手!”扔出棒球,挥动依旧没有 和球,然后用更大的力气对自己喊:“我是世界上最棒的棒球手!”可是接下来的结果,并未如愿。男孩子似乎有些气馁,可是转念一想:我抛球这么刁,一定是个很 喊:“我是世界上最棒的挥球手!”其实,大多数情况下,很多人做不到这看似荒谬的自我鼓励,可是,这故事却深深反映了这个男孩子自我鼓励下的执著,而这执著
高一数学正弦函数y=sinx的性质
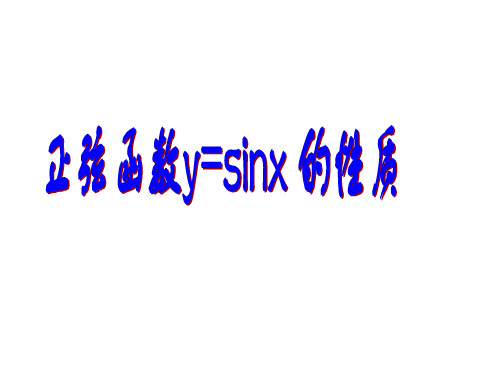
y
1
2
o
-1
2
3 2
2
x
五点法:
( 0, 0 )
( ,1) 2
( ,0)
3 ( ,1) 2
( 2 ,0)
回顾:
2、正弦函数y=sinx,x∈R的图象;
y=sinx x[0,2]
sin(x+2k)=sinx, kZ
y
1
y=sinx xR
-4
-3
-2
-
o
-1
y
1
4
7 2
3
( k Z)
2
3 2
2
2
3
4
5 2
1
0
-1
2
3 2
5 y 1 27 2x Nhomakorabea 3 y sin x的减区间: [ 2k, 2k ] 2 2
( k Z)
性质三:正弦函数 y=sinx 的单调性
增区间:
π [ 2kπ , 2kπ ] 2 2
T 2
1 练习 1、y 的定义域为( sin x A.R B.{x | x kπ ,k Z) C.[1, 0) (0, 1] D.{x | x 0}
)
练习2、y 3 sin (2 x )最小正 6 周期为( ) A.4 π B.2 π Cπ . D.
2
练习3、下列函数为偶函数的 是( ) A. y sin | x | B. y sin 2 x C. y sin x D. y sin x 1
y= -1
思考:y=sinx,x∈R的图象为什么会重复出现形 状相同的曲线呢?
1
2
o
-1
2
3 2
2
x
五点法:
( 0, 0 )
( ,1) 2
( ,0)
3 ( ,1) 2
( 2 ,0)
回顾:
2、正弦函数y=sinx,x∈R的图象;
y=sinx x[0,2]
sin(x+2k)=sinx, kZ
y
1
y=sinx xR
-4
-3
-2
-
o
-1
y
1
4
7 2
3
( k Z)
2
3 2
2
2
3
4
5 2
1
0
-1
2
3 2
5 y 1 27 2x Nhomakorabea 3 y sin x的减区间: [ 2k, 2k ] 2 2
( k Z)
性质三:正弦函数 y=sinx 的单调性
增区间:
π [ 2kπ , 2kπ ] 2 2
T 2
1 练习 1、y 的定义域为( sin x A.R B.{x | x kπ ,k Z) C.[1, 0) (0, 1] D.{x | x 0}
)
练习2、y 3 sin (2 x )最小正 6 周期为( ) A.4 π B.2 π Cπ . D.
2
练习3、下列函数为偶函数的 是( ) A. y sin | x | B. y sin 2 x C. y sin x D. y sin x 1
y= -1
思考:y=sinx,x∈R的图象为什么会重复出现形 状相同的曲线呢?
正弦函数的性质

π
度 为
,k ∈ Z
周 期 的 一 半
变式:求函数 的单调区间. 变式 求函数 y=2sin(-x )的单调区间 的单调区间
解: y = 2 sin(− x) = −2 sin x Q
函数在 [ −
π
2
π
2
+2kπ, 2 +2kπ],k∈Z 上单调递减 π π ∈
3π 2
π
思考:令 思考 令t=-x,则y=2sint 则
Q
函数在 [
+2kπ, π
+2kπ],k∈Z上单调递增 π ∈
不通过求值,比较大小: 例3 不通过求值,比较大小: (1) sin 20 , sin170 (3) sin(− 23π ) 5 解(2) Q ,
0
0
(2) sin( −
)
π
18
), sin( −
π
10
)
π π π π Q 又 y=sinx 在[− , ]上是增函数 − <− <− < 2 2 2 10 18 2 π π sin( − ) < sin(− ) 方法归纳: 方法归纳:利用
再看正弦函数,由诱导公式 一) 再看正弦函数 由诱导公式(一 由诱导公式
sin( x + 2kπ ) = sin x, k ∈ Z
即自变量x的值每增加或减少 即自变量 的值每增加或减少 值重复出现(函数值不变 函数值不变)! 值重复出现 函数值不变
的整数倍,正弦函数的 2π 的整数倍 正弦函数的
一般地,对于函数 如果存在一个非零常数 一般地 对于函数f(x),如果存在一个非零常数 使得定义域 对于函数 如果存在一个非零常数T,使得定义域 内的每一个 值都满足: 每一个x值都满足 内的每一个 值都满足
高一数学正弦函数y=sinx的性质
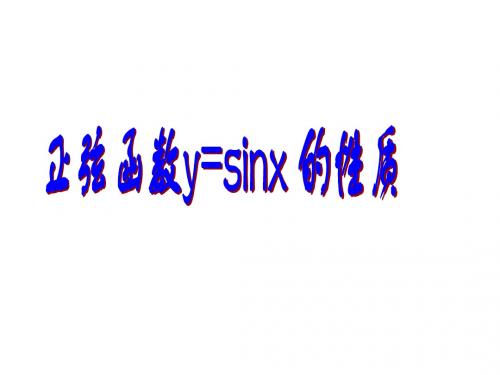
例1、下列各等式能否成立?为什么? (1)2sinx=3; (2)sin2x=0.5
1 sin x 1
例2、设sinx=t-3,x∈R,求t的取值范围。
例3 求下列函数的最值,并求出相应 的x值。 (1) y=2sinx (2)y=sinx+2 (3)y=sin2x
正弦函数 y=sin x(x∈R) 的图象
练习4、y 2 sin x的最大值及取得 最大值时x的值为( A. y 3,x B. y 1,x )
2 2k(k Z)
2
C. y 3,x D. y 1,x
2
2k(k Z) 2kπ (k Z)
2
; / 家具ERP 家具MES 家具生产管理软件 ;
7 2
5 2
2
3 2
5 2
7 2
x
f( x) sin ( x) sin x f(x)
性质四:奇偶性
正弦曲线关于原点(0,0)对称;
正弦函数f(x)=sinx为奇函数。
y
1
4 3 2
3 2
2234 Nhomakorabea
7 2
5 2
2
3 2
2π x y=sinu的周期为 T 8 (2)y sin 4 u →u+2π 2 (3)y A sin ( x ),(A , 0) 3x →3x+2π ( 30x )
T ) f ( x) 2 分析:令3x=u T 3
2 x xx x ? 2 3 T
定义域为R 值域为[-1,1]
y
1
4 3 2
正弦函数、余弦函数的性质 课件

途径:利用单位圆中正弦线来解决.
y
1
..
.o1 .
..
A
o
/2
.
3/2 2 x
-1
函数y=sinx,x[0,2]的图象
1.几何法作图:
3 4
4
3
y
2
1
●
●
●
●
6
●
7 4 63
3 2
5 3
11 6
2
●
O
2
5
●
632 3 6
●
●
x
●
7 -1
4
●
●
●
y=sinx (x∈[0, 2π] )
思考:如何画函数y =sinx(x∈R)的图象?
y
-1
o
x
思考2:一般地,函数y=f(x+a)(a>0)的图象 是由函数y=f(x)的图象经过怎样的变换而得 到的?
向左平移a个单位.
思考3:设想由正弦函数的图象作出余弦函 数的图象,那么先要将余弦函数y=cosx转化 为正弦函数,你可以根据哪个公式完成这个 转化?
二、余弦函数y=cosx(x∈R)的图象
1.正弦线、余弦线的概念
设任意角α的终边与 单位圆交于点P.过点P 做x轴的垂线,垂足为M.
y α 的终边
P(x,y)
oMx
则有向线段MP叫做角α的正弦线.
有向线段OM叫做角α的余弦线.
正弦函数y =sinx与余弦函数y=cosx的定义域都为R
一、正弦函数 y =sinx(x∈R)的图象
1.几何法作图: 问题:如何作出正弦函数的图象?
y=sinx x[0,2]
sin(x+2k)=sinx, kZ
y
1
..
.o1 .
..
A
o
/2
.
3/2 2 x
-1
函数y=sinx,x[0,2]的图象
1.几何法作图:
3 4
4
3
y
2
1
●
●
●
●
6
●
7 4 63
3 2
5 3
11 6
2
●
O
2
5
●
632 3 6
●
●
x
●
7 -1
4
●
●
●
y=sinx (x∈[0, 2π] )
思考:如何画函数y =sinx(x∈R)的图象?
y
-1
o
x
思考2:一般地,函数y=f(x+a)(a>0)的图象 是由函数y=f(x)的图象经过怎样的变换而得 到的?
向左平移a个单位.
思考3:设想由正弦函数的图象作出余弦函 数的图象,那么先要将余弦函数y=cosx转化 为正弦函数,你可以根据哪个公式完成这个 转化?
二、余弦函数y=cosx(x∈R)的图象
1.正弦线、余弦线的概念
设任意角α的终边与 单位圆交于点P.过点P 做x轴的垂线,垂足为M.
y α 的终边
P(x,y)
oMx
则有向线段MP叫做角α的正弦线.
有向线段OM叫做角α的余弦线.
正弦函数y =sinx与余弦函数y=cosx的定义域都为R
一、正弦函数 y =sinx(x∈R)的图象
1.几何法作图: 问题:如何作出正弦函数的图象?
y=sinx x[0,2]
sin(x+2k)=sinx, kZ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦函数 y=sin x(x∈R) 的图象
定义域为R 值域为[-1,1]
y
1
y=1
4
3
2
7 2
5 - 3 21 2
0
2
2
-1
x 2kπ(k Z)
2
x 2kπ(k Z)
2
2
3
4
3 y 1 5
7
x
2
2
2
y= -1
思考:y=sinx,x∈R的图象为什么会重复出现形 状相同的曲线呢?
思考:观察正弦线变化范围,并总结sinx的性质.
x 2kπ(k Z) sinx最大为1
2
x 3 2kπ((kkZ))
22
sinx最小为-1
性质一:正弦函数 y=sinx 定义域和值域
定义域为R,值域为[-1,1]
x
π
2
2kπ(k
Z)时,ymax
1;
x
π
2
2kπ(k
Z)时,ymin
2
3 2
3
4
5
7
x
2
2
性质一:定义域和值域
定义域为R,值域为[-1,1]
增性性性减x质x质质区的y区四三二周间π:: :π2间2A期奇单 周:s[:i偶[为n调 期2(2性k性 性T2kωππx2正((ω22πkφ弦kTπkkπ函),,数(3ZππZ22)f)A(时x时220)kk,,,ππ=ωsy]]yimnmaixxn0为,((x奇1;kk函1R;数) ZZ。))
1;
例1、下列各等式能否成立?为什么? (1)2sinx=3; (2)sin2x=0.5
1 sin x 1
例2、设sinx=t-3,x∈R,求t的取值范围。
例3 求下列函数的最值,并求出相应 的x值。 (1) y=2sinx (2)y=sinx+2 (3) y=(sinx-1)2+2 (4)y=sin2x
y
1
4
3
2
7 2
5
3
2
2
2
2 -1
2
3 2
3
4
5
7
x
2
2
sin(x+2kπ)=sinx(k∈Z)
f(x 2k) f(x),(k Z)
性质二 周期性
一般地,对于函数f(x),如果存在一个非 零常数T,使得定义域内的 每一个x值,都满 足f(x+T)=f(x),那么函数f(x)就叫做 周期函数,非零常数T叫做这个函数的周期。
(2)y sin 2x
f (x) sin x
y
1
4
3
2
7 2
5
3
2
2
2
2 -1
2
3 2
3
4
5
7
x
2
2
f( x) sin( x) sin x f(x)
性质四:奇偶性
正弦曲线关于原点(0,0)对称; 正弦函数f(x)=sinx为奇函数。
y
1
4
3
2
7 2
5
3
2
2
2
2
-1
y 1
o
2
2
-1
五点法:
(0,0) ( ,1) ( ,0)
2
3
2
x
2
(3 ,1) (2 ,0)
2
回顾:
2、正弦函数y=sinx,x∈R的图象;
sin(x+2k)=sinx, kZ
yபைடு நூலகம்sinx x[0,2]
y=sinx xR
y
-4 -3
-2
1
- o
-1
2
3
4
5 6 x
2
2
练习1、y 1 的定义域为(
)
sin x
A.R
B.{x | x kπ,k Z)
C.[1,0)(0,1]
D.{x | x 0}
练习2、y 3sin(2x )最小正
6 周期为( )
A.4π
B.2π
Cπ.
D.
2
练习3、下列函数为偶函数的是( )
A.y sin | x |
B.y sin 2x
2
21 2
0
2
2
3 y 1 5
7
x
2
2
2
-1
y sin x的减区间:[ 2k,3 2k ] (k Z)
2
2
性质三:正弦函数 y=sinx 的单调性
增区间:
[ 2kπ,π 2kπ]
2
2
(k Z)
减区间:
[ 2kπ,3π 2kπ]
2
2
(k Z)
例5、求下列函数的单调区间: (1)y 1 sin x
C.y sin x
D.y sin x 1
练习4、y 2 sin x的最大值及取得 最大值时x的值为( )
A.y 3,x
2
B.y 1,x 2k(k Z)
2
C.y 3,x 2k(k Z)
2
D.y 1,x 2kπ(k Z)
2
回顾: 1、正弦函数y=sinx,x∈[0,2π]的图象;
sin(等x式si2n(kπ4 )2)sinsinx,4 能x 否R说,明k 0
是正弦函数y sin x的周期?为什么?
2
性质二:周期性
对于一个周期函数f(x),如果在它的所有周 期中存在一个最小的正数,那么这个最小的 正数就叫做它的最小正周期。
sin x的周期:...... 4、 2、2、4、6 ......
例如:y=sinx的最小正周期T=2π
例4求下列函数的周期:f(x T ) f(x)
(1)y sin 3x
(2)y sin x 4
分析:令3x=Tu 2
3
y=sinu的周期为2π
T 8
u →u+2π
(3)y Asin(x3x →)3x,+2(πA(30x,2)0)
T xx2xx23?
3
性质二:周期性
正弦函数y sin x的周期2kπ(k Z, k 0)
T 2
y Asin(ωx φ)(A 0,ω 0, x R)
的周期为T
2π ω
正弦函数 y=sin x(x∈R) 的图象
y sin x的增区间:[ 2k, 2k ]
2
2
y
1
(k Z)
4
3
2
2
3
4
7
5 - 3
