816.几何不等式初步-奥数精讲与测试8年级
八年级数学几何中的最值问题
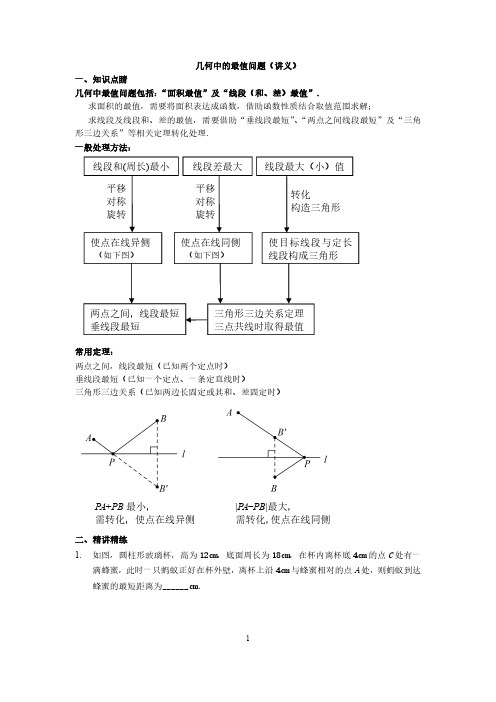
几何中的最值问题(讲义)一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.一般处理方法:常用定理:两点之间,线段最短(已知两个定点时)垂线段最短(已知一个定点、一条定直线时)三角形三边关系(已知两边长固定或其和、差固定时)二、精讲精练1.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm.线段和(周长)最小转化构造三角形两点之间,线段最短垂线段最短PA +PB 最小,需转化,使点在线异侧|PA -PB |最大,需转化,使点在线同侧线段差最大线段最大(小)值三角形三边关系定理三点共线时取得最值平移对称旋转使点在线异侧(如下图)使点在线同侧(如下图)使目标线段与定长线段构成三角形平移对称旋转第1题图第2题图2.如图,点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP2,则△PMN周长的最小值为.3.如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值为.第3题图第4题图4.如图,在菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,则PK+QK的最小值为.5.如图,当四边形PABN的周长最小时,a=.第5题图第6题图6.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,则点F的坐标为.7.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=8,B到MN的距离BD=5,CD=4,-的最大值等于.P在直线MN上运动,则PA PB第7题图第8题图8.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图-的值最大的点,Q是y轴上使得QA+QB的值最小的所示.若P是x轴上使得PA PB⋅=.点,则OP OQ9.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_________.第9题图第10题图10.如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD,则CD长度的最小值为.11.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是________.2,另两边长度不变,则点P到原点的最大距离变为若将△ABP中边PA的长度改为2_________.第11题图第12题图12.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为.13.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.(1)当P落在线段CD上时,PD的取值范围为;(2)当P落在直角梯形ABCD内部时,PD的最小值等于.14.在△ABC中,∠BAC=120°,AB=AC=4,M、N两点分别是边AB、AC上的动点,将△AMN沿MN翻折,A点的对应点为A′,连接BA′,则BA′的最小值是_________.几何中的最值问题(作业)1.如图,在梯形ABCD中,AB∥CD,∠BAD=90°,AB=6,对角线AC平分∠BAD,点E在AB上,且AE=2(AE<AD),点P是AC上的动点,则PE+PB的最小值是__________.第1题图第2题图2.在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________cm(结果不取近似值).3.如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,点M为BC上一动点,则A′M的最小值为.第3题图第4题图AB ∠BAC=45°,∠BAC的平分线交BC于点D,点M,4.如图,在锐角△ABC中,42N分别是AD和AB上的动点,则BM+MN的最小值为___________.5.在Rt△ACB中,∠ACB=90°,AC=6,BC=8,P、Q两点分别是边AC、BC上的动点,将△PCQ沿PQ翻折,C点的对应点为C',连接A C',则A C'的最小值是_________.第5题图第6题图6.如图,在△ABC 中,∠ACB=90°,AC=4,BC=2,点A、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是.7.一次函数y 1=kx -2与反比例函数y 2=m x (m <0)的图象交于A ,B 两点,其中点A 的坐标为(-6,2)(1)求m ,k 的值;(2)点P 为y 轴上的一个动点,当点P 在什么位置时|PA -PB |的值最大?并求出最大值.8.已知点A (3,4),点B 为直线x =-1上的动点,设B (-1,y ).(1)如图1,若点C (x ,0)且-1<x <3,BC ⊥AC ,求y 与x 之间的函数关系式;(2)如图2,当点B 的坐标为(-1,1)时,在x 轴上另取两点E ,F ,且EF =1.线段EF 在x 轴上平移,线段EF 平移至何处时,四边形ABEF 的周长最小?求出此时点E 的坐标.图1图29.如图,已知平面直角坐标系中A,B两点的坐标分别为A(2,-3),B(4,-1).(1)若P(p,0)是x轴上的一个动点,则当p=________时,△PAB的周长最短;(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=________时,四边形ABDC 的周长最短;(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0),N(0,n),使四边形ABMN的周长最短?若存在,请写出m和n的值;若不存在,请说明理由.中考数学几何中的最值问题综合测试卷一、单选题(共7道,每道10分)1.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底5cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿5cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为()cmA. B.15 C. D.122.如图,在矩形ABCD中,AB=2,AD=4,E为CD边的中点,P为BC边上的任一点,那么,AP+EP的最小值为()A.3B.4C.5D.63.如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值为()A. B. C.6 D.34.如图,当四边形PABN的周长最小时,a=().A. B. C. D.5.如图所示,已知A(,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()A. B.(1,0) C. D.6.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为边AB上一动点,且PE⊥AC于点E,PF⊥BC于点F,则线段EF长度的最小值是()A. B. C. D.7.如图,正方形ABCD边长为2,当点A在x轴上运动时,点D随之在y轴上运动,在运动过程中,点B到原点O的最大距离为()A. B. C. D.。
八年级上册湘教版数学几何题及答案

八年级上册湘教版数学几何题及答案一、试题部分1. 三角形相关(20分)已知三角形ABC,∠A = 60°,∠B = 40°,求∠C的度数。
(5分)一个三角形的三条边分别为3cm,4cm,5cm,判断这个三角形是什么类型的三角形(按角分类)。
(5分)在等腰三角形ABC中,AB = AC,∠A = 80°,求∠B的度数。
(10分)2. 四边形部分(30分)平行四边形ABCD中,AB = 6cm,BC = 8cm,求平行四边形ABCD的周长。
(5分)矩形的长为8cm,宽为6cm,求矩形的对角线长度。
(5分)菱形的对角线分别为6cm和8cm,求菱形的面积。
(10分)在梯形ABCD中,AD∥BC,AD = 3cm,BC = 7cm,高为4cm,求梯形ABCD的面积。
(10分)3. 相似图形(25分)已知三角形ABC∽三角形DEF,AB = 3cm,DE = 6cm,若三角形ABC的面积为9cm²,求三角形DEF的面积。
(10分)两个相似多边形的相似比为2:3,其中一个多边形的周长为20cm,求另一个多边形的周长。
(15分)4. 视图与投影(25分)一个圆柱的底面直径为4cm,高为6cm,画出它的主视图、左视图和俯视图。
(10分)已知一个物体在灯光下的影子长为5m,物体本身高为2m,光源到物体的水平距离为3m,求光源到地面的垂直距离。
(15分)二、答案与解析1. 三角形相关答案:因为三角形内角和为180°,∠C = 180° - ∠A - ∠B = 180° - 60° - 40° = 80°。
因为3²+4² = 9 + 16 = 25 = 5²,满足勾股定理的逆定理,所以这个三角形是直角三角形。
因为AB = AC,所以∠B=∠C,又因为∠A = 80°,∠B=(180° - 80°)÷2 = 50°。
几何综合压轴题分类专题(考点梳理与题型分类讲解)(北师大版)(解析版)—24-25学年八年级数学上册

几何综合压轴题分类专题第一部分【考点目录】【考点1】特殊平行四边形与相似综合【考点1】矩形性质与判定与图形相似综合 (1)【考点2】菱形性质与判定与图形相似综合 (7)【考点3】正方形性质与判定与图形相似综合 (10)【考点2】特殊四边形几何变换中的相似【考点4】图形相似中的平行四边形几何变换 (14)【考点5】图形相似中的矩形几何变换 (19)【考点6】图形相似中的菱形几何变换 (27)【考点7】图形相似中的正方形几何变换 (33)第二部分【考点展示与方法点拨】【考点1】矩形性质与判定与图形相似综合【1-1】(24-25九年级上·陕西渭南·期中)【问题探究】(1)如图1,在矩形ABCD 中,点、F 分别是AB BC 、边的中点,连接BD EF ,,求证:BCD FBE ∽△△;【问题拓展】(2)如图2,在四边形ABCD 中,AD BC ∥,90BCD Ð=°,点E 是AB 的中点,点F 是BC 边上一点,连接EF BD ,交于点G ,2AD CF =.①试说明GB GF =;②若23AD CD =,EF AB ^,求GE GB的值.【答案】(1)见解析;(2)见解析;(3)35【分析】问题探究:根据矩形的性质可得AB CD =,90EBF C Ð=Ð=°,根据点E F ,分别是AB BC ,的中点,可得12BE BF AB BC ==,即可求证;问题拓展:①取BD 的中点H ,连接EH HC 、,得EH 是ABD △的中位线,根据已知条件可得EH 平行且等于FC ,进而可得EFCH 是平行四边形,得EF HC ∥,则GFB HCB Ð=Ð,根据直角三角形中斜边上的中线等于斜边的一半得出HB HC =,进而可得HBC HCB Ð=Ð,等量代换可得GBF GFB Ð=Ð,等角对等边,即可得证;②过点F 作FM AD ^,则四边形MFCD 是矩形,连接AG AF 、,设4CD MF x ==,则6AD x =,3CF MD x ==,可得3AM x =,5AF x =,又可得EF 垂直平分AB ,得到AG BG =,AF BF =,即可证明()SSS AFG BFG V V ≌,得到GAF GBF Ð=Ð,GFA GFB Ð=Ð,进而由①BG FG =,可得GAF GBF GFB GFA Ð=Ð=Ð=Ð,设GAF GBF GFB GFA a Ð=Ð=Ð=Ð=,则2BGE a =∠,2AFB a Ð=,即可由AD BC ∥得到2BGE MAF a Ð=Ð=,即可证明BEG FMA V V ∽,得到EG BG AM FA =,即可得3355AM x FA GE GB x ===.解:问题探究:四边形ABCD 是矩形,∴AB CD =,90EBF C Ð=Ð=°,∵E F ,分别是AB BC ,的中点 ,∴12BE BF AB BC ==,即12BE BF CD BC ==,∴BCD FBE ∽△△;问题拓展:如图所示,取BD 的中点H ,连接EH HC 、,∵E 是AB 的中点,H 是BD 的中点,∴12EH AD =,EH AD ∥,又∵2AD CF =,∴EH CF =,∵AD BC ∥,∴EH FC ∥,∴四边形EHCF 是平行四边形,∴EF CH ∥ ,∴GFB HCB Ð=Ð,又∵90BCD Ð=°,H 是BD 的中点,∴12HC BD BH ==,∴HBC HCB Ð=Ð,∴GBF GFB Ð=Ð,∴GB GF =;②如图所示,连接AG AF 、,过点F 作FM AD ^,则四边形MFCD 是矩形,90FMA Ð=°,∵2AD CF =,23AD CD =,∴设4CD MF x ==,则6AD x =,3CF MD x ==,∴633AM AD MD x x x =-=-=,∴5AF x ==,∵90BEF Ð=°,∴EF AB ^,又∵E 是AB 的中点,∴EF 垂直平分AB ,∴AG BG =,AF BF =,∵FG FG =,∴()SSS AGF BGF V V ≌,∴GAF GBF Ð=Ð,GFA GFB Ð=Ð,由①,BG FG =,∴GBF GFB Ð=Ð,∴GAF GBF GFB GFA Ð=Ð=Ð=Ð,设GAF GBF GFB GFA a Ð=Ð=Ð=Ð=,则2BGE a =∠,2AFB a Ð=,∵AD BC ∥,∴2MAF AFB a Ð=Ð=,∴BGE MAF Ð=Ð,又∵90BEG FMA Ð=Ð=°,∴BEG FMA V V ∽,∴EG BG AM FA =,∴3355AM x FA GE GB x ===【点拨】本题考查了矩形的性质,相似三角形的性质与判定,平行四边形的性质与判定,三角形中位线的性质,直角三角形中斜边上的中线等于斜边的一半,全等三角形的性质与判定,线段垂直平分线的性质,平行线的性质,勾股定理,正确作出辅助线是解题的关键.【1-2】(24-25九年级上·山西运城·阶段练习)如图,矩形ABCD 中,6AB =,3BC =.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则AE 的长是( )A B .94C .154D .3.5【答案】C【分析】本题考查了菱形的性质,全等三角形的判定和性质,相似三角形的判定和性质,熟练运用定理是解题的关键.连接EF 交AC 于O ,由四边形EGFH 是菱形,得到EF AC ^,OE OF =,由于四边形ABCD是矩形,得到90B D Ð=Ð=°,AB CD ∥,通过CFO AEO △≌△,得到AO CO =,求出12AO AC ==根据AOE ABC V V ∽,即可得到结果.解;连接EF 交AC 于O ,Q 四边形EGFH 是菱形,EF AC \^,OE OF =,Q 四边形ABCD 是矩形,90B D \Ð=Ð=°,AB CD ∥,ACD CAB \Ð=Ð,在CFO △与AOE △中,FCO OAB FOC AOE OF OE Ð=ÐìïÐ=Ðíï=î,(AAS)CFO AEO \△≌△,AO CO \=,AC ===Q12AO AC \==CAB CAB Ð=ÐQ ,90AOE B Ð=Ð=°,AOE ABC \V V ∽,AE AC,=154AE \=.故选:C【1-3】(24-25九年级上·山东济南·阶段练习)如图,在矩形ABCD 中,DE 平分ADC Ð,交BC 于点E ,EF AE ^,交CD 于点F ,以AE EF ,为边,作矩形AEFG ,FG 与DA 相交于点H .若34CEAH ==,,则AE = .【答案】【分析】本题考查了全等三角形的判定与性质、相似三角形的判定和性质、矩形的性质和正方形的判定与性质,首先证明Rt Rt ASA ECF ABE V V ≌(),推导出AE EF =,结合矩形AEFG ,推导出四边形AEFG 为正方形,然后利用GAH FEC G C ÐÐÐÐ=,=,推导出GAH CEF V V ∽,AG CE AH EF=,进而得到AG EF AH CE ×=×,代入数据得到24312AE =´=,进而即可得出答案.解:∵四边形ABCD 是矩形,∴90AD BC CD AB B C =Ð=Ð=°P ,,,∴90AEB EAB Ð+Ð=°,∵EF AE ^,∴9090AEF AEB CEF Ð=°Ð+Ð=°,,∴EAB CEF Ð=Ð,∵DE 平分ADC Ð,∴1452CDE ADC ÐÐ==°,在Rt CDE △中,CE CD AB ==,在Rt ECF V 和Rt ABE △中,B CCE AB EAB CEFÐ=Ðìï=íï=Ðî,∴Rt Rt ASA ECF ABE V V ≌(),∴AE EF =,在矩形AEFG 中,AG EF AE ==,∴四边形AEFG 为正方形,∴90G Ð=°,∴AG EF P ,∴GAH FEC Ð=Ð,又∵G C Ð=Ð,∴GAH CEF V V ∽,∴AGCEAH EF =,∴AG EF AH CE ×=×,∴24312AE =´=,∴AE =,故答案为:【考点2】菱形性质与判定与图形相似综合【2-1】(24-25九年级上·四川成都·阶段练习)如图,在菱形ABCD 中,点G 在边CD 上,连线AG 并延长交BC 的延长线于点F ,连结BD 交AF 于点E ,连结CE .(1)求证:2EC EF EG =×;(2)若6AB =,3CE EG=,求CF 的长.【答案】(1)见解析 (2)12【分析】本题主要考查菱形的性质以及相似三角形的判定和性质,(1)由菱形的性质可证明DAE DCE F Ð=Ð=Ð,即可证明FEC CEG V V ∽,可得出结论;(2)由FEC CEG V V ∽可得3EC EF CG EG EC CF===,设GC x =,则3CF x =,6DG x =-,证明ADG FCG V V ∽,得出方程求解即可.(1)证明:Q 四边形ABCD 是菱形,∴ADE CDE Ð=Ð,AD CD =,AD BC ∥,∵DE DE =,∴()SAS ADE CDE △△≌,\DAE DCE Ð=Ð.∵AD BC ∥,DAE F \Ð=Ð,DAE DCE F \Ð=Ð=Ð,FEC CEG Ð=ÐQ ,\FEC CEG V V ∽,\EC EF EG EC=,2EC EF EG \=×;(2)解:Q 四边形ABCD 是菱形,6AB =,∴6AB AD CD BC ====,由(1)可知FEC CEG V V ∽,∴EC EF CG EG EC CF ==,∵3CE EG =,∴3EC EF CG EG EC CF===,设GC x =,则3CF x =,6DG DC CG x =-=-,又∵DAE F Ð=Ð,DGA CGF Ð=Ð,\ADG FCG V V ∽,\=AD DG FC CG ,\663x x x-=,解得4x =,经检验,4x =是分式方程的解,312CF x \==.【2-2】(24-25九年级上·黑龙江哈尔滨·阶段练习)如图,点E F 、分别在菱形ABCD 的边AB 、AD 上,且AE DF =,BF 交DE 于点G ,延长BF 交CD 的延长线于点H ,若2AF DF =,则DG GE的值为( )A .23B .712C .12D .34【答案】D【分析】本题考查菱形性质,相似三角形判定及性质等.根据题意设DF x =,则AE DF x ==,2AF BE x ==,3AB x =,证明HFD BFA ∽△△,HDG BEG △∽△,继而得到本题答案.解:∵四边形ABCD 是菱形,∴AB BC CD AD ===,∵2AF DF =,AE DF =,∴设DF x =,则AE DF x ==,2AF BE x ==,3AB x =,∵HD AB ∥,∴,H GBE DGH BGE Ð=ÐÐ=Ð,HFD AFB Ð=Ð,∴HFD BFA ∽△△,HDG BEG △∽△,∴12HD DF HF AB AF FB ===,∴ 1.5HD x =,∴ 1.5324HD DG x BE GE x ===,故选:D .【2-3】(24-25九年级上·广东中山·阶段练习)如图,菱形ABCD 的对角线AC 与BD 分别为8,6,过点O 作OE AD ∥交AB 于点E ,连接DE ,交AC 于点F ,过点F 作FG AD ∥交AB 于点G ,则GE = .【答案】53【分析】本题考查菱形的性质,勾股定理,三角形中位线定理,相似三角形的判定与性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.利用菱形的性质以及勾股定理求出5BC =,再证明:::2AG GE AF OF AD OE ===,可得结论.解:Q 四边形ABCD 是菱形,AC BD \^,142OA OC AC ===,132OB OD BC ===,AD BC AB ==,5BC \=,5AB BC \==,OE BC Q P ,AO AE OC EB\=,AO OC =Q ,AE EB \=,1522OE BC \==,OE BC Q P ,BC AD ∥,OE AD \∥,AFD OFE\V V ∽\12OF OE AF AD ==,FG OE Q ∥,\2AG AF GE FO==,1533GE AB \==.故答案为:53.【考点3】正方形性质与判定与图形相似综合【3-1】(2024·湖北武汉·模拟预测)如图1,在正方形ABCD 中,E 是对角线CA 延长线上的一点,线段BE 绕点B 顺时针旋转90°至BG ,连接CG .(1)求证:AE CG =;(2)如图2,连接EG 交AD 于点F ,并延长与BC 的延长线相交于点H ,若FD CG =,①求证:2FD AD AF =×;②直接写出EF BE的值.【答案】(1)见解析 (2)①见解析;②EF BE =【分析】(1)利用SAS 证明EBA GBC ≌△△,即可得出结论;(2)①根据正方形的性质,证明BAE EAF ∽△△,得AB AE BE AE AF EF==,即2AE AB AF =×,由(1)证得AE CG FD ==,即可得到2FD AD AF =×;②设FD x =,(0,0)AD m x m =>>,则AF m x =-,根据2FD AD AF =×,列出方程,解得x m =进而解决问题.(1)证明:如图1,由旋转的性质,得BE BG =,90EBG Ð=°,90EBA ABG \Ð+Ð=°,Q 四边形ABCD 是正方形,AB BC AD \==,90ABC Ð=°,90ABG GBC \Ð+Ð=°,EBA GBC \Ð=Ð,在EBA △和V GBC 中,BE BG EBA GBC AB BC =ìïÐ=Ðíï=î,(SAS)EBA GBC \V V ≌,AE CG \=;(2)解:①由旋转的性质可得90EBG Ð=°,BE BG =,EBG \V 是等腰直角三角形,45BEF \Ð=°,45BEA AEF \Ð+Ð=°,在正方形ABCD 中,45DAC BAC Ð=Ð=°Q ,135EAB EAF \Ð=Ð=°,45AFE AEF Ð+Ð=°,BEA AFE \Ð=Ð,BAE EAF \V V ∽,\AB AE BE AE AF EF==,即2AE AB AF =×,由(1)证得AE CG =,又FD CG =Q ,AE FD \=,2FD AD AF \=×,②设FD x =,(0,0)AD m x m =>>,则AF m x =-,2()x m m x \=-,整理得220x mx m +-=,\210x x m m æö+-=ç÷èø,解得x m =即FD AB \AE AB =\EF BE =【点拨】本题是相似形综合题,主要考查了相似三角形的判定与性质,正方形的性质,一元二次方程,全等三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.综合性较强,属于中考压轴题.【3-2】(23-24九年级上·江苏无锡·期中)如图,在正方形ABCD 中,5AB =,点E 是CD 边上一点,且23DE CE =,点F 是BD 上一点,若45FAE Ð=°,则AF 的长为( )A .BCD .92【答案】B 【分析】本题主要考查了正方形的性质,勾股定理,相似三角形的性质与判定,由正方形的性质得到545CD AB AD BAC ABD ======°,∠∠∠,90ABC ADE Ð=Ð=°,则由勾股定理得到AC =求出2DE =,则AE ABF ACE ∽△△,得到AB AF AC AE ==得到AF =解:如图所示,连接AC∵四边形ABCD 是正方形,∴545CD AB AD BAC ACD ABD ======°,∠∠∠,90ABC ADE Ð=Ð=°,∴AC ==∵23DE CE =,∴335CE CD ==,∴2DE =,∴AE∵45FAE BAC Ð=Ð=°,∴BAF CAE Ð=Ð,又∵45ABF ACE Ð=Ð=°,∴ABF ACE ∽△△,∴AB AF AC AE==∴AF =故选:B .【3-3】(24-25九年级上·四川成都·阶段练习)如图,正方形ABCD 中,P 为AD 上一点,PE BP ^交BC 的延长线于点E ,交CD 于点F ,若4AB =,3AP =,则EF 的长为 .【答案】6512/5512【分析】此题考查了正方形的性质,相似三角形的性质和判定,勾股定理等知识,解题的关键是掌握以上知识点.首先根据勾股定理求出5BP ==,然后证明出BAP EPB V V ∽,得到AB AP PE BP =,代数求出203PE =,然后证明出BAP PDF V V ∽,得到AB BP PD PF =,代数求出54PF =,进而利用线段的和差求解即可.解:∵四边形ABCD 是正方形,∴90A ABC D Ð=Ð=Ð=°,∵4AB =,3AP =,∴5BP ==,∵BE AP P ,∴EBP APB Ð=Ð,∵PE BP ^,∴90A BPE Ð=Ð=°,∴BAP EPB V V ∽,∴AB AP PE BP=,即435PE =,∴203PE =,∵4AD AB ==,3AP =,∴1PD AD AP =-=,∵90ABP APB FPD APB Ð+Ð=Ð+Ð=°,∴ABP FPD Ð=Ð,又∵90A D Ð=Ð=°,∴BAP PDF V V ∽,∴AB BP PD PF =,即451PF=,∴54PF =,∴6512EF PE PF =-=.故答案为:6512.【考点4】图形相似中的平行四边形几何变换【4-1】(2023·陕西西安·模拟预测)数学活动课上,老师让同学们根据下面情境提出问题并解答.问题情境:在平行四边形ABCD 中,点P 是边AD 上一点,将PDC △沿直线PC 折叠,点D 的对应点为E .数学思考:(1)“兴趣小组”提出的问题是:如图1,若点P 与点A 重合,过点E 作EF AD ∥,与PC 交于点F ,连接DF ,则四边形AEFD 是菱形.请你证明“兴趣小组”提出的问题;拓展探究:(2)“智慧小组”提出的问题是:如图2,当点P 为AD 的中点时,延长CE 交AB 于点F ,连接PF .试判断PF 与PC 的位置关系,并说明理由;问题解决:(3)“创新小组”在前两个小组的启发下,提出的问题是:如图3,当点E 恰好落在AB 边上时,6820AP PD DC ===,,,求AE 的长.【答案】(1)见解析 (2)PF PC ^,见解析 (3)5【分析】(1)由折叠的性质可知,AD AE DF EF DAF EAF ==Ð=Ð,,,再根据平行线的性质推出EFA EAF Ð=Ð,则EA EF =,进而推出AD DF EF AE ===,即可证明四边形AEFD 是菱形;(2)连接AE .由折叠的性质可知,PD PE PEC PDC DPC EPC =Ð=ÐÐ=Ð,,,由180ADC DAB Ð+Ð=°,180PEC PEF Ð+Ð=°,得到DAB PEF Ð=Ð;由点P 是AD 的中点,得到PA PD PE ==,则PAE PEA Ð=Ð,进一步证明AEF EAF Ð=Ð,得到AF EF =,证明PAF PEF △≌△,得到APF EPF Ð=Ð,再根据平角的定义得到90FPC Ð=°,则PF PC ^;(3)延长CP 交BA 的延长线于点T .设AE x =.由折叠的性质可知,20PCD PCE CD CE Ð=Ð==,,再证明T PCE Ð=Ð,得到2020EC ET AT x ===-,,证明PDC PAT △∽△,得到620820x -=,即可求出5AE =.(1)证明:由折叠的性质可知,AD AE DF EF DAF EAF ==Ð=Ð,,,∵EF AD ∥,∴DAF EFA Ð=Ð,∴EFA EAF Ð=Ð,∴EA EF =,∴AD DF EF AE ===,∴四边形AEFD 是菱形;(2)解:结论:PF PC ^.理由:连接AE .由折叠的性质可知,PD PE PEC PDC DPC EPC =Ð=ÐÐ=Ð,,,∵四边形ABCD 是平行四边形,∴180ADC DAB Ð+Ð=°,∵180PEC PEF Ð+Ð=°,∴DAB PEF Ð=Ð,∵点P 是AD 的中点,∴PA PD PE ==,∴PAE PEA Ð=Ð,∴DAB PAE PEF PEA Ð-Ð=Ð-Ð,∴AEF EAF Ð=Ð,∴AF EF =,∵PF PF =,∴()SSS PAF PEF V V ≌,∴APF EPF Ð=Ð,∵180DPC CPE EPF APF Ð+Ð+Ð+Ð=°,∴22180CPE FPE Ð+Ð=°,∴90FPC Ð=°,∴PF PC ^;(3)解:延长CP 交BA 的延长线于点T .设AE x =.由折叠的性质可知,20PCD PCE CD CE Ð=Ð==,,∵CD BT ∥,∴T DCP Ð=Ð,∴T PCE Ð=Ð,∴2020EC ET AT x ===-,,∵AT CD ∥,∴PDC PAT △∽△,∴AP AT PD CD =,∴620820x -=,∴5x =,∴5AE =.【点拨】本题主要考查了平行四边形的性质,折叠的性质,等腰三角形的性质与判定,相似三角形的性质与判定,菱形的判定,全等三角形的性质与判定等等,正确作出辅助线是解题的关键.【4-2】(23-24九年级上·陕西西安·开学考试)已知:如图1,在平行四边形ABCD 中,3cm AB =,5cm =BC ,AC AB ^,ACD V 沿AC 的方向以速度为1cm/s 匀速平移得到PMN V ;同时,点Q 从点C 出发,沿CB 方向匀速运动速度为1cm/s ,当PMN V 停止平移时,点Q 也停止运动,如图2,设运动时间为(s)(04)t t <<,则t 的值为( )s 时,:1:3QMC ABQP S S =四边形△.A .1t =B .4t =C .5t =D .t 不存在【答案】D 【分析】作PF BC ^于点F ,AE BC ^于点E ,利用面积法求AE 的长,利用勾股定理计算CE 的长,证明CPF CAE V V ∽,列式可表示PF 的长,根据面积公式计算△QCM 是面积;根据同底等高的两个三角形面积相等得:PQC MQC S S =V V ,由已知得::1:4MQC ABC S S =V V ,然后得到关于t 一元二次方程求解即可.解:作PF BC ^于点F ,AE BC ^于点E ,∵3cm AB =,5cm =BC ,AC AB ^,∴4AC ==,∵1122ABC S AB AC AE BC =´=´V ,∴1134522AE ´´=´,∴125AE =,则由勾股定理得:165CE ===,∵作PF BC ^,AE BC ^,∴AE PF ∥,∴CPF CAE V V ∽,∴CP CF PF CA CE AE==,即41612455t CF PF -==,解得:1235t PF -=,1645t CF -=,由平移的性质得,PM BC ∥,∴M 到BC 的距离1235h PF -==,∴QCM V 是面积21112336225105t CQ h t t t -=´=´´=-+;∵PM BC ∥,∴PQC MQC S S =V V ,∵:1:3QMC ABQP S S =四边形△,∴:1:4MQC ABC S S =V V ,则23614431052t t æö-+=´´ç÷èø,整理得,2312150t t -+=,∵()21243150D =--´´<,∴该方程无实数根,∴不存在某一时刻t ,:1:3QMC ABQP S S =四边形△.故选D .【点拨】本题考查了平移,勾股定理、相似三角形的性质和判定,一元二次方程根的判别式,熟练掌握平移的性质和相似三角形的判定与性质是解答本题的关键.【4-3】(20-21九年级上·全国·单元测试)如图,将平行四边形ABCD绕点D旋转,点C落在BC上的点H 处,点B恰好落在点A处,得平行四边形DHAE,若BH=2,CH=3,则DC=.【分析】由题意可求AD=BC=5,∠C=∠DHC=∠ADH=∠AHD,即可证△ADH∽△DCH,可得AD DHDC HC=,即可求DC的长.解:∵BH=2,CH=3,∴BC=5,∵四边形ABCD是平行四边形,∴AD=BC=5,AD∥CB,∴∠ADH=∠DHC,∵将平行四边形ABCD绕点D旋转,∴DH=DC,∠C=∠AHD,∵DH=DC,∴∠C=∠DHC,且∠ADH=∠DHC,∠C=∠AHD,∴∠C=∠DHC=∠ADH=∠AHD,∴△ADH∽△DCH,∴AD DH DC HC=,∴DC2=15,∴【点拨】本题考查了旋转的性质,平行四边形的性质,相似三角形的判定和性质,熟练运用这些性质,判定进行推理是本题的关键.【考点5】图形相似中的矩形几何变换【5-1】(2020·四川眉山·模拟预测)如图,矩形ABCO 中,点C 在x 轴上,点A 在y 轴上,点B 的坐标是()12,16-,矩形ABCO 沿直线BD 折叠,使得点A 落在对角线OB 上的点E 处,折痕与OA 、x 轴分别交于点D 、F .(1)直接写出线段OB 的长;(2)求直线BD 解析式;(3)若点N 在直线BD 上,在x 轴上是否存在点M ,使以M 、N 、E 、D 为顶点的四边形是平行四边形?若存在,请求出一个满足条件的点M 的坐标;若不存在,请说明理由.【答案】(1)20 (2)1102y x =-+ (3)存在,()8,0M 【分析】(1)由点的坐标的特点可得12,16CO BC ==,由矩形的性质可得90BCO Ð=°,再利用勾股定理即可求出OB 的长;(2)设OD x =,由矩形的性质得出16AD x =-,由折叠的性质得出BDA BDE @V V ,根据全等三角形的性质得出12,16AB EB AD DE x ====-,90BAD BED Ð=°=Ð,再结合勾股定理求出D 点坐标,最后利用待定系数法求解即可;(3)过点E 作EG x ^轴与点G ,过点E 作EM BD ∥,交x 轴于点M ,过点M 作MN ED ∥,交直线BD 于点N ,此时,四边形MNDE 是平行四边形,EM DE ∥,通过证明EOG BOC V :V ,利用相似三角形的性质可求出点E 的坐标,再利用待定系数法求出直线EM 解析式即可求解.解:(1)∵在矩形ABCO 中,点B 的坐标是()12,16-,∴12,16CO BC ==,90BCO Ð=°,20OB \=;(2)∵四边形ABCO 是矩形,∴12,16AB OC AO BC ====,90BAO Ð=°,设OD x =,16AD x \=-,∵矩形ABCO 沿直线BD 折叠,使得点A 落在对角线OB 上的点E 处,BDA BDE \@V V ,12,16AB EB AD DE x \====-,90BAD BED Ð=°=Ð,90DEO \Ð=°,222DE OE OD \+=,20OB =Q ,8OE OB EB \=-=,()222168x x \-+=,解得10x =,()0,10D \,设直线BD 解析式为y kx b =+,把()()12,16,0,10B D -代入,得161210k bb=-+ìí=î,解得1210k b ì=-ïíï=î,∴直线BD 解析式为1102y x =-+;(3)过点E 作EG x ^轴与点G ,过点E 作EM BD ∥,交x 轴于点M ,过点M 作MN ED ∥,交直线BD 于点N ,此时,四边形MNDE 是平行四边形,EM DE ∥,90EGO BCO \Ð=°=ÐEOG BOCÐ=ÐQ EOG BOC\V :V EO EG OGBO BC OC\==8,20,16,12EO BO BC OC ====Q 8201612EG OG \==3224,55EG OG \==2432,55E æö\-ç÷èø,∵直线BD 解析式为1102y x =-+,∴设直线EM 解析式为12y x t =-+,把点2432,55E æö-ç÷èø代入,得32124525t æö=-´-+ç÷èø解得4t =,\直线EM 解析式为142y x =-+,当0y =时,8x =,()8,0M \.【点拨】本题主要考查了四边形综合问题,求一次函数的解析式,相似三角形的判定和性质,平行四边形的性质,矩形的性质,勾股定理,解题的关键是熟知矩形的性质,折叠的问题利用勾股定理构造直角三角形进行求解,分情况讨论平行四边形的边及对角线的情况.【5-2】(2022·四川绵阳·二模)如图,在平面直角坐标系中,直线122y x =--与x 轴,y 轴分别交于点M ,点N ,矩形ABCD 的顶点,A D 分别在x 轴,y 轴上,对角线BD ∥x 轴,已知()2,0A ,()0,4D .现将直线MN 向上平移m 个单位长度,使平移后的直线恰好平分矩形ABCD 的面积,则m 的值为()A .172B .8C .9D .152【答案】A【分析】作BE x ⊥轴于E ,连接AC ,交BD 于点P ,则P 是BD 的中点,根据矩形的中心对称性可知当经过点P 时,平移后的直线恰好平分矩形ABCD 的面积,求出点N 的坐标和平移后的直线解析式,再求出平移后的直线解析式与y 轴的交点纵坐标,从而得到m 的值.解:作BE x ⊥轴于E ,连接AC ,交BD 于点P ,则P 是BD 的中点,∵对角线BD x ∥轴,()()2,0,0,4A D ,∴2,4OA BE OD ===,∵90BAD AOD Ð=Ð=°,∴90ADO DAO DAO BAE Ð+Ð=Ð+Ð=°,∴ADO BAE Ð=Ð,∵90AOD BEA Ð=Ð=°,∴ADO BAE D D :,∴AE BE OD OA=,即442AE =,∴8AE =,∴8210OE =+=,∴()10,4B ,∴()5,4P ,当0x =时,1222y x =--=-,∴()0,2N -,设平移后的直线为12y x k =-+,∵当经过点P 时,平移后的直线恰好平分矩形ABCD 的面积,∴1452k =-´+,解得132k =,∴平移后的直线为11322y x =-+,当0x =时,11313222y x =-+=,∴()1317222m =--=,∴m 的值为172,故选:A .【点拨】本题考查了一次函数的图象与几何变换,坐标与图形性质,一次函数图象上点的坐标特征,相似三角形的判定和性质,中心对称的性质等知识,明确直线经过矩形对角线的交点时平分矩形的面积是解题的关键.【5-3】(2022·四川绵阳·二模)如图,在平面直角坐标系中,直线122y x =--与x 轴,y 轴分别交于点M ,点N ,矩形ABCD 的顶点,A D 分别在x 轴,y 轴上,对角线BD ∥x 轴,已知()2,0A ,()0,4D .现将直线MN 向上平移m 个单位长度,使平移后的直线恰好平分矩形ABCD 的面积,则m 的值为()A .172B .8C .9D .152【答案】A【分析】作BE x ⊥轴于E ,连接AC ,交BD 于点P ,则P 是BD 的中点,根据矩形的中心对称性可知当经过点P 时,平移后的直线恰好平分矩形ABCD 的面积,求出点N 的坐标和平移后的直线解析式,再求出平移后的直线解析式与y 轴的交点纵坐标,从而得到m 的值.解:作BE x ⊥轴于E ,连接AC ,交BD 于点P ,则P 是BD 的中点,∵对角线BD x ∥轴,()()2,0,0,4A D ,∴2,4OA BE OD ===,∵90BAD AOD Ð=Ð=°,∴90ADO DAO DAO BAE Ð+Ð=Ð+Ð=°,∴ADO BAE Ð=Ð,∵90AOD BEA Ð=Ð=°,∴ADO BAE D D :,∴AE BE OD OA=,即442AE =,∴8AE =,∴8210OE =+=,∴()10,4B ,∴()5,4P ,当0x =时,1222y x =--=-,∴()0,2N -,设平移后的直线为12y x k =-+,∵当经过点P 时,平移后的直线恰好平分矩形ABCD 的面积,∴1452k =-´+,解得132k =,∴平移后的直线为11322y x =-+,当0x =时,11313222y x =-+=,∴()1317222m =--=,∴m 的值为172,故选:A .【点拨】本题考查了一次函数的图象与几何变换,坐标与图形性质,一次函数图象上点的坐标特征,相似三角形的判定和性质,中心对称的性质等知识,明确直线经过矩形对角线的交点时平分矩形的面积是解题的关键.【5-3】(2023·河南信阳·二模)如图,BD 为矩形ABCD 的对角线,5AB =,154BC =,把CD 绕点C 旋转,点D 的对应为点E ,当CE BD ∥时,DE 的长为 .或【分析】分两种情况讨论,通过证明EFC V ∽BCD △,由三角形的性质可求CE ,EF 的长,由勾股定理即可求解.解:如图,当CD 绕点C 顺时针旋转,过点E 作EF CD ^于F ,如图所示:90EFC BCD \Ð=Ð=°,5CE CD ==,BD CE Q ∥,FCE BDC \Ð=Ð,EFC \V ∽BCD △,153454EF BC CF CD \===,5CE =Q ,3EF \=,4CF=,1DF CD CF \=-=,DE \===当CD 绕点C 逆时针旋转,过点D 作DF ¢^直线CE ¢于F ¢,CD CE =Q ,1122DCE S DC EF CE DF ¢\=´×=´×V ,3DF EF ¢\==,1DF EF ¢\==,1019E F ¢¢\=-=,DE ¢\==故答案为:.【点拨】本题考查了旋转的性质,矩形的性质,相似三角形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.【考点6】图形相似中的菱形几何变换【6-1】(24-25九年级上·山西运城·阶段练习)综合与探究问题情境在课外小组活动中,创新小组以“菱形纸片中的图形变换”为主题开展数学活动.如图1,边长为12cm 的菱形纸片ABCD (90BAD Ð>°),对角线8cm AC =.实践探究(1)成员甲:将图1中的ABC V 折叠,使点B 落在线段BC 的延长线上的点G 处,得到折痕AH ,如图2,求折痕AH 的长;(2)成员乙:将图1中菱形纸片ABCD (90BAD Ð>°),沿对角线AC 剪开,得到ABC V 和ACD V .再将ACD V 以点A 为旋转中心,按逆时针方向旋转角a ,使2BAC a =Ð,得到如图3所示的AEF V ,点C 、D 的对应点分别为点E 、F ,连接FB 、EC ,得到四边形BCEF ,请判断四边形BCEF 的形状,并证明;(3)小组组长根据图3,在成员乙发现结论的基础上,提出一个平移问题:将AEF △沿着射线FB 方向平移cm a ,得到A E F ¢¢¢△,连接BF ¢,CE ¢,使四边形BCE F ¢¢恰好为正方形,直接写出a 的值.【答案】(1)AH =;(2)四边形BCEF 是矩形,见解析;(3)12cm ö÷ø或12cm ö÷ø.【分析】(1)过点B 作BM AC ^,交AC 于M ,根据菱形的性质可知14cm 2AM CM AC ===,根据勾股定理,利用等面积法求解即可;(2)利用旋转的性质结合菱形的性质得出,四边形BCEF 是平行四边形,进而得出四边形BCEF 是矩形;(3)首先求出CC ′的长,分别利用①点E ¢在边EC 上,②点E ¢在EC 的延长线上,求出a 的值.解:(1)解:过点B 作BM AC ^,交AC 于M ,由题意可知,12cm AB BC ==,∵BM AC ^,∴14cm 2AM CM AC ===,由勾股定理可得:BM ,由折叠可知,AH BC ^,∵1122ABC S AC BM BC AH =×=×△,∴AC BM AH BC ×==;(2)证明:如图,作AN CE ^于点N ,由旋转得:AC AE =,则12CAN EAN BAC a Ð=Ð==Ð,∵四边形ABCD 是菱形,∴BA BC =,∴BCA BAC Ð=Ð,∴CAN BCA Ð=Ð,∴AN BC ∥,同理可得:AN EF P ,∴BC EF ∥.又∵BC EF =,∴四边形BCEF 是平行四边形.∵AN BC ∥,90CNA Ð=°,∵18090BCE CNA Ð=°-Ð=°,∴四边形BCEF 是矩形;(3)如图,过点B 作BM AC ^,垂足为M ,由(1)可知,BM =,在ACN △和CBM V 中,∵CAN BCM Ð=Ð,90CNA BMC Ð=Ð=°,∴ACN CBM V V ∽,CNBM \=812=,解得:∵AC AE =,AN22CE CN \===,当四边形BCE F ¢¢恰好为正方形时,分两种情况:①点E ¢在边EC 上,1212cm a CE ö=-=÷÷ø,②点E ¢在EC 的延长线上,1212cm a CE ö=+=÷÷ø,综上所述:a 的值为:12cm ö-÷ø或12cm ö÷ø.【点拨】此题主要考查了几何变换综合以及相似三角形的判定与性质、菱形的判定与性质以及矩形的判定方法等知识,正确利用相似三角形的判定与性质得出CE 的长是解题关键.【6-2】(23-24九年级上·四川达州·期中)如图,把菱形ABCD 沿着它的对角线AC 方向平移1cm ,得到菱形EFGH ,若4cm AC =,则图中阴影部分的面积与四边形ENCM 的面积之比为( )A .14:9B .3:2C .4:3D .17:9【答案】A【分析】此题主要考查了菱形的性质以及相似三角形的判定与性质,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.首先得出MEC DAC ∽△△,则 EC MEAC AD =,进而得出916CME ADC S S =△△,即可得出答案.解:ME AD Q ∥,MEC DAC \∽△△,EC MEAC AD\=,Q 菱形ABCD 的对角线4cm AC =,把菱形ABCD 沿着它的对角线AC 方向平移1cm ,得到菱形EFGH ,1cm AE \=,3cm EC =,34EC AC \=,916CME ADC S S \=△△,∴图中阴影部分图形的面积与四边形EMCN 的面积之比为:7777281499189+++==+.故选:A .【6-3】(2022·浙江杭州·二模)如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,将线段AB 绕点B顺时针方向旋转,使点A 落在BD H ,E 为边BC 的中点,连接HE ,交AC 于点P .若12AC =,16BD =,则线段PC 的长为( )A .3B.C .4D .5【答案】D【分析】过E 点作EF ⊥BD 于F ,根据菱形的性质可知OC =6,OB =8,根据勾股定理可以得出BC =10,所以BH =10,OH =2,因为E 、F 是BC 和BO 的中点,由中位线定理可以得出EF ,OF 的长,再根据相似三角形的性质求出OP 的长度,最后由OC ﹣OP =PC 求得结果.解:过E 点作EF ⊥BD 于F,∵四边形ABCD 是菱形,∴AC ⊥BD ,∴EF ∥AC ,∵AC =12,BD =16,∴OC =OA =12AC =6,OB =OD =12BD =8,∴BC ==10,∴BH =AB =BC =10,∴OH =BH ﹣OB =2,∵E 是BC 的中点,EF ∥AC ,∴EF =12OC =3,OF =12OB =4,∴HF =OH +OF =6,∵EF ∥AC ,∴△HOP ∽△HFE ,∴=OP OH EF HF ,∴2=36OP ,∴OP =1,∴CP =OC ﹣OP =5.故选:D .【点拨】此题考查了菱形的性质,勾股定理,旋转的性质,相似三角形的判定和性质,孰练掌握菱形的相关性质,勾股定理以及相似三角形的判定和性质是解决本题的关键.【6-4】(21-22九年级上·山东济南·期末)在菱形ABCD 中,4AC =,BD =,AC ,BD 相交于点O .将一个足够大的直角三角板60°角的顶点放在菱形ABCD 的顶点A 处,绕点A 左右旋转,其中三角板60°角的两边分别与边BC ,CD 相交于点E ,F ,连接EF 与AC 相交于点G .旋转过程中,当点E 为边BC的四等分点时(BE CE >),CG = .【答案】34/0.75【分析】根据菱形的性质,确定△AOB 为直角三角形,然后利用勾股定理求出边AB 的长度;证明△ABE ≌△ACF ,得到AE =AF ,再根据已知条件∠EAF =60°,可以判定△AEF 是等边三角形;得出∠AEF =60°,证明△CAE ∽△CFG ,由对应边的比例关系求出CG 的长度.解:∵四边形ABCD 是菱形,∴AC ⊥BD ,AB =BC =CD =AD ,∴△AOB 为直角三角形,且OA =12AC =2,OB =12BD=在Rt △AOB 中,由勾股定理得:AB4==2.∵AB =BC =AC =4,∴△ABC 与△ACD 均为等边三角形,∴∠BAC =∠BAE +∠CAE =60°,∠∠EBA =∠FCA =60°,又∵∠EAF =∠CAF +∠CAE =60°,∴∠BAE =∠CAF .在△ABE 与△ACF 中,°BAE CAF{AB AC EBA FCA 60ÐÐÐÐ====,∴△ABE ≌△ACF (ASA ),∴BE =CF ,AE =AF ,∴△AEF 是等腰三角形,又∵∠EAF =60°,∴△AEF 是等边三角形.∴∠AEF =60°,∵BC =4,E 为为边BC 的四等分点,且BE >CE,∴CE =1,BE =3.∴CF =BE =3,∵∠EAC +∠AEG +∠EGA =∠GFC +∠FCG +∠CGF =180°,∠AEG =∠FCG =60°,∠EGA =∠CGF ,∴∠EAC =∠GFC .又∵∠ACE =∠FCG =60°,∴△CAE ∽△CFG ,∴CG CE =CF AC ,即1CG =34,解得:CG =34;故答案为34.【点拨】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、菱形的性质、勾股定理、旋转的性质、等边三角形的判定与性质等知识;熟练掌握全等三角形的判定与性质和相似三角形的判定与性质是解题的关键.【考点7】图形相似中的正方形几何变换【7-1】(2024·广东汕头·模拟预测)如图1,在正方形ABCD 中,点E 是CD 边上一点,将BCE V 沿着BE 折叠,点C 落在点F 处,连接CF 交BE 于点O ,延长CF 交AD 于点G .(1)求证:BCE CDG ≌V V ;(2)如图2,若点E 为CD 的中点,连接DF 、DO ,判断DFO V 的形状,并说明理由;(3)如图3,将“正方形ABCD ”改为“矩形ABCD ”,点E 为CD 的中点,同样将BCE V 沿着BE 折叠,CF 的延长线恰好经过点A ,求证:四边形BODF 是平行四边形.【答案】(1)见解析 (2)DFO V 是等腰直角三角形,理由见解析 (3)见解析【分析】(1)利用同角的余角相等得到EBC GCD Ð=Ð,可用ASA 证明三角形全等;(2)根据折叠的性质证明OE 是DF 的中位线,证明OEC OCB △∽△可得1122OE OC OF ==,即可证明DFO V 是等腰直角三角形;(3)证明AFD COB ≌△△即可证明四边形BODF 是平行四边形.解:(1)证明:Q 四边形ABCD 是正方形,BC CD \=,90BCE D Ð=Ð=°,90BCO GCD \Ð+Ð=°,BE CF ^Q ,90BCO OBC \Ð+Ð=°,EBC GCD \Ð=Ð,在BCE V 和CDG V 中,EBC GCD BC CDBCE CDG Ð=Ðìï=íïÐ=ÐîQ (ASA)BCE CDG \≌△△;(2)解:DFO V 是等腰直角三角形.理由如下:BE Q 是CF 的垂直平分线,CO FO \=,CE ED =Q ,EO DF \∥,2FD OE =,CF DF \^,即90DFC Ð=°,在Rt BEC V 中,CO BE ^,∴90COE COB Ð=Ð=°,∵CBO OCE Ð=Ð,CEO BCO \∽△△,12OE CE CO BC \==,2CO OE \=,∴CO FD =,FO FD \=,DFO \△是等腰直角三角形;(3)解:①由(2)可得EO DF ∥,2FD OE =,DF AC ^,OF OD =,Q 四边形ABCD 是矩形,AD CB \=,AD BC ∥,DAF BCO\Ð=ÐQ,Ð=Ð=°AFD COB90△△.\≌(AAS)AFD COB\=,DF BO\四边形BODF是平行四边形.【点拨】本题考查了三角形全等的判定和性质、三角形相似的判定和性质、正方形的性质,平行四边形的判定,等腰三角形的性质与与判定,熟练掌握以上知识是解题的关键.【7-2】(2021·海南海口·一模)如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,平移的距离为()A.2B.3C.4D.5【答案】C【分析】根据已知条件得到AC=6=2,OB=7,求得BC=9,根据正方形的性质得到DE=OC=OE=2,求得O′E′=O′C′=2,根据相似三角形的性质得到BO′=3,于是得到结论.解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,∵顶点A,B的坐标分别为(-2,6)和(7,0),∴AC=6,OC=2,OB=7,∴BC=9,∵四边形OCDE是正方形,∴DE =OC =OE =2,∴O ′E ′=O ′C ′=2,∵E ′O ′⊥BC ,∴∠BO ′E ′=∠BCA =90°,∴E ′O ′∥AC ,∴△BO ′E ′∽△BCA ,∴=¢¢¢E O BO AC BC,∴269¢=BO ,∴BO ′=3,∴OO ′=7-3=4,故选:C .【点拨】本题考查了正方形的性质,坐标与图形性质,相似三角形的判定和性质,正确的识别图形是解题的关键.【7-3】(2022·山东菏泽·二模)如图,在正方形ABCD 中,顶点()5,0A -,()5,10C ,点F 是BC 的中点,CD 与y 轴交于点E ,AF 与BE 交于点G ,将正方形ABCD 绕点O 顺时针旋转,每次旋转90°,则第2022次旋转结束时,点G 的坐标为( )A .()4,3B .()3,4C .()4,3--D .()3,4--【答案】D 【分析】根据正方形的性质得到AB =BC =CD =10,∠C =∠ABF =90°,根据全等三角形的性质得到∠BAF =∠CBE ,根据余角的性质得到∠BGF =90°,过G 作GH ⊥AB 于H ,根据相似三角形的性质得到BH =2,根据勾股定理得到HG =3,求得G (3,4),找出规律即可得到结论.解:∵四边形ABCD 是正方形,。
几何模型之二图形中的最短距离定值及不等式问题

学生: 科目: 数 学 教师: 谭 前 富知识框架在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。
最值问题的解决方法通常有两种: (1) 应用几何性质:① 三角形的三边关系:两边之和大于第三边,两边之差小于第三边; ② 两点间线段最短;③ 连结直线外一点和直线上各点的所有线段中,垂线段最短; ④ 定圆中的所有弦中,直径最长。
⑵运用代数证法:① 运用配方法求二次三项式的最值; ② 运用一元二次方程根的判别式。
【例题精讲】一. 最短路径和几何不等式问题: 考查知识点----:“两点之间线段最短”,“两边之和大于第三边”,“斜边大于直角边”,“垂线段最短”,“点关于线对称”,“线段的平移”。
原型----“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
最短路径和几何不等式问题的两种基本模型----:Ⅰ、归于函数模型:即利用一次函数的增减性和二次函数的对称性及增减性,确定某范围内函数的最大或最小值Ⅱ、归于几何模型,这类模型又分为两种情况:(1)归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
(2)归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
解题总思路----找点关于线的对称点实现“折”转“直”,较难的会出现“三折线”转“直”等变式问题考查。
二.最短距离中的数形结合:例:求代数式9)12(422+-++x x 的最小值.课 题几何模型之二:图形中的最短距离、定值及不等式问题教学内容三.立体几何中的最短路径问题:(1)台阶问题 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm ,3cm 和1cm ,A 和B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到B 点去吃可口的食物.请你想一想,这只蚂蚁从A 点出发,沿着台阶面爬到B 点,最短线路是多少?(2)圆柱问题 有一圆形油罐底面圆的周长为24m ,高为6m ,一只老鼠从距底面1m 的A 处爬行到对角B 处吃食物,它爬行的最短路线长为多少?变式1:有一圆柱形油罐,已知油罐周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周建造梯子,正好到达A 点的正上方B 处,问梯子最短有多长?变式2: 桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A 处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B 处时,突然发现了蜜糖。
初中数学几何模型与最值问题08专题-瓜豆原理中动点轨迹不确定型最值问题(含答案)

初中数学几何模型与最值问题专题8瓜豆原理中动点轨迹不确定型最值问题【专题说明】动点轨迹非圆或直线时,基本上将此线段转化为一个三角形中,(1)利用三角形两边之和大于第三边,两边之差小于第三边求最值。
(2)在转化较难进行时,可借助直角三角形斜边上的中线及中位线或构建全等图形进一步转化求最值。
【知识精讲】所谓“瓜豆原理”,就是主动点的轨迹与从动点的轨迹是相似性,根据主、从动点与定点连线形成的夹角以及主、从动点到定点的距离之比,可确定从动点的轨迹,而当主动点轨迹是其他图形时,从动点轨迹必然也是.【例题】如图,在反比例函数的图像上有一个动点A,连接AO并延长交图像的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数的图像上运动,若tan∠CAB=2,则k的值为()A.2B.4C.6D.8【模型】一、借助直角三角形斜边上的中线1、如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是()A.6B.C.D.【模型】二、借助三角形两边之和大于第三边,两边之差小于第三边1、如图,已知等边三角形ABC边长为A、B分别在平面直角坐标系的x轴负半轴、轴的正半轴上滑动,点C在第四象限,连接OC,则线段OC长的最小值是()A-1B.3C.3D.2、如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是______.3、如图,在ABC △中,90ACB ∠=︒,30CAB ∠=︒,6AB =,以线段AB 为边向外作等边ABD △,点E 是线段AB 的中点,连结CE 并延长交线段AD 于点F .(1)求证:四边形BCFD 为平行四边形;(2)求平行四边形BCFD 的面积;(3)如图,分别作射线CM ,CN ,如图中ABD △的两个顶点A ,B 分别在射线CN ,CM 上滑动,在这个变化的过程中,求出线段CD 的最大长度.4、如图,在Rt ABC ∆中,90ACB ∠=,将ABC ∆绕顶点C 逆时针旋转得到'',A B C M ∆是BC 的中点,N 是''A B 的中点,连接MN ,若4,60BC ABC =∠=︒,则线段MN 的最大值为()A .4B .8C .D .6【模型】三、借助构建全等图形1、如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接B P,以B P为边作等边△B P Q,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.2、如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是()A.6B.3C.2D.1.5【模型】四、借助中位线1、如图,在等腰直角∆ABC中,斜边AB的长度为8,以AC为直径作圆,点P为半圆上的动点,连接B P,取B P的中点M,则CM的最小值为()A.B.C-D.2、如图,抛物线2119y x =-与x 轴交于A B ,两点,D 是以点()0,4C 为圆心,1为半径的圆上的动点,E 是线段AD 的中点,连接,OE BD ,则线段OE 的最小值是()A .2B .322C .52D .3专题8瓜豆原理中动点轨迹不确定型最值问题答案【专题说明】动点轨迹非圆或直线时,基本上将此线段转化为一个三角形中,(1)利用三角形两边之和大于第三边,两边之差小于第三边求最值。
人教版初中数学竞赛专题复习第17章 几何不等式与极值问题(含答案)

第17章 几何不等式与极值问题17.1.1★ 一个凸行边形的内角中,恰好有4个钝角,求n 的最大值. 解析考虑这个凸行边形的n 个外角,有4n -个角90︒≥,故有()490360n -⨯︒<︒(严格小于是由于4个钝角的外角和大于0︒),因此8n <,n 的最大值是7.易构造这样的例子。
如果恰好有k 个钝角,则n 的最大值是3k +.17.1.2★ 在ABC △中,AB AC >,P 为BC 边的高AD 上的一点,求证:AB AC PB PC -<-.PCDB A解析易知AB AC PB PC +>+,又2222AB AC BD CD -=- 22PB PC =-,故有AB AC PB PC -<-. 评注 读者不妨考虑AD 是角平分线与中线的情况.17.1.3 已知四边形ABCD ,AC 、BD 交于O ,ADO △和BCO △的面积分别为3、12,求四边形ABCD 面积的最小值.CB ODA解析易知ABO BCOADO DCOS S BO S DO S ==△△△△,故36ABO CDO ADO BCO S S S S ⋅=⋅=△△△△.从而12ABO CDO S S +△△≥,且当ABO CDO S S =△△(此时四边形ABCD 为一梯形)时等号成立,所以此时四边形ABCD 面积达到最小值27.17.1.4★ 已知:直角三角形ABC 中,斜边BC 上的高6h =. (1)求证:BC h AB AC +>+; (2)求()()22BC h AB AC ++-. 解析()()22BC h AB AC +-+222222BC h BC h AB AC AB AC =++⋅---⋅,由条件,知242ABC BC h S AB AC ⋅==⋅△,且222AB AC BC +=, 于是()()22236BC h AB AC h +-+==.注意:这同时解决了(1)和(2).17.1.5★ 设矩形ABCD ,10BC =,7CD =,动点F 、E 分别在BC 、CD 上,且4BF ED +=,求AFE △面积的最小值.B FCED A解析设 BF x=,()4DE y x ==-,则()()()117101077022ABF ADE ECF S S S x y x y xy ++=++--=+⎡⎤⎣⎦△△△。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.如图,P是△ABC内任一点,求证:
1
2
(a+b+c)<PA+PB+PC<a+b+c。
例2.如图,在△ABC中,∠B=2∠C,求证:AC<2AB 。
例3.如图,设正△AB C的边长为2,M是AB边上的中点,P是BC边上
的任意一点,PA+PM的最大值和最小值分别为S和t,求S2−t2的值。
例4.如图,△ABC中,BC为最大边,AB=AC,CD=BF,BD=CE,求∠
DEF的取值范围。
例5.已知一平面内的任意四点,其中任何三点都不在一条直线上,试问:
是否一定能从这样的四点中选出三点构成一个三角形,使得这个三角形至
少有一内角不大于45°?请证明你的结论。
A
卷
一、填空题
01.在周长为a 的等腰三角形中,腰长x 的取值范围是__________。
02.如图260,在△ABC 中,若AB=5,AC=3,则BC 边上的中线MA 的取值范围是__________。
03.在△ABC 中,若∠A=58°,AB >BC ,那么∠B 的取值范围是__________。
04.根据绝对值的几何意义,代数式321x x x ++-++的最小值为__________。
05.在锐角△ABC 中,a=1,b=3,则第三边。
的变化范围是__________。
06.在△ABC 中AB >AC ,∠A 的平分线交BC 于D ,则BD_____CD (填“>”或“<”)。
07.如图261,设△ABC 为等边三角形,P 是任意点,则PB +PC ____PA (填“<”、“>”或“=”)。
08.已知直角梯形ABCD ,AD ∥BC ,∠DAB=∠CBA=90°,O 为DC 的中点,则OA _____OB (填“>”、“=”或“<”)。
09.如图262,五边形ABCDE 中,AB=AE ,BC +DE=CD ,∠ABC +∠AED=180°,连结AD ,则∠ADE_______∠ADC(填“>”、“=”或“<”)。
10.如图263,△ABC 中,AB >AC ,P 是∠A 平分线AD 上一点,则PB −PC_______(填“>”或“<”)AB −AC 。
二、解答题
11.如图,△ABC 中,D 是BC 的中点,DE ⊥DF ,试判断BE +CF 与EF 的大小关系,并证明你的结论。
12.如图,已知∠MON 内有一点P ,分别在OM 与ON 上,求作点A 与点B ,使△APB 的周长最小。
B 卷
一、填空题
01.已知△ABC 中∠A ≤∠C ≤∠B ,且2∠B=5∠A ,则∠B 的取值范围是__________。
02.△ABC 中,∠A ,∠B ,∠C 的对边为a 、b 、c 。
已知a=b (b +c),为钝角,则a 、2b 、c 的大小__________。
03.如图266,设四边形ABCD 对角线AC 、BD 垂直相交于O ,又OC <OA ,OD <OB ,则BC +AD_______AB +CD (填“>”、“=”或“<”)。
04.如图267,设a 、b 、c 分别表示△ABC 中∠A 、∠B 、∠C 所对的边h 示AB 边上的高。
设M=a +b ,N=2
2
4c h +,其中较大者为__________。
05.如图268,H 为△ABC 的垂心,则__________<AD BE CF
AB BC CA
++++<
__________。
06.如图269,P 为边长为1的等边△ABC 内任意一点.设t=PA +PB +PC ,则t 的取值范围为__________。
07.如图270,已知直线l 的同侧有两点A 与B ,AB=62,A 到l 的距离为1,B 到l 的距离为7,那么l 上存在一点P ,则AP +BP 的最小值是__________。
08.从n ×n 的正方形的一个角上剪去1个1×1的小方块(n >1),则所得图
形最少可分成_________个面积相等的三角形。
09.在△ABC 中,一边是另一边的两倍,该三角形的周长为P ,则最小边长c 的取值范围为__________。
10.若直角三角形两直角边上中线长度之比为m ,则m 的取值范围是__________。
二、解答题
11.已知△ABC 的三边为a 、b 、c ,且()
222a b -=,求证:1<2c b
b
-<3。
12.如图,将面积为1的矩形纸片ABCD 沿一条直线对折,使得C 与A 重合,证明:所得的五边形的面积小于34。
C 卷
解答题
01. 在直角坐标系xoy 中,x 轴上的动点M(x ,0)到定点P(5,5)和Q(2,1)的距离分别为MP 和MQ ,那么当MP +MQ 取最小值时,求点M 的横坐标x 。
02.已知∠MON=40°,P 为∠MON 内一点,A 为OM 上的点,B 为ON 上的点,则当△PAB 的周长取最小时,求∠APB 的度数。
03. 若x +y=12,求2249x y +++的最小值。
04. 设∠MON=20°,A 为OM 上一点,OA=43,D 为ON 上一点,OD=83,C 为AM 上任一点,B 是OD 上任意一点,求折线ABCD 长的最小值。
05.点P 与边长为2的正方形ABCD 在同一平面内,且PA 2+PB 2=PC 2,求PD 的最大值。
06. 在△ABC 中,BC=a ,AC=b ,以AB 为边向外作正DABD ,问当∠ACB 多少时,C 与D 两点间的距离最大,最大值是多少?
07. 已知一平面内的任意四点,其中任何三点都不在一条直线上,试问是否一定能从这样的四点中选出三点构成一个三角形,使得这个三角形至少有一内角不大于45°?请证明你的结论。
08.在△ABC 中,AB=AC ,∠BAC=80°,P 点在△ABC 内,,∠PBC=10°,∠PCB=30°,求∠BAP 。
09.△ABC 中,最大角小于120°,在△ABC 内取一点P ,使P 到三个顶点距离之和PA +PB +PC 为最小。
10.如图,ABCD 是一个边长为1的正方形,U 、V 分别是AB 、CD 上的点,AV 与DU 相交于点P ,BV 与CU 相交于点Q ,求四边形PUQV 面积的最大值。
