随机变量及分布列习题43462
高三数学随机变量的分布列试题

高三数学随机变量的分布列试题1.随机变量X的概率分布规律为P(X=n)=(n=1,2,3,4),其中a是常数,则P(<X<)的值为()A.B.C.D.【答案】D【解析】由题意得,+++=1,解得a=.于是P(<X<)=P(X=1)+P(X=2)=+=a=,故选D.2. [2014·四川模拟]在四次独立重复试验中,事件A在每次试验中出现的概率相同,若事件A至少发生一次的概率为,则事件A恰好发生一次的概率为()A.B.C.D.【答案】C【解析】设事件A在每次试验中发生的概率为p,则事件A在4次独立重复试验中,恰好发生k 次的概率为pk=p k(1-p)4-k(k=0,1,2,3,4),∴p0=p0(1-p)4=(1-p)4,由条件知1-p=,∴(1-p)4=,∴1-p=,∴p=.∴p1=p·(1-p)3=4××()3=,故选C.3.[2014·唐山检测]2013年高考分数公布之后,一个班的3个同学都达到一本线,都填了一本志愿,设Y为被录取一本的人数,则关于随机变量Y的描述,错误的是()A.Y的取值为0,1,2,3B.P(Y=0)+P(Y=1)+P(Y=2)+P(Y=3)=1C.若每录取1人学校奖励300元给班主任,没有录取不奖励,则班主任得奖金数为300Y D.若每不录取1人学校就扣班主任300元,录取不奖励,则班主任得奖金数为-300Y【答案】D【解析】由题意知A、B正确.易知C正确.对于D,若每不录取1人学校就扣班主任300元奖金,录取不奖励,则班主任得奖金数为-300(3-Y)=300Y-900.4.设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此两球所得分数之和,求ξ分布列;(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=,V(η)=,求a∶b∶c.【答案】(1)ξ的分布列为(2)3∶2∶1【解析】(1)由已知得到:当两次摸到的球分别是红红时ξ=2,此时P(ξ=2)==;当两次摸到的球分别是黄黄、红蓝、蓝红时ξ=4时,P(ξ=4)==;当两次摸到的球分别是红黄,黄红时ξ=3时,P(ξ=3)==;当两次摸到的球分别是黄蓝,蓝黄时ξ=5时,P(ξ=5)==;当两次摸到的球分别是蓝蓝时ξ=6时,P(ξ=6)==.所以ξ的分布列为ξ23456由已知得到:η有三种取值即1,,所以η的分布列为所以,所以b=2c,a=3c,所以a∶b∶c=3∶2∶1.5.设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.【答案】(1)0.5(2)0.8(3)ξ0123【解析】解:记A表示事件:进入商场的1位顾客购买甲种商品;记B表示事件:进入商场的1位顾客购买乙种商品;记C表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种;记D 表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种.(1)C=A·B+A·B,P(C)=P(A·B+A·B)=P(A·B)+P(A·B)=P(A)·P(B)+P()·P(B)=0.5×0.4+0.5×0.6=0.5.(2)D=A·B,P(D)=P(A·B)=P(A)·P(B)=0.5×0.4=0.2,P(D)=1-P(D)=0.8.(3)ξ~B(3,0.8),故ξ的分布列P(ξ=0)=0.23=0.008;P(ξ=1)=×0.8×0.22=0.096;P(ξ=2)=×0.82×0.2=0.384;P(ξ=3)=0.83=0.512.6.甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获胜的概率是外,其余每局比赛甲队获胜的概率都是,假设各局比赛结果相互独立.(1)分别求甲队以3∶0,3∶1,3∶2胜利的概率;(2)若比赛结果为3∶0或3∶1,则胜利方得3分,对方得0分;若比赛结果为3∶2,则胜利方得2分、对方得1分.求乙队得分X的分布列.【答案】(1)、、(2)X的分布列为【解析】(1)记“甲队以3∶0胜利”为事件A1,“甲队以3∶1胜利”为事件A2,“甲队以3∶2胜利”为事件A3,由题意,各局比赛结果相互独立,故P(A1)==,P(A2)=××=,P(A3)=××=.所以,甲队以3∶0、3∶1、3∶2胜利的概率分别是、、;(2)设“乙队以3∶2胜利”为事件A4,由题意,各局比赛结果相互独立,所以P(A4)=××=.由题意,随机变量X的所有可能的取值为0,1,2,3,根据事件的互斥性得P(X=0)=P(A1+A2)=P(A1)+P(A2)=,P(X=1)=P(A3)=,P(X=2)=P(A)=,4P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=.故X的分布列为7.一个袋子中装有7个小球,其中红球4个,编号分别为1,2,3,4,黄球3个,编号分别为2,4,6,从袋子中任取4个小球(假设取到任一小球的可能性相等).(1)求取出的小球中有相同编号的概率;(2)记取出的小球的最大编号为,求随机变量的分布列和数学期望.【答案】(1);(2)随机变量的分布列为:346随机变量的数学期望 .【解析】(1)应用古典概型概率的计算公式,关键是利用组合知识,确定事件数;(2) 随机变量的可能取值为.计算相应概率即得随机变量的分布列为:数学期望 .试题解析:(1):设取出的小球中有相同编号的事件为,编号相同可分成一个相同和两个相同 2分4分(2) 随机变量的可能取值为:3,4,6 6分, 7分, 8分9分所以随机变量的分布列为:346所以随机变量的数学期望 . 12分【考点】古典概型,互斥事件,离散型随机变量的分布列及数学期望.8.某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的;若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金;若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其他区域,则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则参与了促销活动.(1)求顾客甲中一等奖的概率;(2)记X为顾客甲所得的奖金数,求X的分布列及其数学期望.【答案】(1)(2)【解析】(1)设事件A表示该顾客中一等奖,P(A)=×+2××=,所以该顾客中一等奖的概率是.(2)X的可能取值为20,15,10,5,0,P(X=20)=×=,P(X=15)=2××=,P(X=10)=×+2××=,P(X=5)=2××=,P(X=0)=×=.所以X的分布列为数学期望E(X)=20×+15×+10×+5×=.9.辽宁某大学对参加全运会的志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为、、,他们考核所得的等次相互独立.(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量X,求随机变量X的分布列.(3)求X的数学期望.【答案】(1)(2)(3)【解析】(1)记“甲考核为优秀”为事件A,“乙考核为优秀”为事件B,“丙考核为优秀”为事件C,“甲、乙、丙至少有一名考核为优秀”为事件E.则P(E)=1-P( )=1-P()P()P( )=1-××=.(2)由题意,得X的可能取值是,2,,3.因为P(X=)=P()=,P(X=2)=P(A )+P(B)+P(C )=,P(X=)=P(AB)+P(A C)+P( B C)==,P(X=3)=P(ABC)=,所以X的分布列为:(3)由(2)知E(X)=×+2×+×+3×==.10.随机变量的分布列如右:其中成等差数列,若,则的值是.【答案】.【解析】由题意,则.【考点】随机变量的期望和方差.11.一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球,现从中有放回地随机抽取2个小球,抽取的球的编号分别记为、,记.(Ⅰ)求取最大值的概率;(Ⅱ)求的分布列及数学期望.【答案】(Ⅰ);(Ⅱ)所以的分布列:数学期望.【解析】(1)随机变量的分布列问题,首先确定随机变量的所有可能值;(2))本题属古典概型,各随机变量所对应的事件包含的基本事件无法用公式求出,需一一列举出来.列举时要注意避免重复和遗漏,这是极易出错的地方试题解析:(Ⅰ)当时,最大。
随机变量及其概率分布典型例题

概率与数理统计课件
天津科技大学理学院数学系
第8讲 随机变量及其概率分布习题课
第8讲 随机变量及其概率分布习题课
教学目的:通过对随机变量(一维,二维为主)及其概率分布的归纳总结, 及典型
知识要点回顾:
1. 一维随机变量及其分布函数. 2. 离散型随机变量及其概率分
5. 二维随机变量(X,Y)及其分布
函数F(x,y).
6. 二维随机变量的边际分布函
布列.
3. 连续型随机变量及其概率密
数及边际概率密度.
7. 随机变量的独立性. 8. 随机变量函数的分布.
度函数.
4. 常用的随机变量.
1 1
0 0
e
x y
dxdy 1 e1 .
2
随机变量及其概率分布典型例题解析
X \Y 7.设二维随机变量 X , Y 的联合概率分布为 1 2 1 1
5 20 3 20 2 20 3 20
返回
2
6 20 1 20
.求(1) X Y ; (2) X Y 的概率分布.
1 1 P X k 2 1 k 3. 3 ,故 P X k 3 ,即 F k 3 ,从而
5) 3 x 6时,F x dx
dx 0dx 1.
6
0 x
1
解
1) 1
f x, y dxdy
题的分析讲解,使学生对概部分内容有较深的理解与认识.
教学重点:随机变量(离散型,连续型),分布函数,六个重要的分布(两点, 二
随机变量与分布列习题

随机变量及分布列1.已知随机变量()20,X N σ~,若(2)P X a <=,则(2)P X >的值为( )A.12a - B. 2a C. 1a - D. 12a+2.已知随机变量,若,则的值为( ) A. 0.4 B. 0.2 C. 0.1 D. 0.6 3.已知,,则的值为( ) A. 10 B. 7 C. 3 D. 64.集装箱有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下并放回,如果两球之积是4的倍数,则获奖.若有4人参与摸奖,恰好有3人获奖的概率是( ) A. B. C. D.5.甲袋中放有大小和形状相同的小球若干,其中标号为0的小球为1个,标号为1的小球2个,标号为2的小球2个.从袋中任取两个球,已知其中一个的标号是1,则另一个标号也是1的概率为__________. 6.设随机变量服从正态分布,,则__________.7.某人通过普通话二级测试的概率是,他连线测试3次,那么其中恰有1次通过的概率是( ) A. B. C. D.8.从1,2,3,4,5,6,7中任取两个不同的数,事件为“取到的两个数的和为偶数”,事件为“取到的两个数均为奇数”,则( ) A. B. C. D.9.班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机 抽取一个容量为8的样本进行分析.(Ⅰ)如果按性别比例分层抽样,求样本中男生、女生人数分别是多少;(Ⅱ)随机抽取8位同学,数学成绩由低到高依次为:6065707580859095,,,,,,,;物理成绩由低到高依次为:7277808488909395,,,,,,,,若规定90分(含90分)以上为优秀,记ξ为这8位同学中数学和物理分数均为优秀的人数,求ξ的分布列和数学期望.10.某品牌汽车的4S 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件A :“至多有1位采用分6期付款“的概率()P A ;(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量η,求η的分布列和数学期望()E η.11.某公司有,,,,A B C D E 五辆汽车,其中,A B 两辆汽车的车牌尾号均为1. ,C D 两辆汽车的车牌尾号均为2,E 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,,,A B E 三辆汽车每天出车的概率均为12,,C D 两辆汽车每天出车的概率均为23,且五辆汽车是否出车相互独立,该公司所在地区汽车(1)求该公司在星期一至少有2辆汽车出国的概率;(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及期望.12.拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为X,试求随机变量X的分布列和数学期望;(Ⅱ)若在犯错误的概率不超过P的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.附:独立性检验统计量()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.13.某高校数学系2016年高等代数试题有6个题库,其中3个是新题库(即没有用过的题库),3个是旧题库(即至少用过一次的题库),每次期末考试任意选择2个题库里的试题考试.(1)设2016年期末考试时选到的新题库个数为,求的分布列和数学期望;(2)已知2016年时用过的题库都当作旧题库,求2017年期末考试时恰好到1个新题库的概率.14.某市举行的“国际马拉松赛”,举办单位在活动推介晚会上进行嘉宾现场抽奖活动,抽奖盒中装有6个大小相同的小球,分别印有“快乐马拉松”和“美丽绿城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球(取出后不再放回),若抽到的两个球都印有“快乐马拉松”标志即可获奖.并停止取球;否则继续抽取,第一次取球就抽中获一等奖,第二次取球抽中获二等奖,第三次取球抽中获三等奖,没有抽中不获奖.活动开始后,一位参赛者问:“盒中有几个印有‘快乐马拉松’的小球?”主持人说:“我只知道第一次从盒中同时抽两球,不都是‘美丽绿城行’标志的概率是(1)求盒中印有“快乐马拉松”小球的个数;(2)若用表示这位参加者抽取的次数,求的分布列及期望.15.为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25) , [25,30) , [30,35), [35,40) , [40,45] ,并得到如下频率分布直方图.(Ⅰ)求图中的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为,求的分布列及数学期望.16.一家医药研究所,从中草药中提取并合成了甲、乙两种抗“病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为.现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”. (1)求一个试用组为“甲类组”的概率;(2)观察3个试用组,用表示这3个试用组中“甲类组”的个数,求的分布列和数学期望.17.某班为了提高学生学习英语的兴趣,在班举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在的人数为12人.(Ⅰ)求此班级人数;(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.(i )甲不排在第一位乙不排在最后一位的概率;(ii )记甲乙二人排在前三位的人数为,求的分布列和数学期望.18.2017年1月1日,作为市打造“千园之城”27个示性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列22⨯愿意不愿意总计男生 女生 总计(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为12,记甲通过的关数为X ,求X的分布列和数学期望. ()20P K k ≥0.1 0.05 0.025 0.01()()()()()22n ad bc K a b c d a c b d -=++++.19.在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,知识告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.(1)求乙班总分超过甲班的概率;(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分, ①请你从平均分和方差的角度来分析两个班的选手的情况;②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为,求的分布列及数学期望.20.一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求: (1)连续取两次都是红球的概率;(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数的概率分布列及期望.21.甲乙两人下棋比赛,规定谁比对方先多胜两局谁就获胜,比赛立即结束;若比赛进行完6局还没有分出胜负则判第一局获胜者为最终获胜且结束比赛.比赛过程中,每局比赛甲获胜的概率为,乙获胜的概率为,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.22.若随机变量()22,3X N ~,且()()1P X P X a ≤=≥,则()52x a ax⎛+ ⎝展开式中3x 项的系数是__________.23.在某项测试中,测量结果服从正态分布,若,则__________.24.某班有50名学生,一次数学考试的成绩ξ服从正态分布,已知,估计该班学生数学成绩在120分以上的有______人.25.某厂生产的零件尺寸服从正态分布N(25,0.032),为使该厂生产的产品有95%以上的合格率,则该厂生产的零件尺寸允许值的围为________.26.已知正态总体的数据落在区间(-3,-1)里的概率和落在区间(3,5)里的概率相等,那么这个正态总体的数学期望为________.27且E (ξ)=1.1,则D (ξ)=________. 28.设p 为非负实数,随机变量X则E (X )的最大值为_______,D (X )的最大值为_____.29.12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,以ξ表示取出次品的个数,则ξ的期望值()E ξ=.参考答案1.A【解析】由题意有正态密度函数的图象关于直线0x =对称,正态密度函数的图象与x 轴围成的面积为1,所以有()1(2)(2)12P X P X a >=<-=-,选A . 2.B 【解析】。
随机变量及其分布列习题(含解析)
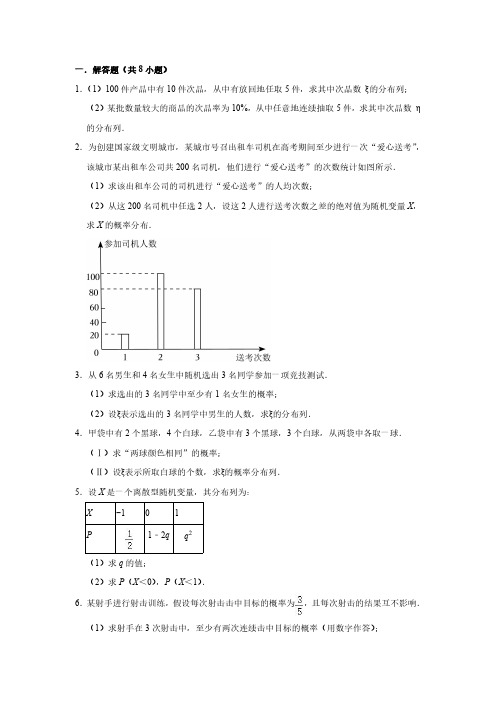
一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.2.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.参考答案与试题解析一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.【解答】解:(1)由题意知ξ的可能取值为0,1,2,3,4,5,每次取出次品的概率为:,相当于5次独立重复实验,ξ~B(5,),P(ξ=0)==0.59059,P(ξ=1)==0.32805,P(ξ=2)==0.07329,P(ξ=3)==0.0081,P(ξ=4)==0.00045,P(ξ=5)==0.00001,∴ξ的分布列为:ξ012345P0.590590.328050.07290.00810.000450.00001(2)由题意知η的可能取值为0,1,2,3,4,5,且η~B(5,0.1),∴η的分布列为:η012345P0.590590.328050.07290.00810.000450.000012.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.【解答】解:(1)由统计图得200名司机中送考1次的有20人,送考2次的有100人,送考3次的有80人,∴该出租车公司的司机进行“爱心送考”的人均次数为;(2)从该公司任选两名司机,记“这两人中﹣人送考1次,另一人送考2次”为事件A,“这两人中一人送考2次,另一人送考3次“为事件B,“这两人中﹣人送考1次,另一人送考3次”为事件C,“这两人送考次数相同”为事件D,由题意知X的所有可能取值为0,1,2,,,,所以X的分布列为:X012P3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【解答】解:(1)由意可知,选出的3名同学全是男生的概率为=,∴选出的3名同学中至少有1名女生的概率为P=1﹣=.(2)根据题意,ξ的可能取值为0,1,2,3,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:ξ0123P4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.【解答】解:(I)从甲中取出黑球的概率为,取出白球的概率为,从乙中取出黑球的概率为,取出白球的概率为,故“两球颜色相同”的概率P=.(II)由题意可得,ξ所有可能取值为0,1,2,P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,故ξ的分布列为:ξ012P5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).【解答】解:(1)依题意,得,解得或(舍去),所以.(2)由(1)得,,所以,.6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.【解答】解:(1)设事件该射手第i次射击,击中目标为A i,i=1,2,3,则,所以,事件射手在3次射击中,至少有两次连续击中目标可表示为,因为事件,,A1A2A3互斥,所以又事件A1,A2,A3相互独立,所以==;(2)事件射手第3次击中目标时,恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标,又各次击中目标的概率为,所以前3次中恰有两次击中目标的概率为,第四次击中目标的概率为,所以事件射手第3次击中目标时,恰好射击了4次的概率;(3)由已知ξ的取值有3,4,5,⋅⋅⋅,n,⋅⋅⋅,又,,,⋅⋅⋅,,所以随机变量ξ的分布列为:ξ345…n…P……7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.【解答】解:(1)由题意可得,X可能取值为0,1,2,3,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,故X的分布列为:X0123P(2)设得分为Y,则得分Y可以取4,5,6,7,分别对应4个黑球,3黑1红,2黑2红,1黑3红四种情况,P(Y≥6)=P(Y=6)+P(Y=7)=,故得分不小于6分的概率为.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.【解答】解:(1)由题意得ξ的可能取值为0,1,2,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,∴随机变量ξ的分布列为:ξ012P(2)事件“选出的2学生至少有一女生”的概率为:P=P(ξ=1)+P(ξ=2)==.。
随机变量分布列练习题二套

16. 某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有 个红球、 个白球 的甲箱和装有 个红球、 个白球的乙箱中,各随机摸出 个球,在摸出的 个球中,若都是红球,则获一 等奖,若只有 个红球,则获二等奖;若没有红球,则不获奖. (1)求顾客抽奖 次能获奖的概率; (2)若某顾客有 次抽奖机会,记该顾客在 次抽奖中获一等奖的次数为 ,求 的分布列和数学期望.
14. 某厂用鲜牛奶在某台设备上生产 , 两种奶制品.生产 吨 产品需鲜牛奶 吨,使用设备 小时,获 利 元;生产 吨 产品需鲜牛奶 吨,使用设备 小时,获利 元.要求每天 产品的产量不超过
产品产量的 倍,设备每天生产 , 两种产品时间之和不超过 小时.假定每天可获取的鲜牛奶数量 (单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利 (单位:元)是一个随 机变量.
(1)求 的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求 天中至少有 天的最大获利超过
元的概率.
15. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人 都猜对,则“星队”得 分;如果只有一个人猜对,则“星队”得 分;如果两人都没猜对,则“星队”得 分.已知甲每轮猜对的概率是 ,乙每轮猜对的概率是 ;每轮活动中甲、乙猜对与否互不影响.各轮结 果亦互不影响.假设“星队”参加两轮活动,求: (1)“星队”至少猜对 个成语的概率; (2)“星队”两轮得分之和为 的分布列和数学期望 .
13. 在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验 的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接 受心理暗示后的结果来评价两种心理暗示的作用,现有 名男志愿者 , , , , , 和 名女志 愿者 , , , ,从中随机抽取 人接受甲种心理暗示,另 人接受乙种心理暗示. (1)求接受甲种心理暗示的志愿者中包含 但不包含 的概率. (2)用 表示接受乙种心理暗示的女志愿者人数,求 的分布列与数学期望 .
高二数学随机变量的分布列试题答案及解析

高二数学随机变量的分布列试题答案及解析1.设随机变量ξ的概率分布列为(k=0,1,2,3),则.【答案】【解析】随机变量ξ的概率分布列为(k=0,1,2,3),且,,即.【考点】随机变量的分布列.2.若随机变量X~B(n,0.6),且E(X)=3,则P(X=1)的值是________.【答案】3×0.44【解析】E(X)=n×0.6=3,∴n=5,∴P(X=1)=C1(0.6)1×0.44=3×0.44.53.为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将从该市某学校抽取的样本数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.(Ⅰ)求该校报考体育专业学生的总人数n;(Ⅱ)若用这所学校的样本数据来估计该市的总体情况,现从该市报考体育专业的学生中任选3人,设表示体重超过60千克的学生人数,求的分布列和数学期望.【答案】(Ⅰ).(Ⅱ)0123(或).【解析】(Ⅰ)设从左至右前3小组的频率分别为由题意得 3分∴ 5分∴ 6分(Ⅱ)由(Ⅰ)得一个报考体育专业学生的体重超过60公斤的概率为8分由题意可知∴, 10分即∴(或) 12分【考点】频率分布直方图,随机变量的分布列及数学期望。
点评:中档题,作为数学应用问题,实际背景学生熟悉,易于理解题意,关键是细心计算。
4.甲、乙两人玩猜数字游戏,规则如下:①连续竞猜次,每次相互独立;②每次竟猜时,先由甲写出一个数字,记为,再由乙猜测甲写的数字,记为,已知,若,则本次竞猜成功;③在次竞猜中,至少有次竞猜成功,则两人获奖.(Ⅰ) 求甲乙两人玩此游戏获奖的概率;(Ⅱ)现从人组成的代表队中选人参加此游戏,这人中有且仅有对双胞胎,记选出的人中含有双胞胎的对数为,求的分布列和期望.【答案】(1)(2)分布列为∴【解析】解:(Ⅰ)记事件为甲乙两人一次竞猜成功,则则甲乙两人获奖的概率为(Ⅱ)由题意可知6人中选取4人,双胞胎的对数取值为0,1,2则,∴分布列为∴【考点】古典概型概率和分布列点评:主要是考查了古典概型概率和分布列的求解,属于基础题。
第2章_随机变量及其分布练习题及答案

第2章 随机变量及其分布(练习、复习题及答案)一、填空题:1.随机变量ξ的分布列为P(ξ=k )=a /N ,(k =1,2,…,N),则a = 1 .2.射手每次射击击中目标的概率为p ,连续向同一目标射击,直到某一次击中目标为止,则射击次数ξ的分布列为 P(ξ=k )=p (1-p )k -1,k =1,2,….3.随机变量ξ服从参数为(2,p )的二项分布,随机变量η服从参数为(4,p )的二项分布,若P(ξ<1)=4/9,则P(η≥1)=_ 65/81_.4.离散型随机变量ξ的概率分布P(ξ=0)=0.2,P(ξ=1)=0.3,P(ξ=2)=0.5,则P(ξ≤1.5)=__0.5__.5.随机变量ξ的分布列为P(ξ=k )=!k Ckλ,k =0,1,2,…(λ>0),则C = e -λ. *λλλλe =++++!3!2!11326.随机变量ξ的分布列为P(ξ=k )=k a -λ,k =1,2,…,其中λ>1,则a = λ-1 .7.一实习生用同一台机器接连独立地制造三个同种零件,第i 个零件是不合格品的概率3,2,1,11=+=i i p i ,以ξ表示三个零件中合格品的个数,则P{ξ=2}= 11/24 .8.随机变量ξ的分布函数为F(x ),则概率P(ξ≥a )用F(x )表示为__ 1-F(a )__. 9.随机变量ξ的分布函数为F(x )=⎪⎩⎪⎨⎧<≥+--0 0 0)1(1x x ex x ,,,则P(ξ≤1)=_1-2e -1_. 10.随机变量ξ的概率密度函数为f (x )=⎪⎩⎪⎨⎧<-其他,), 0 2A(2x x ,则A=__1/4__.11.连续型随机变量ξ的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<=1, 110,0,0)(F 2x x x x x ,则ξ的概率密度f (x )=⎩⎨⎧<<其他, 1 10,2x x .12.连续型随机变量ξ的分布函数为)0(00,0B A )(F >⎪⎩⎪⎨⎧≤>+=-λλx x ex x ,, ,则常数A =_1 ,B =_-1;P{-1<ξ<1}= 1-e -λ.13.随机变量ξ的分布函数为⎪⎩⎪⎨⎧<≥+-=-0, 00,)1(1)(x x ex x F x ,则相应的概率密度是⎪⎩⎪⎨⎧<≥=-0, 00,)(x x xex f x .14.随机变量ξ在[1,4]上服从均匀分布,现在对进行3次独立试验,则至少有2次观察值大于2的概率为_20/27_.15.随机变量ξ ~N(70,102),则P(60<ξ<80)=_0.6826_.(已知Φ(1)=0.8413)16.随机变量ξ服从正态分布N(2,σ2),且P(2<ξ<4)=0.3,则P(ξ<0)=_0.2_.17.随机变量服从正态分布N(μ,σ2),已知P(ξ<9)=0.975,P(ξ<2)=0.062,则P(ξ>6)=_0.3228_. 18.若ξ~N(0,1),则η=ξ3的密度函数为+∞<<-∞--y e yy,231322132π.19.统考成绩服从正态分布N(70,102),在参加统考的人中,及格者100人(及格分数为60分),则不及格人数约为_19_.二、选择题1.在下列结果中,构成概率分布的是( D ).{}{}{}{}),,(D.P ),,,(C.P ),,(B.P ),,,(A.P 2 132 2 1 032 2 131 2 1 031============k k ξk k ξk k ξk k ξkkkk2.随机变量ξ的概率分布为P(ξ=k )=b λk (k =1,2,…), b >0,则( C ). A.λ为任意正实数 B.λ=b +1 C.b+=11λ D.11-=b λ3.常数b =( B )时,),,( 2 1)1(=+=k k k b p k 为离散型随机变量的概率分布.A.2B.1C.0.5D.34.设ξ是一个离散型随机变量,则( D )可以成为ξ的分布列.{}{}, , , n n en ξn n en ξx x x x x R p p p nn210!32 1!30.22.0 .303.0 .10 ,1 0 1 3354321======⎪⎪⎭⎫⎝⎛∈⎪⎪⎭⎫⎝⎛---.D.P,,.C.P B.A.5.随机变量ξ~N(0,1),ξ的分布函数为Φ(x ),则P(⎢ξ⎪<1)的值为( B ).A.2[1-Φ(1)]B.2Φ(1)-1C.1-Φ(1)D.1-2Φ(1)6.随机变量ξ~N(0,1),ξ的分布函数为Φ(x ),则P(⎢ξ⎪>2)的值为( A ). A.2[1-Φ(2)] B.2Φ(2)-1 C.2-Φ(2) D.1-2Φ(2)7.设随机变量ξ的分布函数为F (x ),在下列概率中可表示为F (a +0) - F (a )的是( C ). A.P{ξ≤a } B. P{ξ>a } C. P{ξ=a } D. P{ξ≥a }8.下列函数可以作为某一随机变量ξ的密度函数的是( D ).⎪⎩⎪⎨⎧∈=⎪⎩⎪⎨⎧-∈=⎪⎩⎪⎨⎧∈=⎩⎨⎧∈=其他D. 其他C. 其他B.其他A., 0 ]2,0[,sin )(, 0 ]2,2[,sin )(, 0 ]23,0[,sin )( , 0 ],0[,sin )(πππππx x x f x x x f x x x f x x x f9.设ξ的概率密度为⎪⎩⎪⎨⎧≤>+=0 0 0)(1A )(4x x x x x f ,,,则A=( B ).A.3B.6C.2.5D.4 10.设随机变量ξ的密度函数为f (x )=)(21+∞<<-∞-x ex,则其分布函数的是( B ).⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤-<=⎪⎩⎪⎨⎧≥<-=⎪⎪⎩⎪⎪⎨⎧≥-<=⎪⎩⎪⎨⎧≥<=---1, 1 10,2110, 21 )(0, 1 0,211)(0,2110, 21 )( 0, 0 0,21)(x x e x e x F x x e x F x e x e x F x x e x F x xx x xx D. C. B.A.11.设f (x )是一连续型随机变量ξ的密度函数,其表达式为分段函数,则当x ∈( A )时,f (x )=cos x ,其余f (x )=0.]47,23[],0[],2[]2,0[ππππππ D. C. B.A.12.设随机变量ξ服从[0,5]上的均匀分布,则关于t 的方程4t 2+4ξt+ξ+2=0有实根的概率是( B ).A.0.4B.0.6C.1D.1/313.设随机变量ξ~N(μ, 62),η~ N(μ, 82),记p 1=P{ξ≤μ-6},p 2=P{η≥μ+8},则( A ).A. p 1=p 2B. p 1>p 2C. p 1<p 2D. p 1≤p 2 三、解答题:1.下列表格是概率分布吗?为什么?(1) ξ 1 2 3 4 不是 (2) ξ -1 0 1 4 是 P 0.2 0.3 0.3 0.4 P 0.1 0.2 0.3 0.4 2.求常数C ,使下列函数成为概率分布:P(ξ=k )=Ck ,k =1,2,…, n ; )1(2+=n n C3.随机变量ξ~b (n , p ),已知P(ξ=1)=P(ξ=n -1),试求 p 与P(ξ=2)的值.p =0.5,P(ξ=2)=122)1(21+-=⎪⎭⎫ ⎝⎛n nnn n C4.随机试验中事件A 发生的概率为p ,把这个试验独立重复地做两次。
随机变量及其分布习题及解答

第二章 随机变量及其分布习题1.设连续型随机变量X 的分布函数为0,,()arcsin ,,(0).1,,x a x F x A B a x a a a x a <−⎧⎪⎪=+−≤<>⎨⎪≥⎪⎩ 求:(1)A 和B ;(2)概率密度.)(x f 2.设连续型随机变量X 的密度函数为)(x f X 230,0,2,x x x e x −<⎧⎪=⎨≥⎪⎩0.求:(1);(2)32+=X Y 2X Y =的密度函数. 3.随机变量X 与Y 相互独立,且都服从正态分布)21,0(N ,求22Y X Z +=的概率密度。
4.已知随机变量X 服从区间上的均匀分布,求随机变量)1,1(−122+=X Y 的概率密度函数。
5.设随机变量X 的概率密度为∞<<+=x x x p X 0,)1(2)(2π 求随机变量XY 1=的分布密度函数。
6.袋中有5只同样大小的球,编号为1,2,3,4,5,从中同时取出3只球,令X 表示取出的球的最大号码,求X 的分布律和分布函数。
7、已知随机变量和的概率分布为1X 2X , , ⎭⎬⎫⎩⎨⎧−−4/12/14/1101~1X ⎭⎬⎫⎩⎨⎧2/12/110~2X 而且1}0{21==X X P .(1) 求和的联合分布.1X 2X (2) 问和是否独立?为什么?1X 2X 8.某仪器装有三只独立工作的同型号电气元件,其寿命(单位:小时)都服从同一指数分布,密度函数为⎪⎩⎪⎨⎧≤>−=000600exp(6001)(x x x x f . 试求在仪器使用的最初200h 内,至少有一个电子元件损坏的概率α9.某公共汽车站从上午7时起每15分钟发一班车,即在7:00,7:15,7:30,…有汽车发出。
如果乘客到达此汽车站的时间X 是在7:00~7:30的均匀随机变量,试求乘客在车站等候(1)不超过5分钟的概率;(2)超过10分钟的概率10.假设电路中装有三个同种电器元件,它们的工作状态相互独立,且无故障工作时间都服从参数为0>λ的指数分布,当三个元件都无故障时,电路正常工作,求电路正常工作时间T 的概率分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机变量及分布列1.已知随机变量()20,X N σ~,若(2)P X a <=,则(2)P X >的值为( )A.12a - B. 2a C. 1a - D. 12a+2.已知随机变量,若,则的值为( ) A. 0.4 B. 0.2 C. 0.1 D. 0.6 3.已知,,则的值为( ) A. 10 B. 7 C. 3 D. 64.集装箱有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下并放回,如果两球之积是4的倍数,则获奖.若有4人参与摸奖,恰好有3人获奖的概率是( ) A. B. C. D.5.甲袋中放有大小和形状相同的小球若干,其中标号为0的小球为1个,标号为1的小球2个,标号为2的小球2个.从袋中任取两个球,已知其中一个的标号是1,则另一个标号也是1的概率为__________. 6.设随机变量服从正态分布,,则__________.7.某人通过普通话二级测试的概率是,他连线测试3次,那么其中恰有1次通过的概率是( ) A. B. C. D.8.从1,2,3,4,5,6,7中任取两个不同的数,事件为“取到的两个数的和为偶数”,事件为“取到的两个数均为奇数”,则( ) A. B. C. D.9.班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机 抽取一个容量为8的样本进行分析.(Ⅰ)如果按性别比例分层抽样,求样本中男生、女生人数分别是多少;(Ⅱ)随机抽取8位同学,数学成绩由低到高依次为:6065707580859095,,,,,,,;物理成绩由低到高依次为:7277808488909395,,,,,,,,若规定90分(含90分)以上为优秀,记ξ为这8位同学中数学和物理分数均为优秀的人数,求ξ的分布列和数学期望.10.某品牌汽车的4S 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件A :“至多有1位采用分6期付款“的概率()P A ;(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量η,求η的分布列和数学期望()E η.11.某公司有,,,,A B C D E 五辆汽车,其中,A B 两辆汽车的车牌尾号均为1. ,C D 两辆汽车的车牌尾号均为2,E车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,,,A B E三辆汽车每天出车的概率均为12,,C D两辆汽车每天出车的概率均为23,且五辆汽车是否出车相互独立,该公司所在地区汽车(1)求该公司在星期一至少有2辆汽车出国的概率;(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及期望.12.拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为X,试求随机变量X的分布列和数学期望;(Ⅱ)若在犯错误的概率不超过P的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由.附:独立性检验统计量()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.13.某高校数学系2016年高等代数试题有6个题库,其中3个是新题库(即没有用过的题库),3个是旧题库(即至少用过一次的题库),每次期末考试任意选择2个题库里的试题考试.(1)设2016年期末考试时选到的新题库个数为,求的分布列和数学期望;(2)已知2016年时用过的题库都当作旧题库,求2017年期末考试时恰好到1个新题库的概率.14.某市举行的“国际马拉松赛”,举办单位在活动推介晚会上进行嘉宾现场抽奖活动,抽奖盒中装有6个大小相同的小球,分别印有“快乐马拉松”和“美丽绿城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球(取出后不再放回),若抽到的两个球都印有“快乐马拉松”标志即可获奖.并停止取球;否则继续抽取,第一次取球就抽中获一等奖,第二次取球抽中获二等奖,第三次取球抽中获三等奖,没有抽中不获奖.活动开始后,一位参赛者问:“盒中有几个印有‘快乐马拉松’的小球?”主持人说:“我只知道第一次从盒中同时抽两球,不都是‘美丽绿城行’标志的概率是(1)求盒中印有“快乐马拉松”小球的个数;(2)若用表示这位参加者抽取的次数,求的分布列及期望.15.为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25) , [25,30) , [30,35), [35,40) , [40,45] ,并得到如下频率分布直方图.(Ⅰ)求图中的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为,求的分布列及数学期望.16.一家医药研究所,从中草药中提取并合成了甲、乙两种抗“病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为.现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.(1)求一个试用组为“甲类组”的概率;(2)观察3个试用组,用表示这3个试用组中“甲类组”的个数,求的分布列和数学期望.17.某班为了提高学生学习英语的兴趣,在班举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在的人数为12人.(Ⅰ)求此班级人数;(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.(i)甲不排在第一位乙不排在最后一位的概率;(ii)记甲乙二人排在前三位的人数为,求的分布列和数学期望.18.2017年1月1日,作为市打造“千园之城”27个示性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列22愿意不愿意总计男生女生总计(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为12,记甲通过的关数为X ,求X的分布列和数学期望.()()()()()22n ad bc K a b c d a c b d -=++++.19.在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,知识告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.(1)求乙班总分超过甲班的概率;(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分, ①请你从平均分和方差的角度来分析两个班的选手的情况;②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为,求的分布列及数学期望.20.一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求: (1)连续取两次都是红球的概率;(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数的概率分布列及期望.21.甲乙两人下棋比赛,规定谁比对方先多胜两局谁就获胜,比赛立即结束;若比赛进行完6局还没有分出胜负则判第一局获胜者为最终获胜且结束比赛.比赛过程中,每局比赛甲获胜的概率为,乙获胜的概率为,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.22.若随机变量()22,3X N ~,且()()1P X P X a ≤=≥,则()52x a ax⎛+ ⎝展开式中3x 项的系数是__________.23.在某项测试中,测量结果服从正态分布,若,则__________.24.某班有50名学生,一次数学考试的成绩ξ服从正态分布,已知,估计该班学生数学成绩在120分以上的有______人.25.某厂生产的零件尺寸服从正态分布N(25,0.032),为使该厂生产的产品有95%以上的合格率,则该厂生产的零件尺寸允许值的围为________.26.已知正态总体的数据落在区间(-3,-1)里的概率和落在区间(3,5)里的概率相等,那么这个正态总体的数学期望为________.27.若随机变量ξ的分布列如下表:ξ 01 xP15 p310且E (ξ)=1.1,则D (ξ)=________. 28.设p 为非负实数,随机变量X 的概率分布为X 012P12p - p 12则E (X )的最大值为_______,D (X )的最大值为_____.29.12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,以ξ表示取出次品的个数,则ξ的期望值()E ξ=.参考答案1.A【解析】由题意有正态密度函数的图象关于直线0x =对称,正态密度函数的图象与x 轴围成的面积为1,所以有()1(2)(2)12P X P X a >=<-=-,选A . 2.B 【解析】。
故选B 。
3.A【解析】由题意得 。
故选A 。
4.B【解析】获奖的概率为 ,记获奖的人数为 , ,所以4人中恰好有3人获奖的概率为 ,故选B. 5.【解析】记“一个标号是 ”为事件 ,”另一个标号也是”为事件 ,所以 。
