椭圆_双曲线_抛物线知识点
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总
椭圆双曲线抛物线是数学中的重要概念,它们的知识点汇总如下:
首先是椭圆,它是一种抛物线,其特征是两个轴的长度不相等,形状像一个椭圆。
它的方程式为:x2/a2 + y2/b2 = 1,其中a为椭圆的长轴,b为椭圆的短轴。
其次是双曲线,它也是一种抛物线,其特征是两个轴的长度相等,形状像一个双曲线。
它的方程式为:x2/a2 - y2/b2 = 1,其中a为双曲线的长轴,b为双曲线的短轴。
最后是抛物线,它是一种曲线,其特征是一个轴的长度为零,形状像一个抛物线。
它的方程式为:y2 = 2px,其中p为抛物线的焦点距离。
椭圆双曲线抛物线是数学中重要的概念,它们的方程式分别为:x2/a2 + y2/b2 = 1(椭圆),x2/a2 - y2/b2 = 1(双曲线),y2 = 2px(抛物线)。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总椭圆、双曲线、抛物线知识点汇总一、椭圆(Ellipse)1. 定义:椭圆是平面上所有到两个固定点(焦点)距离之和为常数的点的集合。
2. 标准方程:\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)其中,\(a\) 是椭圆的长半轴,\(b\) 是短半轴。
3. 性质:- 焦点:椭圆上任意一点到两个焦点的距离之和是一个大于两焦点间距离的常数,即 \(2a\)。
- 椭圆的长轴和短轴互相垂直。
- 椭圆的面积 \(A = \pi a b\)。
4. 焦点性质:- 椭圆上任意一点 \(P\) 与两个焦点 \(F_1\) 和 \(F_2\) 构成的三角形中,\(PF_1 + PF_2 = 2a\)。
5. 椭圆的离心率 \(e\):\(e = \frac{c}{a}\)其中,\(c = \sqrt{a^2 - b^2}\) 是焦点到中心的距离。
二、双曲线(Hyperbola)1. 定义:双曲线是平面上所有到两个固定点(焦点)距离之差为常数的点的集合。
2. 标准方程:\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) 为右开口双曲线;\(\frac{y^2}{b^2} - \frac{x^2}{a^2} = 1\) 为上开口双曲线。
3. 性质:- 焦点:双曲线上任意一点到两个焦点的距离之差是一个小于两焦点间距离的常数,即 \(2a\)。
- 双曲线的两个分支分别位于中心点的两侧。
- 双曲线的面积无限大。
4. 焦点性质:- 双曲线上任意一点 \(P\) 与两个焦点 \(F_1\) 和 \(F_2\) 构成的三角形中,\(PF_1 - PF_2 = 2a\)。
5. 双曲线的离心率 \(e\):\(e = \frac{c}{a}\)其中,\(c = \sqrt{a^2 + b^2}\) 是焦点到中心的距离,且 \(e > 1\)。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数(大于|F1F2|)的动点 P 的轨迹,F1、F2 称为椭圆的焦点,两焦点的距离|F1F2|称为椭圆的焦距。
1、椭圆的标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
焦点在 y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\)(\(a > b > 0\))。
2、椭圆的性质范围:对于焦点在 x 轴上的椭圆,\(a \leq x \leq a\),\(b\leq y \leq b\);对于焦点在 y 轴上的椭圆,\(b \leq x \leq b\),\(a \leq y \leq a\)。
对称性:椭圆关于 x 轴、y 轴和原点对称。
顶点:焦点在 x 轴上时,顶点坐标为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点坐标为\((0, \pm a)\),\((\pm b, 0)\)。
离心率:椭圆的离心率\(e =\frac{c}{a}\)(\(0 < e <1\)),它反映了椭圆的扁平程度,\(e\)越接近0,椭圆越接近圆;\(e\)越接近 1,椭圆越扁。
3、椭圆的参数方程焦点在 x 轴上:\(\begin{cases}x = a\cos\theta \\ y =b\sin\theta\end{cases}\)(\(\theta\)为参数)焦点在 y 轴上:\(\begin{cases}x = b\cos\theta \\ y =a\sin\theta\end{cases}\)(\(\theta\)为参数)4、椭圆中的焦点三角形设 P 为椭圆上一点,F1、F2 为焦点,\(\angle F1PF2 =\theta\),则三角形 PF1F2 的面积为\(S = b^2\tan\frac{\theta}{2}\)。
抛物线椭圆双曲线知识点总结知乎

抛物线椭圆双曲线知识点总结知乎抛物线、椭圆和双曲线是三种常见的二次曲线形状,它们在数学和物理学中具有重要的应用。
下面是对这三种曲线的知识点总结: 1. 抛物线:定义,抛物线是一个平面曲线,其定义为到一个定点(焦点)和一条直线(准线)的距离之比等于一个常数(离心率)。
方程形式,一般的抛物线方程可以表示为 y = ax^2 + bx + c,其中 a、b、c 是常数,a ≠ 0。
特点,抛物线是对称的,关于焦点和准线都具有对称性。
焦点和准线的位置和形状取决于抛物线方程中的参数。
2. 椭圆:定义,椭圆是一个平面曲线,其定义为到两个定点(焦点)之和等于一定距离(长轴)的点的集合。
方程形式,一般的椭圆方程可以表示为 (x-h)^2/a^2 + (y-k)^2/b^2 = 1,其中 (h, k) 是椭圆的中心坐标,a 和 b 是长轴和短轴的长度。
特点,椭圆是对称的,关于中心点具有对称性。
长轴和短轴的长度决定了椭圆的形状和大小。
3. 双曲线:定义,双曲线是一个平面曲线,其定义为到两个定点(焦点)之差等于一定距离(距离焦点的距离)的点的集合。
方程形式,一般的双曲线方程可以表示为 (x-h)^2/a^2 (y-k)^2/b^2 = 1,其中 (h, k) 是双曲线的中心坐标,a 和 b 是与中心有关的参数。
特点,双曲线有两个分支,分别向外延伸。
焦点和中心之间的距离决定了双曲线的形状和大小。
这些是抛物线、椭圆和双曲线的基本知识点总结。
它们在数学中有广泛的应用,例如物体的运动轨迹、光学系统的焦点和镜面反射等。
深入了解这些曲线的性质和特点,对于数学和物理学的学习都具有重要意义。
高中数学知识点---椭圆、双曲线、抛物线

高中数学专题四椭圆、双曲线、抛物线《圆锥曲线》知识点小结一、椭圆:(1)椭圆的定义:平面内与两个定点21,F F 的距离的和等于常数(大于||21F F )的点的轨迹。
其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。
注意:||221F F a >表示椭圆;||221F F a =表示线段21F F ;||221F F a <没有轨迹; (2)椭圆的标准方程、图象及几何性质:3.常用结论:(1)椭圆)0(12222>>=+b a by a x 的两个焦点为21,F F ,过1F 的直线交椭圆于B A ,两点,则2ABF ∆的周长=(2)设椭圆)0(12222>>=+b a by a x 左、右两个焦点为21,F F ,过1F 且垂直于对称轴的直线交椭圆于Q P ,两点,则Q P ,的坐标分别是 =||PQ二、双曲线:(1)双曲线的定义:平面内与两个定点21,F F 的距离的差的绝对值等于常数(小于||21F F )的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距。
注意:a PF PF 2||||21=-与a PF PF 2||||12=-(||221F F a <)表示双曲线的一支。
||221F F a =表示两条射线;||221F F a >没有轨迹;(2(3)双曲线的渐近线:①求双曲线12222=-b y a x 的渐近线,可令其右边的1为0,即得02222=-by a x ,因式分解得到0x ya b±=。
②与双曲线12222=-b y a x 共渐近线的双曲线系方程是λ=-2222y x ;(4)等轴双曲线为222t y x =-2(4)常用结论:(1)双曲线)0,0(12222>>=-b a by a x 的两个焦点为21,F F ,过1F 的直线交双曲线的同一支于B A ,两点,则2ABF ∆的周长=(2)设双曲线)0,0(12222>>=-b a by a x 左、右两个焦点为21,F F ,过1F 且垂直于对称轴的直线交双曲线于Q P ,两点,则Q P ,的坐标分别是=||PQ三、抛物线:(1)抛物线的定义:平面内与一个定点的距离和一条定直线的距离相等的点的轨迹。
一轮复习专题48 椭圆、双曲线、抛物线(知识梳理)

专题48椭圆、双曲线、抛物线(知识梳理)一、椭圆(一)椭圆的基本定义和方程1、椭圆的定义:设1F 、2F 是定点,P 为动点,则满足a PF PF 2||||21=+(a 为定值且||221F F a >)的动点P 的轨迹称为椭圆,符号表示:a PF PF 2||||21=+(||221F F a >)。
注意:当||221F F a =时为线段21F F ,当||221F F a <时无轨迹。
2、椭圆的方程及图像性质定义方程a y c x y c x 2)()(2222=+-+++ac y x c y x 2)()(2222=-++++标准方程12222=+b y a x (0>>b a )12222=+b x a y (0>>b a )一般方程122=+ny mx (0>m ,0>n ,n m ≠)推导方程22222b x ab y +-=(0>>b a )22222a x ba x +-=(0>>b a )范围][a a x ,-∈,][b b y ,-∈][b b x ,-∈,][a a y ,-∈图形焦点坐标焦点在x 轴上)0(1,c F -,)0(2,c F 焦点在y 轴上)0(1c F -,,)0(2c F ,对称性对称轴:x 轴、y 轴对称中心:原点(这个对称中心称为椭圆的中心)顶点)0(1,a A -、)0(2,a A 、)0(1b B -,、)0(2b B ,)0(1a A ,、)0(2a A -,、)0(1,b B 、)0(2,b B -轴长轴21A A 的长为:a 2(a 为长半轴)短轴21B B 的长为:b 2(b 为短半轴)离心率椭圆的焦距与长轴长度的比叫做椭圆的离心率ace =,)10(,∈e ,e 越大越扁,e 越小越圆焦距:cF F 221=222c b a +=3、椭圆12222=+by a x (0>>b a )的图像中线段的几何特征(如图):(1)a PF PF 2||||21=+,e PM PF PM PF ==2211,c a PM PM 2212||||=+;(2)a BF BF ==||||21,c OF OF ==||||21,2221||||b a B A B A +=+;(3)c a F A F A -==||||2211,c a F A F A +==||||1221。
(完整版)椭圆,双曲线,抛物线知识点
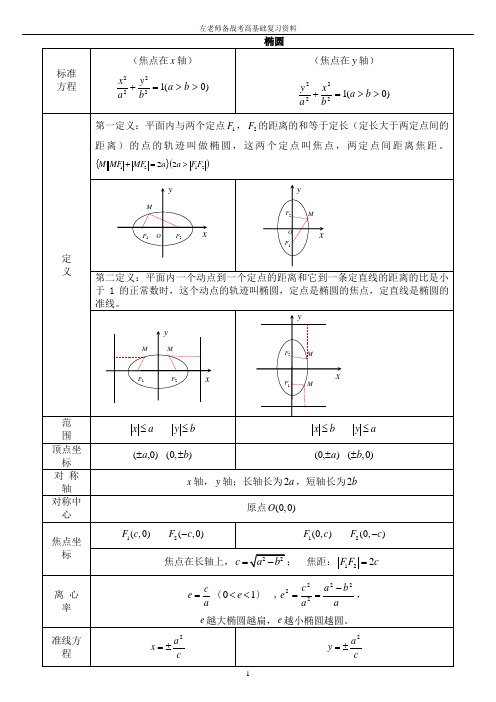
标准
方程
(焦点在 轴)
(焦点在 轴)
定 义
第一定义:平面内与两个定点 , 的距离的和等于定长(定长大于两定点间的距离)的点的轨迹叫做椭圆,这两个定点叫焦点,两定点间距离焦距。
第二定义:平面内一个动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数时,这个动点的轨迹叫椭圆,定点是椭圆的焦点,定直线是椭圆的准线。
顶点到准线的距离
焦点到准线的距离
焦点弦的几条性质
设直线过焦点F与抛物线 >0)交于 ,
则:(1) =
(2)
(3)通径长:
(4)焦点弦长
直线与抛物线的位置
抛物线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
切线
方程
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
椭圆上到焦点的最大(小)距离
最大距离为:
最小距离为:
相关应用题:远日距离
近日距离
椭圆的参数方程
( 为参数)
( 为参数)
椭圆上的点到给定直线的距离
利用参数方程简便:椭圆 ( 为参数)上一点到直线 的距离为:
直线和椭圆的位置
椭圆 与直线 的位置关系:
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
渐近线
方程
( )
( )
共渐近线的双曲线系方程
( )
( )
直线和双曲线的位置
双曲线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
二次方程二次项系数为零直线与渐近线平行。
相交弦AB的弦长
通径:
过双曲线上一点的切线
圆锥曲线(椭圆,双曲线,抛物线)的定义方程和性质知识总结

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2.3. 椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在x 轴上时,设12F F 、分别是椭圆的左、右焦点,()00P x y ,是椭圆上任一点,则10PF a ex =+,20PF a ex =-。
推导过程:由第二定义得11PF e d =(1d 为点P 到左准线的距离), 则211000a PF ed e x ex a a ex c ⎛⎫==+=+=+ ⎪⎝⎭;同理得20PF a ex =-。
简记为:左“+”右“-”。
由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。
22221x y a b +=;若焦点在y 轴上,则为22221y x a b+=。
有时为了运算方便,设),0(122n m m ny mx ≠>=+。
双曲线的定义、方程和性质1. 定义(1)第一定义:平面内到两定点F 1、F 2的距离之差的绝对值等于定长2a (小于|F 1F 2|)的点的轨迹叫双曲线。
说明:①||PF 1|-|PF 2||=2a (2a <|F 1F 2|)是双曲线;若2a=|F 1F 2|,轨迹是以F 1、F 2为端点的射线;2a >|F 1F 2|时无轨迹。
②设M 是双曲线上任意一点,若M 点在双曲线右边一支上,则|MF 1|>|MF 2|,|MF 1|-|MF 2|=2a ;若M 在双曲线的左支上,则|MF 1|<|MF 2|,|MF 1|-|MF 2|=-2a ,故|MF 1|-|MF 2|=±2a ,这是与椭圆不同的地方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通径:
过椭圆上一点的切线
利用导数
利用导数
双曲线
双曲线
标准方程(焦点在 轴)
标准方程(焦点在 轴)
定义
第一定义:平面内与两个定点 , 的距离的差的绝对值是常数(小于 )的点的轨迹叫双曲线。这两个定点叫做双曲线的焦点,两焦点的距离叫焦距。
范围
,
,
对称轴
轴, 轴;实轴长为 ,虚轴长为
对称中心
顶点
离心率
=1
准线
方程
准线与焦点位于顶点两侧且到顶点的距离相等。
顶点到准线的距离
焦点到准线的距离
焦点弦的几条性质
设直线过焦点F与抛物线 >0)交于 ,
则:(1) =
(2)
(3)通径长:
(4)焦点弦长
直线与抛物线的位置
抛物线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
切线
方程
越大椭圆越扁, 越小椭圆越圆。
椭圆上到焦点的最大(小)距离
最大距离为:
最小距离为:
相关应用题:远日距离
近日距离
椭圆的参数方程
( 为参数)
( 为参数)
椭圆上的点到给定直线的距离
利用参数方程简便:椭圆 ( 为参数)上一点到直线 的距离为:
直线和椭圆的Βιβλιοθήκη 置椭圆 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
椭圆
标准
方程
(焦点在 轴)
(焦点在 轴)
定 义
第一定义:平面内与两个定点 , 的距离的和等于定长(定长大于两定点间的距离)的点的轨迹叫做椭圆,这两个定点叫焦点,两定点间距离焦距。
范 围
顶点坐标
对 称 轴
轴, 轴;长轴长为 ,短轴长为
对称中心
原点
焦点坐标
焦点在长轴上, ; 焦距:
离 心 率
( ) , ,
相交弦AB的弦长
通径:
过双曲线上一点的切线
或利用导数
或利用导数
抛物线
抛
物
线
定义
平面内与一个定点 和一条定直线 的距离相等的点的轨迹叫做抛物线,点 叫做抛物线的焦点,直线 叫做抛物线的准线。
{ =点M到直线 的距离}
范围
对称性
关于 轴对称
关于 轴对称
焦点
( ,0)
( ,0)
(0, )
(0, )
焦点在对称轴上
原点
焦点坐标
焦点在实轴上, ;焦距:
顶点坐标
( ,0)( ,0)
(0, ,) (0, )
离心率
1)
准线方程
准线垂直于实轴且在两顶点的内侧;两准线间的距离:
渐近线
方程
( )
( )
共渐近线的双曲线系方程
( )
( )
直线和双曲线的位置
双曲线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
二次方程二次项系数为零直线与渐近线平行。
