matlab数字图像加密
数字图像加密算法的研究与实现

数字图像加密算法的研究与实现摘要数字图像加密是进行数字图像信息保密的一种手段。
随着信息技术的飞速发展,数字图像在各个领域中有着极为广泛的运用,那么数字图像中所包含的信息安全性应受到重视。
数字图像本身具有数据量较大的特点,用传统的的加密方法往往无法达到加密的要求,许多学者对数字图像的信息安全性进行了多次研究并提出了许多强而有效的算法。
本文研究并实现了一种基于混沌序列置乱的数字图像加密算法,通过密钥产生混沌序列,将该混沌序列进行逻辑排序,并以此排列方法对数字图像进行加密。
该算法隐私性较强,在数字图像的加密和解密过程中均需要密钥的参与,因此不知道密钥的用户无法恢复数字图像,具有良好的保密性。
关键词:数字图像混沌加密数据隐藏AbstractDigital image encryption algorithm is a method about keeping the information of digital image secret.With the quick development of informational technology,the digital image has been utilized in many areas,so the security of message that digital images carry should be paid attention.Particularly ,digital images have the characteristic of a large amount of data,it can not meet demands about encryption that encrypting data in traditional way,which leads to a lot of scholars have spent much time and energy on researching the security about digital image information and illustrated many effective algorithm.This article discuss and illustrate a kind of digital image encryption algorithm based on chaotic array disruption,producing chaotic array according to the key,then logically arranging existed chaotic array,finally encrypt digital image with same logic.It shows better privacy.This process requires keys participating in both encryption and deciphering,so anyone does not know the key who can not rebuild the original image.Key words:digital image chaotic encryption hiding data目录摘要 (I)Abstract (II)绪论 (1)1数字图像加密的基础理论 (4)1.1密码学的介绍 (4)1.2 图像加密技术 (4)1.3数字图像的置乱 (5)1.4混沌加密简介 (5)1.5混沌加密安全性分析 (6)2开发工具简介 (8)3基于混沌的数字图像加密算法 (11)3.1数字图像混沌加密算法总体设计 (11)3.2 数字图像混沌加密算法 (11)3.3数字图像混沌解密算法 (13)4实验仿真与结果 (14)4.1编程实现相关函数及其方法 (14)4.2仿真结果 (14)4.2.1非彩色图像实验仿真 (14)4.2.2彩色图像实验仿真 (16)结论 (18)附录1混沌加密与混沌解密算法代码 (19)绪论计算机和网络的飞速发展为多媒体数字产品的使用、传播提供了极其便利的途径,然而由于数字产品具有极易被复制和修改的特性,使得数字作品的信息安全问题和版权保护成为迫切需要解决的难题。
图像加密中测试混沌系统性能的0-1测试0-1Test方法与MATLAB实现代码
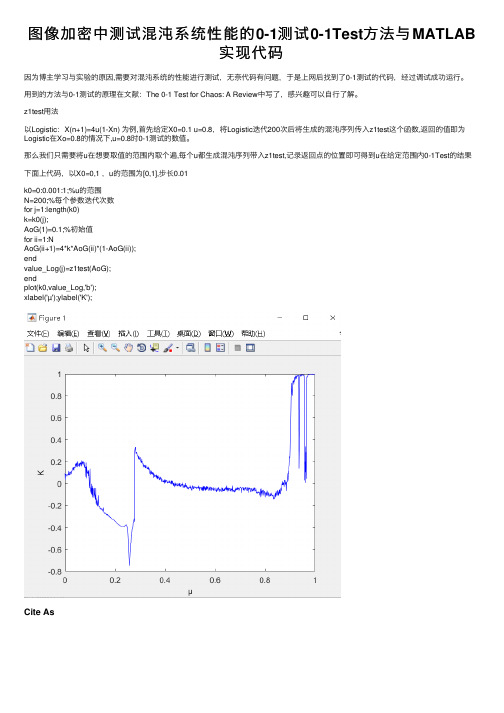
图像加密中测试混沌系统性能的0-1测试0-1Test⽅法与MATLAB
实现代码
因为博主学习与实验的原因,需要对混沌系统的性能进⾏测试,⽆奈代码有问题,于是上⽹后找到了0-1测试的代码,经过调试成功运⾏。
⽤到的⽅法与0-1测试的原理在⽂献:The 0-1 Test for Chaos: A Review中写了,感兴趣可以⾃⾏了解。
z1test⽤法
以Logistic:X(n+1)=4u(1-Xn) 为例,⾸先给定X0=0.1 u=0.8,将Logistic迭代200次后将⽣成的混沌序列传⼊z1test这个函数,返回的值即为Logistic在Xo=0.8的情况下,u=0.8时0-1测试的数值。
那么我们只需要将u在想要取值的范围内取个遍,每个u都⽣成混沌序列带⼊z1test,记录返回点的位置即可得到u在给定范围内0-1Test的结果下⾯上代码,以X0=0,1 ,u的范围为[0,1],步长0.01
k0=0:0.001:1;%u的范围
N=200;%每个参数迭代次数
for j=1:length(k0)
k=k0(j);
AoG(1)=0.1;%初始值
for ii=1:N
AoG(ii+1)=4*k*AoG(ii)*(1-AoG(ii));
end
value_Log(j)=z1test(AoG);
end
plot(k0,value_Log,'b');
xlabel('µ');ylabel('K');
Cite As。
可逆信息隐藏hs算法matlab

可逆信息隐藏是指在保证原始载体数据不受损的情况下,将需要隐藏的信息嵌入到载体数据中,并且可以在需要时将隐藏的信息提取出来。
可逆信息隐藏的应用场景非常广泛,可以用于数字水印、版权保护、隐私保护等领域。
其中,HS算法是一种经典的可逆信息隐藏算法,而MATLAB是一种功能强大的科学计算软件,结合两者可以实现对图像信息的可逆隐藏和提取。
1. 可逆信息隐藏原理可逆信息隐藏是利用载体图像的一些隐含特性来隐藏需要传输的信息,在不损害载体图像质量的前提下,能够完整、准确地提取出隐藏的信息。
可逆信息隐藏主要包括隐写与加密两个主要过程。
隐写是指将需要隐藏的信息写入到载体图像中,而加密则是对隐藏的信息进行加密处理,增强信息的安全性。
2. HS算法原理HS算法是一种经典的可逆信息隐藏算法,其核心思想是利用图像的直方图来隐藏信息。
具体来说,HS算法首先对载体图像进行预处理,然后通过对直方图的调整来实现信息的隐藏。
在提取信息时,再根据调整后的直方图来还原隐藏的信息。
HS算法的优点是对图像没有任何损害,并且隐藏的信息可以完整提取出来。
3. MATLAB在可逆信息隐藏中的应用MATLAB作为一个功能强大的科学计算软件,提供了丰富的图像处理和加密算法库,非常适合用于可逆信息隐藏的实现。
利用MATLAB,可以方便地对图像进行处理、隐藏信息,并且提供了丰富的工具函数,能够直观地展示信息隐藏的效果。
4. 可逆信息隐藏HS算法在MATLAB中的实现通过MATLAB可以很方便地实现可逆信息隐藏HS算法。
需要对载体图像进行预处理,以便后续信息的隐藏。
利用HS算法将需要隐藏的信息写入到载体图像中,并对隐藏的信息进行加密处理。
在需要提取信息时,通过对载体图像的处理和对修改后的载体图像进行比对,可以成功地提取出隐藏的信息。
5. 代码示例以下是一个简单的MATLAB代码示例,演示了如何使用HS算法实现可逆信息隐藏:```matlab读取载体图像carrier_image = imread('carrier.png');进行预处理processed_image = preprocess(carrier_image);隐藏信息hidden_image = HS_algorithm(processed_image,'hidden_message');提取隐藏的信息extracted_message = extract_hidden_message(hidden_image);显示提取的信息disp(extracted_message);```通过以上代码示例,可以清晰地看到MATLAB如何便捷地实现了可逆信息隐藏HS算法的过程,并成功地提取出隐藏的信息。
使用MATLAB进行数据加密和解密

使用MATLAB进行数据加密和解密数据加密和解密是当今信息安全领域中非常重要的问题。
加密算法的设计和实现是确保数据在传输和存储过程中不被未经授权的人访问的一种关键手段。
在本文中,我们将探讨如何使用MATLAB进行数据加密和解密,并介绍一些常用的加密算法和技术。
一、数据加密的基本原理数据加密是通过将原始数据转化为不易被理解的形式,从而防止未经授权的人获取敏感信息。
加密过程主要包括两部分:加密算法和密钥。
加密算法是对原始数据进行数学计算和转换的一种方法。
常见的加密算法有对称加密算法和非对称加密算法。
对称加密算法使用相同的密钥进行加密和解密,加密和解密过程非常高效。
其中,最常用的对称加密算法是AES(Advanced Encryption Standard)算法。
AES算法在MATLAB中有相应的函数可供使用。
非对称加密算法使用两个密钥:公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
公钥可以公开,而私钥需要保密。
RSA算法是一种常见的非对称加密算法,也可以在MATLAB中使用相应的函数实现。
密钥是在加密和解密过程中起到关键作用的参数。
密钥的选择和管理直接影响到加密算法的安全性。
为了确保数据的安全性,密钥应该是足够长的随机数。
同时,密钥的保管也是一个重要的问题,只有授权的人能够访问密钥。
二、使用MATLAB进行数据加密在MATLAB中,我们可以利用现有的加密算法和函数来对数据进行加密。
接下来,我们将使用AES算法来进行示范。
首先,需要准备一个密钥。
在MATLAB中,我们可以通过randi函数生成一个随机的密钥。
例如:```MATLABkey = randi([0 255], 1, 16);```生成了一个16字节长的随机密钥。
然后,我们可以使用AES算法对数据进行加密。
在MATLAB中,通过函数aesencrypt可以实现AES加密。
例如,假设我们要加密一个文本文件:```MATLABplaintext = fileread('plaintext.txt');ciphertext = aesencrypt(plaintext, key);```上述代码将plaintext.txt文件中的内容进行AES加密,并将加密后的结果存储在变量ciphertext中。
MATLAB中的图像压缩和编码方法

MATLAB中的图像压缩和编码方法图像压缩和编码是数字图像处理的重要领域,在各种图像应用中起着至关重要的作用。
在本文中,我们将探讨MATLAB中的图像压缩和编码方法,包括无损压缩和有损压缩,并介绍其中的一些经典算法和技术。
一、图像压缩和编码概述图像压缩是指通过一定的算法和技术来减少图像数据的存储量或传输带宽,以达到节约存储空间和提高传输效率的目的。
而图像编码则是将原始图像数据转换为一系列二进制编码的过程,以便存储或传输。
图像压缩和编码通常可以分为无损压缩和有损压缩两种方法。
无损压缩是指压缩后的数据可以完全还原为原始图像数据,不会引入任何失真或变化。
常见的无损压缩算法有Run-Length Encoding (RLE)、Lempel-Ziv-Welch (LZW)、Huffman编码等。
这些算法通常针对图像中的冗余数据进行编码,如重复的像素值或相似的图像区域。
有损压缩则是在保证一定程度的视觉质量下,通过舍弃或近似原始图像数据来减小存储或传输的数据量。
常见的有损压缩算法有JPEG、JPEG2000、GIF等。
这些算法通过离散余弦变换(DCT)、小波变换或颜色量化等方法,将图像数据转换为频域或颜色空间的系数,并通过量化、编码和压缩等步骤来减小数据量。
二、无损压缩方法1. Run-Length Encoding (RLE)RLE是一种简单高效的无损压缩算法,通过计算连续重复像素值的数量来减小数据量。
在MATLAB中,可以使用`rle`函数实现RLE编码和解码。
例如,对于一幅图像,可以将连续的像素值(如白色)编码为重复的个数,然后在解码时根据重复的个数恢复原始像素值。
2. Lempel-Ziv-Welch (LZW)LZW是一种字典压缩算法,通过将图像中连续的像素序列映射为一个短代码来减小数据量。
在MATLAB中,可以使用`lzwencode`和`lzwdecode`函数实现LZW 编码和解码。
例如,对于一段连续的像素序列,可以将其映射为一个短代码,然后在解码时根据代码恢复原始像素序列。
(绝对可运行)加密图像中的可逆数据隐藏算法matlab代码(基于张新鹏教授的算法)

%This is the program of Reversible Data Hiding in Encrypted Domain clc;clear;%===============Read image===========================original_p=rgb2gray(imread('LENA.tif'));[m,n]=size(original_p);%==============Image encryption====================== random_bits=rand(m,n*8)<=0.5;%伪随机序列for i=1:mfor j=1:ns=0;for k=0:7b(k+1)=mod(fix(double(origi nal_p(i,j))/(2Ak)),2);eb(k+1)=xor(b(k+1),random_bits(i,8*j+k-7)); s=s+eb(k+1)*(2A k);endencrypted_image(i,j)=s;endendfigure(1);subplot(1,2,1);imshow(original_p);hold on;title('Original image','fontsize',16);subplot(1,2,2);encrypted_image=uint8(encrypted_image);imshow(encrypted_image);title('Encrypted image','fontsize',16);%================Data embedding======================size=8; %分块大小N=6;%置乱周期number1=3;number2=N-number1;lim_row=fix(m/size); %图像的分块数lim_col=fix(n/size); %图像的分块数bitts=3;watermessage=rand(lim_row,lim_col)<0.5; %水印信息pseudo_randomly for i=1:lim_rowfor j=1:lim_col block_image{i,j}=encrypted_image((size*i-size+1):size*i,(size*j-size+1):size*j); % 分块for k=1:sizefor t=1:sizeindex=arnold(k,t,size,number1);%arnold is permutateion function;arno_block_image{i,j}(index(1)+1,index(2)+1)=block_image{i,j}(k,t); end end%数据嵌入sum0=zeros(size/2,size); if watermessage(i,j)==0 for k=0:7bbb{k+1}=mod(fix(double(arno_block_image{i,j}(1:size/ 2,:))/(2你)),2);if k<bitts bbb{k+1}=~bbb{k+1};endsum0=sum0+bbb{k+1}*(2A k);enddata_image{i,j}=[sum0;double(arno_block_image{i,j}(size/ 2+1:size,:))];endsum1=zeros(size/2,size);if watermessage(i,j)==1for k=0:7 bbb{k+1}=mod(fix(double(arno_block_image{i,j}(size/ 2+1:size,:))/(2Ak)),2);if k<bittsbbb{k+1}=~bbb{k+1};endsum1=sum1+bbb{k+1}*(2Ak);enddata_image{i,j}=[double(arno_block_image{i,j}(1:size/ 2,:));sum1];endfor k=1:sizefor t=1:size index=arnold(k,t,size,number2);%arnold is permutateion function;re_data_image{i,j}(index(1)+1,index(2)+1)=data_image{i,j}(k,t);endend%合成嵌入数据后的图像data_en_image((size*i-size+1):size*i,(size*j-size+1):size*j)=re_data_image{i,j};endend%=====Encrypt image which contains data====for i=1:lim_row*sizefor j=1:lim_col*sizes=0;for k=0:7b(k+1)=mod(fix(data_en_image(i,j)/(2Ak)),2);eb(k+1)=xor(b(k+1),random_bits(i,8*j+k-7));s=s+eb(k+1)*(2A k);endde_data_image(i,j)=s;endendfigure(2);hold on;subplot(1,2,1);imshow(original_p);title('Original image','fontsize',16);subplot(1,2,2);imshow(uint8(de_data_image));title('Decrypted image contains data','fontsize',16);%直接解密图像的峰值信噪比sumsss=0;for i=1:lim_row*sizefor j=1:lim_col*size sumsss=(de_data_image(i,j)-double(original_p(i,j)))A2+sumsss;endendmse=sumsss/((lim_row*size)*(lim_row*size));psnr=10*log10(255A2 /mse);%======Extract data and recover image=======for i=1:lim_rowfor j=1:lim_col block_de_image{i,j}=de_data_image((size*i-size+1):size*i,(size*j-size+1):size*j);%分块for k=1:sizefor t=1:size index=arnold(k,t,size,number1);%arnold is permutateion function;ar_block_de_image{i,j}(index(1)+1,index(2)+1)=block_de_image{i,j}(k,t);endendsum0=zeros(size/2,size);sum1=zeros(size/2,size);for k=0:7bbbO{k+1}=mod(fix(ar_block_de_image{i,j}(1:size/ 2,:)/(2你)),2);bbb1{k+1}=mod(fix(ar_block_de_image{i,j}(size/ 2+1:size,:)/(2A k)),2);if k<bittsbbb0{k+1}=~bbb0{k+1};bbb1{k+1}=~bbb1{k+1};endsum0=sum0+bbb0{k+1}*(2Ak);sum1=sum1+bbb1{k+1}*(2Ak);endar_H0_image{i,j}=[sum0;ar_block_de_image{i,j}(size/ 2+1:size,:)];ar_H1_image{i,j}=[ar_block_de_image{i,j}(1:size/ 2,:);sum1];for k=1:sizefor t=1:size index=arnold(k,t,size,number2);%arnold is permutateion function;H0_image{i,j}(index(1)+1,index(2)+1)=ar_H0_image{i,j}(k,t);H1_image{i,j}(index(1)+1,index(2)+1)=ar_H1_image{i,j}(k,t);endendf0=0;f1=0;for u=2:size-1for v=2:size-1f0=f0+abs(H0_image{i,j}(u,v)-(H0_image{i,j}(u-1,v)+H0_image{i,j}(u,v-1)+H0_image{i,j}(u+1,v)+H0_image{i,j}(u,v+1))/4);f1=f1+abs(H1_image{i,j}(u,v)-(H1_image{i,j}(u-1,v)+H1_image{i,j}(u,v-1)+H1_image{i,j}(u+1,v)+H1_image{i,j}(u,v+1))/4);endendif (f0-f1)<0extract_bits(i,j)=0; recover_image(size*i-size+1:size*i,size*j-size+1:size*j)=H0_image{i,j};elseextract_bits(i,j)=1; recover_image(size*i-size+1:size*i,size*j-size+1:size*j)=H1_image{i,j};endendendfigure(3);subplot(1,2,1);imshow(original_p);hold on;title('Original image','fontsize',16); subplot(1,2,2);recover_image=uint8(recover_image); imshow(recover_image);hold on; title('Recovered image','fontsize',16);%==============analysis============ diff=original_p(1:lim_row*size,1:lim_col*size)-recover_image;counts=0;for i=1:lim_rowfor j=1:lim_col block_diff{i,j}=diff((size*i-size+1):size*i,(size*j-size+1):size*j); %分块if extract_bits(i,j)~=watermessage(i,j) block_diff{i,j}=ones(size,size)*255;counts=counts+1;else block_diff{i,j}=original_p((size*i-size+1):size*i,(size*j-size+1):size*j);end diff_image((size*i-size+1):size*i,(size*j-size+1):size*j)=block_diff{i,j};endend figure(4); imshow(diff_image); hold on;%title('Blocks of incorrect','fontsize',16); %错误率与分块大小的关系rate=counts/((lim_row)*(lim_col))。
正确运用matlab数字水印技术实现图像版权保护

正确运用matlab数字水印技术实现图像版权保护作者:朱有为来源:《计算机光盘软件与应用》2013年第01期摘要:数字水印技术作为信息保密与媒体版权保护的新技术,在各个行业得到了较为广泛的引用。
本文根据笔者多年的公工作经验,对mat lab数字水印技术进行了介绍,并对mat lab数字水印技术的应用以及实现图象版权保护的流程等因素进行了浅要探讨。
关键词:mat lab;数字水印技术;图像;版权保护中图分类号:TP309.7 文献标识码:A 文章编号:1007-9599(2013)01-0090-02数字水印技术作为一种信息隐藏技术,能在实现与数字签名相同作用的同时,保护媒体内容的真实性与完整性,在现阶段的版权保护工作过程中得到了较为广泛的应用。
对于部分电子档案而言,是以图像的媒体形式显示与存储的。
而随着影响网络安全因素的不断增加,为电子档案的安全造成了严重威胁。
合理利用matlab数字水印技术能保护版权信息,提高电子档案的安全性。
同时,利用matlab数字水印技术将版权信息嵌入图片内,能使媒体内容在出现版权争议时,提取出嵌在图片中的版权信息来解决争议,从而实现电子档案的版权保护。
在此,笔者就mat lab数字水印技术实现图像版权保护问题进行以下探讨:1 matlab数字水印技术简介Matlab是Math Works公司推出的一款高性能的数据计算与可视化软件,具有数据分析、矩阵计算、信号处理以及图形显示等功能,营造出了一种操作方便、界面友好的用户环境,该软件目前在国内有着非常广泛的应用。
同时,用MatIab来研究数字水印技术,更能丰富数字水印技术的功能,并且集成了丰富的工具。
对于基于matlab的数字水印技术而言,具有以下基本特征:1.1 不可见性matlab数字水印技术能将一些具有辨别作用的信息嵌入文档、图象等多媒体数据中,在涉及到版权争议使,能将辨别信息提取出来,起到保护版权的作用。
但对于所嵌入的辨别信息而言,是人们用肉眼所无法辨别的,即嵌入水印的图象与原始图象所带给人们的感觉是一样的。
在Matlab中进行图像压缩与图像解密的方法与技巧

在Matlab中进行图像压缩与图像解密的方法与技巧Matlab是一种强大的工具,被广泛用于图像处理和计算机视觉领域。
在本文中,我们将讨论如何利用Matlab进行图像压缩与图像解密,并探讨一些相应的方法和技巧。
首先,让我们来了解一下图像压缩的基本概念和原理。
图像压缩是通过减少图像占用的存储空间或传输带宽来减小图像文件的大小。
压缩分为有损压缩和无损压缩两种类型。
有损压缩会丢失一些图像信息,以达到压缩的目的,而无损压缩则尽量保留所有图像信息。
在Matlab中,我们可以使用多种方法进行图像压缩。
常见的方法之一是使用离散余弦变换(Discrete Cosine Transform,DCT)。
DCT将图像分解为一系列互不相关的频率成分,然后根据其重要性对这些成分进行量化和编码。
通过调整量化步长可以控制压缩比率和图像质量。
除了DCT,还有其他一些常用的压缩方法,如小波变换(Wavelet Transform),它可以提供更好的局部逼近能力,适用于不同尺度和方向的图像特征。
Matlab中有许多内置函数可以实现小波变换,例如waverec和wavedec函数。
另一个常用的图像压缩方法是基于向量量化(Vector Quantization,VQ)的编码。
VQ将图像划分为不重叠的块,并使用聚类算法将每个块映射到具有较少位数的代表向量。
然后,通过编码代表向量和其在图像中的位置来表示整个图像。
这种方法对于有损压缩非常有效,但在无损压缩方面效果较差。
一旦我们对图像进行了压缩,接下来我们需要了解如何进行图像解密。
在Matlab中,解密可以通过逆向操作来实现。
对于DCT压缩,我们可以通过应用逆离散余弦变换(Inverse Discrete Cosine Transform,IDCT)来恢复原始图像。
同样,对于小波变换压缩,我们可以使用逆小波变换(Inverse Wavelet Transform)来还原图像。
需要注意的是,如果进行了有损压缩,解密后的图像与原始图像之间很可能有一些质量损失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB数字图像加密
一、实验名称
MATLAB数字图像加密
二、实验目的
熟悉MATLAB编译环境;
掌握基本的矩阵操作;
了解初级的加密算法。
三、实验环境
WindowsXP操作系统,MATLABR2010a编译环境
四、实验原理
将数字图像划分成块,对RGB矩阵进行转置、水平翻转、垂直翻转等变换,形成新的矩阵,实现对图像的加密。
五、实验过程
1.获取数字图像存入矩阵;
2.获取矩阵大小存入变量;
3.将矩阵划分成等大的4*4子矩阵;
4.分别对存储图像RGB信息的矩阵进行转置、水平翻转、垂直翻转等变换;
5.再次细化矩阵,将矩阵划分成等大的16*16子矩阵;
6.分别对存储图像RGB信息的矩阵进行转置、水平翻转、垂直翻转等变换;
7.加密完成,存储加密后的图像;
8.逆推过程,完成解密,存储解密后的图像。
六、源程序
a=imread('C:\Documents and Settings\Owner\×ÀÃæ\jm\jmtp.jpg');
subplot(2,2,1);
imshow(a);
[l,m,n]=size(a);
x=l/4;
y=m/4;
for i=0:3
for j=0:3
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),1)=a((j*x+1):((j+1)*x),(i*y+1):
((i+1)*y),1)';
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),2)=flipud(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),2));
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),3)=fliplr(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),3));
end
end
subplot(2,2,3);
imshow(a);
x=l/16;
y=m/16;
a(:,:,1)=flipud(a(:,:,1));
a(:,:,2)=fliplr(a(:,:,2));
a(:,:,3)=a(:,:,3)';
for i=0:15
for j=0:15
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),1)=a((j*x+1):((j+1)*x),(i*y+1): ((i+1)*y),1)';
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),2)=flipud(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),2));
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),3)=fliplr(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),3));
end
end
subplot(2,2,2);
imshow(a);
imwrite(a,'jiamihou.jpg');
for i=0:15
for j=0:15
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),1)=a((j*x+1):((j+1)*x),(i*y+1): ((i+1)*y),1)';
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),2)=flipud(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),2));
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),3)=fliplr(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),3));
end
end
a(:,:,1)=flipud(a(:,:,1));
a(:,:,2)=fliplr(a(:,:,2));
a(:,:,3)=a(:,:,3)';
x=l/4;
y=m/4;
for i=0:3
for j=0:3
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),1)=a((j*x+1):((j+1)*x),(i*y+1): ((i+1)*y),1)';
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),2)=flipud(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),2));
a((j*x+1):((j+1)*x),(i*y+1):((i+1)*y),3)=fliplr(a((j*x+1):((j+1)*x),( i*y+1):((i+1)*y),3));
end
end
subplot(2,2,4);
imshow(a);
imwrite(a,'jiemihou.jpg');
七、实验结果
原图片
加密后的图片解密后的图片
八、实验分析
优点:该加密算法原理简单,编程易实现,加密效果较好。
缺点:解密过程简便,易破解。
