可变R-L-C 元件的SPICE模拟行为建模

合集下载

spice仿真

spice仿真Spice仿真引言Spice (Simulation Program with Integrated Circuit Emphasis) 是一种电路仿真程序，它可以模拟各种电路的性能和行为。

历经多年的发展，Spice已经成为电子设计领域中最为常用和广泛认可的仿真工具之一。

本文将介绍Spice仿真的基本原理、应用领域以及使用方法，帮助读者更好地了解和应用这一强大的工具。

一、Spice仿真的基本原理Spice仿真基于电路的数学模型和电路分析方法，通过求解一组线性或非线性的代数和微分方程来模拟电路的行为。

Spice可以对各种类型的电路进行仿真，包括模拟电路、数字电路以及混合信号电路。

它考虑了电路中各个元件的电性能，并基于电流和电压的关系对电路进行建模和分析。

Spice程序需要用户提供电路的拓扑结构以及各个元件的参数。

通过这些输入，Spice可以根据预定义的电路分析方法和解算器来计算电路中各个节点和元件上的电压、电流以及功率等参数。

通过对电路的相应参数进行实时仿真和分析，Spice可以为设计者提供准确的电路行为信息，帮助他们对电路性能进行优化和改进。

二、Spice仿真的应用领域Spice仿真在电子设计和电路分析中有广泛的应用。

以下列举了几个常见的应用领域：1.模拟电路设计：Spice可以用于模拟电路的设计和验证，帮助设计者检查电路的性能和稳定性。

通过Spice仿真，设计者可以预测电路的频率响应、幅频特性以及相位延迟等参数，从而改进电路的设计方案。

2. 数字电路分析：Spice可以模拟数字电路中的逻辑门、触发器和时序电路等元件，帮助设计者验证电路的正确性和稳定性。

通过仿真结果，设计者可以找出可能存在的逻辑错误和电路延迟，并及时进行优化和调整。

3.射频电路分析：Spice也可以用于射频电路的仿真和分析。

射频电路中经常涉及到高频信号的传输和耦合问题，通过对射频电路进行Spice仿真，设计者可以预测电路中的信号衰减、失真以及噪声等问题，从而优化电路的性能。

PSPICE仿真课件

电路绘制程序 Capture CIS
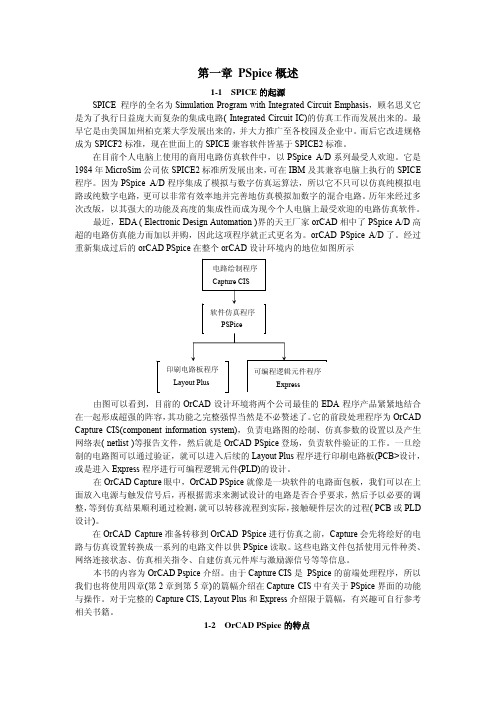
软件仿真程序 PSPice
印刷电路板程序 Layout Plus
可编程逻辑元件程序 Express
由图可以看到，目前的 OrCAD 设计环境将两个公司最佳的 EDA 程序产品紧紧地结合在一起形成超强的阵容，其功能之完整强悍当然是不必赘述了。它的前段处理程序为 OrCAD Capture CIS(component information system)，负责电路图的绘制、仿真参数的设置以及产生网络表( netlist )等报告文件，然后就是 OrCAD PSpice 登场，负责软件验证的工作。一旦绘制的电路图可以通过验证，就可以进入后续的 Layout Plus 程序进行印刷电路板(PCB>设计，或是进入 Express 程序进行可编程逻辑元件(PLD)的设计。在 OrCAD Capture 眼中，OrCAD PSpice 就像是一块软件的电路面包板，我们可以在上面放入电源与触发信号后，再根据需求来测试设计的电路是否合乎要求，然后予以必要的调整，等到仿真结果顺利通过检测，就可以转移流程到实际，接触硬件层次的过程( PCB 或 PLD 设计)。在 OrCAD Capture 准备转移到 OrCAD PSpice 进行仿真之前，Capture 会先将绘好的电路与仿真设置转换成一系列的电路文件以供 PSpice 读取。这些电路文件包括使用元件种类、网络连接状态、仿真相关指令、自建仿真元件库与激励源信号等等信息。本书的内容为 OrCAD Pspice 介绍。由于 Capture CIS 是 PSpice 的前端处理程序，所以我们也将使用四章(第 2 章到第 5 章)的篇幅介绍在 Capture CIS 中有关于 PSpice 界面的功能与操作。对于完整的 Capture CIS, Layout Plus 和 Express 介绍限于篇幅，有兴趣可自行参考相关书籍。 1-2 OrCAD PSpice 的特点

名称晶体管模型(SPICE)到行为级模型(IBIS)的转换工具

名称：晶体管模型(SPICE)到行为级模型(IBIS)的转换工具
参考品牌：Cadence
参考型号：Cadence
数量：1套
技术参数：
1：含1个用户的PSpice 基本数模混合分析工具，辅助用户完成模拟及数字混合电路的仿真分析，包含有直流扫描、交流扫描、瞬态分析，温度参数扫描等功能，同时包含多样的仿真模型并具有建模功能。

2：含1个用户的PSpice 高级仿真分析工具，结合基本分析工具，使用户具备更加强大的分析功能，包括灵敏度分析，优化分析，蒙特卡洛分析，应力分析和参数测绘分析。

3：含1个用户的OrCAD SI信号完整性仿真工具，该工具支持布线前仿真和布线后后仿真两种工作流程，提供了针对PCB板极的信号仿真分析功能。

服务：
供方需要提供完整技术支持服务，包含仿真建模等的指导及培训内容。

验收合格后支付。

spice模型

SPICE中将MOS场效应管模型分成不同级别，并用变量LEVEL来指定所用的模型。
1）LEVEL＝1
级别为1的MOS管模型又称MOS1模型，这是最简单的模型，适用于手工计算。MOS1模型是 MOS晶体管的一阶模型，描述了MOS管电流电压的平方率特性，考虑了衬底调制效应和沟道长度调制效应，适用于精度要求不高的长沟道MOS晶体管。
4）LEVEL＝4 级别为4的MOS4模型又称BSIM（Berkeley short-channel IGFET model）模型。该模型是由美国伯克利大学1984年专门为短沟道MOS 场效应晶体管而开发的模型，是AT&T Bell实验室简练短沟道IGFET模型的改进型。模型是在物理基础上建立的，模型参数由工艺文件经模型参数提取程序自动产生，适用于数字电路和模拟电路，而且运行时间比二级模型平均缩短一半左右。现已发表的有BSIM1、BSIM2、 BSIM3和BSIM4等模型。
Cd

dQ dVD
τT
dI D dVD
τT I D
n Vt
二极管模型参数对照表
参数名
饱和电流发射系数串联体电阻渡越时间零偏置时的势垒
电容梯度因子
PN结内建势垒
公式中符号
IS n RS τT Cj0 m V0
SPICE中符号
IS N RS TT CJ0 M VJ
单位
A Ω Sec F V
SPICE中缺省值
1.0E-14 1 0 0
0
0.5
1
二极管的噪声模型
热噪声：
In2
4kTA RS
闪烁（1/f）噪声和散粒噪声：
In2

KF I D AF

Spice仿真

仿真功能简介
返回
四、 Pspice的基本电路特性分析
1 . 静态工作点分析

静态工作点分析就是将电路中的电容开路，电感短路，对各个信号源取其直流电平值，计算电路的直流偏置量。
例：求基本放大电路的静态工作点。步骤如下：（1）用Capture软件画好电路图
返回
（2）建立模拟类型分组。

仿真步骤
（1）新建仿真设计项目；
（2）输入电路结构；
（3）编辑修改电路元器件标号和参数值，包括直流电源和信号源参数；（4）创建仿真简要表（Simulation Profile），设置分析功能；（5）执行仿真；（6）仿真结果分析及输出。
返回
新建设计项目(File/New/Project)
5.0mV 0V SEL>> -5.0mV 1.0V V(Vs:+) 0V
-1.0V
返回
0s V(Out)
0.4ms
0.8ms Time
1.2ms
1.6ms
2.0ms
频域分析
幅频特性dB(V(Vo)/V(i)) 输入阻抗V(i)/ I(i) 输出阻抗
返回
求解输出阻抗
修改电路：令Vs=0，信号源短路，取掉负载RL，外加一个信号源VSIN(400mv) 其他步骤与“输入电阻的频率响应”分析相同 Ro =V(Vo)/I(Vs)
返回
连线与设置节点名
（1）连线。①启动Place/Wire命令。 ②按对应的绘图快捷键（2）设置节点名。例如，想把输出端的节点起名为Out。步骤如下：
①启动Place/Net Alias命令，或按对应的绘图快捷键，屏幕上出现设置框。在设置框中键入节点名（例Out）。 ② 按OK键，则光标处附着一个小方框，将光标移至设置节点名的位置，按鼠标左键，新节点名即出现在该位置。

SPICE仿真和模型简介

SPICE仿真和模型简介SPICE 仿真和模型简介1、SPICE仿真程序电路系统的设计人员有时需要对系统中的部分电路作电压与电流关系的详细分析，此时需要做晶体管级仿真（电路级），这种仿真算法中所使用的电路模型都是最基本的元件和单管。

仿真时按时间关系对每一个节点的I/V关系进行计算。

这种仿真方法在所有仿真手段中是最精确的，但也是最耗费时间的。

SPICE（Simulation program with integrated circuit emphasis）是最为普遍的电路级模拟程序，各软件厂家提供提供了Vspice、Hspice、Pspice等不同版本spice软件，其仿真核心大同小异，都是采用了由美国加州Berkeley大学开发的spice模拟算法。

SPICE可对电路进行非线性直流分析、非线性瞬态分析和线性交流分析。

被分析的电路中的元件可包括电阻、电容、电感、互感、独立电压源、独立电流源、各种线性受控源、传输线以及有源半导体器件。

SPICE内建半导体器件模型，用户只需选定模型级别并给出合适的参数。

2、元器件模型为了进行电路模拟，必须先建立元器件的模型，也就是对于电路模拟程序所支持的各种元器件，在模拟程序中必须有相应的数学模型来描述他们，即能用计算机进行运算的计算公式来表达他们。

一个理想的元器件模型，应该既能正确反映元器件的电学特性又适于在计算机上进行数值求解。

一般来讲，器件模型的精度越高，模型本身也就越复杂，所要求的模型参数个数也越多。

这样计算时所占内存量增大，计算时间增加。

而集成电路往往包含数量巨大的元器件，器件模型复杂度的少许增加就会使计算时间成倍延长。

反之，如果模型过于粗糙，会导致分析结果不可靠。

因此所用元器件模型的复杂程度要根据实际需要而定。

如果需要进行元器件的物理模型研究或进行单管设计，一般采用精度和复杂程度较高的模型，甚至采用以求解半导体器件基本方程为手段的器件模拟方法。

二微准静态数值模拟是这种方法的代表，通过求解泊松方程，电流连续性方程等基本方程结合精确的边界条件和几何、工艺参数，相当准确的给出器件电学特性。

SPICE模型、命令介绍

SPICE模型、命令介绍SPICE模型、命令介绍下⾯列出常⽤SPICE器件的模型描述。

{ }中的参数是必须的，[ ]中的参数可选，{ }*中的参数需要重复。

此外，每个SPICE模型提供商可能会有其他的参数或命令。

DEVICE：1、C device - Capacitor.C{name} {+node} {-node} [{model}] {value} [IC={initial}]Examples:CLOAD 15 0 20pFCFDBK 3 33 CMOD 10pF IC=1.5v2、D device - Diode.D{name} {+node} {-node} {model} [area]Examples:DCLAMP 14 0 DMOD3、I device - Current Source.I{name} {+node} {-node} [[DC] {value}] [AC {mag} [{phase}]]Examples:IBIAS 13 0 2.3mAIAC 2 3 AC .001IPULSE 1 0 PULSE(-1mA 1mA 2ns 2ns 2ns 50ns 100ns)I3 26 77 AC 1 SIN(.002 .002 1.5MEG)4、J device - Junction FET.J{name} {d} {g} {s} {model} [{area]}Examples:JIN 100 1 0 JFAST5、K device - Inductor Coupling.K{name} L{name} { L{name} }* {coupling}Examples:KTUNED L3OUT L4IN .8KXFR1 LPRIM LSEC .996、L device - Inductor.L{name} {+node} {-node} [model] {value} [IC={initial}]Examples:LLOAD 15 0 20mHL2 1 2 .2e-6LSENSE 5 12 2uH IC=2mA7、M device - MOSFET.M{name} {d} {g} {s} {sub} {mdl} [L={value}] [W={value}] + [AD={value}] [AS={value}] + [PD={value}] [PS={value}]+ [NRD={value}] [NRS={value}]Examples:M1 14 2 13 0 PNOM L=25u W=12uM13 15 3 0 0 PSTRONG8、Q device - Bipolar Transistor.Q{name} {c} {b} {e} [{subs}] {model} [{area}]Examples:Q1 14 2 13 PNPNOMQ13 15 3 0 1 NPNSTRONG 1.59、R device - Resistor.R{name} {+node} {-node} [{model}] {value}Examples:RLOAD 15 0 2k10、S device - Voltage-Controlled Switch.S{name} {+node} {-node} {+control} {-control} {model}Examples:S12 13 17 2 0 SMOD11、T device - Transmission Line.T{name} {A+} {A-} {B+} {B-} Z0={value}[TD={val} | F={val}[NL={val}]]Examples:T1 1 2 3 4 Z0=220 TD=115nsT2 1 2 3 4 Z0=50 F=5MEG NL=0.512、V device - Voltage Source.V{name} {+node} {-node} [[DC] {value}] [AC {mag} [{phase}]]Examples:VBIAS 13 0 2.3mVV AC 2 3 AC .001VPULSE 1 0 PULSE(-1mV 1mV 2ns 2ns 2ns 50ns 100ns)V3 26 77 AC 1 SIN(.002 .002 1.5MEG)13、X device - Subcircuit Call.X{name} [{node}]* {subcircuit name}Examples:X12 100 101 200 201 DIFFAMPCONTROLLED SOURCES14、E device - Voltage Controlled V oltage Source VCVS.E{name} {+node} {-node} {+cntrl} {-cntrl} {gain}E{name} {+node} {-node} POL Y({value}) {{+cntrl} {-cntrl}}* {{coeff}}* Examples: EBUFF 1 2 10 11 1.0EAMP 13 0 POL Y(1) 26 0 50015、F device - Current Controlled Current Source CCCS.F{name} {+node} {-node} {vsource name} {gain}Examples:FSENSE 1 2 VSENSE 10.016、G device - Voltage Controlled Current Source VCCS.G{name} {+node} {-node} {+control} {-control} {gain}Examples:GBUFF 1 2 10 11 1.017、H device - Current Controlled V oltage Source CCVS.H{name} {+node} {-node} {vsource name} {gain}H{name} {+node} {-node} POL Y({value}) { {vsource name} }* {{coeff}}* Examples: HSENSE 1 2 VSENSE 10.0HAMP 13 0 POL Y(1) VIN 500INPUT SOURCES18、EXPONENTIALEXP( {v1} {v2} {trise_delay} {tau_rise} {tfall_delay} {tau_fall) )19、PULSEPULSE( {v1} {v2} {tdelay} {trise} {tfall} {width} {period} )20、PIECE WISE LINEARPWL( {time1} {v1} {time2} {v2} ... {time3} {v3} )21、SINGLE FREQUENCY FMSFFM( {voffset} {vpeak} {fcarrier} {mod_index} {fsignal} )22、SINE WA VESIN( {voffset} {vpeak} {freq} {tdelay} {damp_factor} {phase} )ANALOG BEHA VIORAL MODELING23、V ALUEE|G{name} {+node} {-node} V ALUE {expression}Examples:GMULT 1 0 V ALUE = { V(3)*V(5,6)*100 }ERES 1 3 VALUE = { I(VSENSE)*10K }24、TABLEE|G{name} {+node} {-node} TABLE {expression} = (invalue, outvalue)* Examples: ECOMP 3 0 TABLE {V(1,2)} = (-1MV 0V) (1MV, 10V)25、LAPLACEE|G{name} {+node} {-node} LAPLACE {expression} {s expression} Examples:ELOPASS 4 0 LAPLACE {V(1)} {10 / (s/6800 + 1)}26、FREQE|G{name} {+node} {-node} FREQ {expression} (freq, gain, phase)* Examples:EAMP 5 0 FREQ {V(1)} (1KZ, 10DB, 0DEG) (10KHZ, 0DB, -90DEG)27、POL YE|G{name} {+node} {-node} POL Y(dim) {inputs X} {coeff k0,k1,...} [IC=value] Examples:EAMP 3 0 POL Y(1) (2,0) 0 500EMULT2 3 0 POL Y(2) (1,0) (2,0) 0 0 0 0 1ESUM3 6 0 POL Y(3) (3,0) (4,0) (5,0) 0 1.2 0.5 1.2COEFFICIENTS28、POL Y(1)y = k0 + k1?X1 + k2?X1?X1 + k3?X1?X1?X1 + ...29、POL Y(2)y = k0 + k1?X1+ k2?X2 + k3?X1?X1+ k4?X2?X1 + k5?X2?X2+ k6?X1?X1?X1 + k7?X2?X1?X1 + k8?X2?X2?X1+ k9?X2? X2?X2 + ...30、POL Y(3)y = k0 + k1?X1 + k2?X2 + k3?X3 + k4?X1?X1 + k5?X2?X1 + k6?X3?X1+ k7?X2?X2+ k8?X2?X3 + k9?X3?X3 + ...STATEMENTS31、.AC - AC Analysis..AC [LIN][OCT][DEC] {points} {start} {end}Examples:.AC LIN 101 10Hz 200Hz.AC DEC 20 1MEG 100MEG32、.DC - DC Analysis..DC [LIN] {varname} {start} {end} {incr}.DC [OCT][DEC] {varname} {start} {end} {points}Examples:.DC VIN -.25 .25 .05.DC LIN I2 5mA -2mA 0.1mA VCE 10V 15V 1V 33、.FOUR - Fourier Analysis..FOUR {freq} {output var}*Examples:.FOUR 10KHz v(5) v(6,7)34、.IC - Initial Transient Conditions..IC { {vnode} = {value} }*Examples:.IC V(2)=3.4 V(102)=035、.MODEL – Device Model..MODEL {name} {type}Typename Devname DevtypeCAP Cxxx capacitorIND Lxxx inductorRES Rxxx resistorD Dxxx diodeNPN Qxxx NPN bipolarPNP Qxxx PNP bipolarNJF Jxxx N-channel JFETPJF Jxxx P-channel JFETNMOS Mxxx N-channel MOSFETPMOS Mxxx P-channel MOSFETVSWITCH Sxxx voltage controlled switch Examples:.MODEL RMAX RES (R=1.5 TC=.02 TC2=.005).MODEL QDRIV NPN (IS=1e-7 BF=30)36、.NODESET – Initial bias point guess..NODESET { {node}={value} }*Examples:.NODESET V(2)=3.4 V(3)=-1V37、.NOISE - Noise Analysis..NOISE {output variable} {name} [{print interval}] Examples:.NOISE V(5) VIN38、.PLOT – Plot Output..PLOT [DC][AC][NOISE][TRAN] [ [{output variable}*] Examples: .PLOT DC V(3) V(2,3) V(R1) I(VIN).PLOT AC VM(2) VP(2) VG(2)39、.PRINT – Print Output..PRINT [DC][AC][NOISE][TRAN] [{output variable}*] Examples: .PRINT DC V(3) V(2,3) V(R1) IB(Q13).PRINT AC VM(2) VP(2) VG(5) II(7)40、.PROBE – Save simulation output PSPICE COMMAND. .PROBE [output variable]*Examples:.PROBE.PROBE V(3) VM(2) I(VIN)41、.SENS - Sensitivity Analysis..SENS {output variable}*Examples:.SENS V(9) V(4,3) I(VCC)42、.SUBCKT - Subcircuit Definition..SUBCKT {name} [{node}*]Examples:.SUBCKT OPAMP 1 2 101 10243、.TEMP – Temperature Analysis..TEMP {value}*Examples:.TEMP 0 27 12544、.TF – DC Transfer Function..TF {output variable} {input source name}Examples:.TF V(5) VIN45、.TRAN - Transient Analysis..TRAN {print step value} {final time} [{no print time} [{step ceiling value}]] [UIC] Examples:.TRAN 5NS 100NS。

第七章 Pspice与器件模型

第七章 Pspice与器件模型
另外，不同工艺线的Spice模型参数会有一些差异，所以在进行电路设计前应先选好要去流片的工艺线，从厂家索取 Spice模型文件，并根据这个文件建自己的库。建库要用到 Parts程序，具体操作在后面说明。由于无法知道Pspice自带的库采用的工艺，也不能改变它的参数，如MOS晶体管的沟道宽度、长度，双极型晶体管的发射区面积等。所以要进行具体的集成电路设计用系统自带的库是不够的。
数据的单位应位于比例后缀之后, 如:1E-3V，10MV等。
在完成电路图的输入后,还要把激励源加到电路上，才能模拟电路。
所有的激励源都在SOURCE.SLB和SOURCSTM.SLB库里。较新版本的Pspice中有一个激励信号编辑器叫 Stimulus Editor。在电路图的适当位置放置SOURCSTM库里的VSTIM（电压激励源），ISTIM（电流激励源）或DIGSTIM(数字激励源)，再双击要编辑的激励源，就会弹出Stimulus Editor窗口。在这个激励编辑器窗口中可以编辑瞬态分析的激励波形。
第七章 Pspice与器件模型
3. 蒙特卡罗分析和最坏情况分析
蒙特卡罗分析是对电路所选择的分析(直流、交流、瞬态) 进行了多次运行后,进行的统计分析。第一次运行是用所有元器件的标称值进行运算的。而以后的运行, 则是根据每个模型语句内对各个元器件模型参数的容差规定, 随机选取在其容差限度内偏离其标称值的不定值进行的运算。将各次运行结果同第一次运行结果进行比较, 得出由于元器件的容差而引起输出结果偏离的统计情况。
美国加州大学伯克利分校以Pederson教授为首的计算机辅助集成电路设计小组开发的，经过不断的完善和改进, 从20世纪70年代末开始, Spice向全世界推广。现在, Spice已成为大学、研究机构和公司普遍采用的电路分析程序, 甚至把它当作了一种标准。

SPICE的器件模型..

SPICE的器件模型在介绍SPICE基础知识时介绍了最复杂和重要的电路描述语句，其中就包括元器件描述语句。

许多元器件（如二极管、晶体管等）的描述语句中都有模型关键字，而电阻、电容、电源等的描述语句中也有模型名可选项，这些都要求后面配以.MODEL起始的模型描述语句，对这些特殊器件的参数做详细描述。

电阻、电容、电源等的模型描述语句语句比较简单，也比较容易理解，在SPICE基础中已介绍，就不再重复了；二极管、双极型晶体管的模型虽也做了些介绍，但不够详细，是本文介绍的重点，以便可以自己制作器件模型；场效应管、数字器件的模型过于复杂，太专业，一般用户自己难以制作模型，只做简单介绍。

元器件的模型非常重要，是影响分析精度的重要因素之一。

但模型中涉及太多图表，特别是很多数学公式，都是在WORD下编辑后再转为JEPG图像文件的，很繁琐和耗时，所以只能介绍重点。

一、二极管模型：1.1 理想二极管的I-V特性：1.2 实际硅二极管的I-V特性曲线：折线1.3 DC大信号模型：1.4 电荷存储特性：1.5 大信号模型的电荷存储参数Qd：1.6 温度模型：1.7 二极管模型参数表：二、双极型晶体管BJT模型：2.1 Ebers-Moll静态模型：电流注入模式和传输模式两种2.1.1 电流注入模式：2.1.2 传输模式：2.1.3 在不同的工作区域，极电流Ic Ie的工作范围不同，电流方程也各不相同：2.1.4 Early效应：基区宽度调制效应2.1.5 带Rc、Re、Rb的传输静态模型：正向参数和反向参数是相对的，基极接法不变，而发射极和集电极互换所对应的两种状态，分别称为正向状态和反向状态，与此对应的参数就分别定义为正向参数和反向参数。

2.2 Ebers-Moll大信号模型：2.3 Gummel-Pool静态模型：2.4 Gummel-Pool大信号模型：拓扑结构与Ebers-Moll大信号模型相同，非线性存储元件电压控制电容的方程也相同2.5 BJT晶体管模型总参数表：三、金属氧化物半导体晶体管MOSFET模型：3.1 一级静态模型：Shichman-Hodges模型3.2 二级静态模型（大信号模型）：Meyer模型3.2.1 电荷存储效应：3.2.2 PN结电容：3.3 三级静态模型：3.2 MOSFET模型参数表：一级模型理论上复杂，有效参数少，用于精度不高场合，迅速粗略估计电路二级模型可使用复杂程度不同的模型，计算较多，常常不能收敛三级模型精度与二级模型相同，计算时间和重复次数少，某些参数计算比较复杂四级模型BSIM，适用于短沟道（<3um）的分析，Berkley在1987年提出四、结型场效应晶体管JFET模型：基于Shichman-Hodges模型4.1 N沟道JFET静态模型：4.2 JFET大信号模型：4.3 JFET模型参数表：五、GaAs MESFET模型：分两级模型（肖特基结作栅极）GaAs MESFET模型参数表：六、数字器件模型：6.1 标准门的模型语句：.MODEL <(model)name> UGATE [模型参数] 标准门的延迟参数：6.2 三态门的模型语句：.MODEL <(model)name> UTGATE [模型参数]三态门的延迟参数：6.3 边沿触发器的模型语句：.MODEL <(model)name> UEFF [模型参数]边沿触发器参数：JKFF nff preb,clrb,clkb,j*,k*,g*,gb* JK触发器，后沿触发DFF nff preb,clrb,clk,d*,g*,gb* D触发器，前沿触发边沿触发器时间参数：6.4 钟控触发器的模型语句：.MODEL <(model)name> UGFF [模型参数]钟控触发器参数：SRFF nff preb,clrb,gate,s*,r*,q*,qb* SR触发器，时钟高电平触发DLTCH nff preb,clrb,gate,d*,g*,gb* D触发器，时钟高电平触发钟控触发器时间参数：6.5 可编程逻辑阵列器件的语句：U <name> <pld type> (<#inputs>,<#outputs>) <input_node>* <output_node># +<(timing model)name> <(io_model)name> [FILE=<(file name) text value>]+[DATA=<radix flag>$ <program data>$][MNTYMXDLY=<(delay select)value>] +[IOLEVEL=<(interface model level)value>]其中：<pld type>列表<(file name) text value> JEDEC格式文件的名称，含有阵列特定的编程数据JEDEC文件指定时，DATA语句数据可忽略<radix flag> 是下列字母之一：B 二进制 O 八进制 X 十六进制<program data> 程序数据是一个数据序列，初始都为0PLD时间模型参数：七、数字I/O接口子电路：数字电路与模拟电路连接的界面节点，SPICE自动插入此子电路子电路名（AtoDn和DtoAn）在I/O模型中定义，实现逻辑状态与电压、阻抗之间的转换。

spice仿真

spice仿真简介Spice（Simulation Program with Integrated Circuit Emphasis）是一种电路仿真软件，广泛应用于电子工程领域。

它可以模拟电路中的各种元件和信号，提供了丰富的仿真功能，能够准确地预测电路的行为和性能。

spice软件特点Spice软件具有以下主要特点：1.模型库丰富：Spice软件提供了各种各样的元件模型，包括传输线、电阻、电容、电感、二极管、晶体管等。

用户可以根据自己的需要选择合适的元件模型，进行仿真分析。

2.仿真精度高：Spice软件采用了复杂的数学算法，能够对电路进行准确的仿真计算。

它能够考虑到电路中各种元件的非线性特性，并给出准确的仿真结果。

3.仿真速度快：Spice软件在运行时采用了高效的算法和优化技术，提高了仿真的速度。

用户可以在较短的时间内得到仿真结果，提高工作效率。

4.灵活性强：Spice软件具有丰富的仿真选项和参数配置功能，能够满足不同用户的需求。

用户可以通过调整参数来改变仿真条件，观察电路的行为和性能变化。

5.支持多平台：Spice软件在设计上具有良好的可移植性，能够在不同操作系统上运行。

用户可以根据自己的实际情况选择合适的操作系统进行仿真。

spice仿真流程Spice仿真的基本流程如下：1.定义电路元件：首先，用户需要定义电路中的元件，包括电阻、电容、电感、二极管、晶体管等。

可以通过编辑器或文本方式进行定义。

2.建立电路拓扑：用户需要根据实际电路设计，在编辑器中建立电路的拓扑结构。

可以使用类似于网表的方式描述电路的连接关系。

3.设置仿真参数：用户需要设置仿真的参数，包括仿真时间、仿真步长等。

可以根据需要进行适当的调整。

4.运行仿真：用户可以直接运行仿真，Spice软件会根据定义的电路元件和参数进行仿真计算，并得出仿真结果。

5.结果分析：用户可以通过仿真结果进行电路性能分析，比如电压波形图、电流曲线等。

可以根据需要调整仿真参数，再次进行仿真，以达到理想的仿真效果。

Spice仿真介绍和操作

数字逻辑基础LOGOEDA工具在数字逻辑课程中的应用--Multisim工具之Spice仿真在模拟电子课程中，我们通过使用晶体管的小信号模型，手工计算得到小规模模拟电子电路电压增益、电流增益、输入阻抗、输出阻抗、频率响应特性等。

⏹这种通过人工计算的分析方法就显得效率很低。

⏹随着计算机性能的不断提高，电子设计自动化（ElectronicDesign Automation，EDA）工具出现。

它成为电子系统设计和分析的强有力的助手。

⏹EDA工具取代了传统的手工计算方法，显著的提高了设计电路和分析电路的效率。

EDA工具在数字逻辑课程中的应用--Multisim工具之Spice仿真以集成电路为重点的仿真程序（Simulation Programwith Integrated Circuit Emphasis，SPICE），它是为了执行日益庞大而复杂的集成电路仿真工业而发展起来的，它是一个通用的、开源的模拟电子电路仿真工具。

⏹SPICE是一个程序用于集成电路和板级设计，用于检查电路设计的完整性，并且预测电路的行为。

⏹SPICE最早由加州大学伯克利分校开发，1975年改进成为SPICE2的标准，它使用FORTRAN语言开发。

在1989年，Thomas Quarles 开发出SPICE3，它使用C语言编写，并且增加了窗口系统绘图功能。

EDA 工具在数字逻辑课程中的应用--Multisim 工具之Spice 仿真在目前流行的NI 公司的Mutisim Workbench 工具、Altium 公司的Altium Designer 工具和Cadence 公司的OrCAD 工具中都嵌入了SPICE 仿真工具。

⏹在SPICE仿真工具中，包含下面的模块：☐电路原理图输入程序。

☐激励源编辑程序。

☐电路仿真程序。

☐输出结果绘图程序。

☐模型参数提取程序。

☐元器件模型参数库。

下面将通过Multisim 环境下的设计实例，演示EDA工具在数字逻辑课程中的应用--Multisim工具之Spice仿真SPICE的基本分析功能包含三大类：⏹直流分析⏹交流分析⏹时域分析EDA工具在数字逻辑课程中的应用--Multisim工具之Spice仿真注1：直流分析是所有其它分析的基础。

PSpice电路仿真报告

PSpice 电路仿真报告——11351003 陈纪凯一、实验目的1. 学会Pspice 电路仿真软件的基本使用2. 掌握直流电路分析、瞬态电路分析等仿真分析方法二、实验准备1. 阅读PSpice 软件的使用说明2. 掌握节点法和网孔法来分析直流电路中各元件的电流和电压3. 掌握用函数式表示一阶、二队电路中某些元件的电流和电压三、实验原理用PSpice 仿真电路中各元件属性并与计算理论值比较，得出结论。

四、实验内容 A. P113 3.381. 该测试电路如图a-1所示。

输入该电路图，设置好元件属性和合适的分析方法，按Analysis/Simulate 仿真该电路。

图a -1 图a-22. 仿真结果如图a-2所示。

3. 比较图a-2中仿真出来的数据与理论计算出来的数据。

计算值为： 1.731i A =，153.076V V =，262.885V V = 仿真值为： 1.731i A =，153.08V V =，262.89V V =经比较，发现计算值与仿真值只是精确度不一样，精确值相等。

B. P116 3.571. 该测试电路图如图b-1如示。

设置好元件属性及仿真方法。

图b- 1图b- 22.仿真出来的电路中各支路电流值如图b-2所示。

3.比较仿真值与理论计算值。

计算值：用网孔分析法得到线性方程组如下：用matlab解上述方程得i=1.5835A, i=1.0938A, i=1.2426A, i=-0.8787A即1234i=1.584A, i=1.094A, i=1.243A, i=-0.87872A 从图b-2可以读出仿真值：1234把计算值当作真实值，把仿真值当作测量值，计算相对误差如下表由上表可以看出计算值与仿真值之间的相对误差很小，而从直观上来看，两者只是精确度问题。

4. 图b-2也可以验证一下基尔霍夫电流定律。

如1.584=1.094+489.70m 。

C. P274 Example 7.181. 该测试电路如图c-1所示，设置好元件属性。

SPICE模型的导入及仿真

ADS SPICE模型的导入及仿真SPICE模型的导入1、打开一个新的原理图编辑视窗，暂时不用保存也不要为原理图命名。

2、导入SPICE模型：:BFP&4C_TESl_20110L03.p r j ； untitled；(Schematicpl 1rile Edit Select Viww InEert Options CD Hrv* Dcitin’.Qrl+N Open Design-n Clri+QCJose DesignReyert to Saved Design...wv Save Design QH+S &Save Design 公…静Save Design As Template .CuipxDuGgm..Qelete Desiqr.,.Print.Ctrl+P Print Area...Print Setup-™庠 1 E|P 口!■■!!：■・Export.™1iKfiportsDesig.n ^ar^rT eters...T QC J E Layout Simulate lAindow ^►ynainiiiicLiiib Des ignGtj idle Help p O 月加备\盏＜8＞郞臼庫[mport bFil^K«tli st FileImport File Nam^ (Sourat)New Design Kame QJe^tin^tioit^2▼ Mcpxe OytiOK C axicel HelpJlZW. 2.£>K -0J5H Z.B75A/肝SrnSchem [mport Netlist Options：5FSFICEV] Fir?+ line is a. cfifMfiint两卩res? □爼10 fnuppingTranslated Output FormatQ ALT Schematic [with nwsd coimaatioaCJ ADM 丿Ojti sitsl Direetwy LfiCiti srDirectory To Store kDS ffstliit Cdafaull i toproject dirtctary)ance Hel?3、新建一个原理图，命名为“ BFP640_aII”，利用刚导入的SPICE文件并对照下载的SPICE文件附带的原理图进行连接：附带的原理图连接好后的BFP640 all 原理图如下:門肝轴wj 科T/cni-icHjii."逋抽単 …wv di" ：ie- [jit Ldre 乂* Qpco 昭 Rgic U 帕a 筍仙虹 Bcrriw 吐汕叶口吐临肝门-]& is a*OM 口厂二母鳳録弋/陰睜屢合妨暗罩區IF ；、■ HichFM t-dtJ Lihur *"匚1■士專山 Si \ ±■即’© LJ 粵4、为SPICE 模型创建一个新的电路符号ADS 原理图系统默认的电路符号如下:这里我们为BFP640创建一个新的NPN 电路符号。

第8章SPICE模型及仿真

School of Information Science and Engineering, Shandong University
Chapter 8
通过带限AWGN信道的数字传数字基带传输系统）输（数字基带传输系统）
Principles of the Communications
School of Information Science and Engineering, Shandong University
Chapter 8
假设接收端采用匹配滤波器，假设接收端采用匹配滤波器，则
G R ( f ) = H * ( f ) e − j 2 π ft0
t0表示滤波器输出抽样的时间延迟
在抽样时刻t=t 在抽样时刻 0 ，匹配滤波器输出的信号分量为
y s ( t 0 ) = y s (t ) =∫ =∫ =∫
1 0 .9 0 .8 0 .7 0 .6 0 .5 0 .4 0 .3 0 .2 0 .1 0
Chapter 8
GT ( f )
-4 -3 -2
2
3 − T
2 − T
-1
0
2 T
1
3 T
2
3
4
匹配滤波器H(f)输出的信号分量为匹配滤波器H(f)输出的信号分量为 H(f)
Eh = ∫
W −W
GT ( f ) df
8.1.2 带限带通信道上的数字带限带通信道上的数字PAM传输传输对PAM 信号 u(t ) = v(t )cos2π fct 对QAM和PSK信号 QAM和PSK信号
u (t ) = vc (t ) cos 2π f c t + vs (t ) sin 2π f c t vc (t ) =

几种简单的SPICE程序模拟电路元件模型

几种简单的SPICE程序模拟电路元件模型
史平君
【期刊名称】《火控雷达技术》
【年(卷),期】1993(022)003
【摘要】SPICE(Simulation program with integrated circuit emphasis)电路模拟程序是当前国际上比较流行的一种通用电路分析程序。

但用SPICE程序对电路模拟时,有些电路元件不能被SPICE程序所接受。

文章对可控硅、调制器、变压器建立了可被SPICE接受的电路元件模型。

【总页数】4页(P38-41)
【作者】史平君
【作者单位】无
【正文语种】中文
【中图分类】TN761
【相关文献】
1.应用SPICE程序模拟大功率电路 [J], 高燕梅;付文秀
2.应用SPICE程序模拟振荡器电路 [J], 高燕梅;王学成
3.Spice:IC 设计中的模拟程序 [J], Christophe BASSO
4.高速吞脉冲程序分频器的电路设计与PSPICE模拟 [J], 邝小飞;陈迪平;郭辉;朱小莉;王镇道
5.简单的晶闸管PSPICE模型 [J], 张红庆;路松峰
因版权原因，仅展示原文概要，查看原文内容请购买。

Pspice仿真常用变压器模型

Pspice 仿真一一常用变压器模型屈时间：2012-04-12 2176 次阅读【网友评论0条：］因为电感元件的参数比较单一，而且在仿真中，主要是仿真元件的电子特性。

所以，这里就不谈电感，而主要讨论一下变压器和耦合电感的问题。

不少朋友在使用pspice仿真的时候，只会使用元件库中的几个理想化的耦合电感和变压器模型，却不会用那种带磁芯参数的耦合电感和变压器。

下面让我们画一张原理图，把常用的理想化的和非理想话的耦合电感及变压器包含进去，进行一个仿真比较，这样才能掌握模型的特点，从而在实际工作中运用。

在这张原理图中，我们一共放置了5个耦合电感和变压器模型。

其中左边的2个是理想化的，右边三个是非理想化，模拟的是带着实际的磁芯的磁性元件，磁芯的规格是3C90材质的ER28L。

有必要先简单说一下耦合电感这个模型，让一些刚入门的朋友便于自己动手尝试。

在图中的K1、K2、K3就是以耦合电感为核心构造的几个变压器。

我们构造这种变压器的时候，需要放置一个耦合电感模型K_Linear或K_Break或一个带磁芯的耦合电感模型例如K3所用的ER28L_3C90这个模型。

然后需要根据实际的需要放置一个电感模型作为绕组，有几个绕组就放几个电感模型，但对于一个耦合电感模型，绕组不能超过6个。

下面说说这几个模型的设置。

左边两个理想化模型：K1 ：耦合电感模型为K_Linear，绕组为L1和L2，必须双击K_Linear模型在其参数L1中输入L1，在参数L2中输入L2，才能实现两个绕组的耦合。

耦合系数设定为1，说明是完全耦合。

电感L1和L2的电感量，就代表绕组的电感量。

我们设定L1为250uH，L2为1000UH。

这就意味这初级与次级的匝比为 1 : 2。

因为电感量之比是匝比的平方。

TX1 :采用理想变压器模型XFRM_LINEAR ，这个模型只有两个绕组，双击模型后设定耦合系数为1，两个绕组的电感量也分别设定为250uH 和1000uH。