流体力学课后第七章
流体力学专题课程第七章孔口、管嘴出流与有压管流

ε=0.6f4 0.82
ε=1
(3) 与孔口的对比: 1> 公式形式相同,但系数不同: 2> H0 相同时,若A 也相同,则管嘴出流是孔口出流 量的1.32倍。
二、 收缩断面的真空
与自由出流一致
结论 1、流量公式:
QA 2gH0
2、自由式与淹没式对比: 1> 公式形式相同;
2> φ、μ基本相同,但 H0不同;
3> 自由出流与孔口的淹没深度有关, 淹没出流与上、下游水位差有关。
H v0
z
v0
v2
自由式:
H0 = H +
v02 2g
淹没式:
H0 =
z
+
v02 2g
-
v22 2g
pg AzA2 vg A 2 pg CzC2 vC g 22 vC g 2
pC pa
zAzCpA gpa2 vg A 2 12 vC g 2
H0——自由出流的作用水头
H0
1
vC2
2g
物理意义:促使流体克服阻力,流入大气的全部能量
特例 自由液面:PA=Pa,液面恒定:vA=0
H 0zAzCH
收缩断面流速
一、概念
1、孔口出流 ——容器壁上开孔,流体经容器壁上所开 小孔流出的水力现象,称孔口出流。
2、管嘴出流 ——在孔口上对接长度为3-4倍孔径的短管, 流体经容器壁上所接短管流出的水力 现象,称管嘴出流。
二、任务: 计算过流量Q。 三、依据:
(1)能量方程; (2)总流的连续性方程; (3)能量损失计算式。
vC
1
1
2gH 0 2gH 0
φ——孔口的流速系数,φ=0.97。
流体力学讲义 第七章 孔口及管嘴不可压缩流体恒定流

第七章孔口及管嘴不可压缩流体恒定流本章主要介绍流体力学基本方法和水头损失计算方法在孔口与管嘴出流中的应用,得出了孔口、管嘴出流的基本公式。
概念一、孔口出流(orifice discharge):在容器壁上开孔,水经孔口流出的水力现象就称为孔口出流,如图7-1。
应用:排水工程中各类取水,泄水闸孔,以及某些量测流量设备均属孔口。
图7-11.根据d/H的比值大小可分为:大孔口、小孔口大孔口(big orifice):当孔口直径d(或高度e)与孔口形心以上的水头高H的比值大于0.1,即d/H>0.1时,需考虑在孔口射流断面上各点的水头、压强、速度沿孔口高度的变化,这时的孔口称为大孔口。
小孔口(small orifice ):当孔口直径d(或高度e)与孔口形心以上的水头高度H的比值小于0.1,即d/H<0.1时,可认为孔口射流断面上的各点流速相等,且各点水头亦相等,这时的孔口称为小孔口。
2.根据出流条件的不同,可分为自由出流和淹没出流自由出流(free discharge):若经孔口流出的水流直接进入空气中,此时收缩断面的压强可认为是大气压强,即p c=p a,则该孔口出流称为孔口自由出流。
淹没出流(submerged discharge):若经孔口流出的水流不是进入空气,而是流入下游水体中,致使孔口淹没在下游水面之下,这种情况称为淹没出流。
3.根据孔口水头变化情况,出流可分为:恒定出流、非恒定出流恒定出流(steady discharge):当孔口出流时,水箱中水量如能得到源源不断的补充,从而使孔口的水头不变,此时的出流称为恒定出流。
非恒定出流(unsteady discharge):当孔口出流时,水箱中水量得不到补充,则孔口的水头不断变化,此时的出流称为非恒定出流。
二、管嘴出流:在孔口周边连接一长为3~4倍孔径的短管,水经过短管并在出口断面满管流出的水力现象,称为管嘴出流。
圆柱形外管嘴:先收缩后扩大到整满管。
流体力学 第七章

u2 dq d( ) 0 2 dp
等熵流动,dq=0
dp
u2 d( ) 0 2
积分形式
dp
u2 d( ) C 2
基本方程建立了速度、温度、压力、密度 的相互关系。即使用于可逆的绝热流动过 程,又适用于不可逆的绝热流动过程。
第三节 一元气体的流动特性
微分形式的可压缩气体总流的连续性方程 沿流管流体的速度、密度和流管的断面面积这 三者之间的相对变化量的代数和必然为0
二 可压缩气体的能量方程
由于气体的密度很小,所以质量力可以忽略不计。 气体是一维定常流动,则欧拉运动微分方程为
du dp u dx dx
积分
2
du 1 dp u 0 dx dx
以上分析表明:亚声速运动的点扰动源,扰动点始终 位于扰动波内,在足够长的时间以后,它的扰动总可 以传播到整个空间。因此亚声速运动的点扰动源的影 响域也是全流畅。 3)超声速运动的点扰动源的影响域 扰动点的运动速度 v大于声速c,设 t=0时刻点扰动位 于o点,在3t时刻 扰动到达半径为 3ct的o3球面上
( p dp) A PA dpA
沿活塞运动方向列动量方程
dpAdt cdtA(du 0)
dp du c
cd du d
dp cd c d
c
dp d (1 ) d
因为活塞速度很小,气体受到的扰动也很微弱, 其状态变化量很小,dρ/ρ可以忽略不计
C0 kRT0 1.4 287T0 20.1 273 20 343m / s
C1 kRT1 1.4 287T1 20.1 273 55 296m / s
《工程流体力学》第七章 粘性流体动力学
x方向 : 1)表面力:作用在左右两面上力的合力:
作用在上下两面上力的合力:
作用在前后两面上力的合力:
作用在整个六面体上表面力沿x轴方向的合力:
2) x方向质量力 : 单位质量流体受到的质量力分量:X;
六面体受到的质量力: Xrdxdydz
牛顿第二定律:
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式:
应力:各向同性
运动粘性流体:存在法向、切向表面力 应力:各向异性
流体中:任一点c :绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz:定义c上的应力
需要2个下标表示:9个应力分量
第1个下标i:应力作用方向 第2个下标j:作用面方向
第七章 粘性流体动力学
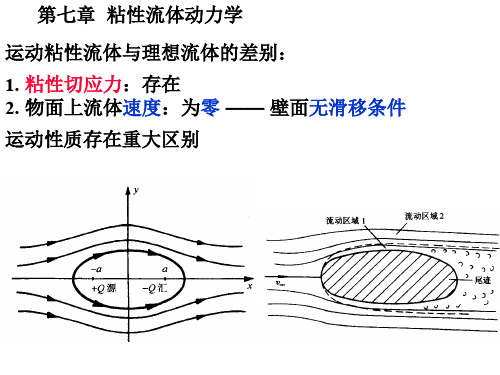
运动粘性流体与理想流体的差别: 1. 粘性切应力:存在 2. 物面上流体速度:为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力: 1.质量力:与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法:和理想流体相同
2. 表面力: 静止和运动理想流体:仅存在指向作用面法向表面力
由于外部无粘流:受到分离流的排挤 明显改变:其中压强分布 实际计算:用实测物面压力分布计算分离点前附面层流动 附面层分离:使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生:是工程上一个重要问 题
边界层分离后:形成尾涡区 尾涡区压强:基本上等于分离点压强 压强:上下对称 若将压强在圆柱面上积分:则得压差阻力
流体在y+l层时均速度:
流体力学第七章不可压缩流体动力学基础
第七章不可压缩流体动力学基础在询面的章节中,我们学习了理想流体和粘性流体的流动分析,按照水力学的 观点,求得平均量。
但是,很多问题需要求得更加详细的信息,如流速、压强等 流动参数在二个或三个坐标轴方向上的分布情况。
本章的容介绍流体运动的基本 规律、基本方程、定解条件和解决流体问题的基本方法。
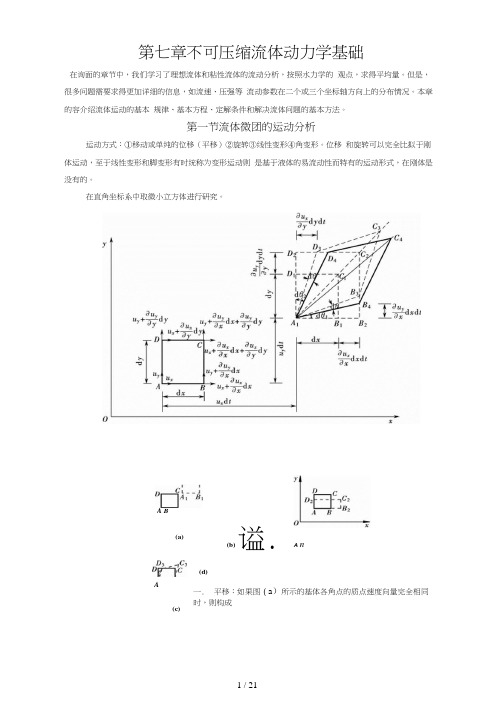
第一节流体微团的运动分析运动方式:①移动或单纯的位移(平移)②旋转③线性变形④角变形。
位移 和旋转可以完全比拟于刚体运动,至于线性变形和脚变形有时统称为变形运动则 是基于液体的易流动性而特有的运动形式,在刚体是没有的。
在直角坐标系中取微小立方体进行研究。
(b)谥.A n(d)一. 平移:如果图(a )所示的基体各角点的质点速度向量完全相同时,则构成(c)A B(a)A了液体基体的单纯位移,其移动速度为心、®、“,。
基体在运动中可能沿直线也 可能沿曲线运动,但其方位与形状都和原来一样(立方基体各边的长度保持不 变)。
二、 线变形:从图(b )中可以看出,由于沿y 轴的速度分量,B 点和C 点都比 A 点和D 点大了竺如 而比就代表〃y = l 时液体基体运动时,在单位时间沿勿dyy 轴方向的伸长率。
du x °"、. du : dxdydz三、 角变形(角变形速度)—BIA ■ dp -------------------------------- Jda-0 = dp + 00 =J"些+些k dz. dx四、旋转(旋转角速度)1O = —0 =—21勿du vdx—dx角变形:血 A那么,代入欧拉加速度表达式,得:du r du Tdu r八 八5=说=古叫 云+"卑+"0+-叭巴加、6仇 du Ya v = ----- = — + u v ---------- + U.0, +ii t a ). -iLCoydt dt dy “'2 …加.du diL q 。
工程流体力学第七章 理想不可压缩流体的有旋流动和无旋流动讲解

x
vx
y
v y
z
vz
t
0
或
(v) 0
t
连续性方程表示了单位时间内控制体内流体质量的增量等于流体在控
制体表面上的净通量。它适用于理想流体和粘性流体、定常流动和非定常
流动。
在定常流动中,由于 0 t
x
0
对于不可压缩流体 vr 1 v vz vr 0
r r z r
式中 r 为极径; 为极角
球坐标系中的表示式为:
1 (vrr 2 ) 1 (v sin ) 1 v 0
t r 2 r
r sin
r sin
在某流场O点邻近的任意点A上的速度可以分成三个部分: 分别为与O点相同的平移速度(平移运动);绕O点转动在A点 引起的速度(旋转运动);由于变形(包括线变形和角变形) 在A点引起的速度(变形运动)。
第三节 有旋流动和无旋流动
根据流体微团在流动中是否旋转,可将流体的流动分为两 类:有旋流动和无旋流动。
vx y
2 x
2 y
2 z
前面在流体微团的分析中,已给出E点的速度为 :
vxE
vx
vx x
dx
vx y
dy
vx z
dz
v yE
vy
vy x
dx
vy y
dy
vy z
dz
vzE
流体力学 第七章 波浪理论

第七章波浪理论课堂提问:为什么海面上“无风三尺浪”船舶与海洋工程中:船舶摇摆和拍击,船舶稳性,兴波阻力。
沿岸工程中:波浪对港口、防波堤的作用。
离岸工程中:钻井平台,海工建筑、海底油管等水波起制约作用的物理因素是重力,粘性力可略而不计,因此可用理想流体的势流理论来研究波浪运动的规律。
本章内容:着重介绍小振幅波(线性波)理论,相关内容为:1.小振幅波的基本方程和边界条件2.波浪运动的有关概念(波速、波长、周期、波数、频率、深水波、浅水波等)3. 流体质点的轨道运动4. 前进水波中的压力分布5. 波群与波群速6. 船波7. 波能传递与兴波阻力7-1 微振幅波的基本方程与边界条件§一简谐前进波沿x轴正向移动,h—水深(从平均水平面到底部的距离)η(x , t)—自由面在平均水面以上的瞬时垂直距离a—振幅H—波高,对于小振幅波 H = 2aL—波长(两相邻波峰或波谷间的距离)T—周期(固定点处重复出现波峰(或波谷)的时间间隔,或波形传播一个波长所需的间。
C—波速,或相速度(波阵面的传播速度) C = L/T (7-2)k—波数(2π距离内波的数目)K = 2π/L (7-3)σ—圆频率(2π时间内波振动的次数)σ=2π/T (7-4)微振幅波理论的基本假设1.理想不可压缩流体,重力不能忽略;2.运动是无旋的,具有速度势;3.波浪是微振幅波(线性波),即H<<L (7-5) 速度势φ(x ,z ,t ),满足xz v x v z ϕϕ∂=∂∂=∂ (7-6)且满足Laplace 方程:22220x zϕϕ∂∂+=∂∂(, )h z x η-<<-∞<<+∞ (7-7)底部条件(不可穿透条件):0z v z ϕ∂==∂( z = -h ) (7-8)自由表面边界条件:1z g t ηϕη=∂=-∂(7-10)令z=η,自由表面上相对压力p=0。
为使边界条件线性化,假定速度平方v 2→0 而得到。
《工程流体力学》第七章 粘性流体动力学

2.附面层位移厚度d*: 设物面P点附面层厚度d ,在垂直于纸面方向取单位宽度,
则该处通过附面层的质量流量:
通过同一面积理想流体流量:
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面,
使两块阴影处面积相同:
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动,整个流场分为三个区域:
1)附面层: 流速:由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向:速度梯度很大
即使流体粘性系数小:粘性应力仍可达到一定数值
由于速度梯度很大: 使得通过附面层物体 涡旋强度很大,流体 是有旋的
2)尾迹流: 附面层内流体:离开物体流入下游,在物体后形成尾迹流
各物理量都是统计平均值, \ 瞬时物理量=平均物理量+脉动物理量, 对整个方程进行时间平均的运算。
一、常用时均运算关系式:
时均运算规律:
推论:脉动量对空间坐标各阶导数的时均值=0。
二、连续方程:对二维流动,瞬态运动连续方程 进行时均运算:
\ 可压缩紊流运动连续方程:
进行时均运算: 上两式相减:
\ 附加法向应力
法向应力: l: 比例系数,与体积变化率有关
三个法向应力平均值的负值:为粘性流体在该点压强
最后得表面应力与变形率之间的关系:
第二节 粘性流体运动的基本方程
一、连续方程:
粘性流体运动:服从质量守恒定律 连续方程:不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程: 粘性流体中:微元六面体 微元六面体中心:c
三、雷诺方程: 二维不可压缩粘性流,不考虑质量力,N-S为:
对上式进行时均运算:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 已知平面流场的速度分布为xy x u x +=2,y xy u y 522+=。
求在点(1,-1)处流体微团的线变形速度,角变形速度和旋转角速度。
解:(1)线变形速度:y x xu x x +=∂∂=2θ 54+=∂∂=xy y u yy θ 角变形速度:()x y y u x u x y z +=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=222121ε 旋转角速度:()x y x u x u x y z -=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=222121ω 将点(1,-1)代入可得流体微团的1=x θ,1=y θ;23/z =ε;21/z =ω2.已知有旋流动的速度场为z y u x 32+=,x z u y 32+=,y x u z 32+=。
试求旋转角速度,角变形速度和涡线方程。
解:旋转角速度:2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=z u y u y z x ω 2121=⎪⎭⎫ ⎝⎛∂∂-∂∂=x u z u z x y ω 2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=y u x u x yz ω 角变形速度:2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=z u y u y z x ε 2521=⎪⎭⎫ ⎝⎛∂∂+∂∂=x u z u z x y ε 2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=y u x u x y z ε 由z y x dz dy dxωωω==积分得涡线的方程为:1c x y +=,2c x z +=3.已知有旋流动的速度场为22z y c u x +=,0=y u ,0=z u ,式中c 为常数,试求流场的涡量及涡线方程。
解:流场的涡量为:0=∂∂-∂∂=zu y u y z x Ω 22z y cz x u z u z x y +=∂∂-∂∂=Ω 22zy cy y u x u x yz +-=∂∂-∂∂=Ω 旋转角速度分别为:0=x ω222zy czy +=ω 222z y cyz +-=ω 则涡线的方程为:c dz dy z y +=⎰⎰ωω 即c y dz z dy +-=⎰⎰可得涡线的方程为:c z y =+224.求沿封闭曲线2 22b y x =+,0=z 的速度环量。
(1)Ax u x =,0=y u ;(2)Ay u x =,0=y u ;(3)0=y u ,r A u =θ。
其中A 为常数。
解:(1)由封闭曲线方程可知该曲线时在z =0的平面上的圆周线。
在z =0的平面上速度分布为:Ax u x =,0=y u涡量分布为:0=z Ω根据斯托克斯定理得:0==⎰z A z s dA ΩΓ(2)涡量分布为:A z -=Ω根据斯托克斯定理得:2b A dA z A z s πΩΓ-==⎰(3)由于0=r u ,r A u =θ 则转化为直角坐标为:22b Ay y r A u x -=-=,2bAx u y =则22bA y u x u x yz =∂∂-∂∂=Ω 根据斯托克斯定理得:A dA z A z s πΩΓ2==⎰5.试确定下列各流场是否满足不可压缩流体的连续性条件?答:不可压缩流体连续性方程 直角坐标:0=∂∂+∂∂+∂∂zu y u x u z y x (1) 柱面坐标:0=∂∂+∂∂+∂∂+zu r u r u r u z r r θθ (2) (1)0,,=-==z y x u ky u kx u 代入(1) 满足(2)y x u x z u z y u z y x +=+=+=,, 代入(1) 满足(3)0),(),(2222=+=-+z y x u y x k u y xy x k u 代入(1) 不满足(4)0,sin ,sin =-==z y x u xy k u xy k u 代入(1) 不满足(5)0,,0===z r u kr u u θ 代入(2) 满足(6)0,0,==-=z r u u rk u θ 代入(2) 满足 (7)0,sin 2,cos sin 22=-==z r u r u r u θθθθ 代入(2) 满足6.已知流场的速度分布为y x u x 2=,y u y 3-=,22z u z =。
求(3,1,2)点上流体质点的加速度。
解:y x y x x y xy y x zu u y u u x u u t u a x z x y x x x x 22322320320-=+⋅-⋅+=∂∂+∂∂+∂∂+∂∂= y z u u y u u x u u tu a y z y y y x yy 9=∂∂+∂∂+∂∂+∂∂= 38z zu u y u u x u u t u a z z z y z x z z =∂∂+∂∂+∂∂+∂∂= 将质点(3,1,2)代入a x 、a y 、a z 中分别得:27=x a ,9=y a ,64=z a7.已知平面流场的速度分布为2224y x y t u x +-=,222y x x u y +=。
求0=t 时,在(1,1)点上流体质点的加速度。
解:()()()⎥⎥⎦⎤⎢⎢⎣⎡+-+-++⎥⎥⎦⎤⎢⎢⎣⎡+⋅⎪⎪⎭⎫ ⎝⎛+-+=∂∂+∂∂+∂∂=2222222222222420222244y x y y x y x x y x y x y x y t y u u x u u t u a x y x x x x 当0=t 时,()()322223222222)(84y x y x x y x xy a x +--+-= 将(1,1)代入得3=x a()()()22222222222224242240y x xy y x x y x x y x y x y t y u u x u u t u a y y y x yy +-⋅++⎥⎥⎦⎤⎢⎢⎣⎡+-+⎪⎪⎭⎫ ⎝⎛+-+=∂∂+∂∂+∂∂= 当t=0时,将(1,1)代入得:1-=y a8.设两平板之间的距离为2h ,平板长宽皆为无限大,如图所示。
试用粘性流体运动微分方程,求此不可压缩流体恒定流的流速分布。
解:z 方向速度与时间无关,质量力:g f x -=运动方程:z 方向:2210dxu d z p υρ+∂∂-= x 方向:→∂∂--=xp g ρ10 积分:)(z f gx p +-=ρ∴p 对z 的偏导与x 无关,z 方向的运动方程可写为z p dyu d ∂∂=μ122 积分:21221C x C x z p u ++∂∂=μ 边界条件:h x ±=,0=u得:01=C ,221h zp C ∂∂-=μ ∴⎥⎦⎤⎢⎣⎡-∂∂-=22)(12h x z p h u μ 9.沿倾斜平面均匀地流下的薄液层,试证明:(1)流层内的速度分布为()θμγsin y by u 222-=;(2)单位宽度上的流量为θμγsin 33b q =。
解:x 方向速度与时间无关,质量力θsin g f x =,θcos g f y -=运动方程:x 方向:221sin 0dyu d x p g υρθ+∂∂-= ① y 方向:yp g ∂∂--=ρθ1cos 0 ②②→积分)(cos x f gy p +-=θρb y = a p p = )(cos x f gb a +-=θρρ∴θρcos )(y h g p p a -+=∵=b 常数 ∴p 与x 无关 ①可变为μθρsin 22g dy u d -= 积分)21(sin 212C y C y g u ++-=μθρ 边界条件:0=y ,0=u ;b y =,0=dy du ∴b C -=1,02=C∴θμμθρsin )2(2)2(2sin 2y by r y b y g u -=-= θμγθμγsin 3sin )2(23200b dy y by udy Q b b =-==⎰⎰ 10.描绘出下列流速场 解:流线方程:y x u dy u dx = (a )4=x u ,3=y u ,代入流线方程,积分:c x y +=43直线族(b )4=x u ,x u y 3=,代入流线方程,积分:c x y +=283抛物线族(c )y u x 4=,0=y u ,代入流线方程,积分:c y =直线族(d )y u x 4=,3=y u ,代入流线方程,积分:c y x +=232抛物线族(e )y u x 4=,x u y 3-=,代入流线方程,积分:c y x =+2243椭圆族(f )y u x 4=,x u y 4=,代入流线方程,积分:c y x =-22双曲线族(g )y u x 4=,x u y 4-=,代入流线方程,积分:c y x =+22同心圆(h )4=x u ,0=y u ,代入流线方程,积分:c y =直线族(i )4=x u ,x u y 4-=,代入流线方程,积分:c x y +-=22抛物线族(j )x u x 4=,0=y u ,代入流线方程,积分:c y =直线族(k )xy u x 4=,0=y u ,代入流线方程,积分:c y =直线族(l )r c u r =,0=θu ,由换算公式:θθθsin cos u u u r x -=,θθθcos sin u u u r y += 220y x cx r x r c u x +=-=,220y x cy r y r c u y +=+= 代入流线方程积分:c y x =直线族(m )0=r u ,r c u =θ,220y x cx r x r c u x +-=-=,220y x cx r x r c u y +=+= 代入流线方程积分:c y x =+22同心圆11.在上题流速场中,哪些流动是无旋流动,哪些流动是有旋流动。
如果是有旋流动,它的旋转角速度的表达式是什么?解:无旋流有:x u y u y x ∂∂=∂∂(或rr u u r ∂∂=∂∂θθ) (a ),(f ),(h ),(j ),(l ),(m )为无旋流动,其余的为有旋流动对有旋流动,旋转角速度:)(21yu x u x y ∂∂-∂∂=ω (b )23=ω (c )2-=ω (d )2-=ω (e )27-=ω (g )4-=ω (i )2-=ω (k )x 2-=ω12.在上题流速场中,求出各有势流动的流函数和势函数。
解:势函数⎰+=dy u dx u y x ϕ流函数⎰-=dx u dy u y x ψ(a )⎰+=+=y x dy dx 3434ϕy x dx dy 4334+-=-=⎰ψ(e )e 为有旋流无势函数只有流函数xy xdx ydy y x 33400=--=⎰⎰ψ其他各题略13.流速场为rc u u a r ==θ,0)(,r u u b r 2,0)(ωθ==时,求半径为1r 和2r 的两流线间流量的表达式。
