北京市延庆县2012年数学初三一模
2012北京市各区中考数学一模试卷及答案试题试卷_1 (2)

顺义区2012届初三第一次统一练习 数学学科参考答案及评分细则二、填空题(本题共16分,每小题4分,)9.4;10.25()x x y -; 11.11.4; 12, 2)π+,π. 三、解答题(本题共30分,每小题5分) 13()12cos303-︒+--1213⎛⎫=+-- ⎪⎝⎭……………………………………………… 4分 113=+ 43= …………………………………………………………………… 5分 14.解: 221x y x y +=⎧⎨-=⎩①②①+②,得 33x =.1x =. …………………………………………………… 2分 把1x =代入①,得 12y +=.1y =. ………………………………………………………… 4分 ∴原方程组的解为 1,1.x y =⎧⎨=⎩ ………………………………………………… 5分15.证明:∵AB=AC ,∴B C ∠=∠. …………………………………………………………… 1分 在△ABD 和△ACE 中,,,,AB AC B C BD CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABD ≌△ACE .……………………………………………………… 3分 ∴ AD=AE . ……………………………………………………………… 4分∴∠ADE =∠AED . ……………………………………………………… 5分16.解:6931x x x x -⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭2693x x x x x -+-=÷ …………………………………………………… 2分 2(3)3x xx x -=-3x =- ……………………………………………………………………… 4分当2012x =时,原式=201232009-=.…………………………………… 5分17.解:(1)∵点(4,)A m 在反比例函数4y x=(0x >)的图象上, ∴414m ==. …………………………………………………………… 1分 ∴(4,1)A .将(4,1)A 代入一次函数y x b =-+中,得 5b =.∴一次函数的解析式为5y x =-+. …………………………………… 2分(2)由题意,得 (0,5)B , ∴5OB =.设P 点的横坐标为P x .∵OBP △的面积为5, ∴1552p x ⨯=.…………………………………………………………… 3分 ∴2P x =±.∴点P 的坐标为(2,3)或(-2,7). ………………………………… 5分 18.解:设A 户型的每户窗户改造费用为x 元,则B 户型的每户窗户改造费用为(500)x -元. ……………………………… 1分 根据题意,列方程得5400004800005x x =-. 解得 4500x =.经检验,4500x =是原方程的解,且符合题意.…………………………… 4分 ∴5004000x -=.答:A 户型的每户窗户改造费用为4500元,B 户型的每户窗户改造费用为4000 元.…………………………………… 5分MF EDCBAFE DCO BA四、解答题(本题共20分,每小题5分)19.解:(1)∵在□ABCD 中,∠B=60°,AB=4,∠ACB=45°,∴∠D=60°,CD=AB=4,AD ∥BC . ……………………………… 1分 ∴∠DAC=45°. 过点C 作CM ⊥AD 于M , 在Rt △CDM 中,sin 4sin 6023CM CD D ==︒=cos 4cos602DM CD D ==︒=.………………………………… 2分在Rt △ACM中,∵∠MAC=45°, ∴AM CM==∴2AD AM DM =+=.…………………………………… 3分∵EF ⊥AD ,CM ⊥AD , ∴EF ∥CM .∴12EF CM ==在Rt △AEF 中,AF EF ==4分∴22DF AD AF =-=-=.……………………… 5分20.(1)证明:连结OD .∵AB 是⊙O 的直径,∴∠ADB=90°. ……………………………………………………… 1分 ∵∠A=30°, ∴∠ABD=60°.∴∠BDC =1302ABD ∠=︒. ∵OD=OB ,∴△ODB 是等边三角形. ∴∠ODB=60°.∴∠ODC=∠ODB+∠BDC =90°. 即OD ⊥DC .∴CD 是⊙O 的切线.…………………………………………………… 2分(2)解:∵OF ∥AD ,∠ADB=90°,∴OF ⊥BD ,∠BOE=∠A =30°. ……………………………………… 3分∴112DE BE BD ===. 在Rt △OEB中,OB=2BE=2,OE ==.………… 4分 ∵OD=OB=2,∠C=∠ABD -∠BDC =30°,∠DOF=30°, ∴CD =tan 30DF OD =︒=∴CF CD DF =-== ……………………………5分21.解:(1)此次共调查了100名学生. …………………………………………………1分(2)填表:…………………………………………………3分(3)补全统计图如下:到校方式条形统计图 到校方式扇形统计图.…………………………………………………………………………5分22.解:(1)四边形DFCE 的面积S = 6 ,△DBF 的面积1S = 6 ,△ADE 的面积2S = 32 . …………………………………… 3分(2)2S = 214S S (用含S 、1S 的代数式表示). ………… 4分 (3)□DEFG 的面积为12. ………………………………………… 5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.解:(1)△=244(1)(3)k k k --+=2244812k k k --+=812k -+ ……………………………………………………………… 1分∵方程有两个不相等的实数根, ∴10,0.k -≠⎧⎨∆>⎩ 即 10,8120.k k -≠⎧⎨-+>⎩∴k 的取值范围是32k <且1k ≠. …………………………………… 3分 (2)当方程有两个相等的实数根时,△=812k -+=0.∴32k =. ………………………………………………………………… 4分 ∴关于y 的方程为2(6)10y a y a +-++=.∴2'(6)4(1)a a ∆=--+2123644a a a =-+--21632a a =-+2(8)32a =--.由a 为正整数,当2(8)32a --是完全平方数时,方程才有可能有整数根. 设22(8)32a m --=(其中m 为整数),32p q =(p 、q 均为整数), ∴22(8)32a m --=.即(8)(8)32a m a m -+--=.不妨设8,8.a m p a m q -+=⎧⎨--=⎩两式相加,得 162p q a ++=.∵(8)a m -+与(8)a m --的奇偶性相同,∴32可分解为216⨯,48⨯,(2)(16)-⨯-,(4)(8)-⨯-, ∴18p q +=或12或18-或12-.∴17a =或14或1-(不合题意,舍去)或2.当17a =时,方程的两根为1172y -±=,即12y =-,29y =-.…… 5分 当14a =时,方程的两根为822y -±=,即13y =-,25y =-.…… 6分当2a =时, 方程的两根为422y ±=,即13y =,21y =. ………… 7分24.解:(1)∵抛物线y =mx 2+2mx +n 经过点A (-4,0)和点B (0,3),∴1680,3.m m n n -+=⎧⎨=⎩ ∴3,83.m n ⎧=-⎪⎨⎪=⎩. ∴抛物线的解析式为:233384y x x =--+.………………………… 2分 (2)令3y =,得2333384x x --+=,得10x =,22x =-, ∵抛物线向右平移后仍经过点B ,∴抛物线向右平移2个单位.……… 3分∵233384y x x =--+ 233(21)388x x =-++++2327(1)88x =-++. ………… 4分∴平移后的抛物线解析式为2327(1)88y x =--+. …………………… 5分(3)由抛物线向右平移2个单位,得'(2,0)A -,'(2,3)B .∴四边形AA ’B ’B 为平行四边形,其面积'236AA OB ==⨯=.设P 点的纵坐标为P y ,由'OA P △的面积=6, ∴1'62P OA y =,即1262P y ⨯= ∴6P y =, 6P y =±.………………………………………………… 6分当6P y =时,方程2327(1)688x --+=无实根, 当6P y =-时,方程2327(1)688x --+=-的解为16x =,24x =-.∴点P 的坐标为(6,6)-或(4,6)--.……………………………… 7分25.解:(1)完成画图如图2,由BAC ∠的度数为 60°,点E 落在 AB 的中点处 ,容易得出BE 与DE 之间的数量关系 为 BE=DE ;…………… 3分(2)完成画图如图3.猜想:BE DE =.证明:取AB 的中点F ,连结EF .∵90ACB ∠=︒,30ABC ∠=︒,∴160∠=︒,12CF AF AB ==. ∴△ACF 是等边三角形.∴AC AF =. ① …… 4分∵△ADE 是等边三角形,∴260∠=︒, AD AE =. ②∴12∠=∠. ∴12BAD BAD ∠+∠=∠+∠.即CAD FAE ∠=∠.③ ………………………………………… 5分 由①②③得 △ACD ≌△AFE (SAS ). …………………………… 6分 ∴90ACD AFE ∠=∠=︒. ∵F 是AB 的中点,∴EF 是AB 的垂直平分线.∴BE=AE . ……………………………………………………… 7分 ∵△ADE 是等边三角形, ∴DE=AE .∴BE DE =. …………………………………………………… 8分EAB C (D )图221F EDB C A图3。
初中数学北京市延庆区中考模拟数学一模考试题考试卷及答案

xx学校xx学年xx 学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx 分)试题1:的绝对值是A. B. C. D.试题2:在第六次全国人口普查,截至2010年11月1日零时,延庆县常住人口为317000人,将317000用科学记数法表示应为A.3.17×105 B.31.7×104 C.3.17×104 D.0.317×106试题3:一个不透明的盒子中装有2个白球,5个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为A.B. C. D.试题4:如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是A.15° B.25°C.45° D.65°试题5:下列图形中,是中心对称图形但不是轴对称图形的是A.等边三角形 B.菱形C. 平行四边形 D.矩形试题6:小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直线上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m(如图所示).已知DE=30cm,EF=20cm,那么树AB的高度等于A.4 m B.5.4 m C.9 m D.10.4 m试题7:某中学足球队9名队员的年龄情况如下:年龄(单位:岁)14 15 16 17人数 1 4 2 2则该队队员年龄的众数和中位数分别是A.15,15 B.15,16 C.15,17 D.16,15试题8:如图,在△ABC中,AB=5cm,BC=12cm,动点D、E同时从点B出发,点D由B到A以1cm/s的速度向终点A作匀速运动,点E沿BC-CA以2.4cm/s的速度向终点A作匀速运动,那么△BDE的面积S与点E运动的时间t 之间的函数图象大致是A.B. C. D.试题9:分解因式:= __________ .试题10:若分式的值为0,则x的值等于.试题11:某一次函数的图象经过点(1,-2),且函数y的值随自变量x的增大而减小,请写出一个满足上述条件的函数关系式:.试题12:如图,正三角形ABC、正四边形ABCM、正五边形ABCMN中,点E在CB的延长线上,点D在另一边反向延长线上,且BE=CD,DB延长线交AE于点F.图1中∠AFB的度数为,图2中∠AFB度数为,若将条件“正三角形、正四边形、正五边形”改为“正n边形”,其它条件不变,则∠AFB度数为.(用含n的代数式表示)图1 图2 图3试题13:如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;求证:∠D=∠A试题14:计算:.试题15:解不等式组:试题16:已知,求代数式的值.试题17:在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象的一个交点为A(1,).(1)求反比例函数的解析式;(2)若P是坐标轴上一点(P不与O重合),且满足,直接写出点P的坐标.试题18:为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多小时.求自驾车平均速度和自行车平均速度各是多少.试题19:如图,在△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使EF=DE,连接CF.(1)求证: 四边形BCFD是平行四边形;(2)若BD=4,BC=6,∠F=60°,求CE的长.试题20:以下是根据2013年某旅游县接待游客的相关数据绘制的统计图的一部分,请根据图1,图2回答下列问题:(1)该旅游县5~8月接待游客人数一共是280万人,请将图1中的统计图补充完整;(2)该旅游县6月份4A级景点接待游客人数约为多少人?(3)小明观察图2后认为,4A级景点7月份接待游客人数比8月多了,你同意他的看某旅游县5~8月4A级景点接待游客人数占该县当月游客人数百分比的统计图某旅游县5~8月各月接待游客人数统计图法吗?说明你的理由.试题21:已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.(1)求证:AD是⊙O的切线;(2)如果PB是⊙O的切线,BC=4,求PE 的长.试题22:阅读下面资料:小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1,求S1的值.小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B=AB,B1C=BC,C1A=CA,根据等高两三角形的面积比等于底之比,图1 图2所以,由此继续推理,从而解决了这个问题.(1)请直接写出S1= ;(用含字母a的式子表示).请参考小明同学思考问题的方法,解决下列问题:(2)如图3,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S2,求S2的值.(3)如图4,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,设△APE的面积为y,△BPF的面积为x,①求△APE ,△BPF,△APF 面积之间的关系;②求△ABC的面积.图3 图4试题23:已知:抛物线与x轴相交于A、B两点,与y轴相交于点C,其中点C的坐标是(0,3),顶点为点D,联结CD,抛物线的对称轴与x轴交于点E.(1)求m的值;(2)求∠CDE的度数;(3)在抛物线对称轴的右侧部分上是否存在一点P,使得△PDC是等腰三角形?如果存在,求出符合条件的点P的坐标;如果不存在,请说明理由.试题24:如图,正方形ABCD的边长是2,M是AD的中点.点E从点A出发,沿AB运动到点B停止.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.(1)设AE=x时,△EGF的面积为y.求y关于x的函数关系式,并写出自变量x的取值范围;(2)P是MG的中点,求点P运动路线的长.试题25:已知:在平面直角坐标系xOy中,给出如下定义:线段AB及点P,任取AB上一点Q,线段PQ长度的最小值称为点P到线段AB的距离,记作d(P→AB).(1)如图1,已知C点的坐标为(1,0),D点的坐标为(3,0),求点P(2,1)到线段CD的距离d(P→CD)为;(2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.图1 图2试题1答案:B试题2答案:A试题3答案:D试题4答案:B试题5答案:C试题6答案:B试题7答案:A试题8答案:D试题9答案:试题10答案:3试题11答案:略试题12答案:60,90,试题13答案:证明:∵AC∥DF∴∠C=∠F在△DEF和△ACB中∴∴∠D=∠A 试题14答案:解:=①②试题15答案:解:由①得:x>-6由①得:∴试题16答案:==∵∴原式=2试题17答案:⑴∵点A(1,n)在一次函数的图象上,∴n=3.∴点A的坐标为(1,3).∵点的反比例函数的图象上,∴k=3.∴反比例函数的解析式为.⑵点P的坐标为(2,0)或(0,6).试题18答案:解:自行车平均速度为x km/h,自驾车平均速度为2x km/h由题意得:解方程得:60-30=2x∴x=15,经检验:x=15是所列方程的解,且符合实际意义,∴2x=30答:自行车速度为15km/h,汽车的速度为30km/h.试题19答案:证明:(1)∵D、E分别是AB、AC的中点∴∵EF=DE∴∴∴四边形BCFD是平行四边形(2)过点C作CM⊥DF于M,∵平行四边形BCFD∴CF=BD=4 DF=BC=6∴EF=DE=3∵∠F=60°∴∠MC F=30°∴Rt△CMF中,Rt△NMF中,试题20答案:(1)图略(2)(万人)(3)(万人)(万人)所以小明说的不对试题21答案:证明:(1)∵AB=AC,点D是边BC的中点∴∠ADC=∠ADB=90°∴AD是⊙O的切线(2)∵AD是⊙O的切线PB是⊙O的切线∴PE=DE连接OP∴∠BPO=90°∴∠BPO=∠ADB =90°∴∽△BPO∴∵BC=4∴CD=BD=2∴OP=1,OB=3∴∴试题22答案:(1)S1=7a;(2)∵A1B=2AB,B1C=2BC,C1A=2CA根据等高两三角形的面积比等于底之比,∴S△A1BC=S△B1CA=S△C1AB=2S△ABC=2a∴S1=19a;(3)①过点C作CG⊥BE于点G,∵S△BPC=BP•CG=70;S△PCE=PE•CG=35,∴∴即:BP=2EP同理,∴S△APB=2S△APF.=x,S△APE=y,∴x+84=2y.②∵,又∵x+84=2y∴∵S△BPF∴S△ABC=315.试题23答案:(1)∵抛物线过点C(0,3)∴1-m=3∴m=-2(2)由(1)可知该抛物线的解析式为y=-x2+2x+3=-(x-1)2+4∴此抛物线的对称轴x=1抛物线的顶点D(1,4)过点C作CF⊥DE,则CF∥OE∴F(1,3)所以CF=1,DF=4-3=1∴CF=DF又∵CF⊥DE∴∠DFC=90°∴∠CDE=45°(3)存在.①延长CF交抛物线于点P1,则CP1∥x轴,所以P1正好是C点关于DE的对称点时,有DC=DP1,得出P1点坐标(2,3);由y=-x2+2x+3得,D点坐标为(1,4),对称轴为x=1.②若以CD为底边,则PD=PC,设P点坐标为(x,y),根据两点间距离公式,得x2+(3-y)2=(x-1)2+(4-y)2,即y=4-x.又P点(x,y)在抛物线上,∴4-x=-x2+2x+3,即x2-3x+1=0,解得:<1,应舍去;∴∴y=4-x=则P2点坐标()∴符合条件的点P坐标为()和(2,3).试题24答案:解:(1)当点E与点A重合时,x=0,y=2-----------2分当点E与点A不重合时,0<x≤2在正方形ABCD中,∠A=∠ADC=90°∴∠MDF=90°,∴∠A=∠MDF在△AME和△DMF中∴△AME≌△DMF(ASA)∴ME=MF在Rt△AME中,AE=x,AM=1,ME=∴EF=2ME=2过M作MN⊥BC,垂足为N(如图)则∠MNG=90°,∠AMN=90°,MN=AB=AD=2AM ∴∠AME+∠EMN=90°∵∠EMG=90°∴∠GMN+∠EMN=90°∴∠AME=∠GMN∴Rt△AME∽Rt△NMG∴即∴MG=2ME=∴∴(2)如图,PP′即为P点运动的距离;在Rt△BMG′中,MG⊥BG′;∴∠MBG=∠G′MG=90°-∠BMG;∴tan∠MBG=∴tan∠GMG′=tan∠MBG=∴GG′=2MG=4;△MGG′中,P、P′分别是MG、MG′的中点,∴PP′是△MGG′的中位线;∴PP′=即:点P运动路线的长为2.试题25答案:(1) d(P→CD)为 1(2)在坐标平面内作出线段DE:y=x(0≤x≤3).∵点G的横坐标为1,∴点G在直线x=1上,设直线x=1交x轴于点H,交DE于点K,①如图2所示,过点G1作G1F⊥DE于点F,则G1F就是点G1到线段DE的距离,∵线段DE:y=x(0≤x≤3),∴△G1FK,△DHK均为等腰直角三角形,∵G1F=∴KF=由勾股定理得G1K=2,又∵KH=OH=1,∴H G1=3,即G1的纵坐标为3;②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,∵OH=1,∴G2O=∴点G2同样是满足条件的点,∴点G2的纵坐标为-1,综上,点G的纵坐标为3或-1.。
北京市延庆县中考数一模试卷 人教版
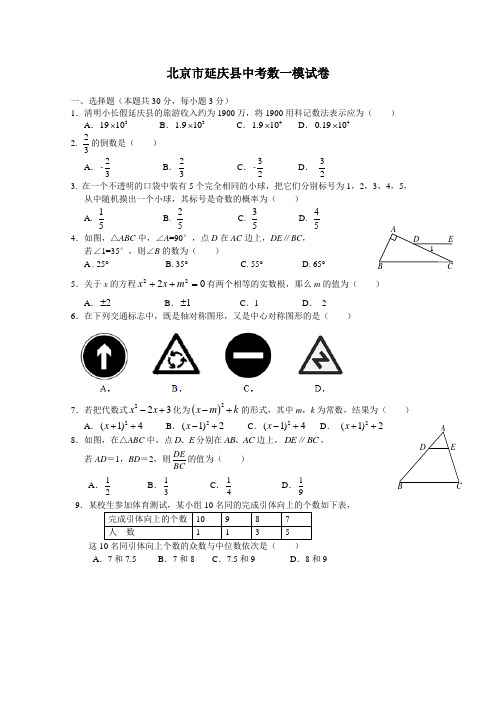
1E DCBAEDCB A 北京市延庆县中考数一模试卷一、选择题(本题共30分,每小题3分)1.清明小长假延庆县的旅游收入约为1900万,将1900用科记数法表示应为( ) A .21910⨯ B .31.910⨯ C .41.910⨯ D .40.1910⨯ 2. 23的倒数是( ) A .23- B .23 C .32- D . 323. 在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5, 从中随机摸出一个小球,其标号是奇数的概率为( ) A.51 B. 52 C. 53 D. 54 4.如图,△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC , 若∠1=35°,则∠B 的数为( ) A . 25° B. 35° C. 55° D. 65°5.关于x 的方程0222=++m x x 有两个相等的实数根,那么m 的值为( ) A .2± B .1± C .1 D . 26.在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )7.若把代数式223x x -+化为()2x m k -+的形式,其中m ,k 为常数,结果为( )A .2(1)4x ++B .2(1)2x -+C .2(1)4x -+D . 2(1)2x ++ 8.如图,在△ABC 中,点D E 、分别在AB AC 、边上,DE BC ∥,若AD =1,BD =2,则DEBC 的值为( )A .12 B .13 C .14 D .199完成引体向上的个数 10 9 8 7 人 数1135这 A .7和7.5 B .7和8 C .7.5和9 D .8和9CABED O10.如图,△ABC 中,∠ACB =90°,∠A =30°,AB =16.点P 是斜边AB 上一点.过点P 作PQ ⊥AB ,垂足为P ,交边AC (或边CB )于点Q ,设AP =x ,△APQ 的面积为y ,则y 与x 之间的函数图象大致是( )二、填空题(本题共18分,每小题3分) 11.分解因式:24x y y -= . 12.若分式1x x-的值为0,则x 的值等于_________ . 13.如图,⊙O 的直径CD 垂直弦AB 于点E ,且CE =2,DE =8,则AB 的长为 .14.请写出一个开口向上,并且与y 轴交于点(0,2)的抛物线的表达式__________ .15. 习勾股定理相关内容后,张老师请同们交流这样的一个问题:“已知直角三角形的两条边长分别为3,4,请你求出第三边.”张华同通过计算得到第三边是5,你认为张华的答案是否正确:________,你的理由是 _______________________________________.16. 将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图161.在图162中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图161所示的状态,那么按上述规则连续完成3次变换后,骰子朝上一面的点数是________;连续完成次变换后,骰子朝上一面的点数是________.三、解答题(本题共30分,每小题5分)17.如图,△ABC 中,∠ACB =90°,延长AC 到D ,使得CD=CB ,过点D 作DE ⊥AB 于点E ,交BC 于F .求证:AB =DF .FED C BA图161 图162向右翻滚90° 逆时针旋转90°18.计算:011(3)4cos 45()2π---︒++-.19.解不等式组: 32,12.3x x x x >-⎧⎪+⎨>⎪⎩20.已知2410x x +-=,求代数式22(2)(2)(2)x x x x +-+-+的值.21.如图,一次函数1y x =+的图象与反比例函数ky x=(k 为常数,且0k ≠)的图象都经过点A (m ,2).(1)求点A 的坐标及反比例函数的表达式;(2) 设一次函数1y x =+的图象与x 轴交于点B ,若点P 是x 轴上一点,且满足△ABP 的面积是2,直接写出点P 的坐标.22.列方程或方程组解应用题:八级的生去距校10千米的科技馆参观,一部分生骑自行车先走,过了20分钟,其余的生乘汽车出发,结果他们同时到达,已知汽车的速是骑自行车生速的2倍,求骑车生每小时走多少千米?四、 解答题(本题共20分,每小题5分)23. 如图,点O 是△ABC 内一点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,得到四边形DEFG .(1)求证:四边形DEFG 是平行四边形;(2)如果∠OBC =45°,∠OCB =30°,OC =4,求EF 的长.G FOBCDE A24. 某区对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A .使用清洁能源B .汽车限行C .绿化造林D .拆除燃煤小锅炉调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:(1)这次被调查的市民共有 人. (2)请你将统计图1补充完整.(3)已知该区人口为00人,请根据调查结果估计该市认同汽车限行的人数.25. 如图,AB 是⊙O 的直径,点C 在⊙O 上,过点C 作⊙O 的切线CM . (1)求证:∠ACM =∠ABC ;(2)延长BC 到D ,使CD = BC ,连接AD 与CM 交于点E ,若⊙O 的半径为2,ED =1,求AC 的长.ODCA BM E26. 阅读下面资料: 问题情境:(1)如图1,等边△ABC ,∠CAB 和∠CBA 的平分线交于点O ,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点与点O 重合,已知OA =2,则图中重叠部分△OAB 的面积是 . 探究:(2)在(1)的条件下,将纸片绕O 点旋转至如图2所示位置,纸片两边分别与AB ,AC 交于点E ,F ,求图2中重叠部分的面积.(3)如图3,若∠ABC =α(0°<α<90°),点O 在∠ABC 的角平分线上,且BO =2,以O 为顶点的等腰三角形纸片(纸片足够大)与∠ABC 的两边AB ,AC 分别交于点E 、F ,∠EOF =180°﹣α,直接写出重叠部分的面积.(用含α的式子表示)五、解答题(本题共22分,第27题7分、28题各7分,29题8分) 27. 二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C .(1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.28. 已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.29. 对于平面直角坐标系xOy 中的点P 和线段AB ,给出如下定义:在线段AB 外有一点P ,如果在线段AB 上存在两点C 、D ,使得∠CPD =90°,那么就把点P 叫做线段AB 的悬垂点.(1)已知点A (2,0),O (0,0)①若1(1,)2C ,D (1,1),E (1,2),在点C ,D ,E 中,线段AO 的悬垂点是______; ②如果点P (m ,n )在直线1y x =-上,且是线段AO 的悬垂点,求m 的取值范围; (2)如下图是帽形M (半圆与一条直径组成,点M 是半圆的圆心),且圆M 的半径是1,若帽形内部的所有点是某一条线段的悬垂点,求此线段长的取值范围.延庆县毕业考试答案初三数题号 1 2 3 4 5 6 7 8 9 104分 4分 5分① ② 5分4分 2分5分5分 4分 2分1分011(3)4cos 45()2123π---︒++-=-+=3分 1分三、解答题(本题共30分,每小题5分) 17. 证明:证明:∵ DE ⊥AB ∴∠DEA=90° ∵∠ACB =90° ∴∠DEA=∠ACB ∴∠D=∠B在△DCF 和△ACB 中DCB ACB DC BC B D ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DCF ACB ∆≅∆∴AB =DF18.解:19. 32,12.3x x x x >-⎧⎪+⎨>⎪⎩解:由①得:x>1 由①得:15x < ∴115x -<<22222220.(2)(2)(2)44448x x x x x x x x x x +-+-+=++-++=++ ∵2410x x +-=∴241x x +=∴原式=921. ⑴ ∵点A (m ,2)在一次函数1y x =+的图象上,5分3分 5分 4分4分 5分 3分2分4分2分60MA FG E BCD∴m=1.∴点A 的坐标为(1,2).∵点A 的反比例函数xky =的图象上,∴k=2.∴反比例函数的解析式为2y x=. ⑵ 点P 的坐标为(1,0)或(3,0).24.(1)200 (2)5分 1分 2分3分 5分O D C A BME(3)8020020000080000÷⨯=25.证明:(1)证明:连接OC . ∵ AB 为⊙O 的直径, ∴ ∠ACB = 90°.∴ ∠ABC +∠BAC = 90°. ∵ CM 是⊙O 的切线, ∴ OC ⊥CM .∴ ∠ACM +∠ACO = 90°. ·································································· 1分[来∵ CO = AO ,∴ ∠BAC =∠ACO . ∴ ∠ACM =∠ABC . ··············································································· 2分 (2)解:∵ BC = CD ,OB=OA ,∴ OC ∥AD. 又∵ OC ⊥CE ,∴CE ⊥AD . 3分[∵ ∠ACD =∠ACB = 90°,∴ ∠AEC =∠ACD . ∴ ΔADC ∽ΔACE .∴AD ACAC AE=. ····················································································· 4分[ 而⊙O 的半径为2, ∴ AD = 4. ∴43AC AC =. ∴ AC = 2 3 . ······················································································ 5分[ 26.(1) 3(2) 连接AO 、BO ,如图②,由题意可得:∠EOF =∠AOB ,则∠EOA =∠FOB . 在△EOA 和△FOB 中,EAO FBO OA OBEOA FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△EOA ≌△FOB . ∴S 四边形AEOF =S △OAB .过点O 作ON ⊥AB ,垂足为N ,如图, ∵△ABC 为等边三角形, ∴∠CAB =∠CBA =60°.∵∠CAB 和∠CBA 的平分线交于点O ∴∠OAB =∠OBA =30°. ∴OB=OA =2. ∵ON ⊥AB ,∴AN=NB ,ON =1.∴AN =N FEOCBA4分 5分D P ABCE FQPFEQD CBA ∴AB=2AN =2. ∴S △OAB =AB •ON =. S 四边形AEOF = (3) S 面积=4sincos.27. 解:(1)∵二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0) ∴4101m nm n=--+⎧⎨=-++⎩∴m=2,n=3∴二次函数的表达式为223y x x =--+ (2)12y x b =-+经过点B ∴12b = 画出图形()211(,),2322M m m m m m -+--+设,则N ∴21123()22MN m m m =--+--+设 ∴23522MN m m =--+∴2349()416MN m =-++ ∴MN 的最大值为491628.解:(1)AE ∥BF ,QE=QF , (2)QE=QF ,证明:如图2,延长EQ 交BF 于D , ∵AE ∥BF ,∴∠AEQ=∠BDQ , 在△BDQ 和△AEQ 中AEQ BDQ AQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDQ ≌△AEQ (ASA ), ∴QE=QD , ∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边上的中线, ∴QE=QF=QD , 即QE=QF . (3)(2)中的结论仍然成立, 证明:如图3,延长EQ 、FB 交于D , ∵AE ∥BF ,7分 2分 6分 5分3分 4分2分3分5分4分∴∠AEQ =∠D ,在△AQE 和△BQD 中AEQ BDQ AQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, 图3 ∴△AQE ≌△BQD (AAS ), ∴QE=QD ,∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边DE 上的中线, ∴QE=QF . 说明:第三问画出图形给1分 29.(1)线段AO 的悬垂点是C ,D ;(2)以点D 为圆心,以1为半径做圆,设1y x =-与⊙D 交于点B ,C与x 轴,y 轴的交点坐标为(1,0),(0,1) ∴∠ODB=45° ∴DE=BE在Rt △DBE 中,由勾股定理得:DE=22∴2211122m m -≤≤+≠且 (3)设这条线段的长为a①当2a <时,如图1,凡是⊙D 外的点不满足条件; ②当2a =时,如图2,所有的点均满足条件; ③当2a >时,如图3,所有的点均满足条件; 综上所述:2a ≥以上答案仅供参考。
归纳总结--2.2012初三一模题答案-延庆

参考答案
一、选择题(共8个小题,每题4分,共32分)
题号
1
2
3
4
5
6
7
8
答案
B
C
D
A
D
B
C
A
二、填空题(共4个小题,每小题4分,共16分)
题号
9
10
11
12
答案
x≥3
a(x+2)(x-2)
;
三、解答题(共5道小题,13-17每小题5分,共25分)
13.解:原式 …………………………………………4分
即:BD+DC> AD------------------- 3分
(2)BD+DC≥ AD---------4分
(3)猜想1:BD+DC〈2AD
证明:把 绕点A顺时针旋转 ,得到
则有 , DC=EB,∠ACD=∠ABE---------5分
∵∠BAC+∠BDC=180º∴∠ABD+∠ACD=180º
当2<t<4时,S=4t-8………………………………7分(各1分)
八、解答题(本题满分7分)
24.(1)证明:把 绕点A瞬时针旋转 得到 ,连接ED,------1分
则有 ,DC=EB
∵AD=AE, ∴ 是等腰直角三角形
∴DE= AD ------------------2分
在 中,BD+EB>DE
.………………………………………………………5分
14.解:
= ……………………………………2分
= ……………………………………3分
∵ =0
∴ ……………………………………4分
初三延庆数学一模试卷答案

一、选择题(每题3分,共30分)1. 若a、b、c是等差数列,且a=2,b=4,c=6,则公差d等于:A. 1B. 2C. 3D. 4答案:B. 2解析:由等差数列的性质,得d = b - a = 4 - 2 = 2。
2. 若函数f(x) = 2x - 1,则f(3)的值为:A. 5B. 6C. 7D. 8答案:C. 7解析:将x = 3代入函数f(x),得f(3) = 23 - 1 = 6 - 1 = 7。
3. 在直角坐标系中,点A(2,3),点B(-1,2)的中点坐标为:A. (1,2.5)B. (1,2)C. (3,2)D. (2,2.5)答案:A. (1,2.5)解析:中点坐标为两点坐标的平均值,即( (2 + (-1)) / 2, (3 + 2) / 2 ) = (1, 2.5)。
4. 下列选项中,不是等比数列的是:A. 2, 4, 8, 16, 32, ...B. 1, 1/2, 1/4, 1/8, ...C. 1, 3, 9, 27, 81, ...D. 0, 0, 0, 0, ...答案:D. 0, 0, 0, 0, ...解析:等比数列的定义是任意两项的比值相等,而0与任何数的比值都是0,因此D选项不是等比数列。
5. 已知三角形ABC的边长分别为a、b、c,且满足a+b+c=12,则三角形ABC的最大角为:A. 60°B. 90°C. 120°D. 180°答案:B. 90°解析:根据三角形的性质,任意两边之和大于第三边,且等腰三角形两边相等时,顶角最大。
当a=b=c时,三角形ABC为等边三角形,最大角为60°。
由于a+b+c=12,且三角形ABC不是等边三角形,故最大角小于60°,只有90°符合条件。
二、填空题(每题4分,共40分)6. 若x^2 - 5x + 6 = 0,则x的值为_________。
2012北京延庆中考一模数学(含解析)

B. 86 103 ) .
3 4
C. 8.6 104
D. 8.6 105
3.下列运算中正确的是( A. a a a
3 2 6
B. ( a ) a 7
C. a 6 a 3 a 2
D. a5 a5 2a5
4.一个布袋中有 4 个除颜色外其余都相同的小球,其中 3 个白球, 1 个红球.从袋中任意摸出 1 个 球是白球的概率是( A.
19.已知:如图,在 △ABC 中, AB BC , D 是 AC 中点, BE 平分 ABD 交 AC 于点 E ,点 O 是
AB 上一点,⊙ O 过 B 、 E 两点,交 BD 于点 G ,交 AB 于点 F .
( 1 )求证: AC 与⊙ O 相切; ( 2 )当 BD 6 , sin C
8 / 16
2012 年北京延庆中考一模数学试卷答案
一、选择题(本题共 32 分,每小题 4 分) 题号 答案 1 B 2 C 3 D 4 A 5 D 6 B 7 C 8 A
二、填空题(本题共 16 分,每小题 4 分) 题号 答案 9
x≥3
10
a( x 2)( x 2)
11
y ( x 1)2 3
3 时,求⊙ O 的半径. 5
4 / 16
五、解答题(本题满分 6 分) 20. 2010 年 4 月 14 日青海玉树发生 7.1 级地震,地震灾情牵动全国人民的心.某社区响应政府的 号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分 捐款户数进行分组统计(统计表如下) ,数据整理成如图所示的不完整统计图.已知 A 、 B 两 组捐款户数直方图的高度比为 1: 5 ,请结合图中相关数据回答下列问题.
[数学]2012年北京各城区中考一模数学试题汇编
![[数学]2012年北京各城区中考一模数学试题汇编](https://img.taocdn.com/s3/m/e0e170791ed9ad51f01df2f2.png)
2012年北京各城区一模试题汇编第8题汇总:1.(12海淀一模)2.(12西城一模)对于实数c 、d ,我们可用min{ c ,d }表示c 、d 两数中较小的数,如min{3,1-}=1-.若关于x 的函数y = min{22x ,2()a x t -}的图象关于直线3x =对称,则a 、t 的值可能是A .3,6B .2,6- C.2,6 D .2-,63.(12丰台一模)如图,矩形ABCD 中,AB =3,BC =5,点P 是BC 边上的一个动点(点P 不与点B 、C 重合),现将△PCD 沿直线PD 折叠,使点C 落到点C’处;作∠BPC’的角平分线交AB 于点E .设BP =x ,BE =y ,则下列图象中,能表示y 与x 的函数关系的图象大致是A .B .C .D .E PC’A DBCA 、CA第8题图D7.(12延庆一模) 将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的A .面CDHEB .面BCEFC .面ABFGD .面ADHG8.(12房山一模) 如图,梯形ABCD 中,AB ∥CD ,∠A =30°,∠B =60°,AD =32,CD =2,点P 是线段AB 上一个动点,过点P 作PQ ⊥AB 于P ,交其它边于Q ,设BP 为x ,△BPQ 的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( ).xy 6312O xy 6312O A Bxy 6312O xy 6312O C D9.(12密云一模)在正方体的表面上画有如图⑴中所示的粗线,图⑵是其展开图的示意图,但只在A 面上画有粗线,那么将 图⑴中剩余两个面中的粗线画入图⑵中,画法正确的是10.(12通州一模)如图,在平行四边形ABCD中,AC = 4,BD = 6,P是BD上的任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F.设BP=x,EF=y,则能大致反映y与x之间关系的图象为()A B C D11.(12顺义一模)12.(12东城一模)如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD—DC—CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是A B C D13.(12朝阳一模)已知关于x 的一元二次方程02=++n mx x 的两个实数根分别为a x =1,b x =2(b a <),则二次函数n mx x y ++=2中,当0<y 时,x 的取值范围是 A .a x < B .b x > C .b x a << D .a x <或b x >第12题汇总:1.(12海淀一模)2.(12西城一模)如图,直角三角形纸片ABC 中,∠ACB =90°,AC=8,BC =6.折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别为D 、E . (1) DE 的长为 ;(2) 将折叠后的图形沿直线AE 剪开,原纸片被剪成三块,其中最小一块的面积等于 .3.(12丰台一模)在数学校本活动课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A 出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D ,第二次逆时针方向跳2步到达顶点B ,第三次顺时针方向跳3步到达顶点C ,第四次逆时针方向跳4步到达顶点C ,… ,以此类推,跳动第10次到达的顶点是 ,跳动第2012次到达的顶点是 .ADCB4.(12石景山一模)一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):则第4行中的最后一个数是 ,第n 行中共有 个数, 第n 行的第n 个数是 .5.(12昌平一模)己知□ABCD 中,AD =6,点E 在直线AD 上,且DE =3,连结BE 与对角线AC 相交于点M ,则MCAM= .6.(12平谷一模)abc 是一个三位的自然数,已知195abc ab a --=,这个三位数是_____________;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果abcd 是一个四位的自然数,且2993abcd abc ab a ---=那么,这个四位数是_____________.7.(12延庆一模) 将1、2、3、6按右侧方式排列.若规定(m,n )表示第m 排从左向右第n 个数,则(7,3)所表示的数是 ;(5,2)与(20,17)表示的两数之积是111122663263323第1排第2排第3排第4排第5排8.(12房山一模)如图,已知Rt △ABC 中,∠ACB =90°,AC =6,BC = 8,过直角顶点C 作CA 1⊥AB ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直作下去,得到了一组线段CA 1,A 1C 1,C 1A 2,A 2C 2,…,A n C n ,则A 1C 1= ,A n C n = .9.(12密云一模)在∠A (0°<∠A <90°)的内部画线段,并使线段的两端点分别落在角的两边AB 、AC 上,如图所示,从点A 1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A 1A 2为第1条线段.设AA 1=A 1A 2=A 2A 3=1,则∠A = ;若记线段A 2n-1A 2n 的长度为a n (n 为正整数),如A 1A 2=a 1,A 3A 4=a 2,则此时a 2= ,a n = (用含n 的式子表示).10.(12通州一模)已知如图,△ABC 和△DCE 都是等边三角形,若△ABC 的边长为1,则△BAE 的面积是 .四边形ABCD 和四边形BEFG 都是正方形,若正方形ABCD 的边长为4,则△FAC 的面积是 .……如果两个正多边形ABCDE …和BPKGY …是正n (n ≥3)边形,正多边形ABCDE …的边长是2a ,则△KCA 的面积是 .(结果用含有a 、n 的代数式表示)ABCA 1A 2A 3A 4A 5 C 1 23 4 5 12题图第12题图E11.(12顺义一模)12.(12东城一模) 如图,正方形ABCD 的边长为10,内部有6个全等的正方形,小正方形的顶点E 、F 、G 、H 分别落在边AD 、AB 、BC 、CD 上,则DE 的长为 .13.(12朝阳一模)如图,在正方形ABCD 中,AB =1,E 、F 分别是BC 、CD 边上点,(1)若CE =12CB ,CF =12CD ,则图中阴影部分的面积是 ;(2)若CE =1n CB ,CF =1nCD ,则图中阴影部分的面积是 (用含n 的式子表示,n 是正整数).第22题汇总: 1.(12海淀一模)A2.(12西城一模)阅读下列材料:问题:如图1,在正方形ABCD内有一点P,PA=5,PB=2,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.请你参考小明同学的思路,解决下列问题:(1) 图2中∠BPC的度数为;(2) 如图3,若在正六边形ABCDEF内有一点P,且P A=132,PB=4,PC=2,则∠BPC的度数为,正六边形ABCDEF的边长为.图1 图3CB A D3.(12丰台一模) 将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼 成一个等腰三角形(不能有重叠和缝隙).小明的做法是:如图1所示,在矩形ABCD 中,分别取AD 、AB 、CD 的中点P 、E 、F ,并沿直线PE 、PF 剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2). (1)在图3中画出另一种剪拼成等腰三角形的示意图;(2)以矩形ABCD 的顶点B 为原点,BC 所在直线为x 轴建立平面直角坐标系(如图4),矩形ABCD 剪拼后得到等腰三角形△PMN ,点P 在边AD 上(不与点A 、D 重合),点M 、N 在x 轴上(点M 在N 的左边).如果点D 的坐标为(5,8),直线PM 的解析式为=y kx b ,则所有满足条件的k 的值为 .图1 图2 图3图4 备用P E FDAPE FD A4.(12石景山一模)生活中,有人用纸条可以折成正五边形的形状,折叠过程是将图①中.(1)将,若将展开,展开后的平面图形是 ;(2)若原长方形纸条(图①)宽为2cm ,求(1)中展开后平面图形的周长(可以用三角函数表示).5.(12昌平一模) 问题探究:(1)如图1,在边长为3的正方形ABCD 内(含边)画出使∠BPC =90°的一个点P ,保留作图痕迹;(2)如图2,在边长为3的正方形ABCD 内(含边)画出使∠BPC =60°的所有的点P ,保留作图痕迹并简要说明作法;(3)如图3,已知矩形ABCD ,AB =3,BC =4,在矩形ABCD 内(含边)画出使∠BPC =60°,且使△BPC 的面积最大的所有点P ,保留作图痕迹.图① 图② 图③图3图2图1A DCBABCDD CBA图1图26.(12平谷一模)如图①,在矩形ABCD 中,将矩形折叠,使点B 落在AD (含端点)上,落点记为E ,这时折痕与边BC 或边CD (含端点)交于点F .然后再展开铺平,则以B E F 、、为顶点的BEF △称为矩形ABCD 的“折痕三角形”.(1)由“折痕三角形”的定义可知,矩形ABCD 的任意一个“折痕BEF △”一定是一个________三角形;(2)如图②,在矩形ABCD 中,24AB BC ==,,当它的“折痕BEF △”的顶点E 位于边AD 的中点时,画出这个“折痕BEF △”,并求出点F 的坐标;(3)如图③,在矩形ABCD 中,24AB BC ==,.当点F 在OC 上时,在图③中画出该矩形中面积最大的“折痕BEF △”,并直接写出这个最大面积.7.(12延庆一模)阅读下面材料:小红遇到这样一个问题,如图1:在△ABC 中,AD ⊥BC ,BD=4,DC=6,且∠BAC=45°,求线段AD 的长.图3小红是这样想的:作△ABC 的外接圆⊙O ,如图2:利用同弧所对圆周角和圆心角的关系,可以知道∠BOC=90°,然后过O 点作OE ⊥BC 于E ,作OF ⊥AD 于F ,在Rt △BOC 中可以求出⊙O 半径及 OE ,在Rt △AOF 中可以求出AF,最后利用AD=AF+DF 得以解决此题。
2012北京市延庆县初三(一模)数 学

2012北京市延庆县初三(一模)数学一、选择题:(共8道小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的,请将所选答案在答题卡相应位置涂黑.1.(4分)﹣3的绝对值是()A.﹣3 B.3 C.D.2.(4分)截至2009年底,我国铁路营业里程达到86 000公里,跃居世界第二位.将86 000用科学记数法表示为()A.0.86×105 B.86×103C.8.6×104D.8.6×1053.(4分)下列运算中正确的是()A.a3a2=a6B.(a3)4=a7C.a6÷a3=a2D.a5+a5=2a54.(4分)一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是()A.B.C.D.5.(4分)若如图是某几何体的三视图,则这个几何体是()A.直棱柱B.球C.圆柱D.圆锥6.(4分)若,则(﹣xy)2的值为()A.﹣6 B.9 C.6 D.﹣97.(4分)如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为()A.20°B.40°C.50°D.60°8.(4分)将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的()二、填空题(共4道小题,每小题4分,共16分)9.(4分)若式子有意义,则实数x的取值范围是.10.(4分)分解因式:ax2﹣4a=.11.(4分)用配方法把y=x2+2x+4化为y=a(x+h)2+k的形式为.12.(4分)将1、、、按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(7,3)所表示的数是;(5,2)与(20,17)表示的两数之积是.三、解答题(共5道小题,每小题5分,共25分)13.(5分)计算:.14.(5分)当2x2+3x+1=0时,求(x﹣2)2+x(x+5)+2x﹣8的值.15.(5分)求不等式组的整数解.16.(5分)已知:如图,▱ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.求证:AB=AF.17.(5分)如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,直线AB与y轴交于点C.(1)求反比例函数和一次函数的关系式;(2)求△AOC的面积;(3)求不等式kx+b﹣<0的解集.(直接写出答案)四、解答题(共2道小题,共10分)18.(5分)如图,小明在楼上点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为12m.求旗杆的高度.19.(5分)已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sinC=时,求⊙O的半径.五、解答题(本题满分6分)20.(6分)2010年4月14日青海玉树发生7.1级地震,地震灾情牵动全国人民的心.某社区响应恩施州政府的号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A 、B 两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.捐款分组统计表:(1)A 组的频数是多少?本次调查样本的容量是多少? (2)求出C 组的频数并补全直方图.(3)若该社区有500户住户,请估计捐款不少于300元的户数是多少?六、解答题(共2道小题,共9分) 21.(5分)列方程(组)解应用题:进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:组别 捐款额(x )元 A 10≤x <100 B 100≤x <200 C200≤x <300 D 300≤x <400 Ex ≥40022.(4分)阅读下面材料:小红遇到这样一个问题,如图1:在△ABC中,AD⊥BC,BD=4,DC=6,且∠BAC=45°,求线段AD的长.小红是这样想的:作△ABC的外接圆⊙O,如图2:利用同弧所对圆周角和圆心角的关系,可以知道∠BOC=90°,然后过O点作OE⊥BC于E,作OF⊥AD于F,在Rt△BOC中可以求出⊙O半径及OE,在Rt△AOF中可以求出AF,最后利用AD=AF+DF 得以解决此题.请你回答图2中线段AD的长.参考小红思考问题的方法,解决下列问题:如图3:在△ABC中,AD⊥BC,BD=4,DC=6,且∠BAC=30°,则线段AD 的长.七、解答题(本题满分7分)23.(7分)在平面直角坐标系xOy中,二次函数y1=mx2﹣(2m+3)x+m+3与x轴交于点A、点B(点A在点B的左侧),与y轴交于点C(其中m>0).(1)求:点A、点B的坐标(含m的式子表示);(2)若OB=4•AO,点D是线段OC(不与点O、点C重合)上一动点,在线段OD的右侧作正方形ODEF,连接CE、BE,设线段OD=t,△CEB的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.24.(7分)如图1,已知:已知:等边△ABC,点D是边BC上一点(点D不与点B、点C重合),求证:BD+DC>AD.下面的证法供你参考:把△ACD绕点A顺时针旋转60°得到△ABE,连接ED,则有△ACD≌△ABE,DC=EB,∵AD=AE,∠DAE=60°,∴△ADE是等边三角形,∴AD=DE.在△DBE中,BD+EB>DE,即:BD+DC>AD实践探索:(1)请你仿照上面的思路,探索解决下面的问题:如图3,点D是等腰直角三角形△ABC边上的点(点D不与B、C重合).求证:BD+DC>AD.(2)如果点D运动到等腰直角三角形△ABC外或内时,BD、DC和AD之间又存在怎样的数量关系?直接写出结论.创新应用:(3)已知:如图4,等腰△ABC中,AB=AC,且∠BAC=α(α为钝角),D是等腰△ABC外一点,且∠BDC+∠BAC=180°,BD、DC与AD之间存在怎样的数量关系?写出你的猜想,并证明.25.(8分)在平面直角坐标系xOy中,已知二次函数y1=ax2+3x+c的图象经过原点及点A(1,2),与x轴相交于另一点B.(1)求:二次函数y1的解析式及B点坐标;(2)若将抛物线y1以x=3为对称轴向右翻折后,得到一个新的二次函数y2,已知二次函数y2与x轴交于两点,其中右边的交点为C点.点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);①当点E在二次函数y1的图象上时,求OP的长.②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,同时线段OC上另一个点Q从C点出发向O点做匀速运动,速度为每秒2个单位长度(当Q点到达O点时停止运动,P点也同时停止运动).过Q点作x轴的垂线,与直线AC交于G点,以QG为边在QG的左侧作正方形QGMN(当Q点运动时,点G、点M、点N也随之运动),若P点运动t秒时,两个正方形分别有一条边恰好落在同一条直线上(正方形在x轴上的边除外),求此刻t 的值.数学试题答案一、选择题:(共8道小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的,请将所选答案在答题卡相应位置涂黑.1.【解答】|﹣3|=3.故﹣3的绝对值是3.故选:B.2.【解答】86 000=8.6×104.故选C.3.【解答】A、应为a3a2=a3+2=a5,故本选项错误;B、应为(a3)4=a3×4=a12,故本选项错误;C、应为a6÷a3=a6﹣3=a3,故本选项错误;D、a5+a5=(1+1)a5=2a5,正确.故选D.4.【解答】因为一共4个球,其中3个白球,所以从袋中任意摸出1个球是白球的概率是.故选A.5.【解答】俯视图为圆的有球,圆锥,圆柱等几何体,再符合主视图和左视图为三角形的只有圆锥.故选D.6.【解答】∵,∴x﹣1=0,y+3=0,∴x=1,y=﹣3.∴(﹣xy)2=9.故选B.7.【解答】∵EF平分∠CEG,∴∠CEG=2∠CEF又∵AB∥CD,∴∠2=∠CEF=(180°﹣∠1)÷2=50°,故选C.8.【解答】由图1中的红心“”标志,可知它与等边三角形相邻,折叠成正方体是正方体中的面CDHE.故选A.二、填空题(共4道小题,每小题4分,共16分)9.【解答】根据题意,得x﹣3≥0,解得,x≥3;故答案是:x≥3.10.【解答】ax2﹣4a,=a(x2﹣4),=a(x+2)(x﹣2).11.【解答】y=x2+2x+4=(x2+2x+1)+3=(x+1)2+3,即y=(x+1)2+3.故答案为:y=(x+1)2+3.12.【解答】(7,3)表示第7排从左向右第3个数,可以看出奇数排最中间的一个数都是1,1+2+3+4+5+6+3=24,24÷4=6,则(7,3)所表示的数是;从图示中知道,(5,2)所表示的数是;∵第19排最后一个数的序号是:1+2+3+4+…+19=190,则(20,17)表示的是第190+17=207个数,207÷4=51…3,∴(20,17)表示的数是.∴(5,2)与(20,17)表示的两数之积是:×=3.故答案为:;.三、解答题(共5道小题,每小题5分,共25分)13.【解答】原式=3﹣2×+2+1=2+3.14.【解答】∵2x2+3x+1=0∴2x2+3x=﹣1∴(x﹣2)2+x(x+5)+2x﹣8=x2﹣4x+4+x2+5x+2x﹣8=2x2+3x﹣4=﹣1﹣4=﹣5.15.【解答】由①得;(2分)由②得x<2.(3分)∴此不等式组的解集为.(4分)∴此不等式组的整数解为0,1.(5分)16.【解答】证明:∵四边形ABCD是平行四边形,∴AB∥CD且AB=CD.∴∠F=∠2,∠1=∠D.∵E为AD中点,∴AE=ED.在△AEF和△DEC中∴△AEF≌△DEC.∴AF=CD.∴AB=AF.17.【解答】(1)∵B(1,4)在反比例函数y=上,∴m=4,又∵A(n,﹣2)在反比例函数y=的图象上,∴n=﹣2,又∵A(﹣2,﹣2),B(1,4)是一次函数y=kx+b的上的点,联立方程组解得,k=2,b=2,∴,y=2x+2;(2)过点A作AD⊥CD,∵一次函数y=kx+b的图象和反比例函数y=的图象的两个交点为A,B,联立方程组解得,A(﹣2,﹣2),B(1,4),C(0,2),∴AD=2,CO=2,∴△AOC的面积为:S=AD•CO=×2×2=2;(3)由图象知:当0<x<1和﹣2<x<0时函数y=的图象在一次函数y=kx+b图象的上方,∴不等式kx+b﹣<0的解集为:0<x<1或x<﹣2.18.【解答】过A作AE⊥BC于E.∵AD∥CE,∴Rt△ACE中,CE=AD=12m,∠CAE=60°,∴AE=CE÷tan60°=4.Rt△AEB中,AE=4,∠BAE=30°,∴BE=AE•tan30°=4.BC=BE+CE=4+12=16.故旗杆的高度为16米.19.【解答】(1)证明:连接OE,∵AB=BC且D是AC中点,∴BD⊥AC,∵BE平分∠ABD,∴∠ABE=∠DBE,∵OB=OE∴∠OBE=∠OEB,∴∠OEB=∠DBE,∴OE∥BD,∵BD⊥AC,∴OE⊥AC,∵OE为⊙O半径,∴AC与⊙O相切.(2)解:∵BD=6,sinC=,BD⊥AC,∴BC=10,∴AB=BC=10,设⊙O 的半径为r,则AO=10﹣r,∵AB=BC,∴∠C=∠A,∴sinA=sinC=,∵AC与⊙O相切于点E,∴OE⊥AC,∴sinA===,∴r=,答:⊙O的半径是.五、解答题(本题满分6分)20.【解答】(1)A组的频数是:(10÷5)×1=2,调查样本的容量是:(10+2)÷(1﹣40%﹣28%﹣8%)=50(2)C组的频数是:50×40%=20,(3)估计捐款不少于300元的户数是:500×(28%+8%)=180户.六、解答题(共2道小题,共9分)21.【解答】设原来每天加固x米,根据题意,得:+=9.去分母,得:1200+4200=18x.(或18x=5400)解得:x=300.检验:当x=300时,2x≠0(或分母不等于0).∴x=300是原方程的解.答:该地驻军原来每天加固300米.22.【解答】(1)∵OE⊥BC于E,∴EC=BC=(BD+CD)=(4+6)=5,又∵∠BOC=2∠BAC=2×45°=90°,∴∠COE=45°,∴直角△OEC中,OC=CE=5,在直角△AOF中,OF=BE﹣BD=5﹣4=1,AF==7,∴AD=AF+FD=7+5=12,故答案是:12;(2)过O点作OE⊥BC于E,作OF⊥AD于F,在Rt△BOC中可以求出⊙O半径及OE,与(1)的解法相同,可以得到:EC=5,∠EOC=30°,则OE=EC=5,OC=2EC=10,在直角△AOF中,利用勾股定理可以得到:AF=3,则AD=AF+FD=3+5.七、解答题(本题满分7分)23.【解答】(1)二次函数y1=mx2﹣(2m+3)x+m+3中,令y=0,得:0=mx2﹣(2m+3)x+m+3,解得:x1=1,x2=;∴A(1,0)、B(,0).(2)由(1)知:OB=,OA=1,已知OB=4•OA,得:=4,解得:m=1;在Rt△OBC中,OB=OC=4,所以∠OBC=45°;①当0<t<2时,如图①;由于四边形ODEF是正方形,所以OF=EF=t,BF=OB﹣OF=4﹣t;∴GF=BF=4﹣t,GE=GF﹣EF=4﹣t﹣t=4﹣2t;∴S=GE•OB=8﹣4t;②当2<t<4时,如图②;同①可得:GE=2t﹣4;S=GE•OB=4t﹣8;综上,得:当0<t<2时,S=8﹣4t;当2<t<4时,S=4t﹣8.八、解答题(本题满分7分)24.【解答】(1)证明:把△ACD绕点A顺时针旋转90°得到△ABE,连接ED则有△ACD≌△ABE,DC=EB∵AD=AE,∠DAE=90°∴△ADE是等腰直角三角形∴DE=AD在△DBE中,BD+EB>DE,即:BD+DC>AD;(2)把△ABD旋转,使AB与AC重合,然后绕AC旋转,得到△ACD′,则BD=CD′,在△CDD′中,CD+CD′>DD′,即BD+CD>DD′,∵△ADD′是钝角三角形,则DD′>AD当D运动到B的位置时,DD′=BC=AD.∴BD+DC≥AD;(3)猜想1:BD+DC<2AD证明:把△ACD绕点A顺时针旋转α,得到△ABE则有△ACD≌△ABE,DC=EB,∠ACD=∠ABE ∵∠BAC+∠BDC=180°∴∠ABD+∠ACD=180°∴∠ABD+∠ABE=180°即:E、B、D三点共线.∵AD=AE,∴在△ADE中,AE+AD>ED,即BD+DC<2AD.九、解答题(本题满分8分)25.【解答】(1)∵二次函数y1=ax2+3x+c的图象经过原点及点A(1,2),∴将(0,0),代入得出:c=0,将(1,2)代入得出:a+3=2,解得:a=﹣1,故二次函数解析式为:y1=﹣x2+3x,∵图象与x轴相交于另一点B,∴0=﹣x2+3x,解得:x=0或3,则B(3,0);(2)①由已知可得C(6,0)如图:过A点作AH⊥x轴于H点,∵DP∥AH,∴△OPD∽△OHA,∴=,即=,∴PD=2a,∵正方形PDEF,∴E(3a,2a),∵E(3a,2a)在二次函数y1=﹣x2+3x的图象上,∴a=;即OP=.②如图1:当点F、点N重合时,有OF+CN=6,∵直线AO过点(1,2),故直线解析式为:y=2x,当OP=t,则AP=2t,∵直线AC过点(1,2),(6,0),代入y=ax+b,,解得:,故直线AC的解析式为:y=﹣x+,∵当OP=t,QC=2t,∴QO=6﹣2t,∴GQ=﹣(6﹣2t)+=t,即NQ=t,∴OP+PN+NQ+QC=6,则有3t+2t+t=6,解得:t=;如图2:当点F、点Q重合时,有OF+CQ=6,则有3t+2t=6,解得:t=;如图3:当点P、点N重合时,有OP+CN=6,则有t+2t+t=6,解得:t=,如图4:当点P、点Q重合时,有OP+CQ=6,则有t+2t=6,解得:t=2.故此刻t的值为:t1=,t2=,t3=,t4=2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6题图
C
A
B
O
E D
数学练习1 姓名_____________分数_________ 一、选择题:(共8个小题,每小题4分, 共32分)
在下列每小题给出的四个选项中,只有一个是符合题目要求的............,请在答题纸上将所选项涂黑..........。
1.2-的倒数是 A . 2- B . 2 C .2
1- D .
2
1
2.大量事实证明,治理垃圾污染刻不容缓.据统计,全球每分钟约有8500000吨污水排入江河湖海,
这个排污量用科学记数法表示是
A .6
105.8⨯吨 B .5
105.8⨯吨 C .7
105.8⨯吨
D .6
1085⨯吨
3.若两圆的半径分别是cm 1和cm 3,圆心距为cm 4,则这两圆的位置关系是
A .内切
B .相交
C .外切
D .外离
4.不等式组 1
103
20.x x ⎧+>⎪⎨⎪-⎩
,
≥的解集是A -3
1
<x ≤2 B .-3<x ≤2 C .x ≥2 D .x <-3
5.为了解居民节约用水的情况,增强居民的节水意识,下表是某个单元的住户当月用水量的调查结果:
则关于这12户居民月用水量(单位:方),下列说法错误..
的是 A .中位数是6 B .众数是6 C .极差是8 D .平均数是5
6.如图,AB 是⊙O 的直径,弦AB CD ⊥于点E , 30=∠CDB , ⊙O 的半径 为cm 3,则弦CD 的长为
A .cm 3
B .cm 2
3
C .cm 32
D .cm 9
7.从1~9这九个自然数中作任取一个,是2的倍数的概率是 A .
9
2 B .
9
4 C .
9
5 D .
3
2
8.定义新运算:1()(0)a a b a b a
a b b b
⎧-⎪
⊕=⎨->≠⎪⎩且≤,则函数3y x =⊕的图象大致是
二、填空题(共4个小题,每小题4分,共16分)
9.把多项式x x x 24223+-分解因式的结果是 . 10.如图,在菱形ABCD 中,对角线4=AC , 120=∠BAD ,
则菱形ABCD 的周长为 .
11.若二次函数52++=bx x y 配方后为k x y +-=2)2(,则b 、k 的值分别 . 12.在平面直角坐标系中,正方形ABCD 的位置如图所示,
点A 的坐标为)0,1(,点D 的坐标为)2,0(. 延长CB 交x 轴于点1A ,作正方形C C B A 111; 延长11B C 交x 轴于点2A ,作正方形1222C C B A … 按这样的规律进行下去,第3个正方形的面积为________; 第n 个正方形的面积为_____________(用含n 的代数式表示). 三、解答题(共6个小题,每小题5分,共30分)
13.计算: ︒+-+---45cos 2|2|)2011(2
1
(02π 14.解方程:
x x +1 + 2
x -1
=1
15.如图,ABC ∆中, 45=∠=∠BAC ABC ,点P 在AB 上,CP AD ⊥于点D ,
E CP BE 延长线于点⊥,求证:BE CD =
16.先化简:1
4
4)11
3(2
++-÷
+-+a a a a a ,并从0,1-,2中选一个合适的数作为a 的值代入求值.
D .
第8题图
C .
B .
A .
第10题图
第15题图
第12题图
BC=BE 17.已知:如图,一次函数m x y +=
3与反比例函数x
y 33=
的图象在第一象限的交点为),3(n A .
(1)求m 与n 的值;
(2)设一次函数的图像与x 轴交于点B ,
连接OA ,求BAO ∠的度数.
18.列方程或方程组解应用题:
为了有效的使用电力资源,电业局对峰谷用电进行试点:每天008:
--0022:,用电 价格是在原电价的基础上每千瓦时上浮30.0元(称“峰电”价),0022:
--次日008:,用电价格是在原电价的基础上每千瓦时下浮25.0元(称“谷电”)。
小林家在5月份使用“峰电”千瓦时30,使用“谷电”千瓦时70,按分段电价付电费92.37元,
(1)问小林家该月支付的峰电、谷电价每千瓦时各是多少元? (2)如不使用分段电价结算,5月份小林家将多支付电费多少元?
四、解答题(共4个小题,第19,20题各5分,第21题6分,第22题4分,共20分)
19.如图,在梯形ABCD 中,AB//CD ,2=AB ,4=AD ,=
C tan 3
4,
90=∠=∠DAB ADC ,P 是腰BC 上一个动点(不含点C 、B ),作A P PQ ⊥交CD 于点Q (图
1)(1)求BC 的长与梯形ABCD 的面积;(2)当DQ PQ =时,求BP 的长;(图2)
20.如图,A B 为O ⊙的直径,劣弧,CE //BD ,
连接A E 并延长交B D 于D . 求证:(1)B D 是O ⊙的切线;
(2)若O ⊙的半径为cm 2,cm AC 3=,求的长B D .
B
第20题图
第17题图 第19题图2
Q
P
D C
B
A
Q
P
D C
B
A
第19题图1
B
21.四中的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机
抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
(1)本次问卷调查取样的样本容量为_______,
表中的m 值为_______;n 值为_______.
(2)根据表中的数据计算等级为“非常了解”的频数
在扇形统计图所对应的扇形的圆心角的度数, 并补全扇形统计图;
(3)若该校有学生1500人,请根据调查结果估计这些
学生中“比较了解”垃圾分类知识的人数约为多少?
22.阅读材料:
(1)操作发现:
如图,矩形ABCD 中,E 是AD 的中点,将△ABE ∆沿BE 折叠后得到GBE ∆,且点 G 在矩形
ABCD 内部.小明将BG 延长交DC 于点F ,
认为DF GF =,你同意吗?说明理由. (2)问题解决:
保持(1)中的条件不变,若DF DC 2=,求AB
AD 的值;
(3)类比探求:
保持(1)中条件不变,若nDF DC =,求AB AD 的值.
五、解答题(共3个小题, 23小题7分,24小题8分,25小题7分,共22分)
23.已知关于x 函数k x x k y +-=2)-2(2(1)若此函数的图像与坐标轴只有2个交点,求k 的值.
(2)求证:关于x 的一元二次方程02)-2(2=+-k x x k 必有一个根是1.
第22题图
24.已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12
y x a =
-分别与x 轴,
y 轴相交于B C ,两点,并且与直线A M 相交于点N .
(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则 ; (2)如图1,将N AC △沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,
A N ′与x 轴交于点D ,连结C D ,求a 的值和四边形A D C N 的面积;
(3)在抛物线2
2y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.
25.如图(1),(2)所示,矩形ABCD 的边长6=AB ,4=BC ,点F 在DC 上,2=DF .动点N
M ,分别从点B D ,同时出发,沿射线DA 、线段BA 向点A 的方向运动(点M 可运动到DA 的延长线上),当动点N 运动到点A 时,N M ,两点同时停止运动.连结FN MN FM ,,,
当M N F ,,不在同一条直线时,可得FMN ∆,过FMN ∆三边的中点作PQW ∆.设动点N M ,的速度都是1个单位/秒,N M ,运动的时间为x 秒.试解答下列问题:
(1)说明FMN ∆∽QWP ∆;
(2)设40≤≤x (即M 从D 到A 运动的时间段).试问x 为何值时,PQW ∆为直角三角形?当x 在何范围时,PQW ∆不为直角三角形?
(3)问当x 为何值时,线段MN 最短?求此时MN 的值.
第24题图1
备用图
M
第25题图1。
