Communications and Signal Processing Group, CENTIA
电子类通信类和计算机类EI期刊(大部分免费)

电子类通信类和计算机类ei期刊(1)Multidimensional Systems and Signal Processing(2)Circuits, Systems and Signal Processing(3)Wireless Personal Communications(4)International Journal of Adaptive Control and Signal Processing(5)Journal of Signal Processing Systems(6)International Journal of Electronics and Communication(7)Journal of Circuits, Systems and Computers(8)Progress in Electromagnetics Research (PIER)(9)Canadian Journal of Electrical and Computer Engineering(10)ETRI Journal(11)IEEE Antennas and Wireless Propagation Letters(12)Signal, Image and Video Processing(13)Wireless Communicatiosn and Mobile Computings***(1)IET Radar Sonar and Navigation(2)IET Signal Processing(3)IET Communications(4)Signal Processing (Elsevier, EURASIP)(5)Eurasip Journal on Advances in Signal Processing (Hindawi)(6)Digital Signal Processing (A Review Journal)(7)IEEE Trans Circuits and Systems(8)IEICE Trans Communications/Fundamentals of Electronics, Communications and Computer Sciences(9)European Trans. Telecommunications(10)Annals of Telecommunications*****(1)IEEE Trans Communications(2)IEEE Trans Signal Processing(3)IEEE Trans Antennas and Propagation(4)IEEE Trans Aerospace and Electronic Systems(5)Electronics Letters(6)IEEE Signal Processing Letters(7)IEEE Communications Letters(8)Radio Science大部分免费------------------------------IEEE communication letter 和electronic letter相对容易IEICE的影响因子太低了,而且版面费出奇的贵,怎么能和IEEE混在一起。
EI会议和期刊(信号处理相关)
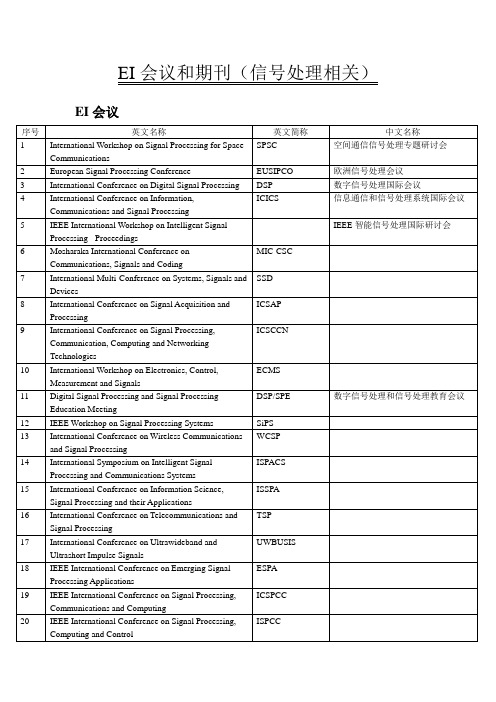
International Workshop on Systems, Signal Processing and their Applications
WoSSPA
28
WSEAS International Conference on Signal Processing
SIP
29
CSI International Symposium on Artificial Intelligence and Signal Processing
ICSCCN
ห้องสมุดไป่ตู้10
International Workshop on Electronics, Control, Measurement and Signals
ECMS
11
Digital Signal Processing and Signal Processing Education Meeting
AISP
30
Asia-Pacific Signal and Information Processing Association Annual Summit and Conference
APSIPA
31
International Symposium on Signals, Systems and Electronics
ISSPA
16
International Conference on Telecommunications and Signal Processing
TSP
17
International Conference on Ultrawideband and Ultrashort Impulse Signals
通讯行业英语词汇

通信测试设备组Communication Test Equipment Group CTEG通信电路芯片Communication Circuit Chip通信管理网Telecommunication Management Network TMN通信控制字段Communication Control Field CCF通信口Com. Port通信量,业务量Amount of Traffic, Traffic通信楼综合定时供给系统Building Integrated Timing Supply BITS通信前置机Communication Front-end Processor通信设备进网Network Access of Communications Equipment通信设备进网质量认证Quality Recognition Certification For Network Access of Communication Equipment通信设施Communication Facilities通信体系结构Communication Architecture通信终端产品Telecom Terminal Product通信阻断Communication Block通讯板卡Communication Card通讯电缆Communication Cable通用Universal, General,Common通用标记语言Generalized Markup Language GML通用参数Common parameter通用插座,万能插座Universal Socket通用分组无线业务General Packet Radio Service GPRS通用个人通信Universal Personal Telecommunications UPT通用接入码Universal Access Number UAN通用时隙交叉连接板General Timeslot Cross-connection GTC通用式的All-Purpose通用移动通讯系统Universal Mobile Telecommunication System UMTS通用中间格式Common Intermediate Format CIF通用总线General Bus GB通针和毛刷(协助焊接)Needle and Hair Brush(Soldering Aid)通知Notification N通知机Announcement Machine ANM通知消息Announcement Message通知音Announcement Tone同波道干扰In-Channel Interference同步synchronization同步保持模式Synchronous holdover mode同步不可用do not use for synchronization DUS同步传递模式Synchronous Transfer Mode STM同步传输Synchronous Transmission同步传输模式synchronous transfer module STM同步传送模块第N级Synchronous Transport Module Level N STM-N同步传送信号等级1 synchronous transport signal level 1 STS-1同步的Synchronous同步定时Synchronization Timing STM同步定时发生器Synchronous Timing Generator STG同步复用器Synchronous Multiplexer SM同步光网络Synchronous Optical Network SONET同步净负荷包络Synchronous Payload Envelope SPE同步设备定时发生器Synchronous Equipment Timing Generator SETG同步设备定时物理接口Synchronous Equipment Timing Physical Interface SETPI同步设备定时源Synchronous Equipment Timing Source SETS同步设备管理功能Synchronous Equipment Management Function SEMF同步时钟Synchronization Clock同步数字系列Synchronous Digital Hierarchy SDH同步数字系列交叉Synchronous Digital hierarchy Cross-Connect SDXC同步网Synchronization Network同步物理接口SDH physical interface SPI同步系统Synchronization System同步线路管理单元信号处理板Administrative Unit Signal Processing ASP同步信息骨干系统Synchronous information Bone System SBS同步序列丢失loss of sequence synchronisation LSS同步源Synchronous source同步振荡器板Synchronization Oscillator Board同步装置Synchronization Equipment同步状态标志synchronization status marker SSM同抢Simultaneously Holding同抢,双占用,双重占线Simultaneous hold同相Cophase同心圆蜂窝Concentric Cell同信[频]道干扰Co-channel interference同信道,同波道Co-Channel同一PLMN内GPRS支持节点间的接口Interface between GPRS Support Nodes (GSNs) within a PLMN Gn interface同轴电缆Coaxial Cable同轴电缆接口板,同轴板Coaxial cable interface board同轴电缆压接钳Coaxial cable press plier同轴连接器Coaxial connector铜缆分布式数据接口Copper Distributed Data Interface CDDI统计日志数据库Statistic Log Database统计时分复用Statistic Time Division Multiplexing STDM统计资料,统计数据Statistical Data统一编码United Coding统一模型,一致化模型United Model投币电话Coin Telephone投币箱,投币电话机Coin Box投标,设标Bidding投标工程物料Bidding Project Materials投标者Bidder投票式信令poll投入运行Put into operation突发传输Burst Transmission突发脉冲序列周期Burst Period BP图标,图像符号Icon图例,图注Legend图形交换格式Graphics Interchange Format GIF图形设备接口Graphic Device Interface GDI图形用户界面Graphic User Interface GUI推荐标准Recommended Standard退席Off Attendance吞吐率Throughput托盘(放置移动机柜用) Pallet脱焊Loose Weld拓扑结构Topology Structure外部成套External Suite外部单根External Single外部告警模块External Alarm Module EAM外部接口External Interface PI外部接入设备External Access Equipment EA外部设备识别寄存器External Identification Register EIR外存储器External Memory外基准输入接口板Line Clock Interface Board LCI外壳Shell外围处理器Peripheral Processor PP外围环境参量检测Peripheral Environment Parameter Detection PEPD 外围设备Peripheral Equipment外线External line, Subscriber line外线测试Loop test外线测试,环路测试External Line Test, Loop Test外线电容(值)Loop Capacitance外线电容测试Loop Capacitance Test外线电压测试Loop V oltage Test外线呼叫External Call外置式External弯角件Angle Support万位千位MyriabitKilobit万用表Multimeter网关Gateway网关GPRS支持节点Gateway GPRS Support Node GGSN网关到网关协议Gateway-Gateway Protocol GGP网关网元Gateway Network Element GNE网关移动业务交换中心Gateway Mobile Switching Center GMSC网关移动业务交换中心Gateway Mobile Switching Center GMSC网关移动业务交换中心Gateway Mobile-services Switching Center GMSC网管Network Management NM网管设备Network Management Equipment网管中心Network Management Centers NMC网卡Network Adapter网络安全性,网络保密Network Security网络操作系统Network Operating System NOS网络操作中心Network Operations Center NOC网络打印机Network Printer网络单元Network element NE网络单元功能Network Element Function NEF网络地址Network Address NA网络电视Web TV网络独立时钟Network Independent Clock NIC网络管理功能Network Management Function NMF网络管理系统Network Management System NMS网络规划和优化测量设备Network Planning & Optimizing Measuring Equipment 网络规模Network Size网络间接口Inter-Network Interface NNI网络监视和测试单元Network Supervision and Test Unit NSTU网络接口单元Network Interface Unit NIU网络接入服务提供商Internet Service Provider ISP网络结点接口Network Node Interface NNI网络礼仪Netiquette网络配件Network Fittings网络驱动器Network Driver NETD网络设备Network Equipment网络实体Network Entity NE网络文件系统Network File System NFS网络用户身份Network User Identity NUI网络运营商Network Operator网络指示Network Indicator NI网络终端Network Terminal NT网平面Network Plane网桥Bridge网外呼叫Off-Net Calling ONC网外接入Off-Net Access OFA网线Network Cable网线接头Network Cable Connector网元Network Element NE网元功能Network Element Function NEF网元图标NE icon网状网Mesh Network往返时间,环程时间Round-Trip Time微波Microwave MW微波接力通信Microwave Radio Relay Communication微波频段Microwave Frequency Band微处理机Microprocessor ΜP微处理器Microprocessor微动开关Micro Switch微蜂窝Micro cell微微蜂窝(针对室内覆盖而设计)Picocellular/in-building, picocell微微小区Picocell微小区Microcell微型同轴电缆细缆粗缆Minitype coaxial cable Thinnet cable Thicknet cable伪网络标识码Pseudo Network Identification Code PNIC尾纤Tail optical fiber, fiber pigtail卫星电路Satellite Circuit卫星通信Satellite Communication SATCOM卫星同步信号接收板Globe Satellite Positioning Receiver GPR卫星直播Direct Broadcasting Satellite DBS未安装Uninstalled未来公用陆地移动通信系统Future Public Land Mobile Telecommunication System FPLMTS 未准备好接收Receive UN-ready RNR位Bit位(比特)同步Bit Synchronization位串,比特串Bit String位交错,比特交错,比特交织Bit Interleave位图,位映象Bitmap位映射Bit Map位置Position POS位置登记Location Registration位置更新Location Update位置区Location Area LA位置区号Location Area Identity LAI位置区码Location Area Code LAC温补晶振Temperature-compensation Crystal Oscillator温度补偿Temperature Compensation温度补偿晶体振荡器Temperature Compensated Crystal Oscillator温度传感器Temperature Sensor温度控制Temperature Control温度值, 湿度值, 烟雾浓度Temperature, Humidity, Smoke Density温湿度传感器Temperature Humidity Sensor温湿度计Hygrothermograph文档Document DOC文件备份File Backup文件传输协议File Transfer Protocol FTP文件分配表File Allocation Table FAT文件结尾End of File EOF文件压缩实用程序File Compression Utility稳压二极管Zener稳压器Voltage Stabilizer问讯台,查询台Information Desk握手Hand Shaking无编号信息Unnumbered Information UI无错的Error-Free EFS无缝的Seamless无缝连接Seamless Connection无光告警No Light Alarm无呼出权限No Call Out Authority无呼出权限No Call Out Authority无接续控制Signal Connectionless Control SCLC无连接的Connectionless CL无连接宽带数据业务Connectionless Broadband Data Services CBDS 无连接协议Connectionless Protocol无屏蔽扭绞线对Unshielded Twisted Pair UTP无屏蔽双绞线Unshielded Twisted Pair UTP无冗余Non-Redundancy无绳电话Cordless Telephone CT无损耗压缩Lossless Compression无条件呼叫前转Call Forwarding Unconditional CFU无线本地环Wireless Local Loop WLL无线本地环路wireless local loop无线测试设备的射频单元Radio Test Equipment (board) RTE无线测试设备的数字处理单元Radio test device RTD无线电干扰Radio jamming无线电话系统Cordless Telephony System CTS无线分系统指定越区切换Radio sub-system directed handover无线分系统准则Radio sub-system criteria无线杆Radio masts无线基站Wireless Base Station无线接口层3 Radio Interface Layer3 RIL3无线接口协议Radio interface protocols无线接入Wireless Access无线链路管理Radio Link Management RLM无线链路控制Radio Link Control RLC无线数字本地环Wireless Digital Local Loop WDLL无线通信OEM专用物料Special Materials for Wireless OEM Products 无线通信设备Wireless Telecom Equipment无线信道控制器Wireless Channel Controller WCC无线信道群Radio Channel Group RCG无线信令链路Radio Signaling Link RSL无线寻呼系统Radio paging system无线应用协议Wireless Application Protocol WAP无线专用芯片Wireless Special-purpose Chip无线资源Radio Resource RR无线子系统管理Radio Sub-system Management RSM (RR’)无效信元Invalid Cell无应答呼叫前转Call Forwarding No Reply CFNR无应答前转补充业务Call Forwarding on No Reply CFNRy 无源光器件Passive Optical Components无源光网络Passive Optical Network PON无源光网络Passive Optical Network APON无源天线Passive antenna无摘机信号,无拔号音No dial tone五类屏蔽Class 5 Shielding物理层Physical Layer PHY物理平面Physical Plane PP物理软件, 嵌入式软件Embeded Software物理实体Physical Entity PE误码Bit Error误码率Bit error rate BER误码率过大BER Excess误码秒Errored Second ES误码秒率Errored Second Rate ESR误码仪Error Detector吸尘器Cleaner吸锡器Solder Removal Tool膝上型电脑Laptop Computer系统崩溃System Breakdown系统集成中心System Integration Center SIC系统图System Diagram系统误码特性Characteristic of BER in System系统中止System Halt细缆Thinnet Cable下话路Down Channel下拉菜单Pull-Down Menu下拉式列表框Pull down List Box下母线Down Highway DHW下行链路Down Link DNL下一批Next Group/Batch。
专业英语翻译之数字信号处理

Signal processingSignal processing is an area of electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time, to perform useful operations on those signals. Signals of interest can include sound, images, time-varying measurement values and sensor data, for example biological data such as electrocardiograms, control system signals, telecommunication transmission signals such as radio signals, and many others. Signals are analog or digital electrical representations of time-varying or spatial-varying physical quantities. In the context of signal processing, arbitrary binary data streams and on-off signalling are not considered as signals, but only analog and digital signals that are representations of analog physical quantities.HistoryAccording to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the "digitalization" or digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s.[2]Categories of signal processingAnalog signal processingAnalog signal processing is for signals that have not been digitized, as in classical radio, telephone, radar, and television systems. This involves linear electronic circuits such as passive filters, active filters, additive mixers, integrators and delay lines. It also involves non-linear circuits such ascompandors, multiplicators (frequency mixers and voltage-controlled amplifiers), voltage-controlled filters, voltage-controlled oscillators andphase-locked loops.Discrete time signal processingDiscrete time signal processing is for sampled signals that are considered as defined only at discrete points in time, and as such are quantized in time, but not in magnitude.Analog discrete-time signal processing is a technology based on electronic devices such as sample and hold circuits, analog time-division multiplexers, analog delay lines and analog feedback shift registers. This technology was a predecessor of digital signal processing (see below), and is still used in advanced processing of gigahertz signals.The concept of discrete-time signal processing also refers to a theoretical discipline that establishes a mathematical basis for digital signal processing, without taking quantization error into consideration.Digital signal processingDigital signal processing is for signals that have been digitized. Processing is done by general-purpose computers or by digital circuits such as ASICs, field-programmable gate arrays or specialized digital signal processors (DSP chips). Typical arithmetical operations include fixed-point and floating-point, real-valued and complex-valued, multiplication and addition. Other typical operations supported by the hardware are circular buffers and look-up tables. Examples of algorithms are the Fast Fourier transform (FFT), finite impulseresponse (FIR) filter, Infinite impulse response (IIR) filter, and adaptive filters such as the Wiener and Kalman filters1.Digital signal processingDigital signal processing (DSP) is concerned with the representation of signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing. DSP includes subfields like: audio and speech signal processing, sonar and radar signal processing, sensor array processing, spectral estimation, statistical signal processing, digital image processing, signal processing for communications, control of systems, biomedical signal processing, seismic data processing, etc.The goal of DSP is usually to measure, filter and/or compress continuousreal-world analog signals. The first step is usually to convert the signal from an analog to a digital form, by sampling it using an analog-to-digital converter (ADC), which turns the analog signal into a stream of numbers. However, often, the required output signal is another analog output signal, which requires a digital-to-analog converter (DAC). Even if this process is more complex than analog processing and has a discrete value range, the application of computational power to digital signal processing allows for many advantages over analog processing in many applications, such as error detection and correction in transmission as well as data compression.[1]DSP algorithms have long been run on standard computers, on specialized processors called digital signal processors (DSPs), or on purpose-built hardware such as application-specific integrated circuit (ASICs). Today thereare additional technologies used for digital signal processing including more powerful general purpose microprocessors, field-programmable gate arrays (FPGAs), digital signal controllers (mostly for industrial apps such as motor control), and stream processors, among others.[2]2. DSP domainsIn DSP, engineers usually study digital signals in one of the following domains: time domain (one-dimensional signals), spatial domain (multidimensional signals), frequency domain, autocorrelation domain, and wavelet domains. They choose the domain in which to process a signal by making an informed guess (or by trying different possibilities) as to which domain best represents the essential characteristics of the signal. A sequence of samples from a measuring device produces a time or spatial domain representation, whereas a discrete Fourier transform produces the frequency domain information, that is the frequency spectrum. Autocorrelation is defined as the cross-correlation of the signal with itself over varying intervals of time or space.3. Signal samplingMain article: Sampling (signal processing)With the increasing use of computers the usage of and need for digital signal processing has increased. In order to use an analog signal on a computer it must be digitized with an analog-to-digital converter. Sampling is usually carried out in two stages, discretization and quantization. In the discretization stage, the space of signals is partitioned into equivalence classes and quantization is carried out by replacing the signal with representative signal of the corresponding equivalence class. In the quantization stage the representative signal values are approximated by values from a finite set.The Nyquist–Shannon sampling theorem states that a signal can be exactly reconstructed from its samples if the sampling frequency is greater than twice the highest frequency of the signal; but requires an infinite number of samples . In practice, the sampling frequency is often significantly more than twice that required by the signal's limited bandwidth.A digital-to-analog converter is used to convert the digital signal back to analog. The use of a digital computer is a key ingredient in digital control systems. 4. Time and space domainsMain article: Time domainThe most common processing approach in the time or space domain is enhancement of the input signal through a method called filtering. Digital filtering generally consists of some linear transformation of a number of surrounding samples around the current sample of the input or output signal. There are various ways to characterize filters; for example:∙ A "linear" filter is a linear transformation of input samples; other filters are "non-linear". Linear filters satisfy the superposition condition, i.e. if an input is a weighted linear combination of different signals, the output is an equally weighted linear combination of the corresponding output signals.∙ A "causal" filter uses only previous samples of the input or output signals; while a "non-causal" filter uses future input samples. A non-causal filter can usually be changed into a causal filter by adding a delay to it.∙ A "time-invariant" filter has constant properties over time; other filters such as adaptive filters change in time.∙Some filters are "stable", others are "unstable". A stable filter produces an output that converges to a constant value with time, or remains bounded within a finite interval. An unstable filter can produce an output that grows without bounds, with bounded or even zero input.∙ A "finite impulse response" (FIR) filter uses only the input signals, while an "infinite impulse response" filter (IIR) uses both the input signal and previous samples ofthe output signal. FIR filters are always stable, while IIR filters may be unstable.Filters can be represented by block diagrams which can then be used to derive a sample processing algorithm to implement the filter using hardware instructions. A filter may also be described as a difference equation, a collection of zeroes and poles or, if it is an FIR filter, an impulse response or step response.The output of a digital filter to any given input may be calculated by convolving the input signal with the impulse response.5. Frequency domainMain article: Frequency domainSignals are converted from time or space domain to the frequency domain usually through the Fourier transform. The Fourier transform converts the signal information to a magnitude and phase component of each frequency. Often the Fourier transform is converted to the power spectrum, which is the magnitude of each frequency component squared.The most common purpose for analysis of signals in the frequency domain is analysis of signal properties. The engineer can study the spectrum todetermine which frequencies are present in the input signal and which are missing.In addition to frequency information, phase information is often needed. This can be obtained from the Fourier transform. With some applications, how the phase varies with frequency can be a significant consideration.Filtering, particularly in non-realtime work can also be achieved by converting to the frequency domain, applying the filter and then converting back to the time domain. This is a fast, O(n log n) operation, and can give essentially any filter shape including excellent approximations to brickwall filters.There are some commonly used frequency domain transformations. For example, the cepstrum converts a signal to the frequency domain through Fourier transform, takes the logarithm, then applies another Fourier transform. This emphasizes the frequency components with smaller magnitude while retaining the order of magnitudes of frequency components.Frequency domain analysis is also called spectrum- or spectral analysis. 6. Z-domain analysisWhereas analog filters are usually analysed on the s-plane; digital filters are analysed on the z-plane or z-domain in terms of z-transforms.Most filters can be described in Z-domain (a complex number superset of the frequency domain) by their transfer functions. A filter may be analysed in the z-domain by its characteristic collection of zeroes and poles.7. ApplicationsThe main applications of DSP are audio signal processing, audio compression, digital image processing, video compression, speech processing, speech recognition, digital communications, RADAR, SONAR, seismology, and biomedicine. Specific examples are speech compression and transmission in digital mobile phones, room matching equalization of sound in Hifi and sound reinforcement applications, weather forecasting, economic forecasting, seismic data processing, analysis and control of industrial processes, computer-generated animations in movies, medical imaging such as CAT scans and MRI, MP3 compression, image manipulation, high fidelity loudspeaker crossovers and equalization, and audio effects for use with electric guitar amplifiers8. ImplementationDigital signal processing is often implemented using specialised microprocessors such as the DSP56000, the TMS320, or the SHARC. These often process data using fixed-point arithmetic, although some versions are available which use floating point arithmetic and are more powerful. For faster applications FPGAs[3] might be used. Beginning in 2007, multicore implementations of DSPs have started to emerge from companies including Freescale and Stream Processors, Inc. For faster applications with vast usage, ASICs might be designed specifically. For slow applications, a traditional slower processor such as a microcontroller may be adequate. Also a growing number of DSP applications are now being implemented on Embedded Systems using powerful PCs with a Multi-core processor.(翻译)信号处理信号处理是电气工程与应用数学领域,在离散的或连续时间域处理和分析信号,以对这些信号进行所需的有用的处理。
雷达信号处理期刊总结
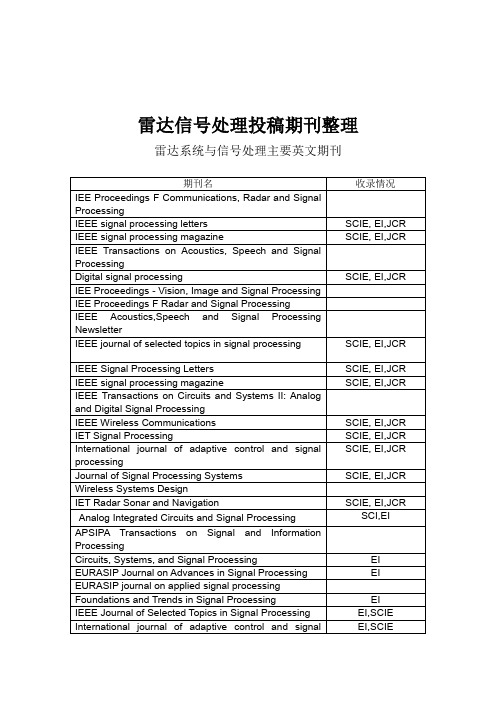
雷达系统与信号处理主要中文期刊
期刊名
收录情况
计算机学报
EI, PKU,CJCR, CSCD
电子学报
EI, PKU,CJCR, CSCD
电子与信息学报
EI, PKU,CJCR, CSCD
现代雷达
PKU, CJCR,CSCD
雷达学报
CJCR, CSCD
导航定位学报
导航与控制
CJCR
SCIE, EI,JCR
Wireless Systems Design
IET Radar Sonar and Navigation
SCIE, EI,JCR
Analog Integrated Circuits and Signal Processing
SCI,EI
APSIPA Transactions on Signal and Information Processing
IEE Proceedings F Radar and Signal Processing
IEEE Acoustics,Speech and Signal Processing Newsletter
IEEE journal of selected topics in signal processing
现代雷达
PKU, CJCR,CSCD
电子科技大学学报
电子测量与仪器学报
PKU, CJCR,CSCD
电子与信息学报
,CSCD
雷达系统与信号处理领域国际会议
国际重要会议
会议中文名称
IEEE Radar Conference
雷达会议
International Conference on Radar
爱思唯尔signal processing分区

爱思唯尔signal processing分区爱思唯尔signal processing分区是一个涉及信号处理领域的学术刊物集合。
在这个分区中,研究者们专注于探索和研究信号处理的各个方面,旨在提高信号处理算法和技术的效果和性能。
信号处理是一种广泛应用于多个学科领域的技术,包括通信、音频和视频处理、雷达和图像处理等。
拥有一个专门的分区,如爱思唯尔signal processing分区,有助于整合相关领域的学术研究成果,进而促进学术交流和产业应用的发展。
在爱思唯尔signal processing分区中,研究论文通常关注以下几个关键领域:1.信号处理算法和技术:这个领域主要关注开发新的信号处理算法和技术,以解决各种实际应用中的问题。
这些算法和技术可以用于信号增强、噪声抑制、压缩和解码等领域。
2.语音和音频处理:这个领域关注语音和音频信号的处理和分析。
研究方向包括语音识别、语音合成、音频编解码、音频增强和音频检索等。
3.图像和视频处理:这个领域致力于图像和视频信号的处理和分析。
研究方向包括图像压缩、图像恢复、图像分割、目标检测和跟踪等。
这些技术可以应用于医学图像、遥感图像和计算机视觉等领域。
4.数字信号处理系统:这个领域关注设计和实现数字信号处理系统的方法和技术。
研究方向包括DSP芯片设计、实时信号处理、并行处理和硬件加速等。
在爱思唯尔signal processing分区发表的论文在学术界具有一定的影响力,并且对相关领域的研究和应用有着重要的推动作用。
通过这个分区,研究者们可以及时了解最新的研究成果,并与其他领域的专家进行交流和合作。
这将有助于进一步推动信号处理领域的发展和创新。
Unit 9 Digital signals and signal processing

Unite 9 Digital signals and signal processingPart 1: Digital signal processingDigital signal processing (DSP) is the study of signals in a digital representation and the processing methods of these signals. DSP and analog signal processing are sub-fields of signal processing. DSP includes sub-fields like audio and speech signal processing, sonar and radar signal processing, sensor array processing, spectral estimation, statistical signal processing, image processing, signal processing for communications, biomedical signal processing, etc.Since the goal of DSP is usually to measure or filter continuous real-world analog signals, the first step is usually to convert the signal form an analog to a digital form, by using an analog to digital converter. Often, the required output signal is another analog output signal, which requires a digital to analog converter.The algorithms required for DSP are sometimes performed using specialized computers, which make use of specialized microprocessors called digital signal processors (also abbreviated DSP). These process signals in real time, and are generally purpose-designed application-specific integrated circuits (ASICs). When flexibility and rapid development are more important than unit costs at high volume, DSP algorithms may also be implemented using field-rogrammable gatearrays (FPGAs).DSP domainsIn DSP, engineers usually study digital signals in one of the following domains: time domain (one-dimensional signals), spatial domain (multidimensional signals), frequency domain, autocorrelation domain, and wavelet domains. They choose the domain in which to process a signal by making an informed guess (or by trying different possibilities) as to which domain best represents the essential characteristics of the signal. A sequence of samples form a measuring device produces a time or spatial domain representation, whereas a discrete Fourier transform produces the frequency domain information, that is, the frequency spectrum. Autocorrelation is defined as the cross-correlation of the signal with itself over varying intervals of time or space.Signal samplingWith the increasing use of computers the usage and need of digital signal processing has increased. In order to use an analog signal on computer it must be digitized with an analog to digital converter (ADC). Sampling is usually carried out in tow stages, discretization and quantization. In the discretization stage, the space of signals is partitioned into equivalence classes and discretization is carried out by replacing thesignal with representative signal of the corresponding equivalence class. In the quantization stage the representative signal values are approximated by values form a finite set.In order for a sampled analog signal to be exactly reconstructed, the Nyquist-Shannon sampling theorem must be satisfied. This theorem states that the sampling frequency must be greater than twice the bandwidth of the signal. In practice, the sampling frequency is often significantly more than twice the required bandwidth. The most common bandwidth scenarios are: DC~BW (“baseband”); and f BW, a frequency band centered on a carrier frequency (“direct demodulation”).Time and space domainsThe most common processing approach in the time or space domain is enhancement of the input signal through a method called filtering. Filtering generally consists of some transformation of a number of surrounding samples around the current sample of the input or output signal. There are various ways to characterize filters; for example: - A “linear” filter is a linear transformation of input samples; other filters are “non-linear.” Linear filters satisfy the superposition condition, i.e., if an input is a weighted linear combination of different signals, the output is an equally weighted linear combination of the corresponding output signals.- A “causal” filter uses only previous samples of the input or output signals; while a “non-causal” filter uses future input samples. A non-causal filter can usually be changed into a causal filter by adding a delay to it.- A “time-invariant” filter has constant properties over time; other filters such as adaptive filters change in time.- Some filters are “stable”, others are “unstable”. A stable filter produces an output that converges to a constant value with time or remains bounded within a finite interval. An unstable filter produces output which diverges.- A “finite impulse response” (FIR) filter uses only the input signal, while an “infinite impulse response” filter (IIR) uses both the input signal and previous samples of the output signal. FIR filters are always stable, while IIR filters may be unstable.Most filters can be described in Z-domain (a superset of the frequency domain) by their transfer functions. A filter may also be described as a difference equation, a collection of zeroes and poles or, if it is an FIR filter, an impulse response or step response. The output of an FIR filter to any given input may be calculated by convolving the input signal with the impulse response. Filters can also be represented by block diagrams which can then be used to derive a sample processing algorithm to implement the filter using hardware instructions.Frequency domainSignals are converted from time or space domain to the frequency domain usually through the Fourier transform. The Fourier transform converts the signal information to a magnitude and phase component of each frequency. Often the Fourier transform is converted to the power spectrum, which is the magnitude of each frequency component squared.The most common purpose for analysis of signals in the frequency domain is analysis of signal properties. The engineer can study the spectrum to get information of which frequencies are present in the input signal and which are missing.There are some commonly used frequency domain transformations. For example, the cepstrum converts a signal to the frequency domain through Fourier transform, takes the logarithm, and then applies another Fourier transform. This emphasizes the frequency components with smaller magnitude while retaining the order of magnitudes of frequency components.ApplicationsThe main applications of DSP are audio signal processing, audio compression, digital image processing, video compression, speech processing, speech recognition, digital communications, radar, sonar,seismology, and biomedicine. Specific examples are speech compression and transmission in digital mobile phones, room matching equalization of sound in HiFi and sound reinforcement applications, weather forecasting, economic forecasting, seismic data processing, analysis and control of industrial processes, computer-generated animations in movies, medical imaging such as CAT scans and MRI, image manipulation, high fidelity loudspeaker crossovers and equalization, and audio effects for use with electric guitar amplifiers.ImplementationDigital signal processing is often implemented using specialized microprocessors such as the MC560000 and the TMS320. These often process data using fixed-point arithmetic, although some versions are available which use floating point arithmetic and are more powerful. For faster applications FPGAs might be used. Beginning in 2007, multicore implementations of DSPs have started to emerge. For faster applications with vast usage, ASICs might be designed specifically. For slow applications, a traditional slower processor such as microcontroller can cope.Part 2: General concepts of digital signal processingThere have been tremendous demands in the use of digital computersand special-purpose digital circuitry for performing varied signal processing functions that were originally achieved with analog equipment. The continued evolution of inexpensive integrated circuits has led to a variety of microcomputers and minicomputers that can be used for various signal processing functions. It is now possible to build special-purpose digital processors within much smaller size and lower cost constraints of systems previously all analog in nature.We will provide a general discussion of the basic concepts associated with digital signal processing. To do so, it is appropriate to discuss some common terms and assumptions. Wherever possible the definitions and terminology will be established in accordance with the recommendations of the IEEEE Group on Audio and Electroacoustics.An analog signal is a function that is defined over a continuous range of time and in which the amplitude may assume a continuous range of values. Common examples are the sinusoidal function, the step function, the output of a microphone, etc. the term analog apparently originated from the field of analog computation, in which voltages and currents are used to represent physical variables, but it has been extended in usage.Continuous-time signal is a function that is defined over a continuous range of time, but in which the amplitude may either have a continuous ranger of values or a finite number of possible values. In this context, an analog signal could be considered as a special case of continuous-timesignal. In practice, however, the terms analog and continuous-time are interchanged casually in usage and are often used to mean the same thing. Because of the association of the term analog with physical analogies, preference has been established for the term continuous-time. Nevertheless, there will be cases in which the term analog will be used for clarity, particularly where it relates to the term digital.The term quantization describes the process of representing a variable by a set of distinct values. A quantized variable is one that may assume only distinct values.A discrete-time signal is a function that is defined only at a particular set of values of time. This means that the independent variable, time, is quantized. If the amplitude of a discrete-time signal is permitted to assume a continuous range of values, the function is said to be a sampled-data signal. A sampled-data signal could arise from sampling an analog signal at discrete values of time.A digital signal is a function in which both time and amplitude are quantized. A digital signal may always be represented by a sequence of numbers in which each number has a finite number of digits.The terms discrete-time and digital are often interchanged in practice and are often used to mean the same thing. A great deal of the theory underlying discreet-time signals is applicable to purely digital signals, so it is not always necessary to make rigid distinctions. The term。
ieee transactions on signal processing 投稿经验分享

ieee transactions on signal processing 投稿经验分享、在IEEE Transactions on Signal Processing(信号处理汇刊)上投稿,你需要遵循一些关键步骤,以下是一些具体的经验分享:1.选择合适的主题和期刊:首先,确保你的研究内容与Signal Processing汇刊的主题相符。
查看期刊的官方网站,了解期刊的范围和要求,以确保你的论文适合该期刊。
2.撰写高质量的论文:论文的质量是决定是否被接受的关键因素。
确保你的论文具有清晰的结构,包括引言、方法、结果和结论。
提供完整的实验数据和详细的分析,使评审员能够理解你的研究方法和结果。
3.仔细阅读投稿指南:每个期刊都有自己的投稿指南,包括格式、提交材料、字数限制等。
确保你仔细阅读并遵循这些指南,以免在初审阶段就被拒绝。
4.准备充分的同行评审材料:提交论文之前,准备一份详细的审稿提纲,包括研究背景、目的、方法、结果和结论。
这将有助于同行评审员更好地理解你的研究,并给出有建设性的反馈。
5.选择合适的审稿人:在提交论文时,你需要为期刊推荐合适的审稿人。
选择那些在你的研究领域内有丰富经验和知识的专家,以确保你的论文得到专业的评审。
6.耐心等待并积极回应:一旦你的论文被接受,你需要等待评审员的反馈。
通常这个过程需要几个月的时间。
在收到反馈后,及时回应评审员的建议并进行修改,以提高论文的质量。
7.不断改进和完善:即使你的论文被接受,也不意味着你的工作已经完成。
你需要不断改进和完善你的研究,以适应不断变化的研究领域和技术发展。
以上是关于在IEEE Transactions on Signal Processing上投稿的一些经验分享,希望对你有所帮助。
祝你成功!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Journal of Applied Research and TecБайду номын сангаасnology
Wave-Network Based on L -Nomr Minimsation For Learning Chaotics Time Series. V. Alarcon-Aquino et al, 211-221
th th
2
Received: April 19 , 2003. Accepted :September 30 , 2005
ABSTRACT This paper presents a wavelet-neural network based on the L1-norm minimisation for learning chaotic time series. The proposed approach, which is based on multi-resolution analysis, uses wavelets as activation functions in the hidden layer of the wavelet-network. We propose using the L1-norm, as opposed to the L2-norm, due to the wellknown fact that the L1-norm is superior to the L2-norm criterion when the signal has heavy tailed distributions or outliers. A comparison of the proposed approach with previous reported schemes using a time series benchmark is presented. Simulation results show that the proposed wavelet-network based on the L1-norm performs better than the standard back-propagation network and the wavelet-network based on the traditional L2-norm when applied to synthetic data. RESUMEN En este artículo se presenta una red neuronal-wavelet basada en la minimización de la norma L1 para aprendizaje de series de tiempo caóticas. El método propuesto, el cuál se basa en un análisis multi-resolución, utiliza wavelets como funciones de activación en la capa oculta de la red neuronal-wavelet. Se propone utilizar la norma L1, en lugar de la tradicional norma L2, debido a que la norma L1 es superior a la norma L2 cuando la señal tiene distribuciones sesgadas o de colas pesadas. Se presenta una comparación del método propuesto con esquemas reportados previamente utilizando series de tiempo caóticas conocidas. Los resultados de simulación revelan que la red neuronal-wavelet basada en la norma L1 tiene una mejor eficiencia que la red neuronal con propagación hacia atrás y la red neuronal-wavelet basada en la tradicional norma L2 cuando se aplica a datos sintéticos. KEYWORDS: Wavelet-networks, Wavelets, Multi-resolution Analysis, Learning Chaotic Time Series.
1. INTRODUCTION Despite the potential of neural networks, there are several problems that remain to be solved. First, it is well known that the back-propagation algorithm for training the multi-layer perceptron, also known as back-propagation network (BPN), suffers for having slow convergence, and the convergence is not normally guaranteed [1 & 9]. Second, the
back-propagation type for the learning of the network. In [3], the off-line learning algorithm is based on the traditional L2-norm, which is basically a non-iterative Least Squares problem and it can be solved using the Moore-Penrose pseudo inverse rule [9]. The L2-norm may be inaccurate especially where the measurements contain large errors [6]. It is well known that the L1-norm outperforms the L2-norm when the signal has heavy tailed distributions or outliers. Generally speaking, the L1-norm is superior to the Lp-norm (with p > 1 i.e., p = 2, ∞ ) criteria if the error distribution has long tails [4&6]. In the work reported in this paper an algorithm is proposed for learning chaotic times series based on waveletnetworks and the L1-norm minimisation. The results reported show that wavelet-networks have better approximation properties than the back-propagation network when applied to synthetic data. This is due to the fact that wavelets, in addition to forming an orthogonal basis, have the capability to explicitly represent the behaviour of a function with different resolutions of input variables [3]. The rest of this paper is organised as follows. Section 2 presents a review of wavelet theory. Section 3, introduces the wavelet-network based on the L1-norm minimisation algorithm, and its implementation through linear programming and the dual simplex method. Section 4 presents a brief description of chaotic time series. In Section 5, a comparison of different approaches reported in the literature and the waveletnetwork based on the L1-norm minimisation using synthetic data is presented. Finally, Section 6 presents the conclusions drawn from previous sections and suggests some future work. 2. A REVIEW OF WAVELET THEORY Wavelet transforms involve representing a general function in terms of simple, fixed building blocks at different scales and positions. These building blocks are generated from a single fixed function called mother wavelet by translation and dilation operations. The continuous wavelet transform considers a family [2 & 5]
