2013届高三人教B版理科数学一轮复习课时作业(42)立体几何中的向量方法(一)——位置关系的证明 2
2013届高考数学一轮复习讲义:8.6 立体几何中的向量方法(Ⅰ) 证明平行与垂直

1 1 3 3 → → ∴AE· =- × + × =0, CD 2 4 6 4 → → ∴AE⊥CD,即 AE⊥CD.
→ 2 3 (2)方法一 ∵P(0,0,1),∴PD=0, ,-1. 3 3 2 3 1 → → 又AE· = × PD + ×(-1)=0, 4 3 2 → → ∴PD⊥AE,即 PD⊥AE. → → → ∵AB=(1,0,0),∴PD· =0, AB
建立如图所示的空间直角坐标系 A—xyz, 则 A(0,0,0)、B(2,0,0)、C(2,2,0)、D(0,2,0)、 P(0,0,2)、E(0,0,1)、F(0,1,1)、G(1,2,0). → → ∴PB=(2,0,-2),FE=(0,-1,0), → FG=(1,1,-1),
→ → → 设PB=sFE+tFG, 即(2,0,-2)=s(0,-1,0)+t(1,1,-1), t=2, ∴t-s=0, -t=-2, 解得 s=t=2.
(-2,1,0). → → 因为 n⊥BA1,n⊥BD,
→ -x+2y+ 3z=0, n· 1=0, BA 故 ⇒ -2x+y=0, → n· =0 BD 令 x=1,则 y=2,z=- 3,故 n=(1,2,- 3)为平面 A1BD 的 → 一个法向量,而AB1=(1,2,- 3), → → 所以AB1=n,所以AB1∥n,故 AB1⊥平面 A1BD.
→ → 设平面 A1BD 的法向量为 n=(x,y,z),BA1=(-1,2, 3),BD=
利用空间向量解决探索 性问题
例 3 如图,四棱锥 P—ABCD 中,PA⊥平 面 ABCD,PB 与底面所成的角为 45° , 底面 ABCD 为直角梯形,∠ABC= 1 ∠BAD=90° ,PA=BC= AD=1. 2 (1)求证:平面 PAC⊥平面 PCD; (2)在棱 PD 上是否存在一点 E, CE∥平面 PAB?若存在, 使 请确定 E 点的位置;若不存在,请说明理由.
高三数学一轮复习试题:立体几何中的向量方法-

高三数学一轮复习试题:立体几何中的向量
方法
导读:高考,比的不是智商高低,比的是谁的耐心好,经过一轮、二轮、三轮复习的摧残还能有几个小伙伴说自己屹立不倒的?今天本文库末宝就给大家带来了高考数学一轮复习的同步练习,快来看看吧。
3.若→(AB)=λ→(CD)+μ→(CE),则直线AB与平面CDE的位置关系是()
A.相交
B.平行
C.在平面内
D.平行或在平面内
【答案】D
【解析】∵→(AB)=λ→(CD)+μ→(CE),∴→(AB)、→(CD)、→(CE)共面,
∴AB与平面CDE平行或在平面CDE内.
5.在正四棱锥SABCD中,O为顶点在底面上的射影,P为侧棱SD 的中点,且SO=OD,则直线BC与平面PAC所成的角是()
A.30°
B.45°
C.60°
D.90°
【答案】A
【解析】如图,以O为原点建立空间直角坐标系Oxyz.
12.如图所示,四棱锥S—ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.
(1)求证:AC⊥SD.
(2)若SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
更多数学复习资讯,尽在本文库。
高三数学(理)一轮复习之双基限时训练:立体几何中的向量方法(人教新课标).pdf

巩固双基,提升能力一、选择题 1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( ) A. B. C. D. 解析:建立空间直角坐标系如图. 则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2). =(-1,0,2),=(-1,2,1), cos〈,〉==. 所以异面直线BC1与AE所成角的余弦值为. 答案:B 2.在正方体ABCD-A1B1C1D1中,若E为A1C1中点,则直线CE垂直于( ) A.AC B.BD C.A1D D.A1A 解析:以A为原点,AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系,设正方体棱长为1,则A(0,0,0),C(1,1,0),B(1,0,0),D(0,1,0),A1(0,0,1),E, =,=(1,1,0),=(-1,1,0), =(0,1,-1),=(0,0,-1). 显然·=-+0=0, ⊥,即CEBD. 答案:B 3.在90°的二面角的棱上有A、B两点,AC、BD分别在这个二面角的两个面内,且都垂直于棱AB,已知AB=5,AC=3,CD=5,则BD=( ) A.4 B.5 C.6 D.7 解析:由条件知ACAB,BDAB,ACBD, 又=++, 2=(++)2 =||2+||2+||2 =32+52+||2=(5)2, ||2=16,BD=4. 答案:A 4.若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于( ) A.120° B.60° C.30° D.以上均错 解析:设l与α所成角为θ,则sinθ=|cos120°|=. 又0°≤θ≤90°,θ=30°. 答案:C5.已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值为( ) A. B. C. D. 解析:如图建立空间直角坐标系, 则B(4,0,0),C(4,4,0),C1(4,4,2), 显然AC平面BB1D1D, =(4,4,0)为平面BB1D1D的一个法向量. 又=(0,4,2), cos〈,〉= = =. 即BC1与平面BB1D1D所成角的正弦值为. 答案:C 6.(2013·德州调研)二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为( ) A.150° B.45° C.60° D.120° 解析:由题意知与所成角即为该二面角的平面角. =++, 2=2+2+2+2·+2·+2·. (2)2=62+42+82+2||||cos〈,〉 =116+2×6×8cos〈,〉, cos〈,〉=-,〈,〉=120°, 〈,〉=60°,该二面角的大小为60°. 答案:C 二、填空题 7.(2013·潍坊考试)如图,平行六面体ABCD-A1B1C1D1,若ABCD是边长为2的正方形,AA1=1,A1AD=A1AB=60°,则BD1的长为__________. 解析:=++, 〈〉2=(++)2=9,故BD1=3. 答案:3 8.(2013·怀化模拟)如图,在直三棱柱中,ACB=90°,AC=BC=1,侧棱AA1=,M为A1B1的中点,则AM与平面AA1C1C所成角的正切值为________. 解析:以C1为原点,C1A1,C1B1,C1C所在直线分别为x,y,z轴建立空间直角坐标系,则平面AA1C1C的法向量为n=(0,1,0),=-(1,0,)=,则直线AM与平面AA1C1C所成角θ的正弦值为sinθ=|cos〈,n〉|==,tanθ=. 答案: 9(2013·东城练习)如图,在正方体ABCD-A1B1C1D1中,E,F,G,H,M分别是棱AD,DD1,D1A1,A1A,AB的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件__________时,就有MNA1C1;当N只需满足条件__________时,就有MN平面B1D1C. 解析:以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系,设正方体的棱长为1,则M,N(x,0,z),=(-1,1,0),因此·=·(-1,1,0)=1-x-=0,即x=,故点N在EG上,就有MNA1C1.设平面B1D1C的一个法向量为n=(-1,1,1),若MN平面B1D1C,则·n=·(-1,1,1)=1-x-+z=0即x-z-=0,故点N在EH上,就有MN平面B1D1C. 答案:点N在EG上 点N在EH上 三、解答题 10.(2012·天津)如图,在四棱锥P-ABCD中,AP平面ABCD,ACAD,ABBC,BAC=45°,PA=AD=2,AC=1. (1)证明PCAD; (2)求二面角A-PC-D的正弦值; (3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长. 解析:方法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0),B,P(0,0,2). (1)易得=(0,1,-2),=(2,0,0), 于是·=0,所以PCAD. (2)=(0,1,-2),=(2,-1,0). 设平面PCD的法向量n=(x,y,z), 则即 不妨令z=1,可得n=(1,2,1). 可取平面PAC的法向量m=(1,0,0). 于是cos〈m,n〉===, 从而sin〈m,n〉=. 所以二面角A-PC-D的正弦值为. (3)设点E的坐标为(0,0,h),其中h[0,2]. 由此得=.由=(2,-1,0),故 cos〈,〉== =, 所以,=cos30°=, 解得h=,即AE=. 方法二: (1)由PA平面ABCD,可得PAAD, 又由ADAC,PA∩AC=A,故AD平面PAC, 又PC平面PAC,所以PCAD. (2)如图,作AHPC于点H,连接DH. 由PCAD,PCAH,可得PC平面ADH. 因此DHPC,从而AHD为二面角A-PC-D的平面角.在RtPAC中,PA=2,AC=1,由此得AH=. 由(1)知ADAH.故在RtDAH中, DH==. 因此sinAHD==. 所以二面角A-PC-D的正弦值为. (3)如图,因为ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF.故EBF或其补角为异面直线BE与CD所成的角. 由于BFCD,故AFB=ADC,在RtDAC中,CD=,sinADC=, 故sinAFB=. 在AFB中,由=,AB=, sinFAB=sin135°=,可得BF=. 由余弦定理,BF2=AB2+AF2-2AB·AF·cosFAB,可得AF=. 设AE=h. 在RtEAF中,EF== . 在RtBAE中,BE== . 在EBF中,因为EF<BE,从而EBF=30°,由余弦定理得cos30°=.可解得h=. 所以AE=. 11.(2012·湖北)如图1,ACB=45°,BC=3,过动点A作ADBC,垂足D在线段BC上且异于点B,连接AB,沿AD将ABD折起,使BDC=90°(如图2所示). (1)当BD的长为多少时,三棱锥A-BCD的体积最大; (2)当三棱锥A-BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得ENBM,并求EN与平面BMN所成角的大小. 图1 图2 解析:(1)方法一:在如图1所示ABC中,设BD=x(0<x<3),则CD=3-x. 由ADBC,ACB=45°知,ADC为等腰直角三角形,所以AD=CD=3-x. 由折起前ADBC知,折起后(如图2),ADDC,ADBD,且BD∩DC=D, 所以AD平面BCD. 又BDC=90°, 所以SBCD=BD·CD=x·(3-x). 于是VA-BCD=AD·SBCD=(3-x)·x(3-x)=·2x(3-x)(3-x)≤3=,当且仅当2x=3-x,即x=1时,等号成立,故当x=1,即BD=1时,三棱锥A-BCD的体积最大. 方法二:同解法1,得 VA-BCD=AD·SBCD =(3-x)·x(3-x) =(x3-6x2+9x). 令f(x)=(x3-6x2+9x), 由f′(x)=(x-1)(x-3)=0,且0<x<3,解得x=1. 当x(0,1)时,f′(x)>0;当x(1,3)时,f′(x)<0. 所以当x=1时,f(x)取得最大值. 故当BD=1时,三棱锥A-BCD的体积最大. (2)方法一:以D为原点,建立如图a所示的空间直角坐标系D-xyz. 由(1)知,当三棱锥A-BCD的体积最大时,BD=1,AD=CD=2. 于是可得D(0,0,0),B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E,且=(-1,1, 1). 设N(0,λ,0),则=. 因为ENBN等价于·=0,即 ·(-1,1,1)=+λ-1=0, 故λ=,N. 所以当DN=(即N是CD的靠近点D的一个四等分点)时,ENBM. 设平面BMN的一个法向量为n=(x,y,z),由及=,得可取n=(1,2,-1). 设EN与平面BMN所成角的大小为θ,则由=,n=(1,2,-1),可得sinθ=cos(90°-θ)===,即θ=60°. 故EN与平面BMN所成角的大小为60°. 图a 图b 图c 图d 方法二:由(1)知,当三棱锥A-BCD的体积最大时,BD=1,AD=CD=2. 如图b,取CD的中点F,连结MF,BF,EF,则MFAD. 由(1)知AD平面BCD,所以MF平面BCD. 如图c,延长FE至P点使得FP=DB,连BP,DP,则四边形DBPF为正方形,所以DPBF.取DF的中点N,连结EN,又E为FP的中点,则ENDP,所以ENBF. 因为MF平面BCD,又EN面BCD,所以MFEN. 又MF∩BF=F,所以EN面BMF.又BM面BMF,所以ENBM. 因为ENBM当且仅当ENBF,而点F是唯一的,所以点N是唯一的. 即当DN=(即N是CD的靠近点D的一个四等分点),ENBM. 连接MN,ME,由计算得NB=NM=EB=EM=,所以NMB与EMB是两个共底边的全等的等腰三角形,如图d所示,取BM的中点G,连接EG,NG,则BM平面EGN. 在平面ENG中,过点E作EHGN于H,则EH平面BMN,故ENH是EN与平面BMN所成的角. 在EGN中,易得EG=GN=NE=,所以EGN是正三角形,故ENH=60°,即EN与平面BMN所成的角的大小为60°. 12.(2012·福建)如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点. (1)求证:B1EAD1; (2)在棱AA1上是否存在一点P,使得DP平面B1AE?若存在,求AP的长;若不存在,说明理由;(3)若二面角A-B1E-A1的大小为30°,求AB的长. 解析:(1)以A为原点,,,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系(如图). 设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E,B1(a,0,1),故= (0,1,1),=,=(a,0,1),=. ·=-×0+1×1+(-1)×1=0, B1E⊥AD1. (2)假设在棱AA1上存在一点P(0,0,z0),使得DP平面B1AE,此时=(0,-1,z0). 又设平面B1AE的法向量n=(x,y,z), n⊥平面B1AE, n⊥,n,得 取x=1,得平面B1AE的一个法向量n=. 要使DP平面B1AE,只要n,有-az0=0,解得z0=. 又DP平面B1AE, 存在点P,满足DP平面B1AE,此时AP=. (3)连接A1D,B1C,由长方体ABCD-A1B1C1D1及AA1=AD=1,得AD1A1D. ∵B1C∥A1D,AD1⊥B1C. 又由(1)知B1EAD1,且B1C∩B1E=B1, AD1⊥平面DCB1A1, 是平面A1B1E的一个法向量,此时=(0,1,1). 设与n所成的角为θ,则 cosθ==. 二面角A-B1E-A1的大小为30°, |cosθ|=cos30°,即=, 解得a=2,即AB的长为2. 。
高中数学选修2-1课时作业4:3.2 立体几何中的向量方法(一)

3.2立体几何中的向量方法(一)——直线的方向向量和平面的法向量1.若n =(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α法向量的是( )A .(0,-3,1)B .(2,0,1)C .(-2,-3,1)D .(-2,3,-1)[答案] D2.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k ),若α∥β,则k =( )A .2B .-4C .4D .-2 [答案] C3.若平面α与平面β的法向量分别是a =(4,0,-2),与b =(1,0,2),则平面α与平面β的位置关系是( )A .平行B .垂直C .相交不垂直D .无法判定[答案] B4.若直线l 1的方向向量与l 2的方向向量的夹角为150°,则l 1与l 2这两条异面直线所成的角等于( )A .30°B .150°C .30°或150°D .以上均错 [答案] A5.若直线l 的方向向量与平面α的法向量的夹角等于120°,则直线l 与平面α所成的角等于( )A .120°B .60°C .30°D .以上均错 [解析] 如下图所示,易知直线l 与平面α所成的角为30°.[答案] C6.已知A (1,0,0),B (0,1,0),C (0,0,1),则平面ABC 的一个单位法向量是( )A.⎝⎛⎭⎫33,33,-33B.⎝⎛⎭⎫33,-33,33C.⎝⎛⎭⎫-33,33,33D.⎝⎛⎭⎫-33,-33,-33 [解析] ∵AB →=(-1,1,0),AC →=(-1,0,1),结合选项,验证知应选D.[答案] D7.已知棱长为1的正方体ABCD -A 1B 1C 1D 1,则平面ACB 1的一个法向量为__________.[解析] 建立空间直角坐标系,如下图所示,则A (1,0,0),B (1,1,0),C (0,1,0),B 1(1,1,1),∴AC →=(-1,1,0),AB 1→=(0,1,1)设平面ACB 1的一个法向量为n =(x ,y ,z ),则由n ⊥AC →,n ⊥AB 1→,得⎩⎪⎨⎪⎧-x +y =0,y +z =0,令x =1,得n =(1,1,-1). [答案] (1,1,-1)8.若两个平面α,β的法向量分别等于u =(1,0,1),v =(-1,1,0)则这两个平面所成的锐二面角的度数是__________.[解析] ∵a =(1,0,1),v =(-1,1,0),∴|u |=2,|v |=2,u ·v =-1.∴cos 〈u ·v 〉=-12. ∴〈u ,v 〉=120°,故两平面所成的锐二面角为60°.[答案] 60°9.若直线a 和b 是两条异面直线,它们的方向向量分别是(1,1,1),和(2,-3,-2),求直线a 和b 的公垂线的一个方向向量.解 设直线a 与b 的公垂线的一个方向向量为n =(x ,y ,z ),则n ⊥(1,1,1),n ⊥(2,-3,-2),∴⎩⎪⎨⎪⎧ x +y +z =0,2x -3y -2z =0,∴⎩⎨⎧ x =-15z y =-45z ,令z =-5,得x =1,y =4,故直线a 和b 的公垂线的一个法向量为(1,4,-5).10.如图,在长方体ABCD -A 1B 1C 1D 1中,AD =DC =3,DD 1=4,E 是A 1A 的中点,求证:A 1C ∥平面BED .证明 以点A 的坐标原点,以AB 、AD ,AA 1所在的直线为x ,y ,z 轴,建立空间直角坐标系,得A 1(0,0,4),C (3,3,0),E (0,0,2).取BD 中点记为F ,则F (32,32,0), ∴A 1C →=(3,3,-4),EF →=(32,32,-2).∴A 1C →=2EF →.∴A 1C →∥EF →,又A 1C 与EF 无交点,A 1C ∥EF ,EF ⊂面BED ,A 1C ⊄平面BED .∴A 1C ∥平面BED .。
2013届高考数学一轮复习课时检测 第七章 第七节 立体几何中的向量方法 理

第七章 第七节 立体几何中的向量方法一、选择题1.若平面α,β的法向量分别为a =(-1,2,4),b =(x ,-1,-2),并且α⊥β,则x 的值为( )A .10B .-10 C.12D .-12解析:∵α⊥β,∴a ²b =0 ∴x =-10. 答案:B2.已知AB =(1,5,-2), BC =(3,1,z ),若 AB ⊥ BC , BP=(x -1,y ,-3),且BP ⊥平面ABC ,则实数x ,y ,z 分别为 ( )A.337,-157,4 B.407,-157,4 C.407,-2,4D .4,407,-15解析: AB ⊥ BC ⇒ AB² BC =3+5-2z =0,∴z =4.又BP ⊥平面ABC ,∴BP ²AB=x -1+5y +6=0,①BP ²BC=3x -3+y -3z =0,②由①②得x =407,y =-157.答案:B3.如图,在正方体ABCD -A 1B 1C 1D 1中,E 为A 1C 1的中点,则异面直线CE 与BD 所成的角为 ( )A .30°B .45°C .60°D .90°解析:以D 点为原点,建立空间直角坐标系,设正方体棱长为1,则相关点的坐标为C (0,1,0),E (12,12,1),B (1,1,0),D (0,0,0),∴ CE =(12,-12,1), BD =(-1,-1,0).∴ CE ² BD =-12+12+0=0.∴ CE ⊥ BD,即CE ⊥BD .答案:D4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是 ( )A .相交B .平行C .垂直D .不能确定解析:分别以C 1B 1,C 1D 1,C 1C 所在直线为x ,y ,z 轴,建立空间直角坐标系.∵A 1M =AN =23a , ∴M (a ,23a ,a 3),N (23a ,23a ,a ).∴ MN =(-a 3,0,23a ).又C 1(0,0,0),D 1(0,a,0),∴ 11C D=(0,a,0).∴ MN ² 11C D =0,∴MN⊥ 11C D .∵ 11C D是平面BB 1C 1C 的法向量,且MN ⊄平面BB 1C 1C , ∴MN ∥平面BB 1C 1C . 答案:B5.如图所示,在三棱柱ABC —A 1B 1C 1中,AA 1⊥底面ABC ,AB =BC =AA 1,∠ABC =90°,点E 、F 分别是棱AB 、BB 1的中点,则直线EF 和BC 1所成的角是( )A .45°B .60°C .90°D .120°解析:以B 点为坐标原点,以BC 、BA 、BB 1分别为x 、y 、z 轴建立空间直角坐标系.设AB =BC =AA 1=2,则B (0,0,0),C 1(2,0,2),E (0,1,0),F (0,0,1),∴ EF =(0,-1,1),1BC=(2,0,2)∴cos 〈 EF , 1BC 〉= EF ²1BC| EF||1BC |=22²8=12.∴EF 与BC 1所成角为60°. 答案:B6.如图,平面ABCD ⊥平面ABEF ,四边形ABCD 是正方形,四边形ABEF 是矩形,且AF =12AD =a ,G 是EF 的中点,则GB 与平面AGC 所成角的正弦值为( )A.66B.33C.63D.23解析:如图,以A 为原点建立空间直角坐标系,则A (0,0,0),B (0,2a,0),C (0,2a,2a ),G (a ,a,0),F (a,0,0), AG =(a ,a,0), AC=(0,2a,2a ),BG =(a ,-a,0),BC=(0,0,2a ),设平面AGC 的法向量为n 1=(x 1,y 1,1),由⎩⎨⎧BG²n 1=0 BG²n 1=0⇒⎩⎪⎨⎪⎧ax 1+ay 1=02ay 1+2a =0⇒⎩⎪⎨⎪⎧x 1=1y 1=-1⇒n 1=(1,-1,1).sin θ=| BG²n 1|| BG ||n 1|=2a 2a ³3=63.答案:C 二、填空题7.已知 AB=(2,2,1), AC =(4,5,3),则平面ABC 的单位法向量是________.解析:设平面ABC 的法向量n =(x ,y,1),则n ⊥ AB且n ⊥ AC ,即n ² AB=0,且n ²AC =0.即⎩⎪⎨⎪⎧2x +2y +1=0,4x +5y +3=0,即⎩⎪⎨⎪⎧x =12,y =-1,∴n =(12,-1,1),单位法向量为±n |n |=±(13,-23,23). 答案:(13,-23,23)或(-13,23,-23)8.在如右图所示的正方体A 1B 1C 1D 1-ABCD 中,E 是C 1D 1的中点,正方体的棱长为2,则异面直线DE 与AC 所成角的余弦值为________.解析:分别以DA ,DC ,DD 1为x ,y ,z 轴建立空间直角坐标系,则C (0,2,0),E (0,1,2),A (2,0,0),AC =(-2,2,0),DE=(0,1,2), ∴cos 〈 AC , DE 〉=1010.答案:10109.正四棱锥S -ABCD 中,O 为顶点在底面上的射影,P 为侧棱SD 的中点,且SO =OD ,则直线BC 与平面PAC 所成的角是________.解析:如图,以O 为原点建立空间直角坐标系O -xyz .设OD =SO =OA =OB =OC =a ,则A (a,0,0),B (0,a,0),C (-a,0,0),P (0,-a 2,a2),则 CA =(2a,0,0) AP =(-a ,-a 2,a2), CB =(a ,a,0),设平面PAC 的法向量为n ,可求得n =(0,1,1),则cos 〈 CB ,n 〉= CB²n | CB |²|n |=a 2a 2²2=12,∴〈 CB,n 〉=60°.∴直线BC 与平面PAC 所成的角为90°-60°=30°.答案:30° 三、解答题10.如图,在△ABC 中,∠ABC =60°,∠BAC =90°,AD 是BC 上的高,沿AD 把△ABD 折起,使∠BDC =90°.(1)证明:平面ADB ⊥平面BDC ;(2)设E 为BC 的中点,求 AE 与 DB夹角的余弦值.解:(1)证明:∵折起前AD 是BC 边上的高, ∴当△ABD 折起后,AD ⊥DC ,AD ⊥DB . 又DB ∩DC =D , ∴AD ⊥平面BDC . ∵AD ⊂平面ABD , ∴平面ABD ⊥平面BDC .(2)由∠BDC =90°及(1)知DA ,DB ,DC 两两垂直,不妨设|DB |=1,以D 为坐标原点,以 DB , DC , DA所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,易得D (0,0,0),B (1,0,0),C (0,3,0),A (0,0,3),E (12,32,0),∴ AE =(12,32,-3), DB =(1,0,0),∴ AE 与 DB夹角的余弦值为cos 〈AE ,DB 〉=AE ²DB| AE|²| DB |=12224³1=2222. 11.(2012²温州模拟)已知四棱锥P -ABCD 的底面为直角梯形,AB ∥DC ,∠DAB =90°,PA ⊥底面ABCD ,且PA =AD =DC =12,AB =1,M 是PB 的中点.(1)证明:平面PAD ⊥平面PCD ; (2)求AC 与PB 所成的角;(3)求平面AMC 与平面BMC 所成二面角的余弦值.解:以A 为坐标原点,AD 长为单位长度,如图建立空间直角坐标系,则各点坐标为A (0,0,0),B (0,2,0),C (1,1,0),D (1,0,0),P (0,0,1),M (0,1,12).(1)证明:因 AP =(0,0,1), DC =(0,1,0),故 AP² DC =0,所以AP ⊥DC .由题设知AD ⊥DC ,且AP 与AD 是平面PAD 内的两条相交直线,由此得DC ⊥平面PAD . 又DC 在平面PCD 上,故面PAD ⊥面PCD .(2)因 AC =(1,1,0), PB=(0,2,-1),故| AC |=2,| PB |=5, AC ² PB=2,所以cos< AC , PB >=AC ² PB| AC |²| PB |=105.(3)在MC 上取一点N (x ,y ,z ),则存在λ∈R ,使 NC =λ MC, NC =(1-x,1-y ,-z ), MC =(1,0,-12),∴x =1-λ,y =1,z =12λ.要使AN ⊥MC ,只需 AN ² MC =0即x -12z =0,解得λ=45.可知当λ=45时,N 点坐标为(15,1,25),能使 AN² MC =0.此时,AN =(15,1,25), BN =(15,-1,25),有 BN² MC =0由 AN ² MC =0, BN² MC =0得AN ⊥MC ,BN ⊥MC .所以∠ANB 为所求二面角的平面角.∵| AN |=305,| BN |=305, AN ² BN =-45.∴cos 〈AN , BN 〉=AN ² BN | AN |²| BN |=-23.∴平面AMC 与平面BMC 所成角的余弦值为-23.12.(2011²福建高考)如图,四棱锥P -ABCD 中,PA ⊥底面ABCD .四边形ABCD 中,AB⊥AD ,AB +AD =4,CD =2,∠CDA =45°.(1)求证:平面PAB ⊥平面PAD ; (2)设AB =AP .(ⅰ)若直线PB 与平面PCD 所成的角为30°,求线段AB 的长;(ⅱ)在线段AD 上是否存在一个点G ,使得点G 到点P 、B 、C 、D 的距离都相等?说明理由.解:(1)证明:因为PA ⊥平面ABCD ,AB ⊂平面ABCD ,所以PA ⊥AB .又AB ⊥AD ,PA ∩AD =A , 所以AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)以A 为坐标原点,建立空间直角坐标系A -xyz (如图).在平面ABCD 内,作CE ∥AB 交AD 于点E , 则CE ⊥AD .在Rt△CDE 中,DE =CD ²cos 45°=1,CE =CD ²sin 45°=1.设AB =AP =t ,则B (t,0,0),P (0,0,t ). 由AB +AD =4得AD =4-t ,所以E (0,3-t,0),C (1,3-t,0),D (0,4-t,0),CD =(-1,1,0), PD=(0,4-t ,-t ).(ⅰ)设平面PCD 的一个法向量为n =(x ,y ,z ),由n ⊥ CD ,n ⊥ PD ,得⎩⎪⎨⎪⎧-x +y =0,4-t y -tz =0.取x =t ,得平面PCD 的一个法向量n =(t ,t,4-t ).又 PB=(t,0,-t ),故由直线PB 与平面PCD 所成的角为30°得cos 60°=|n ² PB|n |²| PB ||, 即|2t 2-4t |t 2+t 2+4-t 2²2t 2=12, 解得t =45或t =4(舍去,因为AD =4-t >0),所以AB =45.(ⅱ)假设在线段AD 上存在一个点G ,使得点G 到P ,B ,C ,D的距离都相等,设G (0,m,0)(其中0≤m ≤4-t ),则 GC=(1,3-t -m,0), GD=(0,4-t -m,0), GP=(0,-m ,t ).由| GC |=| GD |得12+(3-t -m )2=(4-t -m )2, 即t =3-m ;(1)由| GD |=| GP |得(4-t -m )2=m 2+t 2.(2)由(1)、(2)消去t ,化简得m 2-3m +4=0.(3)由于方程(3)没有实数根,所以在线段AD 上不存在一个点G ,使得点G 到点P 、C 、D 的距离都相等.从而,在线段AD 上不存在一个点G ,使得点G 到点P 、B 、C 、D 的距离都相等。
高三数学第一轮复习课时作业(43)立体几何中的向量方法(二)——空间角与距离求解
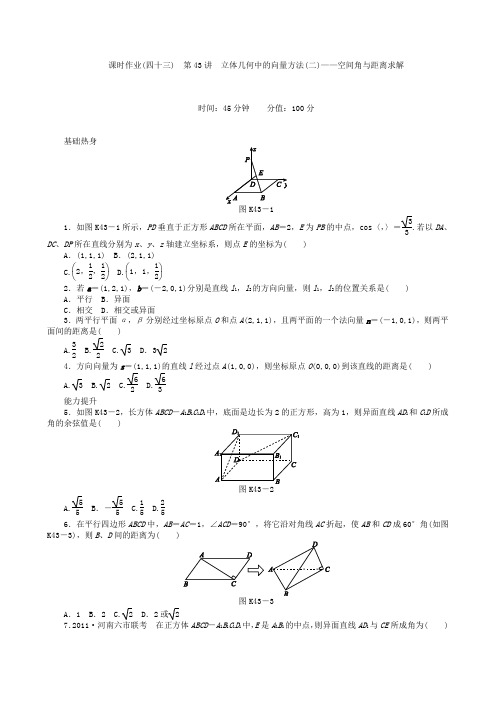
课时作业(四十三) 第43讲 立体几何中的向量方法(二)——空间角与距离求解时间:45分钟 分值:100分基础热身1.如图K43-1所示,PD 垂直于正方形ABCD 所在平面,AB =2,E 为PB 的中点,cos 〈,〉=33.若以DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立坐标系,则点E 的坐标为( )A .(1,1,1)B .(2,1,1)C.⎝⎛⎭⎫2,12,12D.⎝⎛⎭⎫1,1,122.若a =(1,2,1),b =(-2,0,1)分别是直线l 1,l 2的方向向量,则l 1,l 2的位置关系是( ) A .平行 B .异面C .相交D .相交或异面3.两平行平面α,β分别经过坐标原点O 和点A (2,1,1),且两平面的一个法向量n =(-1,0,1),则两平面间的距离是( )A.32B.22C. 3 D .3 2 4.方向向量为s =(1,1,1)的直线l 经过点A (1,0,0),则坐标原点O (0,0,0)到该直线的距离是( ) A. 3 B. 2 C.62 D.63能力提升5.如图K43-2,长方体ABCD -A 1B 1C 1D 1中,底面是边长为2的正方形,高为1,则异面直线AD 1和C 1D 所成角的余弦值是( )A.55 B .-55 C.15 D.256.在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 和CD 成60°角(如图K43-3),则B 、D 间的距离为( )图K43A .1 B .2 C. 2 D .2或 2 7.2011·河南六市联考 在正方体ABCD -A 1B 1C 1D 1中,E 是A 1B 1的中点,则异面直线AD 1与CE 所成角为( )A.π6B.π4C.π3D.π28.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为( )A. 3B.22 C.2λ3 D.559.如图K43-4,四棱锥P -ABCD 中,底面ABCD 是矩形,PD ⊥平面ABCD ,且PD =AD =1,AB =2,点E 是AB 上一点,当二面角P -EC -D 的平面角为π4时,AE =( )A .1 B.12C .2- 2D .2- 310.已知三棱锥O -ABC 的侧棱OA ,OB ,OC 两两垂直,E 为OC 的中点,且OA =1,OB =OC =2,则平面EAB 与平面ABC 夹角的余弦值是________.11.如图K43-5,已知四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为a 的正方形,侧棱AA 1长为b ,且AA 1与A 1B 1,A 1D 1的夹角都是60°,则AC 1的长等于________.-5K43-612.如图K43-6,AO ⊥平面α,BC ⊥OB ,BC 与平面α的夹角为30°,AO =BO =BC =a ,则AC =________________________________________________________________________.13.如图K43-7,在空间直角坐标系中有棱长为a 的正方体ABCD -A 1B 1C 1D 1,点M 是线段DC 1上的动点,则点M 到直线AD 1距离的最小值为________.14.(10分)如图K43-8,放置在水平面上的组合体由直三棱柱ABC -A 1B 1C 1与正三棱锥B -ACD 组成,其中,AB ⊥BC .它的主视图、俯视图、左视图的面积分别为22+1,22+1,1.(1)求直线CA 1与平面ACD 所成角的正弦值;(2)在线段AC 1上是否存在点P ,使B 1P ⊥平面ACD ?若存在,确定点P 的位置;若不存在,说明理由.15.(13分)2011·安徽师大附中三模如图K43-9,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE;(3)求直线BF和平面BCE所成角的正弦值.难点突破16.(12分)2011·湖北卷如图K43-10,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.(1)当CF=1时,求证:EF⊥A1C;(2)设二面角C-AF-E的大小为θ,求tanθ的最小值.图K43-10课时作业(四十三)【基础热身】1.A 解析 可知A (2,0,0)、B (2,2,0)、C (0,2,0), 令P (0,0,2m )(m >0),则E (1,1,m ),=(-1,1,m ),=(0,0,2m ),∴cos 〈,〉=2m 21+1+m 2·2m=33,m =1.∴E 的坐标为(1,1,1).2.D 解析 根据共线向量定理,显然a ,b 不平行,所以l 1,l 2的位置关系是相交或异面.3.B 解析 两平面的一个单位法向量n 0=⎝ ⎛⎭⎪⎫-22,0,22,故两平面间的距离d =|·n 0|=22.4.D 解析 直线l 的一个单位法向量s 0=⎝ ⎛⎭⎪⎫33,33,33,向量=(1,0,0),故点O 到直线l 的距离为d =|OA →|2-|OA →·s 0|2=1-⎝⎛⎭⎪⎫332=63.【能力提升】5.C [解析] 建立如图所示的空间直角坐标系.则A (2,0,0),D (0,0,0),D 1(0,0,1),C 1(0,2,1),1=(-2,0,1),=(0,2,1),故异面直线AD 1和C 1D 所成角的余弦值为|cos 〈1,1〉|==15.6.D [解析] ∵∠ACD =90°,∴·=同理·=0,∵AB 和CD 成60°角,∴〈,〉=60°或120°. ∵=++, ∴2=2+2+2+2·+2·+2· =2+2+2+2·=3+2×1×1×cos 〈,〉 =∴||=2或2,即B 、D 间的距离为2或2,故选D.7.D [解析] 建立如图所示的空间直角坐标系,设正方体棱长为1,则有A (0,0,0),D 1(1,0,1),C (1,1,0),E ⎝⎛⎭⎫0,12,1,所以=(1,0,1),=⎝⎛⎭⎫-1,-12,1,∴·=0,即异面直线AD 1与CE 所成角为π2.8.D [解析] 如图,如果过点G 1H ,如果我们能求出向量,那么||就是点G 到平面D 1EF 的距离.在正方体中,建立空间直角坐标系非常方便,因此用坐标的方法,解决这个问题.如图,以射线DA ,DC ,DD 1分别为x ,y ,z 轴的正方向建立空间直角坐标系,则G (1,λ,1),E ⎝⎛⎭⎫1,0,12,=⎝⎛⎭⎫0,-λ,-12,F ⎝⎛⎭⎫1,1,12,=(0,1,0),D 1(0,0,1),1=⎝⎛⎭⎫-1,0,12.过点G 向平面D 1EF 作垂线,垂足为H ,由于点H 在平面D 1EF 内,故存在实数x ,y 使=+x +y 1=⎝⎛⎭⎫-y ,-λ+x ,-12+12y ,由于GH ⊥EF ,GH ⊥ED 1,所以⎩⎨⎧⎝⎛⎭⎫-y ,-λ+x ,-12+12y ·(0,1,0)=0,⎝⎛⎭⎫-y ,-λ+x ,-12+12y ·⎝⎛⎭⎫-1,0,12=0,解得⎩⎪⎨⎪⎧x =λ,y =15,故=⎝⎛⎭⎫-15,0,-25,所以||=55,即点G 到平面D 1EF 的距离是55.9.D [解析] 以D 为原点,射线DA ,DC ,DP 为x ,y ,z 轴正方向建立空间直角坐标系,如图,设E (1,y 0,0)(0≤y 0≤2),则=(-1,2-y 0,0), 设平面PEC 的法向量为n 1=(x ,y ,z ),∴⇒⎩⎨⎧-x +y (2-y 0)=0,2y -z =0⇒x ∶y ∶z =(2-y 0)∶1∶2,记n 1=(2-y 0,1,2),而平面ECD 的法向量n 2=(0,0,1),则二面角P -EC -D 的平面角θ满足cos θ=|cos 〈n 1,n 2〉|=22, ∴cos θ=|n 1·n 2||n 1|·|n 2|=2(2-y 0)2+12+22·122⇒y 0=2- 3.∴当AE =2-3时,二面角P -EC -D 的平面角为π4.10.7618[解析] 以O 为原点,OB ,OC ,OA 分别为x ,y ,z 轴建立空间直角坐标系,则有A (0,0,1),B (2,0,0),C (0,2,0),E (0,1,0).设平面ABC 的法向量为n 1=(x ,y ,z ),则由11n 1⊥知n 1·=2y -z =0,取n 1=(1,1,2).设平面EAB 的法向量为n =(x ,y ,z ),则由n ⊥知n ·=2x -z =0,由n ⊥知n ·=2x -y =0,取n =(1,2,2).则cos 〈n ,n 1〉=n ·n 1|n ||n 1|=1+2+49×6=7618,所以平面EAB 与平面ABC 夹角的余弦值为7618. 11.2a 2+b 2-2ab [解析] 由已知〈1,〉=〈1,〉=120°,〈,〉=90°. |1|2=|1++|2=|1|2+||2+||2+21·+2·+21·=b 2+a 2+a 2-ab -ab =2a 2+b 2-2ab ,故|1|=2a 2+b 2-2ab . 12.2a [解析] =++, 其中〈,〉=〈,〉=90°,〈,〉=120°,故||2=|++|2=||2+||2+||2+2·+2·+2·=3a 2+2a 2cos120°=2a 2,故||=2a ,即AC =2a .13.33a [解析] 设M (0,m ,m )(0≤m ≤a ),=(-a,0,a ),直线AD 1的一个单位方向向量s 0=⎝ ⎛⎭⎪⎫-22,0,22,由=(0,-m ,a -m ),故点M 到直线AD 1的距离d =|MD 1→|2-|MD 1→·s 0|2=m 2+(a -m )2-12(a -m )2=32m 2-am +12a 2,根式内的二次函数当m =--a 2×32=a 3时取最小值32⎝⎛⎫a 32-a ×a 3+12a 2=13a 2,故d 的最小值为33a . 14.[解答] 由已知可得AB ⊥平面BB 1C 1C ,由于三棱锥B -ACD 是正三棱锥,所以CD ⊂平面BB 1C 1C ,D ,B ,B 1三点共线,AB =BC =BD .设AB =a ,BB 1=b .则其主视图和俯视图的面积都是ab +12a 2,左视图的面积是12a 2,根据已知解得a =2,b=2.以点B 为坐标原点,射线BC ,BB 1,BA 分别为x ,y ,z 轴的正方向建立空间直角坐标系,如图,则A (0,0,2),C (2,0,0),D (0,-22,0),A 1(0,2,2). (1)由于三棱锥B -ACD ⎭⎪⎫,23,则BG ⊥平面ACD ,故可取向量n =(1,-1,1)为平面ACD 的一个法向量,=(-2,2,2),故可取v =(1,-2,-1)为直线CA 1的一个方向向量.设直线CA 1与平面ACD 所成角为θ,则sin θ=|cos 〈n ,v 〉|=|n ·v ||n ||v |=223=66.(2)设=m =(2m,2m ,-2m ),则=+=(2m,2m -2,2-2m ),如果B 1P ⊥平面ACD ,则∥n ,即(2m,2m -2,2-2m )=(λ,-λ,λ),由此得方程组⎩⎨⎧2m =λ,①2m -2=-λ,②2-2m =λ,③由①③得m =12,λ=22,代入②则-1=-22,矛盾,这说明不存在满足题目要求的点P .15.[解答] 方法一:(1)证法一:取CE 的中点G ,连接FG 、BG .∵F 为CD 的中点,∴GF ∥DE 且GF =12DE ,∵AB ⊥平面ACD ,DE ⊥平面ACD , ∴AB ∥DE ,∴GF ∥AB .又AB =12DE ,∴GF =AB .又DE =2AB ,∴四边形GFAB 为平行四边形,则AF ∥BG . ∵AF ⊄平面BCE ,BG ⊂平面BCE , ∴AF ∥平面BCE .证法二:取DE 的中点M ,连接AM 、FM , ∵F 为CD 的中点,∴FM ∥CE .∵AB ⊥平面ACD ,DE ⊥平面ACD ,∴DE ∥AB .又AB =12DE =ME ,∴四边形ABEM 为平行四边形,则AM ∥BE . ∵FM 、AM ⊄平面BCE ,CE 、BE ⊂平面BCE , ∴FM ∥平面BCE ,AM ∥平面BCE .又FM ∩AM =M ,∴平面AFM ∥平面BCE . ∵AF ⊂平面AFM , ∴AF ∥平面BCE .(2)证明:∵△ACD 为等边三角形,F 为∴AF ⊥CD .∵DE ⊥平面ACD ,AF ⊂平面ACD ,∴DE ⊥AF . 又CD ∩DE =D ,故AF ⊥平面CDE . ∵BG ∥AF ,∴BG ⊥平面CDE . ∵BG ⊂平面BCE ,∴平面BCE ⊥平面CDE .(3)在平面CDE 内,过F 作FH ⊥CE 于H ,连接BH , ∵平面BCE ⊥平面CDE ,∴FH ⊥平面BCE . ∴∠FBH 为BF 和平面BCE 所成的角. 设AD =DE =2AB =2a ,则FH =CF sin45°=22a , BF =AB 2+AF 2=a 2+(3a )2=2a ,在Rt △FHB 中,sin ∠FBH =FH BF =24. ∴直线BF 和平面BCE 所成角的正弦值为24. 方法二:设AD =DE =2AB =2a ,建立如图所示的坐标系A -xyz ,则A (0,0,0),C (2a,0,0),B (0,0,a ),D (a ,3a,0),E (a ,3a,2a ).∵F 为CD 的中点,∴F ⎝ ⎛⎭⎪⎫32a ,32a ,0.(1)证明:=⎝ ⎛⎭⎪⎫32a ,32a ,0,=(a ,3a ,a ),=(2a,0,-a ),∵=12(+),AF ⊄平面BCE ,∴AF ∥平面BCE .(2)证明:∵=⎝ ⎛⎭⎪⎫32a ,32a ,0,=(-a ,3a,0),=(0,0,-2a ),∴·=0,·=0,∴⊥,⊥.∴⊥平面CDE ,又AF ∥平面BCE , ∴平面BCE ⊥平面CDE .(3)设平面BCE 的法向量为n =(x ,y ,z ),由n ·=0,n ·=0可得x +3y +z =0,2x -z =0,取n =(1,-3,2).又=⎝ ⎛⎭⎪⎫32a ,32a ,-a ,设BF 和平面BCE 所成的角为θ,则sin θ==2a 2a ·22=24.∴直线BF 和平面BCE 所成角的正弦值为24. 【难点突破】16.[解答] 解法1:过E 作EN ⊥AC 于N ,连接EF .(1)如图①,连接NF 、AC 1,由直棱柱的性质知,底面ABC ⊥侧面A 1C ,又底面ABC ∩侧面A 1C =AC ,且EN ⊂底面ABC ,所以EN ⊥侧面A 1C ,NF 为EF 在侧面A 1C 内的射影, 在Rt △CNE 中,CN =CE cos60°=1,则由CF CC 1=CN CA =14,得NF ∥AC 1.又AC 1⊥A 1C ,故NF ⊥A 1C , 由三垂线定理知EF ⊥A 1C .(2)如图②,连接AF ,过N 作NM ⊥AF 于M ,连接ME , 由(1)知EN ⊥侧面A 1C ,根据三垂线定理得EM ⊥AF ,所以∠EMN 是二面角C -AF -E 的平面角,即∠EMN =θ, 设∠FAC =α,则0°<α≤45°.在Rt △CNE 中,NE =EC ·sin60°=3, 在Rt △AMN 中,MN =AN ·sin α=3sin α, 故tan θ=NE MN =33sin α. 又0°<α≤45°,∴0<sin α≤22, 故当sin α=22,即当α=45°时,tan θ达到最小值, tan θ=33×2=63,此时F 与C 1重合.解法2:(1)建立如图③所示的空间直角坐标系,则由已知可得A (0,0,0),B (23,2,0),C (0,4,0),A 1(0,0,4),E (3,3,0),F (0,4,1),于是=(0,-4,4),=(-3,1,1),则·=(0,-4,4)·(-3,1,1)=0-4+4=0,故EF ⊥A 1C .(2)设CF =λ(0<λ≤4),平面AEF 的一个法向量为m =(x ,y ,z ),则由(1)得F (0,4,λ), =(3,3,0),=(0,4,λ),于是由m ⊥,m ⊥可得即⎩⎪⎨⎪⎧3x +3y =0,4y +λz =0,取m =(3λ,-λ,4),又由直三棱柱的性质可取侧面A 1C 的一个法向量为n =(1,0,0),于是由θ为锐角可得cos θ=|m·n||m|·|n|=3λ2λ2+4,sin θ=λ2+162λ2+4,所以tan θ=λ2+163λ=13+163λ2, 由0<λ≤4,得1λ≥14,即tan θ≥13+13=63, 故当λ=4,即点F 与点C 1重合时,tan θ取得最小值63.。
高考数学一轮复习课后限时集训42立体几何中的向量方法理含解析北师大版

则 =(0,-1,1), =(2,0,2),
∴ · =2,
∴cos〈 , 〉= = ,
∴EF和BC1所成的角为60°.]
7.在正四棱柱ABCDA1B1C1D1中,AA1=2AB,则CD与平面BDC1夹角的正弦值等于________.
[以D为坐标原点,建立空间直角坐标系,如图,设AA1=2AB=2,则D(0,0,0),C(0,1,0),B(1,1,0),C1(0,1,2),则 =(0,1,0), =(1,1,0), =(0,1,2).
A. B.
C. D.
B[建立空间直角坐标系如图.
则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2), =(-1,0,2), =(-1,2,1),cos〈 , 〉= = .
所以异面直线BC1与AE夹角的余弦值为 .]
2.如图,在三棱柱ABCA1B1C1中,底面为等边三角形,侧棱垂直于底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F= CC1,则异面直线A1E与AF夹角的余弦值为( )
[如图所示,建立空间直角坐标系,则依题意可知,
D ,C(1,1,0),S(0,0,1),
可知 = 是平面SAB的一个法向量.
设平面SCD的一个法向量n=(x,y,z),
因为 = ,
= ,
所以n· =0,n· =0,
即 -z=0, +y=0.
令x=2,则有y=-1,z=1,
所以n=(2,-1,1).
设平面SCD与平面SAB所成的锐二面角为θ,
[解]依题意,可以建立以D为原点,分别以 , , 的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),可得
高三数学一轮复习课时作业3:立体几何中的向量方法

9.7立体几何中的向量方法A 级 基础达标1.平面α经过三点A (-1,0,1),B (1,1,2),C (2,-1,0),则下列向量中与平面α的法向量不垂直的是( )A .(12,-1,-1)B .(6,-2,-2)C .(4,2,2)D .(-1,1,4)2.在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为棱AA 1和BB 1的中点,则sin 〈CM →,D 1N →〉的值为( )A.19B.495C.295 D.233.如图,平面ABCD ⊥平面ABEF ,四边形ABCD 是正方形,四边形ABEF 是矩形,且AF =12AD =a ,G 是EF 的中点,则GB 与平面AGC 所成角的正弦值为( )A.66B.33C.63D.234.如图所示,ABCD -A 1B 1C 1D 1是棱长为6的正方体,E 、F 分别是棱AB 、BC 上的动点,且AE =BF .当A 1、E 、F 、C 1共面时,平面A 1DE 与平面C 1DF 所成二面角的余弦值为( )A.32B.12C.15D.2655.『2014·天津十校联考』如图,在四棱锥P -ABCD 中,侧面P AD 为正三角形,底面ABCD 为正方形,侧面P AD ⊥底面ABCD ,M 为底面ABCD 内的一个动点,且满足MP =MC ,则点M 在正方形ABCD 内的轨迹为( )6.如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的和的值为________.7.『2014·佛山质检』已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.8.『2014·合肥调研』已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是________.9.设动点P 在棱长为1的正方体ABCD -A 1B 1C 1D 1的对角线BD 1上,记D 1PD 1B =λ.当∠APC 为钝角时,λ的取值范围是________.10.『2013·江苏高考』如图,在直三棱柱A 1B 1C 1-ABC 中,AB ⊥AC ,AB =AC =2,A 1A =4,点D 是BC 的中点.(1)求异面直线A 1B 与C 1D 所成角的余弦值; (2)求平面ADC 1与平面ABA 1夹角的正弦值.11.『2013·天津高考』如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB ∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.(1)证明:B1C1⊥CE;(2)求二面角B1-CE-C1的正弦值;(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为26,求线段AM的长.12. 『2013·江西七校高三联考』如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.(1)求证:AC⊥平面BDE;(2)求二面角F-BE-D的余弦值;(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.B级知能提升1.『2014·皖北五校联考』在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为()A.64B.-64C.104D.-1042.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1-DC-C1的大小为60°,则AD的长为()A. 2B.3C .2 D.223.『2013·重庆高考』如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,BC =CD =2,AC =4,∠ACB =∠ACD =π3,F 为PC 的中点,AF ⊥PB .(1)求P A 的长;(2)求二面角B -AF -D 的正弦值.解析及答案05限时规范特训A 级 基础达标1.『解析』设平面α的法向量为n ,则n ⊥AB →,n ⊥AC →,n ⊥BC →,所有与AB →(或AC →、BC →)平行的向量或可用AB →与AC →线性表示的向量都与n 垂直,故选D.『答案』D2.『解析』设正方体的棱长为2,以D 为坐标原点,DA 为x 轴,DC 为y 轴,DD 1为z轴建立空间直角坐标系(如图),可知CM →=(2,-2,1),D 1N →=(2,2,-1),cos 〈CM →,D 1N →〉=-19,sin 〈CM →,D 1N →〉=459.『答案』B3.『解析』如图,以A 为原点建立空间直角坐标系,则A (0,0,0),B (0,2a,0),C (0,2a,2a ),G (a ,a,0),F (a,0,0),AG →=(a ,a,0),AC →=(0,2a,2a ),BG →=(a ,-a ,0),BC →=(0,0,2a ),设平面AGC 的法向量为n 1=(x 1,y 1,1),由⎩⎪⎨⎪⎧AG →·n 1=0,AC →·n 1=0⇒⎩⎪⎨⎪⎧ ax 1+ay 1=02ay 1+2a =0⇒⎩⎪⎨⎪⎧x 1=1,y 1=-1⇒n 1=(1,-1,1). sin θ=BG →·n 1|BG →||n 1|=2a 2a×3=63.『答案』C4.『解析』以D 为原点,DA 、DC 、DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,易知当E (6,3,0)、F (3,6,0)时,A 1、E 、F 、C 1共面,设平面A 1DE 的法向量为n 1=(a ,b ,c ),依题意得⎩⎪⎨⎪⎧n 1·DE →=6a +3b =0,n 1·DA 1→=6a +6c =0,可取n 1=(-1,2,1),同理可得平面C 1DF 的一个法向量为n 2=(2,-1,1),故平面A 1DE 与平面C 1DF 所成二面角的余弦值为|n 1·n 2||n1|·|n 2|=12.故选B.『答案』B5.『解析』以D 为原点,DA 、DC 所在直线分别为x 、y 轴建系如图:设M (x ,y,0),设正方形边长为a ,则P (a 2,0,32a ),C (0,a,0),则|MC |=x 2+y -a2,|MP |=x -a22+y 2+32a 2.由|MP |=|MC |得x =2y ,所以点M 在正方形ABCD 内的轨迹为直线y =12x 的一部分.『答案』A6.『解析』以D 1A 1、D 1C 1、D 1D 分别为x ,y ,z 轴建立空间直角坐标系,设CE =x ,DF =y ,则易知E (x,1,1),B 1(1,1,0),∴B 1E →=(x -1,0,1),又F (0,0,1-y ),B (1,1,1),∴FB →=(1,1,y ),由于AB ⊥B 1E ,故若B 1E ⊥平面ABF ,只需FB →·B 1E →=(1,1,y )·(x -1,0,1)=0⇒x +y =1.『答案』17. 『解析』如图建立空间直角坐标系,AB →=(0,1,0),AD 1→=(-1,0,1),AE →=(0,12,1),设平面ABC 1D 1的法向量为n =(x ,y ,z ),由n ·AB →=0,n ·AD 1→=0,可解得n =(1,0,1)设直线AE 与平面ABC 1D 所成的角为θ,则sin θ=|AE →·n ||AE →|·|n |=105『答案』1058.『解析』如图建立空间直角坐标系D -xyz , 则A 1(2,0,4),A (2,0,0), B 1(2,2,4),D 1(0,0,4), AD 1→=(-2,0,4), AB 1→=(0,2,4),AA 1→=(0,0,4),设平面AB 1D 1的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·AD 1→=0,n ·AB 1→=0,即⎩⎪⎨⎪⎧-2x +4z =0,2y +4z =0, 解得x =2z 且y =-2z ,不妨设n =(2,-2,1), 设点A 1到平面AB 1D 1的距离为d ,则d =|AA 1→·n ||n |=43.『答案』439.『解析』本题主要考查了用空间向量求直线间的夹角,一元二次不等式的解法,意在考查考生的空间想象能力以及运算求解能力.以DA →、DC →、DD 1→为单位正交基底,建立如图所示的空间直角坐标系D -xyz ,则有A (1,0,0),B (1,1,0),C (0,1,0),D 1(0,0,1),则D 1B →=(1,1,-1),得D 1P →=λD 1B →=(λ,λ,-λ),所以P A →=PD 1→+D 1A →=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),PC →=PD 1→+D 1C →=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC 不是平角,所以∠APC 为钝角等价于P A →·PC →<0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得13<λ<1,因此λ的取值范围是(13,1).『答案』(13,1)10.『解』(1)以A 为坐标原点,建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (0,2,0),D (1,1,0),A 1(0,0,4),C 1(0,2,4),∴A 1B →=(2,0,-4),C 1D →=(1,-1,-4).∵cos 〈A 1B →,C 1D →〉=A 1B →·C 1D →|A 1B →||C 1D →|=1820×18=31010,∴异面直线A 1B 与C 1D 所成角的余弦值为31010.(2)设平面ADC 1的法向量为n 1=(x ,y ,z ),∵AD →=(1,1,0),AC 1→=(0,2,4),∴n 1·AD →=0,n 1·AC 1→=0,即x +y =0且2y +4z =0,取z =1,得x =2,y =-2,∴n 1=(2,-2,1)是平面ADC 1的一个法向量.取平面AA 1B 的一个法向量为n 2=(0,1,0),设平面ADC 1与平面ABA 1夹角的大小为θ.由cos θ=|n 1·n 2||n 1||n 2|=29×1=23,得sin θ=53.因此,平面ADC 1与平面ABA 1夹角的正弦值为53. 11. 『解』本题可通过建立空间坐标系求解.如图,以点A 为原点建立空间直角坐标系,依题意得A (0,0,0),B (0,0,2),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0).(1)证明:易得B 1C 1→=(1,0,-1),CE →=(-1,1,-1),于是B 1C 1→·CE →=0,∴B 1C 1⊥CE .(2)B 1C →=(1,-2,-1).设平面B 1CE 的法向量m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·B 1C →=0,m ·CE →=0,即⎩⎪⎨⎪⎧x -2y -z =0,-x +y -z =0. 消去x ,得y +2z =0,不妨令z =1,可得一个法向量为m =(-3,-2,1).由(1),B 1C 1⊥CE ,又CC 1⊥B 1C 1,可得B 1C 1⊥平面CEC 1,故B 1C 1→=(1,0,-1)为平面CEC 1的一个法向量.于是cos 〈m ,B 1C 1→〉=m ·B 1C 1→|m |·|B 1C 1→|=-414×2=-277,从而sin 〈m ,B 1C 1→〉=217,故二面角B 1-CE -C 1的正弦值为217. (3)AE →=(0,1,0),EC 1→=(1,1,1).设EM →=λEC 1→=(λ,λ,λ),0≤λ≤1,有AM →=AE →+EM →=(λ,λ+1,λ).可取AB →=(0,0,2)为平面ADD 1A 1的一个法向量.设θ为直线AM 与平面ADD 1A 1所成的角,则sin θ=|cos 〈AM →,AB →〉|=|AM →·AB →||AM →|·|AB →|=2λλ2+λ+12+λ2×2=λ3λ2+2λ+1. 于是λ3λ2+2λ+1=26,解得λ=13(λ=-15舍去),∴AM = 2.12. 『解』(1)∵DE ⊥平面ABCD ,∴DE ⊥AC ,∵ABCD 是正方形,∴AC ⊥BD ,又DE ∩BD =D ,∴AC ⊥平面BDE .(2)∵DE ⊥平面ABCD ,∴∠EBD 就是BE 与平面ABCD 所成的角,即∠EBD =60°. ∴EDBD= 3.由AD =3,得DE =36,AF = 6.如图所示,分别以DA ,DC ,DE 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,则A (3,0,0),F (3,0,6),E (0,0,36),B (3,3,0),C (0,3,0),∴BF →=(0,-3,6),EF →=(3,0,-26). 设平面BEF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n·BF →=0,n ·EF →=0,即⎩⎨⎧-3y +6z =03x -26z =0.令z =6,则n =(4,2,6). ∵AC ⊥平面BDE , ∴CA →=(3,-3,0)为平面BDE 的一个法向量,∴cos 〈n ,CA →〉=n ·CA →|n |·|CA →|=626×32=1313.又二面角F -BE -D 为锐角,故二面角F -BE -D 的余弦值为1313. (3)依题意,设M (t ,t,0)(0≤t ≤3),则AM →=(t -3,t,0),∴AM ∥平面BEF ,∴AM →·n =0, 即4(t -3)+2t =0,解得t =2.∴点M 的坐标为(2,2,0),此时DM →=23DB →,∴点M 是线段BD 上靠近B 点的三等分点.B 级 知能提升1.『解析』取AC 中点E ,连接BE ,则BE ⊥AC , 如图,建立空间直角坐标系B -xyz , 则A (32,12,0),D (0,0,1), 则AD →=(-32,-12,1). ∵平面ABC ⊥平面AA 1C 1C ,BE ⊥AC , ∴BE ⊥平面AA 1C 1C . ∴BE →=(32,0,0)为平面AA 1C 1C 的一个法向量, ∴cos 〈AD →,BE →〉=-64, 设AD 与平面AA 1C 1C 所成的角为α,∴sin α=|cos 〈AD →,BE →〉|=64,故选A. 『答案』A2.『解析』如图,以C 为坐标原点,CA ,CB ,CC 1所在的直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则C (0,0,0),A (1,0,0),B 1(0,2,2),C 1(0,0,2),设AD =a ,则D 点坐标为(1,0,a ),CD →=(1,0,a ),CB 1→=(0,2,2),设平面B 1CD 的一个法向量为m =(x ,y ,z ).则⎩⎪⎨⎪⎧m ·CB 1→=0m ·CD →=0⇒⎩⎪⎨⎪⎧2y +2z =0x +az =0,令z =-1, 得m =(a,1,-1),又平面C 1DC 的一个法向量为n (0,1,0), 则由cos60°=m ·n |m ||n |,得1a 2+2=12,即a =2,故AD = 2. 『答案』A3.『解』(1)如图,连接BD 交AC 于O ,∵BC =CD ,即△BCD 为等腰三角形,又AC平分∠BCD ,故AC ⊥BD ,以O 为坐标原点,OB →,OC →,AP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz ,则OC =CD cos π3=1,而AC =4,得AO =AC -OC=3,又OD =CD sin π3=3,故A (0,-3,0),B (3,0,0),C (0,1,0),D (-3,0,0).∵P A ⊥底面ABCD ,可设P (0,-3,z ),由F 为PC 边中点,得F (0,-1,z2),∴AF →=(0,2,z 2),PB →=(3,3,-z ),∵AF ⊥PB ,∴AF →·PB →=0,即6-z 22=0,z =23(舍去-23),∴|P A →|=2 3.(2)由(1)知AD →=(-3,3,0),AB →=(3,3,0),AF →=(0,2,3).设平面F AD 的法向量为n 1=(x 1,y 1,z 1),平面F AB 的法向量为n 2=(x 2,y 2,z 2),由n 1·AD →=0,n 1·AF →=0,得⎩⎨⎧-3x 1+3y 1=0,2y 1+3z 1=0,因此可取n 1=(3,3,-2), 由n 2·AB →=0,n 2·AF →=0,得⎩⎨⎧3x 2+3y 2=0,2y 2+3z 2=0,故可取n 2=(3,-3,2). 从而法向量n 1,n 2的夹角的余弦值为 cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=18.故二面角B -AF -D 的正弦值为378.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大千教育课时作业(四十二)立体几何中的向量方法(一)——位置关系的证明1.直线l 1,l 2相互平行,则下列向量可能是这两条直线的方向向量的是( ) A .s 1=(0,1,2),s 2=(2,1,0) B .s 1=(0,1,1),s 2=(1,1,0)C .s 1=(1,1,2),s 2=(2,2,4)D .s 1=(1,1,1),s 2=(-1,2,-1)2.直线l 1,l 2相互垂直,则下列向量可能是这两条直线的方向向量的是( ) A .s 1=(1,1,2),s 2=(2,-1,0) B .s 1=(0,1,-1),s 2=(2,0,0)C .s 1=(1,1,1),s 2=(2,2,-2)D .s 1=(1,-1,1),s 2=(-2,2,-2)3.若直线l ∥平面α,直线l 的方向向量为s ,平面α的法向量为n ,则下列结论正确的是( )A .s =(-1,0,2),n =(1,0,-1)B .s =(-1,0,1),n =(1,2,-1)C .s =(-1,1,1),n =(1,2,-1)D .s =(-1,1,1),n =(-2,2,2)4.若直线l ⊥平面α,直线l 的方向向量为s ,平面α的法向量为n ,则下列结论正确的是( )A .s =(1,0,1),n =(1,0,-1)B .s =(1,1,1),n =(1,1,-2)C .s =(2,1,1),n =(-4,-2,-2)D .s =(1,3,1),n =(2,0,-1) 5.若平面α,β平行,则下面可以是这两个平面的法向量的是( ) A .n 1=(1,2,3),n 2=(-3,2,1) B .n 1=(1,2,2),n 2=(-2,2,1)C .n 1=(1,1,1),n 2=(-2,2,1)D .n 1=(1,1,1),n 2=(-2,-2,-2) 6.若平面α,β垂直,则下面可以是这两个平面的法向量的是( ) A .n 1=(1,2,1),n 2=(-3,1,1) B .n 1=(1,1,2),n 2=(-2,1,1)C .n 1=(1,1,1),n 2=(-1,2,1)D .n 1=(1,2,1),n 2=(0,-2,-2)7.直线l 的方向向量为s =(-1,1,1),平面π的法向量为n =(2,x 2+x ,-x ),若直线l ∥平面π,则x 的值为( )A .-2B .-2 C. 2 D .±2 8.[2011·枣庄模拟] 已知A (1,0,0),B (0,1,0),C (0,0,1),则平面ABC 的单位法向量是( )A .s =±(1,1,1)B .s =±⎝⎛⎭⎫22,22,22 C .s =±⎝⎛⎭⎫33,33,33 D .s =±⎝⎛⎭⎫33,-33,33 9.[2011·宁波调研] 已知非零向量a ,b 及平面α,若向量a 是平面α的法向量,则a ·b =0是向量b 所在直线平行于平面α或在平面α内的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件 10.平面α的一个法向量n =(0,1,-1),如果直线l ⊥平面α,则直线l 的单位方向向量是s =________.11.空间中两个有一条公共边AD 的正方形ABCD 与ADEF ,设M ,N 分别是BD ,AE 的中点,给出如下命题:①AD ⊥MN ;②MN ∥平面CDE ;③MN ∥CE ;④MN ,CE 异面.则所有正确命题的序号为________.12.平面α经过点A (0,0,2)且一个法向量n =(1,-1,-1),则x 轴与该平面的交点坐标是________.13.已知AB →=(1,5,-2),BC →=(3,1,z ),若AB →⊥BC →,BP →=(x -1,y ,-3),且BP ⊥平面ABC ,则实数x ,y ,z 分别为________.14.(10分)如图K42-1,在四棱锥P -ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥BP 交BP 于点F .(1)证明:P A ∥平面EDB ; (2)证明:PB ⊥平面EFD .15.(13分)已知三棱柱ABC -A 1B 1C 1的侧棱垂直于底面,∠BAC =90°,AB =AA 1=2,AC =1,M ,N 分别是A 1B 1,BC 的中点.(1)求证:AB ⊥AC 1;(2)求证:MN ∥平面ACC 1A 1.选做题:16.(12分)如图K42-3,已知棱长都为1的三棱锥O -ABC ,棱OA 的中点为M ,自O 作平面ABC 的垂线,垂足为H ,OH 与平面MBC 交于点I .(1)将OI →用OA →,OB →,OC →表示;(2)P 点分线段MB 的比为t1-t(0<t <1),①将OP →用t ,OA →,OB →表示;②若三点P ,I ,C 在同一直线上,求t 的值; ③若PO ⊥P A ,求t 的值.课时作业(四十二)1.C [解析] 两直线平行则其方向向量平行,根据两向量平行的条件检验知正确选项为C.2.B [解析] 两直线垂直,其方向向量垂直,只有选项B 中的两个向量垂直.3.C [解析] 直线与平面平行,直线的方向向量和平面的法向量垂直,检验知正确选项为C.4.C [解析] 线面垂直时,直线的方向向量平行于平面的法向量,只有选项C 中的两向量平行.5.D [解析] 两个平面平行时其法向量也平行,检验知正确选项为D.6.A [解析] 两个平面垂直时其法向量垂直,只有选项A 中的两个向量垂直.7.D [解析] 线面平行时,直线的方向向量垂直于平面的法向量,故x 2-2=0,解得x =±2.8.C [解析] 先求出平面ABC 的一个法向量,再把其单位化.不难求出其一个法向量是n =(1,1,1),单位化得s =±⎝⎛⎭⎫33,33,33. 9.C [解析] 根据向量与平面平行以及平面的法向量与直线的方向向量之间的关系进行判断.a ·b =0说明向量b 垂直于平面α的法向量,故向量b 与平面α共面,此时向量b 所在的直线平行于平面α或在平面α之内;反之a ·b =0.10.±⎝⎛⎭⎫0,22,-22 [解析] 直线l 的方向向量平行于平面α的法向量,故直线l 的单位方向向量是s =±⎝⎛⎭⎫0,22,-22. 11.①②③ [解析] 如图,设AB →=a ,AD →=b ,AF →=c ,则|a |=|c |且a ·b =c ·b =0.MN →=AN →-AM →=12(b +c )-12(a +b )=12(c -a ),MN →·AD →=12(c -a )·b=12(c ·b -a ·b )=0,故AD ⊥MN ;CE →=c -a =2MN →,故MN ∥CE ,故MN ∥平面CDE ,故①②③正确;④一定不正确.12.(-2,0,0) [解析] 设交点M (x,0,0),AM =(x,0,-2),平面的一个法向量是n =(1,-1,-1),故n ⊥AM →,故x +2=0,得x =-2,故x 轴与该平面的交点坐标是(-2,0,0).13.407,-157,4 [解析] 由题知:BP →⊥AB →,BP →⊥BC →. 所以⎩⎪⎨⎪⎧AB →·BC →=0,BP →·AB →=0,BP →·BC →=0,即⎩⎪⎨⎪⎧1×3+5×1+(-2)×z =0,x -1+5y +(-2)×(-3)=0,3(x -1)+y -3z =0.解得x =407,y =-157,z =4.14.[解答] 证明:以D 为坐标原点,射线DA ,DC ,DP 分别为x ,y ,z 轴的正方向建立空间直角坐标系.设DC =a .(1)连接AC ,AC 交BD 于G ,连接EG .依题意得A (a,0,0),P (0,0,a ),E ⎝⎛⎭⎫0,a 2,a 2. 因为底面ABCD 是正方形,所以G 是此正方形的中心,故点G 的坐标为⎝⎛⎭⎫a 2,a 2,0, 且P A →=(a,0,-a ),EG →=⎝⎛⎭⎫a 2,0,-a 2.所以P A →=2EG →,这表明P A ∥EG .而EG ⊂平面EDB 且P A ⊄平面EDB ,所以P A ∥平面EDB . (2)依题意得B (a ,a,0),PB →=(a ,a ,-a ).DE →=⎝⎛⎭⎫0,a 2,a 2,故PB →·DE →=0+a 22-a 22=0,所以PB ⊥DE ,由已知EF ⊥PB ,且EF ∩DE =E ,所以PB ⊥平面EFD .15.[解答] 依条件可知AB ,AC ,AA 1两两垂直.如图,以点A 为原点建立空间直角坐标系A -xyz .A (0,0,0),B (0,2,0),C (-1,0,0),A 1(0,0,2),B 1(0,2,2),C 1(-1,0,2),M (0,1,2),N ⎝⎛⎭⎫-12,1,0. (1)证明:因为AB →=(0,2,0),AC 1→=(-1,0,2),所以AB →·AC 1→=0×(-1)+2×0+0×2=0.所以AB →⊥AC 1→,即AB ⊥AC 1.(2)证明:因为MN →=⎝⎛⎭⎫-12,0,-2,AB →=(0,2,0)是平面ACC 1A 1的一个法向量, 且MN →·AB →=-12×0+0×2-2×0=0,所以MN →⊥AB →.又MN ⊄平面ACC 1A 1, 所以MN ∥平面ACC 1A 1. 【选做题】16.[解答] (1)据已知,H 是正△ABC 的中心,∴OH →=13(OA →+OB →+OC →),又I 在OH →上,故存在实数λ,使OI →=λOH →=λ3(OA →+OB →+OC →)=λ3(2OM →+OB →+OC →),∵I 在平面MBC 内,故2λ3+λ3+λ3=1,即λ=34,于是OI →=14(OA →+OB →+OC →).(2)①MP →=tMB →,PB →=(1-t )MB →,OP →=OM →+MP →=OM →+tMB →=OM →+t (OB →-OM →)=12OA →+t ⎝⎛⎭⎫OB →-12OA →=1-t 2OA →+tOB →;②P 在直线IC 上,故存在实数m ,使 OP →=(1-m )OC →+mOI →=(1-m )OC →+m 4·OA →+m 4·OB →+m 4·OC →=4-3m 4·OC →+m 4·OA →+m 4·OB →,比较①②中两式可得⎩⎪⎨⎪⎧4-3m4=0,m 4=1-t 2,m 4=t ,解得⎩⎨⎧m =43,t =13,故t 的值为13.③OP →·AP →=⎝⎛⎭⎫1-t 2OA →+tOB →·(OP →-OA →)=⎝⎛⎭⎫1-t 2OA →+tOB →·⎝⎛⎭⎫-1+t 2OA →+tOB →=t 2-14OA →2+t 2OB →2-t 2OA →·OB →=t 2-14·12+t 2·12-t 2·1·1·cos60°=3t 2-14,∵OP →⊥P A →,∴OP →·P A →=0,∴3t 2-14=0,即t =±33,又∵0<t <1,∴t =33即为所求.。
