第20讲-《信号与线性系统》第七章-2
吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解-第7~8章【圣才出品】

7.3
如图
7-4
所示的
RC
带通滤波电路,求其电压比函数
H
s
U2 U1
s s
及其零、极点。
图 7-4 解:电路的 s 域模型图如图 7-5 所示。
时域判别:
hk 0, k 0 系统为因果系统
复频域判别:
的收敛域是收敛半径为 的圆外区域 系统为因果系统,换言
之,
的极点都在收敛域
内部。
(2)稳定性判别
稳定系统定义:一个系统,如果对任意的有界输入,其零状态响应也是有界的,则称该
系统是有界输入有界输出
稳定系统。
①对于连续时间系统
时域判别: s 域判别:
(c)输入阻抗为
则零点为 1
0, 2
1, 3
3 ;极点为
P1
1 2
,
P2
3 2
。
(d)输入阻抗为
Z
s
s s
1 s
s
1s
3 s 3
ss
s2 1s2 3 2ss2 2
则零点为 1,2 j, 3,4 j 3 ;极点为 P1=0, P2,3 j 2 。
7.2 图 7-2(a)和(b)所示是两种三阶巴特沃斯型低通滤波电路,图(a)适用于电
极点 和零点 的值可能是实数、虚数或复数。由于 与 的系数都是实数,所 以零、极点若为虚数或复数,则必共轭成对。
系统的极点确定了 的时域波形形式,对 的幅度和相位均有影响,系统的零点 只影响 的幅度和相位,而对 的时域波形形式无影响。
2.系统的因果性和稳定性
1 / 120
圣才电子书
圣才电子书
十万种考研考证电子书、题库视频学习平台
吴大正《信号与线性系统分析》(第4版)笔记和课后习题考研真题详解

吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解
更多资料请在薇♥号精研学习网查找下载
本书是吴大正主编的《信号与线性系统分析》(第4版)的学习辅导书,主要包括以下内容:
(1)整理教材笔记,浓缩内容精华。
本书每章的复习笔记均对该章的知识点进行了整理,突出重点和考点。
(2)解析课后习题,提供详尽答案。
本书参考相关辅导资料,对教材的课后习题进行了详细的解答。
(3)精选考研真题,巩固重难点知识。
本书精选了多所名校近年的考研真题,并提供了详细的解答。
本书提供电子书及打印版,方便对照复习。
第1章信号与系统
1.1复习笔记
1.2课后习题详解
1.3名校考研真题详解
第2章连续系统的时域分析
2.1复习笔记
2.2课后习题详解
2.3名校考研真题详解
第3章离散系统的时域分析
3.1复习笔记
3.2课后习题详解
3.3名校考研真题详解
第4章傅里叶变换和系统的频域分析4.1复习笔记
4.2课后习题详解
4.3名校考研真题详解
第5章连续系统的s域分析
5.1复习笔记
5.2课后习题详解
5.3名校考研真题详解
第6章离散系统的z域分析
6.1复习笔记
6.2课后习题详解
6.3名校考研真题详解
第7章系统函数
7.1复习笔记
7.2课后习题详解
7.3名校考研真题详解
第8章系统的状态变量分析
8.1复习笔记
8.2课后习题详解8.3名校考研真题详解。
信号与系统课件第七章(电子)

虚轴上的极点:
单极点
p0
p1,2
j
A t
Acost t
响应函数幅度不随时间变化。
r重极点
Ajt j t 或 Ajt j cos t j t
j 0,1,2,, 1
响应随t的增大而增大。
右半开平面的极点:
单极点
p 0
p1,2
j
0
Aet t Ae t cost t
左半开平面
H(s)的极点,在s平面的位置
虚轴
左半开平面的极点:
右半开平面
单极点
p 0
p1,2
j
0
Aet t
Ae t cost t
重极点
Ajt jet t 或 Ajt je t cos t j t
j 0,1,2,, 1
响应函数是衰减的, 当t→∞时,响应趋近于零。
j-pi
j
H ( j ) H (s) s j
j 1 n
( j pi )
pi
n1
0
对于任意极点 p和i 零点 ,j 令
j pi j j
Aie Bje
ji j
j
于是
pi
H ( j )
bm B1B2 Bme j( 1 2 m )
A A A e 1 2
j (1 2 n )
n
H ( j ) e j ( )
单位圆外的极点
单极点
pa a 1
Aak (k)
p1,2
ae j
a 1
Aak cos(k ) (k)
如有重极点,其所对应的响应也随k的增加而增大。
由以上讨论可得如下结论:(因果)
H(z)在单位圆内的极点所对应的响应序列都是 衰减的,当k趋于无限时,响应趋于零。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象,其图像为信号的波形。
根据信号的不同特性,可对信号进行不同的分类:确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;实信号与复信号;能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1(t)±f2(t)或f1(t)×f2(t)两信号f1(·)和f2(·)的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2.反转和平移(1)反转f(-t)f(-t)波形为f(t)波形以t=0为轴反转。
图1-1(2)平移f(t+t0)t0>0,f(t+t0)为f(t)波形在t轴上左移t0;t0<0,f(t+t0)为f(t)波形在t轴上右移t0。
图1-2平移的应用:在雷达系统中,雷达接收到的目标回波信号比发射信号延迟了时间t0,利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3.尺度变换f(at)若a>1,则f(at)波形为f(t)的波形在时间轴上压缩为原来的;若0<a<1,则f(at)波形为f(t)的波形在时间轴上扩展为原来的;若a<0,则f(at)波形为f(t)的波形反转并压缩或展宽至。
信号与系统第七章课后答案
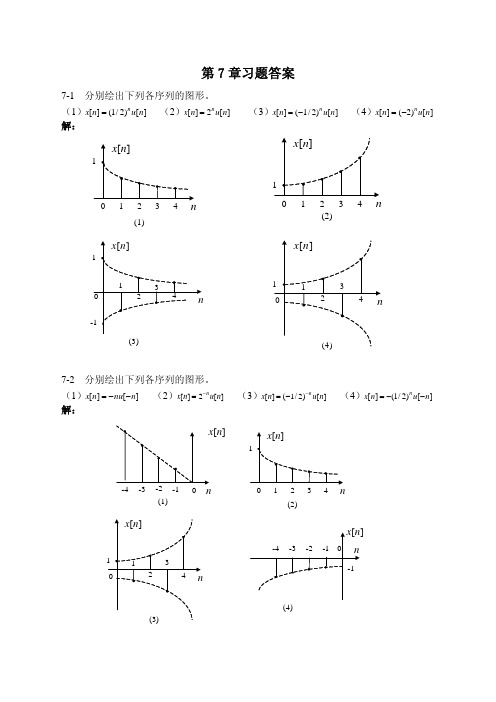
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与线性系统分析-第7章

2
σ
根据初值定理,有
Ks h(0 ) lim sH ( s ) lim 2 K s s s 2 s 5
2s H ( s) 2 s 2s 5
第 3页
二、系统函数H(· )与系统的因果性
因果系统是指:系统的零状态响应yzs(.)不会出现于f(.)
第 13 页
§7.2
一、稳定系统的定义
系统的稳定性
一个系统,若对任意的有界输入,其零状态响应 也是有界的,则称该系统是有界输入有界输出(Bound Input Bound Output------ BIBO)稳定的系统,简称为稳 定系统。 即:若系统对所有的激励 |f(.)|≤Mf ,其零状态响应 |yzs(.)|≤My(M为有限常数),则称该系统稳定。
③ H(s)在虚轴上的高阶极点或右半平面上的极点,其 所对应的响应函数都是递增的。 即当t→∞时,响应均趋于∞。系统稳定?
第 8页
复习:s域与z域的关系
z=esT
s
1 ln z 式中T为取样周期 T
如果将s表示为直角坐标形式 s = +j ,将z表示为 极坐标形式 z = ej = eT , = T 由上式可看出: s平面的左半平面(<0)--->z平面的单 位圆内部(z=<1) s平面的右半平面(>0)--->z平面的单位圆外部(z=>1)
第 6页
系统稳定性问题?
系统的稳定性如何?
系统稳定:若系统对所有的激励 |f(.)|≤Mf ,其零状态 响应 |yzs(.)|≤My(M为有限常数),则称该系统稳定。 (2)在虚轴上 (a)单极点p=0或p12=±jβ, 则响应为Kε(t)或Kcos(βt+θ)ε(t)→稳态分量 (b) r重极点,相应A(s)中有sr或(s2+β2)r,其响应函数为
信号与线性系统分析--吴大正课件

第 18 页
解答
(1)sin2t是周期信号,其角频率和周期分别为 ω1= 2 rad/s , T1= 2π/ ω1= πs
cos3t是周期信号,其角频率和周期分别为 ω2= 3 rad/s , T2= 2π/ ω2= (2π/3) s
由于T1/T2= 3/2为有理数,故f1(t)为周期信号,其周期为 T1和T2的最小公倍数2π。 (2) cos2t 和sinπt的周期分别为T1= πs, T2= 2 s,由于 T1/T2为无理数,故f2(t)为非周期信号。
28k4xk15xk2消去xk得yk2yk13yk24fk15fk2xkfk2xk13xk2系统的特性系统的分析方法16系统的特性与分析方法一系统的特性连续系统与离散系统动态系统与即时系统但输入单输出与多输入多输出系统线性系统与非线性系统时不变与时变系统因果系统与非因果系统稳定系统与不稳定系统常用分类方法
按所具有的时间特性划分:
确定信号和随机信号; 连续信号和离散信号;
周期信号和非周其信号; 能量信号和功率信号;
一维信号和多维信号; 因果信号与反因果信号;
实信号与复信号;
左边信号与右边信号。
第 11 页
1. 确定信号和随机信号
•确定性信号:可用确定的时间函数表示的信号:f(t)
但实际传输的信号是不确定的,常受 到各种干扰及噪声的影响。 •随机信号: 取值具有不确定性的信号: 电子系统中的起伏热噪声、雷电干扰信号。 •伪随机信号:貌似随机而遵循严格规律产生的信号: 伪随机码。
第 19 页
离散周期信号举例1
例 判断正弦序列f(k) = sin(βk)是否为周期信号,若是, 确定其周期。
解 f (k) = sin(βk) = sin(βk + 2mπ) , m = 0,±1,±2,…
信号与线性系统分析课件

04 线性系统的响应
系统的冲激响应
冲激响应定义
01
冲激响应是线性系统对单位冲激函数的响应,反映了系统对瞬
时作用的响应特性。
冲激响应计算
02
通过求解线性系统的微分方程或差分方程,可以得到系统的冲
激响应。
冲激响应的物理意义
03
冲激响应可以理解为系统内部能量的传播和分布,是分析系统
动态特性的重要手段。
卷积积分定义
卷积积分是信号处理中常用的一种运算,用于描述两个函数的相互作用。在线性系统中 ,卷积积分用于描述系统的输出与输入之间的关系。
卷积积分的计算
卷积积分的计算涉及到函数乘积的积分,常用的计算方法包括离散卷积和离散化卷积等 。
卷积积分的物理意义
卷积积分可以理解为系统对输入信号的处理和转换能力,是分析系统动态特性的重要手 段。在信号处理中,卷积积分常用于信号滤波、预测和控制系统设计等领域。
03 信号的傅里叶分析
傅里叶级数
傅里叶级数定义
将周期信号表示为无穷多个正弦和余弦函数 的线性组合。
复指数形式
使用复指数函数来表示周期信号。
三角函数形式
使用正弦和余弦函数来表示周期信号。
傅里叶级数的应用
用于分析信号的频率成分和幅度变化。
傅里叶变换
01
02
03
傅里叶变换定义
将时域信号转换为频域信 号,表示信号的频率分布 。
傅里叶变换的性质
线性、时移、频移、共轭 、对称等性质。
傅里叶变换的应用
用于信号处理、图像处理 、通信等领域。
频域分析
频域分析定义
通过分析信号的频率成分 来理解信号的特征和性质 。
频域分析的应用
用于信号滤波、调制解调 、频谱分析等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可得其模拟框图,如下图所示。
y(k n)
e(k)
y(k 1)
D
D y(k)
an1
a1
a0
15
第七章 离散时间系统的时域分析
若描述系统的差分方程中含有输入函数的移位项,如
y(k n) an1 y(k n 1) a0 y(k) bme(k m) bm1e(k m 1) b0e(k)
t → kT :e(t) → e(kT) = e(k) , y(t) → y(kT) = y(k) , y(t+T) → y[(k+1)T] = y(k+1)
dy(t) yk 1T y(kT)
dt
T
6
第七章 离散时间系统的时域分析
y
dy dt
y(k 1) y(k) T
a0
13
第七章 离散时间系统的时域分析
3.N 阶系统后向差分方程的描述与模拟
对于描述一个n阶系统的后向差分方程
y(k) an1y(k 1) a0 y(k n) e(k)
可改写为
y(k) e(k) an1y(k 1)
可得其模拟框图,如下图所示。
y(k)
a0 y(k n)
一般n阶系统的模拟图
bn1
e(k)
q(k n)
q(k 1)
D
q(k n 1)
an1
b1
q(k) D b0
y(k)
a1 a0
一个系统的模拟图与描述其系统的差分方程一一对应,因此可由系统的差分方程作出模 拟图,也可由模拟图求出描述系统的差分方程。
17
3
第七章 离散时间系统的时域分析
例 2 下图示出电阻梯形网络,其中每一串臂电阻都 为R,每一并臂电阻值都为aR,a为某一正实数。每 个节点对地的电压为 u(k) ,k 0,1,2, ,n 。已知两边界 节点电压为 u(0) E ,u(n) 0 。试写出求第k个节点 电压的差分方程式。
u(0) R u(1) R u(2) R
bme(k m) bm1e(k m 1) b1e(k 1) b0e(k)
8
第七章 离散时间系统的时域分析
(二) 差分方程的算子形式
连续系统的微分算子: p d ,
dt
定义: py(t) dy
dt
n阶微分方程的算子形式:
p n
dn dt n
,
1 p
dt
( An p n An1 p n1 A0 ) y(t) (Bm p m Bm1 p m1 B0 )e(t)
y(t) N ( p) e(t), D( p)
H ( p) y(t) N ( p) e(t) D( p)
N ( p) An pn An1 pn1 A0
且m n 时,需引入一个辅助函数q(k,) 使其满足
q(k n) an1q(k n 1) a0q(k) ek
就有
y k bmq(k m) bm1q(k m 1) b0q(k)
于是,其模拟图如下图所示。
16
第七章 离散时间系统的时域分析
aR
R
R
再经整理即得该系统的差分方程
u(k 2) 2a 1u(k 1) u(k) 0 a
再利用u(0) E ,u(n) 0 两个边界条件,即可求得 u(k)。
差分方程与微分方程在形式上相似!
5
第七章 离散时间系统的时域分析
比较
dy(t) Ay(t) Be(t) dt
y(k) y(k 1) e(k) ——后向形式 问题: 怎样由离散系统得到描述该系统的差分方程?
2
第七章 离散时间系统的时域分析
例1 一质点沿水平方向作直线运动,其在某一秒内 所走过的距离等于前一秒所走过距离的2倍,试 列出该质点行程的方程式。
解: 设k秒末,质点的位移为y(k)
某一秒:第(k+1)秒→第(k+2) 秒 位移 [y(k+2) - y(k+1)]
d dt
(
dy ) dt
1 [ y(t 2T ) y(t T ) y(t T ) y(t)]
T
T
T
令t kT
1
y(k 2)
2
y(k 1)
1
y(k)
T2
T2
T2
A2 y(k 2) A1 y(k 1) A0 y(k)
7
第七章 离散时间系统的时域分析
e(k) D
D
an1
a1
a0
14第七章 离散时间系来自的时域分析4.N 阶系统前向差分方程的描述与模拟
对于描述一个n阶系统的前向差分方程
y(k n) an1y(k n 1) a0 y(k) e(k)
可改写为
y(k n) e(k) an1y(k n 1) a0 y(k)
n阶:
dny dt n
An
y(k
n)
An1 y(k
n
1)
A0 y(k)
n阶微分方程:
An
dny dtn
An1
d n1 y dt n1
A1
dy dt
A0 y
Bm
d me dt m
Bm1
d m1e dt m1
B0e
T足够小时可近似为差分方程:
an y(k n) an1 y(k n 1) a1 y(k 1) a0 y(k)
y(k) N (S) e(k) D(S )
H (S) y(k) N(S) e(k) D(S)
——离散时间系统的转移算子
10
第七章 离散时间系统的时域分析
(三)离散时间系统的模拟
离散系统的模拟与连续系统的模拟具有一定的 相似之处。
连续系统模拟采用三种基本元件:加法器、标 量乘法器、积分器。
y(k 1) ay(k) be(k)
可看出,若 y(k) 与 y(t) 相当,则 y(k+1) 与 y'(t) 相当。在
一定条件下可相互转化。
一阶微分方程 dy(t) y(t) e(t)(1)
dt
考虑离散值(T足够小): dy(t) y(t T ) y(t)
dt
T
令t = 0 , T ,2T ,…,kT
D( p) Bm pm Bm1 pm1 B0
9
第七章 离散时间系统的时域分析
离散系统移序算子:S 定义:Sy(k) y(k 1), S n y(k) y(k n),
1 y(k) y(k 1) S
n阶差分方程的算子形式: (an S n an1S n1 a0 ) y(k) (bm S m bm1S m1 b0 )e(k)
离散系统模拟采用三种基本元件:加法器、标 量乘法器、延时器。
11
第七章 离散时间系统的时域分析
1. 基本模拟元件
x(k) D x (k 1)
(a)单位延时器
x(k) x(k ) y(k )
y(k)
(b)加法器
x(k) ax(k )
a
x(k) a ax(k )
x(k) a ax(k )
R u(n 1) R
E
aR
aR
aR
4
R R u(k)
u(k 1)
u(k 2)
ia
ib
aR ic
第七章 离散时间系统的时域分析
解: 为了写出此系统的差分方程 ,画出系统中第k+1个节点。 对于任一节点k+1,运用KCL不 难写出
u(k 1) u(k) u(k 1) u(k 2) u(k 1)
1 T
y(k 1) 1 T
y(k)
A1 y(k
1)
A0 y(k)
代入(1)式得:
y(k 1) (1 T)y(k) Te(k) y(k 1) (1T)y(k) Te(k)
差分方程的阶数:差分方程中未知函数中变量的最高 和最低序号的差值。
二阶:
d2y dt 2
(c)标量乘法器
12
第七章 离散时间系统的时域分析
2.一阶系统的描述与模拟
描述一阶系统的前向差分方程为 y(k 1) a0 y(k) e(k)
y(k 1)
e(k)
D y(k)
a0
描述一阶系统的后向差分方程为 y(k) a0 y(k 1) e(k)
y(k)
e(k) D
第七章
离散时间系统的时域分析 (二)
第七章 离散时间系统的时域分析 7.3、 离散时间系统的描述和模拟
(一)离散系统的描述——差分方程
连续时间系统的数学模型——微分方程 微分方程:一阶 y(t) y(t) e(t) 差分方程:一阶 y(k 1) y(k) e(k) ——前向形式
前一秒:第 k 秒→第(k+1) 秒 位移 [y(k+1) - y(k)]
依题意: y(k 2) y(k 1) 2[y(k 1) y(k)]
即 y(k 2) 3y(k 1) 2y(k) 0
差分方程是处理离散变量的函数关系的一种数学工具,
但离散变量并不限于时间变量。
