江苏大学-常微分方程-4-2 -高阶线性方程解一般理论、基本解组
江苏大学理力考试大纲

江苏大学硕士研究生入学考试理论力学考试大纲I 考查目标科学、公平、有效地测试考生对理论力学基本概念、基本理论和基本方法的掌握程度,以选拔具有发展潜力的优秀人才入学,为国家建设培养具有较强分析与解决实际问题能力的高层次专业人才。
具体来说,要求考生:1.运用力学的基本理论和基本方法熟练进行研究对象的受力分析,求解静力学平衡问题。
2.运用力学的基本理论和基本方法熟练进行运动分析,求解各运动量。
3.运用力学的基本理论和基本方法熟练进行动力学分析及求解动力学综合问题。
II 考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间180分钟。
二、答题方式答题方式为闭卷、笔试。
允许使用计算器,但不得使用带有公式和文本存储功能的计算器。
三、试卷内容与题型结构计算题为主III 考查内容1.静力学(20 ~40%):(1) 掌握各种常见约束类型。
对物体系统能熟练地进行受力分析。
(2) 熟练计算各类力系的主矢和主矩,对各类力系进行简化计算。
(3) 应用各类力系的平衡方程求解单个物体、物体系统和平面桁架的平衡问题(主要是求约束反力和桁架内力问题)。
(4) 考虑滑动摩擦时平面物体系统的平衡问题。
(5) 物体重心的计算2.运动学(20 ~40%):(1) 理解刚体平移和定轴转动的特征。
熟练求解定轴转动刚体的角速度和角加速度,求解定轴转动刚体上各点的速度和加速度。
(2) 掌握点的合成运动的基本概念。
熟练应用点的速度和加速度合成定理求解平面问题中的运动学问题。
(3) 理解刚体平面运动的特征。
熟练应用基点法、瞬心法和速度投影法求平面机构上各点的速度。
能熟练应用基点法求平面机构上各点的加速度。
(4) 运动学的综合应用。
3.动力学(40 ~60%):(1) 能计算动力学中各基本物理量。
(2) 熟练运用动量定理、质心运动定理求解有关动力学问题。
(3) 熟练运用动量矩定理、定轴转动微分方程、平面运动微分方程求解有关动力学问题。
江苏大学-常微分方程-3-7 - 一阶线性方程与常数变易法

2.2 一阶线性方程与常数变易公式(First order linear differential equationand constant variation formula )[教学内容] 1. 认识一阶线性齐次方程和一阶线性非齐次方程; 2.介绍一阶线性非齐次方程的常数变易公式; 3. 介绍电学知识和基尔霍夫定律; 4. 认识Bernoulli 方程及其通过变量替换化为一阶线性方程的解法; 5. 介绍其他可化为一阶线性方程的例子.[教学重难点] 重点是知道一阶线性非齐次方程的解法,难点是如何根据方程的形式引入新的变量变换使得新方程为一阶线性方程.[教学方法] 自学1、4;讲授2、3 课堂练习 [考核目标]1. 熟练运用常数变易公式;2. 知道⎰dx bx sin e ax 计算和一些三角函数恒等式; 3. 知道电学一些知识,如电容电流公式、电感电压公式和基尔霍夫定律; 4. 知道溶液混合问题建模; 5. 认识Bernoulli 方程并会经过适当变换化为线性方程求解. 6. 知道交换自变量和因变量化非线性方程为一阶线性方程.1. 认识一阶线性齐次方程和一阶线性非齐次方程(First order (non)homogeneous linear differential equation ) (1) 称形如y p(x)dxdy=的方程为一阶线性齐次方程,其中p(x)连续; 称形如q(x)y p(x)dxdy+=的方程为一阶线性非齐次齐次方程,其中q(x) p(x),连续且q(x)不恒为零. (2) 当0y ≠时,改写y p(x)dxdy=为 1C dx p(x)|y |ln ,dx p(x)y dy dx, p(x)y dy +===⎰⎰⎰,其中⎰dx p(x)表示P(x)的一个原函数(antiderivative). 因此,y p(x)dxdy =通解(general solution)为1C p(x)dx e C ~,e C ~y =⎰±=,此外y=0也是解. 综上,y p(x)dxdy =的解为C ,e C y p(x)dx⎰=为任意常数. (3) 常数变易法:如何求q(x)y p(x)dxdy+=的解呢? 假定上述线性非齐次方程有如下形式的解 ⎰=p(x)dxeC(x)y ,则代入原方程来确定C(x),q(x)p(x)C(x)e e p(x) C(x)e (x)' C dxdy p(x)dxp(x)dx p(x)dx +⎰=⎰+⎰=, 即q(x)e(x)' C p(x)dx=⎰,C q(x)dx eC(x) q(x), e(x)' C p(x)dx-p(x)dx+⎰=⎰=⎰-,此处C 为任意常数,⎰⎰q(x)dx ep(x)dx-为函数q(x)ep(x)dx-⎰一个原函数.综上,一阶线性非齐次方程的通解为⎰⎰⎰⎰+⎰=+⎰⋅⎰=q(x)dx eeCeC)q(x)dx e(ey(x)p(x)dx-p(x)dxp(x)dxp(x)dx-p(x)dx.2. 一些实际应用例子(Applications ) 例28. 电容器的充电和放电模型RC 电路:假定开始电容C 上没有电荷,电容两端电压为0,合上开关1后,电池E 对电容C 开始充电,电池电压为E ,电阻阻值为R ,电容C 两端电压逐渐上升. 写出充电过程中,电容C 两端电压随时间变化的规律.解:设U(t)表示在时刻t 时电容两端电压,则根据电学知识,电容两端电量Q=U C ,电流I =dtdU C dt dQ =, 电阻两端电压为R I=dt dUR . 由基尔霍夫定律知,闭合回路上压降为零.即有0dt dU RC U E =--. 改写为 RC EU RC 1dt dU +⋅-=,这是一个一阶线性非齐次方程. 记RCE q(t) ,RC 1p(t)=-=, 由常数变易公式得到, C~e E )C ~(Ee e )C ~dt RCE e (e )C ~q(t)dt e(eU(t)RC tRC t RC t RC t RC t p(t)dtp(t)dt----+=+=+=+⎰⎰=⎰⎰再注意到初始条件U(0)=0,-E C ~0,C ~e Ee U(0)00==+=,因此,RC tEe E U(t)--=.例29. 考察如下RL 电路图,设电源E 的电压为0 U sin wt,U E m m >=为常数,求电感线圈上电流I 随时间的变化规律,设t=0时,I=0.解:设I(t)表示时刻t 时电感线圈上电流强度,则由电学知识有,电感线圈两端电压为dtdI L . 由基尔霍夫定律知,闭合回路电压降为零. 于是 0dtdIL I R E =--. 改写为sin wt U L1L I R dt dIm +-=, 这是一个一阶线性非齐次方程. 记wt sin L Uq(t) ,L R p(t)m =-=, 由常数变易公式得到,)C ~dt sin wt LU e (e )C ~q(t)dt e(eI(t)m L RtL Rt p(t)dtp(t)dt⎰⎰+=+⎰⎰=--.b a bt cos b bt sin a e bt))isin bt (cos e b a ib)(a Im()e ib a 1Im()dt e Im(dt )Im(e e dt bt sin e 22at a 22ib)t(a ib)t (a ibt at at +-=+⋅+-=+===++⎰⎰⎰22t LR m LRtm m LRt w (R/L) wt)cos w sin wt L R(e LU dt sin wt e LUdt sin wt L U e+-==⎰⎰令2222w(R/L)w φsin ,w(R/L)R/L φ cos +-=+=,于是由B sin A cos B cos A sin B)sin(A +=+知,22t LR mm LRt w (R/L)φ)sin(wt e L U dt sin wt L U e++=⎰,于是L Rt22m e C ~w (R/L)φ)sin(wt LU I(t)-+++=.再注意到初始条件I(0)=0,22m0022m w(R/L)φsin L U C ~0,C ~e e w (R/L)φsin LU I(0)+-==++=,因此,t LR 22m22mew(R/L)sin(φL Uw (R/L)φ)sin(wt LUI(t)-+-++=).练习23. (1) 求dt bt cos e at ⎰; (2) 改写 t cos b sin t a +为θ)sin(t ba 122++,给出θ所满足的条件. (3) 由 Euler 公式b sin i b cos e ib+=和R b a, ,e e e b)i(a b i a i ∈=⋅+推导出:b asin sin b cos a cos b)cos(a b,sin a cos b cos a sin b)sin(a -=++=+和b))sin(a b)(sin(a 21b cos a sin -++=, b))cos(a b)(cos(a 21b cos a cos -++=. 作业24. (1) 如例28中RC 电路图,设E=10V , R=100Ω, C=0.01 F, 开始时刻电容C 上电压为零并在此刻合上开关1,问经过多长时间电容C 两端电压为V 5U 1=?(2)如下RL 电路图,设E, R, L 均为正的常数,求开关闭合后电路中电流强度I(t),假定I(0)=0.例30. 溶液混合问题:设容积为V (单位3m )的密封容器装着某种溶液如下图,从A 以速度r (单位/s m 3)流入浓度为0C e >(常数)的相同溶液,经充分混合后在B 以相同速度r 流出容器, 假设时刻t=0时,容器溶液浓度为0,问容器中浓度随时间变化的规律.解:设时刻t 时容器溶液浓度为C(t),则C(0)=0,且由溶质出入平衡,也即流入减去流出等于容器内溶质变化量,由微元法建立如下等式:V C(t))Δt)(C(t C(t)Δt r C Δt r e -+≈-,即e C VrC V r dt dC +-=. (以下略) 作业25. 假设伊利湖的存水量为34m 1048⨯,从休伦湖流入和从安大略湖流出的速度都是每年34m 1035⨯,在t=0时刻,伊利湖的污染物浓度时休伦湖的5倍. 如果流出的水是完全混合好的湖水,问使得伊利湖的污染物浓度减少到休伦湖2倍需要多少时间?(假定休伦湖污染物浓度为常数0C e >) 3. Bernoulli 方程及其解法称形如R n ,y q(x)y p(x)dxdyn ∈+=为Bernoulli 方程. 解法:当0y ≠时,改写原方程1n , n)q(x)(1y p(x) n)(1dxdy y n)-(1n -1n -≠-+-=, 令n)q(x)(1n)p(x)u (1dx du ,y u n1-+-==-,这是一个一阶线性非齐次方程. 例31 求解方程2y x xy6dx dy -=. 解:经过观察,原方程是一个Bernoulli 方程, n=2. (1)当0y ≠时,改写原方程为 x 2)(1y x62)(1dx dy 2)y-(1212---=--,令21y u -=,则 x u x6dx du +-=. 由常数变易公式得到, 6276-dx x6dx x6x C8x C)dx x (x )C xdx e(eu(x)+=+=+⎰⎰=⎰⎰-.返回原变量得到62x C8x y 1+=.(2) 当y=0时,容易验证0y =也是原方程的解. 作业26. 求解方程(1)33y x y x dxdy=+; (2)1y(1) ,y xy 'y x 22==-. 4. 交换自变量和因变量化非线性方程为一阶线性方程 例32. 求解(1)2y 2x y dx dy -=; (2)33yx xy 1dx dy -=. 解:(1) 这是一个一阶方程,非线性方程,不是Bernoulli 方程.(a) 当0y ≠时,交换自变量和因变量而改写原方程为 y x y2y y 2x dy dx 2-=-=. 这是一个一阶线性方程. 由常数变易公式得到, C)y)dy (e(ex dy y2dy y2+-⎰⎰=⎰-,即 |)y |ln (C y C)y)dy (y1(y x 222-=+-=⎰为所求方程的通积分. (b) 当y=0时,已验证y=0也是原方程的一个解. (2) 结合Bernoulli 方程来完成,留作练习.作业27. 求解方程(1)3y x y dx dy +=; (2) y2y x dx dy 22+=.5. 一些一阶线性方程的理论 (1)考虑方程q(x)y p(x)dxdy=+,其中p(x), q(x)都是以w>0为周期的连续函数. 用常数变易公式证明:(a) 若0q(x)≡,则方程任一非零解都以w 为周期的周期函数充要条件是p(x)的平均值.0p(x)dx w 1(x)p w==⎰ (b) 若q(x)不恒为零,则方程有唯一w 周期解充要条件是0p(x)dx w1(x)p w0≠=⎰, 试求出此解. (参见丁同仁、李承治《常微分方程教程》P36 习题5, 6)。
课程介绍-江苏大学842T课程网

空间解析几何课程简介课程编码:课程名称:空间解析几何英文名称:Space Analytic Geometry学分:3学时:45 (其中:讲课学时:45 实验学时:上机学时:)课程内容:《空间解析几何》课程是数学与应用数学专业(师范和非师范)及信息与计算科学专业的一门重要的专业基础课程。
解析几何的基本内容包括:空间直角坐标,向量代数,直线和平面,常见空间曲线和曲面,坐标变换,二次曲线方程的化简等。
通过学习这门课程,学生可以掌握用代数的方法研究空间几何的一些问题,而坐标法、向量法是其基本方法。
选课对象:数学各专业1年级本科生先修课程:平面解析几何教材:蔡国梁等主编,解析几何教程,江苏大学出版社,2012解析几何课一直是数学系各专业的专业基础课和核心课之一。
解析几何产生于十七世纪的欧洲,是由于遇到难以用初等几何、初等代数等常量数学来解决的问题后,人们就相继转而研究变量数学,因此,作为几何与代数相结合的产物——解析几何就问世了。
解析几何的创立者是十七世纪四十年代两位法国数学家费尔马(Pierre de Fermat)和笛卡尔(Rene Descartes),他们把以往对立着的两个研究对象“数”与“形”统一起来了,并在数学中引入了变量的概念,从而完成了数学史上一项划时代的变革。
解析几何的一个重要发展是由平面推广到空间,表示方法上是从两个坐标推广到三个坐标,因而从研究平面图形的问题中很自然地跨入到研究空间图形的问题中。
到了十九世纪后,该学科已经发展得相当完备,但作为二维和三维解析几何所研究问题的代数推广,人们又开始讨论四维解析几何和n维甚至无穷维的解析几何。
正当解析几何蓬勃发展的时候,以光滑曲线、曲面为其研究对象,且以数学分析和微分方程为研究工具的一门几何学的新学科——微分几何诞生了。
虽然微分几何的研究手段不同于解析几何,但是微分几何的内容在很大程度上吸收了解析几何的成果,这就使这两门学科的发展常常交织在一起。
2017年江苏大学硕士研究生入学考试复试科目主要参考书

901
机械制造技术基 础
年;或《机械制造技术基础》(第二版),卢秉恒、赵 万华、洪军.高等教育出版社,2005 年;或《机械制造 技术基础》(第二版),张世昌、李旦、高航.高等教
育出版社
903 光学
《光学教程》(第四版),姚启钧编.高等教育出版社, 2008 年
904 机械原理
《机械原理》,华大年或黄锡恺编.高等教育出版社; 或《机械原理》,申永胜编.清华大学出版社
布丁考研网,在读学长提供高参考价值的复习资料
2004 年
951
信号与线性系统
《信号与线性系统》(第四版),管致中等.高等教育 出版社,2004 年
952 数字信号处理
《数字信号处理》,吴镇扬.高等教育出版社,2004 年 9
953 电磁场理论
《电磁场与电磁波》(第二版),陈邦媛.科学出版社, 2006 年
《新编简明英语语言学教程》(第二版),主编戴炜栋、
917
英语语言文学基 础与汉语写作
何兆熊.上海外语教育出版社,2010 年;《英美文学选 读》(增订版),吴翔林编著.中国对外翻译出版公司,
2005 年 1 月
918 教育技术综合
《计算机应用基础》,全国高等网络教育考试委员会办 公室.清华大学出版社,2013 年。《教学设计》,皮连 生.高等教育出版社,2009 年
954
射频与微波电路
《射频通信电路》(第二版),陈邦媛.科学出版社, 2006 年
955 数据结构
《数据结构》(C 语言版)(第一版),严蔚敏、吴伟 明.清华大学出版社,1997 年;与《数据结构:C++实 现》,缪淮扣.科学出版社,2004 年
《常微分方程》(第二版),王高雄、周之铭等编.高
江苏大学数学与应用数学专业介绍

江苏大学数学与应用数学专业介绍
数学与应用数学
培养目标:本专业培养能主动适应中国特色社会主义建设实际需要,具有良好的思想道德素质、文化素质、身心素质、管理素质,掌握数学基本理论、基本知识和基本技能,具有坚实的数学基础和一定的创造能力,能够从事数学研究、应用、开发和推广工作的专门人才。
培养特色:具有较扎实的数学理论基础,受到比较严格的逻辑思维训练,有数学建模及熟练使用计算机的能力,具有较好的开拓和创新意识,并具备数学理论与应用研究和管理的能力,以及进一步向应用学科发展的素质。
主要课程:数学分析、高等代数、解析几何、微分几何、近世代数、复变函数、实变函数、常微分方程、泛函分析、点集拓扑、概率论、初等数论、计算方法、数学模型、普通物理,计算机基础和程序设计等。
深造机会:该专业所在学科在我校设有基础数学、应用数学、概率与数理统计、系统工程等硕士点,设有系统工程、管理科学与工程等博士点。
目前该专业在校博士生导师和硕士生导师有近20人。
就业状况及趋势:该专业毕业生就业情况良好,就业率始终保持在90%以上。
毕业生可去科研机构、行政机关或企事业单位从事数学模型设计、应用软件开发、网络与网页设计,以及相应的研究和管理工作,也可以到各类中高等职业学校、普通高级和初级中学从事数学及相关课程的教学工作。
江苏大学《825流体力学》历年考研真题汇编

3. 计算题(2S分) 注:本题来解需要计算篱. 确定潜艇它在水面航行的兴波阻力和在水下航行时的粘性阻力,水上航速为&7用/八 水下航速为55*分别在水池和风洞中进行船模试验’设船模的几何尺寸为实船的 i/65r试分别计算船模在水池、风洞中的速度。 (y* =1.145x10^ m2/s, *气=].45心时箫/$,风泅试验时,审脂》Ml『时,可不 考虑旺的影响,共阻方系数基本不受.)
科目代璃;取5科目若称:流体力学第2页井2页
2013年江苏大学能源与动力工程学院825流体力学考研真题
科目代码: 嬴学 科目名称:
江苏大学
满分:座分
L名词解特(用文字、数乳 图3种方式同时简要回答,(括号内的以说清间题为原州 可选择1-2种方式回答)(35分) 1) 定常流与均勾流(举例说明这组觥愈在流体力学的基本方程和教挚实检台中是如何 应用的); 2) 流线与涡线(写出流巍与涡线的方程,对比说明流场与就涡场的异同,乘出直渴线 (即平面点涡)的诱导速度X 3) 动力粘度与涡粘度(写出2种相度的表达式,说明涡粘度是如何产生的,在回管房 流、濡流(粘牲底屋、过渡区、湍流核心中)两种粘度相互的重要怪及太小时比); 4) 边界层与边界层分离(说明列车站台安全线强离的确定,•蛆概念对统流物体摩擦 阻力及压菱航力的影响); 5) 空化与空蚀(空化如何判荆,实睑中如何实现空化现枣的演示,水系等兼直中在何 处可能出现空化与空蚀).
流体力学基本方程
∂t
∂t
单位时段内控制体内流体质量的增量为:
∂ρ dtdxdydz / dt = ∂ρ dxdydz
(2)
∂t
∂t
− [∂(ρ vx ) + ∂(ρ vy ) + ∂(ρ vz )]dxdydz
(1)∂x∂y Nhomakorabea∂z
∂ρ + ∂(ρ vx ) + ∂(ρ vy ) + ∂(ρ vz ) = 0
∂t ∂x
系统:一团流体的集合,在运动过程中,系统始终包含着确定的这些流体 质点。有确定的质量,而这一团流体的表面常常是不断变形的。 控制体:控制体是流场中某一确定的空间区域,即相对于坐标系是固定不 变的。控制体的表面是控制面,控制体的形状是根据流体运动情况和边界 情况选定的。
7
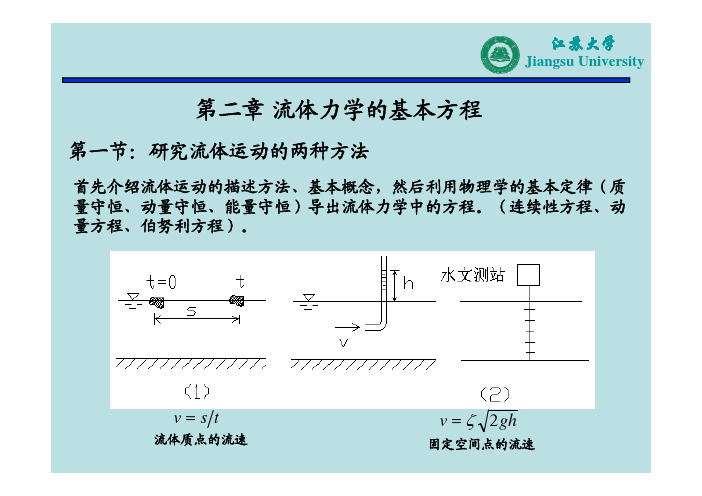
第二节 流体运动的基本概念
一、定常流、非定常流
∂v = 2 ∂y
∂w = 4 ∂z
∂u + ∂v + ∂w = 6 + 2 + 4 = 12 ≠ 0 ∂x ∂y ∂z
对不可压缩流体,以上流动不存在。对可压缩流体,因密度的变化未给 出,故无法判断。
例题3:假定流管形状不随时间变化,设A为流管的横断面积,且在A断面 上流动物理量是均匀的,试证明连续性方程具有下述形式:
20
江苏大学
Jiangsu University
对于定常流动:控制体内的质量增量 ,所以流入 = 流出
单位时间内流入控制体的质量: ρ v1 A1 单位时间内流出控制体的质量: ρ v2 A2
v1 A1 = v2 A2 Q1 = Q2
例1:如上图所示,有二块平 行平板,上板以匀速v向下平 移,间隙中的油向左右挤出 ,前后油液无流动。间隙宽b ,高h(t),求油的平均流速 随位置变化的关系u(x)。
具有功能性反应的微分生态模型的极限环分析

具有功能性反应的微分生态模型的极限环分析刘娟;李医民【摘要】Based on ecosystem with functional response, a differential ecosystem with functional response is established with the application of mathematics ecology. The system is discussed by using differential equations qualities theory. The system' s equilibrium points are studied. The degree and the stability of the center focus are analysed. The existence zone of the system' s limit cycle is given. By using Piocare-Bendixson theorem and Filippov transformation, the existence and uniqueness of the system' s limit cycle are proved in the case that the given parameters satisfy certain conditions. It shows that the densities of preys and predators are stable under some conditions.%在已有的功能性反应生态系统的基础上,应用数学生态学理论建立了一个具有功能性反应的微分生态系统,并应用微分方程定性理论,讨论了该微分生态系统.研究了系统的平衡点,对中心焦点的阶数和稳定性做出了分析,并给出了系统的环域构成图.在给定参数满足一定条件时,利用Poincaré - Bendixson 环域定理和Filippov变换,证明了该系统极限环的存在性和唯一性.结果表明,两种群的密度或产生周期性的变化,或都稳定在一组定值的附近,可以保持一种稳定状态.【期刊名称】《四川师范大学学报(自然科学版)》【年(卷),期】2012(035)004【总页数】5页(P500-504)【关键词】微分生态系统;平衡点;细焦点;稳定性;极限环【作者】刘娟;李医民【作者单位】蚌埠学院理学系,安徽蚌埠233030;江苏大学理学院,江苏镇江212003【正文语种】中文【中图分类】O175.12生物数学的一个重要分支是种群动力学,主要利用数学模型来描述生物系统的一些性质,从而得到现实生活中两种群的生存状态.目前众多学者对于Holling类功能反应的食饵、捕食者系统研究较多[1-5],得到了系统存在平衡点和极限环的一些结论,并讨论了平衡点的稳定性.但生物系统的发展很快,单纯的Holling类模型已不容易实现对生物系统的研究,所以Holling类模型又发展到涉及生物、化学控制[6-7],以实现外部因素对生物系统的影响.随着对生物系统的进一步研究,还可以建立一些其它类型的功能反应系统[8-12],以此说明不同的功能性反应对生物系统的影响是不一样的.文献[13]讨论了一个食饵种群对捕食者种群的影响较为明显的模型.本文在上述模型的基础上,建立了一个具功能性反应的微分生态系统,进一步推广了文献[13]的结论.描述两个种群之间的捕食与被捕食作用、相互竞争作用以及互惠共存作用的一般模型[14]为如果考虑到捕食者种群的增长率与食饵种群的密度密切相关的机理,取其中,选择的生物意义为:与常数相比,食饵种群密度的变化对捕食者种群的影响更为明显.考虑食饵种群的增长是非密度制约的因素,取其中为捕食者种群的功能性反应函数.由此,得到一个具功能性反应的微分生态系统其中,x表示食饵种群的密度,y表示捕食者种群的密度,参数a、b、c、s、m、ω、β各表示一定的生态意义,因此它们均为正常数.设由实际生态意义,只需在D内研究系统(1),作自变数变换变换后仍用t、a、m分别表示则系统(1)化为1 系统平衡点及其性态引理 1 系统(2)有平衡点 O(0,0),A(x0,0),其中且O为不稳定的结点,A为鞍点.证明在O(0,0)处有显然系统(2)的一次近似系统的特征根为所以O(0,0)为不稳定的结点.在A(x0,0)处有显然系统(2)的一次近似系统的特征根为所以A(x0,0)为鞍点.引理2 当aβω>c,abβ>1时,系统(2)在D内有唯一正平衡点其中当时,B是不稳定的焦点或结点;当时,B是稳定的焦点或结点;当时,B是中心型焦点.证明要使系统(2)在D内有正平衡点,则必须方程aβx2+(1-abβ)x-(aβω-c)=0有正根.当aβω>c,abβ>1时,方程aβx2+(1-abβ)x-(aβω-c)=0有唯一正根x1,解得此时系统(2)在 D内有唯一正平衡点容易得到在处,一次近似系统的线性化系数矩阵为设系统(2)的一次近似系统的特征方程为λ2-pλ +q=0,其中1)当时,p>0,所以λ2-pλ+q=0的根均具有正实部,故B为不稳定的焦点或结点;2)当时,p<0,所以λ2-pλ+q=0的根均具有负实部,故B为稳定的焦点或结点;3)当时,p=0,B为为一次近似系统的中心.以下对B作中心焦点判别.令,仍用x 和y分别标记和将系统(2)化为在条件下,于是,当时有其中由文献[15]的焦点判别定理知:当时,O(0,0)为系统(3)的一阶稳定细焦点,故B为系统(2)的一阶稳定细焦点.2 极限环的存在性及唯一性定理当时,系统(2)在D内的正平衡点B外围存在唯一极限环,且为稳定的.证明先证存在性.由系统(2)的奇点讨论知,当时,B为不稳定的焦点或结点,其等倾线如图1所示.其中过A(x0,0)作平行于y轴的直线x=x0,在y轴正向上取一点D(0,yD),并且有过D点作平行于x轴的直线y=yD,与直线x=x0相交于点E(x0,yD),系统(2)在直线AE上:因0<x<x0时,βyD>x0+c,故系统(2)在直线ED上:直线x=0及y=0都是系统(2)的轨线.于是,闭合曲线L=OA∪AE∪ED∪DO内含有一个不稳定的奇点B,且系统(2)的方向场都是自L外部穿向L围成的区域内,当t增加时,系统(2)的一切轨线均跑不出L,所以L构成广义Bendixson环域境界线,由Bendixson环域定理可知L内至少存在一个包含B的极限环.再证唯一性.令将系统(2)化为其中再作自变数变换dt=e-βmudτ,仍用t表示τ,将系统(2)化为Lienard系统其中1)当φ(0)=0,v≠0时表明φ(v)是单调增函数,且φ(v)满足Lipschitz条件.2),故u≠0时,ug(u)>0.易知G(±∞)=+∞.3)经过计算可得其中且有其中由于故T1<0,而所以在条件下,T2>0,故4A1A3-A22>0,所以h(u)>0,因此故单调不减.由文献[16]唯一性定理知,系统(2)围绕B至多存在一个极限环,且它存在时为稳定的.故系统(2)在D内的正平衡点B外围存在唯一极限环.3 结论对于上述具有功能性反应的微分生态系统,我们可以做出一些生物解释.如果系统(2)的轨线趋向于边界平衡点A(x0,0),则意味着捕食者种群将最终走向灭绝,而食饵种群不论初始密度如何取值,都会趋于最终的稳定密度x0.如果系统(2)的轨线趋向于正平衡点则说明尽管在开始阶段食饵种群的密度变化对捕食者种群的影响明显,但在经过一段较长时间后,不论食饵种群的密度初值和捕食者种群的密度初值如何取值,当所给参数满足以上分析得出的条件时,两者的密度或产生周期性的变化,或都稳定在一组定值的附近,可以保持一种平衡状态.致谢蚌埠学院自然科学基金(2010ZR16)对本文给予了资助,谨致谢意.参考文献[1]李秀英,王稳地.具有Holling第Ⅰ类功能反应的食饵-捕食者模型的定性分析[J].西南师范大学学报:自然科学版,2004,29(5):712-717.[2]于勇.一类具有功能性反应的顺环捕食系统概周期解的存在性[J].四川师范大学学报:自然科学版,2008,31(5):546-548.[3]鲁铁军,王美娟.一类基于比率的捕食-食饵系统的全局稳定性分析[J].应用数学和力学,2008,29(4):447-452.[4]Wang Y Q,Ma J Y.Qualitative analysis on a class of predator-prey model with HollingⅢfunctional response[J].J Biomathematics,2004,19(4):395-402.[5]任丽萍,李波.具有HollingIII功能性捕食模型的定性分析[J].四川师范大学学报:自然科学版,2009,32(6):757-762.[6]Liu B,Zhang Y J,Chen L S.Dynamic complexities of a HollingI predator-prey model concerning periodic biological and chemical control [J].Chaos,Solitons and Fractals,2004,22:123-134.[7]王爱丽,薛秋芳.具有多时滞和广义扩散的N-种群竞争反馈控制系统的持久性[J].工程数学学报,2009,26(6):985-989.[8]侯晓星,张群英.一类具时滞的禽流感模型[J].生物数学学报,2010,25(1):43-50.[9]李辉,王艺霏.具有功能性反应的时滞扩散模型的周期解与稳定性[J].东北师大学报:自然科学版,2008,40(2):22-29.[10]Mainik J,Ortlieb C P.Qualitative properties of a niche-model [J].Mathematics and Computer in Simulation,1999,49:353-374. [11]De I M,Fuente L.Diversity of temporal self-organized behaviors in a biochemical system[J].Biosystems,1999,50:83-97.[12]Moereira H N,Wang Y Q.Global stability in a class of competitive cubic system[J].Ecological Modelling,1997,102:273-285.[13]李医民,刘娟.一个微分生态系统的极限环分析[J].江苏大学学报:自然科学版,2008,29(1):89-92.[14]陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1988. [15]韩茂安.动力系统的周期解与分支理论[M].北京:科学出版社,2002. [16]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wronsky 行列式恒等于 0,这是否和教材 P124 定理 4 矛盾?如果不矛盾,它该例说明了什 么? 解:当 t ≥ 0 时, W[x1 (t), x 2 (t)] =
x1 (t) x 2 (t) t2 0 == =0. x1 ' (t) x 2 ' (t) 2t 0
当 t < 0 时, W[x1 (t), x 2 (t)] =
2 2
例 41.
ห้องสมุดไป่ตู้
验 证 x1 = e , x 2 = e
t
−t
为 方 程 x' '− x = 0 的 基 本 解 组 , 并 求 出 满 足 初 始 条 件
x(0) = 1, x' (0) = 1 的特解,其中 x' ' =
解:直接代入验证知, e − e = 0, e
t t −t
d2x . dt 2 − e − t = 0 ,因此, x1 = e t , x 2 = e − t 为方程的两个解 et et e−t = −2 ≠ 0 ,因此,由解函数线性 − e−t
t
dW = 0. dt ψ = 0 . 得证. ψ
由行列式定义的函数的导数公式(参见《数学分析》下 P124 习题 8) ,我们得到
ϕ dW ϕ ' ψ' ϕ ψ = + = ϕ ' ψ' ϕ ' ' ψ' ' − q(t)ϕ dt
(2)仿照(1)可证(a)
ψ ϕ = −q(t) − q(t)ψ ϕ
di x dt i
t=t0
= x i 的唯一解
αx1 (t), βx 2 (t), x1 (t) + x 2 (t), αx1 (t) + βx 2 (t) 都是齐次线性微分方程(*)的解.
(2)设 x1 (t), x 2 (t),⋯ , x k (t) 都是定义在[a, b]上函数,若存在不全为零的常数 c1 , c 2 ,⋯ , c k 使得 c1x 1 (t) + c 2 x 2 (t) + ⋯ c k x k (t) = 0, t ∈ [a, b] ,则称 x1 (t), x 2 (t),⋯ , x k (t) 在区间 [a, b] 上 线性相关,否则则称 x1 (t), x 2 (t),⋯ , x k (t) 在区间[a, b]上线性无关.
为非零函数. 线性方程柯西问题解的存在唯一性定理:考察上述 n 阶非齐次线性微分方程,若
a i (t), f(t), i = 1,2,⋯ , n 都 是 [a, b] 上 连 续 函 数 , 则 对 ∀t 0 ∈ [a, b] 和 任 意 n 个 实 数 x 0 , x1 ,⋯ , x n −1 ,方程 (**) 存在满足初始条件 x(t 0 ) = x 0 , x (i) (t 0 ) = x = ϕ (t), t ∈ [a, b] .
dnx d n −1x dx + a (t) + ⋯ + a n −1 (t) + a n (t)x = 0 为 n 阶齐次线性微分方程; 1 n n −1 dt dt dt
dnx d n −1x dx 称 n + a1 (t) n −1 + ⋯ + a n −1 (t) + a n (t)x = f(t) 为 n 阶非齐次线性微分方程,其中 f(t) dt dt dt
dnx d n −1x dnx d n −1 x 和 + a (t) + ⋯ + a (t)x = f (t) + a (t) + ⋯ + a n (t)x = f 2 (t) 的解. 1 n 1 1 dt n dt n −1 dt n dt n −1
x1 dW x1 ' x 2 ' x1 x 2 = + = x1 ' x 2 ' x1 ' ' x 2 ' ' − a1 (t)x1 '−a 2 (t)x1 dt
结论成立.
x2 x x2 = −a 1 (t) 1 − a1 (t)x 2 '−a 2 (t)x 2 x1 ' x 2 '
t
(b)求解方程 W '+ a1 (t) W = 0 得到,满足 W(t 0 ) = 1 的解 W(t) = e
t −t
函数. 下面验证它们是线性无关的. W[x1 , x 2 ] =
t −t
无 关 判 定 定 理 知 , x1 = e , x 2 = e
是 线 性 无 关 的 . 因 此 , 证 x1 = e , x 2 = e
为方程
x' '− x = 0 的基本解组. 方程的通解为 x = c1e t + c 2 e − t , c1 , c 2 为任意常数.
∫t0 −a1 (s)ds
.
此时相应的 x 2 (t) 和 x1 (t) 是线性无关的, 它们构成了原齐次线性方程的基本解组, 因为它们 Wronsky 行列式不为零. 改写 W(t) = e t0
∫
t
− a1 (s)ds
为 x 1 x 2 '− x 1 ' x 2 = e
−
∫t0 a1 (s)ds
件 是 W '+a 1 (t) W = 0 , 其 中 W = W[x1 (t), x 2 (t)] . (b) 方 程 的 通 解 为
1 ∫ −a1 (s)ds x = c1x1 (t) + c 2 x1 ( t ) ∫ 2 e t0 dt ,其中 c1 , c 2 为任意常数. x1 (t)
(3)已知 x = e t 是微分方程 x' '+ q(t)x = 0 一个特解, 试求该方程的通解, 并确定函数 q(t) ? 证明: (1)记 W(t) = W[ϕ (t), ψ(t)] ,下证
声明:以下总假设方程(*)和(**)满足柯西问题解的存在唯一性定理条件. 2. 齐次线性方程 (*)解的叠加原理、函数的线性无关性、 Wronsky 行列式、方程(*)的通 解结构 (证明细节参见教材 ) (1)叠 加 原 理 : 设 x1 (t), x 2 (t) 为 齐 次 线 性 微 分 方 程 ( * ) 的 解 函 数 , 则
t
t
t
得到解函数 x 2 (t) = x1
∫
1 − ∫t0 a1 (s)ds . 因此,由齐次线性方程通解结构定理知,结论成立. e 2 x1
(3)记 x1 (t) = e t ,由上述公式得到, x 2 (t) = e t
t −t t −t
∫e
− 2t
dt = e − t . 因此,原方程一个基本解
x1 (t) x 2 (t) 0 t 2 = = 0. x1 ' (t) x 2 ' (t) 0 2t
这说明 Wronsky 行列式恒等于 0. 考察方程 c1 x1 (t) + c 2 x 2 (t) = 0, t ∈ R . 当 t ≥ 0 时,上述方程为 c1 t = 0 ,得到 c1 = 0 ; 当 t < 0 时,上述方程为 c 2 t = 0 ,得到 c 2 = 0 . 这说明函数组 x1 (t), x 2 (t) 在 R 上线性无关. 这是否和教材 P124 定理 4 并不矛盾!原因是定理 4 中函数组为齐次线性方程的解函数.
t
,由 x1 (t) ≠ 0 再次改写上述方程为
x' 1 − ∫ a1 (s)ds ,这是一个一阶线性方程. 由常数变易公式得到, x 2 ' = 1 x 2 + e t0 x1 x1 x2 = e ∫
x1 '(t) dt x1 (t) −
t
(∫ e
∫
x 1 ' (t) dt x1 (t)
1 − ∫t0 a1 (s)ds 1 − ∫ a1 (s)ds e dt + C) = x1 ( ∫ 2 e t0 + C) , 特 别 地 , 取 C=0 x1 x1
(3)设 x1 (t), x 2 (t),⋯ , x n (t) 都是定义在[a, b]上具有 k-1 阶连续导函数的函数, 则称如下行
x 1 (t) x 2 (t) ⋯ x n (t) x1 ' (t) x 2 ' (t) ⋯ x n ' (t) 列 式 W(t) = W[x1 (t), x 2 (t),⋯ , x n (t)] = 为这些函数 ⋮ ⋮ ⋮ (n −1) (n −1) (n −1) x1 (t) x 2 (t) ⋯ x n (t)
(2)Liouville 公 式 : 考 察 二 阶 齐 次 线 性 方 程 x' '+ a 1 (t)x'+a 2 (t) x = 0 , 其 中 x' ' =
d2x , dt 2
a i (t) ∈ C[a, b], i = 1,2 . 假设 x1 (t) 为方程的一个非零解,则(a)函数 x 2 (t) 为方程的解充要条
Wronsky 行列式. (4)函数组线性相关的必要条件: 设 x1 (t), x 2 (t),⋯ , x n (t) 都是定义在[a, b]上具有 k-1 阶连 续导函数的函数,若它们线性相关,则它们的 Wronsky 行列式恒为零. (5)方程(*)解函数线性无关充要条件:设 x1 (t), x 2 (t),⋯ , x n (t) 都是定义在[a, b]上方程 (*)的解函数,则它们线性无关 ⇔ 它们的 Wronsky 行列式在[a, b]上处处不为零. (6)若 n 个函数 x1 (t), x 2 (t),⋯ , x n (t) 都是方程(*)的解函数且线性无关,则称其构成了 方程(*)的一个基本解组. (7)齐次线性方程(*)的通解结构定理:设 x1 (t), x 2 (t),⋯ , x n (t) 构成了方程(*)的一个
