流动传热与燃烧的数值计算2差分
传热与流动的数值计算

1.2 传热与流动问题数值计算的基本思想及应用举例
1.2.1 数值解基本思想(基于连续介质假设)
把原来在空间与时间坐标中连续的物理量的场 (如速度场、温度场、浓度场等),用一系列有限 个离散点(称为节点,node)上的值的集合来代替; 通过一定的原则建立起这些离散点上变量值之间关 系的代数方程(称为离散方程,discretization equation);求解所建立起来的代数方程以获得所求 解变量的近似值。
5. 四点说明
1. 所导出的三维非稳态Navier-Stokes方程,无论对 层流或是湍流都是适用的。 2. 当流动与换热过程伴随有质交换时,控制方程中还 应增加组份守恒定律。 3. 虽然假定了比热为常数,也可以近似应用于比热的 变化不是很剧烈的情况。 4. 辐射换热需要用积分方程来描述,本课程中将不涉 及这类问题。
u v w 0 x y z
div( U ) 0 t
称为流动无散(度)条件 (Zero divergence)。
2. 动量守恒方程
对上图所示的微元体分别在三个坐标方向上应用 Newton第2定律(F=ma)在流体中的表现形式: [微元体内动量的增加率]=[作用在微元体上各种力之和] 假设流体中切应力与正应力满足Stokes假定:应 力与应变成线性关系,可得u-动量方程如下:
( u ) ( uu ) ( uv ) ( uw) p u (divU 2 ) t x y z x x x v u u w [ ( )] [ ( )] Fx y x y z z x
导致依赖区(domain of dependence) 与影响区 (domain of influence)的不同。 所谓依赖区是指赖以决定一个节点的变量数值的 区域;影响区是一个节点的变量影响所及的区域。
流动-传热与燃烧数值计算研究生课程教学改革探讨

流动\传热与燃烧数值计算研究生课程教学改革探讨[摘要]流动、传热与燃烧数值计算是中南大学能源科学与工程学院面向全体研究生开设的重要技术基础课程。
由于该课程既基于经典流体力学、传热学与燃烧学理论, 又依赖于现代计算技术,学生学习起来感觉有一定难度。
本文结合教改项目的实施, 探讨该门课程的教学内容和教学方法。
教学实践表明,本课程教学方法既提高了学生的基本技能,又加强了学生对流动、传热与燃烧机理的了解, 为后续的科研工作打下良好的基础。
[关键词]计算流体力学数值传热学教学方法基本技能随着现代科学技术的发展,计算机技术已广泛应用于各行各业中,现在对一个工科研究生,不仅要求有坚实的本领域的专业知识,而且有比较扎实的计算机知识,对能源领域的研究生而言更是如此。
鉴于此,中南大学能源科学与工程学院面向全院研究生开设了《流动、传热与燃烧数值计算》课程,该门课程具有鲜明的专业特色与多学科交叉特点,融合了本学科领域的部分最新科研成果,对培养能源类相关专业的研究型人才,具有重要的支撑作用,是我校能源科学与工程学院研究生教学的特色课程之一。
该课程要求学生具有宽厚的高等流体动力学、高等传热学与燃烧学基础,扎实的计算机编程的基本技能。
国内很多高校根据本校优势学科将计算流体力学、数值传热学等等课程纳入研究生教学体系,但面对研究生开设以流动、传热与燃烧过程为数值模拟对象的课程很少,教学内容和教学方法都需要探索。
本文结合教改项目的实施,以培养学生面向流动、传热与燃烧过程的数值模拟技能为目标,以解决能源领域的相关实际问题为导向,探讨《流动、传热与燃烧数值计算》课程教学内容及教学方法。
一、课程教学内容近年来随着经济快速发展,能源问题日益突出,而能源的利用过程中伴随着大量的流动、传热与燃烧过程,能源的合理利用需要能源领域的研究人员对流动、传热与燃烧过程的机理有深入的认识。
为适应经济社会对能源领域人才的需求,《流动、传热与燃烧数值计算》课程设置的内容以培养研究生的基本技能、适应能源领域的科研工作需要为出发点,围绕能源领域实际需求,将教学内容和科研与工程实际问题密切结合。
CFD2013-第12讲-燃烧的数值计算
1012
H2+OH->H2O+H
1010
H2+O2->OH+OH
Kf
108
106
500
1000 T 1500 2000
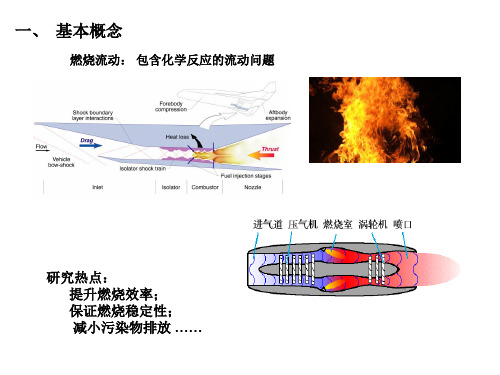
单位摩尔浓度气体反应速度随温度的变化
3) 可逆反应
aA bB eE fF
H O2 OH O
aA bB eE fF eE fF aA bB
正反应 逆反应
i t
iu x
iv y
i w z
( x Sc
ci ) x
( y Sc
ci y
)
z
( Sc
ci z
)
i
对流项
扩散项
源项
L
i qi (vij vij )M j i 1
qi k fi (T ) N X j vji kri (T ) N X j vji
d dt
[H
2
]
1
2
5) 组分生成率的统一表达式
设有N种组分: 有L个化学反应:
X1, X2 ,......X N
反应1 反应2
v11X1 v21X 2 v12 X1 v22 X 2
vN1X N v11X1 v21X 2 vN 2 X N v12 X1 v22 X 2
比例因子,与温度有关
2) Arrhenius公式:
k(T ) AT b exp(EA / RT )
活化能
实验拟合公式
参数A,b,EA等均为物性参数,可查表获得(通常为Chemkin格式)
组分(摩尔浓度)变化率
流动、传热及传质的控制方程

对流传质方程
01
对流传质方程是描述流体流动过程中物质传递的方程,它基于Fick第二定律和 Darcy定律。
02
对流传质方程的一般形式为:ρSc▽·vc = -▽P/ρ + ν▽²vc + (1/ρ)▽·(ρD▽c),其中 Sc是斯密特数,v是速度矢量,P是压力,ν是动力粘度,D是扩散系数,c是浓度。
有限元法在结构分析、固体力学、流体力学等领域有广泛应用。
有限体积法
01
02
03
有限体积法是一种求解偏微分方 程的数值方法,它将连续的求解 区域离散化为有限个小的体积单 元,并对每个体积单元构造近似 函数。
有限体积法特别适合处理流体动 力学问题,因为它能够很好地捕 捉到流体运动的特性,如速度和 压力的连续性。
熵守恒方程
总结词
描述流体熵在空间中的变化。
详细描述
熵守恒方程是热力学的基本方程之一,它表明在封闭系统中,流体的熵不会凭空产生或 消失。该方程基于熵增原理,表示流体在流场中单位时间内熵的增加等于流入该控制体
的净熵流量。
02 传热的控制方程
热传导方程
总结词
描述了物体内部热量的传递过程。
详细描述
热传导方程,也称为傅里叶定律,表 示在物体内部,温度梯度导致热量从 高温区域流向低温区域。该方程基于 能量守恒原理,并考虑了导热系数的 影响。
03
对流传质方程适用于描述流体流动过程中的物质传递过程,如化工、环境、食 品等领域中的流动和传递过程。
化学反应动力学方程
1
化学反应动力学方程是描述化学反应速率和反应 机理的数学模型。
2 3
流动传热与燃烧的数值计算5流场求解

u e u w yz
其中: Ae An At a y z a x z a xy e N n T e : E ae an at Aw As Ab aS s x z aB b x y aW w a yz as ab w aP aE aW aN aS aT aB 0 P P x y z u * u * y z b w e t v* v* xz w* w* xy 0 s n b t
动量方程只有在压力场给定或以某种方式估算出后 才能求解。而且,除非使用的压力场正确,否则由 动量方程求得的速度场不可能满足连续性方程。 求解思路: 假设:p* 试探压力场 u* , v* , w* 基于 p*求出的速度场
* * * * aeue anbunb b ( pP pE ) Ae * * * 则 an vn anb vnb b ( pP p* N ) An a w* a w* b ( p* p* ) A P T t t t nb nb
它流体性质所要求的中间结果。
3 -法的最主要缺点是不易推广到三维。
§4.1求解流场的困难(控制容积法、某些差分格式)
§4.1.1压力梯度的表示 以一维问题为例: 假定控制容积面e和w位于相应结点的正中间 假定压力是分片线性分布的
w
W P
e
E
dp 在控制容积内积分后产生压降的可表示为: dx e pW pP pP pE pW pE dp dx pw pe : w dx 2 2 2 这表明,离散后的动量方程将包含两个相间隔的结点之 压力梯度间的压力差,这意味着求解压力场的网格比实际使用的 更粗,降低了解的精度,而且会产生波形(锯齿形) 压力场。波形压力场显然是不符合实际的,但是对离散 后的动量方程来说,好象是均匀压力场。
数值传热学的通用方程

数值传热学的通用方程数值传热学的通用方程引言:传热学是研究热量在物体内传递的学科,它在实际生活中具有广泛的应用。
数值传热学是传热学的一个重要分支,借助数值计算方法和计算机模拟,能够更准确地预测和模拟热量的传递过程。
在数值传热学中,通用方程是一种重要的工具,它能够描述和计算物体内热量的传递方式。
本文将以数值传热学的通用方程为主题,通过分析其深度和广度,以全面评估和解释这一概念。
一、数值传热学的基础概念1.1 热量传递的三种方式热量传递有三种方式:传导、对流和辐射。
传导是指热量通过物质的直接接触和振动传递,对流是指热量通过流体的传输,辐射是指热量通过电磁波辐射传递。
这三种方式在不同的情况下起着不同的作用,同时它们也相互影响和耦合。
1.2 数值计算方法在传热学中的应用数值计算方法是数值传热学的核心工具,它可以通过数学模型和离散计算,模拟和预测物体内热量的传递过程。
常用的数值计算方法有有限元法、有限差分法和有限体积法等。
通过这些方法,我们可以更准确地计算和研究热量的传递规律。
二、数值传热学的通用方程2.1 传热方程的基本形式传热方程是描述热量传递过程的数学方程,它以物体内部的温度分布、热流和热导率等参数为基础,通过各种数学方法和推导,得到不同传热方式下的通用方程。
2.2 热传导方程热传导方程是描述热量通过传导方式传递的方程。
在传热过程中,热量会从高温处传向低温处,而传热率又与温度梯度和材料的热导率成正比。
热传导方程能够计算和描述热量在物体内部的传递过程,为热传导问题的分析和计算提供了基础。
2.3 流体传热方程流体传热方程是描述热量通过对流方式传递的方程。
流体传热过程中,流体的流动状态和温度梯度会影响热量的传递速率。
流体传热方程能够计算和描述流体内部的热量传递过程,对于流体传热问题的研究和分析具有重要意义。
2.4 辐射传热方程辐射传热方程是描述热量通过辐射方式传递的方程。
辐射传热过程中,热量通过电磁波的辐射传输,与物体的温度和辐射特性有关。
热流问题的数值计算

迭代方法
为了求解非线性热流问题,需要采用迭代方法,如 Newton-Raphson方法、Gauss-Seidel方法和SOR 方法等。这些方法需要在每一步迭代中进行线性化和 求解线性方程组,因此需要高效的算法和数值方法。
04
数值计算的应用
工程传热问题
热传导
在机械、航空航天、能源等领域中, 热传导是常见的传热方式,数值计算 可以模拟热流在固体中的传递过程, 优化热设计。
热对流
流体与固体之间的热量交换,如流体 加热器、核反应堆等,数值计算可以 模拟对流换热过程,优化热工性能。
生物医学中的热流问题
生物传热
生物体内的热量传递对生理功能和疾 病诊断具有重要意义,数值计算可以 模拟生物体内的热量分布和变化,为 医学诊断和治疗提供依据。
06
结论
研究成果总结
01
数值计算方法在热流问题中得到了广泛应用,为解决实际问题提供了 有效的工具。
02
数值计算方法能够模拟复杂的热流现象,为实验研究和理论分析提供 有力支持。
03
数值计算方法在解决实际工程问题中取得了显著成果,如传热、流体 动力学和燃烧等领域的模拟。
04
数值计算方法在热流问题中仍存在一些挑战,如高精度算法、复杂边 界条件和多物理场耦合等。
热流的物理特性
01
热流是热量传递的速率,其大小 取决于温度梯度、材料属性以及 热流方向。
02
在稳态条件下,热流与温度梯度 成正比,即
$பைடு நூலகம் = -k frac{partial u}{partial n}$
03
流体流动与传热的数值计算

12
三、本课程的目的
❖ 数值求解有关过程的方法很多,但本课程不 打算介绍所有现成的方法,这样只会把同学 们搞糊涂,感到茫然、不知所措。
❖ 本课程主要介绍由Patankar教授与Spalding教 授所开创的(通用)数值计算方法。学习和 掌握这一套方法后即可用以计算分析在科研 工作中可能遇到的实际问题,并可在此基础 上学习、掌握其他数值计算方法。
❖ 但试验的代价→昂贵,某些时候甚至不可能实现,尤 其是在大型工业化装置上进行实验更为困难。
❖ →只能针对已有的现象或装置做→很难用于开发。1: 1,逐渐放大→大大影响了我国化学工业的发展。
❖ 对一些基本物理现象的规律并不都能从实物试验中获 得。
20.8.16
15
②相似理论指导下的实验
缩小规模:或取一局部物体作模型试验。如 裂解炉的开发:单管试验、多管缩小尺寸、 传热试验、加热时间等;再如降膜结晶法:a. 短单管→物理现象观察分析;b. 长、单管, 中间实验;c. 多根管的放大试验;d工业装置。 但即使如此,有时也存在不同程度的困难。
2. R.B. Bird & W.E.Steward,Transport Phenomena
3. E.R.G. Eckert,Analysis of heat and mass transfer
4. Jacob,Heat Transfer 5. 王补宣,工程传热与传质学
6. O.C. Zienkiewieg,The finite element method , by 7. H. Schlichting,Boundary layer theory
→所有这些都要求更细的过程、更精密的控制 →有必要预测有关的过程。
20.8.16
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相容性:如果当网格步长Δx→0, Δt→0时,差分 方程的截断误差也E→0 ,此时在每一网格结 点上的差分方程与原微分方程是等同的,则该 差分方程与相应的微分方程是相容的。
以FTCS格式为例: u u u o(Vt ) t Vt j
n n j n 1 j
u u 2 x j
1 n un u j j
Vt
n n un 2 u u j 1 j j 1
j 1, 2, L J 1 n 1, 2, L N
(V x )2 j 0,1, 2, L J n 1, 2, L N n 1, 2, L N
u0 j f ( jV x )
n u0 1 ( nVt ) n uJ 2 ( nVt )
0 xl u 2u 2 t x 0 t T u( x , 0) f ( x ) u(0, t ) 1 ( t ) u( l , t ) 2 ( t )
设: tn=nΔt ,xj=jΔx ,n=0,1,2,….,N,j= 0,1,2,….,J 点( xj , tn)可以用(j ,n)表示 u( xj , tn)用 un 表示 j 令微分方程中的一阶导数用向前差分,二阶导数用 中心差分,则与原微分方程对应的差分方程为:
§1.1.3 差分方程的相容性
用差分方程代替微分方程之后产生了一个问题,即 所采用的差分方程是否逼近原来的微分方程?
相容性是差分方程的一个基本特性,它既反映了差 分方程是否收敛到相应的微分方程,也反映了截 断误差。
截断误差:用ujn代替 u(xj, tn) 的差分方程与在点 (xj, tn)处的微分方程之差。 E=O(Δtq+Δxp) 差分方程的精度:如果 E=O(Δtq+Δxp),则称此差 分方程对t是q阶精度,对x是p阶精度。
2
n
n j 1
2u u
n j
n j 1
(V x )
2
o(V x )
2
E 0时E 0 FTCS 格式是相容的
§1.1.4 差分方程的收敛性
差分方程能否应用,要看差分方程的近似解能否 任意地逼近微分方程的准确解。
首先要考虑差分方程理论上的精确解能否任意地 逼近微分方程的准确解,其次还要考虑求解差 分方程过程中产生的误差。
L E n nVt o(Vt V x 2 ) 当Vt 0,V x 0时, E 1 0, E 2 0, L E n 0 即e n j 0 1 故,在0 s 范围内,FTCS 格式是收敛的。 2
举例:对于FTCS格式,当S=1, 1/2, 1/6时,考察结 点xj=0.4,tn=8处的数值解,并与微分方程在该处 的准确解 u(0.4, 8)=45.03963比较。 其中α=0.01,l=1.0
1 1 n 2 当0 s 时,有 e n E ( s 1 2 s s ) V t o ( V t V x ) j 2 即E n1 E n Vt o(Vt V x 2 )
设微分方程的准确解与差分方程的精确解初始条件 相同,即
0 0 0 1 2 % u u j e j 0 E 0 E Vt o(Vt V x ) 0 j
45.24738 45.13947 45.06459
45.11174 45.05766 45.04414
§1.1.5 差分方程的稳定性
求解差分方程的过程中不可避免地会引入误差(舍 入误差、初始误差等),稳定性讨论差分方程解 的误差在计算过程中的发展问题。 稳定性:如果求解差分方程过程中引入的数值误差 在以后计算步逐步消失或保持有界,则称此差分 方程是稳定的;如果引入的数值误差在以后计算 步被逐渐放大,以致物理问题的解被完全破坏, 则称此差分方程是不稳定的。
则e
n1 j
u
n1 j
n1 % uj
n n 2 se n (1 2 s ) e se o ( V t V x )Vt j 1 j j 1
1 n n n 2 en se (1 2 s ) e se V t o ( V t V x ) j j 1 j j 1 n 1 n 1 令E n Max e n , E Max e j j
J
5 10 15 20
Δx
0.2 0.1 0.06 0.05
S=1 100 12200 197 * 106
u S=1/2 50 47.54791 45.61530 45.66436
S=1/6 46.84500 45.49047 45.23979 45.15231
25 50 100
0.04 0.02 0.01
将上述方程改写成便于计算的形式: Vt n1 n n n n uj uj ( u 2 u u FTCS 格式 j 1 j j 1 ) 2 (V x )
若微分方程中的时间导数用向后差分,空间导数用中心差分, 则与原微分方程对应的差分方程为: Vt n 1 n n n n uj uj ( u 2 u u 全隐式格式 j 1 j j 1 ) 2 (V x )
其中s
Vt
(V x )
2
n n % % 设u j 为微分方程的准确解, u j u( x j , t n ) n1 n n n % % % % 则u j su j 1 (1 2 s )u j su j 1 o(Vt V x 2 )Vt n % 设e u u j n j n j
则
d dx 2
可以表示为:
向前差分 向后差分 中心差分
d 3 2 dx x 2 d 2 1 或 x dx 2 d 3 1 或 2x dx 2
则
d 2 2 dx 2
s2 1 2 2 2 要使 : j (2 s 4 s ) 1 0 s 3 2 1 4 s 6 s 1 M 这个过程可继续下去,在许多时间层以后,各处 的误差趋于相等,但可能正负号相同,也可能 正负号相反。
0 0 则 w0 u j j j n n wn u j j j n j
:
由于 w n j 满足差分方程,则
1 n1 n n n n n n un s ( u ) (1 2 s )( u ) s ( u j j j 1 j 1 j j j 1 j 1 )
收敛性是讨论当 Δx→0, Δt→0 时,差分方程的精 确解是否收敛于原微分方程的准确解。 相容性是讨论当Δx→0, Δt→0 时,差分方程是否 逼近原微分方程,相容并不能保证收敛。
以FTCS格式为例,讨论其收敛性 u
n1 j
su
n j 1
(1 2 s )u su
n j
n j 1
若微分方程中的时间导数用中心差分,空间导数也用中心差分, 则与原微分方程对应的差分方程为: Vt n 1 n 1 n n n u j u j 2 ( u 2 u u j 1 j j 1 ) 2 (V x )
Richardson格式
显式格式:解可以由明显的公式计算出来,不需 要求解方程组。FTCS 隐式格式:解不能简单地求出,需要求解代数方 程组。全隐式格式
一般取时间步长Δt =const.,空间步长Δx =const. 对于二维和三维问题,不要求Δx = Δy= Δz。 tn=nΔt 和xj=jΔx 的直线为网格线,其交点( xj , tn) 称为网格结点。 网格设计好之后,就可以把连续求解域上的微分方 程离散化为有限个网格结点上的差分方程。
例:用差分法求解抛物型方程
§1.1有限差分法
差分法的基本思想是用差商代替微商。 用差分法离散微分方程的具体方法有很多种, 对同一微分方程可以建立不同的差分方程。
§1.1.1差分方程的建立
以一维问题为例,设x3-x2=x2-x1=Δx 由Taylor级数展开可得:
d 2 x 2 d 3 x 3 d 3 2 x 2 3 L dx 2 dx 2 2! dx 2 3! d 2 x 2 d 3 x 3 d 1 2 x 2 3 L dx 2 dx 2 2! dx 2 3! (1) (2)
可以表示为:
d 2 3 22 1 2 2 dx x 2
中心差分
§1.1.2网格划分
离散过程包括两个方面:①微分方程的离散化; ②求解域的离散化。
设微分方程有两个自变量x,t 。 微分方程的解应是x和t的函数u(x,t),而差分法 (数值方法)求的是若干个离散点(x=j Δx, t=nΔt )上u(x,t)的近似值 un j 因此,首先要在求解域上指定一系列离散点。
由于un j 是差分方程的精确解,则
1 n n n un su (1 2 s ) u su j j 1 j j 1 1 n n n 故: n s (1 2 s ) s j j 1 j j 1 误差传播方程
jm 0 设 jm 1 0 0 0 m s (1 2 s ) s 1 m2 m 1 m s 1 0 0 0 m s m 1 (1 2 s ) m s m 1 (1 2 s ) 则 1 0 0 0 s (1 2 s ) s m m 1 m 2 s m 1 其余全部为零
0 j
s 1 1 要使 j (1 2 s ) 1 0 s 1 : s 1 再由误差传播方程可知:
2 2 1 1 1 2 m 2 m 2 s m 3 (1 2 s ) m 2 s m 1 s 2 2 1 1 1 2 s (1 2 s ) s (2 s 4 s ) m 1 m 1 m2 m 1 m 2 1 1 1 2 s (1 2 s ) s ( 1 4 s 6 s ) m 1 m m 1 m 其余全部为零
