L单元 算法初步与复数
L单元算法初步与复数(20200611224528)

L 单元算法初步与复数L1算法与程序框图3. L1 [2017 •天津卷]阅读图1-1所示的程序框图,运行相应的程序,若输入 N 的值为 24,则输出N 的值为()A. 0 B . 1 C . 2 D . 33. C [解析]输入N = 24,第一次执行 N = 8;第二次执行 N = 7;第三次执行 N = 6; 第四次执行N = 2,满足条件,输出2•故选C.x 的值为7,第A . 0, 0B . 1, 1C . 0, 1D . 1, 06. D [解析]当x = 7时,b = 2,此时4<7,且x 不能被2整除,所以此时b = 3,又因 为32>7成立,所以输出a = 1;当x = 9时,b = 2,此时4<9,且x 不能被2整除,所以此时 2 b = 3,又因为3 >9不成立,且x 能被3整除,所以输出a = 0•故选D.& L1 [2017全国卷n ]执行如图1-2所示的程序框图,如果输入的a =- 1,则输出的x6. L1 [2017山东卷]执行两次图1-1所示的程序框图,若第一次输入的 二次输入的A.2 B . 3 C . 4 D . 5& B [解析]逐次计算结果为:S =— 1, a = 1, K = 2; S = 1, a =— 1, K = 3; S = — 2, a = 1, K = 4; S = 2, a =— 1, K = 5; S = — 3, a = 1, K = 6; S = 3, a =— 1, K = 7,此时输 出S.故输出的S = 3.8. L1 [2017全国卷I ]图1-3的程序框图是为了求出满足 3n — 2n >1000的最小偶数n ,那么在”和两个空白框中,可以分别填入( )图1-3A . A>1000 和 n = n + 1 B. A>1000 和 n = n + 2 C. A w 1000 和 n = n + 1 D. A < 1000 和 n = n + 2框" _________ ”中应填入n = n + 2.选D.7. L1 [2017全国卷川]执行下面的程序框图,为使输出 S 的值小于91,则输入的正整S =( )图1-2[解析]判断框中应填入A < 1000,由于是求最小偶数,故处理/输入□/2数N 的最小值为( )A . 5B . 4C . 3D . 27. D [解析]程序运行过程如下所示:SM t 初始状态 0 100 1 第1次循环结束100 —10 2 第2次循环结束9013此时S = 90<91 ,满足条件,程序需在t = 3时跳出循环,即N = 2为满足条件的最小值. 3. L1 [2017北京卷]执行如图1-1所示的程序框图,输出的 s 值为()3A . 2 Bq 5 8 C. D" 3 51 +1 、卄□2 + 13. C [解析]k = 0, s = 1,满足 k<3 ; k = 1, s == 2,满足 k<3; k = 2, s ==5 53不满足k<3.故输出s =3故选C.3 332,满足 k<3; k = 3,图1-2图1-12+114. L1 [2017江苏卷]图1-1是一个算法流程图.若输入 x 的值为16,则输出y 的值是+ a = 0,即 a =— 2.2. L4[2017 •山东卷]已知a € R , i 是虚数单位.若 A . 1 或—1 B. 7或— 7—.3 D. 3A [解析]由 z z = a 2 + (Q3)2= a 2 + 3= 4,得 a 2= 1,所以 a = ±,故选 A.A . 1 + 2iB . 1 — 2iC . 2+ iD . 2— i3+ i (3+ i )( 1 — i )4— 2i1. D [解析]不=(1 + i )( 1 — i )=〒=2— i.3. L4[2017全国卷I ]设有下面四个命题若复数z 满足中€ R ,贝U z € R ; P 2:若复数z 满足Z 2€ R ,则z € R ;P 3:若复数 Z 1, Z 2 满足 Z 122 € R ,贝U Z 1 = Z 2;4. —2 [解析]因为输入 L2 基本算法语句 L3 算法案例L4 复数的基本概念与运算9. 9. 1x 的值为16,不满足1x > 1,所以 y = 2+ Iog 2^6=— 2.a € R , i 为虚数单位,a —i若 为实数,则 a 的值为2+ i(a — i ) (2— i ) (2a — 1) —(2 + a ) i a — i 、(2 + i ) (2— i )=5 ,2+ i 为,二 2z = a + . 3i , z - z = 4,贝U a =( )C . 2.1. L4 [2017 全国卷 II ]汙=()图1-1L4[2017 •天津卷]已知a — i —2 [解析]•••乔P4:若复数z€ R,则z€ R.其中的真命题为()A. p i, P3B. p i, P4C. P2, p3 D . P2, p41 a b i i3. B [解析]设z= a+ bi(a, b€ R).- = 2— 2,若-€ R,则b= 0,此时z€ R,故命题z a 十b zp i为真命题;若z€ R,贝U b= 0,此时z= a_ bi € R,命题p4为真命题;z2= a2_ b2+ 2abi, z2€ R时,a= 0或b = 0,此时z为实数或纯虚数,命题P2为假命题.设Z i= i, z2= 4i,则z i z2€ R,但z 严z2,命题p3为假命题.故选B.2. L4[2017全国卷川]设复数z满足(1 + i)z= 2i,则|z|=( )1 2A.J B^2C. 2D. 22i 2i (1 _ i) 2i + 2 . __2 厂2. C [解析]由题知z= 1 + i = ( 1 + i) ( 1 _ 门 =~2- = i+ 1,贝卩回二"』1+ 1= ,2.2. L4[2017北京卷]若复数(1_ i)(a+ i)在复平面内对应的点在第二象限,则实数a的取值范围是()A.(―汽1)B. (—a, —1)C. (1 ,+a ) D . (—1 ,+a )2. B [解析](1 —i)(a + i) = a+ i —ai —i2= a+ 1 + (1 —a)i,其对应的点为(a +1, 1 —a),1 + a<0,因为复数对应的点在第二象限,所以芒解得a< —1,故选B.1 —a>0,12. L4[2017 浙江卷]已知a,b€ R ,(a+ bi)2= 3+ 4i(i 是虚数单位),则a2+ b2= _________ , ab= ________ .12. 5 2 [解析]由(a+ bi)2= 3 + 4i,得a2+ 2abi+ b2i2= 3 + 4i,即a2—b2+ 2abi = 3 +a2_ b2= 3, 224i,又a, b€ R,所以由复数相等的充要条件,得解得ab= 2, a = 4, b = 1,|2ab = 4,因此a2+ b2= 5.2.L4[2017江苏卷]已知复数z= (1 + i)(1 + 2i),其中i是虚数单位,则z的模是 __________ .2. ,10 [解析]因为z= (1 + i)(1 + 2i),所以|z|= |1 + i| |1•+ 2i|=, 12+ 1冬,12+ 22= 10.L5单元综合1年模拟2. 2017淮北月考执行如图K53-2所示的程序框图,若输出的结果是161,则判断框中正整数k为()图K53-22. C [解析]逐次的计算结果是m = 5, n= 1宀m= 17, n = 2宀m= 53, n = 3宀m= 161 , n= 4,此时结束循环,输出161,故k的值为4.3. 2017枣•庄月考执行如图K53-3所示的程序框图,若输出的结果为一45,则判断框中应填入的是()A. i<10?B. i> 10?图K53-32 2 2 2 n 2 *1 +2 —3 +4 —…+ (—1) n (n€ N )的值,因为一3. C [解析]该程序框图计算的是12+ 22—32+ 42—…一92= 3+ 7+ 11+ 15 —81 = —45,所以判断框中应填入“i<9?6. 2017济南模拟执行如图K53-6所示的程序框图,若输入 a =晋,b=罟则输出的结果是()[幵始]/ 输Afljy/In 5c= T,是是_ __________________ __/皤心//姑出二//输出b /(对束j图K53-6A.3C. bD. c6. C[解析]C B. aa =罟=ln ,2,b=罟=ln33, c=罟=ln 55,又.2= 68<6.9= 3 3, 3.32 的功能是输出三个数中的最大值,故输出结果为 b.2. 2017临沂月考若复数z 满足iz = 3 — i (其中z 为z 的共轭复数),则复数z 对应的点位 于复平面的( )A.第一象限B.第二象限C.第三象限D.第四象限3 一 i2. B [解析]z =-厂=—1 — 3i ,所以z =— 1 + 3i ,其对应的点位于复平面的第二象 限. + i4. 2017枣庄月考已知复数 z = m ~1 (m € R ),若复数z 对应的点在复平面的第二象限, 贝UI ——i m 的取值范围是()A. ( —a, — 1)B. (1 ,+^ )C. [ — 1, 1]D. ( — 1 , 1)面的第二象限,则 m — 1<0且m + 1>0,解得—1<m<1,故m 的取值范围是(—1, 1).15243>15 125 = 5 5, .2」°32>10 25= B ,即 3 3> . 2>55 ,所以c v a v b.该程序框图3. 2017淮北月考复数3+ 4i■1—(其中i 为虚数单位)的运算结果是(7- 2+7- 2B7712+1 2C. - 2 + 2iD. 2+》3. C[解析] 3 + 4i 1 — i (3+ 4i )( 1 + i )(1 — i )( 1 + i ))—1 + 7i 1 , 7 =—— I — 2 2 24. D(m + i ) (1 —i ) (1 + i )(1+ i )(m — 1) + ( m + 1) i其对应的点在复平。
L:算法初步与复数(理科2013年) Word版含答案

L单元算法初步与复数L1算法与程序框图图1-15.L1执行如图1-1所示的程序框图,如果输入的t∈,则输出的s属于( )A.B.C.D.5.A 由框图可知,当t∈时,s=4t-t2=-(t-2)2+4,故此时s∈,综上,s∈.5.L1、L2某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( ) A.这种抽样方法是一种分层抽样B.这种抽样方法是一种系统抽样C.这五名男生成绩的方差大于这五名女生成绩的方差D.该班男生成绩的平均数小于该班女生成绩的平均数5.C 分层抽样是按照比例的抽样,由于男女生人数不同,抽取的人数相同;系统抽样是按照一定规则的分段抽样,故题中抽样方法即不是分层抽样也不是系统抽样.又五名男生的成绩的平均数为90,方差为8,五名女生成绩的平均数是91,方差为6,但该班所有男生成绩的平均数未必小于该班所有女生成绩的平均数.故选项C中的结论正确,选项D中的结论不正确.2.L1如图1-1所示,程序框图(算法流程图)的输出结果是( )图1-1A.16B.2524C.34D.11122.D 依次运算的结果是s =12,n =4;s =12+14,n =6;s =12+14+16,n =8,此时输出s ,故输出结果是12+14+16=1112.4.L1 执行如图1-1所示的程序框图,输出的S 的值为()图1-1A .1 B.23 C.1321 D.6109874.C 执行第一次循环时S =12+12×1+1=23,i =1;第二次循环S =232+12×23+1=1321,i =2,此时退出循环,故选C.6.L1 阅读如图1-2所示的程序框图,若输入的k =10,则该算法的功能是( )图1-2A.计算数列{2n-1}的前10项和B.计算数列{2n-1}的前9项和C.计算数列{2n-1}的前10项和D.计算数列{2n-1}的前9项和6.A S=0,i=1→S=1,i=2→S=1+2,i=3→S=1+2+22,i=4→…→S=1+2+22+…+29,i=11>10,故选A.17.L1某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图1-4所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本均值:(2)日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.图1-417.解:18.L1 如图1-5(1),在等腰直角三角形ABC 中,∠A=90°,BC =6,D ,E 分别是AC ,AB 上的点,CD =BE =2,O 为BC 的中点,将△ADE 沿DE 折起,得到如图1-5(2)所示的四棱锥A′-BCDE ,其中A′O= 3.(1)证明:A′O⊥平面BCDE ;(2)求二面角A′-CD -B 的平面角的余弦值.图1-518.解:19.L1 设数列{a n }的前n 项和为S n ,已知a 1=1,2S n n =a n +1-13n 2-n -23,n∈N *.(1)求a 2的值;(2)求数列{a n }的通项公式;(3)证明:对一切正整数n ,有1a 1+1a 2+…+1a n <74.19.解:20.L1 已知抛物线C 的顶点为原点,其焦点F(0,c)(c>0)到直线l :x -y -2=0的距离为322,设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点.(1)求抛物线C 的方程;(2)当点P(x 0,y 0)为直线l 上的定点时,求直线AB 的方程;(3)当点P 在直线l 上移动时,求|AF|·|BF|的最小值. 20.解:21.L1 设函数f(x)=(x -1)e x-kx 2(k∈R ). (1)当k =1时,求函数f(x)的单调区间;(2)当k∈⎝ ⎛⎦⎥⎤12,1时,求函数f(x)在上的最大值M. 21.解:16.L1 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x∈R . (1)求f ⎝ ⎛⎭⎪⎫-π6的值; (2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎭⎪⎫2θ+π3. 16.解:11.L1 执行如图1-2所示的程序框图,若输入n 的值为4,则输出s 的值为________.图1-211.7 1≤4,s=1+0=1,i=2;2≤4,s=1+1=2,i=3;3≤4,s=2+2=4,i =4;4≤4,s=4+3=7,i=5;5>4,故输出s=7.12.L1阅读如图1-4所示的程序框图,运行相应的程序,输出的结果i=________.图1-412.5 逐次运算结果是a=5,i=2;a=16,i=3;a=8,i=4;a=4,i=5,满足条件,输出i=5.13.L1执行如图1-3所示的程序框图,如果输入a=1,b=2,则输出的a的值为________.图1-313.9 根据程序框图所给流程依次可得,a=1,b=2,①a=3,②a=5,③a=7,④a =9,满足条件输出a=9.5.L1如图1-1是一个算法的流程图,则输出的n的值是________.图1-15.3 逐一代入可得当a=26>20时,n=3,故最后输出3.7.L1阅读如图1-1所示的程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( )图1-1A.S=2*i-2 B.S=2*i-1C.S=2*i D.S=2*i+47.C 依次检验可知选C.13.L1图1-3执行如图1-3所示的程序框图,若输入的ε的值为0.25,则输出的n的值为________.13.3 第一次执行循环体时,F1=3,F0=2,n=1+1=2,1F1=13>0.25;第二次执行循环体时,F1=2+3=5,F0=3,n=2+1=3,1F1=15<0.25,满足条件,输出n=3.18.L1,K6某算法的程序框图如图1-6所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.图1-6(1)分别求出按程序框图正确编程运行时输出y的值为i的概率P i(i=1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.甲的频数统计表(部分)乙的频数统计表(部分)当n =2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为i(i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大;(3)按程序框图正确编写的程序运行3次,求输出y 的值为2的次数ξ的分布列及数学期望.18.解:(1)变量x 是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y 的值为1,故P 1=12;当x 从2,4,8,10,14,16,20,22这8个数中产生时,输出y 的值为2,故P 2=13;当x 从6,12,18,24这4个数中产生时,输出y 的值为3,故P 3=16,所以,输出y 的值为1的概率为12,输出y 的值为2的概率为13,输出y 的值为3的概率为16. (2)当n =2 100时,甲、乙所编程序各自输出y 的值为i(i =1,2,3)的频率如下:比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大. (3)随机变量ξ可能的取值为0,1,2,3. P(ξ=0)=C 03×⎝ ⎛⎭⎪⎫130×⎝ ⎛⎭⎪⎫233=827,P(ξ=1)=C 13×⎝ ⎛⎭⎪⎫131×⎝ ⎛⎭⎪⎫232=49,P(ξ=2)=C 23×⎝ ⎛⎭⎪⎫132×⎝ ⎛⎭⎪⎫231=29,P(ξ=3)=C 33×⎝ ⎛⎭⎪⎫133×⎝ ⎛⎭⎪⎫230=127,故ξ的分布列为所以,E ξ=0×827+1×49+2×29+3×127=1.即ξ的数学期望为1.3.L1 阅读如图1-1所示的程序框图,运行相应的程序,若输入x 的值为1,则输出S的值为( )图1-1A .64B .73C .512D .5853.B 当x =1时,S =0+1=1;当x =2时,S =1+23=9;当x =4时,S =9+43=73满足题意输出.图1-16.L1 执行如图1-1所示的程序框图,如果输入的N =10,那么输出的S =( ) A .1+12+13+…+110B .1+12!+13!+ (110)C .1+12+13+…+111D .1+12!+13!+ (111)6.B k =1,T =1,S =1;k =2,T =12,S =1+12;k =3,T =12×3,S =1+12+12×3;k =4,T =12×3×4,S =1+12!+13!+14!,…,10>10不成立,继续循环.答案为B.5.L1 某程序框图如图1-1所示,若该程序运行后输出的值是95,则( )图1-1A .a =4B .a =5C .a =6D .a =7 5.A S =1+11×2+12×3+…+1k (k +1)=1+1-12+12-13+…+1k -1k +1=1+1-1k +1=2-1k +1=95,故k =4,k =k +1=5,满足k>a 时,即5>a 时,输出S ,所以a =4,选择A.8.L1,L2 执行如图1-4所示的程序框图,如果输出s =3,那么判断框内应填入的条件是( )图1-4A .k ≤6B .k ≤7C .k ≤8D .k ≤98.B 第一次输入得s =log 23,k =3;第二次得s =log 23·log 34=2,k =4;第三次得s =2log 45,k =5;第四次得s =2log 45·log 56=2 log 46,k =6;第五次得s =2log 46·log 67=2log 47,k =7;第六次得s =2log 47·log 78=2log 48=2log 4432=3,k =8,输出,故选B.L2 基本算法语句5.L1、L2 某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )A .这种抽样方法是一种分层抽样B .这种抽样方法是一种系统抽样C .这五名男生成绩的方差大于这五名女生成绩的方差D .该班男生成绩的平均数小于该班女生成绩的平均数5.C 分层抽样是按照比例的抽样,由于男女生人数不同,抽取的人数相同;系统抽样是按照一定规则的分段抽样,故题中抽样方法即不是分层抽样也不是系统抽样.又五名男生的成绩的平均数为90,方差为8,五名女生成绩的平均数是91,方差为6,但该班所有男生成绩的平均数未必小于该班所有女生成绩的平均数.故选项C 中的结论正确,选项D 中的结论不正确.2.L2 根据下列算法语句,当输入x 为60时,输出y 的值为( )输入x ;If x ≤50 Then y =0.5*x Elsey =25+0.6*(x -50) End If 输出y.A .25B .30C .31D .612.C 算法语言给出的是分段函数y =⎩⎪⎨⎪⎧0.5x ,x≤50,25+0.6(x -50),x>50,输入x =60时,y =25+0.6(60-50)=31.8.L1,L2 执行如图1-4所示的程序框图,如果输出s =3,那么判断框内应填入的条件是( )图1-4A .k ≤6B .k ≤7C .k ≤8D .k ≤98.B 第一次输入得s =log 23,k =3;第二次得s =log 23·log 34=2,k =4;第三次得s =2log 45,k =5;第四次得s =2log 45·log 56=2 log 46,k =6;第五次得s =2log 46·log 67=2log 47,k =7;第六次得s =2log 47·log 78=2log 48=2log 4432=3,k =8,输出,故选B.L3 算法案例L4 复数的基本概念与运算2.L4 若复数z 满足(3-4i)z =|4+3i|,则z 的虚部为( ) A .-4 B .-45 C .4 D.452.D z =|4+3i|3-4i =53-4i =5(3+4i )25=35+45i ,故z 的虚部是45.1.L4 设i 是虚数单位,z 是复数z 的共轭复数,若z·zi +2=2z ,则z =( ) A .1+i B .1-i C .-1+i D .-1-i1.A 设z=a+bi(a,b∈R),则z=a-bi,所以z·zi+2=2z,即2+(a2+b2)i=2a+2bi,根据复数相等的充要条件得2=2a,a2+b2=2b,解得a=1,b=1,故z=1+i.2.L4在复平面内,复数(2-i)2对应的点位于( )A.第一象限 B.第二象限C.第三象限 D.第四象限2.D (2-i)2=4-4i+i2=3-4i,对应的复平面内点的坐标为(3,-4),所以选D.1.L4已知复数z的共轭复数z=1+2i(i为虚数单位),则z在复平面内对应的点位于( )A.第一象限 B.第二象限C.第三象限 D.第四象限1.D z=1-2i,对应的点为P(1,-2),故选D.3.L4若复数iz=2+4i,则在复平面内,z对应的点的坐标是( )A.(2,4) B.(2,-4)C.(4,-2) D.(4,2)3.C 设复数z=a+bi,a,b∈R,则iz=i(a+bi)=-b+ai=2+4i,解得b=-2,a=4.故在复平面内,z对应的点的坐标是(4,-2),选C.1.L4在复平面内,复数z=2i1+i(i为虚数单位)的共轭复数对应的点位于( ) A.第一象限 B.第二象限C.第三象限 D.第四象限1.D z=2i1+i=2i(1-i)(1+i)(1-i)=i(1-i)=1+i,z=1-i,z对应的点在第四象限,选D.1.L4复数z=i·(1+i)(i为虚数单位)在复平面上对应的点位于( )A.第一象限 B.第二象限C.第三象限 D.第四象限1.B 由题z=i·(1+i)=i+i2=-1+i,在复平面上对应的点坐标为(-1,1),即位于第二象限,选B.2.L4设z=(2-i)2(i为虚数单位),则复数z的模为________.2.5 因为z=(2-i)2=4-4i+i2=3-4i,所以复数z的模为5.1.A1,L4已知集合M={1,2,zi},i为虚数单位,N={3,4},M∩N={4},则复数z=( )A .-2iB .2iC .-4iD .4i 1.C zi =4z =-4i ,故选C.1.L4 复数z =1i -1的模为( )A.12B.22C. 2 D .2 1.B 复数z =1i -1=-1+i 2,所以|z|=-1+i 2=22,故选B.2.L4 (1+3i)3=( ) A .-8 B .8 C .-8i D .8i2.A (1+3i)3=13+3×12(3i)+3×1×(3i)2+(3i)3=1+33i -9-33i =-8.1.L4 复数z 满足(z -3)(2-i)=5(i 为虚数单位),则z 的共轭复数z 为( ) A .2+i B .2-i C .5+i D .5-i1.D 设z =a +bi ,(a ,b∈R ),由题意得(a +bi -3)(2-i)=(2a +b -6)+(2b -a+3)i =5,即⎩⎪⎨⎪⎧2a +b -6=5,2b -a +3=0,解之得⎩⎪⎨⎪⎧a =5,b =1,∴z =5-i.6.L4 设z 1,z 2是复数,则下列命题中的假.命题是( ) A .若|z 1-z 2|=0,则z 1=z 2 B .若z 1=z 2,则z 1=z 2C .若|z 1|=|z 2|,则z 1·z 1=z 2·z 2D .若|z 1|=|z 2|,则z 21=z 226.D 设z 1=a +bi ,z 2=c +di(a ,b ,c ,d∈R ),若|z 1-z 2|=0,则z 1-z 2=(a -c)+(b -d)i =0a =c ,b =d ,故A 正确.若z 1=z 2,则a =c ,b =-d ,所以z 1=z 2,故B 正确.若|z 1|=|z 2|,则a 2+b 2=c 2+d 2,所以z 1·z 1=z 2·z 2,故C 正确.又z 21=(a 2-b 2)+2abi ,z 22=(c 2-d 2)+2cdi ,由a 2+b 2=c 2+d 2不能推出z 21=z 22成立,故D 错.2.L4 如图1-1所示,在复平面内,点A 表示复数z ,则图1-1中表示z 的共轭复数的点是( )图1-1A .AB .BC .CD .D2.B 复数与共轭复数的几何关系是其表示的点关于x 轴对称.9.L4 已知a ,b∈R ,i 是虚数单位,若(a +i)(1+i)=bi ,则a +bi =________. 9.1+2i (a +i)(1+i)=a -1+(a +1)i =bi ,∴⎩⎪⎨⎪⎧a -1=0,a +1=b ,解得a =1,b =2.故a +bi =1+2i. 2.L4 设复数z 满足(1-i)z =2i ,则z =( ) A .-1+i B .-1-i C .1+i D .1-i2.A (1-i)z =2i ,则z =2i1-i=i(1+i)=-1+i.故选A. 1.L4 已知i 是虚数单位,则(-1+i)(2-i)=( ) A .-3+i B .-1+3i C .-3+3i D .-1+i1.B (-1+i)(2-i)=-2+i +2i +1=-1+3i ,故选择B. 11.L4 已知复数z =5i1+2i (i 是虚数单位),则|z|=________.11. 5 因为z =5i (1-2i )(1+2i )(1-2i )=2+i ,所以|z|=22+12= 5.L5 单元综合。
高考数学一轮复习L单元算法初步与复数(含解析)

L 单元算法初步与复数L1 算法与程序框图3. L1[2014 •安徽卷]如图1-1所示,程序框图(算法流程图)的输出结果是()图1-1A. 34 B . 53 C . 78 D . 893. B [ 解析] 由程序框图可知,变量的取值情况如下:第一次循环, 第二次循环, 第三次循环, 第四次循环, 第五次循环, 第六次循环, 第七次循环, 第八次循环, X= 1, y = 1, z = 2;x= 1, y = 2, z = 3;x= 2, y = 3, z = 5;x= 3, y = 5, z = 8;x= 5,y= 8,z= 13;x= 8, y= 13, z= 21;x= 13, y= 21 , z= 34;x= 21, y= 34, z= 55,不满足条件,跳出循环.4. L1[2014 •北京卷]当m^ 7, n = 3时,执行如图1-1所示的程序框图,输出的S值为()图1-1A.7 B .42C.210 D .8404. C [解析]S= 1X 7X 6X 5= 210.5. L1[2014 •福建卷]阅读如图1-3所示的程序框图,运行相应的程序,输出的S的值等于( )图1-3A. 18B. 20C. 21D. 405. B [ 解析] 输入S= 0,n= 1,第一次循环,S= 0+2+1= 3,n= 2;第二次循环,S=3+2 +2= 9,n= 3;第三次循环,S= 9 + 23+ 3= 20, n = 4,满足S> 15,结束循环,输出S= 20.13. L1[2014 •湖北卷]设a是一个各位数字都不是0且没有重复数字的三位数•将组成a 的 3 个数字按从小到大排成的三位数记为I( a) ,按从大到小排成的三位数记为D(a)( 例如a= 815,贝U 1(a) = 158, D( a) = 851).阅读如图1-2所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b= _________________ .图1-213. 495 [解析]取a1= 815? b1= 851 - 158 = 693工815?比=693;由a2= 693? b2= 963 —369 = 594工693 ? a3= 594;由a3= 594? b3= 954 —459 = 495工594 ? a4= 495;由a4= 495? b4= 954—459= 495= a4? b= 495.6. L1[2014 •湖南卷]执行如图1-1所示的程序框图.如果输入的t € [ —2, 2],则输出的S 属于( )A. [ —6,—2] B . [ —5,—1]C. [ —4, 5] D . [ —3, 6]图1-126. D [解析](特值法)当t = —2 时,t = 2X ( —2) + 1 = 9, S= 9 —3 = 6,所以D正确.7. L1[2014 •江西卷]阅读如图1-3所示的程序框图,运行相应的程序,则程序运行后输出的结果为( )图1-3A. 7 B . 9 C . 10 D . 117. B13.图1-229 11 4 13.石 [解析]当 x = 9 时,y = 5,则 |y — x | = 4;当 x = 5 时,y =—,则 | y — x | =云; 93 3 11 294 29当 x = ~3时,y = ~9",贝u| y —x |=9<1.故输出 y =百.7. L1[2014 •新课标全国卷I ]执行如图 1-2所示的程序框图,若输入的 a , b , k 分别 为1, 2, 3,则输出的M=( )3 3 8 3 8 7. D [解析]逐次计算,依次可得:M= 2, a = 2, b =2 n = 2; M= 3 a =~, b = 3, n2 23 2 315 8 1515=3; M= —, a = 3, b = —, n =4.此时输出M 故输出的是 亍7. L1[2014 •新课标全国卷n ]执行如图 1-2所示的程序框图,如果输入的 x , t 均为2,则输出的S =()图 1-2A .4B .5C . 6D .72-20 16A. 7B. 7C.1518D7 - 27. D [解析]逐次计算,可得M= 2, S= 5, k= 2; M= 2, S=乙k= 3,此时输出S= 7.11. L1[2014 •山东卷]执行如图1-2所示的程序框图,若输入的x的值为1,则输出的n 的值为__ .图1-211. 3 [解析]x=1 满足不等式,执行循环后, x=2, n=1;x= 2满足不等式,执行循环后, x= 3, n= 2;x= 3 满足不等式,执行循环后, x= 4, n= 3;x= 4 不满足不等式, 结束循环,输出的n的值为3.4. L1[2014 •陕西卷]根据如图1-1所示的框图,对大于2的整数N,输出的数列的通项公式是( )图1-1A. a n= 2nB. a n= 2(n—1)C. a n= 2D. a n= 2n—14. C [解析]阅读题中所给的程序框图可知,对大于2的整数N,输出数列:2, 2X2 =22, 2X 22= 23, 2X 2 3= 24,…,2X2 N_ 1= 2N,故其通项公式为a n= 2n.5. E5, L1[2014 •四川卷]执行如图1-1所示的程序框图,如果输入的x, y€ R那么输出的S的最大值为()图1-1A. 0 B . 1 C . 2 D . 3x + y w 1,5. C [解析]题中程序输出的是在x>0, 的条件下S= 2x + y的最大值与1中较y >0大的数•结合图像可得,当x = 1, y= 0时,S= 2x+ y取得最大值2, 2>1,故选C.3. L1[2014 •天津卷]阅读如图1-1所示的程序框图,运行相应的程序,输出S的值为图1-1A. 15B. 105C. 245D. 9453. B [解析]第1 次循环,i = 1, T= 3, S= 1 x 3;第 2 次循环,i = 2, T= 5, S= 1 x 3X 5;第 3 次循环,i = 3,T= 7,S= 1 x 3x 5x 7.执行完后,这时i 变为4,退出循环,故输出S=1x3x5x7=105.11. L1[2014 •浙江卷]若某程序框图如图1-3所示,当输入50时,则该程序运行后输出的结果是__________ .图1-311. 6 [解析]第一次运行,S = 1 , i = 2;第二次运行,S = 4, i = 3;第三次运行,S =11 , i = 4;第四次运行,S = 26, i = 5;第五次运行,S = 57, i = 6,此时S >n ,输出i = 6.5. L1[2014 •重庆卷]执行如图1-1所示的程序框图,若输出 k 的值为6,则判断框内 可填入的条件是()图1-19 9 9得s = 1X ^0= 10, k = 8;第二次循环结束,得s = 10 x 44 7 7,k = 7;第三次循环结束,得 s = x -^-, k = 6,此时退出循环,输出k = 6.故判断55 8 101 A. s >2 B C.5. C [解析]第一次循环结束, 框内可填 3 747L2基本算法语句 L3算法案例L4复数的基本概念与运算1. L4[2014 •重庆卷]复平面内表示复数i(1 — 2i)的点位于()A.第一象限 B .第二象限 C.第三象限D .第四象限 1. A [解析]i(1— 2i) = 2+ i ,其在复平面内对应的点为(2 , 1),位于第一象限.L4、A2[2014 •浙江卷]已知i 是虚数单位,a , b € R,得“ a — b — 1”是“(a + b i) 2 的()A.充分不必要条件B .必要不充分条件C.充分必要条件 D .既不充分也不必要条件2. A [解析]由 a, b € R, (a + b i ) 2= a 2— b 2 + 2ab i = 2i,得 a b 0 所以 a — 1 或2ab = 2,b — 1b —— 1,故选 A. b —— 1.1. L4[2014 •全国卷]设z — ,贝U z 的共轭复数为()3十iA. — 1 十 3i B . — 1 — 3i C. 1十 3i D . 1 — 3i 10i 10i (3 — i ) 10 (1 十 3i ) 1. D [解析]z — — — — 1十3i ,根据共轭复数的定 3 十 i ( 3 十 i ) ( 3— i ) 10义,其共轭复数是1— 3i.一 z1. L4[2014 •安徽卷]设i 是虚数单位,z 表示复数z 的共轭复数.若z — 1 + i ,则i 十i • i —()A. — 2 B . — 2i C. 2 D . 2iz —1. C [解析]因为z — 1 + i ,所以-十i • z — ( — i 十1)十i 十1 —2.2. =2i ”9. L4[2014 •北京卷]复数1+ i 2 1—79.—1 [解析]1十i 21 —i(1 十i ))2(1—i )(1 十i )2i22——1.A. — 2-3i B 2 + 3i C. 2 — 3i D . 2+ 3i1. C [解析]由复数z = (3 — 2i)i = 2 + 3i ,得复数z 的共轭复数z = 2— 3i.2.L4[2014 •广东卷]已知复数z 满足(3 + 4i) z = 25,则z =()A. — 3+ 4i B . — 3 — 4i C. 3 + 4i D . 3— 4i2. D [解析]本题考查复数的除法运算,利用分母的共轭复数进行求解. 因为(3 + 4i) z = 25,1. L4[2014 •湖北卷]i 为虚数单位,A.— 1 B . 1 C . — i D . i 1 — i 2 — 2i1 . A [解析]= =—1.故选A.1 + i 2i1 . L4[2014 •湖南卷]满足= i(i 为虚数单位)的复数z =()1 1. —_ i2 21.B [解析]因为 i '则 z +i =zi '所以 z =T^=( i —(()(—1 — i )二二1. L4[2014 •江西卷]z 是z 的共轭复数,若z + z = 2, ( z — z )i = 2(i 为虚数单位), 则 z =()A. 1 + i B . — 1 —i C. — 1 + i D . 1 —i1. D [解析]设 z = a + b i( a , b € R),贝U z = a — b i ,所以 2a = 2, — 2b = 2,得 a = 1,b = — 1,故 z = 1 — i.2. L4[2014 •辽宁卷]设复数 z 满足(z — 2i)(2 — i) = 5,贝U z =( )A. 2 + 3i B . 2 — 3i C . 3+ 2i D . 3 — 2i52. A [解析]由(z — 2i)(2 — i) = 5,得 z — 2i = ,故 z = 2+ 3i.2 — i(1 + i ) 32. L4[2014 •新课标全国卷I ] (一—=( )(1 — i )1 12 -A.2+》B.所以z =253+ 4i 25 (3— 4i ) (3 — 4i )( 3 + 4i )3 — 4i.C. 1 1 —尹1iA. 1 + i B . 1—i4 C.— 1 + i D 1 — iA.— 5 B . 5 C . — 4+ i D . — 4— i22. A [解析]由题知 Z 2 = — 2 + i ,所以乙Z 2 = (2 + i)( — 2+ i) = i — 4= — 5.1. L4[2014 •山东卷]已知a , b € R , i 是虚数单位,若 a — i 与2 + b i 互为共轭复数,2则(a + b i)=( )A. 5 — 4i B . 5+ 4i C . 3— 4i D . 3+ 4i1 . D [解析]因为a — i 与2 + b i 互为共轭复数,所以a = 2, b = 1,所以(a + b i) 2= (22+ i) = 3 + 4i.故选 D.7 + i1 . L4[2014 •天津卷]i 是虚数单位,复数 3+7 =()A. 1 — i B . — 1 + i 17 31 17 25C.25+ 25i D . —7 + 戶”, 7 + i (7 + i )( 3 — 4i ) 25 — 25i 1. A [解析]3+T = (3 + 4i )( 3 — 4i ) = 32+ 42 = 1 — i.L5单元综合2 . [2014 •合肥质检]已知复数Z = 3+ 4i , Z 表示复数Z 的共轭复数,则 彳=( )A. 5 B . 5 C. ,6 D . 6Z2 . B [解析]因为 |Z | = |Z | = 5,所以 i = 5.4 . [2014 •闽南四校期末]已知复数Z 的共轭复数Z = 1 + 2i(i 为虚数单位),则Z 在复 平面内对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限4 . D [解析]由题意知,Z = 1— 2i ,故其所对应的点(1 , — 2)在第四象限. 9 . [2014 •石家庄质检]运行如图G12-2所示的程序框图,则输出 k 的值是( )2. D [解析](1 + i ) 32(1 + i ) (1 + i )(1 — i )(1 —i )2i (1 + i ) —2i1 — i.2. L4[2014 •新课标全国卷n ]设复数Z Z 1, Z 2在复平面内的对应点关于虚轴对称, Z 1 =11 . L4[2014 •2 — 2i四川卷]复数市11. — 2i [解析] 2 —2i1 + i2 (1— i ) (1+i )(1—i )=—2i.e的值为(A.3412. C343[解析]由题意知sin e = 5, cos e工5 所以cos e =-5 所以tan e =B. 3 C图G12-2A. 4 B . 5 C . 6 D . 79. A [解析]运行程序框图可知,输出k的值为4.10. [2014 •江西名校调研]运行如图G12-3所示的程序框图,若输出的S= 120,则判断框内应为()12. [201441 1 114. [2014 •自贡模拟]如图G12-7所示的四个程序框图都是为了计算 S = 1+ - + - + -+3 5 719的值,其中,错误的算法是( )图 G12-3A. k > 4? B . k > 5? C. k > 6? D . k > 7?10. B [解析] ••• S =1, k = 1; k = 2, S = 4; k = 3, S = 11; k = 4, S = 26; k = 5, S =57; k = 6, S = 120. 故选B.4e— 5是纯虚数,则tan•湖北部分重点中学期末 ]若z = sin e -学+ i cos5图G12-714. C [解析]根据程序框图,易知选项A, B, D正确;对于选项C,由该框图可知当1 1 1i = 1时,S= 1;当i= 7时,S= 1 +孑+匸+亏,程序结束,不符合题意.2 5 7。
L单元 算法初步与复数

数 学L 单元 算法初步与复数L1 算法与程序框图 3.L1[2016·北京卷] 执行如图1-1所示的程序框图,若输入的a 值为1,则输出的k 值为( )图1-1A .1B .2C .3D .43.B [解析] 输入a =1,当k =0时,b =1,a =-12,不满足a =b ;当k =1时,a =-2,不满足a =b ;当k =2时,a =1,满足a =b ,结束循环,输出的k 值是2.6.L1[2016·江苏卷] 图1-1a 的值是________.图1-16.9 [解析] 初始值a =1,b =9,不满足a >b ;第一次执行循环体后a =5,b =7,此时还不满足a >b ;第二次执行循环体后a =9,b =5,满足a >b ,结束循环,故输出的a 的值为9.9.L1[2016·全国卷Ⅰ] 执行图1-3的程序框图,如果输入的x =0,y =1,n =1,则输出x ,y 的值满足( )图1-3A .y =2xB .y =3xC .y =4xD .y =5x9.C [解析] 第一次运行程序,n =1,x =0,y =1;第二次运行程序,n =2,x =12,y=2;第三次运行程序,n =3,x =32,y =6,此时满足条件x 2+y 2≥36,输出x =32,y =6,满足y =4x .7.L1[2016·全国卷Ⅲ] 执行图1-2的程序框图,如果输入的a =4,b =6,那么输出的n =( )图1-2A .3B .4C .5D .67.B [解析] 当n =1时,s =6;当n =2时,s =10;当n =3时,s =16;当n =4时,s =20,故输出的n =4.6.L1[2016·四川卷] 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图1-1所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n ,x 的值分别为3,2,则输出v 的值为( )图1-1A.9 B.18C.20 D.356.B[解析] 初始值n=3,x=2,程序运行过程依次为i=2,v=1×2+2=4,i=1;v=4×2+1=9,i=0;v=9×2+0=18,i=-1,跳出循环,输出v=18.8.L1[2016·全国卷Ⅱ] 中国古代有计算多项式值的秦九韶算法,图1-3是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s =()图1-3A.7 B.12C.17 D.348.C[解析] 第一次运算,a=2,s=2,k=1,不满足k>n;第二次运算,a=2,s=2×2+2=6,k=2,不满足k>n;第三次运算,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17.11.L1[2016·山东卷] 执行图1-3所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为________.图1-311.3[解析] 当i=1时,a=1,b=8;当i=2时,a=3,b=6;当i=3时,a=6,b =3,满足条件.故输出i的值为3.4.L1[2016·天津卷] 阅读如图1-1所示的程序框图,运行相应的程序,则输出S的值为()图1-1A.2 B.4C.6 D.84.B[解析] 第一次执行循环体后S=8,n=2;第二次执行循环体后S=2,n=3;第三次执行循环体后S=4,n=4,满足n>3,结束循环.故输出S=4.L2 基本算法语句L3 算法案例L4 复数的基本概念与运算9.L4[2016·北京卷] 设a∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a=________.9.-1[解析] 复数(1+i)(a+i)=a-1+(a+1)i,因为其对应的点位于实轴上,所以a+1=0,解得a =-1.2.L4[2016·江苏卷] 复数z =(1+2i)(3-i),其中i 为虚数单位,则z 的实部是________. 2.5 [解析] 因为z =(1+2i)(3-i)=3+5i -2i 2=5+5i ,所以其实部为5. 2.L4[2016·全国卷Ⅰ] 设(1+i)x =1+y i ,其中x ,y 是实数,则|x +y i|=( )A .1 B. 2 C. 3 D .22.B [解析] 由已知得x +x i =1+y i ,根据两复数相等的条件可得x =y =1,所以|x +y i|=|1+i|= 2.2.L4[2016·全国卷Ⅲ] 若z =1+2i ,则4izz -1=( )A .1B .-1C .iD .-i2.C [解析] 4i zz -1=4i12+22-1=i.2.J3,L4[2016·四川卷] 设i 为虚数单位,则(x +i)6的展开式中含x 4的项为( ) A .-15x 4 B .15x 4 C .-20i x 4 D .20i x 42.A [解析] 由题可知,含x 4的项为C 26x 4i 2=-15x 4. 1.L4[2016·全国卷Ⅱ] 已知z =(m +3)+(m -1)i 在复平面内对应的点在第四象限,则实数m 的取值范围是( )A .(-3,1)B .(-1,3)C .(1,+∞)D .(-∞,-3)1.A [解析] 由题易知m +3>0,m -1<0,解得-3<m <1. 1.L4[2016·山东卷] 若复数z 满足2z +z =3-2i ,其中i 为虚数单位,则z =( ) A .1+2i B .1-2i C .-1+2i D .-1-2i1.B [解析] 设z =a +b i(a ,b ∈R ).由题意得2a +2b i +a -b i =3-2i ,得⎩⎪⎨⎪⎧a =1,b =-2,∴z =1-2i.9.L4[2016·天津卷] 已知a ,b ∈R ,i 是虚数单位.若(1+i)(1-b i)=a ,则ab的值为________.9.2 [解析] (1+i)(1-b i)=a ,即1+b +i -b i =a ,∴⎩⎪⎨⎪⎧1+b =a ,1-b =0,解得⎩⎪⎨⎪⎧b =1,a =2,∴a b =2. 2.L4[2016·上海卷] 设z =3+2ii,其中i 为虚数单位,则Im z =________. 2.-3 [解析] z =3+2i i =3i +2i 2i 2=2-3i ,所以Im z =-3.[2016·浙江卷]03 “复数与导数”模块(1)已知i 为虚数单位.若复数z 满足(z +i)2=2i ,求复数z . (2)求曲线y =2x 2-ln x 在点(1,2)处的切线方程. 解:(1)设复数z =a +b i ,a ,b ∈R ,由题意得a 2-(b +1)2+2a (b +1)i =2i ,解得⎩⎪⎨⎪⎧a =1,b =0或⎩⎪⎨⎪⎧a =-1,b =-2.故z =1或z =-1-2i.(2)由于(2x 2-ln x )′=4x -1x,则曲线在点(1,2)处的切线的斜率为3.因此,曲线在点(1,2)处的切线方程为y =3x -1.。
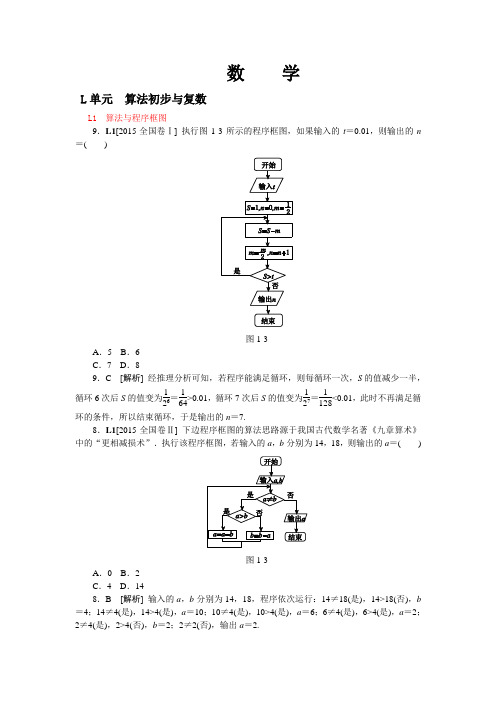
L单元 算法初步与复数

知抛物线 C 的顶点为原点 其焦点 F(0
c)(c>0)到直线 l x
y
设 P 为直线 l
的点 过点 P 作抛物线 C 的两条 线 PA PB 其中
A B为 点 (1)求抛物线 C 的方程 (2)当点 P(x0 y0)为直线 l 的定点时 求直线 AB 的方程 (3)当点 P 在直线 l 移动时 求|AF|·|BF|的最小值
1 4 12 5 [解析] 逐次运算结果是 a=5 i=2 a=16 i=3 a=8 i=4 a=4 i=5 满 足条件 输出 i=5. 13 L1[2013·湖南卷] 执行如 1 3 所示的程序框 如果输入 a=1 b=2 则输出的 a 的值为________
1 3
13 9 [解析] 根据程序框 所给流程依次可得 a=1 b=2 a=3 a=5 a=7 a=9 满足条件输出 a=9. 5 L1[2013·江 卷] 如 1 1 是一个算法的流程 则输出的 n 的值是________
1 1 1 1 所示的程序框
1 1 1 A. 6 3 C. 4 2 D 25 B. 24 11 D. 12 1 [解析] 依次运算的结果是 s= 2 1 4 1 11 = . 6 12 1 1 所示的程序框 输出的 S 的值为( ) n=4 1 1 s= 2 4 1 1 n=6 s= 2 4 1 n=8 6
1 时输出 s 故输出结果是 2 4
L1[2013·北京卷] 执行如
1 1 2 A 1 B. 3 13 610 C. D. 21 987 12 1 22 3 1 13 = 21 1
4
2 C [解析] 执行第一次循环时 S= = 2× × 3
时退出循环 故选 C. 6 L1[2013·福建卷] 阅读如 是( )
L单元 算法初步与复数
数学L单元算法初步与复数L1 算法与程序框图9.L1[2015·全国卷Ⅰ] 执行图1-3所示的程序框图,如果输入的t=0.01,则输出的n =()图1-3A.5 B.6C.7 D.89.C[解析] 经推理分析可知,若程序能满足循环,则每循环一次,S的值减少一半,循环6次后S的值变为126=164>0.01,循环7次后S的值变为127=1128<0.01,此时不再满足循环的条件,所以结束循环,于是输出的n=7.8.L1[2015·全国卷Ⅱ] 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()图1-3A.0 B.2C.4 D.148.B[解析] 输入的a,b分别为14,18,程序依次运行:14≠18(是),14>18(否),b =4;14≠4(是),14>4(是),a=10;10≠4(是),10>4(是),a=6;6≠4(是),6>4(是),a=2;2≠4(是),2>4(否),b=2;2≠2(否),输出a=2.5.L1[2015·北京卷] 执行如图1-1所示的程序框图,输出的k 值为( )图1-1A .3B .4C .5D .65.B [解析] 初值为a =3,k =0,进入循环体后a =32,k =1;a =34,k =2;a =38,k=3;a =316,k =4,此时a <14,退出循环,则输出k =4,故选B.4.L1[2015·福建卷] 阅读如图1-1所示的程序框图,运行相应的程序,若输入x 的值为1,则输出y 的值为( )图1-1A .2B .7C .8D .1284.C [解析] 若输入x 的值为1,则不满足“x ≥2”,所以y =9-1=8. 11.L1[2015·山东卷] 执行图1-2所示的程序框图,若输入的x 的值为1,则输出的y 的值是________.图1-211.13 [解析] 第一次循环,得x =2;第二次循环,不满足x <2,执行y =3×22+1=13,然后输出y .故输出的y 的值为13.7.L1[2015·陕西卷] 根据下面框图,当输入x 为6时,输出的y =( )图1-3A .1B .2C .5D .107.D [解析] 循环体的执行情况是x =3→x =0→x =-3,结束循环,故输出的y =(-3)2+1=10.6.L1[2015·四川卷] 执行如图1-1所示的程序框图,输出S 的值为( )图1-1A .-32 B.32 C .-12 D.126.D [解析] 依据框图循环结构逐次计算.第一次进入循环,运行后,k =2,不满足k >4;第二次进入循环,运行后,k =3,不满足k >4;第三次进入循环,运行后,k =4,不满足k >4;第四次进入循环,运行后k =5,满足k >4,输出S =sin 5π6=12.3.L1[2015·天津卷] 阅读下面的程序框图,运行相应的程序,则输出i 的值为( )A .2B .3C .4D .53.C [解析] 当i =1时,S =9;当i =2时,S =7;当i =3时,S =4;当i =4时,S =0,此时满足条件,故选C.8.L1[2015·重庆卷] 执行如图1-3所示的程序框图,则输出s 的值为( )图1-3A.34B.56C.1112D.25248.D [解析] 第一次循环,得k =2,s =12;第二次循环,得k =4,s =12+14=34;第三次循环,得k =6,s =16+34=1112;第四次循环,得k =8,s =18+1112=2524,退出循环,输出s的值为2524.故选D.7.L1[2015·安徽卷] 执行如图1-1所示的程序框图(算法流程图),输出的n 为( )A .3B .4C .5D .67.B [解析] 初始值,a =1,n =1,|a -1.414|=0.414≥0.005,执行第一次循环,a =1+11+a =32,n =2; |a -1.414|=0.086≥0.005,执行第二次循环,a =1+11+a =75,n =3;|a -1.414|=0.014≥0.005,执行第三次循环,a =1+11+a =1712,n =4;|a -1.414|≈0.002 7<0.005,跳出循环,输出n =4.L2 基本算法语句 L3 算法案例L4 复数的基本概念与运算 1.L4[2015·安徽卷] 设i 是虚数单位,则复数(1-i)·(1+2i)=( )A .3+3iB .-1+3iC .3+iD .-1+i1.C [解析] 由(1-i)(1+2i)=1+2i -i -2i 2=3+i 得C 正确. 2.L4[2015·广东卷] 已知i 是虚数单位,则复数(1+i)2=( ) A .2i B .-2i C .2 D .-22.A [解析] (1+i)2=1+i 2+2i =2i. 1.L4[2015·湖北卷] i 为虚数单位,i 607=( )A .-iB .iC .-1D .11.A [解析] i 607=i 4×151+3=i 3=-i.故选A. 3.L4[2015·全国卷Ⅰ] 已知复数z 满足(z -1)i =1+i ,则z =( ) A .-2-i B .-2+i C .2-i D .2+i3.C [解析] 设复数z =a +b i(a ,b ∈R ),代入(z -1)i =1+i 得(a -1+b i)i =1+i ,即-b +(a -1)i =1+i.根据复数相等可得⎩⎪⎨⎪⎧-b =1,a -1=1,得a =2,b =-1,所以复数z =2-i.2.L4[2015·全国卷Ⅱ] 若a 为实数,且2+a i1+i =3+i ,则a =( )A .-4B .-3C .3D .42.D [解析] 由2+a i1+i =3+i 得2+a i =(3+i)(1+i)=2+4i ,根据复数相等的意义知a=4.9.L4[2015·北京卷] 复数i(1+i)的实部为________. 9.-1 [解析] i(1+i)=i +i 2=-1+i ,所以答案是-1. 1.L42015·福建卷若(1+i)+(2-3i)=a +b i(a ,b ∈R ,i 是虚数单位),则a ,b 的值分别等于( )A .3,-2B .3,2C .3,-3D .-1,41.A [解析] (1+i)+(2-3i)=3-2i ,所以a =3,b =-2.1.L4[2015·湖南卷] 已知(1-i )2z=1+i(i 为虚数单位),则复数z =( )A .1+iB .1-iC .-1+iD .-1-i1.D [解析] 由题得z =(1-i )21+i =-2i1+i=-i(1-i)=-1-i ,故选D.2.L4[2015·山东卷] 若复数z 满足z-1-i =i ,其中i 为虚数单位,则z =( )A .1-iB .1+iC .-1-iD .-1+i2.A [解析] ∵z -1-i=i ,∴z -=i(1-i)=1+i ,即z =1-i.12.K3、L4[2015·陕西卷] 设复数z =(x -1)+y i(x ,y ∈R ),若|z |≤1,则y ≥x 的概率为( )A.34+12πB.12+1πC.14-12πD.12-1π12.C [解析] 由|z |≤1得(x -1)2+y 2≤1,其表示圆心为(1,0),半径为1的圆及其内部.在此区域内y ≥x 表示的区域为图中的阴影部分,其面积为圆(x -1)2+y 2=1面积的四分之一减去一个等腰直角三角形的面积,即为π4-12,故y ≥x 的概率为π4-12π=14-12π.11.L4[2015·四川卷] 设i 是虚数单位,则复数i -1i =________.11.2i [解析] i -1i=i +i =2i.9.L4[2015·天津卷] i 是虚数单位,计算1-2i2+i的结果为________.9.-i [解析] 1-2i 2+i =(1-2i )(2-i )(2+i )(2-i )=-5i5=-i.11.L4[2015·重庆卷] 复数(1+2i)i 的实部为________.11.-2 [解析] 因为(1+2i)i =-2+i ,所以该复数的实部为-2.L5 单元综合 8.[2015·广东实验中学模拟] 已知复数z 1,z 2在复平面上对应的点分别为A (1,2),B (-1,3),则z 2z 1=( )A .1+iB .iC .1-iD .-i8.A [解析] 由复数的几何意义可知,z 1=1+2i ,z 2=-1+3i , ∴z 2z 1=-1+3i 1+2i =(-1+3i )(1-2i )(1+2i )(1-2i )=5+5i 5=1+i.。
[VIP专享]【名校精品解析系列】3月份名校试题解析分类汇编第四期 L单元 算法初步与复数
![[VIP专享]【名校精品解析系列】3月份名校试题解析分类汇编第四期 L单元 算法初步与复数](https://img.taocdn.com/s3/m/9165b6bd0975f46526d3e147.png)
L单元 算法初步与复数目录L单元 算法初步与复数 (1)L1 算法与程序框图 (1)L2 基本算法语句 (4)L3 算法案例 (4)L4 复数的基本概念与运算 (5)L5 单元综合 (7)L1 算法与程序框图【数学理卷·2015届河北省唐山一中高三12月调研考试(201412)】11.已知b为如图所示的程序框图输出的结果,则二项式6-的展开式中的常数项是( )A.-20 B.20C.-540 D.540【知识点】算法与程序框图L1【答案】C=令3-r=0得r=3∴常数项为(-1)3•33=-540.636(1)3r r r r C x ---36C 【思路点拨】根据题意,分析该程序的作用,可得b 的值,再利用二项式定理求出展开式的通项,分析可得常数项.201411)】5.右图给出的是B.C.D.50>i 25<i 25>i 【知识点】程序框图L1【答案】B 【解析】解析:框图首先给变量赋值判断,条件不s n i ,,021s n i ===,,.满足,执行判断,条件不满足,执行102241122s n i =+=+==+=,,;判断,条件不满足,执行1142621324s n i =+=+==+=,,;…由此看出,当执行时,111628314246s n i =++=+==+=,,;11124100s =++⋯+执行,在判断时判断框中的条件应满足,所以判断框100210210151n i =+==+=,中的条件应是,故选择B.i >50?【思路点拨】框图给出的是计算的值的一个程序框图,首先赋值11124100s =++⋯+i=1,执行时同时执行了和式共有50项作和,所以执行完成102s =+,1i i =+,后的值为51,再判断时i=51应满足条件,由此可以得到正确答案.i【数学理卷·2015届四川省成都外国语学校高三12月月考(201412)】11.若某程序框图如图所示,则该程序运行后输出的值为 .【知识点】程序框图L1【答案】【解析】13760解析:第一次执行循环体得s=1,i=2; 第二次执行循环体得s=,i=3; 第三次执行循环32体得s=,i=4; 第四次执行循环体得s=,i=5; 第五次执行循环3111236+=111256412+=体得s=,i=6; 第六次执行循环体得s= 此时25113712560+=1371147279260660604+==>不满足判断框跳出循环,所以输出的值为..14760【思路点拨】一般遇到循环结构的程序框图问题,当运行次数较少时就能达到目的,可依次执行循环体,直到跳出循环,若运行次数较多时,可结合数列知识进行解答.【数学文卷·2015届四川省成都外国语学校高三12月月考(201412)】12.若某程序框图如图所示,则该程序运行后输出的值为 .(第11题)【知识点】程序框图L1【答案】【解析】13760解析:第一次执行循环体得s=1,i=2; 第二次执行循环体得s=,i=3; 第三次执行循环32体得s=,i=4; 第四次执行循环体得s=,i=5; 第五次执行循环3111236+=111256412+=体得s=,i=6; 第六次执行循环体得s= 此时25113712560+=1371147279260660604+==>不满足判断框跳出循环,所以输出的值为.14760【思路点拨】一般遇到循环结构的程序框图问题,当运行次数较少时就能达到目的,可依次执行循环体,直到跳出循环,若运行次数较多时,可结合数列知识进行解答.L2 基本算法语句L3 算法案例(第12题)L4 复数的基本概念与运算【数学理卷·2015届重庆市巴蜀中学高三12月月考(201412)】11设复数,则1iz i=-_____________z =【知识点】复数代数形式的乘除运算.L4【答案】【解析】 解析: 22()()()i 1i i 1i 11z i 1i 1i 1i 222+-+====-+--+,故答案为。
高三数学名校试题分类汇编1月第一期L单元算法初步与复数含解析
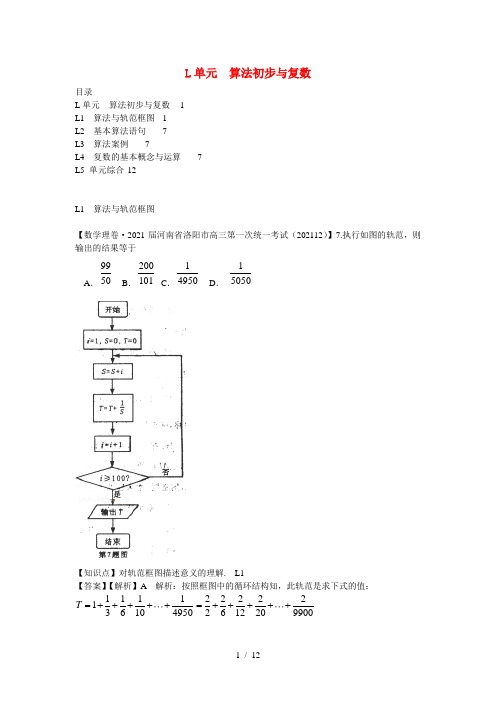
L单元算法初步与复数目录L单元算法初步与复数 1L1算法与轨范框图 1L2基本算法语句7L3算法案例7L4复数的基本概念与运算7L5 单元综合12L1算法与轨范框图【数学理卷·2021届河南省洛阳市高三第一次统一考试(202112)】7.执行如图的轨范,则输出的结果等于A.99 50B.200101C.14950D.15050【知识点】对轨范框图描述意义的理解. L1【答案】【解析】A 解析:按照框图中的循环结构知,此轨范是求下式的值:1111136104950T=+++++222222612209900=+++++1111212233499100⎛⎫=++++ ⎪⨯⨯⨯⨯⎝⎭1111111212233499100⎛⎫=-+-+-++- ⎪⎝⎭1992110050⎛⎫=-= ⎪⎝⎭,故选A.【思路点拨】由轨范框图得其描述的算法意义.【数学理卷·2021届河北省衡水中学高三上学期五调考试(202112)word 版】6.运行如图所示的轨范,若结束时输出的结果不小于3,则t 的取值范围为A .t≥B .t≥ c .t ≤ D .t≤【知识点】算法与轨范框图L1【答案】B【解析】第一次执行循环结构:n←0+2,x←2×t ,a←2-1∵n=2<4,∴继续执行循环结构. 第二次执行循环结构:n←2+2,x←2×2t ,a←4-1;∵n=4=4,∴继续执行循环结构, 第三次执行循环结构:n←4+2,x←2×4t ,a←6-3;∵n=6>4,∴应终止循环结构,并输出38t .由于结束时输出的结果不小于3,故38t≥3,即8t≥1,解得t≥18.【思路点拨】第一次执行循环结构:n←0+2,第二次执行循环结构:n←2+2,第三次执行循环结构:n←4+2,此时应终止循环结构.求出相应的x 、a 即可得出结果.【数学理卷·2021届广东省中山一中等七校高三第二次联考(202112)】11.某轨范框图如图3所示,该轨范运行后,输出的x 值为31,则a 等于______..【知识点】流程图 L1【答案】【解析】3解析:经过第一次循环获得:21,2x a n =+=;因为23≤,所以继续循环获得:()221143,3x a a n =++=+=;因为33≤,所以继续循环获得:()243187,4x a a n =++=+=,因为43≤不成立,所以输出x ,即8731,a +=得3a =,故答案为3.【思路点拨】分析轨范中各变量、各语句的感化,再按照流程图所示的按次,可知:该轨范的感化是利用循环计算并输出x 值.模拟轨范的运行过程,用表格对轨范运行过程中各变量的值进行分析,不难获得最终的输出结果.【数学理卷·2021届四川省德阳市高三第一次诊断考试(202112)word 版】3.如图,若N=5时,则输出的数等于 A. 54B. 45 C. 65 D. 56【知识点】算法与轨范框图L1【答案】56【解析】模拟轨范框图的运行过程,如下;输入N=5,k=1,S=0,S=0+112⨯= 112⨯; 开始1,n x a ==3n ≤ 否输出x结束 是 图3 21x x =+1n n =+k <N ,是,k=2,S= 112⨯+123⨯;k <N ,是,k=3,S=112⨯+123⨯+134⨯;k <N ,是,k=4,S=112⨯+123⨯+134⨯+145⨯;k <N ,是,k=5,S=112⨯+123⨯+134⨯+145⨯+156⨯,k <N ,否,输出S=112⨯+123⨯+134⨯+145⨯+156⨯=(1- 12)+(12-13)+(13-14)+(14- 15)+(15- 16)= 56.【思路点拨】按照题意,模拟轨范框图的运行过程,得出该轨范运行后输出的结果是什么.【数学文卷·2021届广东省中山一中等七校高三第二次联考(202112)】20.(本小题满分14分)按照如图所示的轨范框图,将输出,a b 的值依次分别记为122008122008n n a a a a b b b b ⋯⋯⋯⋯,,,,,;,,,,,.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)写出1234b b b b ,,,,由此猜想{}n b 的通项公式,并证明你的结论; (Ⅲ)在k a 与1k a + 中插入1k b +个3获得一个新数列{}n c ,设数列{}n c 的前n 项和为n S ,问是否存在这样的正整数m ,使数列{}n c 的前m 项的和2008m S =,如果存在,求出m 的值,如果不存在,请说明理由.【知识点】轨范框图,等差数列,等比数列L1 D2 D3【答案】【解析】(Ⅰ)n a n =(Ⅱ)131n n b -=-(Ⅲ)667m = 解析:(Ⅰ)1111n n a a a +=,=+,{}n a ∴是公差为1的等差数列.n a n ∴=.3分 (Ⅱ)123402826b b b b =,=,=,=, 猜想131n n b -=-.证明如下:1132131n n n n b b b b ++=+,+=(+),1{}n b ∴+是公比为3的等比数列.∴1111(1)33n n n b b --+=+=.则131n n b -=-.7分 (Ⅲ)数列{}n c 中,k a 项(含k a )前的所有项的和是121(12)(333)k k -+++++++()13322k k k +-=+,估算知,当7k =时,其和是73328112020082-+=<,当8k =时,其和是83336331520082-+=>,又因为200811208882963-==⨯,是3的倍数,故存在这样的m ,使得2008m S =,此时257(1333)296667m =++++++=.14分【思路点拨】(Ⅰ)由轨范框图可得1111n n a a a +=,=+,可求得n a n =; (Ⅱ)猜想131n n b -=-,1132131n n n n b b b b ++=+,+=(+),1{}n b ∴+是公比为3的等比数列,可求数列131n n b -=-. (Ⅲ)数列{}n c 中,k a 项(含k a )前的所有项的和是121(12)(333)k k -+++++++()13322k k k +-=+,7k =其和73328112020082-+=<,当8k =时,其和2008>,又因为200811208882963-==⨯,是3的倍数,故存在这样的m ,使得2008m S =.【数学文卷·2021届广东省中山一中等七校高三第二次联考(202112)】6.下列算法中,含有条件分支结构的是( )A .求两个数的积B .求点到直线的距离C .解一元二次不等式D .已知梯形两底和高求面积【知识点】条件结构L1【答案】【解析】C 解析:A 、B 、D 不含条件分支,解一元二次不等式要用到条件分支, 故选C .【思路点拨】理解条件结构的适用条件.【数学文卷·2021届安徽省屯溪一中高三第四次月考(202112)】5、如果执行如图的轨范框图,若输入n=6,m=4,那么输出的p等于()A.720B.360C.240D.120【知识点】轨范框图.L1【答案】【解析】B 解析:执行轨范框图,有n=6,m=4,k=1,ρ=1第一次执行循环体,ρ=3满足条件k<m,第2次执行循环体,有k=2,ρ=12满足条件k<m,第3次执行循环体,有k=3,ρ=60满足条件k<m,第4次执行循环体,有k=4,ρ=360不满足条件k<m,输出p的值为360.故选:B.【思路点拨】执行轨范框图,写出每次循环获得的k,ρ的值,当有k=4,ρ=360时不满足条件k<m,输出p的值为360.【数学文卷·2021届四川省德阳市高三第一次诊断考试(202112)word版】3.如图,若N=5时,则输出的数等于A. 5 4B.45 C.65 D.56【知识点】算法与轨范框图L1【答案】D【解析】模拟轨范框图的运行过程,如下;输入N=5,k=1,S=0,S=0+112⨯=112⨯;k<N,是,k=2,S=112⨯+123⨯;k<N,是,k=3,S=112⨯+123⨯+134⨯;k<N,是,k=4,S=112⨯+123⨯+134⨯+145⨯;k<N,是,k=5,S=112⨯+123⨯+134⨯+145⨯+156⨯,k<N,否,输出S=112⨯+123⨯+134⨯+145⨯+156⨯=(1- 12)+(12-13)+(13-14)+(14-15)+(15-16)=56.【思路点拨】按照题意,模拟轨范框图的运行过程,得出该轨范运行后输出的结果是什么.L2基本算法语句L3算法案例L4复数的基本概念与运算【数学(文)卷·2021届四川省成都市高中毕业班第一次诊断性检测(202112)word版】5.复数5i(2i)(2i)=-+z(i是虚数单位)的共轭复数为()(A)5i3-(B)5i3(C)i-(D)i【知识点】复数运算L4【答案】【解析】C解析:5i(2i)(2i)=-+z25545i iii===-,z i∴=-,故选C.【思路点拨】化简得z i=,从而可求z i=-.【数学理卷·2021届辽宁省沈阳二中高三12月月考(202112)】2.已知()2,f x x i =是虚数单位,则在复平面中复数()13f i i ++对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限【知识点】复数的代数运算L4【答案】【解析】A 解析:因为()12133355f i i i ii +==+++,所以选A. 【思路点拨】判断复数对应的点所在的象限,只需先利用复数的代数运算求出该复数即可.【数学理卷·2021届河南省洛阳市高三第一次统一考试(202112)】2.已知i 为虚数单位,复数123,12z ai z i =-=+,若12z z 复平面内对应的点在第四象限,则实数a 的取值范围为A. {}|6a a <- B . 3|62a a ⎧⎫-<<⎨⎬⎩⎭ C .3|2a a ⎧⎫<⎨⎬⎩⎭ D . 3|62a a a ⎧⎫<->⎨⎬⎩⎭或【知识点】复数的运算;复数的几何意义. L4【答案】【解析】B 解析:12z z ()()()()312332612121255ai i ai a a i i i i ----+===-++-,因为12z z 复平面内对应的点在第四象限,所以32036602a a a ->⎧⇒-<<⎨+>⎩,故选 B. 【思路点拨】先把复数z 化为最简形式,在利用复数的几何意义求解.【数学理卷·2021届河北省衡水中学高三上学期四调考试(202112)word 版】2.已知的共轭复数,复数A .B . c .1 D .2【知识点】复数的基本概念与运算. L4【答案】【解析】A 解析:∵()()313323231422321313i i i i z i i i i ++-====+---+-,∴314z i =--,∴22311444z z ⎛⎫⎛⎫⋅=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭.【思路点拨】化简复数z ,按照共轭复数的定义得z ,进而求得结论.【数学理卷·2021届河北省衡水中学高三上学期五调考试(202112)word 版】2.已知复数1-i=(i 为虚数单位),则z 等于 A .一1+3i B .一1+2i C .1—3i D .1—2i【知识点】复数的基本概念与运算L4【答案】A【解析】由题意得z= 241i i +-= (24)(1)(1)(1)i i i i ++-+=-1+3i【思路点拨】化简求出结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数 学
L 单元 算法初步与复数
L1 算法与程序框图 10.L1[2016·全国卷Ⅰ] 执行图1-3所示的程序框图,如果输入的x =0,y =1,n =1,则输出x ,y 的值满足( )
图1-3
A .y =2x
B .y =3x
C .y =4x
D .y =5x
10.C [解析] 第一次循环后,x =0,y =1,n =2;第二次循环后,x =1
2,y =2,n =3;
第三次循环后,x =32,y =6,此时满足条件x 2+y 2≥36,循环结束.故输出x =3
2,y =6,满
足y =4x .
9.L1[2016·全国卷Ⅱ] 中国古代有计算多项式值的秦九韶算法,如图1-3是实现该算法的程序框图.执行该程序框图,若输入的x =2,n =2,依次输入的a 为2,2,5,则输出的s =( )
图1-3
A.7 B.12
C.17 D.34
9.C[解析] 第一次运算,a=2,s=2,k=1,不满足k>n;
第二次运算,a=2,s=2×2+2=6,k=2,不满足k>n;
第三次运算,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17.
8.L1[2016·全国卷Ⅲ] 执行图1-2的程序框图,如果输入的a=4,b=6,那么输出的n =()
图1-2
A.3 B.4
C.5 D.6
8.B[解析] 执行第一次循环,得n=1,s=6;执行第二次循环,得n=2,s=10;执行第三次循环,得n=3,s=16;执行第四次循环,得n=4,s=20,输出n=4.
3.L1[2016·北京卷] 执行如图1-1所示的程序框图,输出的s值为()
图1-1
A.8 B.9
C.27 D.36
3.B[解析] 第一次循环,s=0,k=1;第二次循环,s=1,k=2;第三次循环,s=9,k=3,此时不满足k≤2,故输出的s值是9.
6.L1[2016·江苏卷] 图1-1a的值是________.
图1-1
6.9[解析] 初始值a=1,b=9,不满足a>b;第一次执行循环体后a=5,b=7,此时还不满足a>b;第二次执行循环体后a=9,b=5,满足a>b,结束循环,故输出的a的值为9.
11.L1[2016·山东卷] 执行如图1-3所示的程序框图,若输入n的值为3,则输出的S 的值为________.
图1-3
11.1[解析] 当i=1时,S=0+2-1=2-1;当i=2时,S=2-1+3-2=3-1;当i=3时,S=3-1+4-3=4-1=1,满足条件输出.
11.L1[2016·天津卷] 阅读图1-3的程序框图,运行相应的程序,则输出S的值为________.
图13
11.4 [解析] 第一次执行循环体后S =8,n =2;第二次执行循环体后S =2,n =3;第三次执行循环体后S =4,n =4,结束循环.故输出S 的值是4.
L2 基本算法语句 L3 算法案例
L4 复数的基本概念与运算 2.L4[2016·全国卷Ⅰ] 设(1+2i)(a +i)的实部与虚部相等,其中a 为实数,则a =( ) A .-3 B .-2 C .2 D .3
2.A [解析] 因为(1+2i)(a +i)=a -2+(1+2a )i ,所以由已知,得a -2=1+2a ,解得a =-3.
2.L4[2016·全国卷Ⅱ] 设复数z 满足z +i =3-i ,则=( )
A .-1+2i
B .1-2i
C .3+2i
D .3-2i
2.C [解析] 由z +i =3-i ,得z =3-2i ,故=3+2i.
2.L4[2016·全国卷Ⅲ] 若z =4+3i ,则=( )
A .1
B .-1 C.45+35i D.45-35
i
2.D [解析] =
4-3i
42+32=45-3
5
i.
2.L4[2016·北京卷] 复数1+2i
2-i
=( )
A .i
B .1+i
C .-i
D .1-i 2.A [解析]
1+2i 2-i =(1+2i )(2+i )(2-i )(2+i )=5i
5
=i. 1.L4[2016·四川卷] 设i 为虚数单位,则复数(1+i)2=( ) A .0 B .2
C .2i
D .2+2i
1.C [解析] (1+i)2=1+2i +i 2=2i.
2.L4[2016·山东卷] 若复数z =2
1-i
,其中i 为虚数单位,则
=( )
A .1+i
B .1-i
C .-1+i
D .-1-i
2.B [解析] ∵z =2
1-i =2(1+i )(1-i )(1+i )=2+2i 1-i 2=1+i ,∴
=1-i.
2.L4[2016·上海卷] 设z =
3+2i
i
,其中i 为虚数单位,则z 的虚部等于________. 2.-3 [解析] z =3+2i i =3i +2i 2
i
2=2-3i ,所以z 的虚部为-3.
2.L4[2016·江苏卷] 复数z =(1+2i)(3-i),其中i 为虚数单位,则z 的实部是________.
2.5 [解析] 因为z =(1+2i)(3-i)=3+5i -2i 2
=5+5i ,所以其实部为5. 9.L4[2016·天津卷] i 是虚数单位,复数z 满足(1+i)z =2,则z 的实部为________. 9.1 [解析] 设z =a +b i(a ,b ∈R ),则(1+i)(a +b i)=(a -b )+(a +b )i =2,所以a -b =2且a +b =0,解得a =1,b =-1,所以z 的实部是1.
03 [2016·浙江卷] “复数与导数”模块
(1)已知i 为虚数单位.若复数z 满足(z +i)2=2i ,求复数z . (2)求曲线y =2x 2-ln x 在点(1,2)处的切线方程. 解:(1)设复数z =a +b i ,a ,b ∈R ,由题意得 a 2-(b +1)2+2a (b +1)i =2i ,
解得⎩⎪⎨⎪⎧a =1,b =0或⎩
⎪⎨⎪⎧a =-1,b =-2.
故z =1或z =-1-2i.
(2)由于(2x 2-ln x )′=4x -1
x
,
则曲线在点(1,2)处的切线的斜率为3.
因此,曲线在点(1,2)处的切线方程为y =3x -1.。
