1基于网格的数据流聚类算法
大数据建模练习(习题卷2)

大数据建模练习(习题卷2)第1部分:单项选择题,共39题,每题只有一个正确答案,多选或少选均不得分。
1.[单选题]在黑盒测试方法中,设计测试用例的主要根据是A)程序流程图B)程序内部逻辑C)程序外部功能D)程序数据结构答案:C解析:2.[单选题]以下关于字典类型的描述,正确的是:A)字典类型可迭代,即字典的值还可以是字典类型的对象B)表达式 for x in d: 中,假设d是字典,则x是字典中的键值对C)字典类型的值可以是任意数据类型的对象D)字典类型的键可以是列表和其他数据类型答案:C解析:3.[单选题]已知数据中时间字段的格式为2021-01-01 00:00:00,如果使用过滤算子,过滤出2021年5月1日以来的数据,以下哪个是正确的设置A)大于2021-05-01 00:00:00B)小于2021-05-01 00:00:00C)大于等于2021-05-01 00:00:00D)小于等于2021-05-01 00:00:00答案:C解析:4.[单选题]Jupyter notebook的记事本文件扩展名为:A)mB)pyC)pycD)ipynb答案:D解析:5.[单选题]修改数据库表结构用以下哪一项( )A)UPDATEB)CREATEC)UPDATEDD)ALTER答案:D解析:C)ORDER BY NAME DESCD)ORDER BY DESC NAME答案:A解析:7.[单选题]个栈的初始状态为空。
现将元素 1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是A)12345ABCDEB)EDCBA54321C)54321EDCBAD)ABCDE12345答案:B解析:8.[单选题]在Excel中,数据透视表是汇总、分析、浏览和呈现汇总数据的方法。
插入数据透视表之后,选择一个(),可以实现单元格区域的验证A)单元格B)表/区域C)公式D)文件答案:B解析:9.[单选题]在select语句的where子句中,使用正则表达式过滤数据的关键字是( )A)likeB)againstC)matchD)regexp答案:D解析:10.[单选题]如果要统计某家店铺当天的收益总和,需要按照日期分组,且对收益的统计方式是A)最大B)最小C)总数D)总和答案:D解析:11.[单选题]耦合性和内聚性是对模块独立性度量的两个标准。
基于网格和MST的混合属性流数据聚类算法

abt r hp . ov ep o lm, riaysa eToslet rbe GTMSi p o o e o ls r gsra d t wi x dd t y e, d a dmii m pn igte r h s rp sd frc ti tem aa t mie a tp s 鲥 n nmu sa nn e u en h a r tcnq e i u e ea oi ms s ga ido o t c d cn y a di oma o a u do xn a m l i . p f r eh iu ss s i t g r h , i kn f e me i aj e c f r t n gi f n nmii dt s i r y x e me d nh l t u n g r a n n i no g a i a t E i  ̄l
挖 掘 引起 人们 很 大 兴趣 。 与传 统 的 静 态数 据 仓库 不 同 , 流数 据 具 有 高速 、 时 序 到 达 、 时变 化 和 无 限 的特 点 。 于 流数 据 的这 些 特 按 实 基 点, 流数 据 挖 掘要 求 尽 可 能快 地 处 理 数 据 , 仅使 用 固定 数 量 的 内存 , 且 只 能单 遍 扫 描数 据 。 而
h t : w w.n sn g t / w d z .蠛 n p/ T h 8— 5 一 6 O 6 5 99 4 e + 6 5 l 5 99 3 6 0 6
基于网格的数据流聚类算法

种一次性扫描 的方法 和算法 , 如文[-4等等 , 1 - 1 但它们 的聚类 结果通 常是球形 的, 不能支持对任意形状类的聚类[ 。 5 ]
Gr d b s d Da a S r a u t rng Al o ih i - a e t t e m Cl se i g r t m LI QigB o DAI a F n DENG u Z U n — a o a Ch - S HANG e- ig W i n M
称为 p rmi t r e的结 构储存 下 来 。同时 , ya d i f me a m 使用 另一 个离线的 mar c se 过程 , 据用户 的具 体要求 对 m co co l tr - u 根 i r- c se 聚类 的结果 进行 再分析 。但 它采用 距 离作 为度 量参 l tr u 数, 聚类结果通 常是球 形 的, 不能 支持对 任意形状 类 的聚类 。
( le eo n om ain S se a d M a a e n ,N ain lUnv r i fDee eTe h oo y, a g h 1 0 3 Colg fI f r to y tm n n g me t to a iest o fns c n lg Ch n s a4 0 7 ) y
噪 声干扰 下发现任 意形状 的类, 而且有效地解决 了聚类算 法参数敏感和聚 类结果无法区分密度差异等 问题。
关键词
Ab ta t W i to g a i t rd s o e i g a b t a y s a e cu t r n a d i g n i e g i— a e a as r a cu t — sr c t s r n b l y f ic v rn r ir r h p l s e sa d h n l o s , rd b s d d t t e m l s e h i o n r g ag rt m f ce ty r s l e h s r b e o en e y s n ii e t h s r d f e a a e e s a d d fiu t t i lo ih ef in l e o v st e e p o lm fb i g v r e st o t e u e - e i d p r m t r n i c l o n i v n f d s ig ih t e d n iy d s i c in o l s e s it u s h e st it to f u t r . n n c Ke wo d Cl s e i g,Da a s r a ,Cl s e i a a t r y rs u t rn t te m u t rn p r me e ,Re ai e d n i g ltv e st y
【计算机应用研究】_聚类数据挖掘_期刊发文热词逐年推荐_20140726
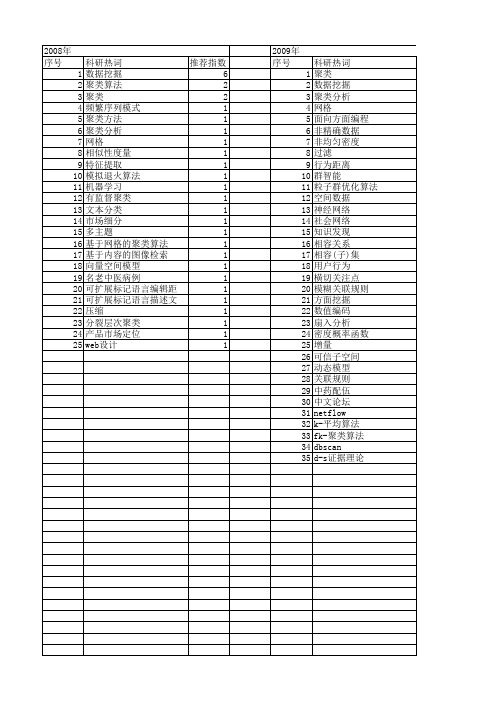
推荐指数 7 7 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 数据挖掘 预处理数据 蚁群聚类 聚类 网格 维数灾 粒子群优化 混合粒子群聚类 并行算法 分布式 分层聚类 入侵检测 主成分分析 web聚类 k均值聚类
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
科研热词 聚类 数据挖掘 聚类分析 网格 面向方面编程 非精确数据 非均匀密度 过滤 行为距离 群智能 粒子群优化算法 空间数据 神经网络 社会网络 知识发现 相容关系 相容(子)集 用户行为 横切关注点 模糊关联规则 方面挖掘 数值编码 扇入分析 密度概率函数 增量 可信子空间 动态模型 关联规则 中药配伍 中文论坛 netflow k-平均算法 fk-聚类算法 dbscan d-s证据理论
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
聚类算法的分类

聚类算法的分类
聚类算法是一种机器学习算法,其目的是将数据集中的对象分成不同的组或簇,使得同一簇内的对象相似度高,不同簇之间的相似度低。
聚类算法的分类可以根据不同的算法思想和应用场景进行划分。
1. 基于原型的聚类算法:该类算法将每个簇表示为一个原型,
如质心、中心点或者最典型的对象,然后通过计算每个对象到原型的距离来确定其所属簇。
常见的算法包括K-means、K-medoids等。
2. 基于层次的聚类算法:该类算法将对象逐层进行分组,直到
达到某个终止条件。
常见的算法包括凝聚层次聚类和分裂层次聚类等。
3. 基于密度的聚类算法:该类算法将簇定义为密度相连的对象,可以处理噪声和离群点。
常见的算法包括DBSCAN、OPTICS等。
4. 基于网格的聚类算法:该类算法将数据集划分为网格,并在
每个网格内进行聚类操作。
常见的算法包括CLIQUE、STING等。
5. 基于模型的聚类算法:该类算法假设数据集由多个组成成分
混合而成,每个组成成分对应一个簇。
常见的算法包括高斯混合模型、潜在狄利克雷分配等。
聚类算法在许多领域都有广泛的应用,如生物学、社交网络分析、文本挖掘等。
选择适合的聚类算法可以有效地提高数据分析的效率和准确性。
- 1 -。
基于网格和密度的数据流聚类算法

whc o i e h p r a h b s d o e st n r .B a so e mo e o o b e—l y rc n t cin,t e ih c mb n d te a p o c a e n d n i a d g d y i y me n ft d l f u l h d a e o s u t r o h
A b t a t Ac o d n o t e c a a trsiso h aa sr a , i p r p e e td a n w l se n lo t m s r c : c r i g t h h r ce it ft e d t te m h spa e r s n e e c u tr g a g r h GTCS c i i
数据流的挖掘要在有限的内存 中完成对数据的及时处理. 通过单次扫描机制 , 在内存中保存数据流的概要信
息 ,以支持后 续 的计 算 , 成挖掘 结果 的近似性 . 形 数据 流是一 个连续 、 在线 的过程 , 传统 的聚类 算法 无法 在数 据 流 中直接 应用 , 因此数 据流 的聚类对 数 据挖 掘 领域 提 出了前 所 未 有 的新 挑 战 , 也成 为许 多学 者 研究 的热
基于动态网格的数据流聚类分析

V0 . 5 No 1 12 . 1 NO . 2 0 V 0 8
基 于 动 态 网格 的数 据 流 聚 类分 析
何
摘
勇, 刘青宝
( 国防科 学技 术 大 学 信 息 系统 与 管理 学院 , 沙 40 7 ) 长 103 要 :提 出的增 量式数 据流 聚类 算 法 D C S结合 网格 和 密度技 术 , GD 能够得 到任 意形状 的聚 类 , 通过 改进 网格
密度的计算方式, 解决了现有网格算法中丢失数据空间影响信息的问题 , 并且实现了关键参数的 自适应设置, 减 小 了 工参数对聚类结果的影响。 人 关键词 :动态网格 ;网格密度 ; 数据流聚类; 聚类参数
中图分 类号 :T 3 1 P9 文献标 志码 :A 文 章编 号 :10 —6 5 20 ) 138.4 0 139 (0 8 1-2 10
提出的增量式数据流聚类算法dgcds结合网格和密度技术能够得到任意形状的聚类通过改进网格密度的计算方式解决了现有网格算法中丢失数据空间影响信息的问题并且实现了关键参数的自适应设置减小了人工参数对聚类结果的影响
第 2 第 1 期 5卷 1
20 0 8年 1 1月
计 算 机 应 用 研 究
Ap l ain Ree rh o mp tr p i t sac fCo ues c o
Dy a c g i — a e l se i g o e aa sra n mi rd b s d cu trn v rd t t m e
HEY n , igbo o g HU Qn —a
( o eefI o a o y e &M n gm n , a o l n e i D e eT hooy C agh 10 3 C i ) Clg n r t n sm l o fm i S t a a e et N t n i rt o e n e nl , h nsa 0 7 , h a i a U v sy f fs c g 4 n
一种基于网格密度的聚类算法

一种基于网格密度的聚类算法作者:刘敏娟,于景茹,张西芝来源:《软件导刊》2012年第12期摘要:提出了一种基于网格密度的聚类算法(DGCA)。
该算法主要利用网格技术去除数据集中的部分孤立点或噪声数据,对类的边缘节点使用一种边缘节点判断函数进行提取,最后利用相近值的方法进行聚类。
实验表明,DGCA算法能够很好地识别出孤立点或噪声,聚类结果可以达到一个较高的精度。
关键词:网格聚类;边界点;网格密度中图分类号:TP312文献标识码:A文章编号:1672-7800(2012)012-0056-020引言聚类是把一组数据按照相似性归成若干类别,它的目的是使得属于同一类别的个体之间的距离尽可能地小而不同类别上的个体间的距离尽可能地大。
聚类的结果可以得到一组数据对象的集合,称其为簇或类。
簇中的对象彼此相似,而与其它簇中的对象相异。
迄今为止,已经提出了许多聚类算法,大体上这些算法可以分为基于距离的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法等。
基于网格的聚类算法首先将d维数据空间的每一维平均分割成等长的区间段,即把数据空间分割成一些网格单元。
若一个网格单元中所含数据量大于给定的值,则将其定为高密度单元;否则将其视为低密度单元。
如果一个低密度网格单元的相邻单元都是低密度的,则视这个低密度单元中的节点为孤立点或噪声节点。
网格聚类就是这些相邻的高密度单元相连的最大集合。
1基本概念1.1相近值网格单元内节点之间的相近值是利用节点间的距离来计算的。
节点间的相近值越大,它们就越相似。
即对这些网格单元内的节点进行聚类时,它们属于同一个类的可能性就越大。
定义1节点集:设P=(U,K),我们用P表示n条记录的集合。
U={U1,U2,…,Un}代表网格单元内的节点集K={K1,K2,…,Kr}代表网格单元内节点的属性其中,,i∈(1,2,…,n),,m∈(1,2,…,r)代表节点Ui的第m个属性Km,因此,用Km代表一个r维的向量(ki1,ki2,…,kir),i∈(1,2,…,n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3)国家自然科学基金(60172012)。
刘青宝 博士生,副教授,主要研究方向为数据仓库技术和数据挖掘;戴超凡 博士,副教授,主要研究方向为数据仓库技术和数据挖掘;邓 苏 博士,教授,主要研究方向指挥自动化、信息综合处理与辅助决策;张维明 博士生导师,教授,主要研究方向为军事信息系统、信息综合处理与辅助决策。
计算机科学2007Vol 134№13基于网格的数据流聚类算法3)刘青宝 戴超凡 邓 苏 张维明(国防科学技术大学信息系统与管理学院 长沙410073)摘 要 本文提出的基于网格的数据流聚类算法,克服了算法CluStream 对非球形的聚类效果不好等缺陷,不仅能在噪声干扰下发现任意形状的类,而且有效地解决了聚类算法参数敏感和聚类结果无法区分密度差异等问题。
关键词 聚类,数据流,聚类参数,相对密度 G rid 2based Data Stream Clustering AlgorithmL IU Qing 2Bao DA I Chao 2Fan DEN G Su ZHAN G Wei 2Ming(College of Information System and Management ,National University of Defense Technology ,Changsha 410073)Abstract With strong ability for discovering arbitrary shape clusters and handling noise ,grid 2based data stream cluste 2ring algorithm efficiently resolves these problem of being very sensitive to the user 2defined parameters and difficult to distinguish the density distinction of clusters.K eyw ords Clustering ,Data stream ,Clustering parameter ,Relative density 随着计算机和传感器技术的发展和应用,数据流挖掘技术在国内外得到广泛研究。
它在网络监控、证券交易分析、电信记录分析等方面有着巨大的应用前景。
特别在军事应用中,为了获得及时的战场态势信息,大量使用了各种传感器,对这些传感器数据流的分析处理已显得极为重要。
针对数据流数据持续到达,且速度快、规模大等特点,数据流挖掘技术的研究重点是设计高效的单遍数据集扫描算法[12]。
数据流聚类问题一直是吸引许多研究者关注的热点问题,已提出多种一次性扫描的方法和算法,如文[1~4]等等,但它们的聚类结果通常是球形的,不能支持对任意形状类的聚类[5]。
本文提出的基于网格的数据流聚类算法,在有限内存条件下,以单遍扫描方式,不仅能在噪声干扰下发现任意形状的类,而且有效地解决了基于绝对密度聚类算法所存在的高密度聚类结果被包含在相连的低密度聚类结果中的问题。
本文第1节简要介绍数据流聚类相关研究,并引出基于网格的数据流聚类算法的思路及其与相关研究的异同;第2节给出基于网格的数据流聚类算法所使用到的基本概念;第3节给出一个完整的基于网格的数据流聚类算法,详细解析算法的执行过程;第4节进行算法性能分析对比;最后总结本文的主要工作和贡献,并指出需要进一步研究和改进的工作。
1 相关研究在有限内存约束下,一般方法很难对数据流进行任意形状的聚类。
第一个增量式聚类挖掘方法是文[6]提出的In 2crementalDBSCAN 算法,它是一个用于数据仓库环境(相对稳定的数据流)的有效聚类算法,可以在有噪声的数据集中发现任意形状的类。
但是,它为了形成任意形状的类,必须用类中的所有点来表示,要求获得整个数据流的全局信息,这在内存有限情况下是难以做到的。
而且,它采用全局一致的绝对密度作参数,使得聚类结果对参数值非常敏感,设置的细微不同即可能导致差别很大的聚类结果。
Aggarwal 在2003年提出的一个解决数据流聚类问题的框架CluStream [1]。
它使用了两个过程来处理数据流聚类问题:首先,使用一个在线的micro 2cluster 过程对数据流进行初级聚类,并按一定的时间跨度将micro 2cluster 的结果按一种称为pyramid time f rame 的结构储存下来。
同时,使用另一个离线的macro 2cluster 过程,根据用户的具体要求对micro 2cluster 聚类的结果进行再分析。
但它采用距离作为度量参数,聚类结果通常是球形的,不能支持对任意形状类的聚类。
而且,它维护的是micro 2cluster 的聚类特征向量(CF 2x ;CF 1x ;CF 2t ;CF 1t ;n ),这在噪声情况下,会产生干扰误差。
2006年,Feng Cao 等人在文[5]中提出了针对动态进化数据流的DenStream 算法。
它相对CluStream 有很大的改进,继承了IncrementalDBSCAN 基于密度的优点,能够支持对有噪声的动态进化(非稳定)的数据流进行任意形状的聚类。
但由于采用全局一致的绝对密度作参数,使得聚类结果对参数值非常敏感。
同时,与CluStream 算法相比,它只能提供对当前数据流的一种描述,不能反映用户指定时间窗内的流数据的变化情况。
朱蔚恒等在文[13]中提出的基于密度与空间的ACluS 2tream 聚类算法,通过引入有严格空间的意义聚类块,在对数据流进行初步聚类的同时,尽量保留数据的空间特性,有效克服了CluStream 算法不能支持对任意形状聚类的缺陷。
但它在处理不属于已有聚类块的新数据点时,使用一种类似“抛硬币”的方法来猜测是否为该点创建一个新的聚类块,误差较大。
而且它以绝对密度做参考,所以在聚类结果中无法区分密度等级不同的簇[7]。
本文提出的基于网格的数据流聚类算法GClustream(Grid Based Data Stream Clustering Algorithm),借鉴算法CluStream的两阶段聚类思想和pyramid time f rame的快照储存结构,采用相对密度作为聚类参数,通过对数据空间进行网格化处理,提高了算法处理速度,并能在噪声干扰条件下发现任意形状的类,同时解决了基于绝对密度聚类算法所存在的高密度聚类结果被包含在相连的低密度聚类结果中的问题[7]。
2 基本概念定义1 网格单元在各维上定义一个单位格长,采用网格方式将n维空间划分为若干个网格单元。
一个网格单元是n维空间中各个维上具有单位格长的n维超立方体,即以n维向量o为起点,向各维的正方向延伸单位格长所形成的一个区间,记为Grid (o)。
定义2 聚合块由若干个网格单元组成的超立方体,称为聚合块,记为Cub(o, r),其中 r为聚合块的各维边长组成的向量。
采用衰变窗口模型[5],数据流上的数据对象,其权重随时间衰减,即w p(t c)=2-λ(t-t)cp,其中λ表示衰减速度,t c表示当前时间,t P表示数据对象p到达时间。
设数据流在时刻t0, t1,t2,…,t c到达的数据对象数n0,n1,n2,…,n c,则数据流的当前时刻t c权重W(t c)为W(t c)=∑c j=0n j2-λ(t c-t j)定义3 网格单元特征向量设起点为o i的网格单元包含n个分别在时刻t i1,t i2,…, t in到达的数据对象p i1,p i2,…,p in,在t c时刻网格单元的特征向量记为(o i,F1,F2,w,t c),其中F1=∑n j=1p ij2-λ(t c-t ij)F2=∑n j=1p2ij2-λ(t c-t ij)w=∑n j=12-λ(t c-t ij)定义4 密集网格单元和候选密集网格单元对于给定的密度阈值ξ(0<ξ<1),设网格单元的特征向量为(o i,F1,F2,w,t c)。
若w>ξW(t c),则称该网格单元在t c 时刻为密集网格单元,记为D—Grid(o i);若0<w<=ξW (t c),则称该网格单元在t c时刻为候选密集网格单元,记为C—Grid(o i)。
定义5 密集聚合块对于给定的密度阈值ξ(0<ξ<1),设聚合块的特征向量为(o i,F1,F2,w,t c, r),若有w>ξW(t c)∏r i,则称该聚合块在t c时刻为密集的。
3 基于网格的数据流聚类算法借鉴算法CluStream的思路[1],基于相对网格的数据流聚类算法GCluStream分为两个阶段:在线的进程和离线的进程。
记录当前数据流聚类特征的在线进程称为GMic2Clus2 ter,而离线的响应查询的进程称为GMac2Cluste。
3.1 G Mic2Cluster过程描述在线进程GMic2Cluster的具体步骤如下:(1)初始化初始时,对每个新到来的数据对象,计算出其所在网格单元的特征向量。
积累一定数量的数据对象后,区分密集网格单元集合和候选密集网格单元集合。
(2)加入数据对象对新到的数据对象p,若它属于一个已存在的密集网格单元或候选密集网格单元,则修改该网格单元的特征向量为(o i,F1+p,F2+p2,w+1,t c)。
否则,直接定位其所在的网格单元,计算该网格单元的特征向量,并把它加入到候选密集网格单元集合。
(3)生成密集聚合块在连续数据流条件下,非密集网格单元通过新数据对象的不断聚集,可以转换为密集网格单元。
在内存空间有限的条件下,随着密集网格单元的数目增大,须把相邻且密度相近的密集网格单元进行聚合,以节省空间消耗。
同样,可把相邻且密度相近的聚合块聚合为更大的块。
这一步的聚合条件是要求相邻、密度相近、同体积大小的两个密集网格单元或两个初级聚类块才能聚合。
(4)密集聚合块的切分聚合块在新数据对象的不断加入下,可能导致内部密度失衡。
在每次加入数据对象时,更新聚合块特征向量,并计算方差,判断失衡程度。
当超过一定阈值δ,则从失衡程度最大、边长超过1的那一维进行居中切分,对切分形成的两个新聚合块或两个新网格单元进行特征向量分割计算。
(5)密集聚合块、密集网格单元的退化由于引进了衰减因子2-λt,若没有新数据对象的加入,初级聚类块特征向量修改为(o i,F132-λΔt,F232-λΔt,w3 2-λΔt,t c, r),密集网格单元特征向量修改为(o i,F132-λΔt, F232-λΔt,w32-λΔt,t c),其中Δt为特征向量上次修改到当前修改的时间间隔。
一旦密集聚合块特征向量(o i,F1,F2, w,t c, r)的w<=ξW(t c)∏ri,则让该密集聚合块“土崩瓦解”成若干个候选密集网格单元。
