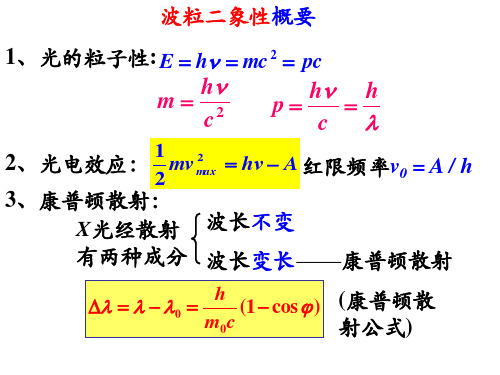
大学物理 波粒二象性(1)黑体辐射和光电效应及康普顿散射共48页文档
合集下载
大学物理-波粒二象性
1 2
mv
2 m
h
A
A：逸出功
光子打出光电子是瞬时发生的(109 s) I N 单位时间打出光电子多 im
h > A 时才能产生光电效应，当 <A/h时，
不发生光电效应，所以存在：
红限频率
0
A h
光量子假设解释了光电效应的全部实验规律！
但是光量子理论在当时并未被物理学界接受， 普朗克在推荐爱因斯坦为柏林科学院院士时说
2h 3
M (T ) c2 eh kT 1
普朗克常量：h 6.626 1034 J s 4.1361015eV s
在全波段与实验曲线惊人地符合！
M (10 - 9 W/(m2 Hz))
2000K
（1900）M
(T
)
2
c2
2
kT
实验曲线
普朗克黑体辐射公式
M
(T )
2h
c2
3
e h kT
1
1926 年 ， 薛 定 谔 (E.Schrodinger) 提出了非相对论粒子（能量远小于 静能）的运动方程—薛定谔方程， 由此方程出发的量子力学称为波动 力学。
同年，狄拉克（P.A.M. Dirac）提出了电子 的相对论性运动方程—狄拉克方程，把狭义相 对论引入薛定谔方程，统一了量子论和相对论 ，为研究粒子物理的量子场论奠定了基础。
光电流 电子电量
单位时间到达光电子数
25
﹡实验规律
(1) 饱和电流
im2
加速电势差增大时光电 im1
流增大，当加速电势差
增大到一定量值时，光
电流达到饱和值。
-Uc
(2) 光电子的最大初动能∝v入 , Uc/V
量子习题解答
n 0,1,2,3...
8、氢原子： 氢原子能级：
me4 1 1 En 2 13.6 2 (e V) 2 2 2 (4 0 ) n n
轨道角动量
L l (l 1)
轨道角动量沿磁场方向分量：Lz m 主量子数 轨道量子数 轨道磁量子数
n=1,2,3…
l=0,1,2,3…,n-1 ml=-l,-(l-1),…,0,1,..,l
h 0 ( 1 cos ) m0 c
4、不确定关系(1927)：
h 2
x p x (或, 或h) 位臵动量不确定关系： 2
能量时间不确定关系：Et / 2
5、氢原子光谱(1913) 谱线的波数
1 1 R ( 2 2 ) T ( m) T ( n) m n
玻尔磁子
电子自旋磁矩在磁场中的能量 Es B B
e B 9.27 10 24 J / T 2me
10、多电子原子的电子组态 电子的状态用4 个量子数n,l,ml,ms确定。n相同 的状态组成一壳层，可容纳2n2个电子；l相同 的状态组成一次壳层，可容纳2（2l+1)个电子。 基态原子电子组态遵循两个规律： （1）能量最低原理，即电子总处于可能最 低的能级。一般n越大，l越大，能量就越高。 （2）泡利不相容原理(1921)，不可能有两个 或两个以上的电子处在同一量子状态。即不 能有两个电子具有相同的n, l, ml , ms。
解： 光子的散射角 θ π 时电子获得的能量最大， v 电子的反冲速度沿入射光子的运动方向.设 为入 pe 射光的频率，为散射光的频率， 为反冲电子的动 v 量。 1 由能量守恒有： h(v v) Ek
由动量守恒有: 2 式得 由1 、
大学物理课件-波粒二象性
)2
R 2eB 2 2m
波长 3000A的紫外线照射某金属表面，光电子能量范围
从0到4.0 1019 J，其遏止电压 |U a | V，金属红限频率 0
1 2
mv
2 max
e |Ua
|
4.0 1019
J
A
h
1 2
mv 2 max
2.63 10 19
J
0
A h
2.63 10 19 6.63 10 34
★光子的品質：
m
h
c2
h
c
m0 m 1 v2 / c2 m0(光子) 0
★光子的動量：p mc h h
c
1
三 光電效應在近代技術中的應用
光控繼電器、自動控制、 自動計數、自動報警等.
光控繼電器示意圖
光
放大器
接控制機構
光電倍增管
例：光 波电长子为（的电单子色电光 量e照，射质某量金m）属， M表进面 入均发匀生磁光场电B效（应v，B)发, 射
4 1014 Hz
|U a | 2.5V
Uc (V)
0
5 -2
(1014Hz)
在某金屬的光電效應實驗中，測得如圖所
示曲線，則該金屬的紅限頻率0= Hz， 逸出功A= eV。
解： ⑴由圖： 0=51014 Hz
⑵
eUc
1 2
mvm2
h A
Uc
h
e
A e
1
A 2V e
A 2eV
[解法二]：
1
一、基本概念
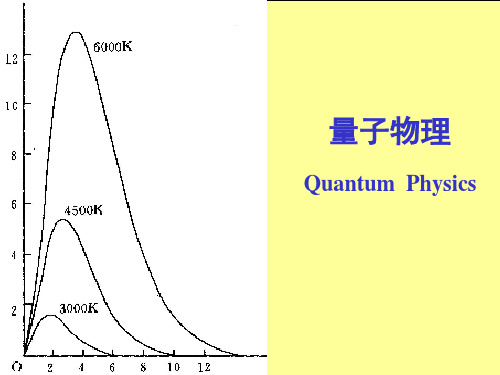
分子热运动导致物体不断向外发射电磁波， 这种与温度有关的辐射称热辐射。
這種輻射可以是紅外線、可見光或紫外線，人眼不一 定可見。
波粒二象性
d M M (T ) d
单色辐出度 M (T ) 与物体的 温度和辐射波长有关。
M ( , T )
2
W /m
3
基尔霍夫
辐射出射度: 辐射出射度:单位时间内，温度为T的物体 单位面积上所发射的各种波长的总辐射能，称 为物体的辐射出射度，简称辐出度。
M (T ) M (T ) d
M 0 (T ) T
斯特藩常数
Байду номын сангаас
4
5.67 10 W/(m K )
8 2 4
热辐射的功率随着温度的升高而迅速增加。
10
（2） 维恩位移定律
对于给定温度T ，黑体的单色辐出度M 0 有一 最大值,其对应波长为 m 。
T m b
b 2.897 10 m K
热辐射的峰值波长随着温度的增加而向着 短波方向移动。
(2) 这些谐振子能量不能连续变化，只能取一些分立值 ，是最小能量 的整数倍,这个最小能量称为能量子。
h
振子从一个状态跃迁到另一个状 态时，辐射出或吸收的能量也是量子 化的。
能量
经典
量子
1918诺贝尔物理学奖
马克斯· 普朗克 1858.4.23.―1947.10.3. 德 国物理学家，量子物理学的 开创者和奠基人，1918年诺 贝尔物理学奖的获得者。 普 朗克的伟大成就，就是创立 了量子理论，这是物理学史 上的一次巨大变革。从此结 束了经典物理学一统天下的 局面。
解：由 Ek A, h
500℃
700
℃
1000℃
1200℃
物体辐射总能量及能量按波长分布都决定于温度。
基本性质 温度,发射的能量,电磁波 的短波成分
波粒二象性1
2、瑞利—金斯公式
利用能量均分定理和电磁理 论得出：
M (T )
瑞利-琼斯
2v M (T )d kTd 2 c 2c M (T )d 4 kTd
2
T=1646k
3、经典物理的困难
在低频（长波）部分与实验曲线相符合，在高频（短波）则完 全不能适用。 在高频部分，黑体辐射的单色辐出度将随着频率的增高而趋于 “无限大”——―紫外灾难”。
A 2.63 1019 0 4 1014 Hz h 6.63 1034
| U a | 2.5V
三、 康普顿效应
一、康普顿效应
1、康普顿散射 单色X射线被物质散射时，散射线中除了有波长与入射线相同的成分外，还有 波长较长的成分，这种波长变长的散射称为康普顿散射。 2、实验装置 X光管发出一定波长的X射线，通过光阑后成为一束狭窄的X射线， 投射到散射物质上，用摄谱仪可以测不同方向上散射光波长及相对 强度。
•从普朗克公式可导出斯特 藩-玻耳兹曼定律，维恩 公式，瑞利—金斯公式
T=1646k
M T d T 4
dM (T ) 0 d
维恩位移定律
斯特藩-玻耳兹曼定律 维恩公式 瑞利—金斯公式
0
0
4、普朗克假说意义
普朗克抛弃了经典物理中的能量可连续变化的旧观点，提出 了能量子、物体辐射或吸收能量只能一份一份地按不连续的 方式进行的新观点。这不仅成功地解决了热辐射中的难题， 而且开创物理学研究新局面，标志着人类对自然规律的认识 已经从从宏观领域进入微观领域，为量子力学的诞生奠定了 基础。X光 管来自光 阑晶体 散射
X光检测 器
0 物质
3、实验现象
第-1-章-波粒二象性
五、粒子的波动性 ➢汤姆逊1927年电子通过金多晶薄膜的衍射 实验
衍射图样
五、粒子的波动性
➢约恩逊1961年电子的单缝、双缝、三缝和 四缝衍射实验
单缝
双缝
三缝 四缝
五、粒子的波动性
➢扫描电子显微镜
当探针针尖与物质表面排布原子的距离小到一 定程度时，其隧道电流会发生明显变化。
五、粒子的波动性 纳米“皇冠”，量子“围栏”
4.光子理论的解释
定性说明
光子与电子作
弹性碰撞，光
子传递一部分
能量给电子，
光子的能量减
少，波长变长。
四、康普顿散射
定量计算
➢X 射 线 光 子 与
“静止”的“自由 电子”弹性碰撞。
h n c
e
h c
0
n0
m
➢碰撞过程中能 量与动量守恒
h 0 m0c2 h mc2
h
0
n0
h
n m
四、康普顿散射
➢散射后的X光子波长偏移
频率足够高，以致每个光量子的能量 h 足够 大时，电子才有可能克服逸出功 A 逸出金属表
面。
逸出电子的最大初动能为
1 2
m
um2
h
A
称为 光电效应方程
三、光的二象性 光子
（2）存在截止频率0
比较
1 2
m um2
eK
eU0
1m 2
um2 h
A
有
h eK
A eU0
由此式可以测量普朗克常数。
红限频率
1.电子双缝衍射实验
➢ 电子通过单缝和双缝的衍射结果不一样！
六、概率波与概率幅
2.玻恩假定
Y
(
波粒二象性
T
单位面积
d E ( d（) 单位时间内）Leabharlann Md E (T )
d
M 取决于T，，物
质种类和表面情况
10
▲（总）辐出度（总发射本领）M(T) （radiant excitance）
M(T ) M (T )d 单位：w/m2
0
▲ 单色吸收比（率） (T)
（monochromatic absorptance）
17
2）斯特藩 — 玻耳兹曼定律 Stefan（德）Boltzman（奥）
M (T ) T 4
5.67108 w/m 2 K4
—— 斯特藩 — 玻耳兹曼常量 1879年斯特藩从实验上总结而得
1884年玻耳兹曼从理论上证明 斯特藩 — 玻耳兹曼定律和维恩位移定律是 测量高温、遥感和红外追踪等的物理基础。
该公式在低频段与实验曲线符合得很好。
时，M ，“紫外灾难”！
21
1904年诺贝尔物理 学奖获得者
——瑞利 • 英国人 • Lord Rayleigh • 1842-1919 • 氩的发现
电子衍射实验
1928 Dirac 相对论波动方程
3
第一章 波粒二象性 （Wave-particle duality）
§1.1黑体辐射 §1.2光电效应 §1.3 光的二象性、光子 §1.4 康普顿散射 §1.5 粒子的波动性 §1.6 概率波与概率幅 §1.7不确定关系
4
§1.1黑体辐射（Black-body radiation）
一. 热辐射的基本概念
▲热辐射 物体受热就会辐射电磁波。温度不同时, 辐射的波长（或频率）也不同。
例如：加热铁块， 温度，铁块颜色由 看不出发光 暗红 橙色 黄白色 蓝白色
大学物理中的波粒二象性问题
大学物理中的波粒二象性问题波粒二象性是指光和其他微观粒子既可以表现出波动性，也可以表现出粒子性的现象。
这种二象性对于理解物理世界的一些基本原理和现象至关重要。
本文将重点讨论大学物理中的波粒二象性问题。
一、光的波粒二象性问题在物理学中，光既可以进行干涉和衍射等波动现象，也可以表现出光的能量是以光量子的形式传递的粒子性。
这种波粒二象性的问题成为光的波粒二象性问题。
波动理论认为，光是由电磁波组成的。
光的干涉和衍射现象可以得到很好的解释。
然而，对于特定实验现象，如光电效应和康普顿散射等，光的粒子性解释更为合理。
这就导致了波粒二象性的存在。
二、粒子的波粒二象性问题对于微观粒子，如电子、中子等，在一些实验中也可以观察到波动现象，如动态干涉和衍射。
例如，电子双缝干涉实验。
当电子通过双缝时，它们会形成干涉条纹，展示出波动性。
这一实验结果表明，尽管电子具有质量和电荷，它们也具有波动性质。
三、波粒二象性解释在20世纪初，普朗克提出了能量量子化的概念，为解释黑体辐射实验结果做出了贡献。
随后，爱因斯坦利用光电效应实验的结果，进一步提出了光的粒子性，并称之为光的能量子。
德布罗意假设是对波粒二象性的一种解释。
德布罗意假设认为，微观粒子具有波动性，其波长与动量呈反比关系。
这一假设通过实验得到了验证，奠定了波粒二象性的理论基础。
四、波粒二象性应用波粒二象性的研究不仅对于理解光和微观粒子的性质有重要意义，也在物理学的其他领域有广泛的应用。
在能谱分析中，波粒二象性可以解释光谱线的产生原理。
在原子物理学中，通过波粒二象性来解释电子在原子轨道中的分布和电子云的性质。
在量子力学中，波粒二象性为物质的波函数理论提供了基础。
此外，波粒二象性被应用于现代技术，如激光、光导纤维通信等。
五、波粒二象性的影响和挑战波粒二象性的存在给物理学家们提出了一些困惑。
到目前为止，波粒二象性的真正本质尚未完全揭示。
这也是量子力学领域仍然存在的挑战之一。
同时，波粒二象性的研究也推动了许多新理论的提出和实验的发展。