沪教版八年级上册-二次根式
沪教版八年级数学上册,二次根式备课笔记

沪教版八年级数学上册,二次根式备课笔记二次根式1.二次根式:形如a的式子(a≥0)叫做二次根式。
在二次根式中,被开放数可以是数,也可以是单项式、多项式、分式等代数式,但必须注意:因为负数没有平方根,所以是为二次根式的前提条件,如,,等是二次根式,而,等都不是二次根式。
2.最简二次根式:必须同时满足下列条件:⑴被开方数中不含开方开的尽的因数或因式;⑵被开方数中不含分母;⑶分母中不含根式。
3.同类二次根式:二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式。
二次根式的运算:①二次根式的加减法:先把二次根式化成最简二次根式再合并同类二次根式.②二次根式的乘除法:二次根式相乘(除),将被开方数相乘(除),所得的积(商)仍作积(商)的被开方数并将运算结果化为最简二次根式.1、二次根式的概念与识别二次根式2、二次根式的化简与运算3、分母含有二次根式的分数进行分母有理化例题1:形如a ()的式子叫做二次根式。
1153a 21b -22a b +220m +144-的个数是().A .4B .3C .2D .12、下列式子一定是二次根式的是()A .2--xB .xC .22+xD .22-x练习:下列各式是二次根式吗?为什么?例2 、二次根式中字母的取值范围a 有意义,被开方数a ≥0,被开方数a 可以是数,也可以是式子x 取何值时,下列根式有意义?4223(8)1(9)42(10)3x -≤++--322(1) 32 (2) 12 (3) 8(4) a (5) -m (m 0) (6)2a -1 (7)a a 21(1)21(2)2(3)(4)1x x x x练习:①、若13-m 有意义,则m 能取的最小整数值是()A .m=0B .m=1C .m=2D .m=3②、二次根式31-x 有意义的条件是。
③、求使下列各式有意义的字母的取值范围:(1)43-x (2)a 831- (3)42+m (4)x1-当x +11x +在实数范围内有意义?例3、最简二次根式被开方数同时符合两个条件:1、被开方数中各因式的指数都为12、被开方数不含分母像这样的二次根式叫做最简二次根式下列二次根式中属于最简二次根式的是()A .14B .48C .ba D .44+a 将下面的两个式子化为最简二次根式 (1).315)2(;72.0练习:将下列二次根式化为最简二次根式将下列二次根式化为最简二次根式0)b >)x y >将下列二次根式化成最简二次二次根式0)a > 0)a > 0)x >例题4:同类二次根式几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式叫做同类二次根式。
沪教版八上教材知识点

角的平分线 →定理:在角的平分线上的点到这个角的两边的距离相等 →逆定理:在一个角的内部(包括顶点)且到角的两边距离相等的点,在 这个角的平分线上 19.6 轨迹(点的轨迹) →和线段两个端点距离相等的点的轨迹是这条线段的垂直平分线 →在一个角的内部 (包括顶点) 且到角两边距离相等的点的轨迹是这个角 的平分线 →到定点的距离等于定长的点的轨迹是以这个定点为圆心, 定长为半径的 圆 第 3 节 直角三角形 19.7 直角三角形全等的判定 →定理:如果两个直角三角形的斜边和一条直角边对应相等,那么这两 个直角三角形全等(简记为 H.L) 19.8 直角三角形的性质 定理 1:直角三角形的两个锐角互余 定理 2:直角三角形斜边上的中线等于斜边的一半 推论 1:在直角三角形中,如果一个锐角等于 300,那么它所对的直角边 等于斜边的一半 推论 2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条 直角边所对应的角等于 300 19.9 勾股定理 →定理:在直角三角形中,斜边大于直角边 →勾股定理:直角三角形两条直角边的平方和,等于斜边的平方 <→勾股定理的逆定理:>如果三角形的一条边的平方等于其他两条边的 平方和,那么这个三角形是直角三角形 19.10 两点的距离公式 19.5 →公式: AB ( X 1 X 2 ) 2 (Y1 Y2 ) 2 本章小结 阅读材料一 《几何原本》古今谈 阅读材料二 勾股定理万花筒
a a (a 0, b 0) b b
→把二次根式里被开方数所含的完全平方因式移到根号外, 或者化去被开 方数的分母的过程,称为“化简二次根式” →通常把形如 m a (a 0) 的式子也叫做二次根式
a a b ab ab (a 0, b 0) b bb b b2
沪教版八年级上册-二次根式的复习与练习题1

二次根式知识点归纳和题型归类 一、知识要点梳理知识点一、二次根式的主要性质:1. ;2. ;3. ;4.积的算术平方根的性质: ;5.商的算术平方根的性质: .6.若 , 则 .知识点二、二次根式的运算1. 二次根式的乘除运算(1) 运算结果应满足以下两个要求: ①应为最简二次根式或有理式;②分母中不含根号.(2) 注意每一步运算的算理;(3) 乘法公式的推广:2. 二次根式的加减运算 先化简, 再运算,3. 二次根式的混合运算 (1)明确运算的顺序, 即先乘方、开方, 再乘除, 最后算加减, 有括号先算括号里;(2)整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.二、分类练习与讲解:1. 二次根式的概念我们把形如 的式子叫做二次根式,如 等, 都是二次根式注意: ① 二次根式都含有二次根号 ; ② 在二次根式中, 被开方数 必须满足 , 当 时, 根式无意义;③ 在二次根式中, 可以是数也可以是一个代数式;④ 二次根式 是 的算术平方根, 所以 。
例1.当 为任意实数时, 下列各式有意义的是( )A. B. C. D.例2、当 为何值时, 下列各式有意义?⑴ 12+x ; ⑵ xx --1132. 二次根式的性质性质:注意:性质 表明:一个数的平方的算术平方根等于这个数的绝对值, 需注意的是 不是等于 , 而是等于 , 再根据 的正、负确定最后的结果。
例3 已知 , 则 的结果是______________例4 已知 满足 , 那么 的值为( )A. 2004B. 2005C. 2006D. 2007练习: 二次根式的意义及性质题组1: (二次根式的识别: 式子 ( ), 叫做二次根式)1. 下列各式中一定是二次根式的是( )A. B. C. D.2.下列各式中, 是二次根式的有_____________________________。
(填序号);; ;; ; 4. 若 , 则下列各式中, 是二次根式的是( )A. B. C. D.题组2: (二次根式有意义的条件)1.当 是怎样的实数时, 下列各式在实数范围内有意义?(1___________;(2__________;(3;(4______。
沪教版八年级上册-二次根式

5、比较大小: ; 。
6、 的整数部分是________;小数部分是_______。
7、求值: =,- =, =,- =_____。
8、若x2=52,则x=,若x2=5,则x=。
9、若3-2x没有平方根,则x
10、若 的正的平方根是3,则x=______________
(1)被开方数中各因数是整数,因式是整式; (2)被开方数中不含能开的尽方的因数或因式。
四、同类二次根式
几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个根式叫做同类二次根式。
同类二次根式可以合并.
注:要判断几个根式是否为同类根式,不一定非要化成最简形式,实际上只要化成某一种形式后,在这种形式下,被开方数相同就可以了。
基本内容 二次根式
知识精要
一、二次根式
在之前数的开方学习中,我们懂得如果一个数的平方等于 (a≥0),即x2=a(a≥0)。那么这个数x叫做 的平方根,写成x= ,即代数式 叫做a的二次根式。其中 是被开方数(可为整式或分式). 有意义的条件是 ,所以 也大于等于0。
2、二次根式的性质
性质1 ;※
性质2 ;
4、如果 在实数范围内有意义,则x的取值范围是____________
5、 成立的条件是
6、 成立的条件是
7、判断下列二次根式是不是最简二次根式:
1) 2) 3) 4)
8、将下列二次根式化成最简二次根式:
1) 2) 3)
化简: = = =
9、下列二次根式,那些是同类二次根式:
, , , , ,
10、若 ,化简
11、计算:
(1) (2)
(3) (4)
(5) (6)
沪教版(五四制)八年级数学上册16.1二次根式初步讲义(无答案)

沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕第十讲二次根式一、二次根式的定义形如a〔a0〕的式子叫做二次根式二、二次根式的根天性质:⑴a0〔a0〕;⑵(a)2a〔a0〕;⑶a2a a(a0)a(a0)三、最简二次根式:二次根式a〔a0〕中a称为被开方数.知足下边条件的二次根式我们称为最简二次根式:⑴被开放数的因数是整数,因式是整式〔被开方数不可以存在小数、分数形式〕⑵被开方数中不含能开得尽方的因数或因式⑶分母中不含二次根式二次根式的计算结果要写成最简根式的形式.四、同类二次根式:几个二次根式化成最简二次根式此后,假如被开方数同样,那么这几个二次根式就叫做同类二次根式。
五、二次根式的乘除二次根式的乘法法那么:a b ab〔a0,b0〕二次根式的除法法那么:a a〔a0,b0〕b b利用这两个法那么时注意a、b的取值范围,关于ab ab,a、b都非负,否那么不建立,如(7)(5)(7)(5)六、分母有理化及其初步应用分母有理化:把分母中的根号化去叫做分母有理化.互为有理化因式:两个含有二次根式的非0代数式相乘,假如它们的积不含有二次根式,我们说这两个代数式互为有理化因式.a b与a b互为有理化因式;分式有理化时,必定要保证有理化因式不为01/11沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕二次根式的观点与意义【例题1】〔1〕求当x知足什么条件时,以下各式在实数范围内存心义?当x时,x22存心义:当x时,2x存心义:2x1当x时,1存心义:当x时,x4存心义。
3x6x3〔2〕当x取何值时,以下二次根式存心义x2(x3)2x x x0〔3〕使等式2a12a 1建立的实数a的取值范围a3a3【例题2】〔1〕在35,a,a2b2,24a,a,x2x2y中,最简根式有个22〔2〕将以下各式化为最简的二次根式13b3=2732a2b=x2y 752(y0)=9xy 〔3〕假定b1,那么化a为最简二次根式得:〔〕b11a(b1)B.1a(b1)C.11)D.(b1)a(b1)A.b a(bb11a2/11沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕【例题3】〔1〕以下二次根式中,哪些是同类二次根式?〔字母均为正数〕①127②48③20④1125⑤1y⑥y x5 2x xy〔2〕以下各式:3,27,1,54,与3是同类二次根式的有个212〔3〕在8,175a,29a,125,23a 3,30.2,21中,与 3a 是同类二次根式的有33 a8个〔4〕在以下各组根式中,是同类二次根式的是〔〕A.3和18B.33a 4b 4和1ab4C.a 2b 和ab 2D.a1和a143〔5〕在1, 2, 3,..., 2021这2021个式子中,与2000是同类二次根式的共有多少个?与2021是同类二次根式的有多少个?〔6〕 2021 x y 且0 x y ,求知足上式的整数对〔 x ,y 〕.二次根式的简单运算3/11沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕【例题4】〔1〕假如 a 2a 建立,那么实数 a 的取值范围是 ___________.〔2〕 xy x y 建立的条件是 .〔3〕实数 a 知足|2021 a| a 2021 a ,求a20212【例题5】〔1〕化简:〔当0 a1时,化简(a1 )21 ______a a〔2〕化简: 1 2 2 3 3 4 4 5〔3〕3322 339〔4〕设等式a(xa)a(y a) xaay 在实数范围内建立,此中 a ,x ,y 是两 两不一样的实数,那么3x 2 xy y 2 的值是〔 〕x 2 xy y 2A .3B .1C .2D .533〔5〕a 为实数,且a26与12 6都是整数,那么a =a【例题6】计算:〔1〕23a46ab〔2〕10mn 26m 2n4/11沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕〔3〕418(28154)〔4〕2a3ab2b27a330,b0〕34aba〔a334【例题7】〔1〕假定abc0,且a b c,化简a4b3c2a1〔2〕化简:〔1〕a2a〔3〕化简:x3x2y1x y21x2yxy2y3(x0,y0)44【例题8】当a1,b5时,1a22abb21b22aba293935/11沪教版〔五四制〕八年级数学上册二次根式初步讲义〔无答案〕【例题9】把以下各式分母有理化:xy 23 5 2 3⑴2(a1) y1 ⑵⑶⑷5 2 32a4xy213【例题10】分母有理化:322 36。
沪教版数学初二上——二次根式概念及性质

【习题7】化简:
(1) ;(2) .
【习题8】计算 的值
【例11】化简:
(1) ;(2) ;
(3) ;(4) ( ).
【例12】化简:
(1) ;(2) ;
(3) ;(4) .
【例13】把下列各式中根号外面的因式移到根号内,并使原式的值不变.
(1) ;(2) ;(3) ;(4) .
【例14】化简:
(1) ;(2) .
【例15】化简:
(1) ;(2) ..
【例16】已知 ,求x的取值范围.
2、二次根式的性质
性质1: 推广性质1可得到:
性质:
性质3:
性质4:
二、例题讲解
【例1】下列各式中,二次根式的个数有()
; ; ; ; ; .
A.2个B.3个C.4个D.5个
【例2】添加什么条件时,下列式子是二次根式?
(1) ;(2) ;(3) ;(4) .
【例3】等式 成立的条件是()
A. B. C. D.
二次根式的概念与性质
一、知识精讲
知识一、二次根式、无理数、实数的概念
当被开方数部分是整数时,该二次根式可以看作一个无理数(开方开不尽的时候),表示对一个整数求算术平方根,联想之前七年级的中点逼近法求范围
知识二、二次根式的概念和性质
1、形如 (a )的代数式,叫做二次根式,a是被开方数.
举例说明: 、 、 、 等都是二次根式.在实数范围内,负数没有平方根,所以像 , 这样的式子没有意义,二次根式有意义的条件是被开方数是非负数.
【例17】
已知 ,求代数式 的值.
【例18】已知 的个位数字.
【例19】已知:m= ,求 的值.
沪教版(上海)八年级第一学期《16.1 二次根式》(共16张PPT)

开平方和平方是互逆的运算——
( a )2 a (a 0) a2 a
a2
a
3/23/2022
2
2
3
3
二次根式的性质
例3
求下列二次根式的值
(1) ( 3 ) 2
(2) x2 2x 1 其中x= 3
(3)
1
(m 2)2
其中m= 5
例4
例4:设a、b、c分别是三角形三边的长, 化简:
被开方数
a
二次根号
a在取值上有什 么要求?
a0
在实数范围内,二次根式有意义的条件就是被开方数是 非负数(即被开方数≥0 )。
3/23/2022
例1
设x是实数,当x满足什么条件时,下列各式有 意义?
(1) 2 x
(2) 2 x 1
(3) 1 x
(4) 1 x 2
巩固练习
设x是实数,当x满足什么条件时,下列各式有 意义?
复习回顾
1、如果 x2 4,那么 x±2 ;
2、3的平方根是_____3___
3、2的算术平方根是___2 _
3/23/2022
x
?
问题情境
1.已知:一个正方形花圃的面积为5㎡,
则它的边长为___5__m;
5
2.已知:一个正方形花圃的面积为(a-5)
㎡,则它的边长为__a__5_m;
3/23/2022
能 力 和 独 立 解决问 题的能 力,积累 了更多 的这些 方面工 作经。 在 完 成 上 述 工作的 同时,还 按照工 委要求 参加了 市直机 关创先 争优和 XX年机关党组
织 书 记 述 职 考评检 查工作 。在参 加这项 工 作 的 过 程 ,自己感 到也是 一个学 习的过 程,学到 了一些 机关党 建
沪教版八年级上册数学 第十六章 二次根式 全章复习 教案
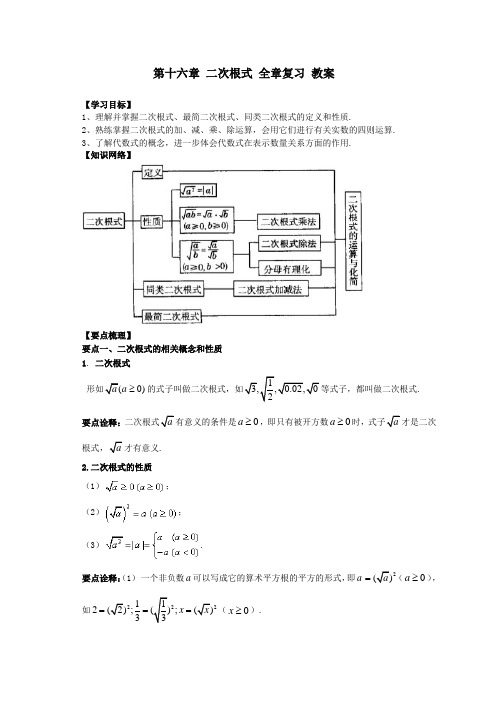
第十六章 二次根式 全章复习 教案【学习目标】1、理解并掌握二次根式、最简二次根式、同类二次根式的定义和性质.2、熟练掌握二次根式的加、减、乘、除运算,会用它们进行有关实数的四则运算.3、了解代数式的概念,进一步体会代数式在表示数量关系方面的作用.【知识网络】【要点梳理】要点一、二次根式的相关概念和性质1. 二次根式形如(0)a a ≥的式子叫做二次根式,如13,,0.02,02等式子,都叫做二次根式. 要点诠释:二次根式a 有意义的条件是0a ≥,即只有被开方数0a ≥时,式子a 才是二次根式,a 才有意义.2.二次根式的性质(1); (2);(3).要点诠释:(1) 一个非负数a 可以写成它的算术平方根的平方的形式,即a 2a =(0a ≥),如2221122););)33x x ===(0x ≥).(2)a 的取值范围可以是任意实数,即不论a .(3a ,再根据绝对值的意义来进行化简.(42的异同a 可以取任何实数,而2中的a 必须取非负数;a ,2=a (0a ≥).相同点:被开方数都是非负数,当a 2.3. 最简二次根式(1)被开方数是整数或整式;(2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式,叫做最简二次根式.次根式.要点诠释:最简二次根式有两个要求:(1)被开方数不含分母;(2)被开方数中每个因式的指数都小于根指数2.4.同类二次根式几个二次根式化成最简二次根式后,被开方数相同,这几个二次根式就叫同类二次根式. 要点诠释:判断是否是同类二次根式,一定要化简到最简二次根式后,看被开方数是否相同,再判断.显然是同类二次根式.要点二、二次根式的运算1. 乘除法(1)乘除法法则:类型法则 逆用法则二次根式的乘法 0,0)a b =≥≥积的算术平方根化简公式:0,0)a b =≥≥二次根式的除法 0,0)a b≥> 商的算术平方根化简公式:0,0)a b=≥> 要点诠释:(1)当二次根式的前面有系数时,可类比单项式与单项式相乘(或相除)的法则,如=(2)被开方数a 、b 一定是非负数(在分母上时只能为正数).≠.2.加减法将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数不变,即合并同类二次根式.要点诠释:二次根式相加减时,要先将各个二次根式化成最简二次根式,再找出同类二次根式,最后合并同类二次根式.如23252(135)22+-=+-=-. 【典型例题】 类型一、二次根式的概念与性质 1. 当________时,二次根式3x -在实数范围内有意义.【答案】x ≥3.【解析】根据二次根式的性质,必须3x -≥0才有意义.【总结升华】本例考查了二次根式成立的条件,要牢记,只有0a ≥时a 才是二次根式. 举一反三【变式】①242x x =-成立的条件是 .②2233x x x x--=--成立的条件是 . 【答案】① x ≤0;(2422x x x x ==-∴≤0.)② 2≤3x <.(20,30,x x -->∴≥2≤3x <) 2.当0≤x <1时,化简21x x +-的结果是__________.【答案】 1.【解析】因为x ≥0,所以2x =x ;又因为x <1,即x -1<0,所以1(1)1x x x -=--=-,所以21x x +-=x +1-x =1.【总结升华】利用二次根式的性质化简二次根式,即2a =a ,同时联系绝对值的意义正确解答.举一反三【变式】已知﹣=2,则+的值为_____________. 【答案】5.解:∵﹣=2, ∴=+2, 两边平方得,25﹣x 2=4+15﹣x 2+4,∴2=3,两边平方得4(15﹣x 2)=9,化简,得x 2=, ∴+=+=5.故答案为:5. 3.下列二次根式中属于最简二次根式的是( ). A. 14 B. 48 C.a b D. 44a + 【答案】A. 【解析】选项B :48=43;选项C :有分母;选项D :44a +=21a +,所以选A.【总结升华】本题考查了最简二次根式的定义.最简二次根式要满足:(1)被开方数是整数或是整式;(2)被开方数中不含能开方的因式或因数.类型二、二次根式的运算 4.下列计算正确的是( )A .﹣= B .3×2=6 C .(2)2=16D .=1 【答案】B.【解析】解:A 、不能化简,所以此选项错误; B 、3×=6,所以此选项正确;C 、(2)2=4×2=8,所以此选项错误;D 、==,所以此选项错误; 故选B .【总结升华】本题考查了二次根式的混合运算,熟练掌握二次根式的计算法则是关键,要注意:①二次根式的运算结果要化为最简二次根式;②与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的;③灵活运用二次根式的性质,选择恰当的解题途径.举一反三【变式】计算:4854453)833【答案】243610-. 5.化简20102011(32)(32)+⋅-.【答案与解析】201020102010=(32)(32)(32)(32)(32)(32)1(32)3 2.+⋅-⋅-⎡⎤=+⋅-⋅-⎣⎦=⋅-=-原式 【总结升华】本题的求解用到了积的乘方的性质,乘法运算律,平方差公式及根式的性质,是一道综合运算题型. 6.已知2231,12x x x x=-+求. 【答案与解析】2231,1=30,(1)133331=33x x x x x x x =+∴->∴=--+==原式当时,原式【总结升华】 化简求值时要注意x 的取值范围,如果未确定要注意分类讨论.举一反三【变式】已知a b +=-3, ab =1,求ab b a +的值. 【答案】∵a b +=-3,ab =1,∴<0a ,<0b11++)=-=3ab ab a b b a ab ∴原式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
※
性质4 ( >0)一般地,我们有
三、最简二次根式
1. 化简二次根式
把二次根式里被开方数所含的完全平方因式移到根号外,或者化去被开方数的分母的过程,称为化简二次根式,通常把形如 的式子叫做最简二次根式。
2. 化简后的二次根式中:
(1)被开方数中各因式的指数都为1; (2)被开方数不含分母。
3.最简二次根式必须满足二个条件:
8、把(a-b) 化成最简二次根式,正确的结果是()
A. ;B. ;C.- ;D.- 。
9、在二次根式 , , , , 中,最简二次根式个数是()
A.1个;B. 2个;C. 3个;D. 4个
10、下列各组二次根式中,同类二次根式是()
A. ,3 ;B. 3 , ;C. , ;D. ,
三、简答题
1、比较大小:
4、 的平方是___, 的平方根是__。
5、比较大小: ; 。
6、 的整数部分是________;小数部分是_______。
7、求值: =,- =, =,- =_____。
8、若x2=52,则x=,若x2=5,则x=。
9、若3-2x没有平方根,则x
10、若 的正的平方根是3,则x=______________
5、最简根式 和 是同类根式,则()
A. a=1,b=1;B. a=1,b=2;C. a=2,b=1;D. a=2,b=2
6、下列各式中与 是同类二次根式的是()。
A. ;B. ;C. ;D.
7、如果最简二次根式 是同类二次根式,那么使 有意义的x的取值范围是()
A. x≤10;B. x≥0;C. x<10;D. x>0
五、二次根式的运算
1.二次根式的加法和减法
一般过程:先把各个二次根式化为最简二次根式,再把同类二次根式分别合并.(化简+合并)
2.二次根式的乘法和除法
(1)两个二次根式相乘,被开方数相乘,根指数不变;
(2)两个二次根式相除,被开方数相除,ቤተ መጻሕፍቲ ባይዱ指数不变.
3.分母有理化
把分母中的根号化去就是分母有理化.即是指分母不含二次根式的运算的技术。
A. ;B. ;C. ;D.
2、已知 ,那么 可化简为()
A. ;B. ;C. ;D.
3、下列二次根式中,与 不是同类二次根式的为()
A. ;B. ;C. ;D.
4、下列说法正确的是()
A、任何两个根式都可化为同类根式;B、最简二次根式一定是同类二次根式;
C、同类根式一定是最简根式;D、 是最简根式。
11、设a、b、c分别是三角形三边的长,化简:
精解名题
例1、
例2、 (a>b>0)
例3、解下列方程和不等式:
(1) (2) (3)
例4、已知 ,求 的值
例5、已知: 是一个正整数
(1)写出最小的正整数a
(2)这样的正整数a有多少个?如果有有限个,请写出来;如果有无数个,则a是怎样的一个整数?
例6、已知: ,求 的平方根。
基本内容 二次根式
知识精要
一、二次根式
在之前数的开方学习中,我们懂得如果一个数的平方等于 (a≥0),即x2=a(a≥0)。那么这个数x叫做 的平方根,写成x= ,即代数式 叫做a的二次根式。其中 是被开方数(可为整式或分式). 有意义的条件是 ,所以 也大于等于0。
2、二次根式的性质
性质1 ;※
性质2 ;
分母有理化的方法是把分子和分母都乘以同一个适当的代数式,使分母不含根号.
上述的适当代数式即是指有理化因式。
热身练习
1、已知x是实数,当x满足什么条件时,下列各式有意义?
1) ;2) ;3) ;4)
2、若5x+1没有平方根,则x的取值范围是____________
3、 是实数,则 =__________
例7、已知:实数 满足 。求: 的值
例8、若 分别表示 的整数部分和小数部分,求 的值。
巩固训练:
一、填空题
1、计算: =。
2、如果 与 是同类二次根式,那么 的值可以是(只需写出一个)。
3、x取6,9,12,18中的________时, 与 是同类二次根式。
4、若最简二次根式 , 是同类二次根式,则a=________。
(1)3 与 ;(2) - 与2 -1;(3) - 与 - 。
2、计算与化简:
(1) ;
(2)[ ]2-( )2;
(3)( -6 )(4 + )-(2 -3 )2;
(4) ;(5) ;
(6) (x>3y)。
自我测试
1、若 ,则 叫做 的,记做 。
2、若最简二次根式 与 是同类二次根式,则 。
3、16的平方根为_______________。
(1)被开方数中各因数是整数,因式是整式; (2)被开方数中不含能开的尽方的因数或因式。
四、同类二次根式
几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个根式叫做同类二次根式。
同类二次根式可以合并.
注:要判断几个根式是否为同类根式,不一定非要化成最简形式,实际上只要化成某一种形式后,在这种形式下,被开方数相同就可以了。
5、计算: · ÷ =; =;( -2)8( +2)8=。
6、当a=_______时,最简根式-2 和3 是同类根式。
7、三角形三边a=7 ,b=4 ,c=2 ,则周长是。
8、若 是最简二次根式,则b可取的自然数有_____。
9、若 和 都是最简二次根式,则 。
二、选择题:
1、下列二次根式中,最简二次根式是()
11、计算:
(1) (2)
(3) (4)
(5) (6)
12、已知m、n为实数,且满足m= ,求6m-3n的值?
13、若x,y为实数,且y= + + .求 - 的值.
14、计算
4、如果 在实数范围内有意义,则x的取值范围是____________
5、 成立的条件是
6、 成立的条件是
7、判断下列二次根式是不是最简二次根式:
1) 2) 3) 4)
8、将下列二次根式化成最简二次根式:
1) 2) 3)
化简: = = =
9、下列二次根式,那些是同类二次根式:
, , , , ,
10、若 ,化简
