计算传热学中国石油大学(华东)第四章大作业
传热学思考题答案-中国石油大学
2.14 冬天新建的居民楼比旧楼房感觉更冷为什么?
答：新建的楼房，墙体中含有较多的水分，导热系数较大，导热能力较强。
2-15 空心砖好，因为空心砖内部充满空气，而空气的导热系数相对较小，热阻
较大，空心砖导热性较之实心砖差，同一条件下空心砖的房间的散热量小，保
温性好。
2-16 棉被中棉絮的中充斥着空气，空气导热系数小，所以棉絮中的热量不容易
������ Δ������，可见ϕ 或 q与λ、δ、A 和 Δt之间的关系，当壁厚，壁温及壁的性质确定时，
������
热流量或热流密度为常数
2 曲线向下弯曲，说明 b＜0，所以������随壁温增加而减小。
3 稳态。根据傅里叶定律，在没有内热源的情况下，及时导热系数随温度变化，
通过平壁的热流密度仍然为常数，通过变物性平壁的的热流密度仍可以按导热
一种经常遇到的恒热流边界：������|������ = 常数
第三类边界条件:规定边界上的换热状况：−������
������������ ������������
|������
=
ℎ(������|������
−
������������ )
2.10 能否将三类边界条件转换成统一的表达式，什么情况下第三类能转换成第
态导热过程的求解需要导热微分方程，而导热微分方程是在傅里叶定律的基础
上推到得到。
2.3 举例说明影响导热系数的因素有哪些？
答： 导热系数与物质的种类、物态、、结构、温度、压力等诸多因素有关。
如：对于同一物质，导热系数固态>液态>气态；金属的导热系数又大于其合金；
有些材料导热系数还与方向有关，如木材，石墨，这类材料被称为各向异性材
计算传热学程序设计
中国石油大学（华东)储运与建筑工程学院热能与动力工程系《计算传热学程序设计》设计报告学生姓名：学号：专业班级:指导教师2012年 7 月 7 日1、设计题目有一房屋的砖墙厚δ=0.3 m ，λ=0.85 W/（m·℃)，ρc=1.05×106 J/( m3·K)，室内温度T f1保持20℃不变，表面传热系数h1=6W/(m2·℃).开始时墙的温度处于稳定状态,内墙表面温度Tw1为15℃寒潮入侵后，室外温度T f2下降为—10℃，外墙的表面传热系数为35W/（m2·℃）.试分析寒潮入侵后多少时间内墙壁面方可感受到外界气温的变化。
图1 墙壁简化图1.1已知参数壁厚，墙壁导热系数，密度与比热容的乘积,室内和寒潮入侵后室外空气温度，室内空气和外墙的表面传热系数，开始时稳定状态下的内墙表面温度.1.2 求解寒潮入侵多少时间后内墙壁面可感受到外界气温的变化？2 物理与数学模型2。
1 物理模型该墙面为常物性，可以假设:（1）其为无限大平面，(2)只有在厚度方向传热，没有纵向传热，则该问题转化为一维常物性无限大平面非稳态导热问题。
2。
2 数学模型以墙外表面为坐标原点，沿厚度方向为坐标正方向，建立坐标系。
基于上述模型,取其在x 方向上的微元作为研究对象，则该问题的数学模型可描述如下：T ()T cx x ρλτ∂∂∂=∂∂∂ （1a)初始条件：(1b)在两侧相应的边界条件是第三类边界条件，分别由傅立叶定律可描述如下： 左边界：0202()x f x T h T T X==∂-λ=-∂ （1c)右边界:11()x f x T h T T X=δ=δ∂-λ=-∂ (1d ）3 数值处理与程序设计3。
1 数值处理采用外点法用均匀网格对求解区域进行离散化，得到的网格系统如图2所示。
一共使用了0~N-1共N 个节点.节点间距δx 为:图2 墙壁内的网格划分此例中墙壁导热系数为常值,无源项。
传热学课后习题第四章答案
选择步长 x y ，又边界为绝热 h 0 ，整理有
t i 1, j t i , j
即
t i , j 1 t i , j 2
t i , j 1 t i , j 2
0
2ti 1, j ti, j 1 ti, j 1 4ti, j 0
4-2 解：根据热平衡方程有
t 2 t10 t5 t 7 4t 6 0
对节点 7
t 3 t11 t 6 t8 4t 7 0
对节点 10
t 6 t14 t9 t11 4t10 0
对节点 11
t 7 t15 t10 t12 4t11 0
对节点 14
t10 t18 t13 t15 4t14 0
hxt f t i , j
t i , j 1 t i , j 2
hx
0
(t i 1, j t i , j 1 ) 2(1
h
x)t i , j 2
tf 0
4-3 解：根据已知条件，划分网格如图所示 第一类边界条件
t w 200C
第二类边界条件
3 200 （2t 4 t 8 100 ） 14 3 3 200 t8 （2t 5 t 7 t 9 ） 14 3 t7
节点 9 为第三类边界条件下的外拐角边界节点
ti1, j ti, j 1 (2Bi 2)ti, j 2Bi t f 0
对节点 20
t16 t 20 t t 24 20 (t19 t 20 ) hy t f t 20 0 2 2
对节点 16
华科传热学04-1,2
2016/1/1
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
3 对流换热系数与对流换热微分方程
①对流换热系数(表面传热系数)
h Φ ( A(t w t )) [W (m2 C)]
——当流体与壁面温度相差 1℃ 时、每单位 壁面面积上、单位时间内所传递的热量.
电子器件散热
2016/1/1
4
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
②对流换热的特点： (1) 导热与热对流同时存在的复杂热传递过 程 (2) 必须有直接接触（流体与壁面）和宏观 运动；也必须有温差 (3) 由于流体的粘性和受壁面摩擦阻力的影 响，紧贴壁面处会形成速度梯度很大的边 界层；热边界层 ③特征：以简单的对流换热过程为例，对 对流换热过程的特征进行粗略的分析。
2016/1/1
y
t∞
u∞
qw
tw
x
6
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
1. they will rebound off the solid surface 2. they will be absorbed into the solid surface 3. they will adhere to the solid surface
第四章 对流换热原理
§4-1 对流换热概述 §4-2 层流流动换热的微分方程组 §4-3 对流换热过程的相似理论 §4-4 边界层理论 §4-5 紊流流动换热
建工版(第5版)《传热学》第4章作业参考解答2-3-7
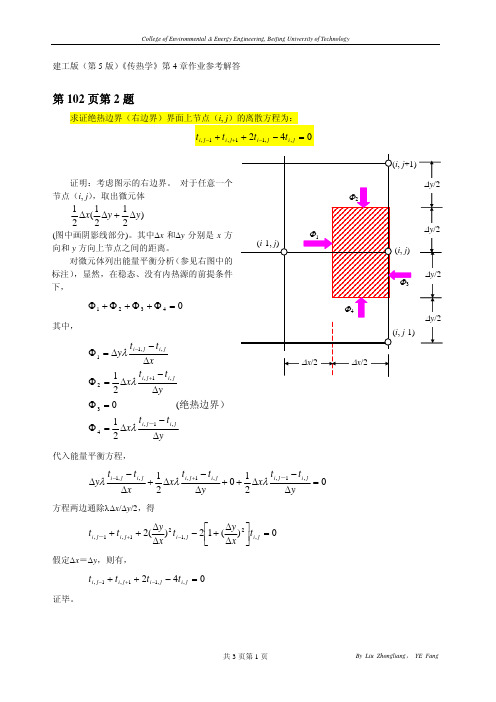
第102页第2题求证绝热边界（右边界）界面上节点（i , j ）的离散方程为：042,,11,1,++−−+−j i j i j i j i t t t t =证明：考虑图示的右边界。
对于任意一个节点（i , j ），取出微元体)2121(21y y x Δ+ΔΔ (图中画阴影线部分)。
其中Δx 和Δy 分别是x 方向和y 方向上节点之间的距离。
对微元体列出能量平衡分析（参见右图中的标注），显然，在稳态、没有内热源的前提条件下，04321=Φ+Φ+Φ+Φ其中，yt t x yt t x xt t y j i j i j i j i ji j i Δ−Δ=Φ=ΦΔ−Δ=ΦΔ−Δ=Φ+−,1,43,1,2,,1121( 021－绝热边界）λλλ代入能量平衡方程，021021,1,,1,,,1=Δ−Δ++Δ−Δ+Δ−Δ+−yt t x y t t x x t t y j i j i j i j i ji j i －λλλ方程两边通除λΔx /Δy /2，得0)(12)(2,2,121,1,=⎥⎦⎤⎢⎣⎡ΔΔ+−ΔΔ++−+j i j i j i j i t x y t x y t t － 假定Δx ＝Δy ，则有，042,,11,1,=−++−+−j i j i j i j i t t t t证毕。
第102页第3题证明：考虑图示的右上角节点（i , j ），取出微元体y x Δ×Δ2121 (图中画阴影线部分)。
其中Δx 和Δy 分别是x 方向和y 方向上节点之间的距离。
对微元体列出能量平衡分析（参见右图中的标注），显然，在稳态、没有内热源的前提条件下，04321=Φ+Φ+Φ+Φ其中，yt t x t t h t t xh x t t y j i j i j i f j i f j i j i Δ−Δ=Φ−Δ=Φ−Δ=ΦΔ−Δ=Φ−,1,4,3,2,,1121( )(y 21( )(2121－牛顿冷却定律）牛顿冷却定律）λλ代入能量平衡方程，021 )(y 21 )(2121,1,,,,,1=Δ−Δ+−Δ+−Δ+Δ−Δ−yt t x t t h t t xh x t t y j i j i j i f j i f j i j i －λλ 方程两边通除λΔy/Δx /2，整理后得到，0)(1)(2,221,2,1=⎟⎟⎠⎞⎜⎜⎝⎛Δ+ΔΔ+⎥⎦⎤⎢⎣⎡Δ+ΔΔ+ΔΔ+−ΔΔ+−f j i j i ji t x h y x h t x h y x h y x t y x t λλλλ－ 假定Δx ＝Δy ，则有，0212,1,,1=Δ+⎟⎠⎞⎜⎝⎛Δ+−+−f ji j i j i t x h t x h t t λλ－ 证毕。
化工原理课后习题答案第4章传热习题解答
习 题1. 如附图所示。
某工业炉的炉壁由耐火砖λ1=1.3W/（m·K）、绝热层λ2=0.18W/（m·K）及普通砖λ3=0.93W/（m·K）三层组成。
炉膛壁内壁温度1100o C ，普通砖层厚12cm ，其外表面温度为50 oC 。
通过炉壁的热损失为1200W/m 2，绝热材料的耐热温度为900 oC 。
求耐火砖层的最小厚度及此时绝热层厚度。
设各层间接触良好，接触热阻可以忽略。
已知：λ1=1.3W/m·K ，λ2=0.18W/m·K ，λ3=0.93W/m·K，T 1＝1100 o C ，T 2＝900 o C ，T 4＝50o C ，3δ＝12cm ，q ＝1200W/m 2，Rc ＝0求： 1δ＝？2δ＝？解： ∵δλT q ∆=∴1δ＝m qTT 22.0120090011003.1211=-⨯=-λ又∵33224234332322λδλδδλδλ+-=-=-=T T T T T T q∴W K m q T T /579.093.012.01200509002334222⋅=--=--=λδλδ得：∴m 10.018.0579.0579.022=⨯==λδ习题1附图习题2附图2. 如附图所示。
为测量炉壁内壁的温度，在炉外壁及距外壁1/3厚度处设置热电偶，测得t 2=300 oC ，t 3=50 o C 。
求内壁温度t 1。
设炉壁由单层均质材料组成。
已知：T 2=300o C ，T 3=50o C 求： T 1=？ 解： ∵δλδλ31323T T TT q -=-=∴T 1－T 3＝3（T 2－T 3）T 1＝2(T 2－T 3)+T 3=3×(300-50)+50＝800 oC 3. 直径为Ø60×3mm 的钢管用30mm 厚的软木包扎，其外又用100mm 厚的保温灰包扎，以作为绝热层。
现测得钢管外壁面温度为–110o C ，绝热层外表面温度10oC 。
化工道理第四版习题解 第四章 传热
Q qll 284 50 1.42104W
1 ln r4
14.2 kW 【4-7】水蒸气管路外径为 108mm，其表面包一层超细玻璃棉毡保温，其热导率随温度
t / ℃ 的变化关系为 0.033 0.00023t W / (m K ) 。水蒸气管路外表面温度为 150℃，希望保温
1.163 0.033 0.002
110 0.036
【4-6】某工厂用 170mm 5mm 的无缝钢管输送水蒸气。为了减少沿途的热损失，在管外
包两层绝热材料，第一层为厚 30mm 的矿渣棉，其热导率为 0.065W / (m K ) ；第二层为厚
30mm 的石棉灰，其热导率为 0.21W / (m K ) 。管内壁温度为 300℃，保温层外表面温度为
的热导率 λ=1.163W/(m·℃)。试计算水垢的热阻是黄铜管 多少倍 [黄铜的热导率 λ=110W/(m·℃)]。
解 因 38 2 ，因算术平均半径计算导热面积。管 32
长用 L 表示。黄铜管的热阻为
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
传热学数值计算大作业
传热学数值计算大作业传热学数值计算大作业一选题《传热学》第四版P179页例题 4-3二相关数据及计算方法1．厚2δ=0.06m的无限大平板受对称冷却，故按一半厚度作为模型进行计算2. δ=0.03m，初始温度t0=100℃,流体温度t∞=0℃；λ=40W/(m.K),h=1000W/(m2.K),Bi=h*△x/λ=0.25；3.设定Fo=0.25和Fo=1两种情况通过C语言编程（源程序文件见附件）进行数值分析计算；当Fo=0.25时，Fo<1/(2*(1+Bi)),理论上出现正确的计算结果；当Fo=1时，Fo>1/(2*(1+Bi))，Fo>0.5,理论上温度分布出现振荡，与实际情况不符。
三网格划分将无限大平面的一半划分为6个控制体，共7个节点。
△x=0.03/N=0.03/6=0.005，即空间步长为0.005m四节点离散方程绝热边界节点即i=1时，tij+1=2Fo△ti+1j+(1-2Fo△)tij 内部节点即0tij+1=tij（1-2Fo△Bo△-2Fo△）+2Fo△ti-1j+2Fo△Bo△tf五温度分布线图（origin）六结果分析1 空间步长，时间步长对温度分布的影响空间步长和时间步长决定了Bo和Fo，两者越小计算结果越精确，但同时计算所需的时间就越长。
2 Fo数的大小对计算结果的影响编程时对Fo=1及0.25的情况分别进行了计算，发现当Fo=1时，各点温度随时间发生振荡，某点的温度高反而会使下一时刻的温度变低，违反了热力学第二定律，因此在计算中对Fo的选取有限制。
为了保证各项前的系数均为正值，对于内节点，Fo>0.5；对于对流边界节点，Fo<1/(2*(1+Bi))。
3 备注在Fo=0.25时，为了反映较长时间后温度的分布，取T=600,并选取了其中部分时刻的温度输出进行画图。
图像显示，随着时间的增长，各点温度趋向一致。
而当Fo=1时由于结果会出现振荡，只取T=6观察即可。
《传热学》课后习题答案-第四章
t 0 850 C, t f 250 C, h 30W /( m 2 .K )
2
.肋高 H=4cm,纵
剖面面积 AL 4cm , 导热系数 20W /( m.K ) 。 解：对于 2 点可以列出：
t t t1 t 2 3 4 2hx(t1 t 2 ) 0; x x 节点 2： t t x 2 3 h(t f t1 ) 2h (t f t 3 ) 0 x 2 2 节点 3： 。
4
22.28027129 22.28881782 22.290955445
15.20263565 15.20690891 15..20797723
其中第五次与第六次相对偏差已小于10 迭代终止。 4-4、 试对附图所示的等截面直肋的稳态导热问题用数值方 法 求 解 节 点 2 ， 3 的 温 度 。 图 中
，
2hxH 2 t 2 t1 t 3 t f hx 2 h t 3 t 2 t f 2 t f
2hxH 2 2
，
4.3636 ， 2.53 85 1.8336 25 215.05 45.84 t2 59.79 59.8 C 4.3636 4.3636 ， 59.8 1.53 25 t3 38.75 38.8 C 2.53 。
n ,i 8．有人对一阶导数 你能否判断这一表达式是否正确，为什么？ 一般性数值计算 4-1、采用计算机进行数值计算不仅是求解偏微分方程的有力工具，而且对一些复杂的经验 公式及用无穷级数 表示的分析 解，也常用计 算机 来获得数值结果。 试用数值方 法对
t x
i i i 3t n 5t n 1 t n 2 2x 2
中国石油大学(华东)《热工基础》期末考试必备通关指导
《热工基础》课程练习题适用层次所有层次适应专业石油工程、油气储运工程使用学期自学学时12021 授学时40 实验学时0使用教材教材名称《工程热力学（第三版）》；《传热学（第二版）》编者沈维道等;戴锅生出版社高等教育出版社参考教材《传热学》俞佐平等，高等教育出版社热力学部分绪论第一章基本概念 1-1～1-5第二章热力学第一定律 2-1～2-5练习题1-1：华氏温标规定，在标准大气压（101325Pa）下纯水的冰点是32℉，汽点是212℉（℉是华氏温标温度单位的符号）。
试推导华氏温度与摄氏温度的换算关系。
1-8：容器被分隔成A、B两室，如图1-19所示。
已知当地大气压=bp，B室内压力表2 的读数04.02,=ep MPa，压力表1的读数294.01,=ep MPa，求压力表3的读数（用MPa表示）。
第二章热力学第一定律 2-6～2-7第三章理想气体的性质 3-1～3-3；3-4～3-6练习题2-5：夏日为避免阳光直射，紧闭门窗，用电扇取凉，电扇功率为60W。
假定房间内初温为28℃、压力为，太阳照射传入的热量为，通过墙壁向外散热1800kJ/h。
室内有3人，每人每小时向环境散发热量为。
试求面积为15m2、高度为3.0m的室内每小时温度的升高值。
已知空气的热力学能与温度的关系为{}KTu∆=∆72.0kJ/kg。
3-4：锅炉燃烧需要的空气量折合为标准状态为30,105⨯=vq m3/h,实际送入的是温度int=250℃、表压力=ep150mmHg的热空气。
已知当地大气压力=bp756mmHg。
设煤燃烧后产生的烟气量与空气量近似相同，烟气通过烟囱排入大气。
已知烟囱出口处烟气的压力=2p，温度T2=480K，要求烟气流速=fc3m/s，试求：（1）热空气实际状态的体积流量vq；（2）烟囱出口内直径的设计尺寸。
见图3-10。
3-8：体积V=0.5m3的密闭容器中装有27℃、的氧气，加热后温度升高到327℃。
(整理)化工原理(第四版)习题解 第四章 传热
第四章 传 热热传导【4-1】有一加热器，为了减少热损失，在加热器的平壁外表面，包一层热导率为0.16W/(m·℃)、厚度为300mm 的绝热材料。
已测得绝热层外表面温度为30℃，另测得距加热器平壁外表面250mm 处的温度为75℃，如习题4-1附图所示。
试求加热器平壁外表面温度。
解 2375℃, 30℃t t ==计算加热器平壁外表面温度1t ，./()W m λ=⋅016℃231212t t t t b b λλ--= (1757530025005016016)t --= ..145025********t =⨯+=℃【4-2】有一冷藏室，其保冷壁是由30mm 厚的软木做成的。
软木的热导率λ=0.043 W/(m·℃)。
若外表面温度为28℃，内表面温度为3℃，试计算单位表面积的冷量损失。
解 已知.(),.123℃, 28℃, =0043／℃ 003t t W m b m λ==⋅=， 则单位表面积的冷量损失为()()../.q t t W m bλ=-=-=-2120043328358 003【4-3】用平板法测定材料的热导率，平板状材料的一侧用电热器加热，另一侧用冷水冷却，同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2，材料的厚度为0.02m 。
现测得电流表的读数为2.8A ，伏特计的读数为140V ，两侧温度分别为280℃和100℃，试计算该材料的热导率。
解 根据已知做图热传导的热量 .28140392Q I V W =⋅=⨯=()12AQ t t bλ=-.().()12392002002280100Qb A t t λ⨯==-- ()./218W m =⋅℃【4-4】燃烧炉的平壁由下列三层材料构成：耐火砖层，热导率λ=1.05W/(m·℃)，厚度230b mm =；绝热砖层，热导率λ=0.151W/(m·℃)；普通砖层，热导率λ=0.93W/(m·℃)。
《传热学》第四章复习题答案
《传热学（第四版）》第四章复习题答案1.试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。
答：基本思想：把原来在时间、空间坐标系中连续的物理量的场，用有限个离散点上的值的集合来代替，通过求解按一定方法建立起来的关于这些值的代数方程，来获得离散点上被求物理量的值。
这些离散点上被求物理量值的集合称为该物理量的数值解。
步骤：①建立控制方程及定解条件；②区域离散化；③建立物理量的代数方程；④用迭代法求解时，设立迭代初场；⑤求解代数方程组；⑥解的分析。
2.试说明用热平衡法对节点建立温度离散方程的基本思想。
答：对以节点所代表的元体用傅立叶定律直接写出其能量守恒表达式，得到以元体为研究对象的传热代数方程。
3.推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似，为什么前者得到的是精确描写，而由后者解出的却是近似解。
答：因为微分方程的研究对象是微元体，而用热平衡法建立的节点温度离散方程的研究对象是元体。
微分方程的微元体可以达到无限小，从而可准确描述物体内任一点的连续函数。
而热平衡法对有限大小元体内的分布函数用节点处的值代替，从而得到近似解，不能得到准确解。
4.第三类边界条件边界节点的离散方程，也可用将第三类边界条件表达式中的一阶导数用差分公式来建立。
试比较这样建立起来的离散方程与用热平衡法建立起来的离散方程的异同与优劣。
答：由教材P175 式(a)，(b)可得：在x方向上有：ðt ðx |m,n≈t m+1,n−t m,nΔxðt ðx |m,n≈t m,n−t m−1,nΔx同理在y方向上有：ðt ðy |m,n≈t m,n+1−t m,nΔyðt ðy |m,n≈t m,n−t m,n−1Δy从而可得：−λðtðx|m,n≈−λt m+1,n−t m,n∆x=ℎ(t f−t m,n)t m,n=t m,n−1−ℎΔxλt f+ℎΔxλt m,n⇒(1−ℎΔxλ)t m,n=t m,n−1−ℎΔxλt f其它式子可类似导出。
传热
d0 2 5m m 0 . 0 2m5 di 2 0m m 0 . 0 2m
整理得
Q KAtm m2Cp 2(t 2 t )1
T t2 '
解得 t2 ' 78.07C 又因为：
m1 ' t 2' t 1 1.36 m1 t 2 t 1 即饱和蒸汽流量变为原来的 1.36 倍。
【例 4-5】【天津大学，1993 年】有一列管式换热器，110℃的饱和水蒸气 在壳程被冷凝为同温度的水，一定流量的某气体在管束内从 30℃加热至 50℃。 现因气体的流量增加，加热蒸汽的压强及气体入口温度均不变，致使气体的出口 温度降至 48℃。换热器的管壁及污垢热阻可忽略，换热器的热损失也可忽略， 气体在管束内均为湍流流动。试求：
m水
mCp(t2
t1 )
0.078kg
Байду номын сангаас
/
s
279.46kg
/
h
（2）由题意，两台换热器串联联使用时，可得：
u ' 2u
Ki ' i '
u( ' 0).8 u
i
6 6 W. 1 6 m2/ (K
)
由
Q
Ki
'
2
Ai
(t2 ' t1) ln T t1
mCp(t2 ' t1) 得，
T t2 '
t2 1 2 1 . 4℃3 由 Q m水 ' mCp(t2 ' t1) 得，
传热学MATLAB温度分布大作业完整版
传热学大作业（第四章）姓名：张宝琪学号：03110608一、题目及要求1.各节点的离散化的代数方程2.源程序3.不同初值时的收敛快慢4.上下边界的热流量（λ=1W/(m℃））5.计算结果的等温线图6.计算小结题目：已知条件如下图所示：二、方程及程序(1)各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 (2)源程序【G-S迭代程序】【方法一】函数文件为：function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为：A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为：function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为：A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746三、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中，本程序应用的收敛条件均为norm(y-x0)>=eps ，即使前后所求误差达到e 的-6次方时，跳出循环得出结果。
传热学数值计算大作业
传热学数值计算大作业传热学是研究物体内部和之间热量传递的科学，其应用范围广泛，例如在工程领域中，传热学的数值计算被广泛用于优化热传递过程，提高能源利用效率。
本文将介绍传热学数值计算的大作业，主要内容包括问题陈述、计算方法和结果分析等。
问题陈述：本次大作业的问题是研究一个热管的热传递特性。
具体来说，热管由内外两个半圆形的金属管组成，内管壁与外管壁之间是一种导热的传热介质。
问题要求计算热管内外壁的温度分布，并分析传热过程的效率和优化热管的设计。
计算方法：计算热传递过程需要运用一些热传导定律和传热方程。
首先，根据Fourier 热传导定律，可得到内外壁的温度梯度。
然后，使用热传导方程来描述热传递过程，其中包括热扩散项和传热源项。
在计算热传导时需要注意材料的热导率、导热介质的热传导性质等参数。
在计算中，可以使用一些数值方法来离散化热传导方程，例如有限差分法、有限元法等。
其中，有限差分法是一种常见的数值方法。
通过将热传导方程中的导数用差分表达式替代，可以将偏微分方程转化为代数方程。
然后，可以使用迭代方法求解代数方程，得到温度分布的数值解。
结果分析：通过数值计算，可以得到热管内外壁的温度分布。
根据温度分布，可以分析热传递过程中的热流分布和传热效果。
例如，可以计算内外壁之间的热传导率，评估热管的热传递效率。
同时，可以对热管的设计进行优化。
例如，可以通过改变热导率高低、加大导热介质的厚度等方式，来提高热传递效果。
此外，对于热管的材料选择和导热介质的设计，还可以进行参数敏感性分析。
通过改变各个参数的数值，可以研究其对热传递过程的影响程度。
这有助于优化热管的设计，并提供一些实际应用方面的建议。
总结：传热学的数值计算是研究热传递现象的重要工具，可以帮助我们深入了解传热过程，优化传热装置的设计。
通过本次大作业，我们可以学习和练习传热学数值计算的方法和技巧，提升对传热现象的理解和分析能力。
希望通过这次大作业，能够更好地应用所学知识，解决实际问题。
《传热学》第四章大作业
《传热学》第四章大作业 ——二维稳态导热问题的数值解法
第一题：
如图所示，一个无限长矩形柱体，其横截面的边长分别为L 1和L 2，常物性。
该问题可视为二维稳态导热问题，边界条件如图中所示，其中L 1=0.6m ，L 2=0.4m ， T w1=60℃，T w2=20℃，λ=200W/(m·K)。
(1) 编写程序求解二维导热方程。
(2) 绘制x =L 1/2和y =L 2/2处的温度场，并与解析解进行比较。
已知矩形内的
温度场的解析解为()()()()1
211w2w1sh sh sin ,L L L y L x t t y x t πππ+=。
第二题
将第一题中y =L 2处的边界条件变为t =t w2，其他条件不变。
(1) 编写程序求解二维导热方程并计算从y =0处导入的热量Φ2。
(2) 当L 2<<L 1时，该二维导热问题可简化为一维导热问题。
在一维的近似下，试计算从y =0处导入的热量Φ1，并比较不同L 2/L 1下Φ2/Φ1的比值。
由该问题的。