维纳滤波(带程序)
完整的维纳滤波器Matlab源程序

subplot(223)
semilogy(t,Py1)
谱图像
title('经过 fir 滤波器后信号在半对数坐标系下频谱图像')
xlabel('x 轴单位:w/rad','color','b')
ylabel('y 轴单位:w/HZ','color','b')
py1n=periodogram(y1n);
%fir 滤波 wp=0.4*pi; ws=0.6*pi; DB=ws-wp; N0=ceil(6.6*pi/DB); M=N0+mod(N0+1,2); wc=(wp+ws)/2/pi; 截止频率(关于 π 归一化) hn=fir1(M,wc); h(n) y1n=filter(hn,1,xn); figure(3) plot(y1n) 图像 title('经过 fir 滤波器后信号图像') xlabel('x 轴单位:f/HZ','color','b') ylabel('y 轴单位:A/V','color','b') y1nmean=mean(y1n) 号均值 y1nms=mean(y1n.^2) 号均方值 y1nvar=var(y1n,1) 方差 Ry1n=xcorr(y1n,Mlag,'biased'); 相关函数 figure(4) subplot(221) plot((-Mlag:Mlag),Ry1n) title('经过 fir 滤波器后信号自相关函数图像')
维纳滤波流程

维纳滤波流程维纳滤波是一种基于图像处理的滤波算法,用于减少图像中的噪声和增强图像的细节。
Wiener filtering is a filtering algorithm based on image processing, used to reduce noise in the image and enhance the details of the image.该算法基于对信号和噪声之间的统计特性进行建模,并利用这些特性来恢复原始的信号。
The algorithm is based on modeling the statistical characteristics between the signal and the noise, and using these characteristics to restore the original signal.维纳滤波常用于医学影像处理、通信系统中的信号处理、雷达系统等领域。
Wiener filtering is commonly used in medical image processing, signal processing in communication systems, radar systems, etc.该滤波器利用信号的功率谱和噪声的功率谱来恢复原始信号,并根据这些谱进行滤波处理。
The filter uses the power spectrum of the signal and the power spectrum of the noise to restore the original signal, and performs filtering based on these spectra.维纳滤波器的主要思想是使信号和噪声之间的功率谱比尽可能保持不变。
The main idea of Wiener filtering is to keep the power spectrum ratio between the signal and the noise as unchanged as possible.理想情况下,维纳滤波器可以最大程度地减少噪声,同时尽可能地保留原始图像的细节。
维纳滤波matlab代码

维纳滤波matlab代码维纳滤波是一种经典的图像复原方法,它可以在图像受到模糊和噪声影响时进行恢复。
在Matlab中,你可以使用以下代码来实现维纳滤波:matlab.% 读取原始图像。
originalImage = imread('input_image.jpg');% 转换为灰度图像。
originalImage = rgb2gray(originalImage);% 显示原始图像。
subplot(1, 2, 1);imshow(originalImage);title('Original Image');% 添加高斯噪声。
noisyImage = imnoise(originalImage, 'gaussian', 0, 0.01);% 显示带噪声的图像。
subplot(1, 2, 2);imshow(noisyImage);title('Noisy Image');% 计算模糊点扩散函数(PSF)。
PSF = fspecial('motion', 21, 11);% 使用逆滤波器和维纳滤波器进行图像复原。
estimated_nsr = 0;wnr3 = deconvwnr(noisyImage, PSF, estimated_nsr);% 显示维纳滤波后的图像。
figure, imshow(wnr3);title('Restored Image using Wiener Filter');在这段代码中,我们首先读取原始图像,然后转换为灰度图像。
接着,我们添加高斯噪声来模拟图像受到的噪声干扰。
然后我们计算模糊点扩散函数(PSF),并使用Matlab内置的`deconvwnr`函数来进行维纳滤波处理。
最后,我们显示经过维纳滤波处理后的图像。
需要注意的是,维纳滤波的参数estimated_nsr需要根据实际情况进行调整,它代表了噪声的方差估计。
wiener滤波程序

基于最小均方误差(MMSE )估计的因果维纳滤波的实现一.功能简介基于最小均方误差(MMSE)估计的因果维纳滤波的Matlab 实现,用莱文森—德宾(Levinson —Durbin)算法求解维纳-霍夫方程(Yule-wa1ker)方程,得到滤波器系数,进行维纳滤波。
二.维纳滤波简介信号处理的实际问题,常常是要解决在噪声中提取信号的问题,因此,我们需要寻找一种所谓有最佳线性过滤特性的滤波器,这种滤波器当信号与噪声同时输入时,在输出端能将信号尽可能精确地重现出来,而噪声却受到最大抑制。
维纳(Wiener )滤波就是用来解决这样一类从噪声中提取信号问题的一种过滤(或滤波)方法.一个线性系统,如果它的单位样本响应为h (n ),当输入一个随机信号x (n ),且)()()(n n s n x υ+=其中s (n )表示信号,)(n υ表示噪声,则输出y (n )为∑-=mm n x m h n y )()()(我们希望x (n )通过线性系统h (n )后得到的y (n )尽量接近于s (n ),因此称y (n )为s (n )的估计值,用)(ˆn s表示,即 )(ˆ)(n sn y =维纳滤波器的输入-输出关系如上图所示。
这个线性系统)(⋅h 称为对于s(n)的一种估计器。
如果我们以ss ˆ与分别表示信号的真值与估计值,而用e (n )表示它们之间的误差,即)(ˆ)()(n sn s n e -= 显然,e (n )可能是正的,也可能是负的,并且它是一个随机变量。
因此,用它的均方值来表达误差是合理的,所谓均方误差最小即它的平方的统计平均值最小:[][]22)ˆ()(ss E n e E -=最小 已知希望输出为:1ˆ()()()()N m y n sn h m x n m -===-∑ 误差为:1ˆ()()()()()()N m e n s n sn s n h m x n m -==-=--∑ 均方误差为:1220()(()()())N m E e n E s n h m x n m -=⎡⎤⎡⎤=--⎢⎥⎣⎦⎣⎦∑ 上式对() m=0,1,,N-1h m 求导得到:102(()()())()00,1,21N opt m E s n h m x n m x n j j N -=⎡⎤---==-⎢⎥⎣⎦∑进一步得:[][]1()()()()()0,1,1N opt m E s n x n j h m E x n m x n j j N -=-=--=-∑从而有:1()()()0,1,2,,1N xs opt xx m R j h m R j m j N -==-=-∑于是就得到N 个线性方程:(0)(0)(0)(1)(1)(1)(1)1(1)(0)(1)(1)(0)(1)(2)1(1)(0)(1)(1)(2)(1)(0)xs xx xx xx xs xx xx xx xs xx xx xx j R h R h R h N R N j R h R h R h N R N j N R N h R N h R N h N R ==+++--⎧⎪==+++--⎪⎨⎪⎪=--=-+-++-⎩写成矩阵形式为:(0)(1)(1)(0)(0)(1)(0)(2)(1)(1)(1)(2)(0)(1)(1)xx xx xx xs xx xx xx xs xx xx xx xs R R R N R h R R R N R h R N R N R R N h N -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦简化形式:xx xs R H R = 其中:H=[h(0) h(1)h(N-1)]'是滤波器的系数[](0),(1),(1)'xs xs xs xs R R R R N =-是互相关序列(0)(1)(1)(1)(0)(2)(1)(2)(0)xx xx xx xxxx xx xx xx xx xx R R R N R R R N R R N R N R -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥--⎣⎦是自相关矩阵由上可见,设计维纳滤波器的过程就是寻求在最小均方误差下滤波器的单位脉冲响应或传递函数的表达式,其实质就是解维纳-霍夫(Wiener -Hopf )方程。
第八章 维纳滤波
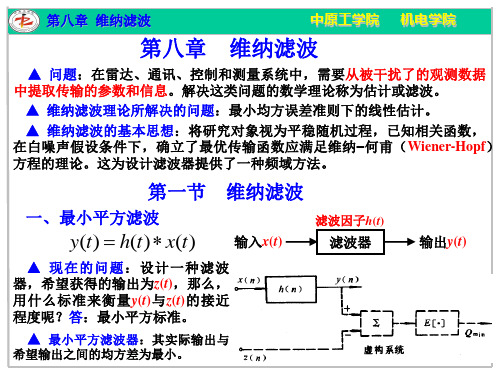
求解此式,可得到最小平方反滤波的滤波因子 h(n) 。然而求 h(n) 值是根据 rpp(i),为了计算rpp(i)就得确切知道干扰系统的冲激响应p(n),这是一个难题。 在许多情况下,希望由x(n)=p(n)*s(n)以及对p(n)的若干特征来寻求p(n)的估计 值。下面给出一种由x(n)计算rpp(i)的近似方法。
n n n n
期望输出s(n)与输入x(n)的互相关函数为
n n
rsx (k ) s(n k ) x(n) s(n k )[s(n) n(n)] rss (k )
如果以 Rss(ejω) 和 Rnn(ejω) 分别表示 rss(k) 和 rnn(k) 的频谱,即分别为 s(n) 和 n(n) 的功率谱,则在对维纳滤波的时间范围不加限制的情况下,由式H(ejω)=Rzs(ejω)/ Rxx(ejω),可以得到维纳滤波器的频率响应应为:
▲ 回声鸣震问题 【例1】
设信号序列为 {s(n)},经过延迟 n0,其一次回声序列为 {rs(n-n0)},二次回声 序列为 {r2s(n-2n0)} ,三次回声序列为 {r3s(n-3n0)} ,等等。其中 r 为反射因子, |r|≤1。滤波器的输入x(n)是信号序列与回声序列的叠加,即
第八章 维纳滤波
Q 0, 0 n N h(n)
x(n) 的 自 相关函数
λ=nT,T 是 采样周期 z(n) 与 x(n) 的 互相关函数
N Q 2[ h(k ) x(n k ) z (n)]x(n h(k ) x(n k ) x(n ) 2 z (n) x(n ) 0
IIR滤波FIR滤波及维纳滤波简介、程序及仿真结果

IIR 滤波器、FIR 滤波器与维纳滤波器所谓数字滤波器,是指输入、输出均为数字信号,通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分的器件。
数字滤波器从实现的网络结构或者从单位脉冲响应分类,可以分为无限脉冲响应(IIR )滤波器和有限脉冲响应(FIR )滤波器。
它们的系统函数分别为:1.1n N n z n h z H --=∑=10)()( 1.21.1中的H(z)成为N 阶IIR 滤波器,1.2中的H(z)称为(N-1)阶FIR 滤波器函数,这两种类型的设计方法有很大的区别。
IIR 数字滤波器的设计既可以从模拟滤波器的设计入手来进行,也可以直接利用指标参数,通过调用滤波器设计子程序或函数来进行。
可以利用脉冲响应不变法来设计IIR 数字低通滤波器,按照技术要求设计一个模拟低通滤波器,得到模拟低通滤波器的传输函数,再按一定的转换关系将传输函数转换成数字低通滤波器的系统函数H(z)。
设模拟滤波器的传输函数是s H a (),相应的单位冲激响应是)(t h a ,对)(t h a 进行等间隔采样,采样间隔为T ,得到)(nT h a ,将h(n)= )(nT h a 作为数字滤波器的单位取样响应,那么数字滤波器的系统函数便是h(n)的z 变换,因此脉冲响应不变法是一种时域上的转换方法,它使h(n)在采样点上等于)(t h a∑=-=Ni iia s s A s H 1)( 1.3 ∑=--=Ni T s iz eA z H i 111)( 1.4 将s H a ()在s 平面上沿虚轴按照周期2pi/T 延括后,再按标准映射关系sT e z =,映射到z 平面上,就得到了H(z)。
脉冲响应不变法的优点是频率坐标变化时线性的,如果不考虑频率混叠现象,用这种方法设计的数字滤波器会很好的重现模拟滤波器的频率特性。
以下为用matlab 仿真的一个IIR 低通滤波器: % IIR Lowpass Use Butterworth % copyright by Etual clear;fs=20;fpass=4;fstop=5;∑∑=-=--=Nk kk Mk k k z a z b z H 101)(Ap=0.5;As=10;wp=2*pi*fpass/fs;ws=2*pi*fstop/fs;omegap=tan(wp/2);omegas=tan(ws/2);ep=sqrt(10^(Ap/10)-1);es=sqrt(10^(As/10)-1);N=ceil(log(es/ep)/log(omegas/omegap));omega0=omegap/ep^(1/N);K=floor(N/2);for i=1:Ktheta(i)=pi*(N-1+2*i)/(2*N);endfor i=1:KG(i)=omega0^2/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka1(i)=2*(omega0^2-1)/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka2(i)=(1+2*omega0*cos(theta(i))+omega0^2)/(1-2*omega0*cos(theta(i))+omeg a0^2);endif K<(N/2)G0=omega0/(omega0+1);a0=(omega0-1)/(omega0+1);endw=0:pi/300:pi;Hw2=1./(1+(tan(w/2)/omega0).^(2*N));plot(w/pi,Hw2);grid;图一IIR滤波器频谱图IIR数字滤波器能保留一些典型模拟滤波器优良的幅度特性,但设计中只考虑了幅度特性,没考虑相位特性,所设计的滤波器相位特性一般是非线性的。
python频域逆滤波和维纳滤波

一、概述Python是一种功能强大的编程语言,可以用于各种领域的科学计算和数据处理。
在信号处理领域,频域逆滤波和维纳滤波是两种常用的技术,用于处理受损信号和去噪。
本文将介绍如何使用Python实现频域逆滤波和维纳滤波,并探讨它们在信号处理中的应用。
二、频域逆滤波1. 概念介绍频域逆滤波是一种用于复原受损信号的技术,它利用信号的频谱信息进行处理。
当信号经过损坏或失真后,可以使用频域逆滤波来尝试恢复原始信号。
2. Python实现在Python中,可以使用`numpy`和`scipy`等库来实现频域逆滤波。
需要获取受损信号的频谱信息,然后根据损坏的模型和系统响应函数,进行逆滤波操作。
通过反变换将处理后的频谱信息还原为时域信号。
3. 应用案例频域逆滤波在医学图像处理、通信系统恢复和地震信号处理等领域有广泛的应用。
通过Python实现频域逆滤波,可以方便地应用于各种实际问题的处理和解决。
三、维纳滤波1. 概念介绍维纳滤波是一种统计信号处理方法,用于在有噪声的环境中对信号进行处理。
它结合了信号的频谱信息和噪声的统计特性,可以实现对受噪声干扰的信号进行有效的去噪处理。
2. Python实现在Python中,可以利用`numpy`和`scipy`等库来实现维纳滤波。
需要获取受噪声信号的频谱信息和噪声的统计特性,然后根据维纳滤波器的设计原理进行滤波处理。
通过反变换将处理后的频谱信息还原为时域信号,以实现信号的去噪处理。
3. 应用案例维纳滤波在语音信号处理、图像去噪和雷达信号处理等领域有着广泛的应用。
通过Python实现维纳滤波,可以实现对受噪声干扰的信号进行有效的去噪处理,提高信号的质量和可靠性。
四、总结频域逆滤波和维纳滤波是两种常用的信号处理技术,在处理受损信号和去噪处理中具有重要的应用价值。
通过Python实现这两种滤波方法,可以方便地进行信号处理实验和应用,为信号处理领域的研究和应用提供了新的工具和方法。
第3讲维纳滤波

第3讲:Wiener 滤波Wiener 滤波器是从统计意义上的最优滤波, 它要求输入信号是宽平稳随机序列, 本章主要集中在FIR 结构的Wiener 滤波器的讨论。
由信号当前值与它的各阶延迟)}1(,),1(),({+--M n u n u n u ,估计一个期望信号)(n d ,输入信号)(n u 是宽平稳的,)(n u 和)(n d 是联合宽平稳的, 要求这个估计的均方误差最小.。
Wiener 滤波器的几个实际应用实例如下: ①通信的信道均衡器。
图1. 信道均衡器的结构示意②系统辨识:图2. 线性系统辨识的结构③一般结构:图3. Wiener 滤波器的一般结构Wiener 滤波器的目的是求最优滤波器系数o w ,使⎥⎦⎤⎢⎣⎡-==22)(ˆ)(]|)([|)(n d n d E n e E n J 最小。
§3.1 从估计理论观点导出Wiener 滤波FIR 结构(也称为横向)的Wiener 滤波器的核心结构如图4所示.图4. 横向Wiener 滤波器为了与第2讲中估计理论一致,假设信号,滤波器权值均为实数由输入)(n u 和它的1至(M-1)阶延迟,估计期望信号)(n d ,确定权系数}1,0,{-=M i w i 使估计误差均方值最小,均方误差定义为:]))(ˆ)([(2n dn d E J -= 这里估计)(ˆn d写为: ∑-=-⋅=10)()(ˆM k k k n u w n d除了现在是波形估计外,与线性Bayesian 估计一一对应。
∑-=⋅=1)(ˆN k kk x a θ∑-=-⋅=10)()(ˆM k k k n u w n dT N a a a ],,[110-= aT N w w w ],,[110-= wT N x x x )]1(),1(),0([-= xT M n u n u n u n )]1(),1(),([)(+--= uθ)(n dxx C R (零均值假设)θx CT M p p p n d n E )]1(),1(),0([)]()([+--=⋅= u P这里)])()([)((n d k n u E k p -=-, Wiener 滤波与线性Bayesian 估计变量之间具有一一对应关系, 设最优滤波器系数为0w ,由线性Bayesian 估计得到Wiener 滤波器系数对应式:p w C =⋅⇒=⋅0R C x xx θa上式后一个方程称为Wiener-Hopf 方程, 或p w ⋅=⇒=--101R C C x xx θa)()()(ˆˆ011n n R n d C C T T xx T x u u ⋅=⋅⋅=⇒⋅⋅=--w p x θθ p p ⋅⋅-=⇒⋅⋅-=--12min 1)ˆ(R J C C C C Bmse T d x xx T x σθθθθθ结论:1) Wiener 滤波器是线性FIR 滤波器中的最优滤波器,但非线性滤波可能会达到更好结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
维纳滤波器的计算机实现专业:信息与通信工程实验一 维纳滤波器的计算机实现一、 实验目的1.MATLAB 编程实现加性干扰信号的维纳滤波。
2.仿真比较实验结果与理论分析结果,分析影响维纳滤波效果的各种因素,从而加深对维纳滤波的理解。
3.利用维纳预测方法实现对AR 模型的参数估计。
二、 实验原理及方法维纳滤波实际上就是在最小均方误差条件下探索和确定滤波器的冲激响应h(n)或系统函数H(z),也就是求解维纳-霍夫方程。
假定一个随机信号x(n)具有以下形式:x (n ) = s (n ) + v (n )其中,s(n)为有用信号,v(n)为噪声干扰,将其输入一个单位脉冲响应为h(n)的线性系统, 则其输出为:()()()()m y n s n h m x n m ∞Λ=-∞==-∑我们希望x (n )在经过系统h(n)后得到y (n ),即s (n )的估计值能尽可能接近s (n ),按照最小均方误差准则,h(n)应满足下面的正则方程:()()()xs xxm k h m k m φφ∞=-∞=-∑其中,()xs k φ是x(n)与s(n)的互相关函数,()xx m φ是x(n)的自相关函数。
在h(n)满足因果性的条件下,,求解维纳-霍夫方程是一个典型的难题。
虽然目前有几种求解h(n)的解析方法,但它们在计算机上实现起来非常困难。
因此,本实验中,利用近似方法,即最佳FIR 维纳滤波方法,在计算机上实现随机信号的维纳滤波。
设h(n)为一因果序列,其长度为N ,则1()()()N m y n h m x n m -==-∑同样利用最小均方误差准则,h(n)满足下面正则方程:xx xs R h r =xx R 为信号x(n)的N 阶自相关矩阵,xs r 为x(n)与s(n)的互相关函数向量。
当xx R 为满秩矩阵时,可得1xx xsh R r -=由此可见,利用有限长的h(n)实现维纳滤波器,只要已知xx R 和xs r 就可以按上式解得满足因果性的h 。
虽然它不同于真正的维纳滤波器,但是只要N 选择的足够大,它就可以很好地逼近真正的维纳滤波器。
利用维纳预测方法来估计AR 模型的参数。
即假定s(n)是一个p 阶AR 模型。
1()(1)()()p s n a s n a s n p w n +-++-=其中w(n)是均值为零,方差等于2w σ的高斯白噪声。
在已知准确自相关函数()ss n φ的情况下,由下面Yule-Walker 方程可以得到AR 模型参数i a (i=1,…p )和2w σ2ss w R A σε=A 为(p+1)╳1 的系数列向量,定义为1[1,,]T p A a a =ε为( p +1)×1的单位列向量,除第一个元素等于1 外,其余元素均为零,即[1,0,0]T ε=三、 仿真结果及分析(1)、L=500,N=10;运行维纳滤波程序得到如下结果:图1 100个是S(n)与X(n)比较图2图3其误差为:不经滤波:The E_xis 0.98152理伦滤波:The E_I is 0.77672维纳滤波:The E_R is 0.809841、通过比较图1与图3可以看出在滤波后,估计值更近似等于S(n),其数据点围绕s(n)的曲线做很小的扰动,其值在s(n)的上下波动。
2、因为只用了有限个数据S(n)和X(n) 来求自相关函数和互相关函数,由此得到的估计值不精确,从而带来了实验误差。
(2)、固定L=500,N=3与N=20的比较结果如下:N=3 N=20N=3 N=20N=3 N=20N=3 N=20分析比较可发现,L=500固定不变,N值越大,误差越小,滤波后的信号更加接近原来的信号,即滤波效果得到改善。
(3)、固定N=10,L=200与L=1000比较:L=200 L=1000L=200 L=1000L=200 L=1000L=200 L=1000当N保持不变,而将数据长度L从200增大到1000,可以发现,均方误差都有增大,而且h(n)其理论值与实验值的差别也变大,这说明单方面增加数据长度将会降低滤波效果。
(4)、AR模型参数估计:1、P=2,a=[0.5,0.6],sigma2=1,L=5002、P=2,a=[0.5,0.6],sigma2=1,L=50从上述两幅图中可以看出样本个数L取的越多对参数a及噪声功率估计的越准确。
(5)、程序代码:维纳滤波:clear;L=input('Please input the value of L: L=');N=input('Please input the value of N: N=');a=0.95;w(1)=0;w=rand(1,L);w=w-mean(w)*ones(1,L);w=w*sqrt(12*(1-a^2));s(1)=1;for n1=2:Ls(n1)=a*s(n1-1)+w(n1-1);endv=rand(1,L);v=v-mean(v)*ones(1,L);v=v*12^(1/2);for n2=1:Lx(n2)=s(n2)+v(n2);endm=100;j=(L-m+1):1:L;sj=s((L-m+1):1:L);xj=x((L-m+1):1:L);figure(1)exp=zeros(1,m);plot(j,sj,'or',j,xj,'*b',j,exp,'-.k');title('100 samples of s(n) and x(n)');xlabel('variable i');ylabel('s(i) and x(i)');legend('s(i)','x(i)');figure(2)PHIxx=xcorr(x,x,'unbiased');PHIxx=PHIxx(L:(L+m-1));Rxx=toeplitz(PHIxx);PHIxs=xcorr(x,s,'unbiased');rxs=PHIxs(L:(L+m-1));inv_Rxx=inv(Rxx);rxs=rxs';h=inv_Rxx*rxs;h=h';for mm=0:(m-1)hd(mm+1)=0.238*(0.724)^mm;endi=0:(m-1);plot(i,h,'or',i,hd,'xb');title('估计h(n)与理想hd(n)比较');xlabel('数值i');ylabel('h(i) and hd(i)');legend('h(i)','hd(i)');grid on;EST_sI=circonv(hd,x,L);EST_sIj=EST_sI((L-m+1):1:L);figure(3)subplot(211)plot(j,sj,'.:r',j,EST_sIj,'x-b');title('真实值s(n)与通过理想滤波器估计值s(n)的比较'); xlabel('数值i');ylabel('s(i)与EST_sI(i)');legend('s(i)','EST_sI(i)');grid on;subplot(212)EST_s=circonv(h,x,L);EST_sj=EST_s((L-m+1):1:L);plot(j,sj,'.:r',j,EST_sj,'+-g');title('真实值s(n) and通过维纳滤波器估计值s(n)的比较'); xlabel('数值i');ylabel('s(i)与EST_s(i)');legend('s(i)','EST_s(i)');grid on;E_x=sum((x-s).^2)/L;E_I=sum((x-EST_sI).^2)/L;E_R=sum((x-EST_s).^2)/L;fprintf('The E_x is %8.5f\n',E_x);fprintf('The E_I is %8.5f\n',E_I);fprintf('The E_R is %8.5f\n',E_R);function y=circonv(x,h,N)x=[x,zeros(1,N-length(x))];h=[h,zeros(1,N-length(h))];m = [0:N-1];hm = h(mod(-m,N)+1);H = toeplitz(hm,[0,h(2:N)]);y = x*H;AR模型:clear;order=input('请输入模型阶数:P=');a=input('请输入系数变量:a=');if ~(order==length(a))dips('the length of coefficients vector should be equal to order!') endvar=input('请输入噪声功率:var=');L=input('请输入样本个数:L=');s=est_AR(order,a,var,L);PHIss=xcorr(s,s,'unbiased');PHIssp=PHIss(L:(L+order));Rss=toeplitz(PHIssp);Rss_l=Rss((2:order+1),(2:(order+1)));Rss_r=Rss((2:order+1),1);Rss_r=(-1)*Rss_r;est_a=inv(Rss_l)*Rss_r;est_var=Rss(1,:)*[1;est_a];est_a=est_a';est_var=est_var';fprintf('\n');fprintf('结果如下:\n');fprintf('a的估计值为: %8.5f\n',est_a);E_a=((a-est_a).^2)/order;fprintf('误差为: %8.5f\n',E_a);fprintf('\n');fprintf('白噪声功率估计为: %8.5f\n',est_var);E_var=sum(var-est_var).^2;fprintf('误差为: %8.5f\n',E_var);function s=est_AR(order,a,var,L)order=2;var=1;L=500;a=[0.5,0.6];a=a';w=randn(1,L);w=w*(var^(1/2));for n1=1:orders(n1)=w(n1);endfor n2=(n1+1):Lsj=[s(n2-1),s(n2-order)]; s(n2)=(-1)*(sj*a)+w(n2); endend。
