用法向量求二面角的大小
用法向量确定二面角大小的三个基本关系

用法向量确定二面角大小的三个基本关系作者:程映军来源:《甘肃教育》2012年第23期〔关键词〕数学教学;法向量;二面角;符号;方向;相关关系〔中图分类号〕 G633.65 〔文献标识码〕 A〔文章编号〕 1004—0463(2012)23—0082—02求二面角平面角的问题在传统立体几何中解决的方法较多,这也是高考的一个重要内容,但新教材对此问题有所淡化,只要求学生能用平面法向量求出二面角平面角的大小.而两个法向量的夹角与二面角的平面角到底何时相等?何时互补?教材中处理得比较含糊,要求借助于图形直观解决,实际上此法可操作性并不大,因此,到了这个部分便常常出现“老师想讲讲不清,学生能学学不透”的尴尬局面.那么,如何在判断方法上兼顾理论依据的正确性和事件操作的可行性、简捷性呢?笔者认为,只要认识清楚以下三个基本关系,我们并不需要借助其他理论工具,就能快速解决这一问题.一、空间向量坐标的符号与向量方向的关系一个向量的坐标并不是刻画这个向量在空间直角坐标系O-xyz中的具体位置,而是刻画向量相对于标准正交基[i][➝]=(1,0,0),[j][➝]=(0,1,0),[k][➝]=(0,0,1)的“分解程度”.如,将向量[m][➝]=(x,y,z)分解,则此向量在x轴、y轴、z轴上的分向量依次是=(x,0,0)=x[i][➝],=(0,y,0)=y[j][➝],=(0,0,z)=z[k][➝],从而x,y,z的正负直接反映这三个分向量与对应的基底是同向还是反向,如下表:二、平面法向量的横、纵、竖之间的相关关系平面α的法向量的坐标之间构成正比例关系.证明:设A0(x0,y0,z0),A1(x1,y1,z1),A2(x2,y2,z2)是平面α上任意三个不共线的点,[m][➝]=(x,y,z)是平面α的法向量,则[m][➝]⊥[m][➝]⊥⇒[m][➝]·=0[m][➝]·=0⇒x(x1-x0)+y(y1-y0)+z(z1-z0)=0x(x2-x0)+y(y2-y0)+z(z2-z0)=0 ,解得y=-x,z=-xy1-y0 z1-z0y2-y0 z2-z0 ≠0. 记λ1=-,μ1=-,则[m][➝]=(x,λ1x,μ1x)=x(1,λ1,μ1);同理,λ2=-,μ2=-x1-x0 z1-z0x2-x0 z2-z0 ≠0,则[m][➝]=(λ2y,y,μ2y)=y(λ2,1,μ2);令λ3=-,μ3=-x1-x0 y1-y0x2-x0 y2-y0 ≠0,则[m][➝]=(λ3z,μ3z,z)=z(λ3,μ3,1).这说明,由A0,A1,A2三点唯一确定的平面α,其法向量可以由x(或y,z)唯一确定.三、二面角的大小与两个法向量相对指向的关系定义1:以l为棱的两个半平面α,β把空间分成两部分,其中使二面角α-l-β的平面角θ∈(0,π)的部分称为二面角的内部,另一部分则称为二面角的外部.定义2:以平面α上任意一个不属于棱的点为起点作该平面的法向量,如果这个法向量的终点总是落在二面角α-l-β的外部,则称该法向量指向二面角α-l-β的外部,反之,称该法向量指向二面角α-l-β的内部.有以下事实:①当α,β的法向量[m][➝],[n][➝]同时指向二面角α-l-β的内部(或外部)时,角与二面角α-l-β互为补角(图1).②当α,β的法向量[m][➝],[n][➝]一个指向二面角α-l-β的内部,另一个指向二面角α-l-β的外部时,角与二面角α-l-β大小相等(图2).对于以上三个基本关系的阐述和证明,我们可以看到,要解决提出的问题,关键是要判断两个法向量的相对方向.而由于平面法向量的方向可以通过点坐标的行列式运算化归为一元线性表达式,所以我们只需要判断出平面法向量的任意一个坐标的符号,就可以确定法向量的相对方向,从而判断出两个法向量夹角与二面角的大小关系,实现整个问题的求解.以下举例说明该方法的具体实施过程.例1:如图3,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边△AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;(2)求点A到平面VBC的距离;(3)求二面角A-VB-C的大小.解析:(1)(2)略.(3)取AC中点O,连接B1O,易知OB1⊥底面ABC,过O作直线OE∥BC交AB于E.取O为空间直角坐标系的原点,以OE,OC,OB1所在直线分别为x轴,y轴,z轴建立如图4所示的空间直角坐标系.则A(0,-a,0),B(a,a,0),C(0,a,0),B1(0,0,a).设平面VBC的一个法向量[n][➝]=(x1,y1,z1),由[n][➝]⊥[n][➝]⊥得-ax1=0-ay1+az1=0,取z1=1,得[n][➝]=(0,,1),此时法向量[n][➝]指向二面角A-VB-C的外侧.同理可得平面VAB的一个法向量[m][➝]=(2,-,1),此时,法向量[m][➝]指向二面角A-VB-C的内侧.∴cos==-.所以,二面角A-VB-C的大小为arccos-.例2:在正方体中,二面角的大小为 .解:如图5,A1C1⊥面BB1D1,A1D⊥面BAD1,所以直线A1C,A1D的方向向量分别为BB1D1和BAD1的法向量,分别令[n1][➝]=,[n2][➝]=,设正方形的边长为1,建立如图所示的空间直角坐标系,则A1(0,1,1), C1(-1,0,1),D1(-1,-1,0).∴ =(-1,-1,0), ||= , =(-1,-2,-1),||=, ·=3.∴cos==.即向量,的夹角为30°,由于,的指向都是向着二面角外,所以二面角A-BD1-B1与向量,的夹角互补,所以二面角A-BD1-B1的大小为150°.。
求二面角的六种方法

求二面角的六种方法求解二面角是空间几何学中常见的问题,它在多个领域如物理学、化学和工程学中都有广泛的应用。
本文将介绍六种求解二面角的方法,包括向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
一、向量法向量法是一种简便的求解二面角的方法。
它利用向量的夹角来表示二面角。
首先,我们需要确定两个平面的法向量,然后计算它们之间的夹角。
通过向量的点积和模长运算,可以得到二面角的大小。
二、坐标法坐标法是一种常用的求解二面角的方法。
它利用坐标系中的点来表示二面角。
我们可以通过给定的坐标点,计算两个平面的法向量,然后利用向量夹角的公式求解二面角。
三、三角法三角法是一种基于三角函数的求解二面角的方法。
它利用三角函数的性质来计算二面角的大小。
通过已知的边长和角度,可以利用正弦定理、余弦定理等公式求解二面角。
四、平面几何法平面几何法是一种利用平面几何关系求解二面角的方法。
它通过已知的平面形状和角度关系,利用平面几何的知识来求解二面角的大小。
例如,可以利用平行线的性质、垂直线的性质等来计算二面角。
五、球面几何法球面几何法是一种利用球面几何关系求解二面角的方法。
它通过已知的球面形状和角度关系,利用球面几何的知识来求解二面角的大小。
例如,可以利用球面上的弧长、球面上的角度等来计算二面角。
六、投影法投影法是一种利用投影关系求解二面角的方法。
它通过已知的投影长度和角度关系,利用投影几何的知识来求解二面角的大小。
例如,可以利用平面上的投影线段、平面上的角度等来计算二面角。
通过以上六种方法,我们可以灵活地求解二面角的大小。
不同的问题和场景可能适用不同的方法,我们可以根据具体情况选择合适的方法来解决问题。
这些方法在实际应用中具有重要的意义,能够帮助我们更好地理解和解决相关问题。
总结起来,求解二面角的六种方法分别是向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
每种方法都有其特点和适用场景,我们可以根据具体问题选择合适的方法来求解二面角。
法向量求二面角-空间向量

精选版ppt
14
利用法向量求二面角利用法向量求二面角如果n那么向量n叫做平面的法向量直线与平面所成的角等于平面的法向量所在的直线与已知直线的夹角的余2利用平面法向量求二面角的大小求二面角的大小先求出两个半平面的法向量的夹角然后根据二面角与其大小相等或互补求出二面角的大小指入指出平面的法向量的夹角的大小就是二面角的大小
C1
A1
B1 E
精选版ppt
C A
D
12
B
2.(广州二模)如图,P A 平 面 A B C , B A C 9 0 0 D,E,F分别是AB,BC,CP的中点,AB=AC =1,PA=2.(1)求直线PA和平面DEF所成的 角的大小; (2)求点P到平面DEF的距离。
P
F
A
C
D
精选版ppt
E
13
B
小结: 1、本节主要复习了法向量在求线面角和二面 角方面的应用,注意所求角与法向量的联系, 掌握基本的思想方法。
2、立体几何问题求解的思想方法的发展趋势
用代数的方法解决立体几何问题是立体几何的发 展趋势,而向量是用代数的方法解决立体几何问 题的主要工具,故,学会用向量法解立体几何问 题是学好立体几何的基础。
cos<ED,n>=1/4<ED,n>=arccos(1/4) 二面角D-BA-C的大小为arccos(1/4)
精选版ppt
例 10
例2.在四面体 ABCD中 ,AB⊥ 面 BCD,
BC=CD,∠BCD=9 0 0,∠ADB= 3 0 0 .E、F
分别是AC、AD的中点。 1)求证 平面BEF⊥平面ABC;
F(1,2,0) E A1
(2,1,2) N
(1,2,2) 则
向量法求二面角大小洋葱数学

向量法求二面角大小洋葱数学【原创实用版】目录一、引言二、向量法求二面角大小的基本原理1.求出所求二面角两个面上的法向量2.计算 cos(法向量 1 法向量 2)/(法向量 1 的模长法向量 2 的模长)3.根据图形判断是锐二面角还是钝二面角4.确定 cos 的符号5.用反三角函数表示这个角三、结论正文一、引言在数学中,二面角是指两个平面之间的夹角,它是一个非常重要的概念。
在实际应用中,求解二面角大小有着广泛的应用,而向量法是求解二面角大小的一种常用方法。
本文将从向量法的角度出发,详细介绍如何求解二面角大小。
二、向量法求二面角大小的基本原理1.求出所求二面角两个面上的法向量在求解二面角大小时,首先需要找到两个平面上的法向量。
法向量是垂直于平面的向量,它可以通过计算平面上两个向量的叉积得到。
假设平面 1 的法向量为 A,平面 2 的法向量为 B,则可以通过计算向量 A 和向量 B 的叉积得到法向量 C。
2.计算 cos(法向量 1 法向量 2)/(法向量 1 的模长法向量 2 的模长)接下来,需要计算二面角大小所对应的 cos 值。
根据向量内积的定义,可以得到 cos(法向量 1 法向量 2)=(法向量 1·法向量 2)/(法向量 1 的模长*法向量 2 的模长)。
其中,法向量 1·法向量 2 表示法向量 1 和法向量 2 的内积,法向量 1 的模长和法向量 2 的模长分别表示它们的模长。
3.根据图形判断是锐二面角还是钝二面角在计算出 cos 值后,需要根据图形来判断这个二面角是锐二面角还是钝二面角。
如果 cos 值为正,那么这个二面角就是锐二面角;如果 cos 值为负,那么这个二面角就是钝二面角。
4.确定 cos 的符号在计算 cos 值时,需要注意 cos 值的符号。
如果法向量 1 和法向量 2 的内积为正,那么 cos 值为正;如果内积为负,那么 cos 值为负。
在实际计算中,需要根据具体情况来确定 cos 值的符号。
高中数学求二面角技巧

高中数学求二面角技巧
高中数学中,求解二面角是一项重要的技巧。
二面角是指两个平面相交而形成的角度,常常出现在几何题目中。
以下是一些求解二面角的技巧:
1. 使用向量法求解二面角
向量法是求解二面角的常用方法。
假设有两个平面AB和CD,且它们相交于一条直线EF。
设向量AB=n,向量CD=m,向量EF=a,则二面角θ的余弦值为:
cosθ=(n·m)/( |n|·|m| )
其中,n·m表示n和m的数量积,|n|和|m|表示向量n和向量m 的模长。
2. 利用三角函数求解二面角
如果已知二面角的两个面的斜率,可以使用三角函数求解二面角。
设两个平面的斜率分别为k1和k2,则二面角的正切值为:
tanθ=(k1-k2)/(1+k1k2)
可以使用反正切函数求解出二面角的值。
3. 利用平面几何知识求解二面角
通过平面几何知识,可以求解出两个平面的交线与一个球面的交线,从而求解二面角。
设两个平面在点O处相交,交线为AB和CD,球心为O,球面与交线AB和CD的交点分别为P和Q,则二面角θ等
于∠POQ。
以上是求解二面角的一些常用技巧,希望对高中数学学习有所帮
助。
用法向量求二面角的大小
解:建立如图空间直角坐标系,
A(2,0,0), C(0,2,0)B( 2,2,0) , E(0,1,1)
解:建立如图空间直角坐标系, D(0,0,0), B( 2,2,0),C(0,2,0), E(0, 2,1),A1(2,0,4)求得平面BDE的法 向量 n1(1,-1,2) ,平面A1DE 的法向量 n2(4,1,2)
cosn1,n2|n n1 1||n n2 2|-4 1 2 4
取内部向量 A 1B(0,2,4)
精选课件
19
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
精选课件
15
练习题2
如图,底面为直角梯形的四棱锥S-ABCD中,AD||BC, ∠ABC=900,SA⊥面ABCD,SA=AD=1, AB=BC=2 ,求侧面 SCD与面SBA所成的二面角的余弦值;
精选课件
16
练习题2
如图,底面为直角梯形的四棱锥S-ABCD中,AD||BC, ∠ABC=900,SA⊥面ABCD,SA=AD=1, AB=BC=2 ,求侧面 SCD与面SBA所成的二面角的余弦值;
为内部向量。
精选课件
12
内部向量MN判定法
MNn1 0 MNn2 0
异 号 互 补
MNn1 0 MNn2 0
精选课件
MNn1 0 MNn2 0
同 号 相 等
MNn1 0 MNn2 0
13
法向量求二面角大小的又一个简单判定方法

法向量求二面角大小的又一个简单判定方法红 岩求二面角大小问题是高考重点考察内容,法向量法是求二面角大小的一种主要方法。
我们知道:二面角大小与其两个平面的法向量夹角相等或互补。
但到底是相等还是互补,教学中很多师生采用直观判断;参考资料涉及此问题也回避不谈,文【1】(数学通讯2013教师版2)给出了一种很好的判定方法,本文给出另一种更为简单的判定方法。
一.判定方法引理:设点A 、B 分别是平面α内、外的点,→n 是平面α的法向量,当→→∙n AB >0 则→n 的方向向上。
(如图) 当→→∙n AB <0 则→n 的方向向下。
(如图)定理:一个起点、终点在不同平面上的向量,分别与这两个平面法向量的数量积,若数量积的符号相同,则这两个平面二面角的大小等于其法向量夹角的大小;若数量积的符号相反,则这两个平面二面角的大小与其法向量夹角的大小互补。
结论可记为“相同相等,相反互补”,或“同等异补”。
已知:设A 、B 分别是βα,上的点,且两点都不在平面βα,交线上(若两点中有在平面βα,交线上,则(→→∙n AB )(→→∙m AB )≠0), →n 、→m 分别是βα,的法向量,θ为平面βα,的平面角。
证明:若(→→∙n AB )(→→∙m AB )>0, 则θ=mn mn∙arccos ;若(→→∙n AB )(→→∙m AB )<0, 则θ=π-mn mn ∙arccos 。
证明:⑴当→→∙n AB >0,→→∙m AB >0,根据引理,得→n 、→m 的方向如图。
βα,的平面角等于→n 、→m 的夹角,∴θ=mn mn ∙arccos⑵当→→∙n AB <0,→→∙m AB <0, 根据引理得→n 、→m 的方向如图。
βα,的平面角等于→n 、→m 的夹角,∴θ=mn mn ∙arccos⑶当→→∙n AB >0,→→∙m AB <0, 根据引理得→n 、→m 的方向如图。
向量法-求二面角大小

空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
① 建立空间直角坐标系; ② 求出所需各点的坐标; ③ 求出两个平面的法向量; ④ 求出两个法向量的夹角; ⑤ 写出所求二面角的大小。
空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
P
M
A
D
B
NC
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
∴ cosq =
6
3
得 tanq =
2
2
∴
所求面SCD与面SBA所成二面角的正切值是22
【练习2】 已知点E、F分别是正方体ABCD-A1B1C1D1的棱BB1、 CC1上的点, 且 BE1=2EB, CF=2FC1 .
(1) 求面AEF与面ABC所成二面角的正切值 .
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
=
3 3
由条件知,二面角A-CD-E为锐角,∴
所求二面角的余弦值为
3 3
【练习1】 如下图, 在底面是直角梯形的四棱锥S-ABCD中,
∠ABC=90O
,
SA⊥面ABCD,SA=AB=BC=1,
AD=
1 2
.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
课堂小结 1、弄清楚两法向量的夹角与二面角的关系。 2、利用内部向量判定二面角的大小。 3、用法向量求二面角大小的一般步骤。 4、感知空间中点、线、面在运动过程中的位 置关系的变化,及空间想象能力的培养。 5、分析、归纳问题的能力。
课后作业
教材112页,A组第6题. B组第2,3题.
根据观察,二面角为………。
齐相国老师刊登在《数学通讯》2009年第4期的《法向量 求二面角时法向量方向的判定法》。 李峰老师发表在《数学通讯》2010年第9期的《对“法向 量求二面角时法向量方向的判定方法”一文的改进 》
内部向量MN判定法
规定:如图,分别在半平面 α,β内各取一点 M,N(不在棱上取),我们称 MN (与法向量不共线) 为内部向量。
n1 n2 14 cos n1 , n2 42 | n1 || n2 |
A1 B (0, 2, 4) 取内部向量 A1 B n1 -10 0, A1 B n2 10 0
故二面角A1-DE-B的余弦值为 14 .
42
用法向量求二面角的大小的一般步骤:
1、建立空间直角坐标系,写出点的坐标。
2、求出两半平面的法向量,并求出其夹角。
3、用观察法,确定二面角的大小。或取内部向量 (同号相等,异号互补),判定二面角的大小。 4、下结论。
练习题2
如图,底面为直角梯形的四棱锥S-ABCD中,AD||BC, ∠ABC=900,SA⊥面ABCD,SA=AD=1, AB=BC=2 ,求侧面 SCD与面SBA所成的二面角的余弦值;
内部向量MN判定法
MN n1 0 MN n2 0 MN n1 0 MN n2 0
异 号 互 补
MN n1 0 MN n2 0
同 号 相 等
练习题2
如图,底面为直角梯形的四棱锥S-ABCD中,AD||BC, ∠ABC=900,SA⊥面ABCD,SA=AD=1, AB=BC=2 ,求侧面 SCD与面SBA所成的二面角的余弦值; 解:建立如图空间直角坐标系, A(0,0,0), B( 0,2,0),C(2,2,0), D(1, 0,0),S(0,0,1) 易知平面SAB的法 向量 AD (1,0,0) ,求出平面 SDC的法向量 n (2, 1,2)
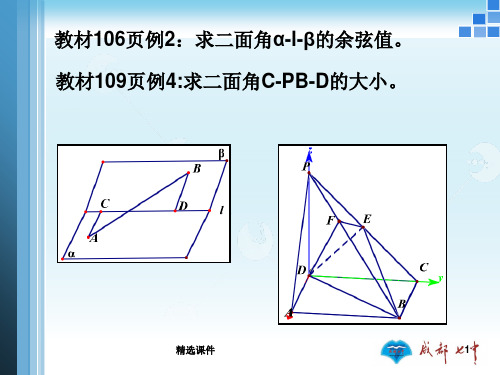
教材106页例2:求二面角α-l-β的余弦值。
教材109页例4:求二面角C-PB-D的大小。
改编教材109页 例4
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. (1)求证:PA||平面EDB; (2)求证:PB⊥平面EFD; (3)(改)求二面角F-BD-E的余弦值;
n1 n2 14 cos n1 , n2 42 | n1 || n2 |
解:建立如图空间直角坐标系, D(0,0,0), B( 2,2,0),C(0,2,0), E(0,2,1),A1(2,0,4) n1 (1, -1, 2) 平面BDE的法向量 平面A1DE的法向量 n2 (4,1, 2)
MN n1 0 MN n2 0
练习题1
如图,正四棱柱ABCD-A1B1C1D1中,A1A=2AB=4,点E在CC1 上,且C1E=3EC.求二面角A1-DE-B的余弦值; 解:建立如图空间直角坐标系, D(0,0,0), B( 2,2,0),C(0,2,0), E(0, 2,1),A1(2,0,4) 求得平面BDE的法 -1, 2) ,平面A1DE 向量 n1 (1, 的法向量 n2 (4,1, 2)
3
判断互补还是相等的简单的方法 是:观察二面角的大小来判定.
练习题1
如图,正四棱柱ABCD-A1B1C1D1中,A1A=4,AB=2,点E在 CC1上,且C1E=3EC.求二面角A1-DE-B的余弦值;
练习题1
如图,正四棱柱ABCD-A1B1C1D1中,A1A=2AB=4,点E在CC1 上,且C1E=3EC.求二面角A1-DE-B的余弦值;
n DE y z 0 n (1, 1,1) y0 n DB 2 x 2 AC n 6 cos AC , n 3 | AC || n |
根据观察,二面角为锐二面角, 故二面角F-BD-E的余弦值为 6 .
用法向量求二面角的大小
成都七中高新校区 康盛
两半平面的法向量与二面角有怎样的关系?
根据上图,分小组进行讨论---“两法向 量的夹角与二面角的关系.”
两法向量的夹角与二面角的关系
θ =π- φ 互补
θ= φ 相等
如何判别互补还是相等?
根据教材109页例4改编
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. (1)求证:PA||平面EDB; (2)求证:PB⊥平面EFD; (3)(改)求二面角F-BD-E的余弦值; 解:建立如图空间直角坐标系, A(2,0,0), C(0,2,0)B( 2,2,0) , E(0,1,1) AC (2,2,0) 易得平面BDF的法向量 设平面 BDE的法向量 n ( x, y, z)
