对称分量法
对称分量法公式

对称分量法公式摘要:一、对称分量法简介1.对称分量法的概念2.应用背景二、对称分量法公式推导1.基本概念与定义2.公式推导过程三、对称分量法的应用1.在电力系统中的应用2.在其他领域的应用四、对称分量法的优缺点1.优点2.缺点五、结论正文:对称分量法是一种分析电气工程、信号处理等领域中复杂系统的方法,通过分解系统中的对称分量,简化问题,从而更好地理解和处理问题。
对称分量法广泛应用于电力系统的故障分析、保护装置设计和运行控制等领域。
1.对称分量法的概念对称分量法是将复杂系统中各变量分解为正、负、零三个对称分量。
正分量表示变量在正序方向上的分量,负分量表示变量在负序方向上的分量,零分量表示变量在零序方向上的分量。
通过分解对称分量,可以简化系统模型,便于分析和处理问题。
2.应用背景对称分量法主要应用于电力系统,包括发电、输电、配电和用电等环节。
在电力系统中,对称分量法可以帮助分析系统中的不对称故障,如两相或三相短路等,并为保护装置的设计和运行提供依据。
此外,对称分量法还应用于信号处理、自动控制、通信等领域。
3.对称分量法公式推导对称分量法的公式推导主要包括基本概念与定义以及公式推导过程。
首先,根据系统中的变量和其正、负、零序分量的关系,可以得到对称分量法的定义。
然后,通过对称分量法的定义,推导出各个分量的计算公式。
4.对称分量法的应用对称分量法在电力系统中的应用主要包括故障分析、保护装置设计和运行控制等。
在故障分析中,通过计算系统中的对称分量,可以判断故障的类型和位置。
在保护装置设计中,根据系统中的对称分量,可以设计出合适的保护装置。
在运行控制中,通过对称分量法,可以实现对电力系统的实时监控和控制。
5.对称分量法的优缺点对称分量法的优点在于能够简化复杂系统的分析过程,便于理解和处理问题。
然而,对称分量法也存在一定的缺点,如在实际应用中,可能需要根据具体情况对对称分量法进行修正。
对称分量法的内容

对称分量法一、什么是对称分量法对称分量法(Symmetrical Component Method,简称SCM)是一种用于解决三相电力系统中不平衡故障问题的分析方法。
在电力系统中,由于各种原因(例如电力负载变化、设备故障等),电源产生的三相电流和电压可能会失去平衡,从而引发各种故障。
对称分量法通过将不平衡信号分解为对称和非对称分量,可以准确地计算电力系统中发生的不平衡故障。
二、对称分量法的基本原理2.1 对称分量的定义在对称分量法中,将三相电源的电压和电流分解为正序、负序和零序三个互相独立的分量。
正序分量表示电压和电流的幅值和相位全都相同,负序分量表示电压和电流的幅值相同但相位互差120度,零序分量表示电压和电流的幅值都为零。
2.2 不平衡故障的分析利用对称分量法,可以将不平衡故障分解为正序、负序和零序三个分量。
通过分析这三个分量在电力系统中的传输和变化,可以准确地确定故障的发生位置和类型。
2.3 对称分量的计算方法对称分量的计算主要基于对称分量正负序的定义和性质。
对于三相对称装置,其中包括电源和电路中没有接地的中性点,正序分量可以通过直接测量获得;负序分量可以通过将三相电流线电压和120度相位互差的关系应用于电压计算得到;零序分量可以通过将三相电压和电流进行相加、平均得到。
三、对称分量法的应用3.1 故障分析与检测对称分量法广泛应用于电力系统中不平衡故障的分析与检测。
通过分析电力系统中各个节点的对称分量,可以判断故障的类型、发生位置以及对系统的影响程度。
这对于保护装置的及时动作以及减小故障对电力系统的影响具有重要意义。
3.2 故障定位与隔离利用对称分量法,可以准确地定位和隔离电力系统中的故障。
通过分析故障点处不同分量的幅值和相位变化,可以确定故障的位置,并采取相应的措施进行隔离和修复。
这可以减少故障造成的停电时间和电力系统的恢复成本。
3.3 电力系统设计和优化对称分量法对于电力系统的设计和优化也具有重要意义。
对称分量法

对称分量法对称分量法是一种强大的数学工具,它可以用来解决各种数学问题,既可以解决大型线性方程组也可以解决高阶非线性方程组。
它的历史可以追溯到古希腊时期,但它的最初形式可以追溯到17世纪的苏格兰数学家詹姆斯拉瓦锡(James Gregory)和英格兰数学家伯纳德罗比(Bernard Robins)。
这种方法的基本思想是用一组标准的的符号,可以用来表示不同的数学结构,这样就可以用不同的语言来解释不同的数学模型。
基本上就是找到一组可以表示和解释不同物理或数学结构的符号。
在一维空间中,只需要表示一个结构,在多维空间中,就需要多个符号来表示。
对称分量法的优点是可以用简单的符号语言来描述各种复杂的几何结构,它可以将模型简化,使其易于推理和理解。
由于它可以通过几何结构定义来表示不同的数学模型,因此它可以用来研究各种大型系统,包括力学、热力学和流体力学等,从而更好地描述和分析它们。
同时,对称分量法也可以用来解决更简单的问题,比如最优化问题和矩阵方程组。
它可以根据解的精度来改变相应的迭代阶数,从而获得最佳的解。
例如,可以用来解决高阶多项式的求根问题,也可以用来解决线性规划问题,这是由于它可以根据精度改变迭代步骤,这样可以使解更具有准确性。
另外,对称分量法也可以提供一种更有效的数值计算方法。
通过它可以实现更快的计算速度,因此可以解决更复杂的问题,比如解决多维的线性或非线性方程组。
总之,对称分量法是一种强大的数学工具,它可以用来解决各种复杂的数学问题,包括大型线性方程组、非线性方程组和最优化问题等。
它可以通过几何结构定义将复杂的模型简化,从而使模型易于推理和理解,并使计算更加高效。
此外,由于它可以根据解的精度来改变迭代步骤,因此可以提供有效的数值计算方法。
因此,对称分量法在许多领域都具有重要的理论意义和应用价值。
对称分量法公式

对称分量法公式摘要:一、对称分量法简介1.对称分量法的概念2.对称分量法在工程中的应用二、对称分量法公式推导1.基本电路分析2.对称分量法的推导过程3.对称分量法公式三、对称分量法应用实例1.三相电路分析2.发电机和变压器分析3.其他应用场景四、对称分量法的优缺点1.优点2.缺点正文:一、对称分量法简介对称分量法是一种电路分析方法,主要用于解决不对称三相电路的问题。
该方法将三相电路分解为三个独立的单相电路,通过对每个单相电路的分析,可以得到三相电路中各相的电流和电压。
对称分量法广泛应用于电力系统、自动化控制等领域。
二、对称分量法公式推导1.基本电路分析首先,我们分析一个简单的不对称三相电路,包含三个相电压U1、U2、U3 和一个中性线N。
我们用矢量表示电压和电流:U1、U2、U3 和I1、I2、I3。
2.对称分量法的推导过程为了方便分析,我们将电压和电流分解为正序和负序两个分量。
正序分量表示三相电压和电流的平衡部分,负序分量表示三相电压和电流的不平衡部分。
正序分量和负序分量的关系如下:U1p = U1 + U2 + U3I1p = I1 + I2 + I3U1n = U1 - U2 - U3I1n = I1 - I2 - I3其中,U1p、I1p 表示正序分量的电压和电流,U1n、I1n 表示负序分量的电压和电流。
3.对称分量法公式根据对称分量法,我们可以得到以下公式:U1p = U1 + jU2 + jU3I1p = I1 + jI2 + jI3U1n = U1 - jU2 - jU3I1n = I1 - jI2 - jI3其中,j 表示虚数单位。
三、对称分量法应用实例1.三相电路分析通过对称分量法,我们可以将复杂的不对称三相电路分解为三个简单的单相电路。
这样,我们可以分别分析每个单相电路,从而简化电路分析过程。
2.发电机和变压器分析对称分量法广泛应用于发电机和变压器的分析。
通过分解发电机和变压器的不对称电流和电压,我们可以了解设备的运行状态,及时发现故障,保证电力系统的稳定运行。
对称分量法(零序,正序,负序)的理解与计算教学文案

对称分量法(零序,正序,负序)的理解与计算对称分量法(零序,正序,负序)的理解与计算1)求零序分量:把三个向量相加求和。
即A相不动,B相的原点平移到A相的顶端(箭头处),注意B相只是平移,不能转动。
同方法把C相的平移到B相的顶端。
此时作A相原点到C相顶端的向量(些时是箭头对箭头),这个向量就是三相向量之和。
最后取此向量幅值的三分一,这就是零序分量的幅值,方向与此向量是一样的。
2)求正序分量:对原来三相向量图先作下面的处理:A相的不动,B相逆时针转120度,C相顺时针转120度,因此得到新的向量图。
按上述方法把此向量图三相相加及取三分一,这就得到正序的A相,用A相向量的幅值按相差120度的方法分别画出B、C两相。
这就得出了正序分量。
3)求负序分量:注意原向量图的处理方法与求正序时不一样。
A相的不动,B 相顺时针转120度,C相逆时针转120度,因此得到新的向量图。
下面的方法就与正序时一样了。
对电机回路来说是三相三线线制,Ia+Ib+Ic=0,三相不对称时也成立;当Ia+Ib+Ic≠0时必有一相接地,对地有有漏电流;对三相四线制则为Ia+Ib+Ic+Io=0成立,只要无漏电,三相不对称时也成立;因此,零序电流通常作为漏电故障判断的参数。
负序电流则不同,其主要应用于三相三线的电机回路;在没有漏电的情况下(即Ia+Ib+Ic=0),三相不对称时也会产生负序电流;负序电流常作为电机故障判断;注意了:Ia+Ib+Ic=0与三相对称不是一回事;Ia+Ib+Ic=0时,三相仍可能不对称。
注意了:三相不平衡与零序电流不可混淆呀!三相不平衡时,不一定会有零序电流的;同样有零序电流时,三相仍可能为对称的。
(这句话对吗?)前面好几位把两者混淆了吧!正序、负序、零序的出现是为了分析在系统电压、电流出现不对称现象时,把三相的不对称分量分解成对称分量(正、负序)及同向的零序分量。
只要是三相系统,一般针对三相三线制的电机回路,就能分解出上述三个分量(有点象力的合成与分解,但很多情况下某个分量的数值为零)。
对称分量法(正序、负序、零序)

对称分量法之宇文皓月创作正序:A相领先B相120度,B相领先C相120度,C相领先A 相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A 相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后。
三相短路故障和正常运行时,系统里面是正序。
单相接地故障时候,系统有正序、负序和零序分量。
两相短路故障时候,系统有正序和负序分量。
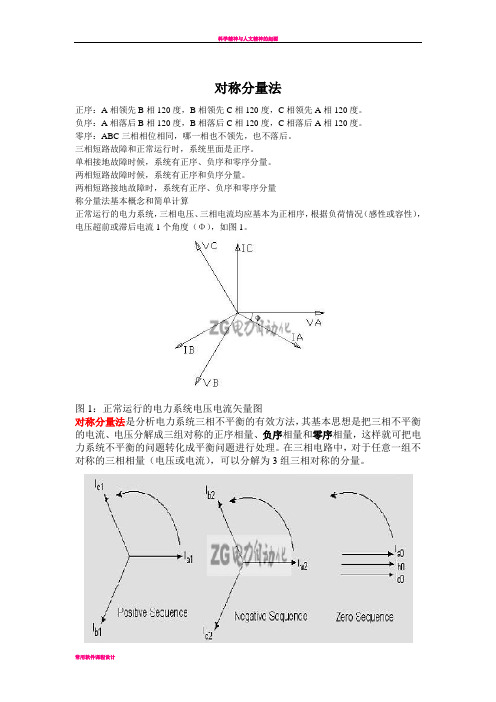
两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1。
图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不服衡的有效方法,其基本思想是把三相不服衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不服衡的问题转化成平衡问题进行处理。
在三相电路中,对于任意一组分歧错误称的三相相量(电压或电流),可以分解为3组三相对称的分量。
图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2 Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0 式中,α为运算子,α=1∠120°有α2=1∠240°, α3=1, α+α2+1=0 由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC) I2=Ia2= 1/3(IA +α2IB +αIC) I0=Ia0= 1/3(IA +IB +IC) 以上3个等式可以通过代数方法或物理意义(方法)求解。
对称分量法

对称分量法
一、概述
1918年,加拿大电气学家Charles LeGeyt Fortescue发明对称分量法(method of symmetrical components),对称分量法(method of symmetrical components)将一个不对称的三个相量,分解为三组对称的相量:正序分量、负序分量和零序分量,对称分量法广泛应用于三相交流电参量的不对称程度分析。
二、计算
下图的图a、b、c分别表示三组对称的三相相量:
1、不对称分量的合成
幅值相等,相位依次差120°,称为正序分量;
幅值相等,相位依次差120°,相序与正序分量相反,称为负序分量;
幅值和相位均相等,称为零序分量。
将上述三组对称的三相相量相加,得到一组不对称的三相相量,不对称的三相相量的数学表达式为:
( 1)
由对称性,参见图a、图b、图c,可知:
(2)
式(2)代入式(1)可得:
(3)
2、不对称分量的分解
式(3)的逆关系为:
上式说明三个不对称的相量可以唯一地分解成为三组对称的相量,即对称分量:正序分量、负序分量和零序分量。
三、应用
对称分量法常用于电力系统的三相不对称分析,国标《GB/T15543-2008电能质量三相电压不平衡》定义的三相电压不平衡度就是采用三相电压的负序分量与正序分量的比值或零序分量与正序分量的比值表示。
WP4000变频功率分析仪依据国标要求,求解三相电参量的基波分量的三相不平衡度。
为了简便运算,国际上还有另外一些相关标准对不平衡度计算采取其它的更为简化的运算方式。
详细请参见银河百科:三相不平衡度。
对称分量法(正序、负序、零序)
对称分量法正序:A相领先B相120度,B相领先C相120度,C相领先A相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后。
三相短路故障和正常运行时,系统里面是正序。
单相接地故障时候,系统有正序、负序和零序分量。
两相短路故障时候,系统有正序和负序分量。
两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1。
图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法,其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理。
在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为3组三相对称的分量。
图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0式中,α为运算子,α=1∠120°有α2=1∠240°, α3=1, α+α2+1=0由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义(方法)求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 3
1 1 1
a a2 1
a2 a
FFba
1
Fc
F120 SFabc
Fabc S 1F120
5
二、序阻抗的概念
• 静止的三相电路元件序阻抗
VVba
Vc
Z Z Z
a 2 Fa1
aFa2
Fa0
Fc
Fc1
Fc2
Fc0
aFa1
a 2 Fa2
Fa0
• 三序量用三相量表示
1 1 1 S 1 a 2 a 1
a a 2 1
Fa1 Fa2
Fa0
• 同步发电机零序电抗在数值上相差很大(绕组结构形式不同):
• 零序电抗典型值
X 0 (0.15 ~ 0.6) X d
20
二、异步电动机和综合负荷的序阻抗
• 异步电机和综合负荷的正序阻抗: Z1=0.8+j0.6或X1=1.2;
• 异步电机负序阻抗:X2=0.2; • 综合负荷负序阻抗:X2=0.35;
➢ 负序网
0 Ia2 (ZG2 Z12 ) Va2
14
三、对称分量法在不对称短路计算中的应用
➢ 零序网
Ia0 Ib0 Ic0 3Ia0
0 Ia0 (Z G0 Z L0 ) 3Ia0 Z n Va0
0 Ia0 (ZG0 Z L0 3Z n ) Va0
结论:在三相参数对称的线性电路中,各序对称分量具有独 立性,因此,可以对正序、负序、零序分量分别进行计算。
7
二、序阻抗的概念
• 序阻抗:元件三相参数对称时,元件两端某一序的电压降与通过该元件的同 一序电流的比值。
正序阻抗 负序阻抗 零序阻抗
Z1 Z2
Va1/ Ia1 Va2 / Ia2
Z0
Va0 /
Ia0
Hale Waihona Puke 8三、对称分量法在不对称短路计算中的应用
• 一台发电机接于空载线路,发电机中性点经阻抗Zn接地。 • a相发生单相接地
Va 0 Vb 0 Vc 0
Ia 0 Ib 0 Ic 0
9
三、对称分量法在不对称短路计算中的应用
• 异步电机和综合负荷的零序电抗:X0=∞。
21
三、变压器的零序电抗及其等值电路
• 正序、负序和零序等值电路结构相同。 • 普通变压器的零序阻抗及其等值电路 • 忽略绕组电阻和铁心损耗时变压器的零序等值电路:
双绕组变压器
三绕组的变压器
22
1 .普通变压器的零序阻抗及其等值电路
➢ 漏磁通的路径与所通电流的序别无关,因此变压器的各序等值漏 抗相等。
• 当元件参数完全对称时
Zs
Z m
Z sc
0
0
Z Z
s
m
0 Z1 0 0
0
0
Z 2
0
0
0
Z s
2Zm
0
0 Z0
V120 Zsc I120
Va1 Va2
Z 1 Ia1 Z 2 Ia2
Va0
Z 0 Ia0
15
E 0
Ia1Z1 Va1 Ia2 Z 2 Va2
0 Ia0 Z 0 Va0
0 Ia2 (ZG2 Z12 ) Va2
Ea Ia1 (Z G1 Z L1 ) Va1
0 Ia0 (ZG0 Z L0 3Z n ) Va0
Fb1 Fb2
a 2 Fa1 , Fc1 aFa2 , Fc2
aFa1 a 2 Fa2
Fb0 Fc0 Fa0
a e j120
4
• 三相量用三序量表示
Fa Fb
Fa1 Fb1
Fa2 Fb2
Fa0 Fb0
➢ 励磁电抗取决于主磁通路径,正序与负序电流的主磁通路径相同, 负序励磁电抗与正序励磁电抗相等。因此,变压器的正、负序等 值电路参数完全相同。
• 变压器的零序励磁电抗与变压器的铁心结构相关。
23
零序励磁电抗等于正序励磁电抗
零序励磁电抗比正序励磁 电抗小得多:Xm0=0.3~1.0 零序励磁电抗等于正序励磁电抗
对称分量法
演讲者:刘煦阳 陈日垚
主要内容:
1、什么是对称分量法?
2、为什么要引入对称分量法?
分析过程是什么?
➢ 对称分量法
1、各元件的序参数是怎样的?
➢ 对称分量法在不对称故障分析2、计如算何中绘的制应电用力系统的序网图?
➢ 电力系统元件序参数及系统的如序何网利图用对称分量法对 简单不对称故障进行分
➢ 简单不对称故障的分析计算 析与计算?
2
4.1 对称分量法
正序分量
负序分量
零序分量
合成
3
一、对称分量法
• 正序分量:三相量大小相等,互差1200,且与系统正常运行相序 相同。
• 负序分量:三相量大小相等,互差1200,且与系统正常运行相序 相反。
• 零序分量:三相量大小相等,相位一致。
逆时针旋转1200
29
4.自耦变压器的零序阻抗及其等值电路
• 中性点直接接地的自耦变压器
30
四、架空线路的零序阻抗及其等值电路
输电线路: • 零序电流必须借助大地及架空地线构成通路
31
四、架空线路的零序阻抗及其等值电路
• 有架空地线的情况:零序阻抗有所减小。
32
• 实际上,由于输电线路所经过地段的大地电阻率一般不是 均匀的,因此零序阻抗一般是通过实测来获得的。在实用 的短路计算中,不同类型架空线路的零序电抗与正序电抗 之间的关系是:
aa ab ac
Z ab Z bb Z bc
Z Z Z
ac bc cc
IIba Ic
Vabc ZI abc
V120 SZS 1 I120 Z sc I120
Z sc SZS 1 称为序阻抗矩阵
6
zaa zbb zcc zs zab zbc zca zm
X2 1.45 Xd
电机类型 电抗
X2
X0
水轮发电机 有阻尼绕组
0.15~0.35
无阻尼绕组 0.32~0.55
汽轮发电机
调相机和 大型同步电动机
0.134~0.18
0.24
0.04~0.125
0.04~0.125
0.036~0.08
0.08
19
2.同步发电机的零序电抗
• 三相零序电流在气隙中产生的合成磁势为零,因此其零序电抗仅 由定子线圈的漏磁通确定。
X d ~ X q X d ~ X q
18
1 同步发电机的负序电抗
• 实用计算中发电X 2机负12序( X电d抗 计X q算)
有阻尼绕组
无阻尼绕组
X 2 X d X q
• 发电机负序电抗X近2 似 估1.算22值X d
有阻尼绕组
无阻尼绕组
• 无确切数值,可取典型值
• 无架空地线的单回路三相输电线路, x0 / x1 3.5;
• 无架空地线的双回路三相输电线路, x0 / x1 5.5; • 有铁磁导体架空地线单回路三相输电线路,x0 / x1 3.0;
• 有铁磁导体架空地线双回路三相输电线路,x0 / x1 4.7;
• 有良导体架空地线单回路三相输电线路, x0 / x1 2.0; • 有良导体架空地线双回路三相输电线路, x0 / x1 3.0;
考虑三个方面: (1)当外电路向变压器某侧施加零序电压时,如果能在该侧 产生零序电流,则等值电路中该侧绕组端点与外电路接通; 反之,则断开。根据这个原则:只有中性点接地的星形接法 绕组才能与外电路接通。 (2)当变压器绕组具有零序电势(由另一侧感应过来)时, 如果它能将零序电势施加到外电路并能提供零序电流的通路, 则等值电路中该侧绕组端点与外电路接通,否则断开。据此: 只有中性点接地星形接法绕组才能与外电路接通。 (3)三角形接法的绕组中,绕组的零序电势虽然不能作用到 外电路中,但能在三相绕组中形成环流。因此,在等值电路 中该侧绕组端点接零序等值中性点(等值中性点与地同电位 时则接地)。
所有同步发电机和调相机以及用等值电源表示的综合负荷,都是正序 网络的电源。
此外,还需在短路点引入代替故障条件的正序电势。从故障端口看正 序网络,它是一个有源网络,可以简化为戴维南等值电路。
37
负序网络
负序电流流通情况和正序电流的流通情况相同,但是所有电源的负序电 势为零,电抗应为负序电抗,在短路点引入代替故障条件的负序电势, 便可得到负序网络,如上图所示。从故障端口看负序网络,踏实一个无 源网络,也可以简化为戴维南等值电路。
根据上述原则,我们结合下图来说明各序网络的制定。
35
电力系统接线图
36
正序网络
正序网络就是通常计算对称短路时所用的等值网络。 除中性点接地阻抗、空载线路(不计导纳时)及空载变压器(不计励
磁电流时)外,电力系统各元件均应包括在正序网络中,并用正序参数 和等值电路表示。如上图所示的正序网络中不包括空载线路L3 和T3 。
Ea Ia1 (Z G1 Z L1 ) (Ia1 a 2 Ia1 aIa1 )Z n Va1 Ia1 Ib1 Ic1
