中考数学数学中考数学压轴题试题附解析(1)
(完整)中考数学压轴题精选及答案
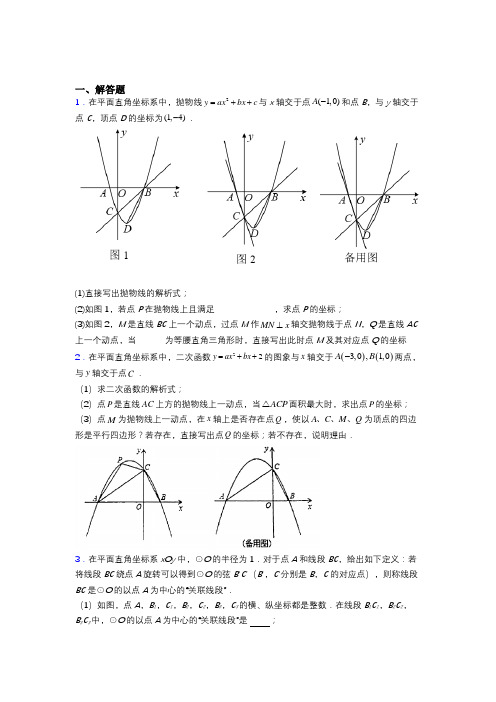
一、解答题1.在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于点(1,0)A -和点B ,与y 轴交于点C ,顶点D 的坐标为(1,4)-.(1)直接写出抛物线的解析式;(2)如图1,若点P 在抛物线上且满足,求点P 的坐标; (3)如图2,M 是直线BC 上一个动点,过点M 作MN x ⊥轴交抛物线于点N ,Q 是直线AC 上一个动点,当为等腰直角三角形时,直接写出此时点M 及其对应点Q 的坐标2.在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △面积最大时,求出点P 的坐标;(3)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A C M Q 、、、为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,说明理由.3.在平面直角坐标系xOy 中,⊙O 的半径为1.对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′(B ′,C ′分别是B ,C 的对应点),则称线段BC 是⊙O 的以点A 为中心的“关联线段”.(1)如图,点A ,B 1,C 1,B 2,C 2,B 3,C 3的横、纵坐标都是整数.在线段B 1C 1,B 2C 2,B 3C 3中,⊙O 的以点A 为中心的“关联线段”是 ;(2)△ABC 是边长为1的等边三角形,点A (0,t ),其中t ≠0.若BC 是⊙O 的以点A 为中心的“关联线段”,求t 的值;(3)在△ABC 中,AB =1,AC =2.若BC 是⊙O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长.4.综合与探究如图,在平面直角坐标系中,点()0,10A ,点B 是x 轴的正半轴上的一个动点,连接AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90°,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(),0t(1)当6t =时,点M 的坐标是 ;(2)用含t 的代数式表示点C 的坐标;(3)是否存在点B ,使四边形AOBD 为矩形?若存在,请求出点B 的坐标;若不存在,请说明理由;(4)在点B 的运动过程中,平面内是否存在一点N ,使得以A 、B 、N 、D 为顶点的四边形是菱形?若存在,请直接写出点N 的纵坐标(不必要写横坐标);若不存在,请说明理由.5.如图(1),在菱形ABCD 中,∠ABC =60°,点E 在边CD 上(不与点C ,D 重合),连结AE ,交BD 于点F .(1)如图(2),若点M 在BC 边上,且DE =CM ,连结AM ,EM .求证:三角形AEM 为等边三角形;(2)设DF x BF=,求tan ∠AFB 的值(用x 的代数式表示); (3)如图(3),若点G 在线段BF 上,且FG =2BG ,连结AG 、CG ,DF x BF =,四边形AGCE 的面积为S 1,ABG 的面积为S 2,求12S S 的最大值.6.如图,在平面直角坐标系中,ABC 的边AB 在x 轴上,且OB OA >,以AB 为直径的圆过点C .若点C 的坐标为()0,4,10AB =,(1)求抛物线的解析式;(2)点P 为该函数在第一象限内的图象上一点(不与BC 重合),过点P 作PQ BC ⊥,垂足为点Q ,连接PC .若以点P 、C 、Q 为顶点的三角形与COA 相似,求点P 的坐标;(3)若ACB ∠平分线所在的直线l 交x 轴与点E ,过点E 任作一直线l '分别交射线CA ,CB (点C 除外)于点M ,N .则11CM CN+的是否为定值?若是,求出该定值;若不是,请说明理由.7.如图1,⊙I 与直线a 相离,过圆心I 作直线a 的垂线,垂足为H ,且交⊙I 于P 、Q 两点(Q 在P 、H 之间).我们把点Q 称为⊙I 关于直线a 的“近点”,点P 称为⊙I 关于直线a 的“远点”把PQ ·QH 的值称为⊙I 关于直线a 的“特征数”.(1)如图2,在平面直角坐标系xOy 中,点E 的坐标为(0,3).半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D .①过点E 画垂直于y 轴的直线m ,则⊙O 关于直线m 的“近点”“远点”分别是点_____和_____(填“A ”、“B ”、“C ”或“D ”),⊙O 关于直线m 的“特征数”为_____;②若直线n 的函数表达式为33y x =-+.求⊙O 关于直线n 的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点M (1,2),点F 是坐标平面内一点,以F 5为半径作⊙F .若⊙F 与直线l 相离,点N (1-,0)是⊙F 关于直线l 的“近点”.且⊙F 关于直线l 的“特征数”是6,求直线l 的函数表达式.8.如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.(1)分别求抛物线和直线AC的解析式;(2)在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.9.已知:如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,以OA,OC为边作矩形ABCO,矩形ABCO的面积是36.(1)求直线AC的解析式.(2)点P为线段AB上一点,点Q为第一象限内一点,连接PO,PQ,∠OPQ=90°,且OP=PQ,设AP的长为t,点Q的横坐标为d,求d与t的函数关系式.(不要求写出自变量t的取值范围)(3)在(2)的条件下,过点Q作QE∥PO交AB的延长线于点E,作∠POC的平分线OF 交PE于点F,交PQ于点K,若KQ=2EF,求点Q的坐标.10.如图,平面直角坐标系中,点O为原点,抛物线交x轴于()2,05,0B两点,交y轴于点C.A-、()(1)求抛物线解析式;(2)点P在第一象限内的抛物线上,过点P作x轴的垂线,垂足为点H,连AP交y轴于点E,设P点横坐标为t,线段EC长为d,求d与t的函数解析式;(3)在(2)条件下,点M在CE上,点Q在第三象限内抛物线上,连接PC、PQ、PM,PQ与y轴交于W,若,,,求点Q的坐标.11.已知:如图1,点A(a,b),AB x⊥轴于点B2++-+=.a b a b24(8)0(1)试判断△AOB的形状,并说明理由;(2)如图2,若点C为线段AB的中点,连OC并作OD OC⊥,且OD OC=,连AD交x轴于点E,试求点E的坐标;(3)如图3,若点M为点B的左边x轴负半轴上一动点,以AM为一边作45∠=︒交MANy轴负半轴于点N,连MN,在点M运动过程中,试猜想式子OM MN ON+-的值是否发生变化?若不变,求这个不变的值;若发生变化,试求它变化的范围.12.直角三角板ABC的斜边AB的两个端点在⊙O上,已知∠BAC=30°,直角边AC与⊙O 相交于点D,且点D是劣弧AB的中点.(1)如图1,判断直角边BC所在直线与⊙O的位置关系,并说明理由;(2)如图2,点P是斜边AB上的一个动点(与A、B不重合),DP的延长线交⊙O于点Q,连接QA、QB.①AD=6,PD=4,则AB= ;PQ= ;②当点P在斜边AB上运动时,求证:QA+QB=3QD.13.如图,已知四边形ABCD内接于⊙O,直径DF交BC于点G.(1)如图1,求证:∠BAD-∠BCF=90°;(2)如图2,连接AC,当∠BAC=∠CFD+∠ACD时,求证:CA=CB;(3)如图3,在(2)的条件下,AC交DF于点H,∠BAC=∠DGB,45CGBG,AC=9,求△CDH的面积.14.同学们学过正方形与等腰三角形发现它们都是轴对称图形,它们之间有很多相似,在正边形ABCD中,E是对角线AC上一点(不与点A、C重合),以AD、AE为邻边作平行四边形AEGD,GE交CD于点M,连接CG.(1)如图1,当12AE AC<时,过点E作EF BE⊥交CD于点F,连接GF并延长交AC于点H.求证:EB EF=;(2)在ABC中,AB AC=,90BAC∠=︒.过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD直线BD交直线AP于点E.如图2,①依题意补全图形;②请用等式表示线段EB,ED,BC之间的数量关系,并予以证明.15.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式.(2)若点P为第三象限内抛物线上一动点,作PD⊥x轴于点D,交AC于点E,过点E作AC 的垂线与抛物线的对称轴和y轴分别交于点F、G,设点P的横坐标为m.①求PE2的最大值;②连接DF、DG,若∠FDG=45°,求m的值.16.【问题提出】如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围.【问题解决】解决此问题可以用如下方法:延长AD 到点E ,使DE =AD ,再连结BE (或将△ACD 绕着点D 逆时针旋转180°得到△EBD ),把AB 、AC ,2AD 集中在△ABE 中,利用三角形三边的关系即可判断.由此得出中线AD 的取值范围是__________【应用】如图②,如图,在△ABC 中,D 为边BC 的中点、已知AB =10,AC =6,AD =4,求BC 的长.【拓展】如图③,在△ABC 中,∠A =90°,点D 是边BC 的中点,点E 在边AB 上,过点D 作D F⊥DE 交边AC 于点F ,连结EF .已知BE =5,CF =6,则EF 的长为__________.17.已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B (1,0)两点,与y 轴交于点()03C -,.(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图象上位于第三象限内的点,若点D 的横坐标为m ,ACD △的面积为S ,求S 与m 之间的函数关系式,并写出ACD △的面积取得最大值时点D 的坐标;(3)M 是二次函数图象对称轴上的点,在二次函数图象上是否存在点N .使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).18.如图,在平面直角坐标系中,已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ,点B 39(2,)16- 是一次函数5119216y x =+上一点.(1)当a =0时,求顶点P 坐标;(2)若a >0,且一次函数2y x b =-+的图象与此抛物线没有交点,请你写出一个符合条件的一次函数关系式(只需写一个,不必写出过程);(3)作直线OC :12y x =与一次函数5119216y x =+交于点C .连结OB ,当抛物线与△OBC 的边有两个交点时,求a 的取值范围.19.已知O 为ABC ∆的外接圆,AC BC =,点D 是劣弧AB 上一点(不与点A ,B 重合),连接DA ,DB ,DC .(1)如图1,若AB 是直径,将ACD ∆绕点C 逆时针旋转得到BCE ∆.若4CD =,求四边形ADBC 的面积;(2)如图2,若AB AC =,半径为2,设线段DC 的长为x .四边形ADBC 的面积为S . ①求S 与x 的函数关系式;②若点M ,N 分别在线段CA ,CB 上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置.DMN ∆的周长有最小值t ,随着点D 的运动,t 的值会发生变化.求所有t 值中的最大值,并求此时四边形ADBC 的面积S .20.如图,在ABCD 中,90ABD ∠=︒,5cm AD =,8cm BD =.点P 从点A 出发,沿折线AB BC -向终点C 运动,点P 在AB 边、BC 边上的运动速度分别为1cm/s 、5cm /s .在点P 的运动过程中,过点P 作AB 所在直线的垂线,交边AD 或边CD 于点Q ,以PQ 为一边作矩形PQMN ,且2QM PQ =,MN 与BD 在PQ 的同侧.设点P 的运动时间为t (秒),矩形PQMN 与ABCD 重叠部分的面积为()2cm S .(1)求边AB 的长.(2)当04t <<时,PQ = ,当48t <<时,PQ = .(用含t 的代数式表示)(3)当点M 落在BD 上时,求t 的值.(4)当矩形PQMN 与ABCD 重叠部分图形为四边形时,求S 与t 的函数关系式.【参考答案】参考答案**科目模拟测试一、解答题1.(1)223y x x =--;(2),; (3),;,;,;,; ,;,. 【解析】【分析】(1)根据顶点的坐标,设抛物线的解析式为y =a (x ﹣1)2﹣4,将点A (﹣1,0)代入,求出a 即可得出答案;(2)利用待定系数法求出直线BD 解析式为y =2x ﹣6,过点C 作CP 1∥BD ,交抛物线于点P 1,再运用待定系数法求出直线CP 1的解析式为y =2x ﹣3,联立方程组即可求出P 1(4,5),过点B 作y 轴平行线,过点C 作x 轴平行线交于点G ,证明△OCE ≌△GCF(ASA),运用待定系数法求出直线CF解析式为y=12x﹣3,即可求出P2(52,﹣74);(3)利用待定系数法求出直线AC解析式为y=﹣3x﹣3,直线BC解析式为y=x﹣3,再分以下三种情况:①当△QMN是以NQ为斜边的等腰直角三角形时,②当△QMN是以MQ为斜边的等腰直角三角形时,③当△QMN是以MN为斜边的等腰直角三角形时,分别画出图形结合图形进行计算即可.(1)解:∵顶点D的坐标为(1,﹣4),∴设抛物线的解析式为y=a(x﹣1)2﹣4,将点A(﹣1,0)代入,得0=a(﹣1﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4=x2﹣2x﹣3,∴该抛物线的解析式为y=x2﹣2x﹣3;(2)解:∵抛物线对称轴为直线x=1,A(﹣1,0),∴B(3,0),设直线BD解析式为y=kx+e,∵B(3,0),D(1,﹣4),∴,解得:,∴直线BD解析式为y=2x﹣6,过点C作CP1∥BD,交抛物线于点P1,设直线CP1的解析式为y=2x+d,将C(0,﹣3)代入,得﹣3=2×0+d,解得:d=﹣3,∴直线CP1的解析式为y=2x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=2x﹣3,解得:x1=0(舍),x2=4,故P1(4,5),过点B作y轴平行线,过点C作x轴平行线交于点G,∵OB=OC,∠BOC=∠OBG=∠OCG=90°,∴四边形OBGC是正方形,设CP1与x轴交于点E,则2x﹣3=0,解得:x=32,∴E(32,0),在x轴下方作∠BCF=∠BCE交BG于点F,∵四边形OBGC是正方形,∴OC=CG=BG=3,∠COE=∠G=90°,∠OCB=∠GCB=45°,∴∠OCB﹣∠BCE=∠GCB﹣∠BCF,即∠OCE=∠GCF,∴△OCE≌△GCF(ASA),∴FG=OE=32,∴BF=BG﹣FG=3﹣32=32,∴F(3,﹣32),设直线CF解析式为y=k1x+e1,∵C(0,﹣3),F(3,﹣32),∴,解得:,∴直线CF解析式为y=12x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=12x﹣3,解得:x1=0(舍),x2=52,∴P2(52,﹣74),综上所述,符合条件的P点坐标为:(4,5)或(52,﹣74);(3)解:(3)设直线AC解析式为y=m1x+n1,直线BC解析式为y=m2x+n2,∵A(﹣1,0),C(0,﹣3),∴,解得:,∴直线AC解析式为y=﹣3x﹣3,∵B(3,0),C(0,﹣3),∴,解得:,∴直线BC解析式为y=x﹣3,设M(t,t﹣3),则N(t,t2﹣2t﹣3),∴MN=|t2﹣2t﹣3﹣(t﹣3)|=|t2﹣3t|,①当△QMN是以NQ为斜边的等腰直角三角形时,此时∠NMQ=90°,MN=MQ,如图2,∵MQ∥x轴,∴Q(﹣13t,t﹣3),∴|t2﹣3t|=|t﹣(﹣13t)|,∴t2﹣3t=±43t,解得:t=0(舍)或t=53或t=133,∴,;,;②当△QMN是以MQ为斜边的等腰直角三角形时,此时∠MNQ=90°,MN=NQ,如图3,∵NQ∥x轴,∴Q(,t2﹣2t﹣3),∴NQ=|t﹣|=13|t2+t|,∴|t2﹣3t|=13|t2+t|,解得:t=0(舍)或t=5或t=2,∴M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);③当△QMN是以MN为斜边的等腰直角三角形时,此时∠MQN=90°,MQ=NQ,如图4,过点Q作QH⊥MN于H,则MH=HN,∴H(t,),∴Q(,),∴QH=|t﹣|=16|t2+5t|,∵MQ=NQ,∴MN=2QH,∴|t2﹣3t|=2×16|t2+5t|,解得:t=7或1,∴M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3);综上所述,点M及其对应点Q的坐标为:,;,;M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3).【点睛】本题是二次函数综合题,主要考查了待定系数法求一次函数和二次函数解析式,求一次函数与二次函数图象交点坐标,全等三角形判定和性质,正方形判定和性质,等腰直角三角形性质等,本题属于中考压轴题,综合性强,难度较大,熟练掌握待定系数法、等腰直角三角形性质等相关知识,运用数形结合思想、分类讨论思想是解题关键.2.(1)224233y x x =--+;(2)35(,)22P -(3)存在,12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【解析】【分析】(1)根据待定系数法求抛物线解析式;(2)设224(,)33P t t --根据(1)的结论求得C 的坐标,进而求得AC 的解析式,过P 作PD ⊥x 轴交AC 于点D ,进而求得PD 的长,根据12APC C A S PD x x =⋅⋅-△求得APC S 的表达式,进而根据二次函数的性质求得取得最大值时,t 的值,进而求得P 点的坐标;(3)分情况讨论,①//CM AQ ,②//AC MQ ,根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标.【详解】(1)二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+ (2)抛物线224233y x x =--+与y 轴交于点C ,令0x =,则2y = (0,2)C ∴设直线AC 的解析式为y kx b =+,由(3,0)A -,(0,2)C ,则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的解析式为223y x =+, 如图,过P 作PD ⊥x 轴交AC 于点D ,设224(,)33P t t --,则2(,2)3D t t +, 2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APC C A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时,APC S 取得最大值,此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P - (3)存在,理由如下抛物线解析式为224233y x x =--+()228133x =-++ ∴抛物线的对称轴为直线1x =①如图,当//CM AQ 时,Q 点在x 轴上,//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称,(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时,如图,设M 的纵坐标为n ,四边形ACQM 是平行四边形,点A ,Q 在x 轴上,则,AQ MC 的交点也在x 轴上, 202n +∴= 解得2n =-设(,2)M m -,2242233x x ∴-=--+ 解得17x =-(17,2)M ∴--A 点到C 点是横坐标加3,纵坐标加2∴M 点到Q 点也是横坐标加3,纵坐标加2 即(173,0)Q -±34(27,0),(27,0)Q Q ∴综上所述,存在点Q ,使得以A C M Q 、、、为顶点的四边形是平行四边形,Q 点的坐标为12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【点睛】本题考查了二次函数综合,待定系数法,二次函数最值,二次函数的图象与性质,平行四边形的性质,综合运用以上知识是解题的关键.3.(1)B 2C 2;(233-3)OA 最小值为1,相应的3BC =OA 最大值为2,相应的6BC =【解析】【分析】(1)结合题意,根据旋转和圆的性质分析,即可得到答案;(2)根据题意,分B C ''在x 轴上方和x 轴上方两种情况;根据等边三角形、勾股定理、全等三角形的性质,得32AD OD ==,从而完成求解; (3)结合题意,得当AC '为⊙O 的直径时,OA 取最小值;当A 、B '、O 三点共线时,OA 取最大值;根据勾股定理、等腰三角形的性质计算,即可得到答案.【详解】(1)线段B 1C 1绕点A 旋转得到的11B C '',均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”;线段B 2C 2绕点A 旋转得到的22B C '',如下图:∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”;线段B 3C 3绕点A 旋转得到的33B C '',均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”;故答案为:B 2C 2;(2)∵△ABC 是边长为1的等边三角形,点A (0,t ),⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况:当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:∵1OB OC ''==∴1122B D B C '''== ∴2232OD OB B D ''=-=∵△ABC 是边长为1的等边三角形,即△AB C ''是边长为1的等边三角形, ∴AC D OC D ''∠=∠,AD B C ''⊥ ∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =;当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:同理,3AO AD OD =+=∴()0,3A -;∴t 3=-;∴3t =或3-;(3)当AC '为⊙O 的直径时,OA 取最小值,如下图:∴OA 最小值为1,90AB C ''∠=︒ ∴223BC B C AC AB ''''==-=;当A 、B '、O 三点共线时,OA 取最大值,2OA AC '== ,如下图:作AE OC '⊥交OC '于点E ,作C F AO '⊥交AO 于点F ,如下图∵2OA AC '==∴1122OE OC '==∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '==∴2214OF OC C F ''=-=∴34B F OB OF ''=-=∴262BC B C C F B F ''''==+=∴OA 最小值为1,相应的3BC =;OA 最大值为2,相应的62BC =. 【点睛】本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识;解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质,从而完成求解.4.(1)(3,5)M ,(2)1(5,)2C t t +;(3)(20,0)B ;(4)154或10. 【解析】 【分析】(1)利用中点坐标公式计算即可.(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .证明()MEB BFC AAS ∆≅∆,利用全等三角形的性质即可解决问题.(3)如图2中,存在.由题意当CF OA =时,可证四边形AOBD 是矩形,构建方程即可解决问题.(4)分三种情形:①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为6.③因为BD AB ≠,所以不存在以AD 为对角线的菱形. 【详解】解:(1)如图1中,(0,10)A ,(6,0)B ,AM BM =, (3,5)M ∴,(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .//ME OA ,AM BM =, 12OE EB t ∴==,152ME OA ==,90MEB CFB CBM ∠=∠=∠=︒,90MBE CBF ∴∠+∠=︒,90MBE BME ∠+∠=︒, BME CBF ∴∠=∠,()MEB BFC AAS ∴∆≅∆,5BF ME ∴==,12CF BE t ==,5OF OB BF t ∴=+=+, 1(5,)2C t t ∴+.(3)存在.如图2中,作ME OB ⊥于E ,CF x ⊥轴于F .理由:由题意当=10CF OA =时,//OA CF , ∴四边形AOFC 是平行四边形,90AOF ∠=︒,∴四边形AOFC 是矩形,90DAO AOB DBO ∴∠=∠=∠=︒,∴四边形AOBD 是矩形,又∵由(2)得12CF BE t ==, 即:1102t =,解得:20t =.(20,0)B ∴.(4)①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.AD BD =, BAD ABD ∴∠=∠,OAB ABD ∴∠=∠,OAB BAD ∴∠=∠. tan tan OAB BAD ∴∠=∠, ∴12OB BC OA BA ==,即1102t =,5t ∴=,5OB ∴=,设AN NB m ==,在Rt OBN △中,则有2225(10)m m =+-, 解得254m =, 25151044ON OA AN ∴=-=-=, ∴点N 的纵坐标为154. ②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为10.③BD AB ≠,∴不存在以AD 为对角线的菱形. 综上所述,满足条件的点N 的纵坐标为154或10. 【点睛】本题属于四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,翻折变换,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.5.(1)证明见解析;(23333xx;(3)194【解析】 【分析】(1)如图,连接,AC 证明,ACB ACD 都为等边三角形,可得,AC AD = 再证明,ACM ADE ≌从而可得答案;(2)如图,记,AC BD 交于点,O 设,,DFa OFb 四边形ABCD 为菱形,60,ABC ∠=︒表示33,33OA OB a b 利用,2DF ax BF a b则2,1a xb x再利用三角函数的定义可得答案;(3)如图,设,DFESn 证明,DFE BFA ∽ 2,BFAnSx 再表示2222,,33ABGAGFn nSS S x x 结合菱形的轴对称的性质可得:2=,3CBG nS x 表示,AFDn S x可得2=,BCD ABDn n S Sxx 可得2212243334,3nn n S x x x x n S x 再利用二次函数的性质可得答案.【详解】证明:(1)如图,连接,AC 菱形ABCD 中,∠ABC =60°,,60,120,60,AB BC CDAD ABC ADC BAD BCD BAC CAD ACB,ACB ACD 都为等边三角形,,AC AD ∴=,60,DE CM ACM ADE,ACM ADE ≌ ,,AMAE MAC EAD 60,MACCAECAEEADAME ∴是等边三角形(2)如图,记,AC BD 交于点,O设,,DF a OF b 四边形ABCD 为菱形,60,ABC ∠=︒,,30,ACBD OB OD a b ABO33,33OAOB a b ,2DF a x BFa b1221,a b bx a a 11,22b ax 则2,1ax bx333tan 13a b OAa AFBOFbb32331,3133xxxx(3)如图,设,DFESn四边形ABCD 是平行四边形,,DFE BFA ∽22=,BFAn DF x S BF2,BFAn SxFG =2BG , 2222,,33ABGAGFn n SS S xx根据菱形的轴对称的性质可得:2=,3CBG n S x ,AFD ABFS DF x SBF2,AFDn n S x x x 2=,BCDABD n n SSxx1222224=333n n n n n nS nn x x x x x x, 2212243334,3n n n S x x x x n S x 30,a所以12S S 有最大值, 当31232x时,最大值为:1119334.424【点睛】本题考查的是菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质,列二次函数关系式,二次函数的性质,锐角三角函数的应用,灵活运用以上知识解题是解本题的关键.6.(1)213442y xx =-++;(2)点P 的坐标为:(6,41,2);(3)11NC MC +=【解析】 【分析】(1)根据题意,先证明AOC ∆∽COB ∆,得到AO OCCO OB=,求出点A 、B 的坐标,然后利用待定系数法,即可求出抛物线解析式;(2)根据题意,可分为两种情况:AOC ∆∽PQC ∆或AOC ∆∽CQP ∆,结合解一元二次方程,相似三角形的判定和性质,分别求出点P 的坐标,即可得到答案;(3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,然后由角平分线的性质定理,得到EI =EJ ,再证明△MEI ∽△MNC ,△NEJ ∽△NMC ,得到111NC MC EI+=,然后求出EI 一个定值,即可进行判断. 【详解】解:(1)∵以AB 为直径的圆过点C , ∴∠ACB =90°, ∵点C 的坐标为()0,4, ∴CO ⊥AB ,∴∠AOC =∠COB =90°,∴∠ACO +∠OCB =∠ACO +∠OAC =90°, ∴∠OCB =∠OAC , ∴AOC ∆∽COB ∆,∴AO OCCO OB=, ∵4CO =,10AO BO AB +==, ∴10AO OB =-, ∴1044OB OB-=, 解得:2OB =或8OB =, 经检验,满足题意, ∵OB OA >, ∴8OB =,∴点A 为(2-,0),点B 为(8,0).设抛物线的解析式为2y ax bx c =++,把点A 、B 、C 三点的坐标代入,有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩,解得:14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式为213442y x x =-++;(2)根据题意,如图:当AOC ∆∽PQC ∆时, ∴ACO PCQ ∠=∠, ∵90ACO OCB ∠+∠=︒, ∴90PCQ OCB ∠+∠=︒, ∴PC ⊥OC , ∴点P 的纵坐标为4,当4y =时,有2134442x x -++=,解得:16x =或20x =(舍去); ∴点P 的坐标为(6,4);当AOC ∆∽CQP ∆时,则此时BC 垂直平分OP ,作PG ⊥y 轴,垂足为G ,如上图, ∴90CQP AOC ∠=∠=︒,∴AC ∥OP , ∴∠ACO =∠POG , ∵90PGO AOC ∠=∠=︒, ∴AOC ∆∽PGO ∆, ∴AO OCPG GO=, 设点P 为(x ,213442x x -++), ∴PG x =,213442GO x x =-++,∴22413442x x x =-++, 解得:171x =±-, ∵点P 在第一象限, ∴171x =-,∴2134217242x x -++=-,∴点P 的坐标为(171-,2172-);综合上述,点P 的坐标为:(6,4)或(171-,2172-); (3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,如图:∵CE 是∠ACB 的角平分线, ∴EI =EJ ,∵EI ∥CN ,EJ ∥CM ,∴△MEI ∽△MNC ,△NEJ ∽△NMC , ∴EI ME NC MN =,EJ NE MC MN =, ∴1EI EJ ME NENC MC MN MN +=+=, ∴1EI EI NC MC +=, ∴111NC MC EI+=, ∵△ACO ∽△AEI ,∴12AI AO EI CO ==,∵AC = ∵AC AI IC AI EI =+=+,12=,解得:EI =∴111NC MC EI +==∴11NC MC+是一个定值. 【点睛】本题考查了二次函数的综合应用,求二次函数的解析式,二次函数的性质,相似三角形的判定和性质,解一元二次方程,角平分线的性质定理等知识,解题的关键是熟练掌握题意,正确的作出辅助线,运用数形结合的思想进行解题.7.(1)①B ;D ;4;②1;(2)1522y x =-+或24y x =-+【解析】 【分析】(1)①根据“近点”、“远点”以及“ 特征数”的定义判断即可;②过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P .先分别求得点E 、F 的坐标,进而可求得EF 的长,再利用等积法求得OH 的长,进而即可解决问题;(2)如图,先求得“近点”N 到直线l 的距离NH AOB AHN △∽△即可求得答案. 【详解】解:(1)①由题意,点B 是O 关于直线m 的“近点”, 点D 是O 关于直线m 的“远点”, ∵点E 的坐标为(0,3).⊙O 的半径为1, ∴OE =3,OB =OD =1,∴BE =OE -OB =2,DB =OB +OD =2,O 关于直线m 的特征数224DB BE =⋅=⨯=, 故答案为:B ;D ;4;②如图,过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P ,设直线33y x =-+交x 轴于点F ,交y 轴于点E , 令y =0,则x =3;令x =0,则y =3, ∴(3F ,0),(0,3)E ,3OE ∴=,3OF =,22223(3)23EF OE OF ∴=+=+=,∵1122EOF S OE OF EF OH =⋅=⋅△, ∴11332322OH ⨯⨯=⨯⋅, 解得:32OH =, 12QH OH OQ ∴=-=, 又∵2PQ OQ OP =+=,O ∴关于直线n 的“特征数” 1212PQ QH =⋅=⨯=;(2)如图,设直线l 交x 轴于点A ,交y 轴于点B ,过点F 作FH ⊥直线l ,垂足为点H ,交⊙F 于N ,G ,∵⊙F 5,∴FN =FG 5,∴GN =FN +FG 5∵⊙F 关于直线l 的“特征数”是6, ∴GN·NH =6,NH =6, 解得:NH设直线l 的解析式是y kx b =+, ∵直线l 经过点M (1,2),∴将(1,2)代入y kx b =+,得:2k b +=, 2b k ∴=-,(2)y kx k ∴=+-,∴当0x =时,2y k =-,∴点B 坐标为(0,2-k ),|2|OB k ∴=-,当0y =时,(2)0kx k +-=, 解得:2k x k-=, ∴点A 坐标为(2k k-,0), 2||k OA k -∴=,22|(1)||1|k k AN k k--=--=+,AB ∴2||k k-= BAO NAH ∠=∠,90AOB AHN ∠=∠=︒, AOB AHN ∴△∽△,∴NH ANOB AB=,∴|2|522|1|||k k k k k-=--+, 整理,得:22520k k ++=,解得:12k =-或2k =-,∴直线l 的解析式为1522y x =-+或24y x =-+.【点睛】本题属于圆综合题,考查了一次函数的性质,相似三角形的判定和性质运用以及勾股定理的运用,远点,近点,特征数等新定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.8.(1)y =-x 2+2x +3,y =-x +3;(2)存在,(-1,0)或(4,-5);(3)存在,(1,2)或(1,-3) 【解析】 【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD AD =,进而判断出ABC 的面积和ACP △的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论. 【详解】(1)把(30)A ,、(10)B -,代入2y x bx c =-++, 解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为(0,3),又(30)A ,,代入1y kx b =+, 得1k =-,13b =, ∴直线AC 的解析式为3y x =-+, (2)如图,连接BC ,∵点D 是抛物线的对称轴与x 轴的交点, ∴AD BD =, ∴2ABCACDSS=,∵2ACP ACD S S =△△,∴ACP ABC S S =△△,此时,点P 与点B 重合, 即:(10)P -,, 过B 点作PB AC ∥交抛物线于点P ,则直线BP 的解析式为1y x =--①, ∵抛物线的解析式为2y x 2x 3=-++②,联立①②解得,10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩,∴P (4,﹣5),∴即点P 的坐标为(﹣1,0)或(4,﹣5); (3)由(1)可知,抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ,如下图所示:22222BM AM ==+,4AB =即222BM AM AB +=则MAB △是等腰直角三角形,符合题意,M 点即为所求Q 点的一种情况,当Q 点在x 轴下方时,设Q 为(1,)m ,0m <, 因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点,则1ADQ QEA ≌ ∴2AD QE ==,1DQ EA m ==- ∴12(1)A m m --,∵点A1恰好落在抛物线2y x 2x 3=-++上, 代入,解得m=-3或2m = (舍去) ∴Q (1,-3)综上,Q 点坐标为(1,2)或(1,-3), 【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,全等三角形的判定与性质,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.9.(1)直线AC 的解析式为y =﹣x +6;(2)d =4-t ;(3)Q (212,1). 【解析】 【分析】(1)先由解析式求出得A 、C 点的坐标,得OA =OC ,得四边形ABCO 为正方形,再根据正方形的面积求得边长,便可得b 的值;(2)过点Q 作QG ⊥AB 交AB 延长沿于点G ,证明Rt △AOP ≌Rt △GPQ (AAS ),得到AP =GQ ,进而求得结论便可;(3)过点P 作PH ⊥OF 于点H ,延长PH 交EQ 的延长线于点R ,EQ 的延长线与x 轴交于点N ,过Q 作QM ⊥x 轴于点M .证明Rt △AOP ≌Rt △GPQ (CCS ),得PK =QR ,∠R=∠OKP,再证明∠R=∠FPR,得EP=ER,再证FE=NR,设FE=NR=k,NQ=m,在Rt△PQE中,由勾股定理列出方程,得到k与m的关系,解Rt△PQE得tan∠PEQ,进而把这个函数值运用到△OAP中,求得t的值,再运用(2)中结论得Q的纵坐标d的值,再运用到△QNM中求得NM,NQ的值,进而求得ON,便可得Q的横坐标的值.【详解】解:(1)∵直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,A b C b,∴(,0),(0,)∴OA=OC=b,∴矩形ABCO为正方形,∵矩形ABCO的面积是36.∴b=6,即直线AC的解析式为y=﹣x+6;(2)如图,过点Q作QG⊥AB交AB延长沿于点G,∵∠OPQ=90°,∴∠APO+∠GPQ=90°,∵∠APO+∠AOP=90°,∴∠AOP=∠GPQ,∵在矩形ABCO,∠OAP=90°,QG⊥AB,∴∠QGP=∠OAP=90°,∵PQ=OP,∴Rt△AOP≌Rt△GPQ(AAS),∴AP=GQ,∵AP=t,∴GQ=t,∴d=4-t;(2)过点P作PH⊥OF于点H,延长PH交EQ的延长线于点R,EQ的延长线与y轴交于点N,过Q作QM⊥y轴于点M.则AP=t,QM=d,且d=6-t.∵OF 平分∠POC , ∴∠POF =∠COF =∠PFO , ∴PF =PO ,∵PH ⊥OF ,∠OPQ =90°, ∴∠OPH =∠FPH ,∠KPH =∠POH , 在△OPK 和△PQR 中, 90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩====, ∴△OPK ≌△PQR (ASA ), ∴PK =QR ,∠R =∠OKP ,∵∠OKP +∠POK =∠POK +∠OPH =90°, ∴∠OKP =∠OPH , ∴∠R =∠OPH , ∵PO =PF ,PH ⊥OF , ∴∠OPH =∠FPH , ∴∠R =∠FPR , ∴EP =ER ,∵PE ∥ON ,OP ∥EN , ∴四边形OPEN 是平行四边形, ∴EN =PO =PF , ∴PE -PF =ER -EN , ∴FE =NR ,设FE =NR =k ,则KQ =2FE =2k , 又设NQ =m ,∴PK=QR=m+k,∴PQ=m+3k,∴PO=EN=PF=m+3k,∴QE=EN-QR=m+3k-m=3k,PE=PF+FE=4k+m,在Rt△PQE中,∵PE2=PQ2+QE2,∴(4k+m)2=(3k+m)2+(3k)2,∴k1=0(舍去),k2=m,∴PQ=4m,QE=3m,∴tan∠PEN=43 PQQE=,∵OP∥EN,∴∠OPA=∠PEN,∴tan∠APO=43,∵AO=6,∴AP=4.5,∴t=4.5,∴QM=d=6-t=1.5,∵PE∥OC,∴∠QNM=∠PEN,∴tan∠QNM=tan∠PEN=43,∴NM=9 tan8QMQNM=∠,∴m=NQ158 =,∴PE=ON=4k+m=5m=758,∴OM=ON+NM=212,∴Q(212,1).【点睛】本题是一次函数与四边形的综合题,主要考查了一次函数的图象与性质,全等三角形的性质与判定,正方形的性质,旋转的性质,解直角三角形的应用,等腰三角形的性质与判定,平行四边形的性质与判定,是一道综合性极强的题目,解决这类问题常用到数形结合、方程和转化等数学思想方法.构造全等三角形是解题的关键,也是问题的突破口.10.(1);(2);(3)【解析】 【分析】(1)由抛物线的二次项系数 再根据交点式可得抛物线为从而可得答案;(2)先画好图形,证明利用相似三角形的性质求解从而可得答案;(3)如图,过P 作轴于,K 过M 作于,N 证明即再求解则,再解方程可得 4,t = 再求解的解析式,再联立解析式解方程可得答案. 【详解】 解:(1) 抛物线交x 轴于()2,0A -、()5,0B 两点,所以可得抛物线为:(2)如图,过P 作于,H 连AP 交OC 于则,x 则令0,(3)如图,过P作轴于,K过M作于,N 由(2)得:,,轴,则轴,,即结合(1)可得:四边形为矩形,。
【精品】人教版九年级数学中考压轴试题(含答案解析)

【精品】人教版九年级数学中考压轴试题(含答案)1.(8分)如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转90°,得到线段CF,连结EF.设∠BCE度数为α.(1)①补全图形.②试用含α的代数式表示∠CDA.(2)若=,求α的大小.(3)直接写出线段AB、BE、CF之间的数量关系.【分析】(1)①根据要求画出图形即可;②利用三角形的外角的性质计算即可;(2)只要证明△FCE∽△ACB,可得==,Rt△CFA中,∠CFA=90°,cos∠FCA=,推出∠FCA=30°,即α=30°.(3)在Rt△ABC,和Rt△CBE中,利用勾股定理即可解决问题;【解答】解:(1)①补全的图形如图所示:②∵CA=CB,∠ACB=90°,∴∠A=∠ABC=45°,∴∠CDA=∠DBC+∠BCD=45°+α.(2)在△FCE和△ACB中,∠CFE=∠CAB=45°,∠FCE=∠ACB=90°,∴△FCE∽△ACB,∴=∵=∴=连结FA,∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,∴∠FCA=∠BCE=α,在Rt△CFA中,∠CFA=90°,cos∠FCA=∴∠FCA=30°,即α=30°.(3)结论:AB2=2CF2+2BE2.理由:∵AB2=AC2+BC2=2BC2,BC2=CE2+BE2=CF2+BE2,∴AB2=2CF2+2BE2.【点评】本题考查相似三角形综合题、相似三角形的判定和性质、等腰直角三角形的性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.2.(8分)已知在平面直角坐标系xOy中的点P和图形G,给出如下的定义:若在图形G上存在一点Q,使得P、Q之间的距离等于1,则称P为图形G的关联点.(1)当⊙O的半径为1时,①点P1(,0),P2(1,),P3(0,3)中,⊙O的关联点有P1,P2.②直线经过(0,1)点,且与y轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标x的取值范围.(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径r的取值范围.【分析】(1)①利用两圆的位置关系即可判断;②根据定义分析,可得当最小y=﹣x上的点P到原点的距离在1到3之间时符合题意,设P(x,﹣x),根据两点间的距离公式即可得到结论;(2)根据关联点的定义求出圆的半径r的最大值与最小值即可解决问题;【解答】解:(1)①∵点P1(,0),P2(1,),P3(0,3)∴OP1=,OP2=2,OP3=3,∴半径为1的⊙P1与⊙O相交,半径为1的⊙P2与⊙O相交,半径为1的⊙P3与⊙O相离1,∴⊙O的关联点是P1,P2;故答案为:P1,P2;②如图,以O为圆心,2为半径的圆与直线y=1交于 P1,P2两点.线段P1,P2上的动点P(含端点)都是以O为圆心,1为半径的圆的关联点.故此﹣≤x≤.(2)由已知,若P为图形G的关联点,图形G必与以P为圆心1为半径的圆有交点.∵正方形ABCD边界上的点都是某圆的关联点,∴该圆与以正方形边界上的各点为圆心1为半径的圆都有交点故此,符合题意的半径最大的圆是以O为圆心,3为半径的圆;符合题意的半径最小的圆是以O为圆心,2﹣1 为半径的圆.综上所述,2﹣1≤r≤3.【点评】本题考查一次函数综合题、圆、正方形的有关性质等知识,解题的关键是理解题意,学会用转化的思想思考问题,学会用分类讨论的思想思考问题,属于中考压轴题.3.(5分)如图,Rt△ABC中,∠C=90°,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为xcm,BD长为ycm(当D与A重合时,y=4;当D与B重合时y=0).小云根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小云的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm 0 0.5 1 1.5 2 2.5 3 3.5 4y/cm 4 3.5 3.2 2.8 2.1 1.4 0.7 0补全上面表格,要求结果保留一位小数.则t≈ 2.9 .(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为2.3 cm.【分析】(1)按题意,认真测量即可;(2)利用数据描点、连线;(3)当DB=AE时,y=x,画图形测量交点横坐标即可.【解答】解:(1)根据题意量取数据为2.9故答案为:2.9(2)根据已知数据描点连线得:(3)当DB=AE时,y与x满足y=x,在(2)图中,画y=x图象,测量交点横坐标为2.3.故答案为:2.3【点评】本题以考查画函数图象为背景,应用了数形结合思想和转化的数学思想.4.(7分)已知抛物线:y=mx2﹣2mx+m+1(m≠0).(1)求抛物线的顶点坐标.(2)若直线l1经过(2,0)点且与x轴垂直,直线l2经过抛物线的顶点与坐标原点,且l1与l2的交点P在抛物线上.求抛物线的表达式.(3)已知点A(0,2),点A关于x轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出m的取值范围.【分析】(1)利用配方法把解析式配成顶点式即可得到抛物线的顶点坐标;(2)先确定P点坐标,然后把P点坐标代入y=mx2﹣2mx+m+1求出m 即可;(3)分别把A、B点的坐标代入y=mx2﹣2mx+m+1求出对应的m的值,然后根据二次函数的性质确定满足条件的m的范围.【解答】(1)解:∵y=mx2﹣2mx+m+1=m(x﹣1)2+1,∴抛物线的顶点坐标为(1,1);(2)易得直线l2的表达式为y=x,当x=2时,y=x=2,则P(2,2),把P(2,2)代入y=mx2﹣2mx+m+1得4m﹣4m+m+1=2,解得m=1,∴抛物线解析式为y=x2﹣2x+2;(3)点A(0,2)关于x轴的对称点B的坐标为(0,﹣2),当抛物线过A(0,2)时,把A(0,2)代入y=mx2﹣2mx+m+1得m+1=2,解得m=1,结合图象可知,当抛物线开口向上且和线段AB恰有一个公共点时,0<m≤1;当抛物线过B(0,﹣2)时,把B(0,﹣2)代入y=mx2﹣2mx+m+1得m+1=﹣2,解得m=﹣3,结合图象可知,当抛物线开口向上且和线段AB恰有一个公共点时,﹣3≤m<0;综上所述,m的取值范围是 0<m≤1或﹣3≤m<0.【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质.5.(5分)如图,AB是⊙O的直径,C、D是⊙O上两点, =.过点B作⊙O的切线,连接AC并延长交于点E,连接AD并延长交于点F.(1)求证:AC=CE.(2)若AE=8,sin∠BAF=求DF长.【分析】(1)连接BC,想办法证明AC=BC,EC=BC即可解决问题;(2)首先证明∠DBF=∠BAF,可得sin∠BAF=sin∠DBF==,由此即可解决问题;【解答】(1)证明:连结BC.∵AB是的直径,C在⊙O上∴∠ACB=90°,∵=,∴AC=BC∴∠CAB=45°.∵AB是⊙O的直径,EF切⊙O于点B,∴∠ABE=90°,∴∠AEB=45°,∴AB=BE,∴AC=CE.(2)在Rt△ABE中,∠ABE=90°,AE=8,AE=BE ∴AB=8,在Rt△ABF中,AB=8,sin∠BAF=,解得:BF=6,连结BD,则∠ADB=∠FDB=90°,∵∠BAF+∠ABD=90°,∠ABD+∠DBF=90°,∴∠DBF=∠BAF,∵sin∠BAF=,∴sin∠DBF=,∴=,∴DF=.【点评】本题考查切线的性质、圆周角定理、解直角三角形、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.(5分)在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于点A(2,0),与反比例函数y=的图象交于点B(3,n).(1)求一次函数与反比例函数的表达式;(2)若点P为x轴上的点,且△PAB的面积是2,则点P的坐标是(﹣2,0)或(6,0).【分析】(1)利用待定系数法即可解决问题;(2)利用三角形的面积公式求出PA的长即可解决问题;【解答】解:(1)∵一次函数y=x+b的图象与x轴交于点A(2,0),∴2+b=0,∴b=﹣2,∴y=x﹣2,当x=3时,y=1,∴B(3,1),代入y=中,得到k=3,∴反比例函数的解析式为y=.(2)∵△PAB的面积是2,∴PA=4,∴P(﹣2,0)或(6,0).【点评】本题考查一次函数的性质、反比例函数的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.7.(5分)如图,小明想测量山的高度.他在点B处仰望山顶A,测得仰角∠ABN=30°,再向山的方向(水平方向)行进100m至索道口点C处,在点C处仰望山顶A,测得仰角∠ACN=45°.求这座山的高度.(结果精确到0.1m,小明的身高忽略不计)(参考数据:≈1.41,≈1.73)【分析】作AH⊥BN于H,设AH=xm,根据正切的概念表示出CH、BH,根据题意列出方程,解方程即可.【解答】解:如图,作AH⊥BN于H,设AH=xm,∵∠ACN=45°,∵tanB=,∴BH=x,则BH﹣CH=BC,即x﹣x=100,解得x=50(+1).答:这座山的高度为50(+1)m;【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,正确作出辅助线、熟记锐角三角函数的概念是解题的关键.8.(5分)如图,四边形ABCD是平行四边形,CE⊥AD于点E,DF⊥BA交BA的延长线于点F.(1)求证:△ADF∽△DCE;(2)当AF=2,AD=6,且点E恰为AD中点时,求AB的长.【分析】(1)由平行四边形的性质知CD∥AB,即∠DAF=∠CDE,再由CE⊥AD、DF⊥BA知∠AFD=∠DEC=90°,据此可得;(2)根据△ADF∽△DCE知=,据此求得DC=9,再根据平行四边形的性质可得答案.【解答】解:(1)∵四边形ABCD是平行四边形,∴CD∥AB,∴∠DAF=∠CDE,又∵CE⊥AD、DF⊥BA,∴∠AFD=∠DEC=90°,∴△ADF∽△DCE;(2)∵AD=6、且E为AD的中点,∴DE=3,∵△ADF∽△DCE,∴=,即=,解得:DC=9,∵四边形ABCD是平行四边形,∴AB=CD=9.【点评】本题主要考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质及平行四边形的性质.9.(5分)二次函数y=x2﹣2mx+5m的图象经过点(1,﹣2).(1)求二次函数图象的对称轴;(2)当﹣4≤x≤1时,求y的取值范围.【分析】(1)根据抛物线的对称性和待定系数法求解即可;(2)根据二次函数的性质可得.【解答】解:(1)把点(1,﹣2)代入y=x2﹣2mx+5m中,可得:1﹣2m+5m=﹣2,解得:m=﹣1,所以二次函数y=x2﹣2mx+5m的对称轴是x=﹣,(2)∵y=x2+2x﹣5=(x+1)2﹣6,∴当x=﹣1时,y取得最小值﹣6,由表可知当x=﹣4时y=3,当x=﹣1时y=﹣6,∴当﹣4≤x≤1时,﹣6≤y≤3.【点评】本题考查了二次函数图象与性质及待定系数法求函数解析式,熟练掌握二次函数的图象与性质是解题的关键.10.(6分)如图,AC是⊙O的直径,点D是⊙O 上一点,⊙O的切线CB与AD的延长线交于点B,点F是直径AC上一点,连接DF并延长交⊙O于点E,连接AE.(1)求证:∠ABC=∠AED;(2)连接BF,若AD=,AF=6,tan∠AED=,求BF的长.【分析】(1)直接利用圆周角定理以及切线的性质定理得出∠ACD=∠ABC,进而得出答案;(2)首先得出DC的长,即可得出FC的长,再利用已知得出BC的长,结合勾股定理求出答案.【解答】(1)证明:连接DC,∵AC是⊙O的直径,∴∠BDC=90°,∴∠ABC+∠BCD=90°,∵⊙O的切线CB与AD的延长线交于点B,∴∠BCA=90°,∴∠ACD+∠BCD=90°,∴∠ACD=∠ABC,∴∠ABC=∠AED;(2)解:连接BF,∵在Rt△ADC中,AD=,tan∠AED=,∴tan∠ACD==,∴DC=AD=,∴AC==8,∵AF=6,∴CF=AC﹣AF=8﹣6=2,∵∠ABC=∠AED,∴tan∠ABC==,∴=,解得:BD=,故BC=6,则BF==2.【点评】此题主要考查了切线的性质与判定以及勾股定理等知识,正确得出∠ACD=∠ABC是解题关键.11.(7分)在平面直角坐标系xOy中,抛物线y=﹣x2+mx+n经过点A (﹣1,0)和B(0,3).(1)求抛物线的表达式;(2)抛物线与x轴的正半轴交于点C,连接BC.设抛物线的顶点P 关于直线y=t的对称点为点Q,若点Q落在△OBC的内部,求t的取值范围.【分析】(1)利用待定系数法即可解决问题;(2)分别求出点Q落在直线BC和x轴上时的t的值即可判断;【解答】解:(1)∵抛物线y=﹣x2+mx+n经过点A(﹣1,0)和B(0,3),∴,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,易知抛物线的顶点坐标为(1,4).观察图象可知当点P关于直线y=t的对称点为点Q中直线BC上时,t=3,当点P关于直线y=t的对称点为点Q在x轴上时,t=2,∴满足条件的t的值为2<t<3.【点评】本题考查二次函数的性质、待定系数法、轴对称等知识,解题的关键是熟练掌握基本知识,学会寻找特殊点解决问题,属于中考常考题型.。
【中考数学压轴题专题突破41】一次函数综合问题(1)

【中考压轴题专题突破41】一次函数综合问题(1)1.在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y1=x 交于点C.(1)当直线AB解析式为y2=﹣x+10时,如图1.①求点C的坐标;②根据图象求出当x满足什么条件时﹣x+10<x.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为9,且OA=6.P,Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.2.如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B 的直线交x轴于点C,且AB=BC.(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);(3)在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.3.如图1,在平面直角坐标系中,OB=10,F是y轴正半轴上一点.(1)若OF=2,求直线BF的解析式;(2)设OF=t,△OBF的面积为s,求s与t的函数关系(直接写出自变量t的取值范围);(3)如图3,在(2)的条件下,过点B作BA⊥x轴,点C在x轴上,OF=OC,连接AC,CD⊥直线BF于点D,∠ACB=2∠CBD,AC=13,OF=OC,AC.BD交于点E,求此时t的值.4.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB =OA,直线l2:y=k2x+b经过点C(,1),与x轴、y轴、直线AB分别交于点E、F、D三点.(1)求直线l1的解析式;(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.5.对于两个一次函数y1=k1x+b1和y2=k2x+b2(其中k1、k2、b1,b2均为常数且k1、k2均不为0),任取一个自变量x,当x<0时,y=y12+y2;当x≥0时,y=y12﹣y2,我们称这样的函数为函数y1=k1x+b1和y2=k2x+b2的“组合函数”.例如:y1=x﹣1和y2=x+1的“组合函数“为y=(1)已知一次函数y1=x﹣1和y2=4x﹣1.①求一次函数y1=x﹣1和y2=4x﹣1的“组合函数”所对应的函数表达式.②一次函数y1=x﹣1和y2=4x﹣1的“组合函数”的函数值y随x的增大而减小时,x的取值范围是.③当﹣4≤x≤4时,该“组合函数”的函数值y的取值范围是.(2)记一次函数y1=x﹣n(n>0)和y2=4nx+n2(其中n为常数)的“组合函数”的图象为G.①当n=1时,若直线y=a(a为常数)与图象G有三个不同的交点时,记三个交点的横坐标分别为x1、x2、x3(x1<x2<x3),求x1+x2+x3的取值范围.②在平面直角坐标系中,正方形ABCD的对称中心与原点重合,顶点A的坐标为(2,2),点B在第二象限.图象G与正方形ABCD的边恰好有两个公共点时,直接写出n的取值范围.6.如图,点O是平面直角坐标系的原点,直线y=kx+3交x轴于点A,交y轴于点B,OA =OB.(1)求k的值;(2)点P为第一象限内线段AB上方一点,点P的坐标为(t,),连接P A,PB,设△P AB的面积为S,求S关于t的函数关系式;(3)在(2)的条件下,在PB上方取一点C,连接BC,PC,使∠BCP=90°,且BC =PC.点D在线段AP上,且横坐标为,连接OC,CD,当∠OCD=45°时,求点P 的坐标.【中考压轴题专题突破41】一次函数综合问题(1)参考答案与试题解析1.解:(1)①由題意,,解得:,所以C(4,4).②观察图象可知x>4时,直线AB位于直线OC的下方,即x>4时,﹣x+10<x.(2)由题意,在OC上截取OM=OP,连结MQ,∵ON平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ.∴△POQ≌△MOQ(SAS),∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直銭上,且AM⊥OC吋,AQ+MQ最小,即AQ+PQ存在最小値;∴AB⊥ON,∴∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=6,∵△OAC的面积为9,∴OC•AM=9,∴AM=3,∴AQ+PQ存在最小值,最小值为3.2.解:(1)∵直线y=2x+6与x轴交于点A,与y轴交于点B,∴点B(0,6),点A(﹣3,0)∴AO=3,BO=6,∴AO=CO=3,∴点C(3,0),设直线BC解析式为:y=kx+b,则,解得:∴直线BC解析式为:y=﹣2x+6;(2)如图1,过点P作PG⊥AC于点G,过点Q作HQ⊥AC于点H,∵点Q横坐标为m,∴点Q(m,﹣2m+6),∵AB=CB,∴∠BAC=∠BCA=∠CHQ,∠PGA=∠QHC=90°,AP=CQ,∴△PGA≌△QHC(AAS),∴PG=HQ=2m﹣6,故点P的纵坐标为:2m﹣6,直线AB的表达式为:y=2x+6,即2m﹣6=2x+6,解得:x=m﹣6,故点P(m﹣6,2m﹣6);(3)如图2,连接AM,CM,过点P作PE⊥AC,∴BO是AC的垂直平分线,∴AM=CM,且AP=CQ,PM=MQ,∴△APM≌△CQM(SSS)∴∠P AM=∠MCQ,∠BQM=∠APM=45°,∵AM=CM,AB=BC,BM=BM,∴△ABM≌△CBM(SSS)∴∠BAM=∠BCM,∴∠BCM=∠MCQ,且∠BCM+∠MCQ=180°,∴∠BCM=∠MCQ=∠P AM=90°,且∠APM=45°,∴∠APM=∠AMP=45°,∴AP=AM,∵∠P AO+∠MAO=90°,∠MAO+∠AMO=90°,∴∠P AO=∠AMO,且∠PEA=∠AOM=90°,AM=AP,∴△APE≌△MAO(AAS)∴AE=OM,PE=AO=3,∴2m﹣6=3,∴m=,∴Q(,﹣3),P(﹣,3)设直线PQ的解析式为:y=ax+c,∴,解得:∴直线PQ的解析式为:y=﹣x+.3.解:(1)∵OB=10,OF=2,∴B(﹣10,0),F(0,2),设直线BF的解析式为y=kx+b,∵直线y=kx+b经过点B(﹣10,0),F(0,2),∴,解得:,∴直线BF的解析式为y=x+2;(2)△OBF的面积为S==5t(t>0);(3)如图,延长AB至点R,使BR=AB,连接CR,延长CD交y轴于点T,过点T,作TM∥x轴交BA的延长线于点M,过点T作TK⊥CR交RC的延长线于点K,连接RT,∵AB⊥BC,AB=BR,∴BC垂直平分AR,∴AC=CR=13,∴∠ACB=∠RCB,设∠CBD=α,则∠ACB=2α,∵BD⊥CD,∴∠BDC=90°,∴∠BCD=90°﹣α,∵∠ACB=∠RCB=2α,∴∠ACK=180°﹣4α,∴∠KCT=∠BCK﹣∠BCD=∠BCA+∠ACK﹣∠BCD=90°﹣α,∴∠KCT=∠BCD,∵TK⊥KR,OT⊥OC,∴OT=TK,∵TC=TC,∴Rt△OTC≌Rt△KTC(HL),∴OC=CK=TK=t,∵OF=OC,∠BOF=∠TOC,∠FBO=∠OTC,∴△BOF≌△TOC(AAS),∴OB=OT=10,∴TK=10,∵∠ABO+∠BOT=90°+90°=180°.∴MB∥OT,∵MT∥OB,∴四边形OBMT为平行四边形,∵OB=OT,∠BOT=90°.∴四边形OBMT为正方形,∴MB=MT=OT=10,∴MT=TK,∵RT=RT,∴Rt△RMT≌Rt△RTK(HL),∴RK=RM=CR+CK=13+t,∴BR=RM﹣MB=3+t,∵BC=OB+OC=10+t,在Rt△BRC中,BR2+BC2=RC2,∴(3+t)2+(10+t)2=132,解得:t=2(t=﹣15舍去).∴t的值为2.4.解:(1)y=k1x+6,当x=0时,y=6,∴OB=6,∵OB=OA,∴OA=2,∴A(﹣2,0),把A(﹣2,0)代入:y=k1x+6中得:﹣2k1+6=0,k1=,∴直线l1的解析式为:y=x+6;(2)如图1,过C作CH⊥x轴于H,∵C(,1),∴OH=,CH=1,Rt△ABO中,AB==4,∴AB=2OA,∴∠OBA=30°,∠OAB=60°,∵CD⊥AB,∴∠ADE=90°,∴∠AED=30°,∴EH=,∴OE=OH+EH=2,∴E(2,0),把E(2,0)和C(,1)代入y=k2x+b中得:,解得:,∴直线l2:y=﹣x+2,∴F(0,2)即BF=6﹣2=4,则,解得,∴D(﹣,3),∴S△BCD=BF(x C﹣x D)==4;(3)分四种情况:①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,∵△QCD是以CD为底边的等腰直角三角形,∴∠CQD=90°,CQ=DQ,∴∠DMQ=∠CNQ=90°,∴∠MDQ=∠CQN,∴△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=,设D(m,m+6)(m<0),则Q(0,﹣m+1),∴OQ=QN+ON=OM+QM,即﹣m+1=m+6+,m==1﹣2,∴Q(0,2);②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=1,设D(m,m+6)(m<0),则Q(m+1,0),∴OQ=QN﹣ON=OM﹣QM,即m+6﹣=﹣m﹣1,m=5﹣4,∴Q(6﹣4,0);③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=1,设D(m,m+6)(m<0),则Q(m﹣1,0),∴OQ=QN﹣ON=OM+QM,即﹣m﹣6﹣=﹣m+1,m=﹣4﹣5,∴Q(﹣4﹣6,0);④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=,设D(m,m+6)(m<0),则Q(0,m+1),∴OQ=QN﹣ON=OM+QM,即﹣m﹣6+=﹣m﹣1,m=﹣2﹣1,∴Q(0,﹣2);综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2)或(6﹣4,0)或(﹣4﹣6,0).5.解:(1)①当x≥0时,y=y12﹣y2,=(x﹣1)2﹣(4x﹣1)=x2﹣6x+2,当x<0时,y=y12+y2=,=(x﹣1)2+(4x﹣1)=x2+2x,∴y=②∵当x≥0时,函数解析式为:y=x2﹣6x+2,∴当0≤x≤3时,y随x的增大而减小.当x<0时,函数解析式为:y=x2+2x,∴x≤﹣1时,y随x的增大而减小.故答案为:x≤﹣1或0≤x≤3;③∵当﹣4≤x<0时,函数解析式为:y=x2+2x,∴﹣1≤y≤8,当0≤x≤4时,函数解析式为:y=x2﹣6x+2,∴﹣7≤y≤2,∴当﹣4≤x≤4时,﹣7≤y≤8;故答案为:﹣7≤y≤8;(2)①当n=1时,y1=x﹣1,y2=4x+1,∴组合函数为:y=∵直线y=a(a为常数)与图象G有三个不同的交点,∴1<a<2,∴当x2﹣6x=1时,x=3+,x=3﹣(舍去),当x2﹣6x=2时,x=3+,x=3﹣(舍去),∵x1+x2=﹣2,∴1+<x1+x2+x3<1+;②∵一次函数y1=x﹣n(n>0)和y2=4nx+n2,∴组合函数y=若y=x2﹣6nx(x>0)的顶点在正方形ABCD内时,∴﹣9n2>﹣2,0<3n<2,∴n2<,且0<n<,∴0<n<,此时y=x2+2nx+2n2与正方形ABCD的边也有1个交点,∴0<n<符合题意;若y=x2﹣6nx(x>0)的顶点不在正方形ABCD内部时,且与正方形ABCD的边有一个交点,∴22﹣6×n×2<﹣2,∴n>即y=x2+2nx+2n2与正方形ABCD的边有一个交点,∴2n2≤2∴n≤1,∴<n≤1;若y=x2+2nx+2n2的顶点在正方形ABCD的AB边上时,图象G与正方形ABCD的边恰好有两个公共点,∴n2=2,∴n=,综上所述:当0<n<或<n≤1或n=时,图象G与正方形ABCD的边恰好有两个公共点.6.解:(1)∵直线y=kx+3交y轴于点B,∴点B坐标(0,3),∴OB=3,∵OA=OB=3,∴点A(3,0),∴0=3k+3,∴k=﹣1;(2)如图1,过点P作PQ⊥OA,交AB于点Q,由(1)知,AB的解析式为:y=﹣x+3,∵点P的坐标为(t,),∴Q点的坐标为(t,﹣t+3),∴PQ=t+,∵,∴;(3)如图2,过点P作PM⊥OA于M,过点D作DN⊥OA于N,过点O作OH⊥OC,交CD的延长线于点H,连接AH,∵∠OCD=45°,∴∠OCH=∠OHC=45°,∴OC=OH,∵∠AOB=∠COH=90°,∴∠BOC=∠AOH,在△OBC和△OAH中,,∴△OBC≌△OAH(SAS),∴BC=AH,∠OCB=∠OHA,∵BC=CP,∴AH=PC,∵∠BCP=90°,∠OCD=45°,∴∠PCD=45°﹣∠OCB,∵∠AHD=45°﹣∠OHA,∴∠PCD=∠AHD,在△PCD和△AHD中,,∴△PCD≌△AHD(AAS),∴PD=P A,∵PM∥DN,∴MN=AN,∵D的横坐标为,点P的坐标为(t,),∴M(t,0),N(,0),∴﹣t=3﹣,∴t=,∴P(,).。
满分突破中考数学压轴题之专题练习(一)—解答压轴题方法与技巧

满分突破中考压轴题之专题练习(一)1.等腰△ ABC中,CA=CB点D为边AB上一点,沿CD折叠△ CAD得到△ CFD边CF交边(2)连接AF交CD的延长线于点M,连接ME交线段DF于点N,若EF=4EC AB=22,求MN的长.【考点】翻折变换(折叠问题);等腰三角形的性质.菁优网版权所有【解答】(1) 证明:如图1,•/ CA=CB •••/ A=Z ABC,•/ CD=CE CDE=/ CED,'Z A=Z ABC在厶ACE与厶BCD 中,,ZAEC二ZBDC t AC=C&•△ACE^A BCD (AAS)•AE=BD, AD=EB•/ AD=DF, • DF=EBI F二EB在厶DCF与厶ECB中 , “ CF二CBLCD=CE•••△DCF^A ECB ( SSS ,/ DCE=/ ECB / DFE=/ EBC,•/ FDE=Z BCE•••/ DEC=ZFEB•/ DCE=/ EBF,•△DEF^A CEBAB 于点E, CD=CE 连接BF.• FD=FB•△DE3A FEB, •/ FDB=/ FBD,(2) 解:•••沿CD 折叠△ CAD 得到△ CFD,••• CA=CF / CAD=Z CFD,•••/ CAD=Z CBE•••/ DEF=Z CEB又•••/ CED=/ BEF•••/ CFD=/ CBE, • △ DEF ^A CEB • △ CED^A BEF,•/ CD=CE• BE=BF , △ EBF 为等腰三角形,•/ CF=CBBCF 为等腰三角形, 则/ BCF=Z EBF,• / DCE=/ BCF, CEBCD 和/ BCD 的平分线,由角平分线定理,可得 CB _ EB CE+EF CD^ED ? CE =ED ?•/ EF=4EC•「_5・・ =5 ,ED•/ AB=AD+ED+EB=22,• 5ED+ED+5ED=22 ,解得ED=2,• •匸■ W TT•- 4CW=5ED 2 , EC=",由余弦定理,可得 ED 2=C D 2+C E ?- 2CD X CEcos / DCE cos / DCE=;.5如图2,过点M 作AE 的平行线分别交 FD EF 于点G 、H ,• M 为AF 边的中点,•••点G 、H 是FD EF 的中点,•/ EF=4EC• EH=2EC• MD=2CD , MH=3ED , •/ GH=- ED, 2• / DCE=/ EBF郢2•/△MNG s^ END,,讥=,MN= ME,ED EN EN 2 7在厶MCE中,由余弦定理,可得ME2=MC2+EC? - 2MC X EC X cos/ DCEME2=10EC - 3.6EC=6.4E(C ,• ME=4 二MN」2 .如图,Rt A ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点MB、MC、AC于点D、E、P,以DE为边向下作等边厶DEF,设厶DEF与厶MBC重叠部分的面积为S( cm2),直线I的运动时间为t (秒).(1) 求边BC的长度;(2) 求S与t的函数关系式;(3) 在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.(4) 在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.【考点】几何变换综合题.菁优网版权所有【解答】解:(1)设/ B=a,•/ MB=MC,M时停止•直线I分别交线段A•/ MC=MA,•••/ A=Z AMC=a ,•••/ B+Z A=90 ,•- a+2 a =90;•a =30°•Z B=30°;■/ cotB= I -;AC•BC=AC X cotB=8 ;厂;;(2)由题意,若点F恰好落在BC上,• MF=4 ( 4 - t) =4;--1=3.当0v t w3时,如图,• BD=2t;DM=8 - 2t ;•/ l // BC,•時」,•L1 :J-•: :,•DE= : (8 - 2t).•点D到EF的距离为FJ= DE=3 (4 - t),2•/ l // BC,•:V i;l】• ---DE"FJ•/ FN=FJ- JN=3 (4 - t)- t=12 - 4t,• "= 一( 3-t)S=S弟形DHG (HG+DE)X FN=-当3 v t w 4时,重叠部分就是厶DEF,S=S年匚詔=3二t2- 24和48 =.即:S= 3 2 砺t+4 结血(3<t<4)(3) 当 O v t w 3 时,/ FC 禺 90°••• Fd CP,•••△ PCF 不可能为等腰三角形当3 v t w 4时,若△ PCF 为等腰三角形,•只能FC=FP•-=3( 4 - t ), 2• t (7)•••存在这样的时刻t=— 时,使得以P 、C 、F 为顶点的三角形为等腰三角形,7 (4 )若相切,理由:•••/ B=30° ,• BD=2t , DM=8 - 2t ,•/ l // BC,…時」,•li :: ■'•-,• DE=二(8 - 2t ).• 2t=3 (4 - t ),解得t=—. 5•••存在这样的时刻t=l —时,使得以点D 为圆心、BD 为半径的圆与直线 EF 相切.^t Z +8V3t(O<t<3) DE=3 (4 - t )3.在Rt A ABC 中,/ ACB=90°, AC=BC=2点P 为BC 边上的一个动点 (不与B 、C 重合).点 第7页(共25页)• AP=AM=AN ,Z 1 = / 2,7 3=/4,•••/ CAB=/ 2+/ 3=45°,MAN=90(1) 当点P 为线段BC 的中点时,求/ M 的正切值;(2) 当点P 在线段BC 上运动时(不与 B 、C 重合),连接AM 、AN ,求证:① 厶AMN 为等腰直角三角形;② 厶 AEF ^A BAM .【考点】相似形综合题.菁优网版权所有【解答】(1 )解:连接NB ,如图1 ,•••在 Rt A ABC 中,/ ACB=90 , AC=BC•••△ ACB 为等腰直角三角形,•••/ A=Z CBA=45 ,•••点P 关于直线AB 的对称点为N ,关于直线AC 的对称点为M ,• AB 垂直 PN, BN=BP,•••/ NBA=Z PBA=45 ,•••/ PBN=90 ,•••点P 为BC 的中点,BC=2,• MC=CP=PB=NB=1• tan / M= m =X 1厂二(2)证明:①连接AP,如图2,•••点P 关于直线AC AB 的对称点分别为M 、N , P 关于直线AC 、AB 的对称点分别为 M 、N ,连接MN 交AC 于点E,交AB 于点F .•••△AMN为等腰直角三角形;②•••△ AMN为等腰直角三角形,•••/ 5=/ 6=45°,•••/ AEF=/ 5+/ 仁45° + / 1 ,•// EAF=45•/ BAM=/ EAF+/ 仁45° + / 1,•/ AEF=/ BAM,又•••/ B=/ EAF=45•△AEF^A BAM.d4. 已知:在梯形ABCD中,AD// BC, AC=BC=10cos/ ACB=:,点E在对角线AC上,且CE=AD,5BE的延长线与射线AD、射线CD分别相交于点F、G,设AD=x,A AEF的面积为y.(1 )求证:/ DCA=/ EBC;(2) 如图,当点G在线段CD上时,求y关于x的函数解析式,并写出它的定义域;(3) 如果△ DFG是直角三角形,求△ AEF的面积.【考点】相似形综合题.菁优网版权所有【解答】(1)证明:T AD / BC,•/ DAC=/ ECB 在厶DCA和厶ECB中,r AD=CE,ZDAC^ZECB ,M 二BC•△DCA^A ECB( SAS,• / DCA=/ EBC(2)T AD// BC,•••△ AEF^A CEB,• .': T !\ : 即I J…茁—:T.,: ,,解得:AF=』'',X作EH丄AF于H ,如图1所示,• EH=;AE=;(10 -x),5 51 3--y=S^ AEF= x —25(10- x)10(10-x) =3(10P)2•- 0v x w 5訂.:-5 ,• y关于x的函数解析式为: y_ " ' ||:, ' 11y=(0v x< 5 , I - 5); (3)分两种情况考虑:①当/ FDG_90时,如图2所示:A在Rt A ADC 中,AD_AC X—_8 ,即x_8 ,5• S L :…AAEF_y_ —②当/ DGF_90时,过E作EM丄BC于点M,如图3所示,由(1)得:CE_AF_x3 4在Rt A EMC 中,EM_ x , MC_ x ,5 5•BM_BC- MC_10-二x,5•••/ GCE_/ GBC, / EGC_/ CGB,•△CGE^A BGC,.CE_CG 即工_CG•g_ j ' : _ ,•••点G在线段CD上,• AF> AD ,即 _ > x,(1) (2)(3) 求厶BCQ 的面积S 与t 的函数关系式.t 为何值时,QP// AC ?t 为何值时,直线 QR 经过点P ?当点P 在AB 上运动时,以PQ 为边在AB 上方所作的正方形 PQMN 在 Rt A ABC 内部,求此时t 的取值范围.【考点】相似形综合题.菁优网版权所有【解答】解:(1 )过C 作CD 丄AB 于D 点,如图所示:•/ AB=10, AQ=2+2t ,• QB=AB- AQ=10-( 2+2t ) =8 - 2t ,在 Rt A ABC 中,AB=10, AC=8,根据勾股定理得:BC=6,•••/ EBM=Z CBG, / BME=Z BGC=90 ,•••△ BMEs^ BGC,-■<?1!=匸''丽硕io4/53• 1 =,即 x=5, 10碍 5此时 y= ;「’=15,综上,此时△ AEF 的面积为「或15.5. 在 Rt A ABC 中,/ C=90° AB=10, AC=8,点 Q 在 AB 上,且 AQ=2,过 Q 做 QR 丄 AB,垂 足为Q , QR 交折线AC- CB 于R (如图1),当点Q 以每秒2个单位向终点B 移动时,点P 同时从A 出发,以每秒6个单位的速度沿 AB - BC- CA 移动,设移动时间为t 秒(如图2).•••丄AC?BC= AB?CD,即卩-X 6X X 10X CD,2 2 2 2••• CD二,5则S^BCQ F QB?CD= (8- 2t) =- 〔t+ ( 0 < t w 4);2 5 5 5(2)当PQ// AC 时,可得/ BPQ=Z C,Z BQP=Z A,• △ BPQ^A BCA, 又BQ=8- 2t, BP=6t- 10,•讥=[F 即-'■ J" -一…, i _ -,整理得:6 (8 - 2t) =10 (6t - 10),解得:t=',18则t= 1时,QP/ AC;18(3)①当Q、P 均在AB 上时,AP=6t , AQ=2+2t ,可得:AP=AQ,即6t=2+2t,解得:t=0.5s ;②当P在BC上时,P与R重合,如图所示:•••/ PQB=Z ACB=90 , / B=Z B ,•△BP2A BAC,•—,又BP=6t- 10 , AB=10 , BQ=8- 2t ,BC=6 AB BC'1= :,即6 (6t - 10) =10 (8 - 2t),10 6解得:t=2.5s;③当P在AC上不存在QR经过点P ,综上,当t=0.5s或2.5s时直线QR经过点P;(4) 当点P在点Q的左侧时,若点N落在AC上,如图所示:•/ AP=6t , AQ=2+2t ,•PQ=AQ- AP=2+2t - 6t=2 - 4t ,•••四边形PQMN是正方形,•PN=PQ=2- 4t,•••/ APN=Z ACB=90 , / A=Z A ,第10页(共25页)。
中考数学压轴题之一元二次方程组(中考题型整理,突破提升)附答案解析

(2)若方程两实根 x1 , x2 满足 x1 x2 x1x2 1 0 ,求 k 的值.
【答案】(1) k< 1 ;(2) k=0. 4
【解析】 【分析】 (1)根据一元二次方程的根的判别式得出△ >0,求出不等式的解集即可; (2)根据根与系数的关系得出 x1+x2=-(2k-1)=1-2k,x1•x2=k2,代入 x1+x2+x1x2-1=0,即可 求出 k 值. 【详解】 解:(1)∵ 关于 x 的一元二次方程 x2+(2k-1)x+k2=0 有两个不等实根 x1,x2,
月份
用水量 (吨)
水费 (元)
四月
35
59.5
五月
80
151
【答案】
5.有一个人患了流感,经过两轮传染后共有 36 人患了流感. (1)求每轮传染中平均一个人传染了几个人? (2)如果不及时控制,第三轮将又有多少人被传染? 【答案】(1)5;(2)180 【解析】 【分析】 (1)设平均一人传染了 x 人,根据有一人患了流感,经过两轮传染后共有 36 人患了流 感,列方程求解即可; (2)根据每轮传染中平均一个人传染的人数和经过两轮传染后的人数,列出算式求解即 可. 【详解】 (1)设每轮传染中平均一个人传染了 x 个人,根据题意得: x+1+(x+1)x=36, 解得:x=5 或 x=﹣7(舍去). 答:每轮传染中平均一个人传染了 5 个人; (2)根据题意得:5×36=180(个), 答:第三轮将又有 180 人被传染.
2a
2 2
2
∴ x1=-1+ 6 ,x2=-1- 6
2
2
(2)(y+2)2-(3y-1)2=0
中考数学28道压轴题含答案解析

中考数学选填压轴题练习一.根的判别式(共1小题)1.(2023•广州)已知关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,则的化简结果是()A.﹣1B.1C.﹣1﹣2k D.2k﹣3【分析】首先根据关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,得判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,由此可得k≤1,据此可对进行化简.【解答】解:∵关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,∴判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,整理得:﹣8k+8≥0,∴k≤1,∴k﹣1≤0,2﹣k>0,∴=﹣(k﹣1)﹣(2﹣k)=﹣1.故选:A.二.函数的图象(共1小题)2.(2023•温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.【问题】路线①③⑥⑦⑧各路段路程之和为()A.4200米B.4800米C.5200米D.5400米【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.【解答】解:由图象可知:小州游玩行走的时间为75+10﹣40=45(分钟),小温游玩行走的时间为205﹣100=105(分钟),设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米由图象可得:,解得:x+y+z=2700,∴游玩行走的速度为:(2700﹣2100)÷10=60 (米/分),由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为:3x+3y=105×60=6300,∴x+y=2100,∴路线①③⑥⑦⑧各路段路程之和为:2x+2y+z=x+y+z+x+y=2700+2100=4800(米).故选:B.三.动点问题的函数图象(共1小题)3.(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.D.【分析】如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=,易知∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,可知AO=OB=,过点O作OD⊥AB,解直角三角形可得AD=AO•cos30°,进而得出等边三角形ABC的边长.【解答】解:如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,\结合图象可知,当点P在AO上运动时,,∴PB=PC,,又∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∴△APB≌△APC(SSS),∴∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,∴OB=,即AO=OB=,∴∠BAO=∠ABO=30°,过点O作OD⊥AB,垂足为D,∴AD=BD,则AD=AO•cos30°=3,∴AB=AD+BD=6,即等边三角形ABC的边长为6.故选:A.四.反比例函数系数k的几何意义(共1小题)4.(2023•宁波)如图,点A,B分别在函数y=(a>0)图象的两支上(A在第一象限),连结AB交x 轴于点C.点D,E在函数y=(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若AC =2BC,△ABE的面积为9,四边形ABDE的面积为14,则a﹣b的值为12,a的值为9.【分析】依据题意,设A(m,),再由AE∥x轴,BD∥y轴,AC=2BC,可得B(﹣2m,﹣),D (﹣2m,﹣),E(,),再结合△ABE的面积为9,四边形ABDE的面积为14,即可得解.【解答】解:设A(m,),∵AE∥x轴,且点E在函数y=上,∴E(,).∵AC=2BC,且点B在函数y=上,∴B(﹣2m,﹣).∵BD∥y轴,点D在函数y=上,∴D(﹣2m,﹣).∵△ABE的面积为9,∴S△ABE=AE×(+)=(m﹣)(+)=m••==9.∴a﹣b=12.∵△ABE的面积为9,四边形ABDE的面积为14,∴S△BDE=DB•(+2m)=(﹣+)()m=(a﹣b)••()•m=3()=5.∴a=﹣3b.又a﹣b=12.∴a=9.故答案为:12,9.五.反比例函数图象上点的坐标特征(共2小题)5.(2023•德州)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(6,3),D是OA的中点,AC,BD交于点E,函数的图象过点B.E.且经过平移后可得到一个反比例函数的图象,则该反比例函数的解析式()A.y=﹣B.C.D.【分析】先根据函数图象经过点B和点E,求出a和b,再由所得函数解析式即可解决问题.【解答】解:由题知,A(6,0),B(6,3),C(0,3),令直线AC的函数表达式为y1=k1x+b1,则,解得,所以.又因为点D为OA的中点,所以D(3,0),同理可得,直线BD的函数解析式为y2=x﹣3,由得,x=4,则y=4﹣3=1,所以点E坐标为(4,1).将B,E两点坐标代入函数解析式得,,解得.所以,则,将此函数图象向左平移3个单位长度,再向下平移4个单位长度,所得图象的函数解析式为:.故选:D.6.如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.(1)k=;(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2﹣BD2的值为4.【分析】(1)根据直角三角形的性质,求出A、B两点坐标,作出辅助线,证得△OPC≌△APC(HL),利用勾股定理及待定系数法求函数解析式即可解答.(2)求出AC、BD的解析式,再联立方程组,求得点D的坐标,分两种情况讨论即可求解.【解答】解:(1)在Rt△OAB中,AB=2,∠AOB=30°,∴,∴,∵C是OB的中点,∴OC=BC=AC=2,如图,过点C作CP⊥OA于P,∴△OPC≌△APC(HL),∴,在Rt△OPC中,PC=,∴C(,1).∵反比例函数y=(k>0)的图象经过斜边OB的中点C,∴,解得k=.故答案为:.(2)设直线AC的解析式为y=k1x+b(k≠0),则,解得,∴AC的解析式为y=﹣x+2,∵AC∥BD,∴直线BD的解析式为y=﹣x+4,∵点D既在反比例函数图象上,又在直线BD上,∴联立得,解得,,当D的坐标为(2+3,)时,BD2==9+3=12,∴OB2﹣BD2=16﹣12=4;当D的坐标为(2﹣3,)时,BD2=+=9+3=12,∴OB2﹣BD2=16﹣12=4;综上,OB2﹣BD2=4.故答案为:4.六.反比例函数与一次函数的交点问题(共1小题)7.(2023•湖州)已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t,p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠﹣2),点C(t,m)和点D(t+2,n)在函数的图象上.当p﹣m与q﹣n的积为负数时,t的取值范围是()A.或B.或C.﹣3<t<﹣2或﹣1<t<0D.﹣3<t<﹣2或0<t<1【分析】将交点的横坐标1代入两个函数,令二者函数值相等,得k1=k2.令k1=k2=k,代入两个函数表达式,并分别将点A、B的坐标和点C、D的坐标代入对应函数,进而分别求出p﹣m与q﹣n的表达式,代入解不等式(p﹣m)(q﹣n)<0并求出t的取值范围即可.【解答】解:∵y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,∴k1=k2.令k1=k2=k(k>0),则y=k1x=kx,=.将点A(t,p)和点B(t+2,q)代入y=kx,得;将点C(t,m)和点D(t+2,n)代入y=,得.∴p﹣m=kt﹣=k(t﹣),q﹣n=k(t+2)﹣=k(t+2﹣),∴(p﹣m)(q﹣n)=k2(t﹣)(t+2﹣)<0,∴(t﹣)(t+2﹣)<0.∵(t﹣)(t+2﹣)=•=<0,∴<0,∴t(t﹣1)(t+2)(t+3)<0.①当t<﹣3时,t(t﹣1)(t+2)(t+3)>0,∴t<﹣3不符合要求,应舍去.②当﹣3<t<﹣2时,t(t﹣1)(t+2)(t+3)<0,∴﹣3<t<﹣2符合要求.③当﹣2<t<0时,t(t﹣1)(t+2)(t+3)>0,∴﹣2<t<0不符合要求,应舍去.④当0<t<1时,t(t﹣1)(t+2)(t+3)<0,∴0<t<1符合要求.⑤当t>1时,t(t﹣1)(t+2)(t+3)>0,∴t>1不符合要求,应舍去.综上,t的取值范围是﹣3<t<﹣2或0<t<1.故选:D.七.二次函数图象与系数的关系(共3小题)8.(2023•乐至县)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).现有以下结论:①abc<0;②5a+c=0;③对于任意实数m,都有2b+bm≤4a﹣am2;④若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,则y1<y2,其中正确的结论是()A.①②B.②③④C.①②④D.①②③④【分析】根据题意和函数图象,利用二次函数的性质,可以判断各个小题中的结论是否正确,从而可以解答本题.【解答】解:由图象可得,a>0,b>0,c<0,∴abc<0,故①正确,∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).∴﹣=﹣2,a+b+c=0,∴b=4a,∴a+b+c=a+4a+c=0,故5a+c=0,故②正确,∵当x=﹣2时,y=4a﹣2b+c取得最小值,∴am2+bm+c≥4a﹣2b+c,即2b+bm≥4a﹣am2(m为任意实数),故③错误,∵抛物线开口向上,对称轴为直线x=﹣2,若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,∴y1<y2,故④正确;故选:C.9.(2023•丹东)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为A(﹣3,0),与y轴交于点C,点D是抛物线的顶点,对称轴为直线x=﹣1,其部分图象如图所示,则以下4个结论:①abc>0;②E(x1,y1),F(x2,y2)是抛物线y=ax2+bx(a≠0)上的两个点,若x1<x2,且x1+x2<﹣2,则y1<y2;③在x轴上有一动点P,当PC+PD的值最小时,则点P的坐标为;④若关于x的方程ax2+b(x﹣2)+c =﹣4(a≠0)无实数根,则b的取值范围是b<1.其中正确的结论有()A.1个B.2个C.3个D.4个【分析】根据所给函数图象可得出a,b,c的正负,再结合抛物线的对称性和增减性即可解决问题.【解答】解:根据所给函数图象可知,a>0,b>0,c<0,所以abc<0,故①错误.因为抛物线y=ax2+bx的图象可由抛物线y=ax2+bx+c的图象沿y轴向上平移|c|个单位长度得到,所以抛物线y=ax2+bx的增减性与抛物线y=ax2+bx+c的增减性一致.则当x<﹣1时,y随x的增大而减小,又x1<x2,且x1+x2<﹣2,若x2<﹣1,则E,F两点都在对称轴的左侧,此时y1>y2.故②错误.作点C关于x轴的对称点C′,连接C′D与x轴交于点P,连接PC,此时PC+PD的值最小.将A(﹣3,0)代入二次函数解析式得,9a﹣3b+c=0,又,即b=2a,所以9a﹣6a+c=0,则c=﹣3a.又抛物线与y轴的交点坐标为C(0,c),则点C坐标为(0,﹣3a),所以点C′坐标为(0,3a).又当x=﹣1时,y=﹣4a,即D(﹣1,﹣4a).设直线C′D的函数表达式为y=kx+3a,将点D坐标代入得,﹣k+3a=﹣4a,则k=7a,所以直线C′D的函数表达式为y=7ax+3a.将y=0代入得,x=.所以点P的坐标为(,0).故③正确.将方程ax2+b(x﹣2)+c=﹣4整理得,ax2+bx+c=2b﹣4,因为方程没有实数根,所以抛物线y=ax2+bx+c与直线y=2b﹣4没有公共点,所以2b﹣4<﹣4a,则2b﹣4<﹣2b,解得b<1,又b>0,所以0<b<1.故④错误.所以正确的有③.故选:A.10.(2023•河北)已知二次函数y=﹣x2+m2x和y=x2﹣m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.m2C.4D.2m2【分析】求出三个交点的坐标,再构建方程求解.【解答】解:令y=0,则﹣x2+m2x=0和x2﹣m2=0,∴x=0或x=m2或x=﹣m或x=m,∵这四个交点中每相邻两点间的距离都相等,若m>0,则m2=2m,∴m=2,若m<0时,则m2=﹣2m,∴m=﹣2.∵抛物线y=x2﹣m2的对称轴为直线x=0,抛物线y=﹣x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选:A.八.二次函数图象上点的坐标特征(共1小题)11.(2023•广东)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac 的值为()A.﹣1B.﹣2C.﹣3D.﹣4【分析】过A作AH⊥x轴于H,根据正方形的性质得到∠AOB=45°,得到AH=OH,利用待定系数法求得a、c的值,即可求得结论.【解答】解:过A作AH⊥x轴于H,∵四边形ABCO是正方形,∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m),则B(0,2m),∴,解得am=﹣1,m=,∴ac的值为﹣2,故选:B.九.二次函数与不等式(组)(共1小题)12.(2023•西宁)直线y1=ax+b和抛物线(a,b是常数,且a≠0)在同一平面直角坐标系中,直线y1=ax+b经过点(﹣4,0).下列结论:①抛物线的对称轴是直线x=﹣2;②抛物线与x轴一定有两个交点;③关于x的方程ax2+bx=ax+b有两个根x1=﹣4,x2=1;④若a >0,当x<﹣4或x>1时,y1>y2.其中正确的结论是()A.①②③④B.①②③C.②③D.①④【分析】根据直线y1=ax+b经过点(﹣4,0).得到b=4a,于是得到=ax2+4ax,求得抛物线的对称轴是直线x=﹣﹣=2;故①正确;根据Δ=16a2>0,得到抛物线与x轴一定有两个交点,故②正确;把b=4a,代入ax2+bx=ax+b得到x2+3x﹣4=0,求得x1=﹣4,x2=1;故③正确;根据a>0,得到抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,于是得到结论.【解答】解:∵直线y1=ax+b经过点(﹣4,0).∴﹣4a+b=0,∴b=4a,∴=ax2+4ax,∴抛物线的对称轴是直线x=﹣﹣=2;故①正确;∵=ax2+4ax,∴Δ=16a2>0,∴抛物线与x轴一定有两个交点,故②正确;∵b=4a,∴方程ax2+bx=ax+b为ax2+4ax=ax+4a得,整理得x2+3x﹣4=0,解得x1=﹣4,x2=1;故③正确;∵a>0,抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,∴当x<﹣4或x>1时,y1<y2.故④错误,故选:B.一十.三角形中位线定理(共1小题)13.(2023•广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 1.2.若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是3≤S≤4.【分析】依据题意,根据三角形中位线定理可得DE=AM=1.2;设AM=x,从而DE=x,由DE∥AM,且DE=AM,又FG∥AM,FG=AM,进而DE∥FG,DE=FG,从而四边形DEFG是平行四边形,结合题意可得DE边上的高为(4﹣x),故四边形DEFG面积S=4x﹣x2,进而利用二次函数的性质可得S的取值范围.【解答】解:由题意,点D,E分别是AB,MB的中点,∴DE是三角形ABM的中位线.∴DE=AM=1.2.如图,设AM=x,∴DE=AM=x.由题意得,DE∥AM,且DE=AM,又FG∥AM,FG=AM,∴DE∥FG,DE=FG.∴四边形DEFG是平行四边形.由题意,GF到AC的距离是x,BC==8,∴DE边上的高为(4﹣x).∴四边形DEFG面积S=2x﹣x2,=﹣(x﹣4)2+4.∵2.4<x≤6,∴3≤S≤4.故答案为:1.2;3≤S≤4.一十一.矩形的性质(共2小题)14.(2023•宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连结AE,AD,设△AED,△ABE,△ACD的面积分别为S,S1,S2,若要求出S﹣S1﹣S2的值,只需知道()A.△ABE的面积B.△ACD的面积C.△ABC的面积D.矩形BCDE的面积【分析】作AG⊥ED于点G,交BC于点F,可证明四边形BFGE是矩形,AF⊥BC,可推导出S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,所以只需知道S△ABC,就可求出S﹣S1﹣S2的值,于是得到问题的答案.【解答】解:作AG⊥ED于点G,交BC于点F,∵四边形BCDE是矩形,∴∠FBE=∠BEG=∠FGE=90°,BC∥ED,BC=ED,BE=CD,∴四边形BFGE是矩形,∠AFB=∠FGE=90°,∴FG=BE=CD,AF⊥BC,∴S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,∴只需知道S△ABC,就可求出S﹣S1﹣S2的值,故选:C.15.(2023•河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为2或1+.【分析】以点D,M,N为顶点的三角形是直角三角形时,分两种情况:如图1,当∠MND=90°时,如图2,当∠NMD=90°时,根据矩形的性质和等腰直角三角形的性质即可得到结论.【解答】解:以点D,M,N为顶点的三角形是直角三角形时,分两种情况:①如图1,当∠MND=90°时,则MN⊥AD,∵四边形ABCD是矩形,∴∠A=90°,∴MN∥AB,∵M为对角线BD的中点,∴AN=DN,∵AN=AB=1,∴AD=2AN=2;如图2,当∠NMD=90°时,则MN⊥BD,∵M为对角线BD的中点,∴BM=DM,∴MN垂直平分BD,∴BN=DN,∵∠A=90°,AB=AN=1,∴BN=AB=,∴AD=AN+DN=1+,综上所述,AD的长为2或1+.故答案为:2或1+.一十二.正方形的性质(共2小题)16.如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为()A.B.C.D.【分析】由正方形ABCD的边长为4及BG=3CG,可求出BG的长,进而求出AG的长,证△ADE∽△GAB,利用相似三角形对应边成比例可求得AE、DE的长,证△ABF≌△DAE,得AF=DE,根据线段的和差求得EF的长即可.【解答】解:∵四边形ABCD是正方形,AB=4,∴BC=CD=DA=AB=4,∠BAD=∠ABC=90°,AD∥BC,∴∠DAE=∠AGB,∵BG=3CG,∴BG=3,∴在Rt△ABG中,AB2+BG2=AG2,∴AG=,∵DE⊥AG,∴∠DEA=∠DEF=∠ABC=90°,∴△ADE∽△GAB,∴AD:GA=AE:GB=DE:AB,∴4:5=AE:3=DE:4,∴AE=,DE=,又∵BF∥DE,∴∠AFB=∠DEF=90°,又∵AB=AD,∠DAE=∠ABF(同角的余角相等),∴△ABF≌△DAE,∴AF=DE=,∴EF=AF﹣AE=,∴tan∠EDF=,故选:A.17.(2023•湖州)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.(1)若EF=3cm,AE+FC=11cm,则BE的长是4cm.(2)若,则tan∠DAH的值是3.【分析】(1)将AE和FC用BE表示出来,再代入AE+FC=11cm,即可求出BE的长;(2)由已知条件可以证明∠DAH=∠CDG,从而得到tan∠DAH=tan∠CDG,设AH=x,DG=5k,GH =4k,用x和k的式子表示出CG,再利用tan∠DAH=tan∠CDG列方程,解出x,从而求出tan∠DAH 的值.【解答】解:(1)∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∵AE+FC=11cm,∴BE+BF=11cm,即BE+BE+EF=11cm,即2BE+EF=11cm,∵EF=3cm,∴2BE+3cm=11cm,∴BE=4cm,故答案为:4;(2)设AH=x,∵,∴可设DG=5k,GH=4k,∵四边形EFGH是正方形,∴HE=EF=FG=GH=4k,∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∠ABE=∠CBF=45°,∴CG=CF+GF=BF+4k=BE+8k=AH+12k=x+12k,∠ABC=∠ABE+∠CBF=45°+45°=90°,∵四边形ABCD对角互补,∴∠ADC=90°,∴∠ADH+∠CDG=90°,∵四边形EFGH是正方形,∴∠AHD=∠CGD=90°,∴∠ADH+∠DAH=90°,∴∠DAH=∠CDG,∴tan∠DAH=tan∠CDG,∴,即,整理得:x2+12kx﹣45k2=0,解得x1=3k,x2=﹣15k(舍去),∴tan∠DAH===3.故答案为:3.一十三.正多边形和圆(共1小题)18.(2023•河北)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:(1)∠α=30度;(2)中间正六边形的中心到直线l的距离为2(结果保留根号).【分析】(1)作图后,结合正多边形的外角的求法即可得到结论;(2)把问题转化为图形问题,首先作出图形,标出相应的字母,把正六边形的中心到直线l的距离转化为求ON=OM+BE,再根据正六边形的性质以及三角函数的定义,分别求出OM,BE即可.【解答】解:(1)作图如图所示,∵多边形是正六边形,∴∠ACB=60°,∵BC∥直线l,∴∠ABC=90°,∴α=30°;故答案为:30°;(2)取中间正六边形的中心为O,作图如图所示,由题意得,AG∥BF,AB∥GF,BF⊥AB,∴四边形ABFG为矩形,∴AB=GF,∵∠BAC=∠FGH,∠ABC=∠GFH=90°,∴△ABC≌△GFH(SAS),∴BC=FH,在Rt△PDE中,DE=1,PE=,由图1知AG=BF=2PE=2,OM=PE=,∵,∴,∴,∵,∴,∴.∴中间正六边形的中心到直线l的距离为2,故答案为:2.一十四.扇形面积的计算(共1小题)19.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为5.若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为.【分析】根据不共线三点确定一个圆,根据对称性得出圆心的位置,进而垂径定理、勾股定理求得r,连接OE,取ED的中点T,连接OT,在Rt△OET中,根据勾股定理即可求解.【解答】解:如图所示,依题意,GH=2=GQ,∵过左侧的三个端点Q,K,L作圆,QH=HL=4,又NK⊥QL,∴O在KN上,连接OQ,则OQ为半径,∵OH=r﹣KH=r﹣2,在Rt△OHQ中,OH2+QH2=QO2,∴(r﹣2)2+42=r2,解得:r=5;连接OE,取ED的中点T,连接OT,交AB于点S,连接PB,AM,过点O作OU⊥AM于点U.连接OA.由△OUN∽△NPM,可得==,∴OU=.MN=2,∴NU=,∴AU==,∴AN=AU﹣NU=2,∴AN=MN,∵AB∥PN,∴AB⊥OT,∴AS=SB,∴NS∥BM,∴NS∥MP,∴M,P,B共线,又NB=NA,∴∠ABM=90°,∵MN=NB,NP⊥MP,∴MP=PB=2,∴NS=MB=2,∵KH+HN=2+4=6,∴ON=6﹣5=1,∴OS=3,∵,设EF=ST=a,则,在Rt△OET中,OE2=OT2+TE2,即,整理得5a2+12a﹣32=0,即(a+4)(5a﹣8)=0,解得:或a=﹣4,∴题字区域的面积为.故答案为:.一十五.轴对称-最短路线问题(共1小题)20.(2023•安徽)如图,E是线段AB上一点,△ADE和△BCE是位于直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,则下列结论错误的是()A.P A+PB的最小值为3B.PE+PF的最小值为2C.△CDE周长的最小值为6D.四边形ABCD面积的最小值为3【分析】延长AD,BC交于M,过P作直线l∥AB,由△ADE和△BCE是等边三角形,可得四边形DECM 是平行四边形,而P为CD中点,知P为EM中点,故P在直线l上运动,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB=P A'+PB最小,即可得P A+PB 最小值A'B==2,判断选项A错误;由PM=PE,即可得当M,P,F共线时,PE+PF 最小,最小值为MF的长度,此时PE+PF的最小值为2,判断选项B正确;过D作DK⊥AB于K,过C作CT⊥AB于T,由△ADE和△BCE是等边三角形,得KT=KE+TE=AB=2,有CD≥2,故△CDE周长的最小值为6,判断选项C正确;设AE=2m,可得S四边形ABCD=(m﹣1)2+3,即知四边形ABCD面积的最小值为3,判断选项D正确.【解答】解:延长AD,BC交于M,过P作直线l∥AB,如图:∵△ADE和△BCE是等边三角形,∴∠DEA=∠MBA=60°,∠CEB=∠MAB=60°,∴DE∥BM,CE∥AM,∴四边形DECM是平行四边形,∵P为CD中点,∴P为EM中点,∵E在线段AB上运动,∴P在直线l上运动,由AB=4知等边三角形ABM的高为2,∴M到直线l的距离,P到直线AB的距离都为,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB =P A'+PB最小,此时P A+PB最小值A'B===2,故选项A错误,符合题意;∵PM=PE,∴PE+PF=PM+PF,∴当M,P,F共线时,PE+PF最小,最小值为MF的长度,∵F为AB的中点,∴MF⊥AB,∴MF为等边三角形ABM的高,∴PE+PF的最小值为2,故选项B正确,不符合题意;过D作DK⊥AB于K,过C作CT⊥AB于T,如图,∵△ADE和△BCE是等边三角形,∴KE=AE,TE=BE,∴KT=KE+TE=AB=2,∴CD≥2,∴DE+CE+CD≥AE+BE+2,即DE+CE+CD≥AB+2,∴DE+CE+CD≥6,∴△CDE周长的最小值为6,故选项C正确,不符合题意;设AE=2m,则BE=4﹣2m,∴AK=KE=m,BT=ET=2﹣m,DK=AK=m,CT=BT=2﹣m,∴S△ADK=m•m=m2,S△BCT=(2﹣m)(2﹣m)=m2﹣2m+2,S梯形DKTC =(m+2﹣m)•2=2,∴S四边形ABCD=m2+m2﹣2m+2+2=m2﹣2m+4=(m﹣1)2+3,∴当m=1时,四边形ABCD面积的最小值为3,故选项D正确,不符合题意;故选:A.一十六.翻折变换(折叠问题)(共2小题)21.(2023•乐至县)如图,在平面直角坐标系xOy中,边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动,将△ABC沿BC所在直线翻折得到△DBC,则OD的最大值为+1.【分析】过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,在Rt△ABO 中利用斜边中线性质求出OE,根据OE+DE≥OD确定当D、O、E三点共线时OD最大,最大值为OD =OE+DE.【解答】解:如图,过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,∵等边三角形ABC的边长为2,∴AB=2,∠ABC=60°,由翻折可知:∠DBC=∠ABC=60°,DB=AB=2,∴∠DBF=60°,∵DF⊥AB,∴∠DFB=90°,∴∠BDF=30°,∴BF=BD=1,∴DF=BF=,∵E是AB的中点,∴AE=BE=OE=AB=1,∴EF=BE+BF=2,∴DE===,∴OD≤DE+OE=+1,∴当D、E、O三点共线时OD最大,最大值为+1.故答案为:+1.22.(2023•南京)如图,在菱形纸片ABCD中,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB′⊥AD,垂足为F.若CF=4cm,FB′=1cm,则BE=cm.【分析】作EH⊥BC于点H,由CF=4cm,FB′=1cm,求得B′C=5cm,由折叠得BC=B′C=5cm,由菱形的性质得BC∥AD,DC=BC=5cm,∠B=∠D,因为CB′⊥AD于点F,所以∠BCB′=∠CFD =90°,则∠BCE=∠B′CE=45°,DF==3cm,所以∠HEC=∠BCE=45°,则CH=EH,由=sin B=sin D=,=cos B=cos D=,得CH=EH=BE,BH=BE,于是得BE+BE =5,则BE=cm.【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,∵CF=4cm,FB′=1cm,∴B′C=CF+FB′=4+1=5(cm),由折叠得BC=B′C=5cm,∠BCE=∠B′CE,∵四边形ABCD是菱形,∴BC∥AD,DC=BC=5cm,∠B=∠D,∵CB′⊥AD于点F,∴∠BCB′=∠CFD=90°,∴∠BCE=∠B′CE=∠BCB′=×90°=45°,DF===3(cm),∴∠HEC=∠BCE=45°,∴CH=EH,∵=sin B=sin D==,=cos B=cos D==,∴CH=EH=BE,BH=BE,∴BE+BE=5,∴BE=cm,故答案为:.一十七.旋转的性质(共1小题)23.(2023•西宁)如图,在矩形ABCD中,点P在BC边上,连接P A,将P A绕点P顺时针旋转90°得到P A′,连接CA′,若AD=9,AB=5,CA′=2,则BP=2.【分析】过A′点作A′H⊥BC于H点,如图,根据旋转的性质得到P A=P A′,再证明△ABP≌△PHA′得到PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=4﹣x,然后在Rt△A′CH中利用勾股定理得到x2+(4﹣x)2=(2)2,于是解方程求出x即可.【解答】解:过A′点作A′H⊥BC于H点,如图,∵四边形ABCD为矩形,∴BC=AD=9,∠B=90°,∵将P A绕点P顺时针旋转90°得到P A′,∴P A=P A′,∵∠P AB+∠APB=90°,∠APB+∠A′PH=90°,∴∠P AB=∠A′PH,在△ABP和△PHA′中,,∴△ABP≌△PHA′(AAS),∴PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=9﹣x﹣5=4﹣x,在Rt△A′CH中,x2+(4﹣x)2=(2)2,解得x1=x2=2,即BP的长为2.故答案为:2.一十八.相似三角形的判定与性质(共2小题)24.(2023•杭州)如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设=k,若AD=DF,则=(结果用含k的代数式表示).【分析】方法一:先根据轴对称的性质和已知条件证明DE∥AC,再证△BDE∽△BAC,推出EC=k•AB,通过证明△ABC∽△ECF,推出CF=k2•AB,即可求出的值.方法二:证明AD=DF=BD,可得BF⊥AC,设AB=AC=1,BC=k,CF=x,则AF=1﹣x,利用勾股定理列方程求出x的值,进而可以解决问题.【解答】解:方法一:∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB,∵AD=DF,∴∠A=∠DF A,∵点B和点F关于直线DE对称,∴∠BDE=∠FDE,∵∠BDE+∠FDE=∠BDF=∠A+∠DF A,∴∠FDE=∠DF A,∴DE∥AC,∴∠C=∠DEB,∠DEF=∠EFC,∵点B和点F关于直线DE对称,∴∠DEB=∠DEF,∴∠C=∠EFC,∵AB=AC,∴∠C=∠B,∵∠ACB=∠EFC,∴△ABC∽△ECF,∴=,∵DE∥AC,∴∠BDE=∠A,∠BED=∠C,∴△BDE∽△BAC,∴==,∴EC=BC,∵=k,∴BC=k•AB,∴EC=k•AB,∴=,∴CF=k2•AB,∴====.方法二:如图,连接BF,∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB=DF,∴BF⊥AC,设AB=AC=1,则BC=k,设CF=x,则AF=1﹣x,由勾股定理得,AB2﹣AF2=BC2﹣CF2,∴12﹣(1﹣x)2=k2﹣x2,∴x=,∴AF=1﹣x=,∴=.故答案为:.25.(2023•广东)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为15.【分析】根据相似三角形的性质,利用相似比求出梯形的上底和下底,用面积公式计算即可.【解答】解:如图,∵BF∥DE,∴△ABF∽△ADE,∴=,∵AB=4,AD=4+6+10=20,DE=10,∴=,∴BF=2,∴GF=6﹣2=4,∵CK∥DE,∴△ACK∽△ADE,∴=,∵AC=4+6=10,AD=20,DE=10,∴=,∴CK=5,∴HK=6﹣5=1,∴阴影梯形的面积=(HK+GF)•GH=(1+4)×6=15.故答案为:15.一十九.相似三角形的应用(共1小题)26.(2023•南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB 的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是()A.36cm B.40cm C.42cm D.45cm【分析】过点B作BC⊥AH,垂足为C,再证明A字模型相似△AOH∽△ABC,从而可得=,过点A作AD⊥BH,垂足为D,然后证明A字模型相似△ABD∽△OBH,从而可得=,最后进行计算即可解答.【解答】解:如图:过点B作BC⊥AH,垂足为C,∵OH⊥AC,BC⊥AC,∴∠AHO=∠ACB=90°,∵∠BAC=∠OAH,∴△AOH∽△ABC,∴=,∴=,如图:过点A作AD⊥BH,垂足为D,∵OH⊥BD,AD⊥BD,∴∠OHB=∠ADB=90°,∵∠ABD=∠OBH,∴△ABD∽△OBH,∴=,∴=,∴+=+,∴+=,∴+=1,解得:OH=36,∴跷跷板AB的支撑点O到地面的高度OH是36cm,故选:A.二十.解直角三角形(共1小题)27.(2023•丹东)如图,在平面直角坐标系中,点O是坐标原点,已知点A(3,0),B(0,4),点C在x 轴负半轴上,连接AB,BC,若tan∠ABC=2,以BC为边作等边三角形BCD,则点C的坐标为(﹣2,0);点D的坐标为(﹣1﹣2,2+)或(﹣1+2,2﹣).【分析】过点C作CE⊥AB于E,先求处AB=5,再设BE=t,由tan∠ABC=2得CE=2t,进而得BC =,由三角形的面积公式得S△ABC=AC•OB=AB•CE,即5×2t=4×(3+OC),则OC=﹣3,然后在Rt△BOC中由勾股定理得,由此解出t1=2,t2=10(不合题意,舍去),此时OC=﹣3=2,故此可得点C的坐标;设点D的坐标为(m,n),由两点间的距离公式得:BC2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,由△BCD为等边三角形得,整理:,②﹣①整理得m=3﹣2n,将m=3﹣2n代入①整理得n2﹣4n+1=0,解得n=,进而再求出m即可得点D的坐标.【解答】解:过点C作CE⊥AB于E,如图:∵点A(3,0),B(0,4),由两点间的距离公式得:AB==5,设BE=t,∵tan∠ABC=2,在Rt△BCE中,tan∠ABC=,∴=2,∴CE=2t,由勾股定理得:BC==t,∵CE⊥AB,OB⊥AC,AC=OC+OA=3+OC,∴S△ABC=AC•OB=AB•CE,即:5×2t=4×(3+OC),∴OC=﹣3,在Rt△BOC中,由勾股定理得:BC2﹣OB2=OC2,即,整理得:t2﹣12t+20=0,解得:t1=2,t2=10(不合题意,舍去),∴t=2,此时OC=﹣3=2,∴点C的坐标为(﹣2,0),设点D的坐标为(m,n),由两点间的距离公式得:BC2=(﹣2﹣0)2+(0﹣4)2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,∵△BCD为等边三角形,∵BD=CD=BC,∴,整理得:,②﹣①得:4m+8n=12,∴m=3﹣2n,将m=3﹣2n代入①得:(3﹣2n)2+n2﹣8n=4,整理得:n2﹣4n+1=0,解得:n=,当n=时,m=3﹣2n=,当n=时,m=3﹣2n=,∴点D的坐标为或.故答案为:(﹣2,0);或.二十一.解直角三角形的应用(共1小题)28.(2023•杭州)第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连接BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1:n,tanα=tan2β,则n=()A.5B.4C.3D.2【分析】设AE=a,DE=b,则BF=a,AF=b,解直角三角形可得,化简可得(b﹣a)2=ab,a2+b2=3ab,结合勾股定理及正方形的面积公式可求得S正方形EFGH;S正方形ABCD=1:3,进而可求解n的值.【解答】解:设AE=a,DE=b,则BF=a,AF=b,∵tanα=,tanβ=,tanα=tan2β,∴,∴(b﹣a)2=ab,∴a2+b2=3ab,∵a2+b2=AD2=S正方形ABCD,(b﹣a)2=S正方形EFGH,∴S正方形EFGH:S正方形ABCD=ab:3ab=1:3,∵S正方形EFGH:S正方形ABCD=1:n,∴n=3.故选:C.。
中考数学—一元二次方程组的综合压轴题专题复习附答案解析
中考数学—一元二次方程组的综合压轴题专题复习附答案解析一、一元二次方程1.如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q 两点之间的距离是多少cm?(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C 同时出发,问经过多长时间P、Q两点之间的距离是10cm?(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?【答案】(1)PQ=62cm;(2)85s或245s;(3)经过4秒或6秒△PBQ的面积为12cm2.【解析】试题分析:(1)作PE⊥CD于E,表示出PQ的长度,利用PE2+EQ2=PQ2列出方程求解即可;(2)设x秒后,点P和点Q的距离是10cm.在Rt△PEQ中,根据勾股定理列出关于x的方程(16-5x)2=64,通过解方程即可求得x的值;(3)分类讨论:①当点P在AB上时;②当点P在BC边上;③当点P在CD边上时.试题解析:(1)过点P作PE⊥CD于E.则根据题意,得EQ=16-2×3-2×2=6(cm),PE=AD=6cm;在Rt△PEQ中,根据勾股定理,得PE2+EQ2=PQ2,即36+36=PQ2,∴cm;∴经过2s时P、Q两点之间的距离是;(2)设x秒后,点P和点Q的距离是10cm.(16-2x-3x)2+62=102,即(16-5x)2=64,∴16-5x=±8,∴x1=85,x2=245;∴经过85s或245sP、Q两点之间的距离是10cm;(3)连接BQ.设经过ys后△PBQ的面积为12cm2.①当0≤y≤163时,则PB=16-3y,∴12PB•BC=12,即12×(16-3y)×6=12,解得y=4;②当163<x≤223时,BP=3y-AB=3y-16,QC=2y,则1 2BP•CQ=12(3y-16)×2y=12,解得y1=6,y2=-23(舍去);③223<x≤8时,QP=CQ-PQ=22-y,则1 2QP•CB=12(22-y)×6=12,解得y=18(舍去).综上所述,经过4秒或6秒△PBQ的面积为 12cm2.考点:一元二次方程的应用.2.在等腰三角形△ABC中,三边分别为a、b、c,其中ɑ=4,若b、c是关于x的方程x2﹣(2k+1)x+4(k﹣12)=0的两个实数根,求△ABC的周长.【答案】△ABC的周长为10.【解析】【分析】分a为腰长及底边长两种情况考虑:当a=4为腰长时,将x=4代入原方程可求出k值,将k值代入原方程可求出底边长,再利用三角形的周长公式可求出△ABC的周长;当a=4为底边长时,由根的判别式△=0可求出k 值,将其代入原方程利用根与系数的关系可求出b+c 的值,由b+c=a 可得出此种情况不存在.综上即可得出结论.【详解】当a =4为腰长时,将x =4代入原方程,得:()214421402k k ⎛⎫-++-= ⎪⎝⎭解得:52k =当52k =时,原方程为x 2﹣6x +8=0, 解得:x 1=2,x 2=4,∴此时△ABC 的周长为4+4+2=10;当a =4为底长时,△=[﹣(2k +1)]2﹣4×1×4(k ﹣12)=(2k ﹣3)2=0, 解得:k =32, ∴b +c =2k +1=4.∵b +c =4=a ,∴此时,边长为a ,b ,c 的三条线段不能围成三角形.∴△ABC 的周长为10.【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系,分a 为腰长及底边长两种情况考虑是解题的关键.3.解方程:(x+1)(x ﹣3)=﹣1.【答案】x 1x 2=1【解析】试题分析:根据方程的特点,先化为一般式,然后利用配方法求解即可.试题解析:整理得:x 2﹣2x=2,配方得:x 2﹣2x+1=3,即(x ﹣1)2=3,解得:x 1,x 2=14.已知关于x 的方程x 2﹣(2k +1)x +k 2+1=0.(1)若方程有两个不相等的实数根,求k 的取值范围;(2)若方程的两根恰好是一个矩形两邻边的长,且k =2,求该矩形的对角线L 的长.【答案】(1)k >34;(2 【解析】【分析】(1)根据关于x 的方程x 2-(2k +1)x +k 2+1=0有两个不相等的实数根,得出△>0,再解不等式即可;(2)当k=2时,原方程x2-5x+5=0,设方程的两根是m、n,则矩形两邻边的长是m、n,利用根与系数的关系得出m+n=5,mn=5,利用完全平方公式进行变形即可求得答案.【详解】(1)∵方程x2-(2k+1)x+k2+1=0有两个不相等的实数根,∴Δ=[-(2k+1)]2-4×1×(k2+1)=4k-3>0,∴k>34;(2)当k=2时,原方程为x2-5x+5=0,设方程的两个根为m,n,∴m+n=5,mn=5,∴==.【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等,一元二次方程根的情况与判别式△的关系:(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;(3)△<0时,方程没有实数根.5.已知:关于x的方程x2-4mx+4m2-1=0.(1)不解方程,判断方程的根的情况;(2)若△ABC为等腰三角形,BC=5,另外两条边是方程的根,求此三角形的周长.2【答案】(1) 有两个不相等的实数根(2)周长为13或17【解析】试题分析:(1)根据方程的系数结合根的判别式,可得出△=4>0,由此可得出:无论m 为何值,该方程总有两个不相等的实数根;(2)根据等腰三角形的性质及△>0,可得出5是方程x2﹣4mx+4m2﹣1=0的根,将x=5代入原方程可求出m值,通过解方程可得出方程的解,在利用三角形的周长公式即可求出结论.试题解析:解:(1)∵△=(﹣4m)2﹣4(4m2﹣1)=4>0,∴无论m为何值,该方程总有两个不相等的实数根.(2)∵△>0,△ABC为等腰三角形,另外两条边是方程的根,∴5是方程x2﹣4mx+4m2﹣1=0的根.将x=5代入原方程,得:25﹣20m+4m2﹣1=0,解得:m1=2,m2=3.当m=2时,原方程为x2﹣8x+15=0,解得:x1=3,x2=5.∵3、5、5能够组成三角形,∴该三角形的周长为3+5+5=13;当m=3时,原方程为x2﹣12x+35=0,解得:x1=5,x2=7.∵5、5、7能够组成三角形,∴该三角形的周长为5+5+7=17.综上所述:此三角形的周长为13或17.点睛:本题考查了根的判别式、等腰三角形的性质、三角形的三边关系以及解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)代入x =5求出m 值.6.已知关于x 的一元二次方程()222130x k x k --+-=有两个实数根. ()1求k 的取值范围;()2设方程两实数根分别为1x ,2x ,且满足221223x x +=,求k 的值.【答案】(1)134k ≤;(2)2k =-. 【解析】【分析】 ()1根据方程有实数根得出()()22[2k 1]41k 38k 50=---⨯⨯-=-+≥V ,解之可得. ()2利用根与系数的关系可用k 表示出12x x +和12x x 的值,根据条件可得到关于k 的方程,可求得k 的值,注意利用根的判别式进行取舍.【详解】解:()1Q 关于x 的一元二次方程()222130x k x k --+-=有两个实数根, 0∴≥V ,即()()22[21]4134130k k k ---⨯⨯-=-+≥, 解得134k ≤. ()2由根与系数的关系可得1221x x k +=-,2123x x k =-,()222222121212()2(21)23247x x x x x x k k k k ∴+=+-=---=-+,221223x x +=Q , 224723k k ∴-+=,解得4k =,或2k =-,134k ≤Q , 4k ∴=舍去,2k ∴=-.【点睛】本题考查了一元二次方程2ax bx c 0(a 0,++=≠a ,b ,c 为常数)根的判别式.当0V >,方程有两个不相等的实数根;当0=V ,方程有两个相等的实数根;当0<V ,方程没有实数根.以及根与系数的关系.7.解方程: 2212x x 6x 9-=-+() 【答案】124x x 23==-, 【解析】试题分析:先对方程的右边因式分解,直接开平方或移项之后再因式分解法求解即可.试题解析:因式分解,得2212x x 3-=-()()开平方,得12x x 3-=-,或12x x 3-=--()解得124x x 23==-, 8.已知为正整数,二次方程的两根为,求下式的值:【答案】【解析】 由韦达定理,有,.于是,对正整数,有原式=9.元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.(1)求甲、乙两种苹果的进价分别是每千克多少元?(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x 元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x 的值.【答案】(1)甲、乙两种苹果的进价分别为10元/千克,8元/千克;(2)x 的值为2或7.【解析】【分析】(1)根据题意列二元一次方程组即可求解,(2)根据题意列一元二次方程即可求解.【详解】(1)解:设甲、乙两种苹果的进价分别为a 元/千克, b 元/千克.由题得:()()18344282a b a b +=⎧⎨+++=⎩解之得:108a b =⎧⎨=⎩ 答:甲、乙两种苹果的进价分别为10元/千克,8元/千克(2)由题意得:()()()()410010214010960x x x x +-++-=解之得:12x =,27x =经检验,12x =,27x =均符合题意答:x 的值为2或7.【点睛】本题考查了二元一次方程组和一元二次方程的实际应用,中等难度,列方程是解题关键.10.已知关于x 的方程mx 2+(3﹣m)x ﹣3=0(m 为实数,m≠0).(1) 试说明:此方程总有两个实数根.(2) 如果此方程的两个实数根都为正整数,求整数m 的值.【答案】(1)()2243b ac m -=+≥0;(2)m=-1,-3.【解析】分析: (1)先计算判别式得到△=(m -3)2-4m •(-3)=(m +3)2,利用非负数的性质得到△≥0,然后根据判别式的意义即可得到结论;(2)利用公式法可求出x 1=3m ,x 2=-1,然后利用整除性即可得到m 的值. 详解: (1)证明:∵m ≠0,∴方程mx 2+(m -3)x -3=0(m ≠0)是关于x 的一元二次方程,∴△=(m -3)2-4m ×(-3)=(m +3)2,∵(m +3)2≥0,即△≥0,∴方程总有两个实数根;(2)解:∵x =()()332m m m --±+ , ∴x 1=-3m,x 2=1, ∵m 为正整数,且方程的两个根均为整数,∴m =-1或-3.点睛: 本题考查了一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式△=b 2-4ac :当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程.11.已知关于x 的方程(x-3)(x-2)-p 2=0.(1)求证:无论p 取何值时,方程总有两个不相等的实数根;(2)设方程两实数根分别为x 1、x 2,且满足x 12+x 22=3 x 1x 2,求实数p 的值.【答案】(1)详见解析;(2)p=±1.【解析】【分析】(1)先把方程化成一般形式,再计算根的判别式,判定△>0,即可得到总有两个不相等的实数根;(2)根据一元二次方程根与系数的关系可得两根和与两根积,再把2212123x x x x +=变形,化成和与乘积的形式,代入计算,得到一个关于p 的一元二次方程,解方程即可求解.【详解】证明:(1)(x ﹣3)(x ﹣2)﹣p 2=0,x 2﹣5x+6﹣p 2=0,△=(﹣5)2﹣4×1×(6﹣p 2)=25﹣24+4p 2=1+4p 2,∵无论p 取何值时,总有4p 2≥0,∴1+4p 2>0,∴无论p 取何值时,方程总有两个不相等的实数根;(2)x 1+x 2=5,x 1x 2=6﹣p 2,∵2212123x x x x +=, ∴(x 1+x 2)2﹣2x 1x 2=3x 1x 2,∴52=5(6﹣p 2),∴p=±1.考点:根的判别式;根与系数的关系.12.解方程:(x 2+x )2+(x 2+x )=6.【答案】x 1=﹣2,x 2=1【解析】【分析】设x 2+x =y ,将原方程变形整理为y 2+y ﹣6=0,求得y 的值,然后再解一元二次方程即可.【详解】解:设x 2+x =y ,则原方程变形为y 2+y ﹣6=0,解得y 1=﹣3,y 2=2.①当y =2时,x 2+x =2,即x 2+x ﹣2=0,解得x 1=﹣2,x 2=1;②当y =﹣3时,x 2+x =﹣3,即x 2+x+3=0,∵△=12﹣4×1×3=1﹣12=﹣11<0,∴此方程无解;∴原方程的解为x 1=﹣2,x 2=1.【点睛】本题考查了换元法和一元二次方程的解法,设出元化简原方程是解答本题的关键.13.阅读材料:若22228160m mn n n -+-+=,求m 、n 的值.解: 22228160m mn n n -+-+=Q ,222(2)(816)0m mn n n n ∴-++-+=22()(4)0m n n ∴-+-=,0,40m n n ∴-=-=,4,4n m ∴==.根据你的观察,探究下面的问题:(1)己知2222210x xy y y ++++=,求x y -的值.(2)已知△ABC 的三边长a 、b 、c 都是正整数,且满足2268250a b a b +--+=,求边c 的最大值.(3) 若己知24,6130a b ab c c -=+-+=,求a b c -+的值.【答案】(1)2(2)6(3)7【解析】【分析】(1)将多项式第三项分项后,结合并利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出x 与y 的值,即可求出x ﹣y 的值;(2)将已知等式25分为9+16,重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出a 与b 的值,根据边长为正整数且三角形三边关系即可求出c 的长;(3)由a ﹣b =4,得到a =b +4,代入已知的等式中重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出b 与c 的值,进而求出a 的值,即可求出a ﹣b +c 的值.【详解】(1)∵x 2+2xy +2y 2+2y +1=0∴(x 2+2xy +y 2)+(y 2+2y +1)=0∴(x +y )2+(y +1)2=0∴x +y =0 y +1=0解得:x =1,y =﹣1∴x ﹣y =2;(2)∵a 2+b 2﹣6a ﹣8b +25=0∴(a 2﹣6a +9)+(b 2﹣8b +16)=0∴(a ﹣3)2+(b ﹣4)2=0∴a ﹣3=0,b ﹣4=0解得:a =3,b =4∵三角形两边之和>第三边∴c<a+b,c<3+4,∴c<7.又∵c是正整数,∴△ABC的最大边c的值为4,5,6,∴c 的最大值为6;(3)∵a﹣b=4,即a=b+4,代入得:(b+4)b+c2﹣6c+13=0,整理得:(b2+4b+4)+(c2﹣6c+9)=(b+2)2+(c﹣3)2=0,∴b+2=0,且c﹣3=0,即b=﹣2,c=3,a=2,则a﹣b+c=2﹣(﹣2)+3=7.故答案为7.【点睛】本题考查了因式分解的应用,以及非负数的性质,熟练掌握完全平方公式是解答本题的关键.14.若两个一次函数的图象与x轴交于同一点,则称这两个函数为一对“x牵手函数”,这个交点为“x牵手点”.(1)一次函数y=x﹣1与x轴的交点坐标为;一次函数y=ax+2与一次函数y=x﹣1为一对“x牵手函数”,则a=;(2)已知一对“x牵手函数”:y=ax+1与y=bx﹣1,其中a,b为一元二次方程x2﹣kx+k﹣4=0的两根,求它们的“x牵手点”.【答案】(1)(1,0),a=﹣2;(2)“x牵手点”为(12-,0)或(12,0).【解析】【分析】(1)根据x轴上点的坐标特征可求一次函数y=x-1与x轴的交点坐标;把一次函数y=x-1与x轴的交点坐标代入一次函数y=ax+2可求a的值;(2)根据“x牵手函数”的定义得到a+b=0,根据根与系数的关系求得k=0,可得方程x2-4=0,解得x1=2,x2=-2,再分两种情况:①若a=2,b=-2,②若a=-2,b=2,进行讨论可求它们的“x牵手点”.【详解】解:(1)当y=0时,即x﹣1=0,所以x=1,即一次函数y=x﹣1与x轴的交点坐标为(1,0),由于一次函数y=ax+2与一次函数y=x﹣1为一对“x牵手函数”,所以0=a+2,解得a=﹣2;(2)∵y=ax+1与y=bx﹣1为一对“x牵手函数”∴11a b-=,∴a+b=0.∵a,b为x2﹣kx+k﹣4=0的两根∴a+b=k=0,∴x2﹣4=0,∴x1=2,x2=﹣2.①若a =2,b =﹣2则y =2x+1与y =﹣2x ﹣1的“x 牵手点”为1,02⎛⎫-⎪⎝⎭; ②若a =﹣2,b =2则y =﹣2x+1与y =2x ﹣1的“x 牵手点”为(12,0 ) ∴综上所述,“x 牵手点”为1,02⎛⎫-⎪⎝⎭或(12,0) 【点睛】 本题考查了根与系数的关系、一次函数的性质和一次函数图象上点的坐标特征的运用.15.阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a 的形式。
中考数学与一元二次方程组有关的压轴题附详细答案
中考数学与一元二次方程组有关的压轴题附详细答案一、一元二次方程1.关于x 的方程x 2﹣2(k ﹣1)x +k 2=0有两个实数根x 1、x 2. (1)求k 的取值范围;(2)若x 1+x 2=1﹣x 1x 2,求k 的值. 【答案】(1)12k ≤;(2)3k = 【解析】试题分析:(1)方程有两个实数根,可得240b ac ∆=-≥,代入可解出k 的取值范围; (2)由韦达定理可知,()2121221,x x k x x k +=-=,列出等式,可得出k 的值.试题解析:(1)∵Δ=4(k -1)2-4k 2≥0,∴-8k +4≥0,∴k ≤12; (2)∵x 1+x 2=2(k -1),x 1x 2=k 2,∴2(k -1)=1-k 2, ∴k 1=1,k 2=-3. ∵k ≤12,∴k =-3.2.如图,抛物线y=ax 2+bx+c 与x 轴交于点A 和点B (1,0),与y 轴交于点C (0,3),其对称轴l 为x=﹣1.(1)求抛物线的解析式并写出其顶点坐标;(2)若动点P 在第二象限内的抛物线上,动点N 在对称轴l 上. ①当PA ⊥NA ,且PA=NA 时,求此时点P 的坐标;②当四边形PABC 的面积最大时,求四边形PABC 面积的最大值及此时点P 的坐标.【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P ﹣1,2);②P (﹣32,154) 【解析】试题分析:(1)将B 、C 的坐标代入已知的抛物线的解析式,由对称轴为1x =-即可得到抛物线的解析式;(2)①首先求得抛物线与x 轴的交点坐标,然后根据已知条件得到PD=OA ,从而得到方程求得x 的值即可求得点P 的坐标;②ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形,表示出来得到二次函数,求得最值即可.试题解析:(1)∵抛物线2y ax bx c =++与x 轴交于点A 和点B (1,0),与y 轴交于点C (0,3),其对称轴l 为1x =-,∴0{312a b c c ba++==-=-,解得:1{23a b c =-=-=,∴二次函数的解析式为223y x x =--+=2(1)4x -++,∴顶点坐标为(﹣1,4);(2)令2230y x x =--+=,解得3x =-或1x =,∴点A (﹣3,0),B (1,0),作PD ⊥x 轴于点D ,∵点P 在223y x x =--+上,∴设点P (x ,223x x --+), ①∵PA ⊥NA ,且PA=NA ,∴△PAD ≌△AND ,∴OA=PD ,即2232y x x =--+=,解得1(舍去)或x=1,∴点P(1,2);②设P(x ,y),则223y x x =--+,∵ΔOBC ΔAPD ABCP C =PDO S S S S ++四边形梯形 =12OB•OC+12AD•PD+12(PD+OC)•OD=11131+(3)(3)()222x y y x ⨯⨯⨯+++-=333222x y -+ =2333(23)222x x x -+--+=239622x x --+=23375()228x -++, ∴当x=32-时,ABCP S 四边形最大值=758,当x=32-时,223y x x =--+=154,此时P(32-,154).考点:1.二次函数综合题;2.二次函数的最值;3.最值问题;4.压轴题.3.机械加工需用油进行润滑以减小摩擦,某企业加工一台设备润滑用油量为90kg ,用油的重复利用率为60%,按此计算,加工一台设备的实际耗油量为36kg ,为了倡导低碳,减少油耗,该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关. (1)甲车间通过技术革新后,加工一台设备润滑油用油量下降到70kg ,用油的重复利用率仍然为60%,问甲车间技术革新后,加工一台设备的实际油耗量是多少千克?(2)乙车间通过技术革新后,不仅降低了润滑油用油量,同时也提高了用油的重复利用率,并且发现在技术革新前的基础上,润滑用油量每减少1kg,用油的重复利用率将增加1.6%,例如润滑用油量为89kg时,用油的重复利用率为61.6%.①润滑用油量为80kg,用油量的重复利用率为多少?②已知乙车间技术革新后实际耗油量下降到12kg,问加工一台设备的润滑用油量是多少千克?用油的重复利用率是多少?【答案】(1)28(2)①76%②75,84%【解析】试题分析:(1)直接利用加工一台设备润滑油用油量下降到70kg,用油的重复利用率仍然为60%,进而得出答案;(2)①利用润滑用油量每减少1kg,用油的重复利用率将增加1.6%,进而求出答案;②首先表示出用油的重复利用率,进而利用乙车间技术革新后实际耗油量下降到12kg,得出等式求出答案.试题解析:(1)根据题意可得:70×(1﹣60%)=28(kg);(2)①60%+1.6%(90﹣80)=76%;②设润滑用油量是x千克,则x{1﹣[60%+1.6%(90﹣x)]}=12,整理得:x2﹣65x﹣750=0,(x﹣75)(x+10)=0,解得:x1=75,x2=﹣10(舍去),60%+1.6%(90﹣x)=84%,答:设备的润滑用油量是75千克,用油的重复利用率是84%.考点:一元二次方程的应用4.解方程:233230 2121x xx x⎛⎫⎛⎫--=⎪ ⎪--⎝⎭⎝⎭.【答案】x=15或x=1【解析】【分析】设321xyx=-,则原方程变形为y2-2y-3=0, 解这个一元二次方程求y,再求x.【详解】解:设321xyx=-,则原方程变形为y2-2y-3=0.解这个方程,得y1=-1,y2=3,∴3121xx=--或3321xx=-.解得x=15或x=1. 经检验:x=15或x=1都是原方程的解. ∴原方程的解是x=15或x=1. 【点睛】考查了还原法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.5.解下列方程: (1)2x 2-4x -1=0(配方法); (2)(x +1)2=6x +6.【答案】(1)x 1=1+2x 2=1-21=-1,x 2=5. 【解析】试题分析:(1)根据配方法解一元二次方程的方法,先移项,再加减一次项系数一半的平方,完成配方,再根据直接开平方法解方程即可;(2)根据因式分解法,先移项,再提公因式即可把方程化为ab=0的形式,然后求解即可.试题解析:(1)由题可得,x 2-2x =12,∴x 2-2x +1=32.∴(x -1)2=32.∴x -1=.∴x 1=1x 2=1 (2)由题可得,(x +1)2-6(x +1)=0,∴(x +1)(x +1-6)=0. ∴x +1=0或x +1-6=0. ∴x 1=-1,x 2=5.6.某社区决定把一块长50m ,宽30m 的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小形状都相同的矩形) ,空白区域为活动区,且四周的4个出口宽度相同,当绿化区较长边x 为何值时,活动区的面积达到21344m ?【答案】当13x m =时,活动区的面积达到21344m 【解析】 【分析】根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出方程,可解答. 【详解】解:设绿化区宽为y ,则由题意得502302x y -=-.即10y x =-列方程: 50304(10)1344x x ⨯--= 解得13x =- (舍),213x =.∴当13x m =时,活动区的面积达到21344m 【点睛】本题是一元二次方程的应用题,确定等量关系是关键,本题计算量大,要细心.7.已知关于x 的一元二次方程()2211204x m x m +++-=. ()1若此方程有两个实数根,求m 的最小整数值;()2若此方程的两个实数根为1x ,2x ,且满足22212121184x x x x m ++=-,求m 的值.【答案】(1)m 的最小整数值为4-;(2)3m = 【解析】 【分析】(1)根据方程有两个实数根得0∆≥,列式即可求解,(2)利用韦达定理即可解题. 【详解】(1)解:()22114124m m ⎛⎫∆=+-⨯⨯-⎪⎝⎭22218m m m =++-+29m =+方程有两个实数根0∴∆≥,即290m +≥92m ∴≥-∴ m 的最小整数值为4-(2)由根与系数的关系得:()121x x m +=-+,212124x x m =- 由22212121184x x x x m ++=-得:()22211121844m m m ⎛⎫⎡⎤-+--=- ⎪⎣⎦⎝⎭13m ∴=,25m =-92m ≥-3m ∴=【点睛】本题考查了根的判别式和韦达定理,中等难度,熟悉韦达定理是解题关键.8.已知关于x 的一元二次方程x 2+(k +1)x +214k =0 有两个不相等的实数根. (1)求k 的取值范围;(2)当k 取最小整数时,求此时方程的解. 【答案】(1)k >﹣12;(2)x 1=0,x 2=﹣1. 【解析】 【分析】(1)由题意得△=(k +1)2﹣4×14k 2>0,解不等式即可求得答案; (2)根据k 取最小整数,得到k =0,列方程即可得到结论. 【详解】(1)∵关于x 的一元二次方程x 2+(k +1)x +214k =0 有两个不相等的实数根, ∴△=(k +1)2﹣4×14k 2>0, ∴k >﹣12; (2)∵k 取最小整数, ∴k =0,∴原方程可化为x 2+x =0, ∴x 1=0,x 2=﹣1. 【点睛】本题考查了一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式△=b 2﹣4ac :当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.9.关于x 的一元二次方程ax 2+bx+1=0.(1)当b=a+2时,利用根的判别式判断方程根的情况;(2)若方程有两个相等的实数根,写出一组满足条件的a ,b 的值,并求此时方程的根. 【答案】(1)方程有两个不相等的实数根;(2)b=-2,a=1时,x 1=x 2=﹣1. 【解析】 【详解】分析:(1)求出根的判别式24b ac ∆=-,判断其范围,即可判断方程根的情况. (2)方程有两个相等的实数根,则240b ac ∆=-=,写出一组满足条件的a ,b 的值即可.详解:(1)解:由题意:0a ≠.∵()22242440b ac a a a ∆=-=+-=+>, ∴原方程有两个不相等的实数根.(2)答案不唯一,满足240b ac -=(0a ≠)即可,例如: 解:令1a =,2b =-,则原方程为2210x x -+=, 解得:121x x ==.点睛:考查一元二次方程()200++=≠ax bx c a 根的判别式24b ac ∆=-,当240b ac ∆=->时,方程有两个不相等的实数根. 当240b ac ∆=-=时,方程有两个相等的实数根. 当240b ac ∆=-<时,方程没有实数根.10.某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.(1)该项绿化工程原计划每天完成多少米2?(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?【答案】(1)2000;(2)2米 【解析】 【分析】(1)设未知数,根据题目中的的量关系列出方程; (2)可以通过平移,也可以通过面积法,列出方程解:(1)设该项绿化工程原计划每天完成x米2,根据题意得:4600022000x-﹣46000220001.5x-= 4解得:x=2000,经检验,x=2000是原方程的解;答:该绿化项目原计划每天完成2000平方米;(2)设人行道的宽度为x米,根据题意得,(20﹣3x)(8﹣2x)=56解得:x=2或x=263(不合题意,舍去).答:人行道的宽为2米.11.工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)求长方体底面面积为12dm2时,裁掉的正方形边长多大?【答案】裁掉的正方形的边长为2dm,底面积为12dm2.【解析】试题分析:设裁掉的正方形的边长为xdm,则制作无盖的长方体容器的长为(10-2x)dm,宽为(6-2x)dm,根据长方体底面面积为12dm2列出方程,解方程即可求得裁掉的正方形边长.试题解析:设裁掉的正方形的边长为xdm,由题意可得(10-2x)(6-2x)=12,即x2-8x+12=0,解得x=2或x=6(舍去),答:裁掉的正方形的边长为2dm,底面积为12dm2.12.已知关于x的方程x2-(m+2)x+(2m-1)=0。
中考数学压轴题方程和不等式综合问题解答题解析版
26.如图1,数轴上,O点与C点对应的数分别是0,单位:单位长度,将一根质地均匀的直尺AB放在数轴上在B的左边,若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.请直接写出直尺的长为______个单位长度;如图2,直尺AB在数轴上移动,有,求此时A点所对应的数;如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处看不到直尺的任何部分,A在B的左边,将直尺AB沿数轴以4个单位长度秒的速度分别向左、右移动,直到完全看到直尺,所经历的时间分别为、,若秒,求直尺放入篷内时,A点所对应的数为多少?【答案】(1)20;(2)或10;(3)A点在蓬内所对应的数为38.当直尺AB在数轴上移动时,符合的情况如下所示:设BO为x:,所对应的数为设OA为x:,所对应的数为10综上所述,A在数轴上所对应的数分别为或10.设,如下图,根据题意,解得所以A点在蓬内所对应的数为38【关键点拨】本题通过直尺两端相对固定的两个点在数轴上移动时和数轴上固定的点之间长度关系的变化来确定移动点的位置,根据已知条件来分析移动点的可能性是解题的关键.月使用费主叫限定时间(分钟) 主叫超时费(元/分钟) 被叫方式一65 160 0.20 免费方式二100 380 0.25 免费被叫免费)(1)若张聪某月主叫通话时间为200分钟,则他按方式一计费需____元,按方式二计费需____ 元;李华某月按方式二计费需107元,则李华该月主叫通话时间为_____分钟;(2)是否存在某主叫通话时间(分钟),按方式一和方式二的计费相等?若存在,请求出的值;若不存在,请说明理由。
(3)直接写出当月主叫通话时间(分钟)满足什么条件时,选择方式一省钱。
【答案】(1)73,100,408;(2)存在某主叫通话时间t=300或560分钟,按方式一和方式二的计费相等;(3)当每月通话时间大于560分钟时,选择方式一省钱.(2)①当t≤160时,不存在;②当160<t≤380时,设每月通话时间为t分钟时,两种计费方式收费一样多,65+0.20×(t-160)=100,解得t=335,符合题意;③当t>380时,设每月通话时间为t分钟时,两种计费方式收费一样多,65+0.20×(t-160)=100+0.25(t-380),解得t=560,符合题意.故存在某主叫通话时间t=300或560分钟,按方式一和方式二的计费相等;(3)由(2)可得,当每月通话时间大于560分钟时,选择方式一省钱.【关键点拨】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.28.同学们,今天我们来学习一个新知识,形如的式子叫做二阶行列式,它的运算法则用公式表示为:利用此法则解决以下问题:(1)仿照上面的解释,计算出的结果;(2)依此法则化简的结果;(3)如果那么的值为多少?【答案】(1)11;(2)5a−b−ab;(3).(3)∴5x-3(x+1)=4∴5x−3x−3=4∴2x=7∴x=【关键点拨】[来源:]此题考查了解一元一次方程,以及有理数的混合运算,理解题中的新定义是解题的关键. 29.阅读探索知识累计解方程组解:设a﹣1=x,b+2=y,原方程组可变为解方程组得:即所以此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组:(2)能力运用已知关于x,y的方程组的解为,直接写出关于m、n的方程组的解为_____________.【答案】(1)(2)解得:,故答案为:【关键点拨】二元一次方程组解法的拓展是本题的考点,熟练掌握基础知识进行换元是解题的关键. 30.如图,在数轴上,点O为原点,点A表示的数为a,点B表示的数为b,且a,b满足,B两点对应的数分别为______,______;若将数轴折叠,使得A点与B点重合,则原点O与数______表示的点重合;若点A、B分别以4个单位秒和3个单位秒的速度相向而行,则几秒后A、B两点相距1个单位长度?若点A、B以中的速度同时向右运动,点P从原点O以7个单位秒的速度向右运动,是否存在常数m,使得为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.【答案】(1)-10;5; (2)-5;(3)2或秒;(4)存在,当m=3时,4AP+3OB-mOP为定值55.(2)∵|AB|=5-(-10)=15,=7.5,∴点A、点B距离折叠点都是7.5个单位所以折叠点上的数为-2.5.所以与点O重合的点表示的数为:-2.5×2=-5.即原点O与数-5表示的点重合.故答案为:-5.(3)设x秒后A、B相距1个单位长度,当点A在点B的左侧时,4x+3x=15-1,解得,x=2,当点A在点B的右侧时,4x+3x=15+1,解得,x=答:2或秒后A、B相距1个单位长度;【关键点拨】本题考查一元一次方程的应用,非负数的性质及数轴上两点间的距离.题目综合性较强,难度较大.解决(1)需利用非负数的性质,解决(3)注意分类思想的运用,解决(4)利用数轴上两点间的距离公式.31.(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:例如,若数轴上点、点表示的数分别为、,则、两点之间的距离,线段的中点表示的数为.(问题情境)在数轴上,点表示的数为-20,点表示的数为10,动点从点出发沿数轴正方向运动,同时,动点也从点出发沿数轴负方向运动,已知运动到4秒钟时,、两点相遇,且动点、运动的速度之比是(速度单位:单位长度/秒).备用图(综合运用)(1)点的运动速度为______单位长度/秒,点的运动速度为______单位长度/秒;(2)当时,求运动时间;(3)若点、在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点、的运动,线段的中点也随着运动.问点能否与原点重合?若能,求出从、相遇起经过的运动时间,并直接写出点的运动方向和运动速度;若不能,请说明理由.【答案】(1)动点P运动的速度为4.5单位长度/秒,动点Q运动的速度为3单位长度/秒;(2)运动时间为或秒;(3)点M能与原点重合,它沿数轴正方向运动,运动速度为或沿数轴正方向运动,运动速度为,理由见解析(2)设运动时间为t秒.由题意知:点P表示的数为-20+4.5t,点Q表示的数为10-3t,根据题意得:|(-20+4.5t)-(10-3t)|=×|(-20)-10|整理得:|7.5t-30|=107.5t-30=10或7.5t-30=-10解得:t=或t=.答:运动时间为或秒.(3)P、Q相遇点表示的数为-20+4×4.5=-2(注:当P、Q两点重合时,线段PQ的中点M也与P、Q两点重合)设从P、Q相遇起经过的运动时间为t秒时,点M与原点重合.①点P、Q均沿数轴正方向运动,则:解得:t=.此时点M能与原点重合,它沿数轴正方向运动,运动速度为2÷(单位长度/秒);②点P沿数轴正方向运动,点Q沿数轴负方向运动,则:解得:t=.此时点M能与原点重合,它沿数轴正方向运动,运动速度为2÷=(单位长度/秒);③点P沿数轴负方向运动,点Q沿数轴正方向运动,则:解得:t=-(舍去).此时点M不能与原点重合;④点P沿数轴负方向运动,点Q沿数轴负方向运动,则:解得:t=-(舍去).此时点M不能与原点重合.综上所述:点M能与原点重合,它沿数轴正方向运动,运动速度为或沿数轴正方向运动,运动速度为.【关键点拨】本题考查了一元一次方程的应用应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程,再求解.32.小明每隔一小时记录某服装专营店8:00~18:00的客流量(每一时段以200人为标时段8:00~9:00 10:00~11:00 12:00~13:0014:00~15:0016:00~17:00客流量(人)-21 +33 -12 +21 +54(1)若服装店每天的营业时间为8:00~18;00,请你估算一周(不休假)的客流量;(单位:人)(精确到百位)(2)若服装店在某天内男女装共卖出135套,据统计,每15名女顾客购买一套女装,每20名男顾客购买一套男装,则这一天卖出男、女服装各多少套?(3)若每套女装的售价为80元,每套男装的售价为120元,则此店一周的营业额约为多少元?【答案】(1)1.51×104人;(2)这一天卖出男装25套,女装110套.(3) 此店一周的营业额约为82600元.(2)设这一天卖出女装x套,男装(135-x)套,根据题意得,15x+20(135-x)=2150,解得,x=110,135-x=135-110=25.故这一天卖出男装25套,女装110套.(3)因为第二问中某一天出售男装25套,女装110套,每套女装的售价为80元,每套男装的售价为120元所以此店一周的营业额约为:[(25×120)+(110×80)]×7=[3000+8800]×7=11800×7=82600(元)故此店一周的营业额约为82600元.【关键点拨】本题考查正数和负数的加法、解方程组、数据的估算,注意第一问中精确到百位.33.某市两超市在元旦节期间分别推出如下促销方式:甲超市:全场均按八八折优惠;乙超市:购物不超过200元,不给予优惠;超过了200元而不超过500元一律打九折;超过500元时,其中的500元优惠10%,超过500元的部分打八折;已知两家超市相同商品的标价都一样.(1)当一次性购物总额是400元时,甲、乙两家超市实付款分别是多少?(2)当购物总额是多少时,甲、乙两家超市实付款相同?(3)某顾客在乙超市购物实际付款482元,试问该顾客的选择划算吗?试说明理由.【答案】(1)甲超市实付款352元,乙超市实付款360元;(2)购物总额是625元时,甲、乙两家超市实付款相同;(3)该顾客选择不划算.(3)设购物总额是x元,购物总额刚好500元时,在乙超市应付款为:500×0.9=450(元),482>450,故购物总额超过500元.根据题意得:500×0.9+0.8(x-500)=482∴x=540∴0.88x=475.2<482∴该顾客选择不划算.【关键点拨】本题考查了一元一次方程的应用,解题的关键是:(1)根据两超市的促销方案,列式计算;(2)找准等量关系,正确列出一元一次方程;(3)求出购物总额.34.某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.(1)符合公司要求的购买方案有几种?请说明理由;(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于1500元,那么应选择以上哪种购买方案?【答案】(1) 有三种购买方案,理由见解析;(2)为保证日租金不低于1500元,应选择方案三,即购买5辆轿车,5辆面包车(2)方案一的日租金为3×200+7×110=1370(元)<1500元;方案二的日租金为4×200+6×110=1460(元)<1500元;方案三的日租金为5×200+5×110=1550(元)>1500元.所以为保证日租金不低于1500元,应选择方案三,即购买5辆轿车,5辆面包车.【关键点拨】本题主要考查对于一元一次不等式组的应用,要注意找好题中的不等关系.解题的关键是:(1)根据数量关系列出关于x的一元一次不等式;(2)求出三种购买方案的日租金35.如图是某景区的环形游览路线ABCDA,已知从景点C到出口A的两条道路CBA和CDA 均为1600米,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形道路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车的速度均为200米/分,每一个游客的步行速度均为50米/分.(1)探究(填空):①当两车行驶分钟时,1、2号车第一次相遇,此相遇点到出口A的路程为米;②当1号车第二次恰好经过点C,此时两车行驶了分钟,这一段时间内1号车与2号车相遇了次.(2)发现:若游客甲在BC上K处(不与点C、B重合)候车,准备乘车到出口A,在下面两种情况下,请问哪种情况用时较少(含候车时间)?请说明理由.情况一:若他刚好错过2号车,便搭乘即将到来的1号车;情况二:若他刚好错过1号车,便搭乘即将到来的2号车.(3)决策:①若游客乙在DA上从D向出口A走去,游客乙从D出发时恰好2号车在C处,当步行到DA上一点P(不与A,D重合)时,刚好与2号车相遇,经计算他发现:此时原地(P点)等候乘1号车到出口与直接从P步行到达出口A这两种方式,所花时间相等,请求出D点到出口A的路程.②当游客丙逛完景点C后准备到出口A,此时2号车刚好在B点,已知BC路程为600米,请你帮助游客丙做一下决策,怎样到出口A所花时间最少,并说明理由.【答案】(1)①4,800;②24,3;(2)情况一所用时间比较少,理由详见解析;(3)①D到A的路程为800 米;②丙应该选择乘坐1 号车所需时间最少.412分钟,第三次相遇时间为1220分钟,第四次相遇时间为2028分钟,∴这一段时间内1号车与2号车相遇了3次.故答案为:24,3;(2)情况一所用时间比较少,设CK=x米,由题意知,情况一需要时间为:16,情况二需要的时间为:16,∴情况一所用时间比较少;(3)①设P到A的路程为a米,则2号车从C→B→A→P的时间为分钟,∴D到P的路程为50,由题意知,,解得:a=320,∴D到P的路程为50=480米,∴D到A的路程为320+480=800米;②若丙选择乘坐1号车,所需时间为13分钟,若丙选择乘坐2号车,所需时间为21分钟,若丙选择步行到出口A,所需时间为32分钟,所以丙应该选择乘坐1号车所需时间最少.【关键点拨】本题考查了一元一次方程的应用,理解题意仔细剖析每种情形下路程的变化是解题的关键.36.已知一个四位自然数M的千、百、十、个位上的数字分别是、、、,若,且,则称自然数M是“关联数”,且规定.例如5326,因为,所以5326是“关联数”,且现已知式子(、、都是整数,,,)的值表示四位自然数,且是“关联数”,的各位数字之和是8的倍数.(1)当时,求;(2)当时,求的和.【答案】(1)3544,(2)-72.∴,,.∴.(2)当时,的千、百、十、个位上的数字分别是3、、、.∵是“关联数”,∴,∴.∴的各位数字之和为.由题意,知是8的倍数,且,,,∴,,,或,,.∴,或3562.[来源]∴,.当时,的千、百、十、个位上的数字分别是3、、、.∵是“关联数”,∴,∴.∴的各位数字之和为.由题意,知是8的倍数,且,,,∴,,,或,,.∴,或3984.∴,.∴.∴的和是-72.【关键点拨】此题主要考察不等式的应用,正确理解题意,再列出相应的式子,但是要注意分开来求解. 37.百脑汇商场中路路通商店有甲、乙两种手机内存卡,买2个甲内存卡和1个乙内存卡用了90元,买3个甲内存卡和2个乙内存卡用了160元.(1)求甲、乙两种内存卡每个各多少元?(2)如果小亮准备购买甲.乙两种手机内存卡共10个,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?(3)某天,路路通售货员不小心把当天上午卖的甲、乙种手机内存卡的销售量统计单丢失了,但老板记得每件甲内存卡每个赚10元,乙内存卡每个赚15元,一上午售出的内存卡共赚了100元,请你帮助老板算算有几种销售方案?并直接写出销售方案.【答案】(1) 甲内存卡每个20元,乙内存卡每个50元;(2) 有两种购买方案,方案一:购买A商品5件,B商品5件;方案二:购买A商品6件,B商品4件,其中方案二费用最低;(3) 共有4种销售方案:方案一:卖了甲内存卡10个,乙内存卡0个;方案二:卖了甲内存卡7个,乙内存卡2个;方案三:卖了甲内存卡4个,乙内存卡4个;方案四:卖了甲内存卡1个,乙内存卡6个.(2)解:设小亮准备购买A甲内存卡a个,则购买乙内存卡(10﹣a)个,则解得5≤a≤6,根据题意,a的值应为整数,所以a=5或a=6.方案一:当a=5时,购买费用为20×5+50×(10﹣5)=350元;方案二:当a=6时,购买费用为20×6+50×(10﹣6)=320元;∵350>320∴购买A商品6件,B商品4件的费用最低.答:有两种购买方案,方案一:购买A商品5件,B商品5件;方案二:购买A商品6件,B商品4件,其中方案二费用最低[来源:(3)解:设老板一上午卖了c个甲内存卡,d个乙内存卡,则10c+15d=100.整理,得2c+3d=20.∵c、d都是正整数,∴当c=10时,d=0;当c=7时,d=2;当c=4时,d=4;当c=1时,d=6.综上所述,共有4种销售方案:方案一:卖了甲内存卡10个,乙内存卡0个;方案二:卖了甲内存卡7个,乙内存卡2个;方案三:卖了甲内存卡4个,乙内存卡4个;方案四:卖了甲内存卡1个,乙内存卡6个.【关键点拨】此题考查二元一次方程组及一元一次不等式方程组的应用,解题关键是读懂题意,找到关键描述语,找到所求的量的大小关系.38.三亚市某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生(2)如果该工厂生产一件A产品可获利80元,生产一件B产品可获利120元,那么该工厂应该怎样安排生产可获得最大利润?【答案】(1)见解析;(2)见解析.(2)方案(一)A,30件,B,20件时,20×120+30×80=4800(元).方案(二)A,31件,B,19件时,19×120+31×80=4760(元).方案(三)A,32件,B,18件时,18×120+32×80=4720(元).故方案(一)A,30件,B,20件利润最大【关键点拨】本题主要考查一元一次不等式组的应用.39.小王是“新星厂”的一名工人,请你阅读下列信息:信息一:工人工作时间:每天上午8:00﹣12:00,下午14:00﹣18:00,每月工作25天;信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元.信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元,请根据以上信息,解答下列问题:(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?【答案】(1)生产一件甲产品需要15分,生产一件乙产品需要20分;(2)小王该月最多能得3544元,此时生产甲、乙两种产品分别60,555件.解这个方程组得:,答:生产一件甲产品需要15分,生产一件乙产品需要20分.(2)设生产甲种产品共用x分,则生产乙种产品用(25×8×60-x)分.则生产甲种产品件,生产乙种产品件.∴w总额=1.5×+2.8×=0.1x+×2.8=0.1x+1680-0.14x[来源]=-0.04x+1680,又≥60,得x≥900,由一次函数的增减性,当x=900时w取得最大值,此时w=0.04×900+1680=1644(元),则小王该月收入最多是1644+1900=3544(元),此时甲有=60(件),乙有:=555(件),答:小王该月最多能得3544元,此时生产甲、乙两种产品分别60,555件.【关键点拨】本题考查了用一元二次方程组的实际应用,一次函数的实际应用问题,建立函数模型是解题关键.40.如图,在平面直角坐标系中,点M的坐标为(2,8),点N的坐标为(2,6),将线段MN向右平移4个单位长度得到线段PQ(点P和点Q分别是点M和点N的对应点),连接MP、NQ,点K是线段MP的中点.(1)求点K的坐标;(2)若长方形PMNQ以每秒1个单位长度的速度向正下方运动,(点A、B、C、D、E分别是点M、N、Q、P、K的对应点),当BC与x轴重合时停止运动,连接OA、OE,设运动时间为t秒,请用含t的式子表示三角形OAE的面积S(不要求写出t的取值范围);(3)在(2)的条件下,连接OB、OD,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积?若存在,请求出t值;若不存在,请说明理由.【答案】(1)(4,8)(2)S△OAE=8﹣t(3)2秒或6秒(2)如图1所示,延长DA交y轴于F,则OF⊥AE,F(0,8﹣t),∴OF=8﹣t,∴S△OAE=OF•AE=(8﹣t)×2=8﹣t;(3)存在,有两种情况:,①如图2,当点B在OD上方时,②如图3,当点B在OD上方时,过点B作BG⊥x轴于G,过D作DH⊥x轴于H,则B(2,6﹣t),D(6,8﹣t),∴OG=2,GH=4,BG=6﹣t,DH=8﹣t,OH=6,S△OBD=S△ODH﹣S四边形DBGH﹣S△OBG,=OH•DH﹣(BG+DH)•GH﹣OG•BG,【关键点拨】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识,解题关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.。
(完整)中考数学压轴题精选含答案
一、解答题1.如图,在直角梯形ABCD 中,AB ∥CD ,∠B =90°,AB =4,BC =8,CD =2m (m >2),P 为CD 中点,以P 为圆心,CP 为半径作半圆P ,交线段AC 于点E ,交线段AD 于点F .(1)当E 为CA 中点时,①求证:E 是弧CF 的中点.②求此时m 的值.(2)连结PF ,若PF 平行△ABC 的某一边时求出满足条件的m 值.(3)连结PE ,将PE 绕着点E 顺时针旋转90°得到EP ',连结AP ',当AP '⊥AC 时,求此时CE 的长.2.如图1,在菱形ABCD 中,∠D =120°,AB =8,点M 从A 开始,以每秒1个单位的速度向点B 运动;点N 从C 出发,沿C →D →A 方向,以每秒2个单位的速度向点A 运动,若M 、N 同时出发,其中一点到达终点时,另一个点也随之停止运动.设运动的时间为t 秒,过点N 作NQ ⊥DC ,交AC 于点Q .(1)当t =2时,求线段NQ 的长;(2)设△AMQ 的面积为S ,直接写出S 与t 的函数关系式及t 的取值范围;(3)在点M 、N 运动过程中,是否存在t 值,使得△AMQ 为等腰三角形?若存在,请求出t 的值;若不存在,请说明理由.3.如图,在平面直角坐标系中,抛物线2y x bx c =-++,与y 轴交于点A 与x 轴交于点E 、B .且点()0,5A ,()5,0B ,点P 为抛物线上的一动点.(1)求二次函数的解析式;(2)如图1,过点A 作AC 平行于x 轴,交抛物线于点C ,若点P 在AC 的上方,作PD 平行于y 轴交AB 于点D ,连接PA ,PC ,当245AOE APCD S S ∆=四边形时,求点P 坐标; (3)设抛物线的对称轴与AB 交于点M ,点Q 在直线AB 上,当以点M 、E 、P 、Q 为顶点的四边形为平行四边形时,请直接写出点Q 的坐标.4.如图,抛物线2y ax bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,OA =1,OB =OC =3.(1)求抛物线的表达式;(2)如图1,点D 为第一象限抛物线上一动点,连接DC ,DB ,BC ,设点D 的横坐标为m ,△BCD 的面积为S ,求S 的最大值;(3)如图2,点P (0,n )是线段OC 上一点(不与点O 、C 重合),连接PB ,将线段PB 以点P 为中心,旋转90°得到线段PQ ,是否存在n 的值,使点Q 落在抛物线上?若存在,请求出满足条件的n 的值,若不存在,请说明理由.5.如图,抛物线223y x x =--+与x 轴交于A 、B 两点,与y 轴交于C 点.(1)在第二象限内的抛物线上确定一点P ,使四边形PBOC 的面积最大.求出点P 的坐标.(2)点M 为抛物线上一动点,x 轴上是否存在一点Q ,使点B 、C 、M 、Q 的顶点的四边形是平行四边形,若存在,请直接写出Q 点的坐标;若不存在,请说明理由.6.已知抛物线经过()30A -,,()1,0B ,52,2C ⎛⎫ ⎪⎝⎭三点,其对称轴交x 轴于点H ,一次函数()0y kx b k =+≠的图象经过点C ,与抛物线交于另一点D (点D 在点C 的左边),与抛物线的对称轴交于点E . (1)求抛物线的解析式;(2)在抛物线上是否存在点F ,使得点A 、B 、E 、F 构成的四边形是平行四边形,如果存在,求出点F 的坐标,若不存在请说明理由(3)设∠CEH=α,∠EAH =β,当αβ>时,直接写出k 的取值范围7.如图1,直线l 1:y =kx 与直线l 2:y =﹣12x +b 相交于点A (4,3),直线l 2:y =﹣12x +b 与x 轴交于点B ,点E 为线段AB 上一动点,过点E 作EF ∥y 轴交直线l 1于点F ,连接BF .(1)求k、b的值;(2)如图2,若点F坐标为(8,6),∠OFE的角平分线交x轴于点M.①求线段OM的长;②点N在直线l1的上方,当△OFN和△OFM全等时,直接写出点N的坐标.8.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的坐标为(4,3).(1)求抛物线的解析式与直线l的解析式;(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当△PAD面积最大时点P 的坐标及该面积的最大值;(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.9.如图,在△ABC中,AB=AC,⊙是△ABC的外接圆,连接BO并延长交边AC于点D.(1)如图1,求证:∠BAC=2∠ABD;(2)如图2,过点B作BH⊥AC于点H,延长BH交⊙O于点G,连接OC,CG,OC交BG于点F,求证:BF=2HG;(3)如图3,在(2)的条件下,若AD=2,CD=3,求线段BF的长.10.如图1,在平面直角坐标系中,抛物线y=ax2+154x+c与x轴负半轴相交于点A(﹣20,0),与y轴相交于点B(0,﹣15).(1)求抛物线的函数表达式及直线AB的函数表达式;(2)如图2,点C是第三象限内抛物线上的一个动点,连接AC、BC,直线OC与直线AB 相交于点D,当△ABC的面积最大时,求此时△ABC面积的最大值及点C的坐标;(3)在(2)的条件下,点E为线段OD上的一个动点,点E从点O开始沿OD以每秒10个单位长度的速度向点D运动(运动到点D时停止),以OE为边,在OD的左侧做正方形OEFG,设正方形OEFG与△OAD重叠的面积为S,运动时间为t秒.当t>3时,请直接写出S与t之间的函数关系式为(不必写出t的取值范围).11.在平面直角坐标系xOy中,点A(a,b)和点B(c,d).给出如下定义:以AB为边,作等边三角形ABC,按照逆时针方向排列A,B,C三个顶点,则称等边三角形ABC为点A,B的逆序等边三角形.例如,当1,0,3,0a b c d=-===时,点A,B的逆序等边三角形ABC如图①所示.(1)已知点A(-1,0),B(3,0),则点C的坐标为___;请在图①中画出点C,B的逆序等边三角形CBD,点D的坐标为___.(2)图②中,点B(3,0),点A在以点M(-2,0)为圆心1为半径的圆上,求点A,B的逆序等边三角形ABC的顶点C的横坐标取值范围.(3)图③中,点A在以点M(-2,0)为圆心1为半径的圆上,点B在以N(3,0)为圆心2为半径的圆上,且点B的纵坐标0d>,点A,B的逆序等边三角形ABC如图③所示.若点C 恰好落在直线y x t=+上,直接写出t的取值范围.12.已知:如图1,一次函数y=mx+5m的图像与x轴、y轴分别交于点A、B,与函数y=-23x的图像交于点C,点C的横坐标为-3.(1)求点B的坐标;(2)若点Q为直线OC上一点,且S△QAC=2S△AOC,求点Q的坐标;(3)如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.①在图2中,只利用圆规.....作图找到点P的位置; (保留作图痕迹,不得在图2中作无关元素.)②求点P的坐标.13.在平面直角坐标系xOy中,⊙O的半径为1.对于线段AB,给出如下定义:若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′,则称线段AB是⊙O的以直线l为对称轴的“反射线段”,直线l称为“反射轴”.(1)如图,线段CD,EF,GH中是⊙O的以直线l为对称轴的“反射线段”有;(2)已知A点坐标为(0,2),B点坐标为(1,1),①若线段AB是⊙O的以直线l为对称轴的“反射线段”,求反射轴l与y轴的交点M的坐标.②若将“反射线段”AB沿直线y=x的方向向上平移一段距离S,其反射轴l与y轴的交点的纵坐标yM的取值范围为12≤yM136≤,求S.(3)已知点M,N是在以原点为圆心,半径为2的圆上的两个动点,且满足MN=1,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,求反射轴l未经过的区域的面积.(4)已知点M,N是在以(2,013MN2=MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,请直接写出反射轴l与y轴交点的纵坐标的取值范围.14.△ABC为等边三角形,AB=4,AD⊥BC于点D,点E为AD的中点.(1)如图1,将AE绕点A顺时针旋转60°至AF,连接EF交AB于点G,求证:G为EF中点.(2)如图2,在(1)的条件下,将△AEF绕点A顺时针旋转,旋转角为α,连接BE,H为BE的中点,连接DH,GH.当30°<α<120°时,猜想∠DHG的大小是否为定值,并证明你的结论.(3)在△AEF绕点A顺时针旋转过程中,H为BE的中点,连接CH,问线段CH何时取得最大值,请说明理由,并直接写出此时△ADH的面积.15.在ABC中,AB AC=,D是边AC上一点,F是边AB上一点,连接BD、CF交于点E,连接AE,且.(1)如图1,若90BAC∠=︒,,,求点B到AE的距离;(2)如图2,若E为BD中点,连接FD,FD平分,G为CF上一点,且,求证:;(3)如图3,若,12BC=,将ABD△沿着AB翻折得,点H为的中点,连接HA、HC,当周长最小时,请直接写出的值.16.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于C点,D为抛物线顶点.(1)连接AD,交y轴于点E,P是抛物线上的一个动点.①如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接,若,求点P的坐标.②如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w有最大值还是最小值?w的最值是多少?(2)如图三,点P是第四象限抛物线上的一点,过A、B、P三点作圆N,过点P作PM x⊥轴,垂足为I,交圆N于点M,点P在运动过程中,线段是否变化?若有变化,求出MI的取值范围;若不变,求出其定值.(3)点Q是抛物线对称轴上一动点,连接OQ、AQ,设AOQ外接圆圆心为H,当的值最大时,请直接写出点H的坐标.17.如图,在平面直角坐标系中,矩形OABC,点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣34x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D (﹣2,﹣1)在直线BC 上,点E 为y 轴右侧抛物线上一点,连接BE 、AE ,DE ,若S △BDE =4S △ABE ,求E 点坐标;(3)如图2,在(2)的条件下,P 为射线DB 上一点,作PQ ⊥直线DE 于点Q ,连接AP ,AQ ,PQ ,若△APQ 为直角三角形,请直接写出P 点坐标.18.如图1,点A ,点B 的坐标分别(a ,0),(0,b ),且b =+4,将线段BA 绕点B 逆时针旋转90°得到线段BC .(1)直接写出a = ,b = ,点C 的坐标为 ;(2)如图2,作CD ⊥x 轴于点D ,点M 是BD 的中点,点N 在△OBD 内部,ON ⊥DN ,求2+ON =DN .(3)如图3,点P 是第二象限内的一个动点,若∠OPB =90°,求线段CP 的最大值.19.如图1,已知抛物线)(3343y x x =+-与x 轴交于A 、B 两点,与y 轴交于点C ,(1)写出A 、B 、C 三点的坐标.(2)若点P 为OBC 内一点,求OP BP CP ++的最小值.(3)如图2,点Q 为对称轴左侧抛物线上一动点,点()4,0D ,直线DQ 分别与y 轴、直线AC 交于E 、F 两点,当CEF △为等腰三角形时,请直接写出CE 的长.20.已知等边△ABC ,M 在边BC 上,MN ⊥AC 于N ,交AB 于点P .(1)求证:BP =BM ;(2)若MC =2BM ,求证:MP =MN .(3)若E ,F 分别在AB 、AC 上,且△MEF 为等边三角形,当MEF ABC S S ∆∆的值最小时,BM BC= .【参考答案】**科目模拟测试 一、解答题 1.(1)①见解析;②5m =;(2)m 的值为25或6;(3)25CE =【解析】【分析】(1)①连接DE ,证明ADC ∆是等腰三角形,根据“三线合一”的性质可得ADE CDE ∠=∠,证得EC EF =,从而可得结论;②根据勾股定理得到AC 45=,由E 为AC 中点得EC 25=,再证明DEC CBA ,由相似三角形的性质列出比例式,求出m 的值即可;(2)分PF //AC 和PF //BC 两种情况求解即可; (3)设CE =x ,作PG ⊥AC ,则2x GE =,45AE x =- 证明PGE EAP '≅得AP GE '=,再证明AP EBAC ',列比例式求出x 的值即可.【详解】解:(1)如图,连接DE∵CD 是圆P 的直径,∴∠DEC =90°,即DE ⊥AC∵E 为CA 中点∴AE =CE∴AD =CD∴ADE CDE ∠=∠∴EC EF =∴E 是CF 的中点;②在Rt △ABC 中,∠B =90°,AB =4,BC =8,∴22224845AC AB BC +=+∵E 是AC 的中点∴11452522EC AC ==⨯= ∵AB //CD ,90B ∠=︒∴90B DCB ∠+∠=︒∴90DCB∠=︒,即90DCE BCA∠+∠=︒∵90CDE DCE∠+∠=︒∴CDE BCA∠=∠又90B DEC∠=∠=︒∴DEC CBA∆∆∽∴CE DCAB AC=,即252=445m解得,5m=;(2)分两种情况:①当PF//AC时,如图,则有PDF CDA∆∆∴PF PDAC CD=,即245PF mm=∴25=PF∴25m=②当PF//BC时,如图,过点A作AH⊥DC,垂足为H,则四边形AHCB是矩形,∴AH//BC,HC=AB=4,AH=BC=8∴PF//AH∵90DCB∠=︒∴90FPD∠=︒∴45PDF PFD∠=∠=︒∴45HAD HDA∠=∠=︒∴DH=AH,即248m-=解得,6m=综上,m的值为256;(3)过点P 作PG AC ⊥于点G ,如图,∵PE =PC ∴1,2GE CE EPG CPG =∠=∠ ∵90PEP '∠=︒∴90P EA PEG '∠+∠=︒又90PEG GPE ∠+∠=︒∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒,PE P E '=∴P AE EPG '∆≅∆∴AP GE '=设CE x =,则45,2x AE x GE AP '=== ∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒∴GPC BCA ∠=∠∴EPG BCP ∠=∠∴P EA BCA '∠=∠又90P AE B '∠=∠=︒∴AP E BAC '∆∆ ∴AP AB AE BC '=42825x = ∴5x =25CE =【点睛】本题主要考查了全等三角形的判定与性质,圆的基本概念,相似三角形的判定与性质,正确作出辅助线以及进行分类讨论是解答本题的关键.2.(143;(2)S =()()22330434348t t t ⎧+≤≤⎪⎪⎨⎪≤⎪⎩<;(3)存在,当t =247s 或(32-163)s或163s时,△AMQ为等腰三角形.【解析】【分析】(1)首先求得CN的长,在直角△CNQ中利用三角函数即可求得NQ的长;(2)当0≤t≤4时,N在CD上,首先求得CQ,则AQ长即可求得,再根据△CAB=30°,AM=t,据此即可求得△AMQ的长;当4<t≤8时,利用相似求得AQ的长,进而求得△AMQ的面积,得到函数解析式;(3)分三种情形讨论求解即可.【详解】解:(1)当t=2时,CN=2×2=4,∵在△ACD中,AD=DC,∴∠DCA=1801202︒-︒=30°,在直角△CNQ中,NQ=CN•tan30°=4×33=433;(2)由题意得,AM=t,当0≤t≤4时,CN=2t,∵∠D=120°,AB=CD=8,∴∠DCA=30°,连接BD,与AC相交于点定O,过点Q作QG⊥AB于点G,∴OC=CD•cos30︒3AC3∴在Rt△CNQ中,NQ23t,CQ43t,∴AQ=AC-CQ343,QG=12AQ,∴S=12AM• QG =233t+,当4<t≤8时,延长QN,交AB于G,交CD延长线于H,如图:ND =2t -8,∠HDN =60°,∴HD =12ND =t -4, ∴CH =t -4+8=t +4,∴CQ =23cos303CH =︒(t +4), ∴AQ =AC -CQ =83-233(t +4),QG =12AQ , S =12•AM • QG 234363t t =-+. 综上,S =()()223230433434863t t t t t t ⎧-+≤≤⎪⎪⎨⎪-+≤⎪⎩<; (3)①当0<t ≤4时,只有MA =MQ 符合条件,过点M 作ME ⊥AC 于点E ,则AE =EQ =AM •cos30︒=32t , ∴AQ =3t ,由(2)知AQ 343, 3433, 解得t =247; ②当4<t ≤8时,由(2)知AQ 323t +4),AQ =AM 时,)4t +=t ,解得tAQ =MQ 时,AM ,t )4t ⎤+⎥⎦, 解得t =163.综上所述,当t =247s 或(s 或163s 时,△AMQ 为等腰三角形. 【点睛】本题考查了菱形的性质以及三角函数,正确进行分请情况进行讨论是关键.3.(1)245y x x =-++;(2)1(2,9)P ,2(3,8)P ;(3)1(9,4)Q -,2(0,5)Q ,3(1,6)Q -,4(5,10)Q -【解析】【分析】(1)直接将(0,5)A ,(5,0)B 代入2y x bx c =-++,求解即可;(2)先求出AB 的解析式,设点P 的横坐标为t ,则()2,45P t t t -++,(,5)D t t -+,用t 表示出PD ,最后利用245AOE APCD S S ∆=四边形求出结果; (3)分三种情况讨论解答:①当EM 为平行四边形的对角线时;②当EP 为对角线时;③当EQ 为对角线时.【详解】(1)将点(0,5)A ,(5,0)B 分别代入2y x bx c =-++得25505b c c -++=⎧⎨=⎩, 45b c =⎧∴⎨=⎩, ∴二次函数的解析式为245y x x =-++;(2)//AC x 轴,点()0,5A ,∴当5y =时,2455x x -++=,10x ∴=,24x =,()4,5C ∴,4AC ∴=,设直线AB 的解析式为y mx n =+,将(0,5)A ,(5,0)B 分别代入得505n m n =⎧⎨=+⎩, 解得:1m =-,5n =∴直线AB 的解析式为5y x =-+;设点P 的横坐标为t ,则()2,45P t t t -++,(,5)D t t -+()2245(5)5PD t t t t t ∴=-++--+=-+,4AC =,()22114521022APCD S AC PD t t t t ∴=⨯=⨯⨯-+=-+四边形 函数245y x x =-++,当0y =时,有2450x x -++=,11x ∴=-,25x =,(1,0)E ∴-,1OE ∴=,又5OA =,11515222AOE S OE OA ∆∴=⨯⨯=⨯⨯=, 245AOE APCD S S ∆=四边形, 22452101252t t ∴-+=⨯=, 解得:12t =,23t =,∴点1(2,9)P ,2(3,8)P ;(3)∵2(2)9y x =--+,∴当x =2时,y =-2+5=3,∴M (2,3),设P (m ,2(2)9m --+,(,5)Q n n -+,而E (-1,0),①当EM 为平行四边形的对角线时,(平行四边形的对角线互相平分)得:21222(2)950322m n m n +-+⎧=⎪⎪⎨--+-++⎪=⎪⎩, 解得121261,52m m n n ==-⎧⎧⎨⎨=-=⎩⎩ (舍), ∴点Q 的坐标为(-5,10);②当EP 为对角线时,212220(2)93522m m m n -++⎧=⎪⎪⎨--+-+⎪=⎪⎩,解得121223,10m m n n ==⎧⎧⎨⎨=-=⎩⎩, ∴点Q 的坐标为(-1,6)或(0,5);③当EQ 为对角线时,21222053(2)922n m n m -++⎧=⎪⎪⎨-+--+⎪=⎪⎩, 解得121261,92m m n n ==-⎧⎧⎨⎨==⎩⎩(舍), 点Q 的坐标为(9,-4),综上所得:1(9,4)Q -,2(0,5)Q ,3(1,6)Q -,4(5,10)Q -.【点睛】本题考查了待定系数法求函数关系式,平行四边形的性质和判定,解本题的关键是分类思想的运用.4.(1)2y x 2x 3=-++;(2)278;(3)存在,n =1或n 3+33- 【解析】【分析】(1)通过待定系数法求解函数解析式即可;(2)作DF ⊥x 轴于点F ,交BC 于点E ,根据12S DE OB =⋅求得S 关于m 的解析式,根据二次函数的性质求解即可;(3)过点P 作PB 的垂线,交抛物线于点1Q 和2Q ,作1Q M y ⊥轴于点M ,2Q N y ⊥轴于点N ,利用全等三角形的性质求解即可.【详解】解:(1)设函数关系式为2y ax bx c =++由题意,得A (-1,0),B (3,0),C (0,3)∴(1)(3)y a x x =+-把C (0,3)代入得,1a =-∴2y x 2x 3=-++(2)作DF ⊥x 轴于点F ,交BC 于点E设直线BC 关系式为y =kx +b ,代入(3,0),(0,3)得k =-1,b =3,∴y =-x +3∵点D 的横坐标为m ,则DF =223m m -++,EF =-m +3∴DE =23m m -+22133327(3)()22228S DE OB m m m =⋅=-+=--+ ∵302-<,∴S 的最大值是278(3)过点P 作PB 的垂线,交抛物线于点1Q 和2Q ,作1Q M y ⊥轴于点M ,2Q N y ⊥轴于点N∴1290Q MP Q NP BOP ∠=∠=∠=︒∵1190Q PM PQ M ∠+∠=︒,190Q PM BPO ∠+∠=︒,∴1PQ M BPO ∠=∠又∵1BP PQ =,∴1Q PM PBO △≌△∴1MQ OP n ==,3MP OB ==,∴1()3Q n n +,代入抛物线,得2323n n n +=-++解得11n =,20n =(舍去)同理,2PN Q PBO ≌,∴2Q (-n ,n -3)代入抛物线,得2323n n n =-+-- 解得13+33n -=2333n --=舍去) 综上,存在n 的值,n =1或n 3+33-【点睛】 此题考查了二次函数与几何的综合应用,涉及了待定系数法求解析式,二次函数的性质,全等三角形的判定与性质,解题的关键是熟练掌握二次函数以及全等三角形的判定与性质.5.(1)315,24⎛⎫- ⎪⎝⎭;(2)Q 1(-5,0),Q 2(-1,0),Q 3 ()720,,Q 4)720,. 【解析】【分析】(1)分别求出点B 、C 的坐标,连接PB ,PC ,PO ,设点P 坐标为()2,23m m m --+,四边形PBOC 的面积为S ,根据=BOP COP S S S +△△得到S 关于m 的二次函数解析式,根据二次函数的性质即可求解;(2)分点M 在x 轴上方或点M 在x 轴下方两种情况讨论,分别求出点M 的坐标,根据平行四边形的性质即可求出点Q 的坐标. 【详解】解:(1)把0x =代入223y x x =--+得y =3, ∴点C 坐标为(0,3);把y =0代入223y x x =--+得2x 2x 30--+=, 解得123,1x x =-=, ∵点B 在x 轴负半轴上, ∴点B 坐标为(-3,0); 如图1,连接PB ,PC ,PO ,∵点P 在第二象限抛物线223y x x =--+上,∴设点P 坐标为()2,23m m m --+(-3<m <0),设四边形PBOC 的面积为S , ∴=BOP COP S S S +△△2211232m m OB O m C =--++ ()()2332223m m m +=+--- 2399222m m =--+, ∵302-<,∴当322b m a =-=-时,S 有最大值, 此时,215234m m --+=, ∴当点P 坐标为315,24⎛⎫- ⎪⎝⎭时,四边形PBOC 的面积最大;(2)存在,如图2,分点M 在x 轴上方或点M 在x 轴下方两种情况讨论. ①当点M 在x 轴上方时,点M 与点C 纵坐标相等,∴2233x x --+=, 解得122,0x x =-=, ∴CM 1=2,∵四边形BQCM 1是平行四边形, ∴CM =BQ =2,∴满足条件的点Q 有两个,分别是Q 1(-5,0),Q 2(-1,0); ②当点M 在x 轴下方时,点M 与点C 纵坐标互为相反数, ∴2233x x --+=-, 解得1271,71x x =--=-,∴点M 2坐标为()713---,,点M 3坐标为()713--,,由平行四边形的性质得点B 向右平移3个单位,向上平移3个单位得到点C ,∴点M 2向右平移3个单位,向上平移3个单位得到点Q 3,点M 3向右平移3个单位,向上平移3个单位得到点Q 4,∴Q 3的坐标为()720-+,,Q 4的坐标为()720+,;综上所述,满足条件的点Q 的坐标有四个,分别是Q 1(-5,0),Q 2(-1,0),Q 3()720-+,,Q 4()720+,.【点睛】本题为二次函数综合题,难度较大,解决第(1)步,关键是理解函数图象上点的坐标特点,将四边形分割为两个三角形,分别表示出三角形面积,得到函数解析式,并利用二次函数性质求解;解决第(2)步关键是理解平行四边形的性质,利用分类讨论思想求解,注意要充分考虑各种情况,不要漏解.6.(1)y =12x 2+x −32;(2)(3,6)或(-5,6)或(−1,-2);(3)−12<k <56且k≠0或56<k<43【解析】【分析】(1)把A(−3,0),B(1,0),52,2C⎛⎫⎪⎝⎭代入y=ax2+bx+c,解方程组即可;(2)把C点坐标代入直线CD,得2k+b=52,分两种情况:①若AB为平行四边形的边时,②若AB为平行四边形的对角线时,得关于k、b的方程组,解方程组即可求解;(3)分两种情况:①当E点在x轴上方时,②E点在x轴下方时,根据当α=β时,列方程,可求出k的值,进而求出k的取值范围.【详解】解:(1)设抛物线的解析式为y=ax2+bx+c,∵抛物线经过A(−3,0),B(1,0),C(2,52)三点,∴9305 422a b ca b ca b c⎧⎪-+=⎪++=⎨⎪⎪++=⎩,∴12132abc⎧⎪⎪⎨⎪⎪-⎩===,∴抛物线的解析式为y=12x2+x−32;(2)如图1所示,将C点坐标代入直线CD,得2k+b=52,当x=−1时,y=−k+b,即E(−1,−k+b).①若AB为平行四边形的边时,则F(-1+4,−k+b)或F(-1-4,−k+b),即:F(3,−k +b )或F (-5,−k +b ), 把F (3,−k +b )代入y =12x 2+x −32,得−k +b =6, 把F (-5,−k +b ),代入y =12x 2+x −32,得−k +b =6, 又∵2k +b =52, ∴k =76-,b =296∴F (3,6)或(-5,6);②若AB 为平行四边形的对角线时,则F 和E 关于x 轴对称, ∴F (−1,k -b ), ∴k -b =-2, 又∵2k +b =52, ∴k =16,b =136,∴F (−1,-2),综上所述:F 的坐标为(3,6)或(-5,6)或(−1,-2); (3)如图2所示,①当E 点在x 轴上方时,如图2所示,当α=β时,∵∠EHA =90°, ∴∠AEC =90°, ∴∠AEH =∠EGH , ∵∠AHF =∠FHG =90°, ∴AHF FHG ∽, ∴AE AHEG EH=, ∵A (−3,0),E (−1,−k +b ),G (bk-,0),∴()()2222221k bk bbk bk+-+=-+⎛⎫-++-+⎪⎝⎭,∴k2−bk−2=0,联立方程220522k bkk b⎧--=⎪⎨+=⎪⎩,解得k=−12(k=43舍去),随着E点向下移动,∠CEH的度数越来越大,∠EAH的度数越来越小,当E点和H点重合时(如图3所示),α和β均等于0,此时联立方程522k bk b⎧+⎪⎨⎪-+⎩==,解得5656kb⎧=⎪⎪⎨⎪=⎪⎩,因此当−12<k<56且k≠0时,α>β;②E点在x轴下方时,如图4所示,当α=β时,∵∠EHA=90°,∴∠AEC=90°,根据①可得此时k=43(k=−12舍去),随着E点向下移动,∠CEH的度数越来越小,∠EAH的度数越来越大,因此当56<k <43时,α>β.综上所述可得,当α>β时,k 取值范围为−12<k <56且k ≠0或56<k <43.【点睛】本题考查的是一次函数、二次函数和相似三角形的判定和性质的综合应用,掌握待定系数法求函数解析式和数形结合思想方法是解题的关键.7.(1)34k =,5b =;(2)①OM =5;②()3,6N 或724,55N ⎛⎫ ⎪⎝⎭【解析】 【分析】(1)分别将将(4,3)A 代入y kx =和12y x b =-+中,求解即可;(2)①设直线AB 与y 轴交与点C ,与FM 交于点D ,证明△AFD ≌△EFD ,得到AD =ED ,利用中点坐标公式求得点D 坐标,用待定系数法求得直线FD 的函数表达式,令0y =,即可求得点M 的坐标,从而求得OM ;②点N 在直线l 1的上方,当△OFN 和△OFM 全等时,满足题意的点N 有两个,分别画出相关的图形,分类讨论求解即可. 【详解】解:(1)∵直线l 1:y kx =和直线l 2:12y x b =-+相交于点A∴将(4,3)A 代入y kx =中,得:43k = 解得:34k =∴将(4,3)A 代入12y x b =-+中,得:1432b -⨯+=解得:5b =∴3,54k b == (2)① 设直线AB 与y 轴交与点C ,与FM 交于点D ,如下图:∵34k =,5b = ∴直线l 1的函数表达式为34y x =,直线l 2的函数表达式为152y x =-+∵(4,3)A ∴22345OA +设直线AB 与y 轴交与点C ,与FM 交于点D 则()0,5C ∴5OC = ∴5OA OC == ∴∠OCA =∠OAC ∵//FE y 轴 ∴∠OCA =∠FEA 又∵∠OAC =∠FAE ∴∠FAE =∠FEA ∴FA =FE又∵FM 是∠OFE 的角平分线 ∴∠AFM =∠EFM 又∵FD =FD ∴△AFD ≌△EFD ∴AD =ED ∴点D 为AE 的中点 ∵//FE y 轴∴点F 和点E 的横坐标相同 将8x =代入152y x =-+中,得1y =∴()8,1E ∵(4,3)A ,()8,1E ∴()6,2D设线段FM 所在的直线函数表达式为()0y ax b a =+≠将()()8,6,6,2F D 代入y ax b =+中,得:8662k b k b +=⎧⎨+=⎩解得:210k b =⎧⎨=-⎩∴线段FM 所在的直线函数表达式为210y x =- 令0y =,得2100x -= 解得:5x = ∴()5,0M ∴OM =5② 当,OFN FOM 全等时,有两种情况,情况一,如下图所示:∵OFN FOM ≅△△∴∠OFN =∠FOM ,FN =OM ,ON =FM ∴//FN OM ∵OM =5 ∴FN =5,8F x =∴853N x =-=,6N F y y == ∴()3,6N情况二,当△OMF 和△ONF 关于直线l 1对称时,如下图所示:∵OFN FOM ≅△△∴ON =OM =5,∠NOF =∠MOF ∵OP =OP ∴△NOP ≌△MOP ∴PN =PM ∵()8,6F∴10OF 又∵1122OMFF SOM y OF PM =⋅=⋅ ∴F OM y OF PM ⋅=⋅ ∴56==310PM ⨯∴MN =2PM =6,OP 4 ∵1122OMN N S MN OP OM y =⋅=⋅△ ∴642455N y ⨯==∴75N x ==∴724,55N ⎛⎫⎪⎝⎭综上所述,满足题意点有两个,分别是:()3,6N 或724,55N ⎛⎫⎪⎝⎭【点睛】本题考查用待定系数法求一次函数表达式,三角形全等的性质和证明,两条直角交点的求法以及三角形的等面积法等知识点,牢记相关内容并能灵活应用数形结合思想解题是本题的关键.8.(1)y 14=-x 2+x +3;y 12=x +1;(2)△PAD 的面积的最大值为274,P (1,154);(3)点Q 的坐标为(0,133)或(0,﹣9) 【解析】 【分析】(1)由A (﹣2,0)、B (6,0)设抛物线的解析式为y =a (x +2)(x ﹣6),把D (4,3)的代入解析式解方程即可,再利用待定系数法求解一次函数的解析式; (2)如图1中,过点P 作PT y ∥轴交AD 于点T .设P (m ,14- m 2+m +3),则T(m,12m+1),再利用面积列函数关系式,再利用二次函数的性质求解最值即可;(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,则T(﹣5,6),设DT交y轴于点Q,则∠ADQ=45°,再求解直线DT的解析式为y13=-x133+,作点T关于AD的对称点T′(1,﹣6),求解直线DT′的解析式为y=3x﹣9,设DQ′交y轴于点Q′,则∠ADQ′=45°,从而可得答案.【详解】解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,∴设抛物线的解析式为y=a(x+2)(x﹣6),∵D(4,3)在抛物线上,∴3=a(4+2)×(4﹣6),解得a14 =-,∴抛物线的解析式为y14=-(x+2)(x﹣6)14=-x2+x+3,∵直线l经过A(﹣2,0)、D(4,3),设直线l的解析式为y=kx+m(k≠0),则2043k mk m-+=⎧⎨+=⎩,解得,121km⎧=⎪⎨⎪=⎩,∴直线l的解析式为y12=x+1;(2)如图1中,过点P作PT y∥轴交AD于点T.设P(m,14-m2+m+3),则T(m,12m+1).∵S△PAD12=•(xD﹣xA)•PT=3PT,∴PT的值最大值时,△PAD的面积最大,∵PT14=-m2+m+312-m﹣114=-m212+m+214=-(m﹣1)294+,∵14-<0,抛物线开口向下,∴m=1时,PT的值最大,最大值为94,此时△PAD的面积的最大值为274,P(1,154).(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,过D作DM x⊥轴于,M过T作TN x轴于,N90,,TNA AMD TAD AD AT90,TAN ATN TAN DAM,ATN DAM,ATN DAM≌6,3,235,TN AM AN DM ON∴T(﹣5,6),设DT交y轴于点Q,则∠ADQ=45°,∵D(4,3),∴直线DT的解析式为y13=-x133+,∴Q(0,133),作点T关于AD的对称点T',同理可得T'(1,﹣6),则直线DT′的解析式为y=3x﹣9,设DQ′交y轴于点Q′,则∠ADQ′=45°,∴Q′(0,﹣9),综上所述,满足条件的点Q的坐标为(0,133)或(0,﹣9).【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,待定系数法,等腰直角三角形的性质等知识,解题的关键是学会利用参数构建二次函数解决最值问题,学会构造特殊三角形解决问题,属于中考压轴题.二次函数综合题中面积问题的解题通法:(1)直角坐标系中图形面积的求法,以“S三角形=12×水平底×铅直高”为基础求解.(2)图形面积的数量关系:①找出所求图形的顶点,其中动点的坐标根据函数关系式用含未知数的代数式表示出来;②结合图形作辅助线,并将关键线段的长度用含未知数的代数式表示出来;③利用面积公式用含未知数的代数式表示出图形的面积;④列方程求解.(3)图形面积的最值,解题思路跟(1)中的前三步相同,然后利用函数的增减性求解.9.(1)证明见解析;(2)证明见解析,(3)15714BF=.【解析】【分析】(1)连接OA并延长AO交BC于E,证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论,(2)利用直角三角形两锐角互余、圆周角定理进行导角,得出MCG△和△FCG是等腰三角形,得出BM=MC=FG=CG,MH=HG,进而由BF=BM+MH-FH=FG-FH+HG,得出结论;(3)过O点作OP⊥AC,由垂径定理得出12PD=,再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==,由勾股定理进而可求BH,再利用相似三角形对应边成比例求出HG,即可得BF长.【详解】解:(1)连接OA并延长AO交BC于E,∵AB=AC,∴AB AC=,∵AE过圆心O,∴AE BC⊥,BE EC=,∴∠BAC=2∠BAE,∵OA=OB,∴∠ABD=∠BAE,∴∠BAC=2∠ABD;(2)如解图(2),连接OA并延长AO交BC于E,AE交BF于M,连接MC,设2BACα∠=,则ABD BAE EACα∠=∠=∠=∵AE =EC ,AE ⊥BC ,∴BM =MC ,∴∠MBC =∠MCB ,∵BG ⊥AC ,AE ⊥BC ,∴∠EAC +∠ACE =90°,∠HBC +∠ACE =90°,∴EAC HBC MCB α∠=∠=∠=,∴2CMG MBC MCB α∠=∠+∠=,∵BC BC =,∴2G BAC α∠=∠=,∴∠G =∠CMG ,∴CG =CM =BM ,∵AC ⊥BG ,∴MH =HG ,∵OA =OC ,∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-,∵180FCG CFG G ∠=︒-∠-∠,即180(90)290FCG ααα∠=︒-︒--=︒-,∴FCG CFG ∠=∠,∴FG =CG ,∴BM =MC =FG =CG ,又∵MH =HG ,∴BF =BM +MH -FH =FG -FH +HG ,∴BF =2HG .(3)过O 点作OP ⊥AC ,如解图(3)∵AO 是∠BAC 的角平分线,∴点O 到AB 、AC 的距离相等, ∴ABO ADO SAB BO S AD OD==, ∵AD =2,CD =3,∴AB =AC =5, ∴5=2BO OD ,即:2=7OD BD , ∵OP ⊥AC ,∴52AP PC ==,12PD =, ∵BH AC ⊥, ∴OP //BH ,∴27DP OP OD DH BH BD ===, ∴7724DH DP ==, ∴154AH AD DH =+=,5-4HC DC DH ==,∵在Rt ABH中,BH == ∵BAH G ∠=∠,AHB GHC ∠=∠, ∴AHB GHC △△,∴AH BH HG CH = 即:AH HC BHHG =, 51544=⨯, ∴HG =, 由(2)得BF =2HG ,∴BF = 【点睛】 本题是圆的综合题,主要考查了圆周角定理,涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点,解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系,从而利用相似或勾股定理解题.10.(1)291515404y x x =+-,y =﹣34x ﹣15;(2)面积最大值225,C (﹣10,﹣30);(3)S =﹣2553t +160t ﹣240. 【解析】【分析】(1)利用待定系数法将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 即可求出抛物线的函数表达式;设AB 的函数表达式是y =kx +b ,然后利用待定系数法将点A (﹣20,0),B (0,﹣15)代入y =kx +b 即可求出直线AB 的函数表达式;(2)作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15),根据题意表示出CF 的长度,进而表示出ABC S ∆,然后利用二次函数的性质求解即可;(3)作AN ⊥OD 于N ,AD 与FG 交于点I ,首先根据题意求出OC 的解析式,然后联立33154y x y x =⎧⎪⎨=--⎪⎩求出点D 的坐标,然后求出AD OD =,利用等腰三角形三线合一性质求出ON 的长度,进而利用勾股定理求出AN 的长度,表示出S △AON ,然后证明出△GFI ∽△OGH ∽△ANO ,利用相似三角形的性质表示出S △IJF =803(t ﹣3)2,S △GOH =253t ,最后利用面积之间的关系即可求出S 与t 之间的函数关系式.【详解】解:(1)由题意得,将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 得, 21515(20)(20)04c a c =-⎧⎪⎨-+⨯-+=⎪⎩, ∴15940c a =-⎧⎪⎨=⎪⎩, ∴291515404y x x =+-, 设AB 的函数表达式是y =kx +b ,将点A (﹣20,0),B (0,﹣15)代入y =kx +b 得,∴15200b k b =-⎧⎨-+=⎩, ∴1534b k =-⎧⎪⎨=-⎪⎩, ∴y =﹣34x ﹣15; (2)如图1,作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15), ∴FC =(﹣315)4a -﹣(2940a +154a ﹣15)=﹣2940a ﹣92a , ∴ABC S ∆=12CF •AO =12(﹣2940a ﹣92a )×20=﹣94(a +10)2+225, ∴当a =﹣10时,ABC S ∆=225, 当a =﹣10时,y =29(10)40⨯-+()15104⨯-﹣15=﹣30, ∴C (﹣10,﹣30);(3)如图2,作AN ⊥OD 于N ,∵C (﹣10,﹣30),∴OC 的解析式是:y =3x ,由33154y x y x =⎧⎪⎨=--⎪⎩得, 412x y =-⎧⎨=-⎩, ∴D (﹣4,﹣12),∵A (﹣20,0),OD 22412+10∴AD ()2220412-++=20,∴AD OD=,又∵AN⊥OD,∴ON=12OD=AN=S△AON=1160 22AN ON=⨯=,∵OE,OD=,∴DE=,∴JE=3(),∴FJ=EF﹣JEt﹣3(t)=(t﹣3),∵OG AN FJ∥∥,∴GOH OAN DAN AJF∠=∠=∠=∠,又∵90G ANO F∠=∠=∠=︒,∴△GFI∽△OGH∽△ANO,∴IJFAONSS∆∆=(FJAN)2=2,GOHAONSS∆∆=(OGAN)2)2,∴S△IJF=803(t﹣3)2,S△GOH=253t,∴S=S正方形OEFG﹣S△IJF﹣S△GOH=10t2﹣53t2﹣803(t﹣3)2=﹣2553t+160t﹣240,故答案是:S=﹣2553t+160t﹣240.【点睛】此题考查了待定系数法求二次函数和一次函数表达式,二次函数与一次函数综合问题,相似三角形的性质和判定,二次函数中最大面积问题等知识,解题的关键是正确分析题目中的条件,设出点的坐标,根据相似三角形的性质以及勾股定理表示出相应的线段和面积.11.(1)(1,,图见解析(2)1322Cx-≤≤1122t<≤【解析】【分析】(1)根据等边三角形的性质,勾股定理求解即可;(2)根据题意以MB为边作等边三角形MM B',以M'为圆心1为半径作M',根据线段中点坐标公式求解即可;(3)在(2)的基础上,先求得最小值,再确定2个圆心,第1个是A 点运动点C 对应的圆心P ',第2个是点B 的运动时点C 轨迹的对应的圆心P ,进而根据线段和最大,当,,P P Q '共线时候,t 最大,根据(2)的方法求解即可.(1)过点C 作CE x ⊥轴于点E ,作出点C ,B 的逆序等边三角形CBD ,如图1,()()1,03,0A B -,,ABC 是等边三角形()1131222AE BE AB ∴===--=,33CE AE ==()1,0E ∴,(1,3C ,ABC BCD 是等边三角形∴60DCB ABC ∠=∠=︒,AB AC BC CD BD ====,CD AB CD AB ∴=∥(5,23D ∴ 故答案为:(1,23,(5,23(2)如图2,以MB 为边作等边三角形MM B ',以M '为圆心1为半径作M ', 点B (3,0),点A 在以点M (-2,0)为圆心1为半径的圆上, ∴点A ,B 的逆序等边三角形ABC 的顶点C 在M '23122M x '-+∴== M '的半径为1∴111122C x -≤≤+ 即1322C x -≤≤(3)如图3,设N 与x 轴交于点G ,以GM 为边向上作等边三角形MGH ,以点H 为圆心1为半径,作H ,设直线y x =为1l ,y x t =+为2l ,过点H 作1HJ l ⊥,交x 轴于点J ,交1l 于点S ,交2l 于点L ,过点H ,作HI x ⊥轴于点I ,设2l 与x 轴的交点为T ,则OT t =根据题意,当C 点在第二象限时,能找到t 的最小值,根据定义可知,B 点与G 点重合时,A 点在M 上运动,则C 点在H 上运动,当2l 与H 相切时,t 最小, ()2,0M -,()3,0N ,M 的半径为1,N 的半径为2, 2,321OM OG ∴==-=3MG ∴=33HI ∴=1322MI MG == 1,02I ⎛⎫∴- ⎪⎝⎭ 1332H ⎛∴- ⎝⎭1l 与x 轴的夹角为45°,1HJ l ⊥,HI x ⊥轴, HIJ ∴是等腰直角三角形 HI IJ ∴=HJ ∴===12OI =12OJ ∴1,02J ⎫∴⎪⎪⎝⎭1LJ HJ HL ∴=-=12l l ∥ LTJ ∴是等腰直角三角形1TJ ∴===⎝3122OJ =1122TO TJ JO ⎫=-==⎪⎪⎝⎭即t 12, B 的纵坐标0d >,则12t > 如图4,作,M N 的逆序等边三角形MNP ',以P '为圆心,1为半径作P ',则1PP AM '==,连接,AM PP ',ANP MNP '是等边三角形,,,60AN NP MN NP ANP MNP ''∴==∠=∠=︒PNP ANM '∴∠=∠PP N AMN '≌∴当,,P P Q '共线时候,t 最大以P 为圆心,2为半径作半圆P ,当直线y x t =+与半圆P 相切时,设切点为Q ,当C 点与Q 点重合时,即可取得t 的最大值,最大值即为T O '的长,()()2,0,3,0M N - ∴1532P ⎛' ⎝⎭过点P '作P P x '''⊥轴于点P '',如图,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、中考数学压轴题1.如图,等腰△ABC ,AB =CB ,边AC 落在x 轴上,点B 落在y 轴上,将△ABC 沿y 轴翻折,得到△ADC(1)直接写出四边形ABCD 的形状:______;(2)在x 轴上取一点E ,使OE =OB ,连结BE ,作AF ⊥BC 交BE 于点F .①直接写出AF 与AD 的关系:____(如果后面的问题需要,可以直接使用,不需要再证明);②取BF 的中点G ,连接OG ,判断OG 与AD 的数量关系,并说明理由;(3)若四边形ABCD 的周长为8,直接写出GE 2+GF 2=____.2.在学习了轴对称知识之后,数学兴趣小组的同学们对课本习题进行了深入研究,请你跟随兴趣小组的同学,一起完成下列问题.(1)(课本习题)如图①,△ABC 是等边三角形,BD 是中线,延长BC 至E ,使CE=CD . 求证:DB=DE(2)(尝试变式)如图②,△ABC 是等边三角形,D 是AC 边上任意一点,延长BC 至E ,使CE=AD .求证:DB=DE .(3)(拓展延伸)如图③,△ABC 是等边三角形,D 是AC 延长线上任意一点,延长BC 至E ,使CE=AD 请问DB 与DE 是否相等? 并证明你的结论.3.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度1y (米/分钟)与时间x (分钟)前2分钟满足二次函数21y ax ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.(1)求第一颗弹珠的速度1y (米/分钟)与时间x (分钟)之间的函数关系式;(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度2y(米/分钟)与弹出第一颗弹珠后的时间x(分钟)之间的函数关系式;(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.4.综合与实践4A纸是我们学习工作最常用的纸张之一,其长宽之比是2:1,我们定义:长宽之比是2:1的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2=是一张“标准纸”,将纸片折叠一次,使点()ABCD AD ABAB=求CF的B与D重合,再展开,折痕EF交AD边于点,E交BC边于点F,若1,长,()2如图2,在()1的基础上,连接,BD折痕EF交BD于点O,连接,BE判断四边形BFDE的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A与点C重合,再展开,痕MN交AD边于点M,BC交边于点,N交BD也是点O.然后将四边形ENFM剪下,探究纸片ENFM是否为“标准纸”,说明理由.5.如图,直线y=12x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣32x+c经过A,B两点,与x轴的另一交点为C.(1)求抛物线的解析式;(2)M为抛物线上一点,直线AM与x轴交于点N,当32MNAN=时,求点M的坐标;(3)P为抛物线上的动点,连接AP,当∠PAB与△AOB的一个内角相等时,直接写出点P 的坐标.6.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(2,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)点E (m ,2)是直线AC 上方的抛物线上一点,连接EA 、EB 、EC ,EB 与y 轴交于D .①点F 是x 轴上一动点,连接EF ,当以A 、E 、F 为顶点的三角形与△BOD 相似时,求出线段EF 的长;②点G 为y 轴左侧抛物线上一点,过点G 作直线CE 的垂线,垂足为H ,若∠GCH =∠EBA ,请直接写出点H 的坐标.7.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC =-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.8.如图,在平面直角坐标系xoy 中,直线122y x =-+与x 轴交于点B ,与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点.(1)求抛物线的解析式;(2)点M 为抛物线对称轴上一动点,当BM CM -的值最小时,请你求出点M 的坐标;(3)抛物线上是否存在点N ,过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似?若存在,请直接写出点N 的坐标;若不存在,请说明理由.9.问题背景:如图(1),ABC 内接于O ,过点A 作O 的切线l ,在l 上任取一个不同于点A 的点P ,连接PB PC 、,比较BPC ∠与BAC ∠的大小,并说明理由.问题解决:如图(2),A (0,2)、B (0,4),在x 轴正半轴上是否存在一点P ,使得cos APB ∠最小?若存在,求出点P 的坐标;若不存在,请说明理由.拓展应用:如图(3),四边形ABCD 中,//AB CD ,AD CD ⊥于D ,E 是AB 上一点,AE AD =,P 是DE 右侧四边形ABCD 内一点,若8AB =,11CD =,tan 2C =,9DEP S =,求sin APB ∠的最大值.10.如图,在ABC 中,90ABC ∠=︒,AB BC <,O 为AC 中点,点D 在BO 延长线上,CD BC =,AE BC ∥,CE CA =,AE 交BD 于点G .(1)若28DCE ∠=︒,求AOB ∠的度数;(2)求证:AG GE =;(3)设DC 交GE 于点M .①若3AB =,4BC =,求::AG GM ME 的值;②连结DE ,分别记ABG ,DGM ,DME 的面积为1S ,2S ,3S ,当AC DE 时,123::S S S = .(直接写出答案)11.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(13),(13)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.12.如图1,已知抛物线21833y x x c =--+与x 轴相交于A 、B 两点(B 点在A 点的左侧),与y 轴相交于C 点,且10AB =.(1)求这条抛物线的解析式;(2)如图2,D 点在x 轴上,且在A 点的右侧,E 点为抛物线上第二象限内的点,连接ED 交抛物线于第二象限内的另外一点F ,点E 到y 轴的距离与点F 到y 轴的距离之比为3:1,已知4tan 3BDE ∠=,求点E 的坐标; (3)如图3,在(2)的条件下,点G 由B 出发,沿x 轴负方向运动,连接EG ,点H 在线段EG 上,连接DH ,EDH EGB ∠=∠,过点E 作EK DH ⊥,与抛物线相交于点K ,若EK EG =,求点K 的坐标. 13.如图,直线y =﹣x+4与抛物线y =﹣12x 2+bx+c 交于A ,B 两点,点A 在y 轴上,点B 在x 轴上.(1)求抛物线的解析式;(2)在x 轴下方的抛物线上存在一点P ,使得∠ABP =90°,求出点P 坐标;(3)点E 是抛物线对称轴上一点,点F 是抛物线上一点,是否存在点E 和点F 使得以点E ,F ,B ,O 为顶点的四边形是平行四边形?若存在,求出点F 的坐标;若不存在,请说明理由.14.如图①,在△ABC 中,∠ACB =90°,∠B =30°,AC =1,D 为AB 的中点,EF 为△ACD 的中位线,四边形EFGH 为△ACD 的内接矩形(矩形的四个顶点均在△ACD 的边上). (1)计算矩形EFGH 的面积;(2)将矩形EFGH 沿AB 向右平移,F 落在BC 上时停止移动.在平移过程中,当矩形与△CBD 重叠部分的面积为316时,求矩形平移的距离; (3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形1111E F G H ,将矩形1111E F G H 绕1G 点按顺时针方向旋转,当1H 落在CD 上时停止转动,旋转后的矩形记为矩形2212E F G H ,设旋转角为α,求cos α的值.15.如图,在平面直角坐标系中,点O 为坐标原点,直线y =-x + m 交 y 轴的正半轴于点A ,交x 轴的正半轴于点B ,过点A 的直线AF 交x 轴的负半轴于点F ,∠AFO=45°. (1)求∠FAB 的度数;(2)点 P 是线段OB 上一点,过点P 作 PQ ⊥OB 交直线 FA 于点Q ,连接 BQ ,取 BQ 的中点C ,连接AP 、AC 、CP ,过点C 作 CR ⊥AP 于点R ,设 BQ 的长为d ,CR 的长为h ,求d 与 h 的函数关系式(不要求写出自变量h 的取值范围);(3)在(2)的条件下,过点 C 作 CE ⊥OB 于点E ,CE 交 AB 于点D ,连接 AE ,∠AEC=2∠DAP ,EP=2,作线段 CD 关于直线AB 的对称线段DS ,求直线PS 与直线 AF 的交点K 的坐标.16.如图①,△ABC 是等腰直角三角形,在两腰AB 、AC 外侧作两个等边三角形ABD 和ACE ,AM 和AN 分别是等边三角形ABD 和ACE 的角平分线,连接CM 、BN ,CM 与AB 交于点P .(1)求证:CM=BN;(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;(3)在(2)的条件下,求PFBN的值.17.已知菱形ABCD中,∠ABC=60°,AB=4,点M在BC边上,过点M作PM∥AB交对角线BD于点P,连接PC.(1)如图1,当BM=1时,求PC的长;(2)如图2,设AM与BD交于点E,当∠PCM=45°时,求证:BEDE=33;(3)如图3,取PC的中点Q,连接MQ,AQ.①请探究AQ和MQ之间的数量关系,并写出探究过程;②△AMQ的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.18.在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A 顺时针旋转90°,得到线段AE,连接DE.(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.(3)如图3,点F为线段DE中点,AB=2a,求出动点D从B运动到C,点F经过的路径长度.19.如图1,在平面直角坐标系中,O是坐标原点,矩形OACB的顶点A、B分别在x轴和y轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为t秒.(1)点P运动到与点C重合时,求直线DP的函数解析式;(2)求△OPD的面积S关于t的函数解析式,并写出对应t的取值范围;(3)点P在运动过程中,是否存在某些位置使△ADP是不以DP为底边的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.20.发现来源于探究.小亮进行数学探究活动,作边长为a的正方形ABCD和边长为b的正方形AEFG(a>b),开始时,点E在AB上,如图1.将正方形AEFG绕点A逆时针方向旋转.(1)如图2,小亮将正方形AEFG绕点A逆时针方向旋转,连接BE、DG,当点G恰好落在线段BE上时,小亮发现DG⊥BE,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG的长.(2)如图3,小亮旋转正方形AEFG,点E在DA的延长线上,连接BF、DF.当FG平分∠BFD时,请你帮他求a:b及∠FBG的度数.(3)如图4,BE的延长线与直线DG相交于点P,a=2b.当正方形AEFG绕点A从图1开始,逆时针方向旋转一周时,请你帮小亮求点P运动的路线长(用含b的代数式表示).21.如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转α°(0°<α<180°),分别交直线BC、AD于点E、F.(1)当α=_____°时,四边形ABEF是平行四边形;(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形,①当α=_______°时,构造的四边形是菱形;②若构造的四边形是矩形,求该矩形的两边长.22.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角:;所有与∠C相等的角:.(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .①求∠B的度数;②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.23.已知,抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ,B ,且B 点的坐标为()2,0. (1)求该抛物线的解析式.(2)如图1,若点P 是线段AB 上的一动点,过点P 作//PE AC ,交BC 于E ,连接CP ,求PCE ∆面积的最大值.(3)如图2,若直线y x m =+与线段AC 交于点M ,与线段BC 交于点N ,是否存在M ,N ,使得OMN ∆为直角三角形,若存在,请求出m 的值;若不存在,请说明理由.24.综合与探究:如图1,抛物线24832999y x x =-++与x 轴交于,A B 两点(点A 在点B 的左侧),顶点为D ,P 为对称轴右侧抛物线的一个动点,直线AD 与y 轴于点C ,过点P 作//PF AD ,交x 轴于点F .(1)求直线AD 的函数表达式及点C 的坐标;(2)如图2,当//PC x 轴时,将AOC ∆以每秒1个单位长度的速度沿x 轴的正方向平移,当点C 与点P 重合时停止平移.设平移t 秒时,在平移过程中AOC ∆与四边形AFPC 重叠部分的面积为S ,求S 关于t 的函数关系式,并写出自变量t 的取值范围; (3)如图3,过点P 作x 轴的平行线,交直线AD 于点E ,直线DF 与PE 交于点M ,设点P 的横坐标为m .①当3DM MF =时,求m 的值;②试探究点P 在运动过程中,是否存在值m ,使四边形AFPE 是菱形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.25.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)菱形;(2)①AF =ADAF ⊥AD ;②2AD OG =,理由见解析;(3)4【解析】【分析】(1)由折叠的性质可得AB=AD=BC=CD ,可得四边形ABCD 是菱形;(2)①由菱形的性质可得AD ∥BC ,且AF ⊥BC ,可得AD ⊥AF ,由等腰三角形的性质和外角的性质可求∠OBE=∠OEB=45°,∠ABE=∠AFB ,可得AF=AB ;②取AB 中点M ,由三角形中位线定理可得MO ∥AD ,AD=2MO ,AF ∥MG ,AF=2MG ,且AF=AD ,AD ⊥AF ,可得MO=MG ,MG ⊥MO ,可得2OM ,即可得OG 与AD 的数量关系;(3)连接AG ,由等腰三角形的性质可得AG ⊥BF ,且∠BEO=45°,可得AG=GE ,由勾股定理可求解.【详解】解:(1)∵将△ABC沿y轴翻折∴AB=AD,BC=CD又∵AB=CB∴AB=AD=BC=CD∴四边形ABCD是菱形故答案为:菱形;(2)①∵四边形ABCD是菱形∴AD∥BC,且AF⊥BC∴AD⊥AF,∴∠FAC+∠CAD=90°,且∠CAD+∠ADO=90°,∴∠FAC=∠ADO,∵AB=AD∴∠ABD=∠ADB,∴∠ABD=∠FAC∵OE=OB∴∠OBE=∠OEB=45°∴∠ABD+∠OBE=∠FAC+∠OEB∴∠ABE=∠AFB∴AF=AB∴AF=AD,故答案为:AF=AD,AD⊥AF;②AD=2OG;如图,取AB中点M,∵点M是AB的中点,点G是BF的中点,点O是AC的中点,∴MO∥AD,AD=2MO,AF∥MG,AF=2MG,且AF=AD,AD⊥AF ∴MO=MG,MG⊥MO∴2OM∵2GO;(3)∵四边形ABCD的周长为8,∴AB=BC=CD=AD=2=AF如图,连接AG,∵AB=AF,点G是BF的中点,∴AG⊥BF,且∠BEO=45°∴∠GAE=∠BEO=45°∴AG=GE,∵AG2+GF2=AF2=4,∴GE2+GF2=4,故答案为:4;【点睛】本题是四边形综合题,考查了菱形的判定和性质,等腰直角三角形的性质,三角形中位线定理,折叠的性质,添加恰当辅助线是本题的关键.2.D解析:(1)见详解;(2)见详解;(3)DB=DE成立,证明见详解【解析】【分析】(1)由等边三角形的性质,得到∠CBD=30°,∠ACB=60°,由CD=CE,则∠E=∠CDE=30°,得到∠E=∠CBD=30°,即可得到DB=DE;(2)过点D作DG∥AB,交BC于点G,证明△BDC≌△EDG,根据全等三角形的性质证明结论;(3)过点D作DF∥AB交BE于F,由“SAS”可证△BCD≌△EFD,可得DB=DE.【详解】证明:(1)∵△ABC是等边三角形∴∠ABC=∠BCA=60°,∵点D为线段AC的中点,∴BD平分∠ABC,AD=CD,∴∠CBD=30°,∵CD=CE,∴∠CDE=∠CED,又∵∠CDE+∠CED=∠BCD,∴2∠CED=60°,∴∠CED=30°=∠CBD,∴DB=DE;(2)过点D 作DG ∥AB ,交BC 于点G ,如图,∴∠DGC=∠ABC=60°,又∠DCG=60°,∴△DGC 为等边三角形,∴DG=GC=CD ,∴BC-GC=AC-CD ,即AD=BG ,∵AD=CE ,∴BG=CE ,∴BC=GE ,在△BDC 和△EDG 中,60DC DG BCD EGD BC EG =⎧⎪∠=∠=︒⎨⎪=⎩,∴△BDC ≌△EDG (SAS )∴BD=DE ;(3)DB=DE 成立,理由如下:过点D 作DF ∥AB 交BE 于F ,∴∠CDF=∠A ,∠CFD=∠ABC ,∵△ABC 是等边三角形∴∠ABC=∠BCA=∠A=60°,BC=AC=AB ,∴∠CDF=∠CFD=60°=∠ACB=∠DCF ,∴△CDF 为等边三角形∴CD=DF=CF ,又AD=CE ,∴AD-CD=CE-CF ,∴BC=AC=EF ,∵∠BCD=∠CFD+∠CDF=120°,∠DFE=∠FCD+∠FDC=120°,∴∠BCD=∠DFE ,且BC=EF ,CD=DF ,∴△BCD ≌△EFD (SAS )∴DB=DE .【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,以及平行线的性质,正确添加恰当辅助线构造全等三角形是本题的关键.3.(1)212(02)16(25)x x y x x ⎧≤≤⎪=⎨≤≤⎪⎩;(2)220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析【解析】【分析】(1)将(1,2)代入21y ax =,得2a =,从而得到212y x =,再代入2x =求出18y =,即可得到反比例函数解析式,即可得解;(2)当01x ≤≤时,第二颗弹珠未弹出,故第二颗弹珠的解析式为20y =;再分别根据(1)中的结论,即可求出当13x <≤和36x <≤时第二颗弹珠的解析式;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,则第2分钟末两颗弹珠速度相差最大,分别求出第2分钟末时两颗弹珠的速度,再相减即可的解;(4)第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻.【详解】(1)当02x ≤≤时,将(1,2)代入21y ax =,得2a =,212y x ∴=,∵当2x =时,18y =,∴当25x ≤≤时,116y x=, 1y ∴与x 的函数关系式为212(02)16(25)x x y x x⎧≤≤⎪=⎨≤≤⎪⎩;(2)当01x ≤≤时,第二颗弹珠未弹出,∴第二颗弹珠的解析式为20y =;当13x <≤时,第二颗弹珠的解析式为222(1)y x =-;当36x <≤时,第二颗弹珠的解析式为2161y x =-; ∴2y 与x 的函数关系式为220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,∴第2分钟末两颗弹珠速度相差最大,∵第一颗弹珠的速度为2218222y x =⨯==米/分钟,第二颗弹珠的速度为2122(1)212y x =⨯==-米/分钟,∴两颗弹珠的速度最大相差8-2=6米/分钟;(4)存在,理由如下:第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟, 第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同. 这个时刻可以通过解方程2162(1)x x =-求得. 【点睛】本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息,明确自变量的取值范围和图象所经过的点的坐标.4.(1) CF长为4 ;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析【解析】【分析】(1)1AB =,则AD =ABCD是矩形,得到1,CD AB BC AD ==-=FB FD =,设CF x =,则FB FD x ==,在Rt DCF △中,222+=CD CF DF,可得)2221x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOE DAB ,再根据2AD AB =,可得222OE AB OD AD ===,进而得到22OE OD =,22EF BD =,同理可得,22MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM 是矩形,90EMF ∠=,2MF OD tan FEM ME OE ∠===,2MF ME =,即可求证纸片ENFM 是“标准纸".【详解】解:()11,AB =则2,2AD AB ==四边形ABCD 是矩形1,2CD AB BC AD ∴==-=由折叠得FB FD =设CF x =,则2FB FD x ==-在Rt DCF △中,222+=CD CF DF()22212x x +=- 24x = 答:CF 长为24 ()2四边形BFDE 是菱形.理由:当顶点B 与点D 重合时,折痕EF 垂直平分,BDOB OD ∴=,90BOF DOE ∠=∠=在矩形ABCD 中,//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠, BOF DOE ∴≅OE OF ∴=OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下:由()2可知,,OE OF =同理可知,,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒DOE DAB ∴2AD =222OE AB OD AD ∴===22OE OD ∴=2EF BD ∴=同理可得,2MN AC =四边形ABCD 是矩形,AC BD ∴=, EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.2,MF ODtan FEM ME OE∴∠=== 2MF ME ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数,灵活运用判定和性质是解题关键.5.B解析:(1)y=12x2﹣32x﹣2;(2)点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)点P的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2).【解析】【分析】(1)根据题意直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,-2)、(4,0),即可求解;(2)由题意直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MNAN=32时,则NHON=32,即4343mmm---=32,进行分析即可求解;(3)根据题意分∠PAB=∠AOB=90°、∠PAB=∠OAB、∠PAB=∠OBA三种情况,分别求解即可.【详解】解:(1)直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,﹣2)、(4,0),则c=﹣2,将点B的坐标代入抛物线表达式并解得:a=12,故抛物线的表达式为:y=12x2﹣32x﹣2①;(2)设点M(m,12m2﹣32m﹣2)、点A(0,﹣2),将点M、A的坐标代入一次函数表达式:y=kx+b并解得:直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MNAN=32时,则NHON=32,即:4343mmm---=32,解得:m=5或﹣2或2或1,故点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)①∠PAB=∠AOB=90°时,则直线AP的表达式为:y=﹣2x﹣2②,联立①②并解得:x=﹣1或0(舍去0),故点P(﹣1,0);②当∠PAB=∠OAB时,当点P在AB上方时,无解;当点P在AB下方时,将△OAB沿AB折叠得到△O′AB,直线OA交x轴于点H、交抛物线为点P,点P为所求,则BO=OB=4,OA=OA=2,设OH=x,则sin∠H=BO OAHB HA'=,即:2444x x=++,解得:x=83,则点H(﹣83,0),.则直线AH的表达式为:y=﹣34x﹣2③,联立①③并解得:x=32,故点P(32,﹣258);③当∠PAB=∠OBA时,当点P在AB上方时,则AH =BH ,设OH =a ,则AH =BH =4﹣a ,AO =2, 故(4﹣a )2=a 2+4,解得:a =32, 故点H (32,0), 则直线AH 的表达式为:y =43x ﹣2④, 联立①④并解得:x =0或173(舍去0), 故点P (173,509); 当点P 在AB 下方时, 同理可得:点P (3,﹣2); 综上,点P 的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2). 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、勾股定理的运用等,要注意分类讨论,解题全面.6.E解析:(1)y =﹣21122x -x+3;(2)①EF 的长为2;②点H 的坐标为(﹣45,135)或(﹣445,99). 【解析】 【分析】(1)用待定系数法求出函数解析式即可;(2)①得出EAB ODB ∠=∠,当时,当时,可求出的长; ②(Ⅰ)求出直线CE 的解析式为132y x =+,得出APE EBA ∠=∠,则GCH APE EBA CHN MGH ∠=∠=∠=∠=∠,得出//GC PB ,由1tan tan tan 2AE EBA CHN MGH BE ∠=∠=∠==,设CN MG m ==,则2HN m =,12MH m =,则1212MH HN m m +=+=,解得,25m =,可求出H 点的坐标;(Ⅱ)过点H 作MN PB ⊥,过点C 作CN MH ⊥于点N ,过点G 作GM HM ⊥于点M ,证得GCH EBA HCN MHG ∠=∠=∠=∠,由(Ⅰ)知:1tan 2EBA ∠=,则1tan tan 2GM HG MHG GCH HM CH ∠==∠==,设MG a =,则2MH a =,证明HMG CNH ∆∆∽,则2NH a =,4CN a =,又(0,3)C ,得出(3,34)G a a --,代入211322y x x =--+中,得449CN =,可求出H 点坐标.【详解】解:(1)将A (﹣3,0)、B (2,0)、C (0,3)代入y =ax2+bx+c 得,0930423a b ca b c c =-+⎧⎪=++⎨⎪=⎩, 解得:12123a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩,∴抛物线的解析式为:y =﹣21122x -x+3; (2)①将E (m ,2)代入y =﹣21122x -x+3中, 得﹣21122m -m+3=0,解得m =﹣2或1(舍去), ∴E (﹣2,2),∵A (﹣3,0)、B (2,0), ∴AB =5,AE =5,BE =25, ∴AB2=AE2+BE2, ∴∠AEB =∠DOB =90°,∴∠EAB+∠EBA =∠ODB+∠EBA =90°, ∴∠EAB =∠ODB , (Ⅰ)当△FEA ∽△BOD 时,∴∠AEF =∠DOB =90°, ∴F 与B 点重合, ∴EF =BE =5(Ⅱ)当△EFA∽△BOD时,∴∠AFE=∠DOB=90°,∵E(﹣2,2),∴EF=2,故:EF的长为25或2;②点H的坐标为4(5-,13)5或44(9-,5)9,(Ⅰ)过点H作HN⊥CO于点N,过点G作GM⊥HN于点M,∴∠GMN=∠CNH=90°,又∠GHC=90°,∴∠CHN+∠GHM=∠MGH+∠GHM=90°,∴∠CHN=∠MGH,∵HN⊥CO,∠COP=90°,∴HN∥AB,∴∠CHN=∠APE=∠MGH,∵E(﹣2,2),C(0,3),∴直线CE的解析式为y=12x+3,∴P(﹣6,0),∴EP=EB=5∴∠APE=∠EBA,∵∠GCH =∠EBA ,∴∠GCH =∠APE =∠EBA =∠CHN =∠MGH , ∴GC ∥PB , 又C (0,3),∴G 点的纵坐标为3,代入y =﹣21122x -x+3中,得:x =﹣1或0(舍去), ∴MN =1,∵∠AEB =90°,AE =5,BE =25, ∴tan ∠EBA =tan ∠CHN =tan ∠MGH =12AE BE =, 设CN =MG =m ,则HN =2m ,MH =12m , ∴MH+HN =2m+12m =1, 解得,m =25, ∴H 点的橫坐标为﹣45,代入y =12x+3,得:y =135,∴点H 的坐标为(﹣45,135). (Ⅱ)过点H 作MN ⊥PB ,过点C 作CN ⊥MH 于点N ,过点G 作GM ⊥HM 于点M ,∴CN ∥PB , ∴∠NCH =∠APE ,由(Ⅰ)知:∠APE =∠EBA ,则∠NCH =∠EBA , ∵∠GMN =∠CNH =90°, 又∠GHC =90°,∴∠HCN+∠NHC =∠MHG+∠NHC =90°, ∴∠HCN =∠MHG , ∵∠GCH =∠EBA ,∴∠GCH =∠EBA =∠HCN =∠MHG ,由(Ⅰ)知:APE EBA ∠=∠,则NCH EBA ∠=∠, 90GMN CNH ∠=∠=︒,又90GHC ∠=︒,90HCN NHC MHG NHC ∴∠+∠=∠+∠=︒, HCN MHG ∴∠=∠, GCH EBA ∠=∠,GCH EBA HCN MHG ∴∠=∠=∠=∠,由(Ⅰ)知:1tan 2EBA ∠=, 则1tan tan 2GM HG MHG GCH HM CH ∠==∠==, 设MG a =,则2MH a =, NCH MHG ∠=∠,N M ∠=∠, HMG CNH ∴∆∆∽,∴12MH MG HG CN NH CH ===, 2NH a ∴=,4CN a =,又(0,3)C ,(3,34)G a a ∴--,代入211322y x x =--+中,得,119a =或0(舍去),449CN ∴=, H ∴点的橫坐标为449-,代入132y x =+,得,59y =.∴点H 的坐标为445(,)99-. 综合以上可得点H 的坐标为4(5-,13)5或445(,)99-.【点睛】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、两点间的距离公式、锐角三角函数、相似三角形的判定与性质及分类讨论思想的运用.7.A解析:(1;(23)存在,6 【解析】 【分析】(1)作A 1H ⊥AB 于H ,连接BD ,BD 1,则四边形ADA 1H 是矩形.解直角三角形,求出∠ABA 1,得到旋转角即可解决问题;(2)由△BCE ∽△BA 2D 2,推出222A D CE n CB A B m ==,可得CE=2n m,由11A E EC =推出16A C EC =,推出A 1C=26n m •,推出BH=A 1C=26n m•,然后由勾股定理建立方程,解方程即可解决问题;(3)当A 、P 、F ,D ,四点共圆,作PF ⊥DF ,PF 与CD 相交于点M ,作MN ⊥AB ,此时PF 的长度为最小值;先证明△FDG ∽△FME ,得到3FG F FM FE D ==,再结合已知条件和解直角三角形求出PM 和FM 的长度,即可得到PF 的最小值. 【详解】解:(1)作A 1H ⊥AB 于H ,连接BD ,BD 1,则四边形ADA 1H 是矩形.∴AD=HA 1=n=1,在Rt △A 1HB 中,∵BA 1=BA=m=2, ∴BA 1=2HA 1, ∴∠ABA 1=30°, ∴旋转角为30°, ∵22125+= ∴D 到点D 1所经过路径的长度3055π⋅⋅=; (2)∵△BCE ∽△BA 2D 2,∴222A D CE nCB A B m==, ∴2n CE m =,∵161EA EC =, ∴16A CEC = ∴A 126n m,∴BH=A 12226n m n m-=,∴42226nm nm-=⋅,∴m4﹣m2n2=6n4,∴2424 16n nm m-=•,∴33nm=(负根已舍去).(3)当A、P、F,D,四点共圆,作PF⊥DF,PF与CD相交于点M,作MN⊥AB,此时PF 的长度为最小值;由(2)可知,3 BE nBG m==,∵四边形BEFG是矩形,∴33 FGFE=,∵∠DFG+∠GFM=∠GFM+∠MFE=90°,∴∠DFG=∠MFE,∵DF⊥PF,即∠DFM=90°,∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°,∴∠FDG=∠FME,∴△FDG∽△FME,∴33FGFFM FED==,∵∠DFM=90°,tan3FDFMDFM∠==,∴∠FDM=60°,∠FMD=30°,∴3FM DM=;在矩形ABCD中,有33 ADAB=3=,则3AD =, ∵MN ⊥AB ,∴四边形ANMD 是矩形,∴MN=AD=3,∵∠NPM=∠DMF=30°,∴PM=2MN=6,∴NP=AB =,∴DM=AN=BP=2,∴2FM DM ===∴6PF PM MF =+=【点睛】本题考查点的运动轨迹,旋转变换、解直角三角形、弧长公式、矩形的性质、相似三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于压轴题,中考常考题型.正确作出辅助线,正确确定动点的位置,注意利用数形结合的思想进行解题.8.B解析:(1)213222y x x =-++;(2)3(,0)2;(3)存在;(0,2)N 或(3,2)N 或(2,3)--N 或(5,18)--N【解析】【分析】(1)由直线122y x =-+可得B 、C 两点的坐标,根据二次函数的对称轴求得A 点坐标,可设抛物线的解析式为(1)(4)y a x x =+-,将C 点坐标代入可求得a ,即可得抛物线的解析式;(2)根据绝对值的性质得出BM CM -的值最小时,点M 为BC 的垂直平分线与直线32x =的交点,求得BC 垂直平分线的解析式,联立直线32x =即可求得点M ; (3)分四种情况进行讨论,设出N 的坐标,根据相似三角形的对应边成比例的性质,求得N 的横坐标与纵坐标的关系,然后联立抛物线解析式即可求解.【详解】 解:∵直线122y x =-+与x 轴交于点B ,与y 轴交于点C , ∴当y =0时,即1022x =-+,解得:x =4,则点B 的坐标为(4,0),当x =0时,10222=-⨯+=y ,则点C 的坐标为(0,2),由二次函数的对称性可知:点A 与点B 关于直线32x =对称, ∴点A 的坐标为(1,0)-,∵抛物线与x 轴的交点为点(1,0),(4,0)A B -,∴可设抛物线的解析式为(1)(4)y a x x =+-,又∵抛物线过点(0,2)C ,∴2(01)(04)a =+-,解得:12a =-, ∴2113(1)(4)2222y x x x x =-+-=-++ ∴抛物线的解析式为213222y x x =-++; (2)如图1,连结CM 、BM ,作线段BC 的垂直平分线l 分别交BC 、直线32x =于点'、N M ,则N 为BC 中点;由绝对值的性质可得:0≥-BM CM ,∴当BM CM -的值最小时,即0=-BM CM ,则此时CM BM =,∴点M 为l 与直线32x =的交点,此时M 与'M 重合, 设l 的解析式为:y kx b =+,∵直线BC 的解析式为:122y x =-+,BC l ⊥ ∴112-⋅=-k ,解得:2k =,则l 的解析式可化为:2y x b =+, 由(4,0),(0,2)B C 得点N 的坐标为(2,1),将(2,1)N 代入2y x b =+得:14b =+,解得:3b =-,∴23y x =-, 将32x =代入23y x =-,得323=02=⨯-y ,即3'(,0)2M , ∴当BM CM -的值最小时,点M 的坐标为3(,0)2,(3)抛物线上存在点N ,使得以点、、B N H 为顶点的三角形与ABC 相似; ∵(1,0),(4,0),(0,2)-A B C∴1,4==OA OB ,2OC =,5AB =,∴2222125=+=+=AC OA OC ,22224225BC OB OC =+=+=, ∵22252025+=+==AC BC AB ,∴ABC 为直角三角形,90ACB ∠=︒,∵NH x ⊥轴,∴90∠=︒NHB ,则90∠=∠=︒NHB ACB ,如图2所示,分四种情况,点N 的坐标分别为1234、、、N N N N ,设点N 的坐标为(,)m n ,①当点1N 在x 轴的上方,要使11N BH ABC ,则11∠=∠N BH ABC ,则此时点1N 与点C 重合,则此时点1H 与点O 重合,则11≅N BH ABC ,满足题意,∴此时点1N 的坐标为(0,2);②当点2N 在x 轴的上方,要使22BN H ABC ,则2222==N H BC BH AC , ∴24=-n m,即28n m =-+,代入抛物线的解析式得: 21328222mm m ,化简得:27120m m , 解得:13m =,24m =(不符合题意,故舍去),将3m =代入抛物线解析式得:2n =,∴此时点2N 的坐标为(3,2);③当点3N 在x 轴的下方,要使33N BH ABC ,则3332==BH BC N H AC , ∴42-=-m n ,即42-=m n ,代入抛物线的解析式得: 24132222m m m ,化简得:2280m m --=, 解得:12m =-,24m =(不符合题意,故舍去),将2m =-代入抛物线解析式得:3n =-,∴此时点3N 的坐标为(2,3)--;④当点4N 在x 轴的下方,要使44BN H ABC ,则4442==N H BC BH AC , ∴24-=-n m,即28=-n m ,代入抛物线的解析式得: 21328222m m m ,化简得:2200m m , 解得:15m =-,24m =(不符合题意,故舍去),将5m =-代入抛物线解析式得:18n =-,∴此时点4N 的坐标为(5,18)--;综上所述,抛物线存在点N 的坐标为(0,2)或(3,2)或(2,3)--或(5,18)--使得以点、、B N H 为顶点的三角形与ABC 相似.【点睛】本题主要考查了一次函数与二次函数的性质、相似三角形的性质,运用数形结合与分类讨论的方法是解题的关键.9.B解析:(1)∠BPC <∠BAC ;(2)点P 坐标为(0);(3)sin ∠APB 的最大值为1.【解析】【分析】。
