指数函数习题精选精讲
指数函数经典例题(问题详细讲解)
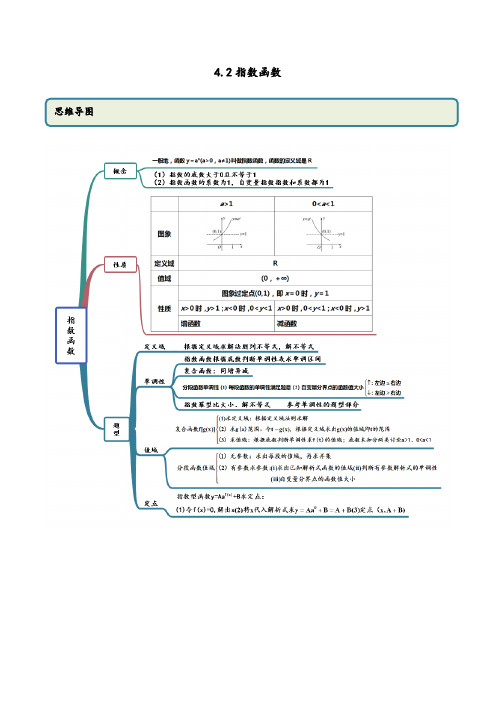
指数函数1．指数函数の定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数の图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101の图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且の图象和性质。
a>1 0<a<1图象00性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在 R上是增函数（4）在R上是减函数指数函数是高中数学中の一个基本初等函数，有关指数函数の图象与性质の题目类型较多，同时也是学习后续数学容の基础和高考考查の重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c=-+满足(1)(1)f x f x+=-，且(0)3f=，则()xf b与()x f c の大小关系是_____．分析：先求b c ，の值再比较大小，要注意x x b c ，の取值是否在同一单调区间． 解：∵(1)(1)f x f x +=-， ∴函数()f x の对称轴是1x =． 故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x x f f >． 综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x の取值围是___________． 分析：利用指数函数の单调性求解，注意底数の取值围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x の取值围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y = 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x の定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数の值域是[)01，．评注：利用指数函数の单调性求值域时，要注意定义域对它の影响． 4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a の值是_______．分析：令x t a =可将问题转化成二次函数の最值问题，需注意换元后t の取值围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤． ∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤，∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a の值是3或13．评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等． 5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程の解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例6 为了得到函数935x y =⨯+の图象，可以把函数3x y =の图象（ ）． A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象の平移规律进解：∵293535x x y +=⨯+=+，∴把函数3x y =の图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+の图象，故选（C ）． 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等． 习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较 与 ；（4）若 ，且 ，比较a 与b ； （5）若 ，且 ，比较a 与b ． 解：（1）由 ，故 ，此时函数 为减函数．由 ，故 ． （2）由 ，故 ．又 ，故 ．从而 ．（3）由 ，因 ，故 ．又 ，故 ．从而 ．（4）应有 ．因若 ，则 ．又 ，故 ，这样 ．又因 ，故 ．从而 ，这与已知 矛盾．（5）应有 ．因若 ，则 ．又 ，故 ，这样有 ．又因 ，且 ，故 ．从而 ，这与已知 矛盾．小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线 分别是指数函数 , 和 の图象,则 与1の大小关系是 ( ). (分析:首先可以根据指数函数单调性,确定 ,在 轴右侧令 ,对应の函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型の数形结合の题目,第(1)题是由数到形の转化,第(2)题则是由图到数の翻译,它の主要目の是提高学生识图,用图の意识.3，求下列函数の定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x の定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x の值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1の定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1の值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x の最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。
4.2 指数函数(精讲)(原卷版附答案).docx
4.2指数函数考点一 指数函数的判断【例1-1】（2019·河北桥西.邢台一中高一月考）下列函数中指数函数的个数是（ ）①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-（a 为常数,12a >,1a ≠） ⑤3y x = ⑥4xy =- ⑦()4xy =-A ．1B ．2C ．3D ．4【例1-2】（2019·河南中原.郑州一中高一开学考试）函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为（ ） A ．1 B ．3 C ．2 D ．1或3【一隅三反】1．（2019·山东高三学业考试）函数()2xy a a =-是指数函数,则（ ）A ．1a =或3a =B ．1a =C ．3a =D ．0a >且1a ≠2．（2019·呼和浩特开来中学高一期中）若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A ．2B ．-2C ．-D ．3．（2019·辽宁葫芦岛.高一月考）下列函数不是指数函数的是（ ） A ．12x y +=B ．3x y -=C ．4x y =D ．32x y =考点二 定义域和值域【例2-1】（2020·全国高一课时练习）求下列函数的定义域和值域：（1）142x y -=；（2）23y ⎛= ⎪⎝⎭（3）22312x x y --⎛⎫=⎪⎝⎭.【例2-2】（2018·湖南开福.长沙一中高一月考）若函数y =的值域为[0,+∞）,则实数a 的取值范围是_____．【一隅三反】1．（2020·全国高一课时练习）求下列函数的定义域和值域； （1）12x y +=；（2）y =（3）y =2．（2020·全国高一课时练习）求下列函数的定义域与值域.（1）y =（2）1(0,1x x a y a a -=>+且1)a ≠（3）110.3;x y -=（4）y =3．（2020·河北新华.石家庄二中高二期末）若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为（ ）A ．1,4⎡⎫+∞⎪⎢⎣⎭B ．11,42⎡⎤⎢⎥⎣⎦C ．1,12⎡⎤⎢⎥⎣⎦D ．1,14⎛⎤⎥⎝⎦4．（2020·云南五华.昆明一中高三其他（理））设函数y =A ,函数12x y -=的值域为B ,则AB =( )A ．()0,1B ．(]0,1C ．()1,1-D ．[]1,1-5．（2019·湖南高一期中）若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为（ ）A ．2-B ．1-C ．1D ．2考点三 指数函数性质【例3】（1）（2020·贵溪市实验中学高二期末（文））若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3（2）（2019·湖南岳阳楼.岳阳一中高一期中）已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)（3）（2019·湖北襄阳）如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么（ ）A ．a b a a a b <<B ．a a b a b a <<C ．b a a a a b <<D ．b a a a b a <<【一隅三反】1．（2019·浙江南湖.嘉兴一中高一月考）函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是（ ）A ．[)1,-+∞B ．(],1-∞-C ．[)1,+∞D ．(],1-∞2．（2019·浙江柯城.衢州二中高三一模）已知定义在R 上的函数()||32x m f x -+=+m 为实数）为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )A ．c b a <<B ．c a b <<C ．a c b <<D ．a b c <<3．（2020·浙江高一课时练习）设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则（ ）A ．312y y y >>B ．213y y y >>C ．123y y y >>D ．132y y y >>1.指数函数性质记忆口诀指数增减要看清,抓住底数不放松； 反正底数大于0,不等于1已表明； 底数若是大于1,图象从下往上增； 底数0到1之间,图象从上往下减； 无论函数增和减,图象都过(0,1)点． 2.比较幂值大小的三种类型及处理方法4．（2020·永安市第三中学高二月考）若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是（ ）A ．(,8][0,)-∞-+∞B ．(),4-∞-C ．[8,4)--D ．(,8]-∞-5（2020·上海高一课时练习）已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.6．（2020·上海普陀.曹杨二中高一期末）函数12x y =-的单调递增区间为________7．（2020·全国高一课时练习）比较下列各题中的两个值的大小． （1）0.10.8-,0.21.25；（2）1ππ-⎛⎫ ⎪⎝⎭,1；（3）30.2-,()0.23-.考点四 定点【例4】（2020·浙江高一课时练习）函数()-1=4+x f x a （0a >,且1a ≠）的图象过定点P ,则P 点的坐标为（ ） A ．(1,5) B ．(1,4) C ．(0,5)D ．(0,4)【一隅三反】1．（2019·涡阳县第九中学高二期末）函数()10,1xy a a a =+>≠的图象必经过点（ ）A ．(0,1)B ．(1,1)C ．()0,2D ．(2,2)2．（2019·贵州省织金县第二中学高一期中）函数21()x f x a-=(0a >且1)a ≠过定点（ ） A ．(1,1) B ．1(,0)2C ．(1,0)D ．1(,1)23．（2020·宁夏贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（ ）A ．（1,1）B ．（1,3）C ．（2,0）D ．（4,0）考点五 图像【例5-1】（2020·广东顺德一中高一期中）函数1(0,1)xy a a a a=->≠的图像可能是（ ）． A ． B ．C ．D ．【例5-2】（2020·浙江高一课时练习）若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则（ ） A ．1a >B ．1a >,且0m <C ．01a <<,且0m >D ．01a <<【一隅三反】1．（2019·浙江高一期中）函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A ．B ．C ．D ．2．（2020·全国高一课时练习）在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是（ ）A ．B ．C ．D ．3．（2020·上海高一课时练习）若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A ．m 1≥B ．1m <C ．1m >-D ．1m ≤-4．（2020·内蒙古集宁一中高二期末（理））若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a的取值范围是___________4.2指数函数考点一 指数函数的判断【例1-1】（2019·河北桥西.邢台一中高一月考）下列函数中指数函数的个数是（ ）①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-（a 为常数,12a >,1a ≠） ⑤3y x = ⑥4xy =- ⑦()4xy =-A ．1B ．2C ．3D ．4【参考答案】B【解析】对①：指数式的系数为2,不是1,故不是指数函数；对②：其指数为1x +,不是x ,故不是指数函数； 对③④：满足指数函数的定义,故都是指数函数； 对⑤：是幂函数,不是指数函数；对⑥：指数式的系数为-1,不是1,故不是指数函数；对⑦：指数的底数为-4,不满足底数大于零且不为1的要求,故不是； 综上,是指数函数的只有③④,故选：B.【例1-2】（2019·河南中原.郑州一中高一开学考试）函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为（ ） A ．1B ．3C ．2D ．1或3【参考答案】C【解析】因为函数f (x )=(a 2﹣3a +3)a x 是指数函数,故可得2331a a -+=解得1a =或2a =, 当1a =时,不是指数函数,舍去.故选：C.【一隅三反】1．（2019·山东高三学业考试）函数()2xy a a =-是指数函数,则（ ）A ．1a =或3a =B ．1a =C ．3a =D ．0a >且1a ≠【参考答案】C【解析】因为函数()2xy a a =-是指数函数所以21a -=,0a >且1a ≠,解得3a =.故选：C.2．（2019·呼和浩特开来中学高一期中）若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A ．2B ．-2C．-D．【参考答案】D【解析】∵函数f （x ）＝（12a ﹣3）•a x 是指数函数,∴12a ﹣3＝1,a ＞0,a ≠1,解得a ＝8, ∴f （x ）＝8x ,∴f （12）==,故选：D ． 3．（2019·辽宁葫芦岛.高一月考）下列函数不是指数函数的是（ ） A ．12x y += B ．3x y -= C ．4x y = D ．32x y =【参考答案】A【解析】指数函数是形如xy a =（0a >且1a ≠）的函数. 对于A ：1222x x y +==⨯,系数不是1,所以不是指数函数；对于B ：133xx y -⎛⎫== ⎪⎝⎭,符合指数函数的定义,所以是指数函数；对于C ：4xy =,符合指数函数的定义,所以是指数函数；对于D ：382x xy ==,符合指数函数的定义,所以是指数函数.故选：A.考点二 定义域和值域【例2-1】（2020·全国高一课时练习）求下列函数的定义域和值域： （1）142x y -=；（2）23y ⎛= ⎪⎝⎭（3）22312x x y --⎛⎫=⎪⎝⎭.【参考答案】（1）定义域{|4}x x ≠,值域为{|0y y >且1}y ≠； （2）定义域{|0}x x =,值域{|1}y y =；（3）定义域R ,值域(]0,16【解析】（1）要使函数式有意义,则40x -≠,解得4x ≠.所以函数142x y -=的定义域为{|4}x x ≠.因为104x ≠-,所以1421x -≠,即函数142x y -=的值域为{|01}y y y >≠，且. （2）要使函数式有意义,则||0x -,解得0x =,所以函数23y ⎛= ⎪⎝⎭{|0}x x =.因为0x =,所以022133⎛⎛⎫== ⎪ ⎪⎝⎭⎝⎭,即函数23y ⎛= ⎪⎝⎭{|1}y y =.（3）函数的定义域为R .因为2223(1)44x x x --=--≥-,所以2234111622x x ---⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭. 又223102x x --⎛⎫>⎪⎝⎭,所以函数22312x x y --⎛⎫= ⎪⎝⎭的值域为(]0,16.【例2-2】（2018·湖南开福.长沙一中高一月考）若函数y =的值域为[0,+∞）,则实数a 的取值范围是_____． 【参考答案】（﹣∞,﹣2]【解析】设()421x x g x a =+⋅+,若函数y =的值域为[0,)+∞,则等价于[0,)+∞是()g x 值域的子集,2()421(2)21x x x x g x a a =+⋅+=+⋅+,设2x t =,则0t >,则2()1y h t t at ==++,(0)10h =>,∴当对称轴02at =-,即0a 时,不满足条件． 当02at =->,即0a <时,则判别式△240a =-,即022a a a <⎧⎨-⎩或,则2a -, 即实数a 的取值范围是(-∞,2]-.故参考答案为：(-∞,2]-【一隅三反】1．（2020·全国高一课时练习）求下列函数的定义域和值域； （1）12x y +=；（2）y =（3）y =【参考答案】（1）定义域为R ,值域为(0,)+∞；（2）(,0]-∞,[0,1)；（3）[0,)+∞,[1,)+∞.【解析】（1）12x y +=的定义域为R ,值域为(0,)+∞.（2）由120x -≥知0x ,故y =(,0]-∞；由0121x -<知0121x -<,故y =[0,1).（3）y =[0,)+∞0x 知1x,故y =[1,)+∞.2．（2020·全国高一课时练习）求下列函数的定义域与值域.（1）y =（2）1(0,1x x a y a a -=>+且1)a ≠（3）110.3;x y -=（4）y =【参考答案】（1）定义域为[0,)+∞；值域为[0,1)；（2）定义域为R ；值域为(－1,1)；（3）定义域为{1}xx ≠∣；值域为{0y y >∣且1}y ≠；（4）定义域为15xx ⎧⎫≥⎨⎬⎩⎭∣；值域为{1}yy ≥∣. 【解析】（1）1102x⎛⎫-≥ ⎪⎝⎭,解得：0x ≥, ∴原函数的定义域为[0,)+∞,令11(0)2xt x ⎛⎫=-≥ ⎪⎝⎭,则01,01t ≤<∴≤∴原函数的值域为[0,1) （2）原函数的定义域为R.设x a t =,则(0,)t ∈+∞,11221111t t y t t t -+-===-+++, 0,11t t >∴+>,1201,2011t t -∴<<∴-<<++,21111t ∴-<-<+,即原函数的值域为(1,1)-. （3）由10x -≠得1x ≠,所以函数定义域为{|1}x x ≠,由101x ≠-得1y ≠, 所以函数值域为{|0y y >且1}y ≠.(4)由510x -≥得15x ≥,所以函数定义域为15x x ⎧⎫≥⎨⎬⎩⎭∣,0≥得1y ≥,所以函数值域为{1}yy ≥∣. 3．（2020·河北新华.石家庄二中高二期末）若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为（ ）A ．1,4⎡⎫+∞⎪⎢⎣⎭B ．11,42⎡⎤⎢⎥⎣⎦C ．1,12⎡⎤⎢⎥⎣⎦D ．1,14⎛⎤ ⎥⎝⎦【参考答案】B【解析】当1x <时,()1,212xf x ⎛⎫∈+∞⎛ ⎪⎝⎫= ⎪⎭⎭⎝ 当1≥x 时,()114,4xf x a a a ⎛⎤∈+⎛⎫=+ ⎪⎝⎭ ⎥⎝⎦ 函数()f x 的值域为(),+∞a 114212a a ⎧+≥⎪⎪∴⎨⎪≤⎪⎩,即11,42a ⎡⎤∈⎢⎥⎣⎦故选：B 4．（2020·云南五华.昆明一中高三其他（理））设函数y =A ,函数12x y -=的值域为B ,则AB =( )A ．()0,1B ．(]0,1C ．()1,1-D ．[]1,1-【参考答案】A【解析】函数定义域满足：210x ->,即11x -<<,所以{}11A x x =-<<,函数12x y -=的值域{}0B y y =>,所以()0,1AB =,故选：A.5．（2019·湖南高一期中）若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为（ ）A ．2-B ．1-C ．1D ．2【参考答案】D【解析】由于函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,所以0a >,且当422x a a-=-=时,()f x 取得最大值为2224411412113333a a a aaf a ⎛⎫⋅-⋅+-+ ⎪-⎝⎭⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故4411,2,2a a a-===.故选：D 考点三 指数函数性质【例3】（1）（2020·贵溪市实验中学高二期末（文））若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3（2）（2019·湖南岳阳楼.岳阳一中高一期中）已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)（3）（2019·湖北襄阳）如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么（ ）A ．a b a a a b <<B ．a a b a b a <<C ．b a a a a b <<D ．b a a a b a <<【参考答案】（1）B （2）B(3)C【解析】（1）函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增,()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ．（2）可知函数()f x 为减函数,由2(4)(3)f a f a ->,可得243a a-<,整理得2340a a --<,解得14a -<<,所以不等式的解集为(1,4)-．故选B.(3) 根据函数()1()2x f x =在R 是减函数,且1111222ba⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,所以10b a >>>,所以a a b a b a <<,故选C.【一隅三反】1．（2019·浙江南湖.嘉兴一中高一月考）函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是（ ）A ．[)1,-+∞B ．(],1-∞-C ．[)1,+∞D ．(],1-∞【参考答案】C【解析】∵13uy ⎛⎫= ⎪⎝⎭是减函数,222(1)1u x x x =-+=--+在(,1]-∞上递增,在[1,)+∞上递减,∴函数2213x xy -+⎛⎫= ⎪⎝⎭的增区间是[1,)+∞．故选：C ．2．（2019·浙江柯城.衢州二中高三一模）已知定义在R 上的函数()||32x m f x -+=+m 为实数）为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )11.指数函数性质记忆口诀指数增减要看清,抓住底数不放松； 反正底数大于0,不等于1已表明； 底数若是大于1,图象从下往上增； 底数0到1之间,图象从上往下减； 无论函数增和减,图象都过(0,1)点． 2.比较幂值大小的三种类型及处理方法A ．c b a <<B ．c a b <<C ．a c b <<D ．a b c <<【参考答案】B【解析】()f x 为偶函数,()()f x f x ∴-=,||||3232x m x m --+-+∴+=+,||||x m x m ∴-+=+；0m ∴=；||()32x f x -∴=+；()f x ∴在[0,)+∞上单调递减,并且0.25(|log 3|)(log 3)a f f ==,5(log )b f e =,()()c f m f ππ=+=550log log 3e π<<<c a b ∴<<．故选：B ．3．（2020·浙江高一课时练习）设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则（ ）A ．312y y y >>B ．213y y y >>C ．123y y y >>D ．132y y y >>【参考答案】D【解析】 1.50.920.9 1.80.4830.481.44 1.35121422,22282,y y y -⨯⨯⎛⎫======⎝== ⎪⎭,因为函数2xy =在定义域上为单调递增函数,所以132y y y >>．故选：D ．4．（2020·永安市第三中学高二月考）若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是（ ）A ．(,8][0,)-∞-+∞B ．(),4-∞-C ．[8,4)--D ．(,8]-∞-【参考答案】D【解析】由9(4)340x xa ++⋅+=,得443(4)0,(4)3433xxx x a a +++=∴-+=+≥（当且仅当32x =时等号成立）,解得8a ≤-故选D5（2020·上海高一课时练习）已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.【参考答案】(,1]-∞-【解析】由题得函数的定义域为R . 设2122,()2uu x x v =++=,函数222,u x x =++在∞(-,-1]单调递减,在[1,)-+∞单调递增,函数1()2uv =在其定义域内单调递减,所以2221()2x x f x ++⎛⎫= ⎪⎝⎭在∞(-,-1]单调递增,在[1,)-+∞单调递减.故参考答案为：(,1]-∞-.6．（2020·上海普陀.曹杨二中高一期末）函数12x y =-的单调递增区间为________【参考答案】(,0]-∞【解析】函数12,010221,1x xxy x x ⎧->⎪=⎨⎛⎫-≤⎪ ⎪⎝⎭=⎩-, 根据指数函数单调性可得,函数在(,0]-∞单调递增,在0,单调递减,所以函数12xy =-的单调递增区间为(,0]-∞.故参考答案为：(,0]-∞ 7．（2020·全国高一课时练习）比较下列各题中的两个值的大小． （1）0.10.8-,0.21.25；（2）1ππ-⎛⎫ ⎪⎝⎭,1；（3）30.2-,()0.23-.【参考答案】（1）0.10.20.81.25-<（2）11ππ-⎛⎫> ⎪⎝⎭（3）()0.230.23->-【解析】（1）因为0.10.10.1450.854--⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭, 0.20.251.254⎛⎫= ⎪⎝⎭, 又指数函数54xy ⎛⎫= ⎪⎝⎭为增函数,且0.10.2<,所以0.10.25544⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭,即0.10.20.8 1.25-<. （2）1ππ-⎛⎫ ⎪⎝⎭01πππ=>=,（3）30.2-00.21>=,()()10.25330-=-=<,所以()0.230.23->-.考点四 定点【例4】（2020·浙江高一课时练习）函数()-1=4+x f x a （0a >,且1a ≠）的图象过定点P ,则P 点的坐标为（ ） A ．(1,5) B ．(1,4) C ．(0,5)D ．(0,4)【参考答案】A【解析】因为xy a =的图象恒过(0,1)点,则1x y a-=的图象恒过(1,1)点,所以()-1=4+x f x a恒过定点()1,5P .故选A .【一隅三反】1．（2019·涡阳县第九中学高二期末）函数()10,1xy a a a =+>≠的图象必经过点（ ）A ．(0,1)B ．(1,1)C ．()0,2D ．(2,2)【参考答案】C【解析】函数x y a =的图象过点(0,1),而函数1x y a =+的图象是把函数x y a =的图象向上平移1个单位,∴函数1x y a =+的图象必经过的点(0,2)．故选：C ．2．（2019·贵州省织金县第二中学高一期中）函数21()x f x a-=(0a >且1)a ≠过定点（ ） A ．(1,1) B ．1(,0)2C ．(1,0)D ．1(,1)2【参考答案】D【解析】令12102x x -=⇒=,所以函数21()x f x a -=(0a >且1)a ≠过定点1(,1)2． 3．（2020·宁夏贺兰县景博中学高一月考）函数y=a x ﹣1+2（a ＞0且a≠1）图象一定过点（ ）A ．（1,1）B ．（1,3）C ．（2,0）D ．（4,0）【参考答案】B 由x ﹣1=0,解得x=1,此时y=1+2=3,即函数的图象过定点（1,3）,故选B考点五 图像【例5-1】（2020·广东顺德一中高一期中）函数1(0,1)xy a a a a=->≠的图像可能是（ ）． A ． B ．C ．D ．【参考答案】D 【解析】∵0a >,∴10a>,∴函数x y a =需向下平移1a 个单位,不过（0,1）点,所以排除A,当1a >时,∴101a <<,所以排除B,当01a <<时,∴11a>,所以排除C,故选D. 【例5-2】（2020·浙江高一课时练习）若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则（ ） A ．1a >B ．1a >,且0m <C ．01a <<,且0m >D ．01a <<【参考答案】B【解析】因为函数xy a =的图像在第一、二象限内,所以欲使其图像在第三、四象限内,必须将xy a =向下移动,因为当01a <<时,图像向下移动,只能经过第一、二、四象限或第二、三、四象限, 所以只有当1a >时,图像向下移动才可能经过第一、三、四象限,故1a >,因为图像向下移动小于一个单位时,图像经过第一、二、三象限,而向下移动一个单位时,图像恰好经过原点和第一、三象限,所以欲使图像经过第一、三、四象限,则必须向下平移超过一个单位, 故11m -<-,0m <,故选：B.【一隅三反】1．（2019·浙江高一期中）函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A ．B ．C ．D ．【参考答案】D【解析】因为函数y x a =+单调递增,所以排除AC 选项；当1a >时,y x a =+与y 轴交点纵坐标大于1,函数xy a =单调递增,B 选项错误；当01a <<时,y x a =+与y 轴交点纵坐标大于0小于1,函数xy a =单调递减；D 选项正确.故选：D2．（2020·全国高一课时练习）在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是（ ）A ．B ．C ．D ．【参考答案】A【解析】根据选项中二次函数图象,可知0c ,根据选项中指数函数的图象,可知01b a <<,所以1022b a-<-<, 所以二次函数2y ax bx c =++的对称轴在y 轴左侧,且1,022b x a ⎛⎫=-∈- ⎪⎝⎭, 所以可排除B 、C 、D,只有A 符合题意.故选：A.3．（2020·上海高一课时练习）若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A ．m 1≥B ．1m <C ．1m >-D ．1m ≤-【参考答案】D【解析】指数函数2x y =过点0,1,则函数2xy m =+过点()0,1m +,若图像不经过第二象限,则10m +≤,即1m ≤-,故选：D4．（2020·内蒙古集宁一中高二期末（理））若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a 的取值范围是___________【参考答案】102⎛⎫ ⎪⎝⎭，【解析】当01,1a a <<>时,做出|1|xy a =-图象,如下图所示,直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点时,1021,02a a <<<<. 故参考答案为:102⎛⎫ ⎪⎝⎭，知识改变命运。
专题4.1 指数与指数函数(精讲精析篇)(解析版)
专题4.1指数与指数函数（精讲精析篇）提纲挈领点点突破热门考点01 根式的化简与求值(1)任意实数的奇次方根只有一个，正数的偶次方根有两个且互为相反数． (2)(na )n 是实数a 的n 次方根的n 次幂，其中实数a 的取值由n 的奇偶性决定．n a ⎩⎪⎨⎪⎧n 为偶数，a 为非负实数n 为奇数，a 为任意实数，且n a 符号与a 的符号一致【典例1】化简下列各式： ①4(x －2)4； ②5(x －π)5. 【答案】见解析. 【解析】 ①4(x －2)4＝|x －2|＝⎩⎪⎨⎪⎧x －2，x ≥2，－x ＋2，x <2.②5(x －π)5＝x －π. 【典例2】化简下列各式：(1)x 2－2x ＋1－x 2＋6x ＋9(－3<x <3)； (2)(a －1)2＋1－2a ＋a 2＋3(1－a )3.【答案】见解析.【解析】(1)原式＝(x －1)2－(x ＋3)2＝|x －1|－|x ＋3|.∵－3<x <3，∴当－3<x <1时，原式＝－(x －1)－(x ＋3)＝－2x －2； 当1≤x <3时，原式＝(x －1)－(x ＋3)＝－4.∴原式＝⎩⎪⎨⎪⎧－2x －2，－3<x <1，－4，1≤x <3.(2)由a －1知a －1≥0，∴原式＝a －1＋(a －1)2＋1－a ＝a －1. 【规律方法】1.根式化简或求值的注意点解决根式的化简或求值问题，首先要分清根式为奇次根式还是偶次根式，然后运用根式的性质进行化简或求值．2．对n a n 与(na )n 的进一步认识(1)对(n a )n 的理解：当n 为大于1的奇数时，(n a )n 对任意a ∈R 都有意义，且(na )n ＝a ，当n 为大于1的偶数时，(n a )n 只有当a ≥0时才有意义，且(na )n ＝a (a ≥0)．(2)对na n的理解：对任意a ∈R 都有意义，且当n 为奇数时，n a n ＝a ；当n 为偶数时，n a n＝|a |＝⎩⎪⎨⎪⎧a a ≥0－a a ＜0.(3)对于根式的运算还要注意变式，整体代换，以及平方差、立方差和完全平方、完全立方公式的运用，做到化繁为简，必要时进行讨论． 3.有限制条件的根式化简的步骤热门考点02 指数幂的化简与求值指数幂运算的一般原则：(1)指数幂的运算首先将根式、分数指数幂统一为分数指数幂，以便利用法则计算． (2)先乘除后加减，负指数幂化成正指数幂的倒数．(3)底数是负数，先确定符号；底数是小数，先化成分数；底数是带分数的，先化成假分数． (4)运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数． 【典例3】计算：．【答案】12. 【解析】．【典例4】已知则的值为__________．【答案】【解析】题意，∴，∴，故答案为．【典例5】（2020·上海高三专题练习）若1a >，0b <，且22b b a a -+=b b a a --=_________. 【答案】2- 【解析】22b ba a-+=()22228b bb b a a a a --+=++=，故226b b a a -+=，()22224b b b b a a a a ---=+-=，1a >，0b <，故0b b a a --<，故2b b a a -=--.故答案为：2-. 【特别提醒】根式、指数幂的条件求值，是代数式求值问题的常见题型，一般步骤是： (1)审题：从整体上把握已知条件和所求代数式的形式和特点；(2)化简：①化简已知条件；②化简所求代数式；（3）求值：往往通过整体代入，简化解题过程.如本题求值问题实质上考查整体思想，考查完全平方公式、立方和（差）公式的应用，如，，，解题时要善于应用公式变形．热门考点03 指数函数的图象及应用常考题型及技法(1)已知函数解析式判断其图象一般是取特殊点，判断选项中的图象是否过这些点，若不满足则排除． (2)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a 与1的大小关系不确定时应注意分类讨论．(3)有关指数方程、不等式问题的求解，往往是利用相应的指数型函数图象，数形结合求解． (4)判断指数函数图象上底数大小的问题，可以先通过令x ＝1得到底数的值再进行比较．【典例6】（2020·上海高一课时练习）函数xy a =和(1)y a x =+（其中0a >且1a ≠）的大致图象只可能是( )A ．B ．C ．D ．【答案】C 【解析】由于(1)y a x =+过点()1,0-，故D 选项错误.当1a >时，xy a =过()0,1且单调递增；(1)y a x =+过点()1,0-且单调递增，过()0,a 且1a >.所以A 选项错误.当01a <<时，xy a =过()0,1且单调递减，(1)y a x =+过点()1,0-且单调递增，过()0,a 且01a <<.所以B 选项错误.综上所述，正确的选项为C. 故选：C【典例7】（2019·贵州省织金县第二中学高一期中）函数21()x f x a -=(0a >且1)a ≠过定点（ ）A ．(1,1)B ．1(,0)2C ．(1,0)D ．1(,1)2【答案】D 【解析】令12102x x -=⇒=，所以函数21()x f x a-=(0a >且1)a ≠过定点1(,1)2． 【总结提升】1.对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a 与1的大小关系不确定时应注意分类讨论．2.判断指数函数图象上底数大小的问题，可以先通过令x ＝1得到底数的值再进行比较．3.识图的三种常用方法（1）抓住函数的性质，定性分析：①从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置；②从函数的单调性，判断图象的变化趋势；③从周期性，判断图象的循环往复；④从函数的奇偶性，判断图象的对称性．⑤从函数的特征点，排除不合要求的图象. (2)抓住函数的特征，定量计算：从函数的特征点，利用特征点、特殊值的计算分析解决问题． （3）根据实际背景、图形判断函数图象的方法：①根据题目所给条件确定函数解析式，从而判断函数图象(定量分析)； ②根据自变量取不同值时函数值的变化、增减速度等判断函数图象(定性分析)． 4.过定点的图象(1)画指数函数y ＝ax(a ＞0，a≠1)的图象，应抓住三个关键点(0,1)，(1，a)， .特别注意，指数函数的图象过定点（0，1）； (2) xy a ＝与xy a-＝的图象关于y 轴对称；(3)当a ＞1时，指数函数的图象呈上升趋势，当0＜a ＜1时，指数函数的图象呈下降趋势；简记：撇增捺减．热门考点04 指数函数的性质及应用1.指数函数图象的变化规律指数函数的图象随底数变化的规律可归纳为：在第一象限内，图象自下而上对应的底数依次增大． 2.有关指数函数性质的问题类型及解题思路(1)比较指数幂大小问题．常利用指数函数的单调性及中间值(0或1)．(2)简单的指数不等式的求解问题．解决此类问题应利用指数函数的单调性，要特别注意底数a 的取值范围，并在必要时进行分类讨论．(3)求解与指数函数有关的复合函数问题，首先要熟知指数函数的定义域、值域、单调性等相关性质，其次要明确复合函数的构成，涉及单调性问题时，要借助“同增异减”这一性质分析判断． 【典例8】（2016新课标全国III ）已知，，，则（ ）A. B. C. D.【答案】A 【解析】因为，，所以，故选A ．【典例9】（2017·北京高考真题（理））已知函数1()3()3x x f x =-，则()f xA ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数【答案】A 【解析】分析：讨论函数()133xxf x ⎛⎫=- ⎪⎝⎭的性质，可得答案. 详解：函数()133xxf x ⎛⎫=- ⎪⎝⎭的定义域为R ，且()()111333,333xxx xxx f x f x --⎡⎤⎛⎫⎛⎫⎛⎫-=-=-+=--=-⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦即函数()f x 是奇函数，又1y 3,3xx y ⎛⎫==- ⎪⎝⎭在R 都是单调递增函数，故函数()f x 在R 上是增函数.故选A.【典例10】(2019·天津河西区一模)已知f (x )＝|2x －1|，当a ＜b ＜c 时，有f (a )＞f (c )＞f (b )，则必有( ) A ．a ＜0，b ＜0，c ＜0 B ．a ＜0，b ＞0，c ＞0 C ．2－a ＜2c D ．1＜2a ＋2c ＜2【答案】D【解析】作出函数f (x )＝|2x －1|的图象， 如图所示，因为a ＜b ＜c ，且有f (a )＞f (c )＞f (b )，所以必有a ＜0,0＜c ＜1，且|2a －1|＞|2c －1|，所以1－2a ＞2c －1，则2a ＋2c ＜2，且2a ＋2c ＞1，故选D.【典例11】（2019·浙江学军中学高一期中）已知函数1()421x x f x a +=-⋅+． （1）若函数()f x 在[]0,2x ∈上有最大值8-，求实数a 的值； （2）若方程()0f x =在[]1,2x ∈-上有解，求实数a 的取值范围． 【答案】（1）5；（2）1718a ≤≤ 【解析】（1）因为[]0,2x ∈，所以令[]21,4xt =∈，所以得到函数()221f t t at =-+，开口向上，对称轴为t a =，当52a ≤时，则在4t =时，()f t 取最大值，即()()max 48f t f ==-， 所以16818a -+=-，解得258a =，不满足52a ≤，所以舍去，当52a >时，则1t =时，()f t 取最大值，即()()max 18f t f ==-，所以1218a -+=-，解得5a =，满足52a >，综上，a 的值为5.（2）因为[]1,2x ∈-，所以令12,42xm ⎡⎤=∈⎢⎥⎣⎦，所以得到函数()221f m m am =-+令()0f m =，得2210m am -+=，即12a m m=+， 所以要使()0f m =有解， 则函数2y a =与函数1y m m=+有交点， 而函数1y m m =+，在1,12⎡⎤⎢⎥⎣⎦上单调递减，在[]1,4上单调递增， 故在1x =时，有min 2y =，在4x =时，有max 174y =， 所以可得21724a ≤≤， 所以a 的范围为1718a ≤≤. 【典例12】（2020·上海高三专题练习）已知函数22513x x y ++⎛⎫= ⎪⎝⎭，求其单调区间及值域．【答案】在(),1-∞-上是增函数，在()1,-+∞上是减函数，值域为10,81⎛⎤ ⎥⎝⎦【解析】根据复合函数单调性“同增异减”的法则，将问题转化为求二次函数的单调递减区间问题.解：令13Uy ⎛⎫= ⎪⎝⎭,225U x x =++，则y 是关于U 的减函数，而U 是(),1-∞-上的减函数，()1,-+∞上的增函数，∴2251 3x xy++⎛⎫= ⎪⎝⎭在(),1-∞-上是增函数，而在()1,-+∞上是减函数，又∵()2225144U x x x=++=++≥, ∴22513x xy++⎛⎫= ⎪⎝⎭的值域为4110,0,381⎛⎤⎛⎫⎛⎤=⎥⎪ ⎥⎝⎭⎝⎦⎥⎝⎦．【总结提升】1在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，既不同底又不同次数的幂函数值比较大小：常找到一个中间值，通过比较幂函数值与中间值的大小进行判断．准确掌握各个幂函数的图象和性质是解题的关键.2.指数函数的图象在第一象限内底大图高(逆时针方向底数依次变大)．当幂的底数不确定时，要注意讨论底数的不同取值情况.3.根据指数函数图象判断底数大小的问题，可以通过直线x＝1与图象的交点进行判断．如图是指数函数(1)y ＝a x，(2)y＝b x，(3)y＝c x，(4)y＝d x的图象，底数a，b，c，d与1之间的大小关系为c＞d＞1＞a＞b.规律：在y轴右(左)侧图象越高(低)，其底数越大．4.幂函数y＝xα的形式特点是“幂指数坐在x的肩膀上”，图象都过点(1,1)．它们的单调性要牢记第一象限的图象特征：当α>0时，第一象限图象是上坡递增；当α＜0时，第一象限图象是下坡递减．然后根据函数的奇偶性确定y轴左侧的增减性即可．巩固提升1.（2019·华东师大二附中前滩学校高三月考）函数1(0,1)xy a a aa=->≠的图象可能是（）．A．B．C ．D ．【答案】D 【解析】∵0a >，∴10a>，∴函数x y a =需向下平移1a 个单位，不过（0,1）点，所以排除A ，当1a >时，∴101a <<，所以排除B ，当01a <<时，∴11a>，所以排除C ，故选D.2．（2020·宾县第二中学高二期末（文））已知,a b ∈R ，则“ln ln a b >”是“11()()33a b<”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A 【解析】 ∵ln ln a b > ∴0a b >>∵1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭∴a b >∵0a b >>是a b >的充分不必要条件∴ln ln a b >是1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭的充分不必要条件 故选A3．（2019·贵州省织金县第二中学高一期中）函数(01)||xxa y a x =<<的图像的大致形状是（ ）A ．B ．C ．D ．【答案】D 【解析】 根据01a <<(01)||x xa y a x =<<,0,0x x a x y a x ⎧>∴=⎨-<⎩01a <<，∴x y a =是减函数，x y a =-是增函数.(01)||xxa y a x =<<在(0)+∞，上单调递减，在()0-∞，上单调递增 故选：D.4．（2020·上海高三专题练习）函数()12x f x -的定义域是 （ ） A ．(],0-∞ B ．[)0,+∞C ．(),0-∞D ．(),-∞+∞【答案】A【解析】120x -≥，解得0x ≤， ∴函数的定义域(],0-∞，故选A.5.（2020·四川省高一期末）设.1084y =，0.728y =，3434y =，则（ ）A ．312y y y >>B ．213y y y >>C ．132y y y >>D ．123y y y >>【答案】B 【解析】()20.80.81.16224y ===，()0.70.73 2.12822y ===，()332 1.5443422y ===.因为 2.1 1.6 1.5222>>，故213y y y >>. 故选：B6．（2020·上海高三专题练习）函数f (x )=x a －b 的图象如图，其中a 、b 为常数，则下列结论正确的是（ ）A ．a >1，b <0B ．a >1，b >0C ．0 <a <1，b >0D ．0 <a <1，b <0【答案】C 【解析】从曲线走向结合指数函数的单调性可知0<a<1, 又f (0)=1－b 1<，所以b >0， 故选：C.7．（2020·上海高三专题练习）已知01,1a b <<<-,则函数x y a b =+的图像必定不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 【解析】此题考查指数函数的图像的性质和指数函数的上下平移；有已知得到：此指数函数是减函数，分布在第一，二象限，渐近线是x 轴，即0y =；xy a b =+（1b <-）是由指数函数向下平移大于1个单位得到的，即原来指数函数所过的定点(0,1)向下平移到原点的下方了，所以图像不经过第一象限，所以选A ，如下图所示：8．（2020·上海高三专题练习）若函数1()21x f x =+, 则该函数在(-∞,+∞)上是 ( ) A ．单调递减无最小值 B ．单调递减有最小值 C ．单调递增无最大值 D ．单调递增有最大值【答案】A 【解析】设21x t =+，则当(),x ∈-∞+∞时为增函数，且1t >；于是()11121xy t t ==>+为减函数，其图象如图所示： 则故121x y =+为减函数且1y <；图象在y 轴上方，0y >，所以原函数既无最小值，也无最大值.故正确答案为A.9．（2019·天津高三高考模拟）若，则函数的值域是（ ）A ．B ．C ．D ．【答案】B 【解析】 将化为，即，解得，所以，所以函数的值域是.故选C.10.（2020·上海高一课时练习）已知实数a ，b 满足01a b <<<，则下列各式中正确的是( ) A ．221333b a b<<B ．122333b a b<<C ．212333a b b<<D ．221333a b b<<【答案】D 【解析】当0α>时，幂函数y x α=在()0,x ∈+∞上为增函数，所以当01a b <<<时有2233a b <， 因为01b <<，所以指数函数xy b =在x ∈R 上为减函数， 因此有 2133b b <， 所以有：221333a b b <<故选：D11.(2018届山东、湖北部分重点中学冲刺（二）)定义在上的奇函数，当时，，则关于的函数的所有零点之和为（ ）A.B.C.D.【答案】C【解析】当时，又是奇函数，画出函数的图象，由函数图象可知： ，有个零点，其中有两个零点关于对称，还有两个零点关于对称，所以这四个零点的和为零，第五个零点是直线与函数，交点的横坐标，即方程的解，，故选C.12.（2015·江苏高考真题）不等式224x x-<的解集为________.【答案】(1,2).- 【解析】,2222,xx-∴<是一个递增函数；故答案为：.13.（2019·安徽马鞍山二中高三月考（文））若函数3x m y a n -=+-（0a >且1a ≠）的图象恒过定点(3,2)，则m n +=______． 【答案】7 【解析】 ∵函数3x my an -=+-（0a >且1a ≠）的图象恒过定点，令0x m -=，可得x m =，2y n =-，可得函数的图象经过定点(),2m n -.再根据函数的图象经过定点()3,2， ∴3m =，22n -=，解得3m =，4n =，则7m n +=， 故答案为：7．14. （2020·湖北省高一期末）当生物死亡后，它机体内原有的碳14会按确定的规律衰减.按照惯例，人们将每克组织的碳14含量作为一个单位大约每经过5730年，一个单位的碳14衰减为原来的一半，这个时间称为“半衰期”.当死亡生物组织内的碳14的含量不足死亡前的千分之一时，用一般的放射性探测器就测不到碳14了.如果用一般的放射性探测器不能测到碳14，那么死亡生物组织内的碳14至少经过了_____个“半衰期”.（提示：910.001952=）【答案】10 【解析】设生物组织内原有的碳14含量为x ，需要经过n 个“半衰期”才不能测到碳14，则1121000n x x ⋅<，即10.0012n <， 由参考数据可知，910.001950.0012=>，10110.001950.0009750.00122=⨯=<，所以10n =， 故答案为：10.15.（2015·湖南高考真题（理））已知函数32,(),x x m f x x x m ⎧≤=⎨>⎩，，若存在实数a ，使函数g(x)=f(x)-a 有两个零点，则实数m 的取值范围是________． 【答案】()(),01,-∞⋃+∞ 【解析】∵()()g x f x a =-有两个零点， ∴()f x a =有两个零点，即()y f x =与y a =的图象有两个交点， 由32x x =可得，0x =或1x =．①当1m >时,函数()f x 的图象如图所示，此时存在a 满足题意，故1m >满足题意．②当1m =时,由于函数()f x 在定义域R 上单调递增，故不符合题意． ③当01m <<时,函数()f x 单调递增，故不符合题意．④0m =时,()f x 单调递增，故不符合题意． ⑤当0m <时,函数()y f x =的图象如图所示,此时存在a 使得()y f x =与y a =有两个交点．综上可得0m <或1m >．所以实数m 的取值范围是()(),01,-∞⋃+∞．16.（2019·上海市高桥中学高一期末）在下列命题中：①两个函数的对应法则和值域相同，则这两个是同一个函数；②()222xxf x -=在R 上单调递增，③若函数()1f x -的定义域为[]0,2，则函数()1f x +的定义域为[]2,0-；④若函数()f x 在其定义域内不是单调函数，则()f x 不存在反函数；⑤()42222xx f x =+++函数的最小值为4；⑥若关于x 的不等式1202xxm --<在[]0,1区间内恒成立，则实数m 的范围是()0,2其中真命题的序号有_________. 【答案】③ 【解析】对于①：对应法则和值域相同的两个函数，其定义域不一定相同， 如f （x ）＝x 2，x ∈R 与g （x ）＝x 2，x ∈[0，+∞），∴①错误； 对于②： ()222xxf x -=在(),1-∞ 上单调递减，在()1,+∞ 上单调递增，故②错误；对于③：∵函数()1f x -的定义域为[]0,2，∴111x -≤-≤ ，即()f x 的定义域为[]1,1-，∴111x -≤+≤，即20x -≤≤，∴函数()1f x +的定义域为[]2,0-，∴③正确；对于④：函数f （x ）1x=在定义域上不单调，但函数f （x ）存在反函数，∴④错误； 对于⑤：()42222xxf x =+++，令()222,xt =+∈+∞ 则()4f x t t=+在()2,+∞上单调递增，没有最小值，∴⑤错误. 对于⑥：由|2x ﹣m |12x -＜0，得|2x﹣m |12x ＜，∴11222x x xm --＜＜， 即112222x xx x m -+＜＜在区间[0，1]内恒成立，∵函数f （x ）122xx =-在区间[0，1]内单调递增，∴f （x ）的最大值为32；令g （x ）122xx =+，t ＝2x （1≤t ≤2），则y ＝t 1t+在[1，2]上为增函数，由内函数t ＝2x 为增函数，∴g （x ）122x x =+在区间[0，1]内单调递增，g （x ）的最小值为2．∴322m ＜＜．∴⑥错误.故答案为：③。
4.2 指数函数(精练)(解析版) -人教版高中数学精讲精练(必修一)
x
2
1 ，故值域为 y
|
0
y
1
.
8．（2021·黑龙江·绥化市第一中学高一期中）已知函数 f x 4x a 2x 3 ， a R ．
(1)当 a 4 ，且 x 0, 2 时，求函数 f x 的值域；
(2)若函数 f x 在0, 2 的最小值为1，求实数 a 的值；
【答案】(1)1,3 (2) a 2 2
③
y
2
x
是指数函数；
④ y xx 的底数是 x 不是常数，不是指数函数；
⑤
y
3
1 x
的指数不是自变量
x
，不是指数函数；
1
⑥ y x3 是幂函数．
故答案为：③
9．（2021·全国·高一专题练习）函数 y a2 5a 5 ax 是指数函数，则 a 的值为________．
【答案】 4
f
x
ax2 2x ,
a
1 x
x 1
3a,
x
1 的最小值为
2，则实数
a 的取值范围是______.
【答案】1,
【解析】由题意，函数
f
x
ax2 2x ,
a 1 x
x 1
3a, x
1 的最小值为
2
，
因为函数 f x 在[1, ) 上为增函数，可得 x 1时，函数 f x 有最小值为 2 ，
则当 x (,1) 时，函数 f x 2 ， min
）
A． c a b
B． c b a
【答案】A
1
2
【解析】
b
1 4
3
1 2
3
，
C． b c a
指数函数典型例题详细解析
.指数函数·例题解析第一课时【例 1】（基础题）求下列函数的定义域与值域：1(2)y ＝ 2 x 2(3)y ＝ 3 3x 1(1)y ＝ 32 x 1解(1) 定义域为 {x|x ∈ R 且 x≠ 2} ．值域 {y|y ＞0 且 y≠ 1} ．(2)由 2x+2－ 1≥ 0，得定义域 {x|x ≥－ 2}，值域为 {|y|y ≥0} ．(3)由 3－ 3x-1≥ 0，得定义域是 {x|x≤ 2}，∵ 0≤ 3－ 3x －1＜3，∴值域是 0≤ y＜3．1.指数函数 Y=ax （ a>0 且 a≠ 1）的定义域是 R，值域是（ 0， +∞）2.求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为０③形如 a0,(a ≠ 0)3. 求函数的值域 : ①利用函数 Y=ax 单调性②函数的有界性 (x2 ≥0;ax>0) ③换元法 . 如 :y=4x+6 × 2x-8(1 ≤ x ≤ 2) 先换元 , 再利用二次函数图象与性质( 注意新元的范围)【例 2】（基础题）指数函数 y＝a x， y＝ b x， y＝ c x， y＝ d x的图像如图 2． 6－ 2 所示，则 a、 b、 c、 d、1 之间的大小关系是[ ] A． a＜ b＜ 1＜ c＜dB． a＜ b＜ 1＜ d＜cC． b ＜a＜ 1＜ d＜cD． c＜ d＜ 1＜ a＜b..解选 (c) ，在 x 轴上任取一点(x ， 0) ，则得 b＜ a＜ 1＜d＜ c．【例 3】（基础题）比较大小：(1) 2、3 2、54、8 8、916的大小关系是：．143(2)0.6 5 2( )2(3)4.5 4.1 ________3.7 3.6..1 1234 解 (1)∵ 2 22 ，3 2 23，5 4 25 ，88 28，9 16 2 9，函数＝x ，2＞，该函数在(－∞，＋∞)上是增函数，y 2 1又1＜3＜2＜4＜1，∴32＜88＜5＜9＜．3 8 5 9 24 16 24 1解(2) ∵ 0.6 5＞1，1＞( 3) 2 ，24 1∴0.6 5＞(3) 2．2解(3) 借助数4.5 3.6打桥，利用指数函数的单调性， 4.5 4.1＞ 4.5 3.6，作函数 y ＝ 4.5x，y ＝3.7 x的图像如图 2．6－ 3，取 x＝ 3.6 ，得 4.5 3.6＞3.7 3.61 2∴4.5 4.1＞ 3.7 3.6．说明如何比较两个幂的大小：若不同底先化为同底的幂，再利用指数函数的单调性进行比较，如例 2 中的 (1) ．若是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助 1 作桥梁，如例 2 中的 (2) ．其二构造一个新的幂作桥梁，这个新的幂具有与 4.5 4.1同底与 3.7 3.6同指数的特点，即为4.5 3.6 ( 或 3.7 4.1 ) ，如例 2 中的 (3) ．例题 4（中档题）..【例 4】 比较大小 n 1a n与 n an 1(a ＞ 0且a ≠1，n ＞1)．n 1 a n 1a n( n 1)解a n 1 n1当 0＜a ＜1，∵ n ＞1，＞0，n( n 1)1∴an( n 1) ＜1，∴ n 1 a n ＜ n a n 11＞ 0，当a ＞1时，∵ n ＞1，n( n1)1∴an( n 1) ＞1， n 1 a n ＞ n a n 1【例 5】（中档题）作出下列函数的图像：图像变换法(1)y ＝ ( 1 ) x 1 (2)y ＝ 2 x－ 2，2(3)y ＝2|x-1|(4)y ＝|1 －3x|解 (1)y ＝ ( 1) x 1的图像 (如图 2． 6－ 4) ，过点 (0， 1) 及 (－ 1， 1) ．2 21 x 的图像向左平移1个单位得到的．是把函数 y ＝ ( ) 2 解 (2)y ＝ 2x－ 2 的图像 ( 如图 2． 6－ 5) 是把函数 y ＝ 2x的图像向下平移 2 个单位得到的．..解 (3) 利用翻折变换，先作 y＝ 2|x|的图像，再把y＝ 2|x|的图像向右平移1个单位，就得 y＝ 2|x-1|的图像 ( 如图 2． 6－6) ．解(4) 作函数 y＝3x的图像关于 x 轴的对称图像得 y＝－ 3x的图像，再把 y＝－ 3x 的图像向上平移 1 个单位，保留其在 x 轴及 x 轴上方部分不变，把 x 轴下方的图像以 x 轴为对称轴翻折到 x 轴上方而得到． ( 如图 2． 6－7)例6（中档题）：用函数单调性定义证明：当 a＞1 时， y = a x是增函数 ...【解析】设 x ， x ∈R且 x ＜ x，并令 x2 = x 1 + h (h ＞0，h ∈R) ，很独特的方 1 2 1 2式则有 a x2 a x 1 a x 1 h a x1 a x1 (a h1) ， ∵a ＞ 1， h ＞ 0，∴a x0, a h1， 1 ∴ ax2 a x 1 0 ，即故 y = a x(a ＞ 1) 为 R 上的增函数，同理可证 0＜ a ＜ 1 时， y = a x a x 1a x2 是 R 上的减函数 .例题 7 中档题）指数函数与二次函数的 复合函数 (由内到外分析）二次函数为内层函数，指数函数为外层函数【例 6】 求函数 y ＝ ( 3 ) x2－ 5x ＋ 6的单调区间及值域．42 3 u 2 －5x解 令 u ＝x － 5x ＋ 6，则 y ＝ ( )是关于 u 的减函数，而 u ＝x4＋ 6在 x ∈ ( ∞， 5] 上是减函数，在 x ∈ [ 5， ∞ ) 上是增函数．∴函数22y ＝ ( 3 ) x2 － 5x ＋ 6的单调增区间是 ( ∞， 5] ，单调减区间是 [ 5， ∞)．422..2－ 5x ＋ 6 ＝ ( x 5 2 1 1 又∵ u ＝ x ) 4 ≥，2 43 ) u ，在 u ∈ [ 1 ∞ ) 上是减函数， 函数 y ＝ (， 44所以函数 y 3 ) x 2－ 5x ＋6的值域是 4108＝ ( (0 ，]．43变式 1 求函数 y=（ 1 ） x22 x的单调区间，并证明之 .2解法一（在解答题） ：在 R 上任取 x1、 x2，且 x1＜ x2，则y2 ( 1 ) x 2 2 2 x 2）（ x2－x1 ）（ x2+x1－ 2）【（ 1）为底数，红色部分为指数】= 2 =（ 1，y 1( 1 ) x 122 x 1222∵x1 ＜x2，∴ x2－ x1＞ 0.当 x1、x 2∈（－∞， 1］时， x1+x2－ 2＜ 0. 这时（ x2－ x1）（ x2+x1－ 2）＜ 0，则 y2＞ y 11.∴y2 ＞y1，函数在（－∞，1］上单调递增 .当 x1、x 2∈［ 1，+∞）时， x1+x2－ 2＞ 0，这时（ x2－ x1）（ x2+x1－ 2）＞0，即 y2＜ y 11.调性）∴ y2＜ y1 ，函数在［ 1，+∞上单调递减.综上，函数 y 在（－∞， 1］上单调递增，在［1，+∞）上单调递减 .合作探究：在填空、选择题中用上述方法就比较麻烦，因此我们可以考虑用复合函数的单调性来解题 ...解法二 、在填空、选择题中 （用复合函数的单调性） ： 设： u x 22xu1则： y2 对任意的 1 x 1 x 2 ，有u 1 u 2 ，1u是减函数又∵ y2x 22 x ∴ y 1 y 2 1 在 [1, ) 是减函数∴ y 2对任意的 x 1 x 2 1，有 u u 2 1 1 u又∵ y 是减函数21 x 22 x ∴ y 1y 2 ∴ y在 [1,) 是增函数 2在该问题中先确定内层函数（ u x 2 2x 1）和外层函数（ y2根据内外层函数的单调性确定复合函数的单调性 .u）的单调情况，再变式 2 已知 a 0 且 a 1，讨论 f (x) a x 23 x 2的单调性 .【分析】这是一道与指数函数有关的复合函数讨论单调性题，指数 x 23x 2 (x 3 )217 ，当 x ≥ 3 时是减函数， x ≤ 3 时是增函数，2 4 2 2 而 f (x) 的单调性又 1 两种范围有关， 应分类讨【解析】设 u x23x 2(x 3 )217 ，2 4..则当 x ≥3时， u 是减函数，当 x ≤3时， u 是增函数，2 2又当 a 1 时， y a u是增函数，当 0 a 1 时，y a u是减函数，所以当 a 1时，原函数 f(x) ax23 x 2 在[ 3 ,) 上是减函数，在( ,3]上是2 2增函数 .当 0 a 1 时，原函数 f( x) a x23x 2 在[ 3 ,) 上是增函数，在 ( , 3] 上是减2 2函数 .【小结】一般情况下，两个函数都是增函数或都是减函数，则其复合函数是增函数；；如果两个函数中一增一减，则其复合函数是减函数，但一定注意考虑复合函数的定义域.第二课时例题 8：（疑难题）指数函数与二次函数的复合函数换元法先换元 , 再利用二次函数图象与性质( 注意新元 u 的范围 )1 ) x 1【例 7】求函数 y＝ ( ( ) x＋1(x≥ 0)的单调区间及它的最大值．2 2 2 2 4 2∴＜≤，又∵＝1x 是∈，＋∞上的减函数，函数y＝ 1 )20 u 1 u ( ) x [ 0 ) ( u2 2 ..3在 ∈， 1 上为减函数，在 [ 1 ， 1) 上是增函数．但由 0 ＜ 1 ) x ≤ 14u (0 2 ] 2 ( 2≥，由11 11 2得 ≤ x ≤ ，得 ≤ ≤ ，∴函数y ＝ x x＋ 单调增x 1 2 ( ) 10 x 1 ( ) ( ) 124 2 区间是 ，＋∞ )，单调减区间 [0 ，1] [1 当 x ＝ 0 时，函数 y 有最大值为 1．内层指数函数 u=(1/2)x 为减，当 u 在（ 0，1/2 】时，此时外层二次 f （u) 为减函数 ，即 x 在【1，正无穷大），，则复合函数 为增（画草图分析法）点评：（1）指数函数的有界性（值域） ： x2≥0;ax>0（ 2）上述证明过程中，在两次求 x 的范围时，逆向利用了指数函数的值域及逆向利用了指数函数的单调性，是关键及疑难点。
4.2 指数函数(精练)-2022版高中数学新同步精讲精炼(必修第一册)(教师版含解析)
4.2指数函数【题组一指数函数的判断】1(2019·南昌市新建一中高一月考)下列函数中，指数函数的个数为()①112x y -⎛⎫= ⎪⎝⎭②y ＝a x ()01a a >≠且；③y ＝1x ；④2112xy ⎛⎫=- ⎪⎝⎭A ．0B ．1C ．3D ．4【答案】B【解析】由指数函数的定义可判定，只有②正确．故选B 2．(2020·全国高一课时练习)下列各函数中，是指数函数的是()A ．(3)xy =-B ．3xy =-C ．13x y -=D ．13xy ⎛⎫= ⎪⎝⎭【答案】D【解析】根据指数函数的定义知，()0,1xy a a a =>≠，A 选项底数错误，B 选项系数错误，C 选项指数错误；D 正确.故选：D3．(2020·全国高一课时练习)下列函数是指数函数的是________(填序号)．①y ＝4x ；②y ＝x 4；③y ＝(－4)x ；④y ＝4x 2.【答案】①【解析】形如(0x y a a =>且1a ≠)的函数，叫指数函数.由指数函数定义，只有①是指数函数；②y ＝x 4是幂函数；③y ＝(－4)x ，由于底数4(0,1)(1,)-∉+∞ ，所以③不是指数函数；④y ＝4x 2不是指数函数.故答案为：①4．(2020·浙江高一课时练习)下列函数中是指数函数的是________.①13xy ⎛⎫= ⎪⎝⎭；②23x y =⨯；③13x y -=；④4x y =；⑤31xy =+；⑥3131x x y -=+.【答案】①④【解析】函数13xy ⎛⎫= ⎪⎝⎭是指数函数，且4x y =也是指数函数，其它函数不符合指数函数的三个特征.故答案为：①④.5．(2020·河北鹿泉区第一中学高二月考)若函数()()21xf x a a a =--是指数函数，则()A ．1a =B ．2a =C ．1a =或2a =D ．0a >且1a ≠【答案】B【解析】由指数函数的定义，得21101a a a a ⎧--=⎪>⎨⎪≠⎩，解得2a =．故选：B6．(2020·全国高一课时练习)若函数()21xy a =-(x 是自变量)是指数函数，则a 的取值范围是()A ．0a >且1a ≠B ．0a ≥且1a ≠C ．12a >且1a ≠D ．12a ≥【答案】C【解析】由于函数()21xy a =-(x 是自变量)是指数函数，则210a ->且211a -≠，解得12a >且1a ≠.故选：C.【题组二定义域和值域】1．(2020·沙坪坝.重庆八中高一期末)已知实数0a >且1a ≠,若函数6,2(),2x x x f x a x -≤⎧=⎨>⎩的值域为[4,)+∞,则a 的取值范围是()A ．()1,2B ．(2,)+∞C ．(0,1)(1,2]⋃D ．[2,)+∞【答案】D【解析】实数0a >且1a ≠,若函数6,2(),2xx x f x a x -≤⎧=⎨>⎩的值域为[4,)+∞,当01a <<时,当2x >时,()f x 的值域为()20,a ,与值域为[4,)+∞矛盾,所以01a <<不成立当1a >时,对于函数()6f x x =-,2x ≤,函数的值域为[4,)+∞.所以只需当2x >时值域为[4,)+∞的子集即可.即24a ≥,解得2a ≥(舍去2a ≤-)综上可知a 的取值范围为[2,)+∞故选:D2．(2020·上海市新中高级中学高一月考)函数65()1f x x =-__________.【答案】(2,1)-【解析】函数()1f x x =+-的自变量x 满足：2650140210xx x x ⎧--≥⎪⎪⎛⎫->⎨⎪⎝⎭⎪⎪-≠⎩，解得6121x x x -≤≤⎧⎪>-⎨⎪≠⎩即21x -<<.故答案为：(2,1)-3．函数()f x =______________．【答案】[1,)+∞【解析】换元20x t =>，得出220t t --≥，解得1t ≤-(舍去)或2t ≥，即22x ≥，解得1x ≥.因此，函数()y f x =的定义域为[)1,+∞，故答案为[)1,+∞.4．(2020·浙江金华.高一期末)已知函数()321,0331,0x xx x f x x ⎧+≥=⎨-+<⎩，则()f x 的最小值是_____________.【答案】34【解析】当0x ≥时，函数31y x =+单调递增，此时()min 01f f ==；当0x <时，设()30,1xt =∈，()2213()124f xg t t t t ⎛⎫==-+=-+ ⎪⎝⎭，此时，min 1324f g ⎛⎫==⎪⎝⎭．综上可知，函数()f x 的最小值是34．故答案为：34．5．(2020·山东滨州.高三三模)已知函数()()()221,412x x x f x h x a a x -+==->-．若[)123,,x x ∀∈+∞∃∈[)3,+∞，使得()()12f x h x =，则实数a 的最大值为__________．【答案】2【解析】由题意可知，函数()f x 在[)3,+∞的值域是函数()h x 在[)3,+∞上值域的子集，()()()2222212122x x x x f x x x -+-+-+==--，3x ≥122242x x =-++≥+=-，等号成立的条件是122x x -=-，即3x =，成立，即函数()f x 在[)3,+∞的值域是[)4,+∞()()41x h x a a =->，是增函数，当[)3,x ∈+∞时，函数()h x 的值域是)34,a ⎡-+∞⎣，所以344a -≤，解得：12a <≤，所以实数a 的最大值是2.故答案为：26．(2020·吉林南关.长春市实验中学高二期中(文))已知函数21(),()()2xf x x mg x =+=，若“对任意[]11,3x ∈-，存在[]20,2x ∈，使12()()f x g x ≥”是真命题，则实数m 的取值范围是__________.【答案】1,4⎡⎫+∞⎪⎢⎣⎭【解析】因为“对任意[]11,3x ∈-，存在[]20,2x ∈，使12()()f x g x ≥”是真命题，所以只需min min ()()f x g x ≥，因为函数2()f x x m =+在[]1,0-上单调递减，在[]0,3上单调递增，所以min ()(0)f x f m ==，因为函数1()()2x g x =在[]0,2上单调递减，所以min 1()(2)4g x g ==所以14m ≥，故答案为：1,4⎡⎫+∞⎪⎢⎣⎭7．(2020·贵州高三其他(理))函数12()(0)12xx f x x +=>+的值域为____________.【答案】11,32⎛⎫⎪⎝⎭【解析】121()(0)1222x x xf x x +-==>++，0x >，0x ∴-<，021x -<<，所以2223x -<+<，则11()32f x <<.故答案为：11,32⎛⎫⎪⎝⎭8．(2020·上海高三专题练习)函数22811(31)3x x y x --+⎛⎫=-≤≤ ⎪⎝⎭的值域是_________.【答案】991,33⎡⎤⎛⎫⎢⎥⎪⎝⎭⎢⎥⎣⎦【解析】设22281229t x x x =--+=-++（），31x -≤≤ ，∴当2x =-时，t 有最大值是9；当1x =时，t 有最小值是-9，99t ∴-≤≤，由函数1()3x y =在定义域上是减函数，∴原函数的值域是99[33]-，．故答案为99[33]-，．9．(2020·陕西新城.西安中学高二期末(文))若函数()24113ax x f x -+⎛⎫= ⎪⎝⎭有最大值3，则实数a 的值为__________.【答案】2【解析】令241t ax x =-+，则13t y ⎛⎫= ⎪⎝⎭，由题意13ty ⎛⎫= ⎪⎝⎭有最大值3，则241t ax x =-+有最小值1-，所以0a >且24(4)14a a--=-，解得2a =.故答案为：210．(2020·上海高一课时练习)函数112142xxy a ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭在[1,)x ∈-+∞的最大值为1-，那么a =________.【答案】3-【解析】令1()(0,2]2xt =∈，则221y t t a =++-，对称轴为12t =-，221y t t a =++-在(0,2]t ∈单调递增，所以2max 22211y a =++-=-，解得3a =-.故答案为：3-11．(2020·上海黄浦.高三二模)已知函数()(0,1)x f x a b a a =+>≠的定义域和值域都是[2,0]-，则(1)f -=________．3-【解析】当1a >时，函数()(0,1)x f x a b a a =+>≠在[2,0]-上单调递增，所以()()2200f f ⎧-=-⎪⎨=⎪⎩，即()()22200f a b f a b -⎧-=+=-⎪⎨=+=⎪⎩，此时方程组无解.当01a <<时，函数()(0,1)x f x a b a a =+>≠在[2,0]-上单调递减，所以()()2002f f ⎧-=⎪⎨=-⎪⎩，即()()22002f a b f a b -⎧-=+=⎪⎨=+=-⎪⎩，解得：333a b ⎧=⎪⎨⎪=-⎩所以()33xf x ⎛=- ⎝⎭，则(1)3f -=-3-.【题组三指数函数性质】1．(2019·宁夏贺兰县景博中学高一月考)函数22311()2x x f x -+⎛⎫=⎪⎝⎭的增区间是________________.【答案】3,4⎛⎤-∞ ⎥⎝⎦【解析】函数()f x 的定义域为R ，令2231t x x =-+，则12ty ⎛⎫= ⎪⎝⎭，因为12ty ⎛⎫= ⎪⎝⎭在R 上单调递减，而2231231248t x x x ⎛⎫=-+=-- ⎪⎝⎭在3,4⎛⎤-∞ ⎥⎝⎦上单调递减，所以函数()f x 的增区间为3,4⎛⎤-∞ ⎥⎝⎦.故答案为：3,4⎛⎤-∞ ⎥⎝⎦2．(2020·四川泸县五中高一月考)若函数()22313x mx f x +-⎛⎫= ⎪⎝⎭在区间()1,1-上单调递减，则实数m 的取值范围是__________．【答案】[)4,+∞【解析】本题等价于223y x mx =+-在()1,1-上单调递增，对称轴4m x =-，所以14m-≤-，得4m ≥．即实数m 的取值范围是[)4,+∞．3．(2020·黑龙江萨尔图.大庆实验中学高二期末(文))已知0.60.4a =，0.20.4b =，0.22c =，则a ，b ，c 的大小关系是______．【答案】c b a>>【解析】∵指数函数()0.4xf x =是单调减函数，()()0.6,0.4a f b f ==，∴()01a b f <<=,()2x g x =是单调增函数，∴()()0.201c g g =>=，∴c b a >>，故答案为：c b a >>.4．(2019·贵州高二学业考试)已知21x m ≤+在[0,)x ∈+∞上恒成立，则实数m 的最大值是__________.【答案】2【解析】由指数函数的性质，可得2x y =在[0,)+∞为单调递增函数，所以21x ≥，可得212x +≥，即21x +最小值为2，又由21x m ≤+在[0,)x ∈+∞上恒成立，所以2m ≤，即实数m 的最大值2.故答案为：2.5．(2020·上海高一课时练习)求下列函数的定义域和值域，并写出其单调区间.(1)()f x =(2)121()3xf x -⎛⎫= ⎪⎝⎭；(3)223()2xx f x --+=；(4)121()1,[2,3]933xxf x x ⎛⎫⎛⎫=-⋅+∈- ⎪ ⎪⎝⎭⎝⎭.【答案】(1)定义域：(,2]-∞-，值域：[0,1)，减区间：(,2]-∞-；(2)定义域：(,2)(2,)-∞⋃+∞，值域：(0,1)(1,)⋃+∞，减区间：(,2)-∞和(2,)+∞；(3)定义域：R ，值域：(0,16]，增区间：(,1]-∞-，减区间：[1,)-+∞；(4)值域8,769⎡⎤⎢⎥⎣⎦，减区间：[2,1]-，增区间：[1,3]【解析】(1)由2130x +-≥得2x -≤，所以定义域为(,2]-∞-，又230x +>，所以20131x +≤-<，01y ≤<，所以值域中[0,1)，213x u +=-在R 上是减函数，所以()f x =的减区间是(,2]-∞-；(2)由20x -≠得2x ≠，所以定义域是(,2)(2,)-∞⋃+∞，又102x ≠-，所以值域是(0,1)(1,)⋃+∞，12u x=-在(,2)-∞和(2,)+∞上都是增函数，所以121()3xf x -⎛⎫= ⎪⎝⎭的减区间是(,2)-∞和(2,)+∞；(3)定义域是R ，又2223(1)44x x x --+=-++≤，所以值域中(0,16]，2(1)4u x =-++在(,1]-∞-上递增，在[1,)-+∞上递减，所以223()2xx f x --+=的增区间(,1]-∞-，减区间是[1,)-+∞；(4)定义域是[2,3]-，令1()3xt =，由[2,3]x ∈-，所以1[,9]27t ∈，222181()339y t t t =-+=-+，所以876]9y ≤≤，值域8,769⎡⎤⎢⎥⎣⎦，又222181(339y t t t =-+=-+在11[,273上递减，在1[,9]3上递增，而1(3x t =是减函数，所以121()1,[2,3]933xxf x x ⎛⎫⎛⎫=-⋅+∈- ⎪ ⎪⎝⎭⎝⎭的减区间是[2,1]-，增区间[1,3]．6．(2019·江西省遂川中学)若函数2121x xa ay ⋅--=-为奇函数．(1)求a 的值；(2)求函数的定义域；(3)求函数的值域．【答案】(1)12-；(2)(,0)(0,)-∞+∞ ；(3)11(,(,)22-∞-+∞ ．【解析】(1)记21()21x xa af x ⋅--=-，∵()f x 是奇函数，∴2121()()2121x x x x a a a a f x f x --⋅--⋅---+=+--(1)2211221x x x xa a a a -+⋅⋅--=+--21a =+0=，∴12a =-；(2)210x -≠，0x ≠，∴定义域为(,0)(0,)-∞+∞ ；(3)由(1)1211211()(1)221221221x x x xf x +=-⋅=-+=-----，∵0x ≠，∴021x <<或21x >，∴1121x <--或1021x >-，∴1112212x -->-或1112212x--<--．∴值域为11(,)(,)22-∞-+∞ ．【题组四定点】1．(2020·全国高一课时练习)已知函数1()4x f x a +=+的图象经过定点P ，则点P 的坐标是()A ．(－1，5)B ．(－1，4)C ．(0，4)D ．(4，0)【答案】A【解析】当10x +=，即1x =-时，011x a a +==，为常数，此时()415f x =+=，即点P 的坐标为(－1，5).故选：A.2．(2020·吉化第一高级中学校高二期末(理))函数1()21(0x f x a a -=+>且1)a ≠的图象过定点，这个点的坐标为______【答案】(1,3)【解析】令10x -=，1,3x y ==，所以函数()f x 过定点(1,3).故答案为:(1,3).3．(2020·公主岭市第一中学校高一期中(理))函数()110,1x y a a a -=+>≠的图象恒过定点P ，则点P 的坐标为________.【答案】()1,2【解析】由指数函数()0,1xy aa a =>≠过定点()0,1且x y a =图像向右平移1个单位，向上移动1个单位得到11x y a -=+图像，所以函数11x y a -=+过定点()1,2故答案为：()1,24．(2019·全国高三其他(文))函数2019()2020x f x a -=+(0a >且1a ≠)的图象过定点A ，则点A 的坐标为______.【答案】()2019,2021【解析】由20190x -=得=2019x ,此时0(2019)2020=2021f a =+,即函数()f x 过定点()2019,2021A ，故答案为:()2019,2021.【题组五图像】1．(2020·浙江高一课时练习)二次函数24(2)y x x x =-->-与指数函数12xy ⎛⎫= ⎪⎝⎭的图像的交点个数为()A ．3B ．2C ．1D ．0【答案】C【解析】二次函数224(2)4(2)y x x x x =--=-++>-，且1x =-时，3y =；2x =-时，4y =.指数函数12xy ⎛⎫= ⎪⎝⎭,当1x =-时，2y =；2x =-时，4y =.两个函数()2,-+∞上均单调递减，在坐标系中画出24(2)y x x x =-->-与12xy ⎛⎫= ⎪⎝⎭的图象，如图所示，由图可得，两个函数图像的交点个数为1.故选：C.2．(2020·河南林州一中高二月考(理))函数()112x f x +⎛⎫= ⎪⎝⎭的图象大致为()A ．B ．C ．D ．【答案】B【解析】作出函数1(012220x x x x y x ⎧≥⎪==⎨⎪<⎩的图象，如下图所示，将12x y =的图象向左平移1个单位得到()112x f x +⎛⎫= ⎪⎝⎭图象.故选：B3．(2019·辛集市第二中学高二期中)已知a ＞1，则函数y =a x 与y =(a -1)x 2在同一坐标系中的图象可能是()A ．B．C．D．【答案】A【解析】∵a ＞1，∴函数y =a x 为增函数，函数y =(a -1)x 2在(-∞，0)上为减函数，在(0，+∞)上为增函数．故选：A ．4．(2020·上海高三专题练习)已知01,1a b <<<-,则函数x y a b =+的图像必定不经过()A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A【解析】此题考查指数函数的图像的性质和指数函数的上下平移；有已知得到：此指数函数是减函数，分布在第一，二象限，渐近线是x 轴，即0y =；x y a b =+(1b <-)是由指数函数向下平移大于1个单位得到的，即原来指数函数所过的定点(0,1)向下平移到原点的下方了，所以图像不经过第一象限，所以选A ，如下图所示：5．(2020·四川成都七中高一月考)设0a >且1,a ≠则函数x y a b =+与y b ax =-在同一坐标系中的图象可能是()A ．B ．C ．D ．【答案】C【解析】对A ，y b ax =-中的10,01b a -<<<<，x y a b =+中的1a >，不能统一，错误；对B ，y b ax =-中的0,1a b ><-，x y a b =+中的0,10a b >-<<，不能统一，错误；对C ，y b ax =-中的10,01b a -<<<<，x y a b =+中的10,01b a -<<<<，正确；对D ，y b ax =-中的1b <-，x y a b =+中的10b -<<，不能统一，错误；故选：C.6．(2019·安徽省肥东县第二中学高一期中)已知在同一坐标系下，指数函数x y a =和x y b =的图象如图，则下列关系中正确的是()A ．1a b <<B ．1b a <<C ．1a b >>D ．1b a >>【答案】C 【解析】很显然a ，b 均大于1；x y a =与1x =的交点在x y b =与1x =的交点上方，故b a <，综上所述:1a b >>.故选:C.7．(2019·伊宁市第八中学高一期中)若函数()21()x f x b b R =+-∈的图象不经过第二象限，则有()A ．1b B ．1b C ．0b D ．0b 【答案】D 【解析】因为2x y =，当0x <时，()01y ∈，，所以函数()21()x f x b b R =+-∈的图象不经过第二象限，则有11b -≤-，解得0b ≤，故选：D .8．(2019·安徽高一月考)若函数x y a b =-，(0a >，且1a ≠)的图像经过第一，第三和第四象限，则一定有()A ．01a <<且1b >B ．1a >且1b >C ．01a <<且1b <D ．1a >且1b <【答案】B【解析】根据指数函数的图象和性质可知，要使函数y ＝a x ﹣(b +1)(a ＞0且a ≠1)的图象经过第一、三、四象限，则函数为增函数，∴a ＞1，且f (0)＜0，即f (0)＝1﹣b ＜0，解得b ＞1，故选：B ．9．(2019·河南中原.郑州一中高一开学考试)若函数1x y a b =+-(0a >且1a ≠)的图象经过第二、三、四象限，则一定有()．A ．01a <<且0b >B ．1a >且0b >C ．01a <<且0b <D ．1a >且0b <【答案】C【解析】1x y a b =+-，经过二、三、四象限，则其图像应如图所示：所以01a <<，010a b +-<，即0b <，故选B.10．(2020·全国高一课时练习)函数()218x f x +⎛⎫= ⎪⎝⎭的部分图象大致为()A ．B ．C ．D ．【答案】B【解析】由题意得，()f x 的定义域为R ，排除C,D ；当2x ≥-时，()218x f x +⎛⎫= ⎪⎝⎭，∵1018<<，∴()f x 在[)2,-+∞上单调递减，排除A ，故选B.【题组六综合运用】1．(2020·安徽贵池池州一中高二期中(文))已知函数()423x xf x a =+⋅+，a R ∈.(1)当4a =-时，[]0,2x ∈，求函数()f x 的值域；(2)若对于任意的()0,x ∈+∞，()0f x >恒成立，求实数a 的取值范围．【答案】(1)[]1,3-；(2)a >-【解析】(1)当4a =-时，令2x t =，由[]0,2x ∈，得[]1,4t ∈，()224321y t t t =-+=--，当2t =时，min 1y =-；当4t =时，max 3y =．∴函数()f x 的值域为[]1,3-；(2)设2x t =，则1t >，()0f x >在()0,∞+对任意的实数x 恒成立，等价于230t at ++>在()1,t ∈+∞上恒成立，∴3a t t ⎛⎫>-+ ⎪⎝⎭在()1,+∞上恒成立，∴max3a t t ⎡⎤⎛⎫>-+ ⎪⎢⎥⎝⎭⎣⎦，设()3g t t t ⎛⎫=-+⎪⎝⎭，1t >，函数()g t在(上单调递增，在)+∞上单调递减，∴()max g t g ==-∴a >-2．(2020·河北承德高一期末)已知函数1()422x x f x k k +=-+⋅-，[0,1]x ∈.(1)当1k =-时，求()f x 的值域；(2)若()f x 的最大值为34-，求实数k 的值.【答案】(1)[6,1]--(2)32【解析】(1)当1k =-时，1()422x x f x +=--+在[0,1]上单调递减，故max ()(0)1f x f ==-，min ()(1)6f x f ==-，所以()f x 的值域为[6,1]--.(2)()2()2222x x f x k k =-+⋅-，令2x t =，[1,2]t ∈则原函数可化为2()22g t t kt k =-+-，其图象的对称轴为t k =.①当1k 时，()g t 在[1,2]上单调递减，所以max 3()(1)1224g t g k k ==-+-=-，无解；②当12k <<时，2max 3()()24g x g k k k ==-=-，即23204k k -+=，解得32k =；③当2k ≥时，()g t 在[1,2]上单调递增，所以max 3()(2)424g x g k ==-+=-，解得138k =，不合题意，舍去.综上，k 的值为32.3．(2019·甘肃城关兰州五十一中高一期中)已知函数2431()3ax x f x -+⎛⎫= ⎪⎝⎭，(1)若1a =-，求()f x 的单调区间；(2)若()f x 有最大值3，求a 的值.(3)若()f x 的值域是(0,)+∞，求a 的取值范围.【答案】(1)函数f (x )的递增区间是(−2,+∞),递减区间是(−∞,−2)；(2)a =1；(3){0}【解析】(1)当a =−1时,2431()3x x f x --+⎛⎫= ⎪⎝⎭，令()243g x x x =--+，由于g (x )在(−∞,−2)上单调递增,在(−2,+∞)上单调递减，而13ty ⎛⎫= ⎪⎝⎭在R 上单调递减，所以f (x )在(−∞,−2)上单调递减,在(−2,+∞)上单调递增，即函数f (x )的递增区间是(−2,+∞),递减区间是(−∞,−2).(2)令()243h x ax x =-+,()13h x y ⎛⎫= ⎪⎝⎭,由于f (x )有最大值3，所以h (x )应有最小值−1，因此12164a a-=−1，解得a =1.即当f (x )有最大值3时，a 的值等于1.(3)由指数函数的性质知，要使y =h (x )的值域为(0,+∞).应使()243h x ax x =-+的值域为R ，因此只能有a =0.因为若a ≠0,则h (x )为二次函数，其值域不可能为R .故a 的取值范围是{0}.4．(2019·浙江高二学业考试)已知函数()22x x f x k -=+⋅，k ∈R ．(1)若函数()f x 为奇函数，求实数k 的值．(2)若对任意的[0,)x ∈+∞都有()2x f x ->成立，求实数k 的取值范围．【答案】(I)(II)【解析】(1)已知函数为奇函数，由()(),R f x f x x -=-∈，求得k 的值；(2)恒成立问题通常是求最值，将原不等式整理为212x k -<对0x ≥恒成立，进而求22x y =在[0,)+∞上的最小值，得到结果.试题解析：(1)因为()22,x x f x k k R -=+⋅∈是奇函数，所以()(),R f x f x x -=-∈，即22(22),x x x x k k --+⋅=-+⋅所以2(1)(1)20x k k +++⋅=对一切R x ∈恒成立，所以1k =-.(2)因为[)0,x ∈+∞，均有()2,x f x ->即222x x x k --+⋅>成立，所以212x k -<对0x ≥恒成立，所以2min 1(2)x k -<,因为22x y =在[)0,+∞上单调递增，所以2min (2)1x =，所以0k >.。
指数函数复习专题(含详细解析)
第讲指数函数时间：年月日刘老师学生签名：一、兴趣导入二、学前测试1．在区间上为增函数的是（ B ）A．B．C ．D．2．函数是单调函数时，的取值范围（ A ）A．B． C ．D．3．如果偶函数在具有最大值，那么该函数在有（ A ）A．最大值B ．最小值 C ．没有最大值D．没有最小值4．函数，是（ B ）A．偶函数B ．奇函数C．不具有奇偶函数D．与有关5．函数在和都是增函数，若，且那么（ D ）A ．B．C．D．无法确定6．函数在区间是增函数，则的递增区间是（ B ）A．B．C．D．12三、方法培养☆专题1：指数函数的定义一般地，函数xy a =（a ＞0且a ≠1）叫做指数函数，其中x 是自变量，函数的定义域为R .例1指出下列函数那些是指数函数：（１）4xy =（２）xy 4=（３）4xy -= （４）)4(-=xy （５）π=y x（6）xy 24=（7）xxy =（８）)1,21(()12≠>=-a a y a x解析：利用指数函数的定义解决这类问题。
解：（１），（５），（８）为指数函数变式练习1 1函数2(33)xy a a a=-+⋅是指数函数，则有（ ）Ａ．ａ＝１或ａ＝２ Ｂ．ａ＝１ Ｃ．ａ＝２ Ｄ．ａ＞０且1≠a 答案:C 2. 计算:105432)(0625.0833416--+++π; 解：(1)105432)(0625.0833416--+++π =(425)21+(827)31+(0.062 5)41+1-21=(25)2×21+(23)313⨯+(0.5)414⨯+21 =25+23+0.5+21 =5;☆专题2：指数函数的图像与性质一般地,指数函数y=a x在底数a ＞1及0＜a ＜1这两种情况下的图象和性质如下表所示：a ＞10＜a ＜1图象3性质①定义域：R ②值域：（0,+∞）③过点（0,1）,即x=0时y=1④在R 上是增函数,当x ＜0时,0＜y ＜1;当x ＞0时,y ＞1④在R 上是减函数,当x ＜0时,y ＞1;当x ＞0时,0＜y ＜1在同一坐标系中作出y=2x和y=(21)x两个函数的图象,如图2-1-2-3.经过仔细研究发现,它们的图象关于y 轴对称.图2-1-2-3例3比较下列各题中的两个值的大小:（1）1.72.5与1.73; (2)0.8-0.1与0.8-0.2; (3)1.70.3与0.93.1. 利用函数单调性,①1.72.5与1.73的底数是1.7,它们可以看成函数y=1.7x,当x=2.5和3时的函数值；因为1.7>1,所以函数y=1.7x 在R 上是增函数,而2.5<3,所以1.72.5<1.73；②0.8-0.1与0.8-0.2的底数是0.8,它们可以看成函数y=0.8x,当x=-0.1和-0.2时的函数值；因为0<0.8<1,所以函数y=0.8x 在R 上是减函数,而-0.1>-0.2,所以0.8-0.1<0.8-0.2；③因为1.70.3>1,0.93.1<1,所以1.70.3>0.93.1..变式练习31.已知a=0.80.7,b=0.80.9,c=1.20.8,按大小顺序排列a,b,c.答案：b<a<c(a 、b 可利用指数函数的性质比较,而c 是大于1的).2. 若指数函数y=（2a －1）x是减函数,则a 的范围是多少？ 答案：21＜a ＜1. 3. 设m<1,f(x)=244+x x,若0<a<1,试求:(1)f(a)+f(1-a)的值; (2))10011000()10013()10012()10011(f f f f ++++ 的值. 活动：学生思考,观察,教师提示学生注意式子的特点,做这种题目,一定要有预见性,即第(2)问要用到第(1)问的结果,联系函数的知识解决.解：(1)f(a)+f(1-a)=24424411+++--a aa a=24444244+++a a a a=a a a 4244244•+++4=aa a 422244+++=2424++a a =1. (2))10011000()10013()10012()10011(f f f f ++++ =［)]1001501()1001500([)]1001999()10002([)]10011000()10001([f f f f f f ++++++=500×1=500.☆专题3：求函数的定义域与值域 例4求下列函数的定义域 （１）241-=x y （2）15-=x y解析：求定义域注意分母不为零，偶次根式里面为非负数。
指数函数常考题型归纳含详解
A． a b 1 c b B． b a 1 d c C．1 a b c d D． a b 1 d c 3、已知函数 f (x) (x a)(x b) （其中 a b) 的图象如图所示，则函数 g(x) ax b 的图象是（ ）
A．
B．
C．
D．
4、画出下列函数的图像
D．
0,
1 2
A． ab aa
B． ba bb
C． ab bb
D． ab ba
2、设 a ， b ， c R ，且 a b ，则（ ）
A． a2 b2
B．
1 2
a
1 2
b
C． a3 b3
D． 1 1 ab
3、已知集合 A {x | x2 3x 2 0}, B {x |1 2 x 4} ，则 A B （ ）
题型九：复合函数的单调性
C． f x x 1
x
1、函数
y
1 2
82 xx2
的单调递增区间为_________．
D． f x 3 x
2、求下列函数的定义域和值域，并写出其单调区间.
（1） f ( x) 1 3x2 ；
1
（2）
f
(x)
1 2x 3
；
（3） f ( x) 2x22x3 ；
A．{x |1 x 2} B．{x |1 x 2} C．{x |1 x 2} D．{x | 0 x 2}
4、已知 a 0.20.3 ， b 0.30.3 ， c 0.20.2 ，则（ ）
A． a b c
B． b a c
题型八：指数函数的单调性
C． b c a
D． a c b
A．函数 f x 在 R 上既是奇函数，也是增函数 B．函数 f x 在 R 上既是奇函数，也是减函数
高考数学复习指数与指数函数-重难点题型精讲(解析)
专题2.11 指数与指数函数-重难点题型精讲1．分数指数幂 （1)m na ＝n，a m (a >0，m ,n ∈N ＊，且n 〉1);m na＝1m na（a >0，m ，n ∈N ＊,且n 〉1);0的正分数指数幂等于0；0的负分数指数幂没有意义．(2）有理数指数幂的运算性质：a r a s ＝a r ＋s ，（a r )s ＝a rs ，(ab ）r ＝a r b r ，其中a 〉0，b >0，r ,s ∈Q . 2．指数函数的图象与性质（1）R 【思考】1。
如图所示是指数函数(1）y ＝a x ，(2）y ＝b x ,（3)y ＝c x ，(4）y ＝d x 的图象，则a ，b ，c ，d 与1之间的大小关系为________．提示 c 〉d >1〉a 〉b >02．结合指数函数y ＝a x (a >0，a ≠1）的图象和性质说明a x >1(a >0,a ≠1）的解集是否与a 的取值有关． 提示 当a >1时，a x >1的解集为｛x |x >0}；当0<a <1时，a x >1的解集为｛x ｜x <0｝．【题型1 指数幂的运算】【例1】(2020秋•荔湾区校级期中）化简下列各式．（1)（√23⋅√3）6﹣4•（1649）−12−√24•80.25﹣（2020）0；（2）√a 3b 2⋅√ab 23(a 14b 12)4⋅√a3(a ＞0，b ＞0）．【解题思路】利用有理数指数幂的运算性质求解． 【解答过程】解：（1）原式=(213×312)6−4×(47)2×(−12)−214×814−1 ＝4×27﹣7−(2×8)14−1 ＝108﹣7﹣2﹣1 ＝98． （2)原式=a 32⋅b 22⋅a 16⋅b 26a⋅b2⋅a −13⋅b 13=a 53⋅b 43a 23⋅b 73＝ab ﹣1．【变式1—1】（2020秋•济宁期中）（1）计算：（94）12−（﹣9.6）0﹣（278）−23+(23)−2;（2)已知a 12+a−12=3，求a 2+a −2+1a+a −1+2的值．【解题思路】（1）根据指数幂的运算法则即可求出；(2)根据完全平方公式即可求出． 【解答过程】解：（1）原式=32−1﹣（32）3×(−23)+94=32−1−49+94=8336， （2)∵a 12+a −12=3，∴a +a ﹣1＝（a 12+a −12）2﹣2＝7，∴a 2+a ﹣2＝(a +a ﹣1）2﹣2＝47，∴原式=47+17+2=489=163．【变式1-2】(2020秋•新泰市校级期中）化简求值：（请写出化简步骤过程）①0.064−13−(−59)0+[(−2)3]−43+16−0.75+0.0112；②1.5−13×(−76)0+814×√24+(√23×√3)6−√(−23)23．【解题思路】把根式化为分数指数幂,根据幂的运算法则计算即可． 【解答过程】解：①0.064−13−(−59)0+[(−2)3]−43+16−0.75+0.0112 =(0.43)−13−1+(−2)3×(−43)+（24）﹣0。
《指数函数》经典讲义(完整版)
指数函数讲义经典整理（含答案）一、同步知识梳理知识点1：指数函数函数(01)xy a a a =>≠且叫做指数函数，其中x 是自变量，函数的定义域是R知识点2：指数函数的图像和性质知识点3：指数函数的底数与图像的关系指数函数在同一直角坐标系中的图像的相对位置与底数大小的关系 如图所示，则01c d a b <<<<<，在y 轴右侧，图像从下到上相应的底数也由小变大， 在y 轴左侧，图像从上到下相应的底数也由小变大 即无论在y 轴左侧还是右侧，底数按逆时针方向变大在第一象限内，“底大图高”知识点4：指数式、指数函数的理解① 分数指数幂与根式或以互化，通常利用分数指数幂进行根式的运算② 根式的运算、变形、求值、化简及等式证明在数学中占有重要的地位，是研究方程、不等式和函数的基础，应引起重视③ 在有关根式、分数指数幂的变形、求值过程中，要注意运用方程的观点处理问题，通过解方程或方程组来求值④ 在理解指数函数的概念时，应抓住定义的“形式”，像1223,,21xx y y x y y =⋅===- 等函数均不符合形式()01x y a a a =>≠且，因此，它们都不是指数函数⑤ 画指数函数x y a =的图像，应抓住三个关键点：()()11,,0,1,1,a a ⎛⎫- ⎪⎝⎭二、同步题型分析题型1：指数函数的定义、解析式、定义域和值域例1：已知函数，且． （1）求m 的值；（2）判定f （x ）的奇偶性；（3）判断f （x ）在（0，+∞）上的单调性，并给予证明．考点：指数函数的定义、解析式、定义域和值域；函数单调性的判断与证明． 专题： 计算题． 分析：（1）欲求m 的值，只须根据f （4）=的值，当x=4时代入f （x ）解一个指数方程即可；（2）求出函数的定义域x|x≠0}，利用奇偶性的定义判断f （x ）与f （﹣x ）的关系，即可得到答案； （3）利用单调性的定义证明即可．任取0＜x1＜x2，只要证明f （x1）＞f （x2），即可． 解答： 解：（1）因为，所以，所以m=1．（2）因为f （x ）的定义域为{x|x≠0}，又，所以f （x ）是奇函数． （3）任取x1＞x2＞0，则，因为x1＞x2＞0，所以，所以f （x1）＞f （x2），所以f（x）在（0，+∞）上为单调增函数．点评：本题主要考查了函数单调性的判断、函数奇偶性的判断，与证明及指数方程的解法．在判定函数奇偶性时，一定注意函数的定义域关于原点对称，属于基础题．例2：已知函数，（1）讨论函数的奇偶性；（2）证明：f（x）＞0．考点：指数函数的定义、解析式、定义域和值域；函数奇偶性的判断；函数奇偶性的性质．专题：计算题．分析：（1）由2x﹣1≠0解得义域为{x|x≠0}，关于原点对称．f（﹣x）=（）（﹣x）=（）x=f（x），故该函数为偶函数．（2）任取x∈{x|x≠0}，当x＞0时，2x＞20=1且x＞0，故，从而．当x＜0时，﹣x＞0，故f（﹣x）＞0，由函数为偶函数，能证明f（x）＞0在定义域上恒成立．解答：解：（1）该函数为偶函数．由2x﹣1≠0解得x≠0即义域为{x|x≠0}关于原点对称…（2分）f（﹣x）=（）（﹣x）=﹣（+）x=（）x=（）x=（）x=f（x）（6分）故该函数为偶函数．…（7分）（2）证明：任取x∈{x|x≠0}当x＞0时，2x＞20=1且x＞0，∴2x﹣1＞0，故从而…（11分）当x＜0时，﹣x＞0，∴f（﹣x）＞0，…（12分）又因为函数为偶函数，∴f（x）=f（﹣x）＞0，…（13分）∴f（x）＞0在定义域上恒成立．…（14分）点评：本题考查函数的奇偶性的判断和证明f（x）＞0．解题时要认真审题，注意指数函数性质的灵活运用．例3：已知函数y=ax（a＞0且a≠1）在[1，2]上的最大值与最小值之和为20，记．（1）求a的值；（2）求f（x）+f（1﹣x）的值；（3）求的值．考点：指数函数的定义、解析式、定义域和值域．专题：综合题；函数的性质及应用．分析：（1）由y=ax单调得a+a2=20，由此可求a；（2）写出f（x），代入运算可得；（3）借助（2）问结论分n为奇数、偶数讨论可求；解答：解：（1）∵函数y=ax（a＞0且a≠1）在[1，2]上的最大值与最小值之和为20，且y=ax单调，∴a+a2=20，得a=4，或a=﹣5（舍去）；（2）由（1）知，∴====1；（3）由（2）知f（x）+f（1﹣x）=1，得n为奇数时，=×1=；n为偶数时，=+f（）==；综上，=．点评：本题考查指数函数的单调性、最值等知识，属中档题．题型2：指数函数的图像变换．例1：已知函数y=|2x﹣2|（1）作出其图象；（2）由图象指出函数的单调区间；（3）由图象指出当x取何值时，函数有最值，并求出最值．考点：指数函数的图像变换．专题：综合题；函数的性质及应用．分析：（1）函数y=|2x﹣2|图象是由y=2x的图象向下平移2个单位，再将x轴下方的部分翻着到x轴上方得到．（2）结合函数的图象，可得函数的减区间和增区间．（3）数形结合可得，当x=1时，ymiin=0．解答：解：（1）函数y=|2x﹣2|图象是由y=2x的图象向下平移2个单位，再将x轴下方的部分翻着到x轴上方得到，如图所示：（2）结合函数的图象，可得函数的减区间为（﹣∞，1]，增区间为（1，+∞）．（3）数形结合可得，当x=1时，ymiin=0．点评：本题主要考查指数函数的图象和性质综合，体现了数形结合的数学思想，属于中档题．题型3：指数函数单调性例1：已知函数f（x）=a•2x+b•3x，其中常数a，b满足a•b≠0（1）若a•b＞0，判断函数f（x）的单调性；（2）若a=﹣3b，求f（x+1）＞f（x）时的x的取值范围．考点：指数函数的单调性与特殊点；函数单调性的判断与证明；函数单调性的性质．专题：函数的性质及应用．分析：（1）分a＞0，b＞0和a＜0，b＜0两种情况讨论，运用单调性的定义可作出判断；（2）当a=﹣3b时，f（x）=﹣3b•2x+b•3x=b（3x﹣3•2x），分b＞0，b＜0两种情况进行讨论，整理可得指数不等式解出即可；解答：解：（1）当a＞0，b＞0时，任意x1，x2∈R，且x1＜x2，则f（x1）﹣f（x2）=a（﹣）+b（﹣），∵＜，＜，a＞0，b＞0，∴a（﹣）＜0，b（﹣）＜0，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），故函数f（x）在R上是增函数；当a＜0，b＜0时，同理，可判断函数f（x）在R上是减函数；（2）当a=﹣3b时，f（x）=﹣3b•2x+b•3x=b（3x﹣3•2x），则f（x+1）＞f（x）即化为b（3x+1﹣3•2x+1）＞b（3x﹣3•2x），若b＞0，则有3x+1﹣3•2x+1＞3x﹣3•2x，整理得，解得x＞1；若b＜0，则有3x+1﹣3•2x+1＜3x﹣3•2x，整理得，解得x＜1；故b＞0时，x的范围是x＞1；当b＜0时，x的范围是x＜1．点评：本题考查函数单调性的判断、指数函数的单调性的应用，考查分类讨论思想，属基础题．例2：已知定义在（﹣1，1）上的奇函数f（x）．在x∈（﹣1，0）时，f（x）=2x+2﹣x．（1）试求f（x）的表达式；（2）用定义证明f（x）在（﹣1，0）上是减函数；（3）若对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立，求实数t的取值范围．考点：指数函数综合题；奇偶性与单调性的综合．专题：计算题；函数的性质及应用．分析：（1）由f（x）是定义在（﹣1，1）上的奇函数可得f（0）=0，x∈（0，1）时，f（x）=﹣f（﹣x）=﹣（2x+2﹣x）；从而写出f（x）的表达式；（2）取值，作差，化简，判号，下结论五步；（3）对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立转化为对于x∈（0，1）上的每一个值，不等式t＞﹣恒成立，从而可得．解答：解：（1）∵f（x）是定义在（﹣1，1）上的奇函数，∴f（0）=0，设∈（0，1），则﹣x∈（﹣1，0），则f（x）=﹣f（﹣x）=﹣（2x+2﹣x），故f（x）=；（2）任取x1，x2∈（﹣1，0），且x1＜x2，则f（x1）﹣f（x2）=+﹣（+）=，∵x1＜x2＜0，∴﹣＜0，0＜＜1，故f（x1）﹣f（x2）＞0，故f（x）在（﹣1，0）上是减函数；（3）由题意，t•2x•f（x）＜4x﹣1可化为t•2x•（﹣（2x+2﹣x））＜4x﹣1，化简可得，t＞﹣，令g（x）=﹣=﹣1+，∵x∈（0，1），∴g（x）＜﹣1+=0，故对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立可化为t≥0．点评：本题考查了函数的性质的综合应用及恒成立问题的处理方法，属于难题．例3：已知函数f（x）=|2x﹣1﹣1|，（x∈R）．（1）证明：函数f（x）在区间（1，+∞）上为增函数，并指出函数f（x）在区间（﹣∞，1）上的单调性；（2）若函数f（x）的图象与直线y=t有两个不同的交点A（m，t），B（n，t），其中m＜n，求m+n 的取值范围．考点：指数函数综合题．专题：计算题；证明题．分析：（1）函数单调性的证明，通常依据定义，步骤为：取值，作差，变形，定号，下结论，由于与指数函数有关，求解时要利用到指数函数的单调性；（2）由（1）可知，函数的值域为（0，1），要使函数f（x）的图象与直线y=t有两个不同的交点，故有t∈（0，1）又函数f（x）的图象与直线y=t有两个不同的交点，所以A（m，t），B（n，t）分别位于直线x=1的两侧，由m＜n，得m＜1＜n，故可以求出m+n，进而由t∈（0，1），可求m+n的取值范围．解答：解：（1）证明：任取x1∈（1，+∞），x2∈（1，+∞），且x1＜x2，=，∵x1＜x2，∴，∴，∴f（x1）＜f（x2）．所以f（x）在区间（1，+∞）上为增函数．（5分）函数f（x）在区间（﹣∞，1）上为减函数．（6分）（2）因为函数f（x）在区间（1，+∞）上为增函数，相应的函数值为（0，+∞），在区间（﹣∞，1）上为减函数，相应的函数值为（0，1），由题意函数f（x）的图象与直线y=t有两个不同的交点，故有t∈（0，1），（8分）易知A（m，t），B（n，t）分别位于直线x=1的两侧，由m＜n，得m＜1＜n，故2m﹣1﹣1＜0，2n ﹣1﹣1＞0，又A，B两点的坐标满足方程t=|2x﹣1﹣1|，故得t=1﹣2m﹣1，t=2n﹣1﹣1，即m=log2（2﹣2t），n=log2（2+2t），（12分）故m+n=log2（2﹣2t）+log2（2+2t）=log2（4﹣4t2），当0＜t＜1时，0＜4﹣4t2＜4，﹣∞＜log2（4﹣4t2）＜2．因此，m+n的取值范围为（﹣∞，2）．（17分）点评：本题的考点是指数函数综合问题，主要考查函数单调性的证明，考查函数图形的性质，有较强的综合性．依据定义，证明函数的单调性的步骤通常为：取值，作差，变形，定号，下结论三、课堂达标检测检测题1：已知函数f（x）=（其中e=2.71828…是一个无理数）．（1）求函数f（x）的定义域；（2）判断奇偶性并证明之；（3）判断单调性并证明之．考点：指数函数的定义、解析式、定义域和值域；函数单调性的判断与证明；函数奇偶性的判断．专题：计算题；证明题．分析：（1）把分子整理变化成和分母相同的一部分，进行分子常数化，则变量只在分母上出现，根据分母是一个指数形式，恒大于零，得到函数的定义域是全体实数．（2）根据上一问值函数的定义域关于原点对称，从f（﹣x）入手整理，把负指数变化为正指数，就得到结果，判断函数是一个奇函数．（3）根据判断函数单调性的定义，设出两个任意的自变量，把两个自变量的函数值做差，化成分子和分母都是因式乘积的形式，根据指数函数的性质，判断差和零的关系．解答：解：f（x）==1﹣（1）∵e2x+1恒大于零，∴x∈R（2）函数是奇函数∵f（﹣x）==又由上一问知函数的定义域关于原点对称，∴f（x）为奇函数（3）是一个单调递增函数设x1，x2∈R 且x1＜x2则f（x1）﹣f（x2）=1﹣=∵x1＜x2，∴∴f（x1）﹣f（x2）＜0即f（x1）＜f（x2）∴f（x）在R是单调增函数点评：本题考查函数的定义域，考查函数的奇偶性的判断及证明．考查函数单调性的判断及证明，考查解决问题的能力，是一个综合题目．检测题2：已知函数f（x）=2ax+2（a为常数）（1）求函数f（x）的定义域．（2）若a=1，x∈（1，2]，求函数f（x）的值域．（3）若f（x）为减函数，求实数a的取值范围．考点：指数函数的定义、解析式、定义域和值域；指数函数的单调性与特殊点．专题：常规题型；转化思想．分析：（1）利用指数函数的定义域来考虑．（2）利用函数f（x）在（1，2]上的单调性求函数的值域．（3）根据复合函数的单调性，函数u=ax+2必须为减函数．解答：解：（1）函数y=2ax+2对任意实数都有意义，所以定义域为实数集R．（2）因为a=1，所以f（x）=2x+2．易知此时f（x）为增函数．又因为1＜x≤2，所以f（1）＜f（x）≤f（2），即8＜f（x）≤16．所以函数f（x）的值域为（8，16]．（3）因为f（x）为减函数，而y=2u是增函数，所以函数u=ax+2必须为减函数．所以得a＜0点评：本题考查指数函数的定义域、值域、单调性，复合函数的单调性，体现转化的数学思想．检测题3：设f（x）的定义域是（﹣∞，0）∪（0，+∞），且f（x）对任意不为零的实数x都满足f（﹣x）=﹣f（x）．已知当x＞0时（1）求当x＜0时，f（x）的解析式（2）解不等式．考点：指数函数的定义、解析式、定义域和值域；函数奇偶性的性质．专题：常规题型．分析：（1）求当x＜0时，f（x）的解析式，在哪个区间上求解析式，就在哪个区间上取值x，再转化到已知区间上求解析式，由f（﹣x）=﹣f（x）解出f（x）即可．（2）解不等式f（x）＜﹣，分x＞0和x＜0两种情况，根据求得的解析式求解即可．解答：解：（1）当x＜0时，﹣x＞0，=又f（﹣x）=﹣f（x）所以，当x＜0时，（2）x＞0时，，∴化简得∴，解得1＜2x＜4∴0＜x＜2当x＜0时，∴解得2x＞1（舍去）或∴x＜﹣2解集为{x|x＜﹣2或0＜x＜2}点评：本题考查分段函数解析式的求法，注意在哪个区间上求解析式，就在哪个区间上取值，再转化到已知的区间上求解析式，再根据奇偶性，解出f（x）来．解不等式也要分段求解，注意x的取值范围．11。
指数函数-重难点题型精讲(教师版)
3
3
)
2−8
＞3−2的解集．
1 2
1 2
【解答过程】解：∵( ) −8＞3−2 = ( ) ，
3
3
∴x2﹣8＜2x，
解得﹣2＜x＜4．
故选：A．
【变式 3-2】（2024 秋•黄埔区校级期中）已知 a＞0，且 a≠1，若函数 y＝xa﹣1 在（0，+∞）内单调递减，
则不等式 a3x+1＞a﹣2x 中 x 的取值范围是（ ）
【方法点拨】
①指数函数图象的识别：对于所给函数解析式，研究函数的单调性、特殊值等，利用排除法，得出正确的
函数图象.
②指数函数图象的应用：对于与指数函数有关的函数的作图问题，一般宜用变换作图法作图，这样有利于
从整体上把握函数的性质，从而指数函数的图象来比较大小、解不等式、求最值等.
【例 4】（2024 秋•临渭区期末）函数 y＝x+a 与 y＝a﹣x（a＞0 且 a≠1）在同一坐标系中的图像可能是（ ）
【方法点拨】
根据指数函数的定义，结合具体条件，进行求解即可.
【例 1】（2024 秋•南宁期末）函数 f（x）＝2x 的定义域为（ ）
A．[1，+∞）
B．（0，+∞）
C．[0，+∞）
D．R
【解题思路】由指数函数的性质可得其定义域．
【解答过程】解：函数 f（x）＝2x 的定义域为 R，
故选：D．
【变式 1-1】（2024 秋•阎良区期末）函数 y＝2x（x≤0）的值域是（ ）
当底数 a＞1 时，函数单调递增，当 0＜a＜1 时，函数单调递减，
当底数 a＞1，满足底数越大函数的图象在 x＞0 时，越靠近 y 轴，
4.2指数函数(精讲)(原卷版)2024-2025学年高一数学必修第一册(人教版)同步讲练
4.2 指数函数（精讲）一．指数函数的概念1.定义：一般地，函数y ＝a x (a >0，且a ≠1)叫做指数函数，其中指数x 是自变量，定义域是R.2.具有三个特征：(1)底数a 为大于0且不等于1的常数；(2)指数位置是自变量x ；(3)a x 的系数是1. 二．指数函数的图象和性质R1.由指数函数y ＝a x 的图象与直线x ＝1相交于点(1，a )可知在y 轴右侧，图象从下到上相应的底数由小变大．2.由指数函数y ＝a x 的图象与直线x ＝－1相交于点⎝⎛⎭⎫－1，1a 可知，在y 轴左侧，图象从下到上相应的底数由大变小．如图所示，指数函数底数的大小关系为0＜a 4＜a 3＜1＜a 2＜a 1.四．单调性的应用 3.解指数型不等式(1)形如a f (x )>a g (x )的不等式，可借助y ＝a x 的单调性求解；(2)形如a f (x )>b 的不等式，可将b 化为以a 为底数的指数幂的形式，再借助y ＝a x 的单调性求解； (3)形如a x >b x 的不等式，可借助两函数y ＝a x ，y ＝b x 的图象求解. 4.与指数函数复合的函数单调性一般地，形如y ＝a f (x )(a >0，且a ≠1)函数的性质有： (1)函数y ＝a f (x )与函数y ＝f (x )有相同的定义域.(2)当a >1时，函数y ＝a f (x )与y ＝f (x )具有相同的单调性；当0<a <1时，函数y ＝a f (x )与y ＝f (x )具有相反的单调性.一．函数图象1.抓住特殊点：指数函数的图象过定点(0，1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y 的值，即可得函数图象所过的定点.2.巧用图象变换：函数图象的平移变换(左右平移、上下平移).3.利用函数的性质：奇偶性与单调性.4.在y 轴右侧，图象从上到下相应的底数由大变小，即“底数大图象高”； 在y 轴左侧，图象从上到下相应的底数由小变大，即“底数大图象低”.二.y ＝a f (x )型函数的定义域、值域的求法 (1)形如y ＝a f (x )的函数的定义域就是f (x )的定义域.(2)形如y ＝a f (x )的函数的值域，先求出u ＝f (x )的值域，再结合y ＝a u 的单调性求出y ＝a f (x )的值域.若a 的取值范围不确定，则需对a 进行分类讨论. 2.y ＝f (a x )型函数的定义域、值域的求法 三．比较指数幂大小的常用方法1.底数相同，指数不同：利用指数函数的单调性来判断2.底数不同，指数相同：利用底数不同的指数函数的图象的变化规律来判断或者按幂函数性质判断3.底数不同，指数不同：通过中间量来比较考点一 指数函数的概念【例1-1】（2023秋·高一课时练习）下列函数：①23x y =⨯；②13x y +=；③πx y =；④x y x =．其中为指数函数的个数是（ ） A ．0 B ．1 C ．2D ．3【例1-2】（2023秋·吉林长春·高一长春外国语学校校考期末）若函数()222x y m m m =--⋅是指数函数，则m等于（ ） A ．1-或3 B ．1- C ．3D ．13【一隅三反】1．（2023·全国·高一课堂例题）下列函数为指数函数的是（ ） A ．4x y =-B ．()4xy =-C ．πx y =D ．24x y =2．（2023秋·高一课时练习）（多选）下列函数是指数函数的是（ ）A ．25x y =B ．4x y =-C ．3y x =D ．()63xy a =-（12a >且23a ≠） 3．（2023·全国·高一假期作业）（多选）下列函数中，是指数函数的是（ ）A ．()3xy =-B ．()121,12x y m m m ⎛⎫=->≠ ⎪⎝⎭C ．()0.19xy =D ．23x y =⋅考点二 指数函数的解析式与函数值【例2】（2023春·新疆）指数函数()(0xf x a a =>且)0a ≠图像经过点()3,27，则()2f =（ ）A ．3B ．6C ．9D ．12【一隅三反】1．（2023·全国·高一专题练习）函数()(0x f x a a =>，且1)a ≠的图象经过点()3,27P ，则()2f =（ ）A ．19BC ．13D ．92．（2023秋·高一课时练习）若指数函数()y f x =的图象经过点12,16⎛⎫- ⎪⎝⎭，则32f ⎛⎫-= ⎪⎝⎭． 3．（2023春·贵州黔东南·高一校考期末）已知指数函数()f x 的图像经过点12,16⎛⎫- ⎪⎝⎭，则12f ⎛⎫-= ⎪⎝⎭． 考点三 定义域与值域【例3-1】（2023秋·高一课前预习）求下列函数的定义域： （1）y （2）y =【例3-2】（2023秋·江西）求下列函数的值域； (1)12x y +=；(2)y(3)y =【例3-3】（2023·全国·高三专题练习）已知函数,1()12,1x xx f x x a x ⎧<⎪=-⎨⎪-≥⎩的值域为R ，则实数a 的取值范围是（ ）A ．(,0)-∞B ．(0,)+∞C ．(,1]-∞D ．[1,)+∞【一隅三反】1．（2023秋·高一课时练习）函数y = ）A ．[2,)-+∞B ．[1,)-+∞C ．(,1]-∞-D ．(,2]-∞- 2．（2022秋·高一课时练习）函数()f x =+的定义域为 .3．（2023秋·高一课时练习）函数42x y =+的值域是 ．4．（2023秋·高一单元测试）函数()[]2,1,1x f x x x =+∈-的值域为 ．5．（2023·上海）已知()2,01,0x x f x x ⎧>=⎨≤⎩，则()f x 的值域是 ；6．（2023黑龙江）已知函数()()22223,121,1x x a x a x f x x +-⎧-+<⎪=⎨-≥⎪⎩的值域为R ，则a 的取值范围是考点四 指数函数的图像【例4-1】（2022春·北京）已知对不同的a 值，函数1()2(0,1)x f x a a a -=+>≠的图象恒过定点P ，则P 点的坐标是 .【例4-2】（2023秋·高一单元测试）函数()x b f x a -=的图象如图所示，其中a ，b 为常数，则下列结论正确的是（ ）A ．1,0a b ><B ．1,0a b >>C ．01,0a b <<>D ．01,0a b <<<【一隅三反】1．（2023秋·高一课时练习）函数1xy a a=-（0a >，且1a ≠）的图象可能是（ ）A ．B ．C ．D ．2．（2023·西藏林芝）()2e xf x x=的图像大致是（ ）A ．B ．C ．D ．3．（2023·全国·高三专题练习）（多选）对于函数()(0xf x a a =>且1a ≠），()2g x ax x =-，在同一直角坐标系下的图象可能为（ ）A ．B ．C ．D ．4．（2023秋·宁夏石嘴山 ）函数212(01)x y a a a -=->≠且，无论a 取何值，函数图像恒过一个定点，则定点坐标为 .5．（2023·全国·高一课堂例题）利用函数()2x y f x ==的图象，作出下列各函数的图象：(1)()1f x -；(2)()f x ；(3)()1f x -；(4)()f x -；(5)()1f x -．考点五 指数函数型的单调性及应用【例5-1】（2023秋·高一课时练习）函数()f x = ）A ．(],2-∞B ．[]1,2C ．[]2,3D ．[)2,+∞【例5-2】（2023春·山东菏泽）设函数()()2x x a f x -=在区间()1,0-单调递增，则a 的取值范围是（ ）A ．(],2-∞-B ．[)2,0-C ．(]0,2D ．[)2,+∞【例5-3】（1）（2023·全国·高一专题练习）已知0.143a -⎛⎫= ⎪⎝⎭，0.134b -⎛⎫= ⎪⎝⎭，c = ）. A ．b c a >> B ．b a c >> C ．a b c >>D ．c b a >>（2）（2022秋·浙江宁波·高一校联考期中）下列大小关系正确的是（ ）A ．0.20.20.50.50.20.2>>B ．0.50.20.20.20.50.2>>C ．0.50.20.20.20.20.5>>D ．0.20.20.50.20.50.2>>【例5-4】（2023·广东）已知函数()21,233,2x x f x x x ⎧-≥=⎨-<⎩，则不等式()()342f x f x -<+的解集为 ．【一隅三反】1．（2023秋·广东湛江）已知函数()2313xx f x -+=，则()f x 的增区间为（ ）A ．3,2⎛⎫+∞ ⎪⎝⎭B ．3,2⎛⎫-+∞ ⎪⎝⎭C ．3,2⎛⎫-∞- ⎪⎝⎭D ．3,2⎛⎫-∞ ⎪⎝⎭2．（2023春·宁夏石嘴山）设函数()2212x mxf x -⎛⎫= ⎪⎝⎭在区间()1,2上单调递增，则m 的取值范围为（ ）A ．(],2-∞-B ．[]2,1--C ．[]1,2D ．[)2,+∞3．（2022秋·青海海东·高一校考阶段练习）已知0.533,0.5,a b c === ）A ．b a c <<B ．a b c <<C ．b c a <<D ．c b a <<4．（2022秋·江西南昌·高一统考期中）已知2π,2a b c ===，则,,a b c 的大小关系为（ ）A ．a b c <<B ．b a c <<C ．b c a <<D ．c b a <<5（2023·河北）已知函数()e e x xf x -=-，则不等式()()110f x f -+>的解集是（ ）A ．(),2-∞B ．()2,+∞C ．()2,0-D ．()0,2考点六 指数函数性质的综合运用【例6-1】（2023春·河北石家庄·高一校考期末）已知函数()131xmf x =++为奇函数． (1)求实数m 的值；(2)求不等式()21102f x x --+<的解集．【例6-2】（2023秋·新疆塔城·高一乌苏市第一中学校考期末）已知函数()22x xf x a -=+奇函数．(1)求a 的值；(2)判断()f x 在(),-∞+∞上的单调性并用定义证明；(3)设()()22222x xF x mf x -=+-，求()F x 在[]0,1上的最小值．【一隅三反】1．（2023秋·安徽）已知函数()32,32x xxxa f x a ⋅-=∈+R ． (1)若()f x 为奇函数，求a 的值； (2)在（1）的条件下，求()f x 的值域．2．（2023秋·河北衡水 ）已知函数()x x f x a k a -=-⋅（0a >，且1a ≠）是奇函数，且3(1)2f =． (1)求a ，k 的值；(2)若对于[1,2]x ∀∈，不等式(2)()0f x mf x +≥成立，求m 的取值范围．3．（2023秋·江苏南通 ）已知二次函数()2f x x bx c =++，且不等式()2f x x <的解集为(1,3).(1)求()f x 解析式；(2)若不等式()2210x xkf -+≤在[1,2]x ∈上有解，求实数k 的取值范围.。
指数函数习题（经典含答案及详细解析）
2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且A ．f (b x )≤f (c x) B ．f (b x )≥f (c x) lg(a x －2x－5 ≥5 [9，(9，1，，1[1，[1，，1)上的最大值比最小值大，则234x x ---+11．(2011·银川模拟)若函数y ＝a 2x ＋2a x－1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x的定义域为[0,1]． (1)求a 的值；的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．的取值范围．指数函数答案指数函数答案1.1.解析：由解析：由a ⊗b ＝îïíïìa a ≤bba >b得f (x )＝1⊗2x＝îïíïì2xx，1x答案：答案：A A 2. 2. 解析：∵解析：∵f (1(1＋＋x )＝f (1(1－－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)(0)＝＝3，∴c ＝3.3.∴∴f (x )在(－∞，－∞，1)1)1)上递减，在上递减，在上递减，在(1(1(1，＋∞)上递增．，＋∞)上递增．，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0<0，则，则3x<2x<1<1，∴，∴f (3x)>f (2x)． ∴f (3x )≥f (2x )． 答案：答案：A A3.3.解析：由于函数解析：由于函数y ＝|2x－1|1|在在(－∞，－∞，0)0)0)内单调递减，在内单调递减，在内单调递减，在(0(0(0，＋∞)内单调递增，而函数在，＋∞)内单调递增，而函数在区间区间((k －1，k ＋1)1)内不单调，所以有内不单调，所以有k －1<0<k ＋1，解得－，解得－1<1<k <1. 答案：答案：C C4. 4. 解析：由题意得：解析：由题意得：A ＝(1,2)(1,2)，，a x －2x >1且a >2>2，由，由A ⊆B 知a x －2x>1在(1,2)(1,2)上恒成立，即上恒成立，即a x －2x －1>0在(1,2)(1,2)上恒成立，令上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0ln2>0，所以函数，所以函数u (x )在(1,2)(1,2)上单调递增，则上单调递增，则u (x )>u (1)(1)＝＝a －3，即a ≥3.≥3. 答案：答案：B B5. 5. 解析：数列解析：数列解析：数列{{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，为增函数，注意a 8－6>(3>(3－－a )×7－)×7－33，所以îïíïìa >13－a >0a8－6－a －3，解得2<a <3.答案：答案：C C6. 6. 解析：解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，的图象，当a >1时，必有a －1≥12，即1<a ≤2，≤2，当0<a <1时，必有a ≥12，即12≤a <1<1，，综上，12≤a <1或1<a ≤2.≤2.答案：答案：C C7. 7. 解析：当解析：当a >1时，y ＝a x 在[1,2][1,2]上单调递增，故上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax 在[1,2][1,2]上单调递减，故上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 8. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线曲线||y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果的图象如图所示，由图象可得：如果||y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]1,1]．． 答案：答案：[[－1,1]9. 9. 解析：如图满足条件的区间解析：如图满足条件的区间解析：如图满足条件的区间[[a ，b ]，当a ＝－＝－11，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－＝－11，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：答案：1 110. 10. 解：要使函数有意义，则只需－解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.≤1. ∴函数的定义域为∴函数的定义域为{{x |－4≤x ≤1}．≤1}． 令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－＝－((x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－＝－44或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝2341()2x x ---+的值域为的值域为[[28，1]1]．．＋)＋(≤－时，≤234()2x x ---+在，－32]－32，－32，，－32][1a，，1a ]＝1a，即(1a＋＝13或－15(或13.。
指数函数典型例题详细解析
指数函数典型例题详细解析指数函数·例题解析第一课时例1：求下列函数的定义域与值域：1) $y=\frac{3}{2-x}$解：定义域为$x\in R$且$x\neq 2$，值域为$y>0$且$y\neq1$。
2) $y=2x+2-1$解：由$2^{\frac{x+2}{2}-1}\geq 0$，得定义域为$x\geq -2$，值域为$|y|\geq 0$。
3) $y=3-3x-1$解：由$3-3^{\frac{x-1}{2}}\geq 0$，得定义域为$x\leq 2$，由$3-3^{\frac{x-1}{2}}<3$，得值域为$y<3$。
1.指数函数$y=a^x$（$a>0$且$a\neq 1$）的定义域是$R$，值域是$(0,+\infty)$。
2.求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为$0$③形如$a^0$，($a\neq 0$)3.求函数的值域：①利用函数$y=a^x$单调性②函数的有界性($x^2\geq 0;a^x>0$)③换元法。
例如：$y=4x+\frac{6}{2x-8}$($1\leq x\leq 2$)，先换元，再利用二次函数图象与性质（注意新元的范围）。
例2：指数函数$y=a^x$，$y=b^x$，$y=c^x$，$y=d^x$的图像如图2.6-2所示，则$a$、$b$、$c$、$d$、$1$之间的大小关系是？解：选$(c)$，在$x$轴上任取一点$(x,0)$，则得$b<a<1<d<c$。
例3：比较大小：1)$2$、$3^2$、$5^4$、$8^8$、$9^{16}$的大小关系是：$2<3^2<5^4<8^8<9^{16}$。
2)$\frac{0.6}{4}-\frac{5}{13}-2$，$2$的大小关系是：$\frac{0.6}{4}-\frac{5}{13}-2<2$。
精讲指数和指数函数(有答案解析)
2.5 指数和指数函数例1 （济南市历城二中·月考）计算：⎝⎛⎭⎫－27823－＋0.00212－－10(5－2)－1＋π0＝ . 【答案】－1679【解析】原式＝⎝⎛⎭⎫－32－2＋12500－10(5＋2)(5－2)(5＋2)＋1 ＝49＋105－105－20＋1＝－1679. 例2（青岛市高三月考）化简：412333223384a a ba ab a -⎛⎫-÷- ⎪⎝⎭+＝ (a >0)． 【答案】a 2 【解析】原式＝11111251111333333336223331111111111223333353362[()(2)]2()(2).()(2)(2)()2a a b a b a a a a a a b a aa ab b a a a b b --⋅÷⨯⨯⨯+⋅+⋅-＝－＝ 例3 （济南市高三月考）已知11223a a-+=，求下列各式的值．（1）11a a -+；（2）22a a -+；（3）22111a a a a --++++.【答案】（1）7；（2）47；（3）6. 【解析】（1）将11223a a-+=两边平方得1129a a -++=，所以117a a -+=．（2）将117a a -+=两边平方得22249a a -++=，所以2247a a -+=．（3）由（1）（2）可得22114716.171a a a a --+++==+++【题型精练】1．（全国高三专题练习）计算020.75357818log 7log 25⎛++⋅⎝=__________ 【答案】18【解析】原式020.75357818log 7log 25+-⎛= ⎝+⋅ ()()3243554355log 7log 25133212712218.log 5log 7=+-⨯+⨯=+-+=故答案为：182．（全国高三专题练习）化简121332140.1()a b ---⎛⎫⎪⎝⎭⨯(0,0)a b >>＝________.【答案】85【解析】原式＝2×333223322210a b a b--⋅⋅⋅⋅168105==.故答案为：85. 3. （全国·高三专题练习）化简： （1）126016(2018)449-⎛⎫+--⨯ ⎪⎝⎭（2111332ab a b -⎫⎪⎭a >0，b >0). （3）312211122211111a a aa a a a a -+--++++-.【答案】（1）99π+；（2）a b；（3）12a . 【解析】（1）原式6614342717399πππ=⨯+--=⨯+-+-=+ （2）原式＝11121082232333354331127272333333a b a b a b a b a b ab a b a b a b -⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭===.（3）原式1122313122221211111a a a a a a a a a a a a a ⎛⎫⎛⎫-⋅++ ⎪ ⎪-+--+-+⎝⎭⎝⎭=--++1122111a a a a -=--=-.【题型二 指数函数的图像】例4 （安徽高三月考）如图是指数函数①y ＝a x ，②y ＝b x ，③y ＝c x ，④y ＝d x 的图象，则a ，b ，c ，d 与1的大小关系是( )A.a ＜b ＜1＜c ＜dB.b ＜a ＜1＜d ＜cC.1＜a ＜b ＜c ＜dD.a ＜b ＜1＜d ＜c【答案】B【解析】方法一 在y 轴的右侧，指数函数的图象由下到上，底数依次增大. 由指数函数图象的升降，知c ＞d ＞1，b ＜a ＜1. ∴b ＜a ＜1＜d ＜c .方法二 作直线x ＝1，与四个图象分别交于A 、B 、C 、D 四点，由于x ＝1代入各个函数可得函数值等于底数的大小，所以四个交点的纵坐标越大，则底数越大，由图可知b ＜a ＜1＜d ＜c .故选B. 例5 （浙江高三课时练习）函数()-1=4+x f x a （0a >，且1a ≠）的图象过定点P ，则P 点的坐标为（ ） A ．(1,5) B ．(1,4) C ．(0,5) D ．(0,4)【答案】A【解析】因为x y a =的图象恒过(0,1)点，则1x y a -=的图象恒过(1,1)点，所以()-1=4+x f x a恒过定点()1,5P .故选A .例6 （河南林州一中高三月考）函数()112x f x +⎛⎫= ⎪⎝⎭的图象大致为（ ）A ．B ．C ．D ．【答案】B【解析】作出函数1()012220xx x x y x ⎧≥⎪==⎨⎪<⎩的图象，如下图所示，将12x y =的图象向左平移1个单位得到()112x f x +⎛⎫= ⎪⎝⎭图象.故选： B【题型精练】1.（高邮市临泽中学高三月考）已知函数2()3x f x a+=-（0a >且1a ≠）的图象恒过定点A ，若点A 在一次函数y mx n =-的图象上，其中实数m ，n 满足0mn >，则12m n+的最小值为______． 【答案】4【解析】∵函数2(03x y a a +-=>，且1)a ≠的图象恒过定点A ，可得()22A --， ，∵点A 在一次函数y mx n=-的图象上，∴22m n +=，∵0m n >，，所以()12112141()2(4)(44222n m m n m n m n m n +=++=++≥+= ，当且仅当,112m n ==时取得等号；2.（辛集市第二中学高二期中）已知a ＞1，则函数y =a x与y =（a -1）x 2在同一坐标系中的图象可能是（ ）A ．B ．C ．D ．【答案】A【解析】∵a ＞1，∴函数y =a x为增函数，函数y =（a -1）x 2在（-∞，0）上为减函数，在（0，+∞）上为增函数．故选：A ．3. （全国·高三专题练习）函数()21xf x m =--恰有一个零点，则m 的取值范围是（ ）A ．()1,+∞B ．{}()01,∞⋃+C ．{}[)01,∞⋃+D ．[)1,+∞【答案】C【解析】由题设，|1|2x y =-与y m =只有一个交点， 又|1|2x y =-的图象如下：∴m ∈{}[)01,∞⋃+. 故选：C.【题型三 指数函数的性质】例7 （全国高三课时练习）求下列函数的定义域和值域： (1)y ＝1-42x ；(2)y ＝1－2x ；(3)y ＝22312--⎛⎫⎪⎝⎭x x .【解析】(1)由x －4≠0，得x ≠4，故y ＝1-42x 的定义域为{x |x ≠4，x ∈R }.又1x －4≠0，即21x －4≠1，故y ＝1-42x 的值域为{y |y ＞0，且y ≠1}. (2)由1－2x ≥0，得2x ≤1，∴x ≤0，∴y ＝1－2x 的定义域为(－∞，0]. 由0＜2x ≤1，得－1≤－2x ＜0，∴0≤1－2x ＜1，∴y ＝1－2x 的值域为[0,1). (3)y ＝22312--⎛⎫⎪⎝⎭x x 的定义域为R .∵x 2－2x －3＝(x －1)2－4≥－4，∴22312--⎛⎫⎪⎝⎭x x ≤⎝⎛⎭⎫12－4＝16.又∵22312--⎛⎫⎪⎝⎭x x ＞0，故函数y ＝22312--⎛⎫⎪⎝⎭x x 的值域为(0,16].例8 （1）（贵溪市实验中学高三期末）若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,3（2）（湖南岳阳楼.岳阳一中高三期中）已知函数1()2xf x ⎛⎫= ⎪⎝⎭，则不等式()24(3)f a f a ->的解集为( )A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)（3）（湖北襄阳高三月考）如果1111222ba⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭，那么（ ）A ．a b a a a b <<B ．a a b a b a <<C ．b a a a a b <<D ．b a a a b a <<【答案】（1）B （2）B(3)C【解析】（1）函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩…单调递增，()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ． （2）可知函数()f x 为减函数，由2(4)(3)f a f a ->，可得243a a-<，整理得2340a a --<，解得14a -<<，所以不等式的解集为(1,4)-．故选B.(3) 根据函数()1()2x f x =在R 是减函数，且1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭，所以10b a >>>，所以a a b a b a <<，故选C. 【题型精练】1．（河南高三期末）函数4422x x x x y --=++-的最小值为（ ） A ．12 B ．1 C ．2 D ．74【答案】D【解析】令22x x t --=，则2442x x t -=+-， 故原函数化为2217224⎛⎫=++=++ ⎪⎝⎭y t t t ，当12t =-时，可得最小值为74． 故选：D ．2.（浙江南湖.嘉兴一中高三月考）函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是（ ）A ．[)1,-+∞B ．(],1-∞-C ．[)1,+∞D ．(],1-∞【答案】C【解析】∵13uy ⎛⎫= ⎪⎝⎭是减函数，222(1)1u x x x =-+=--+在(,1]-∞上递增，在[1,)+∞上递减，∴函数2213x xy -+⎛⎫= ⎪⎝⎭的增区间是[1,)+∞．故选：C ．3.（浙江高三课时练习）设0.914y =，0.4828y =， 1.5312y -⎛⎫= ⎪⎝⎭，则（ ）A ．312y y y >>B ．213y y y >>C ．123y y y >>D ．132y y y >>【答案】D【解析】 1.50.920.9 1.80.4830.481.44 1.35121422,22282,y y y -⨯⨯⎛⎫======⎝== ⎪⎭，因为函数2x y =在定义域上为单调递增函数，所以132y y y >>．故选：D ． 【题型四 指数函数综合问题】例9 （安徽贵池池州一中高三期中）已知函数()423xxf x a =+⋅+，a R ∈.（1）当4a =-时，[]0,2x ∈，求函数()f x 的值域；（2）若对于任意的()0,x ∈+∞，()0f x >恒成立，求实数a 的取值范围． 【答案】（1）[]1,3-；（2）a >-【解析】（1）当4a =-时，令2x t =，由[]0,2x ∈，得[]1,4t ∈，()224321y t t t =-+=--，当2t=时，min 1y =-；当4t =时，max3y =．∴函数()f x 的值域为[]1,3-；（2）设2x t =，则1t >，()0f x >在()0,∞+对任意的实数x 恒成立， 等价于230t at ++>在()1,t ∈+∞上恒成立，∴3a t t ⎛⎫>-+ ⎪⎝⎭在()1,+∞上恒成立， ∴max3a t t ⎡⎤⎛⎫>-+ ⎪⎢⎥⎝⎭⎣⎦，设()3g t t t ⎛⎫=-+ ⎪⎝⎭，1t >，函数()g t在(上单调递增，在)+∞上单调递减，∴()maxg t g==-∴a >-例10 （永安市第三中学高三月考）若关于x 的方程()94340xxa ++⋅+=有解，则实数a 的取值范围是（ ）A ．(,8][0,)-∞-+∞B ．(),4-∞-C ．[8,4)--D ．(,8]-∞-【答案】D【解析】由9(4)340x x a ++⋅+=，得443(4)0,(4)3433xxx x a a +++=∴-+=+≥（当且仅当32x =时等号成立），解得8a ≤-故选D 【题型精练】1．（辽宁葫芦岛市·高三二模）已知函数()22x x f x k -=+⋅，k ∈R ． （1）若函数()f x 为奇函数，求实数k 的值．（2）若对任意的[0,)x ∈+∞都有()2x f x ->成立，求实数k 的取值范围． 【答案】（I ）(II)【解析】（1） 已知函数为奇函数，由()(),R f x f x x -=-∈，求得k 的值；（2）恒成立问题通常是求最值，将原不等式整理为212x k -<对0x ≥恒成立，进而求22x y =在[0,)+∞上的最小值，得到结果. 试题解析：（1）因为()22,x x f x k k R -=+⋅∈是奇函数，所以()(),R f x f x x -=-∈，即22(22),x x x x k k --+⋅=-+⋅所以2(1)(1)20x k k +++⋅=对一切R x ∈恒成立，所以1k =-.（2）因为[)0,x ∈+∞，均有()2,x f x ->即222x x x k --+⋅>成立， 所以212x k -<对0x ≥恒成立， 所以2min 1(2)x k-<,因为22x y =在[)0,+∞上单调递增，所以2min (2)1x=，所以0k>.2.（全国高三专题练习）已知函数3()13xxa f x -=+是R 上的奇函数.（1）求a 的值；（2）用定义证明()f x 在R 上为减函数；（3）若对于任意[2,5]t ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求实数k 的取值范围. 【答案】（1）1a =；（2）证明见解析；（3）(,8)-∞.【解析】（1）由函数3()13x xa f x -=+是R 上的奇函数知(0)0f =， 即102a -=，解得1a =. （2）由（1）知13()13xxf x -=+.任取1,212x x R x x ∈<且，则12122121121212121313(13)(13)(13)(13)2(33)()()1313(13)(13)(13)(13)x x x x x x x x x x x x x x f x f x ---+--+--=-==++++++因为12x x <，所以1233x x <，所以21330x x ->，又因为12130130x x +>+>且，故21122(33)0(13)(13)x x x x ->++， 所以12())0(f x f x ->，即12()()f x f x > 所以()f x 在R 上为减函数.（3）不等式22(2)(2)0f t t f t k -+-<可化为22(2)(2)f t t f t k -<-- 因为()f x 是奇函数，故22(2)(2)f t k f k t --=-所以不等式22(2)(2)f t t f t k -<--可化为22(2)(2)f t t f k t -<- 由（2）知()f x 在R 上为减函数，故2222t t k t ->-即232k t t <- 即对于任意[2,5]t ∈，不等式232k t t <-恒成立. 设2()32,[2,5]g t t t t =-∈易知8()65g t ≤≤因此min ()8k g t <=所以实数k 的取值范围是(,8)-∞.。
高一指数函数的图形习题精讲精练
高一指数函数的图形习题精讲精练1.指数函数的定义：设0>a ，1≠a ，x 是任意实数，我们称x a x f =)(为以a 为底数的指数函数。
2. 递增函数和递减函数的定义：(1)设f （x ）为递增函数，则对所有x 1＜x 2，都满足f （x 1）≤ f （x 2）。
(2)设f （x ）为严格递增函数，则对所有x 1＜x 2，都满足f （x 1）＜f （x 2）。
(3)设f （x ）为递减函数，则对所有x 1＜x 2，都满足f （x 1）≥ f （x 2）。
(4)设f （x ）为严格递减函数，则对所有x 1＜x 2，都满足f （x 1）＞f （x 2）。
3.指数函数的图形：(1)当1a >时，如图一，由图形可以看出： ①图形必通过(0,1)﹐且渐近线为x 轴﹒②对于任意实数x ﹐皆使得x a 大于0﹐所以图形必在x 轴上方﹒③在x 轴上方的任一条水平线都与图形恰有一个交点﹐即若a a αβ=﹐则αβ=﹒④图形的凹口向上（即22a a a αβαβ++>）﹒ ⑤()x f x a =为严格递增函数﹐即a a αβαβ>⇔> (1)图形必通过(0,1)，且渐近线为x 轴 (2)当01a <<时，如图二，由图形可以看出： ①图形必通过(0,1)﹐且渐近线为x 轴﹒②对于任意实数x ﹐皆使得x a 大于0﹐所以图形必在x 轴上方﹒③在x 轴上方的任一条水平线都与图形恰有一个交点﹐即若a a αβ=﹐则αβ=﹒④图形的凹口向上（即22a a a αβαβ++>）﹒ ⑤()x f x a =为严格递减函数﹐即a a αβαβ>⇔<0< a <1x图二a >1x图一4.函数x y a =与1()x y a=的图形对称于y 轴6.对于任意实数21,x x 恒有)()()(2121x f x f x x f ⋅=+。
7.由函数图形求方程式实根的个数：给予方程式()()f x g x =，则其相异实根的个数等于两函数1()y f x =与2()y g x =之图形的交点数，又其交点坐标的x 坐标，即为方程式的实根。
指数函数精讲
指数函数指数函数是高中数学中的一个基本初等函数，有关指数函数的图象与性质的题目类型较多，同时也是学习后续数学内容的基础和高考考查的重点，本文对此部分题目类型作了初步总结1．比较大小例1 已知函数2()f x x bx c =-+满足(1)(1)f x f x +=-，且(0)3f =，则()x f b 与()x f c 的大小关系是_____．2 例23 例34 例45 例56 例6 A B C D习题1、比较下列各组数的大小：（1）若 ，比较 与 ；（2）若 ，比较 与 ；（3）若，比较与；（4）若，且，比较a与b；（5）若，且，比较a与b．2曲线分别是指数函数 ,和的图象,则与1的大小关系是 ( ).(3(1)y＝4 已知-1≤x5、设，求函数的最大值和最小值．6（9．解：y当7．已知函数（且）（1）求的最小值；（2）若，求的取值范围．8（10分）（1）已知m x f x +-=132)(是奇函数，求常数m 的值；（2）画出函数|13|-=x y 的图象，并利用图象回答：k 为何值时，方程|3Ｘ－１｜＝k 无9．若函数 是奇函数，求 的值．10. 已知911．已知 ，求函数 的值域．12. (9分)13 求函数y ＝23231+-⎪⎭⎫ ⎝⎛x x 的单调区间.14 已知函数f(x)＝11+-x x a a (a>0且a ≠1).(1)求f(x)的定义域和值域；(2)讨论f(x)的奇偶性；(3)讨论f(x)的单调性.(2)∵(3)f(x)16、定义在（1（3）当函数y ＝a ｜x ｜(a>1)的图像是( )。
考点09 指数函数(练习)(解析版)
考点9指数函数【题组一定义辨析】1.下列函数中指数函数的个数是。
①y =2x ；②y =x 2；③y =2x +1；④y =x x ；⑤y =（6a –3）x 12(23a a >≠，且．【答案】2【解析】只有①⑤是指数函数；②底数不是常数，故不是指数函数；③1222x x y +==⨯是2与指数2x y =的乘积；④中底数x 不是常数，不符合指数函数的定义，所以指数函数的个数是2．2．下列函数中，指数函数的个数为。
①112x y -⎛⎫= ⎪⎝⎭②y ＝a x ()01a a >≠且；③y ＝1x ；④2112xy ⎛⎫=- ⎪⎝⎭【答案】1【解析】由指数函数的定义可判定，只有②正确．3．函数2(232)xy a a a =-+是指数函数，则a 的取值范围是。
【答案】12⎧⎫⎨⎬⎩⎭【解析】 函数2(232)x y a a a =-+是指数函数，22321a a ∴-+=且0a >，1a ≠，由22321a a -+=解得1a =或12a =，12a ∴=，4．已知函数2()(1)(1)x f x a a a =+-+为指数函数，则a =.【答案】1【解析】 函数()()()211xf x a a a =+-+为指数函数，21110a a a ⎧+-=∴⎨+>⎩解得1a =【题组二定义域】1．函数()1f x x =+-的定义域为__________.【答案】(2,1)-【解析】函数()1f x x =-x 满足：2650140210xx x x ⎧--≥⎪⎪⎛⎫->⎨⎪⎝⎭⎪⎪-≠⎩，解得6121x x x -≤≤⎧⎪>-⎨⎪≠⎩即21x -<<.故答案为：(2,1)-2．函数31()log f x x=的定义域为。
【答案】{}1|0x x <<【解析】要使函数有意义，则01220x x x >⎧⎪≠⎨⎪-≥⎩，解得0＜x <1，3．设函数()f x =，则函数2(log )y f x =的定义域为。
指数函数典型例题讲解
指数函数典型例题讲解27的3次方根3273=， 27-的3次方根3273-=-， 32的5次方根2325=， 32-的5次方根2325-=-． 例1．求下列各式的值：（1）()338- （2）()210- （3）()443π- 例2．已知,0<<b a *∈>N n n ,1， 化简：()()n n n n b a b a ++-． 解：当n 是奇数时，原式a b a b a 2)()(=++-=当n 是偶数时，原式a b a a b b a b a 2)()(||||-=--+-=++-=所以，()()n n n n b a b a ++-22a n a n ⎧=⎨-⎩为奇数为偶数．例3．计算：407407-++解：407407-++52)25()25(22=-++=例4．求值：54925-+． 解：54925-+425254549252）（-+=-+= 452622525+=-+=2154152+=+=）（ 例5． 用分数指数幂的形式表示下列各式()a o >：2a 3a .解：2a 11522222a a aa +⋅==；3a =211333a a a ⋅=；=1113322224a a a a ⎛⎫⎛⎫⋅== ⎪ ⎪⎝⎭⎝⎭．例6．计算下列各式的值（式中字母都是正数）．（1）211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭； （2）83184m n -⎛⎫ ⎪⎝⎭；解（1）211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭=()()211115326236263a b+-+-⨯-÷-⎡⎤⎣⎦=044ab a =；（2） 83184m n -⎛⎫ ⎪⎝⎭=883184m n -⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭=2233m m n n -=．例7．计算下列各式：（1）（2)20a >．解：（1）231324555⎛⎫-÷ ⎪⎝⎭=213134245555÷-÷=5512455-= （22=5262132a a a a==．综合应用例1．化简：11555x x x -+++.解：11555x x x -+++=15(1525)x -++=1315x -⨯=3155x⨯. 例2．化简：)()(41412121y x y x -÷-.解：11112244()()x y x y -÷-111111444444()()()x y x y x y =+-÷- 1144x y =+． 评述：此题注重了分子、分母指数间的联系，即21241)(x x =，由此联想到平方差公式的特点，进而使问题得到解决。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
指数函数指数函数是高中数学中的一个基本初等函数，有关指数函数的图象与性质的题目类型较多，同时也是学习后续数学内容的基础和高考考查的重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c =-+满足(1)(1)f x f x +=-，且(0)3f =，则()x f b 与()xf c 的大小关系是_____．分析：先求b c ，的值再比较大小，要注意x x b c ，的取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-，∴函数()f x 的对称轴是1x =．故2b =，又(0)3f =，∴3c =． ∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x xf f >．综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥． 评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x 的取值范围是___________．分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵2225(1)441a a a ++=++>≥， ∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x 的取值范围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．3．求定义域及值域问题例3 求函数y = 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-，∞．令26x t -=，则y =又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤．∴011t -<≤，即01y <≤． ∴函数的值域是[)01，．评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．4．最值问题例4 函数221(01)x x y aa a a =+->≠且在区间[11]-，上有最大值14，则a 的值是_______． 分析：令x t a =可将问题转化成二次函数的最值问题，需注意换元后t 的取值范围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤． ∴当t a =时，2max (1)214y a =+-=．解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤， ∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a 的值是3或13． 评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程的解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根．6．图象变换及应用问题例6 为了得到函数935x y =⨯+的图象，可以把函数3x y =的图象（ ）．A ．向左平移9个单位长度，再向上平移5个单位长度B ．向右平移9个单位长度，再向下平移5个单位长度C ．向左平移2个单位长度，再向上平移5个单位长度D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象的平移规律进行判断． 解：∵293535x x y +=⨯+=+，∴把函数3x y =的图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+的图象，故选（C ）． 评注：用函数图象解决问题是中学数学的重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数的图象，并掌握图象的变化规律，比如：平移、伸缩、对称等．习题1、比较下列各组数的大小：（1）若，比较 与 ； （2）若，比较 与 ； （3）若，比较 与 ； （4）若，且 ，比较a 与b ； （5）若 ，且 ，比较a 与b ．解：（1）由 ，故 ，此时函数 为减函数．由 ，故 ．（2）由 ，故 ．又 ，故 ．从而 ．（3）由 ，因 ，故 ．又 ，故 ．从而 ．（4）应有．因若 ，则 ．又 ，故 ，这样 ．又因 ，故 ．从而 ，这与已知矛盾． （5）应有 ．因若 ，则 ．又 ，故 ，这样有 ．又因 ，且 ，故．从而 ，这与已知 矛盾．小结：比较通常借助相应函数的单调性、奇偶性、图象来求解．2曲线分别是指数函数 , 和 的图象,则 与1的大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定 ,在 轴右侧令,对应的函数值由小到大依次为 ,故应选 . 小结:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.求最值3 求下列函数的定义域与值域.(1)y ＝231 x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x 的定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1， ∴y ＝231-x 的值域为｛y ｜y>0且y ≠1｝. (2)y ＝4x +2x+1+1的定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1的值域为｛y ｜y>1｝.4 已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x 的最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。
5、设 ，求函数 的最大值和最小值． 分析：注意到，设 ，则原来的函数成为 ，利用闭区间上二次函数的值域的求法，可求得函数的最值．解：设 ，由 知， ，函数成为 ， ，对称轴 ，故函数最小值为，因端点较 距对称轴 远，故函数的最大值为 ．6（9分）已知函数)1(122>-+=a a a y x x 在区间[－1,1]上的最大值是14，求a 的值. ．解： )1(122>-+=a a a y x x ， 换元为)1(122a t at t y <<-+=，对称轴为1-=t . 当1>a ，a t =，即x =1时取最大值，略解得 a =3 (a = －5舍去)7．已知函数（ 且 ） （1）求 的最小值； （2）若 ，求 的取值范围．．解：（1） ， 当 即 时，有最小值为 （2），解得 当时， ； 当 时， ．8（10分）（1）已知m x f x +-=132)(是奇函数，求常数m 的值； （2）画出函数|13|-=x y 的图象，并利用图象回答：k 为何值时，方程|3Ｘ－１｜＝k 无解？有一解？有两解？解： （1）常数m =1 （2）当k <0时，直线y =k 与函数|13|-=x y 的图象无交点,即方程无解;当k =0或k ≥1时, 直线y =k 与函数|13|-=x y 的图象有唯一的交点，所以方程有一解; 当0<k <1时, 直线y =k 与函数|13|-=x y 的图象有两个不同交点，所以方程有两解。
9．若函数是奇函数，求 的值． ．解： 为奇函数， ，即 ，则 ，10. 已知9x -10.3x +9≤0，求函数y=（41）x-1-4·（21）x +2的最大值和最小值 解：由已知得（3x ）2-10·3x +9≤0 得（3x -9）（3x -1）≤0∴1≤3x ≤9 故0≤x ≤2而y=(41)x-1-4·(21)x +2= 4·（21）2x -4·（21）x +2 令t=（21）x （141≤≤t ） 则y=f （t ）=4t 2-4t+2=4（t-21）2+1 当t=21即x=1时，y min =1 当t=1即x=0时，y max =211．已知 ，求函数 的值域．解：由 得 ，即 ，解之得 ，于是 ，即，故所求函数的值域为12. (9分)求函数2222++-=x x y 的定义域，值域和单调区间 定义域为R 值域（0，8〕。
（3）在（-∞， 1〕上是增函数 在〔1，+∞）上是减函数。
13 求函数y ＝23231+-⎪⎭⎫ ⎝⎛x x 的单调区间. 分析 这是复合函数求单调区间的问题 可设y ＝u ⎪⎭⎫ ⎝⎛31,u ＝x 2-3x+2，其中y ＝u ⎪⎭⎫ ⎝⎛31为减函数∴u ＝x 2-3x+2的减区间就是原函数的增区间(即减减→增)u ＝x 2-3x+2的增区间就是原函数的减区间(即减、增→减) 解：设y ＝u ⎪⎭⎫ ⎝⎛31,u ＝x 2-3x+2,y 关于u 递减， 当x ∈(-∞，23)时，u 为减函数， ∴y 关于x 为增函数；当x ∈［23，+∞)时，u 为增函数，y 关于x 为减函数. 14 已知函数f(x)＝11+-x x a a (a>0且a ≠1). (1)求f(x)的定义域和值域；(2)讨论f(x)的奇偶性；(3)讨论f(x)的单调性.解：(1)易得f(x)的定义域为｛x ｜x ∈R ｝.设y ＝11+-x x a a ,解得a x ＝-11-+y y ①∵a x>0当且仅当-11-+y y >0时，方程①有解.解-11-+y y >0得-1<y<1. ∴f(x)的值域为｛y ｜-1＜y ＜1}.(2)∵f(-x)＝11+---x x a a ＝x xa a +-11＝-f(x)且定义域为R ，∴f(x)是奇函数.(3)f(x)＝12)1(+-+x x a a ＝1-12+x a . 1°当a>1时，∵a x +1为增函数，且a x+1>0. ∴12+x a 为减函数，从而f(x)＝1-12+x a ＝11+-x x a a 为增函数.2°当0<a<1时，类似地可得f(x)＝11+-x x a a 为减函数. 15、已知函数f （x ）=a －122+x （a ∈R ）， （1） 求证：对任何a ∈R ，f （x ）为增函数．（2） 若f （x ）为奇函数时，求a 的值。