(完整版)六年级下册比和比例
(完整版)六年级下册比和比例练习题
比和比例填空:1. 甲乙两数的比是11:9,甲数占甲、乙两数和的"■）,乙数占甲、乙两数和的H。
甲、乙两数的比是3:2，甲数是乙数的（）倍，乙数是甲数的H。
.. ............................. .. 3 ............. .................... ... ................................................ 2. 某班男生人数与女生人数的比是▼,女生人数与男生人数的比是（），男生人数和女生人4数的比是（）。
女生人数是总人数的比是（）。
, _________ ..... ___ 2 .............. 一、3. 一本书，小明计划每天看这本书计划（）看完。
4. 一根绳长2米，把它平均剪成5段，每段长是"日米，每段是这根绳子的H。
5. 王老师用180张纸订5本本子，用纸的张数和所订的本子数的比是（），这个比的比值的意义是（）。
6. 一个正方形的周长是7 8米，它的面积是（）平■方米。
57 9 10 11 12 13吨大豆可榨油1吨，1吨大豆可榨油（）吨，要榨1吨油需大豆（）吨。
8 3__ . 2 .................... 2.. ................... ...8 甲数的一等丁乙数的一，甲数与乙数的比是（）。
3 514. 12的约数有（），选择其中的四个约数，把它们组成一个比例是（）。
写出两个比值是8的比（）、（）。
15. 加工零件的总个数一定，每小时加工的零件个数的加工的时间（）比例；订数学书的本数与所需要的钱数（）比例；加工零件的总个数一定，已经加工的零件和没有加工的零件个数（）比例。
16. 如果x +y = 712 x2,那么x和y成（）比例；如果x:4=5:y，那么x和y成（）比例。
二、判断1 .由两个比组成的式子叫做比例。
（）2. 正方形的面积一定，它的边长和边长不成比例。
(完整版)六年级比和比例复习知识点及典型例题
比和比例知识点：2、按比分配的实际应用：例：一辆货车和一列客车同时从相距135km 的两地相向而行，经过1.5小时相遇。
已知货车和客车的速度比是7:8，求货车行驶速度。
135÷1.5×＝427153、比例综合应用：例：在一幅比例尺为1:4000000的中国地图上，量得浙江湖州到山东日照的图书距离为15cm 。
陈老师早上6:00从湖州出发开车去日照旅游，下午2:00到达目的地。
途中陈老师开车的平均速度是多少？75练一练：1、北京到济南高速公路距离大约为430km ，北京到天津大约为120km 。
一辆汽车从北京出发开往济南，当行驶到天津时用了1.5小时。
按照这个速度，北京到济南全程需要多少小时？5.3752、刘大伯家养鸡、鸭、鹅共1800只，这三种家禽的只数比是5:3:1.刘大伯家养鸡、鸭、鹅各多少只？3、为创建海华公司，张、王、李三人分别投资100万元、120万元和80万元。
在他们三人的共同努力下，到年末，公司共盈利60万元，你认为该如何合理分配这笔钱，每人分别得多少？4、在比例尺是1:3000000的地图上，量得A、B两城之间的距离是2.4厘米。
在A、B两城之间有一中途停靠站C，A、B两城到C站的距离比是7：5。
一辆汽车从B城到C站共用了0.6小时,求这辆汽车的速度。
5、甲乙两人分别从相距255千米的两地同时出发相向而行，已知甲乙速度比为10:7，两人相遇时各行了多少千米？6、小淘气看一本科技书，第一天看了全书的，第二天看了42页，这时看了的页数与剩下的页数比是2：5，这本科技书一共有多少页？7、某车间生产了甲、乙、丙三种配套机件共1280只，其中甲乙两种机件只数的比是3∶2，丙种机件比甲种多80只，丙种机件生产了多少只？8、把长35厘米的圆柱体按3∶2截成了一长一短两个小圆柱体后，表面积总和增加了30平方厘米。
求截成的较长一个圆柱的体积。
9、一批零件分给甲、乙、丙三人完成，甲完成了总任务的30%，其余的由乙、丙按3∶4来做，丙共做了200个，问这批零件共有多少个？10、一本书小明第一天读了全部的40%，第二天比第一天少读了30页。
人教版六年级数学下《比和比例》(共11张PPT)
谢谢大家
9、 人的 价值， 在招收 诱惑的 一瞬间 被决定 。21.2. 2721.2 .27Sat urday, Febru ary 27 , 2021 10、低头 要有勇 气，抬 头要有 低气。1 5:28:5 815:28 :5815: 282/27 /2021 3:28:5 8 PM 11、人总 是珍惜 为得到 。21.2. 2715:2 8:5815 :28Feb -2127- Feb-21 12、人乱 于心， 不宽余 请。15: 28:581 5:28:5 815:28 Saturd ay, Fe bruary 27, 2 021 13、生气 是拿别 人做错 的事来 惩罚自 己。21. 2.2721 .2.271 5:28:5 815:28 :58Feb ruary 27, 20 21 14、抱最 大的希 望，作 最大的 努力。2 021年2 月27日 星期六 下午3 时28分5 8秒15: 28:582 1.2.27 15、一个 人炫耀 什么， 说明他 内心缺 少什么 。。202 1年2月 下午3 时28分2 1.2.27 15:28F ebruar y 27, 2021 16、业余 生活要 有意义 ，不要 越轨。2 021年2 月27日 星期六 3时28 分58秒1 5:28:5 827 Fe bruary 2021 17、一个 人即使 已登上 顶峰， 也仍要 自强不 息。下 午3时28 分58秒 下午3 时28分1 5:28:5 821.2. 27
比和比例
国旗长2.4米，宽1.6米
国旗长60厘米，宽40厘米
操场上国旗：2.4:1.6 商场里的国旗：60:40
这两个比能组成比例式2.4:1.6=60:40
1.什么叫比?举例说明,各部分名称是什么? 2.什么叫做比的基本性质?举例说明. 3.什么叫做比例?举例说明,各部分名称. 4.什么叫做比例的基本性质?举例说明. 5.比．比例的基本性质的用处． 6. 比和分数,除法的关系.
六年级下册数学知识点解析：比和比例
小升初数学知识点解析：比和比例两个数相除又叫做两个数的比．一、比和比例的性质性质1：若a: b=c：d，则(a + c)：(b + d)= a：b=c：d；性质2：若a: b=c：d，则(a - c)：(b - d)= a：b=c：d；性质3：若a: b=c：d，则(a +x c)：(b +x d)=a：b=c：d；(x为常数)性质4：若a: b=c：d，则a×d = b×c；(即外项积等于内项积)正比例：如果a÷b=k(k为常数)，则称a、b成正比；反比例：如果a×b=k(k为常数)，则称a、b成反比．二、比和比例在行程问题中的体现在行程问题中，因为有速度=路程时间，所以：当一组物体行走速度相等，那么行走的路程比等于对应时间的反比；当一组物体行走路程相等，那么行走的速度比等于对应时间的反比；当一组物体行走时间相等，那么行走的速度比等于对应路程的正比．1．A和B两个数的比是8：5，每一数都减少34后，A是B的2倍，试求这两个数．【分析与解】方法一：设A为8x，则B为5x，于是有(8x-34):(5x-34)=2：1，x=17，所以A为136，B为85．方法二：因为减少的数相同，所以前后A 、B的差不变，开始时差占3份，后来差占1份且与B 一样多，也就是说减少的34，占开始的3-1=2份，所以开始的1份为34÷2=17，所以A为17×8=136，B为17×5=85．2．近年来火车大提速，1427次火车自北京西站开往安庆西站，行驶至全程的511再向前56千米处所用时间比提速前减少了60分钟，而到达安庆西站比提速前早了2小时．问北京西站、安庆西站两地相距多少千米?【分析与解】设北京西站、安庆西站相距多少千米？(511x+56)：x=60：120，即(511x+56)：x=1：2，即x=1011x+112，解得x=1232．即北京西站、安庆西站两地相距1232千米，3．两座房屋A和B各被分成两个单元．若干只猫和狗住在其中．已知：A房第一单元内猫的比率(即住在该单元内猫的数目与住在该单元内猫狗总数之比)大于B房第一单元内猫的比率；并且A房第二单元内猫的比率也大于B房第二单元内猫的比率．试问是否整座房屋A内猫的比率必定大于整座房屋B内猫的比率?【分析与解】如下表给出的反例指出：对所提出问题的回答应该是否定的．表中具体写出了各个单元及整座房屋中的宠物情况和猫占宠物总数的比率．4．家禽场里鸡、鸭、鹅三种家禽中公篱与母篱数量之比是2：3，已知鸡、鸭、鹅数量之比是8：7：5，公鸡、母鸡数量之比是1：3，公鸭、母鸭数量之比是3：4．试求公鹅、母鹅的数量比．【分析与解】公鸡占家禽场家禽总数的=21124615:(3544)45:46:(3544)46:47.333345⨯⨯+⨯⨯=⨯⨯+⨯⨯=8118751310⨯=+++，母鸡占总数的3 10；公鸭占总数的8338753420⨯=+++，母鸭占总数的420；公鹅占总数的213332102020-+=+（），母鹅占总数的234232102020-+=+（），公鹅、母鹅数量之比为322020：：3：2．5．在古巴比伦的金字塔旁，其朝西下降的阶梯旁6m的地方树立有1根走子，其影子的前端正好到达阶梯的第3阶(箭头)．另外，此时树立l根长70cm自杆子，其影子的长度为175cm，设阶梯各阶的高度与深度都是50cm，求柱子的高度为多少？【分析与解】70cm的杆子产生影子的长度为175cm;所以影子的长度与杆子的长度比为：175：70=2.5倍．于是，影子的长度为6+1.5+1.5×2.5=11.25，所以杆子的长度为11.25÷2.5=4.5m．6．已知三种混合物由三种成分A、B、C组成，第一种仅含成分A和B，重量比为3：5；第二种只含成分B和C，重量比为I：2；第三种只含成分A和C，重量之比为2：3．以什么比例取这些混合物，才能使所得的混合物中A，B和C，这三种成分的重量比为3：5：2 ?【分析与解】注意到第一种混合物种A、B重量比与最终混合物的A、B重量比相同，均为3：5.所以，先将第二种、第三种混合物的A 、B 重量比调整到 3：5，再将第二种、第三种混合物中A 、B 与第一种混合物中A 、B 视为单一物质.第二种混合物不含A ，第三种混合物不含B ，所以1.5倍第三种混合物含A 为3，5倍第二种混合物含B 为5，即第二种、第三种混合物的重量比为5：1.5．于是此时含有C 为5×2+1.5×3=14.5，在最终混合物中C 的含量为3A ／5B 含量的2倍．有14.5÷2-1=6.25，所以含有第一种混合物6.25．即第一、二、三这三种混合物的比例为6.25：5：1.5=25：20：6．7．现有男、女职工共1100人，其中全体男工和全体女工可用同样天数完成同样的工作；若将男工人数和女工人数对调一下，则全体男25天完成的工作，全体女工需36天才能完成，问：男、女工各多少人?【分析与解】 直接设出男、女工人数，然后在通过方程求解，过程会比较繁琐．设开始男工为“1”，此时女工为“k ”，有1名男工相当k 名女工．男工、女工人数对调以后，则男工为“k ”，相当于女工“k 2”，女工为“I”．有k 2：1=36：25，所以k=65． 于是，开始有男工数为11k +×1100=500人，女工600人．8．有甲乙两个钟，甲每天比标准时间慢5分钟，而乙每天比标准时间快5分钟，在3月15日的零点零分的时候两钟正好对准．若已知在某一时刻，乙钟和甲钟时针与分针都分别重合，且在从3月15日开始到这个时候，乙钟时针与分针重合的次数比甲钟多10次，那么这个时候的标准时间是多少?【分析与解】 标准的时钟每隔56511分钟重合一次． 假设经历了x 分钟． 于是，甲钟每隔52460651124605⨯⨯⨯-分钟重合一次，甲钟重合了246052460⨯-⨯×x 次； 同理，乙钟重合了246052460⨯+⨯×x 次； 于是，需要乙钟比甲钟多重合 246052460⨯+⨯×x-246052460⨯-⨯×x=102460⨯×x=10; 所以，x=24×60；所以要经历24×60×65511分钟，则为524606551165246011⨯⨯=⨯天. 于是为65天510(24)10()1111⨯=小时106(60)541111⨯=分钟．9．一队和二队两个施工队的人数之比为3：4，每人工作效率之比为5：4，两队同时分别接受两项工作量与条件完全相同的工程，结果二队比一队早完工9天．后来，由一队工人23与二队工人13组成新一队，其余的工人组成新二队．两支新队又同时分别接受两项工作量与条件完全相同的工程，结果新二队比新一队早完工6天．试求前后两次工程的工作量之比?【分析与解】一队与二队的工作效率之比为：(3×5)：(4×4)=15：16．一队干前一个工程需9÷116=144天．新一队与新二队的工作效率之比为：2112(3544):(3544)46:47.3333⨯⨯+⨯⨯⨯⨯+⨯⨯=新一队干后一个工程需6÷147=282天．一队与新一队的工作效率之比为2115:(3544)45:46 33⨯⨯+⨯⨯=所以一队干后一个工程需282×4645天．前后两次工程的工作量之比是144：(282×4645)=(144×45)：(282×46)=540：1081.。
六年级下册数学比和比例人教版(35张ppt)标准课件
量就叫做成反比例的量，他们的关系叫做 例6：甲、乙两车同时从AB两地相向而行，当甲到达B地时，乙车距A地30千米，当乙车到达A地时，甲车超过B地40千米，AB两地相距多少千米？
例3：甲、乙两车同时从AB两地相对而行，5小时相遇，已知甲、乙两车速度的比是2：3，甲车行完全程需多少小时？ 比、除法、分数之间的关系
用字母表示 x k （一定） y
知识梳理
例5：甲、乙两车同时从AB两地相向而行，4小时后相遇，相遇后甲又行了3小时到达B地，这时乙车离A地70千米，AB两地相距多少千米？ 2500000×8=20000000（厘米） 求比例中的未知项，叫做解比例。
(2)成反比例的量:两种相关联的量，一种 将水泥和黄沙按3∶5搅拌成混凝土，水泥正好用完，黄沙还剩多少吨？
比 和 比 例
比的意义
比的2种写法
比的基本性质
比、除法、分数之间的关系 比的计算
比例的意义 比例的基本性质 解比例 比例尺 按比例分配
正比例与反比例
进入奥数
题型一：复杂的解比例
(3x - 0.5）：（4x +3) = 4 ： 9
9（3x-0.5)=4(4x+3)
4x 3 5 2x 6 6
甲、乙两个正方形边长的比是3∶4，周长的比 是( 3:4 )，面积的比是( 9:16 )。
知识梳理
5、比的计算
(1)求比值:前项除以后项。[结果一般用分数 表示]
(2)化简比:将一个比化作前、后项互质的整 数比。
注意：如果比是带有单位的单位比，化简 前应先将单位统一。
知识梳理
化简比
①整数比(前后项都是整数):把比的前后项 同时除以它们的最大公因数。
(完整版)小学六年级_比和比例知识点梳理
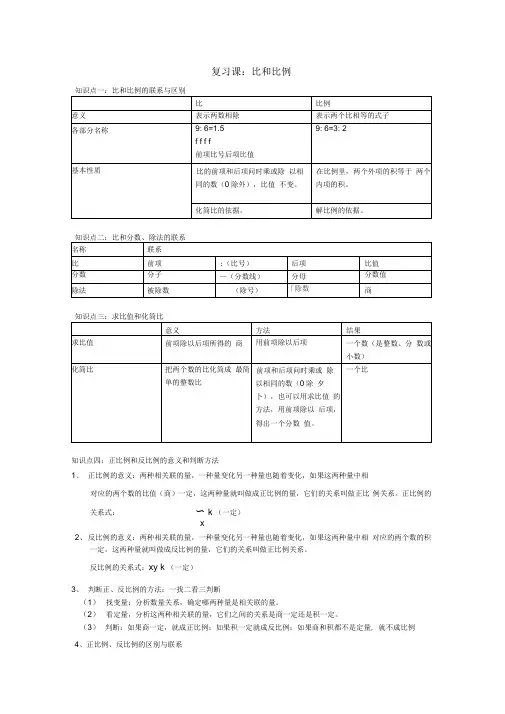
复习课：比和比例知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。
正比例的关系式：〜 k （一定）x2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。
反比例的关系式：xy k （一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。
（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。
（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量, 就不成比例4、正比例、反比例的区别与联系知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。
（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量总份数=平均每份的量（归一）"，再用"一份的量各部分量所对应的份数”,求出各部分的量。
用比例知识解答：首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式，再解比例求出X。
2、用正、反比例知识解答应用题的步骤（1）分析数量关系。
判断成什么比例。
（2）找等量关系。
如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。
（3）解比例式。
设未知数为X,并代入等量关系式，得正比例式或反比例式。
（4）解比例。
（5）检验并写出答语。
精讲典型题例题1填空（1）一项工程，甲单独做要4天，乙单独做要5天完成，甲和乙的工作效率比是（）: （）（2）把2米：4厘米化成最简单的整数比是（），比值是（）。
人教版六年级数学下册第六单元第十三课时_比和比例—比例
32 32 9 2 两个圆面积的比： 2 5 5 25
结论：两个圆半径的比=两个圆直径的比=两个圆周长的比 两个圆面积的比=两个圆半径的平方的比
4
李阿姨是剪纸艺人。平时李阿 姨每天工作6小时，剪出72张 纸；节日期间，李阿姨每天要 工作8小时，能剪出96张剪纸。
（1）写出李阿姨平时和节日期间剪 纸张数及相应工作时间的比。
102 x 360 82 360 64 x 10 x 230.4
x 231
答：需要231块。
变化2:会场铺地, 360块可铺40 平方米,再添 540块,一共铺地多少平方米? 解：设一共铺地x平方米。
40 x 360 360 540
ห้องสมุดไป่ตู้
x 100
答：一共铺地100平方米。
解比例的方法： 根据比例的基本性质，把比例式转化为乘积相 等的等式，再根据以前学过的解方程的方法求解。
比例尺：
一幅图的图上距离和实际距离的比，叫做 这幅图的比例尺。
图上距离 ：实际距离 比例尺
或
图上距离 比例尺 实际距离
图上距离 比例尺 实际距离 实际距离 比例尺 图上距离
比例尺的分类：
数值比例尺 按形式分： 线段比例尺
0 50km
1:5000000
缩小比例尺
1:5000000 50:1
按用途分：
放大比例尺
正比例和反比例的对比：
正比例 反比例
相同点 都是两种相关联的量，一种量随着另一种量变化。 变 化 规 律 关 系 式 变化的方向相同，一种 量扩大(或缩小)，另一 种量也扩大(或缩小)。 相对应的两个数的比值 （商）一定。
人教版六年级数学下册第六单元
比和比例(课件)-六年级数学下册人教版
答：需要糖0.1千克，水1.9千克。
➢ 用正、反比例的知识解决问题
甲工程队铺一条路，前5天 乙工程队铺路，原计划每天
铺了16千米，照这样的速度， 铺3.2千米，15天铺完。实
铺完这条路用了15天。这条 际每天铺4千米，实际需要
路长多少千米？ 正比例
多少天铺完？ 反比例
在练习本上解 答这两题。
➢ 用正、反比例的知识解决问题 • 解题步骤 ✓ 分析数量关系，判断成什么比例关系。 ✓ 找等量关系。若成正比例，则按“等比”找等量关系式; 若成反比例，则按“等积”找等量关系式。 ✓ 列比例。设未知数x，并代入等量关系式。 ✓ 解比例。 ✓ 检验写答。
＝
5 32
前比 后
比
项号 项
值
3∶ 2 ＝ 6 ∶4
内项 外项
➢ 比和比例的区别
• 基本性质
化简比 的根据
比的基本性质：比的前项和后项同时乘或除以 解比例 相同的数（0除外），比值相等。
的根据
比例的基本性质：在比例里，两个外项的积等于
两个内项的积。
➢ 比和比例的联系 • 比是比例的基础，比例是比的扩展； • 两个相等的比可以组成比例。
➢ 判断正、反比例的方法
一找：分析数量关系，确定哪两种量是相关联的量 二看：分析这两种相关联的量，看它们之间的关系是
乘积一定还是比值一定 三判断：如果乘积一定，成反比例
如果比值一定，成正比例 如果乘积和比值都不一定，不成比例
用比和比例的知识解决问题
➢ 按一定的比分配问题
一种糖水是糖与水按1∶19的比例配制而成的。要配制 这种糖水2千克，需要糖和水各多少千克？
成整数比再化简。 把比的前、后项同时乘分母的最小公倍数，转化成整 分数比 数比再化简。
六年级数学比和比例
六年级数学比和比例
（实用版）
目录
1.比和比例的定义
2.比和比例的性质
3.比和比例的应用
4.提高比和比例的解题技巧
正文
1.比和比例的定义
比和比例是数学中常见的概念，比是指两个数相除的结果，比例则是指两个比相等的式子。
比如，如果我们说一个长度为 10 厘米的线段是另一个长度为 5 厘米的线段的两倍，我们就可以说这两个线段的比是 2:1，也可以说这两个线段的比例是 2/1。
2.比和比例的性质
比和比例有一些基本的性质。
比如，如果两个比的比值相等，那么这两个比就是相等的，也就是说，如果 a:b=c:d，那么 a/b=c/d。
另外，比例也有一个基本性质，那就是如果两个比例相等，那么它们的乘积也相等，也就是说，如果 a:b=c:d，那么 a*d=b*c。
3.比和比例的应用
比和比例在实际生活中应用广泛，比如在商业中，我们常常需要通过比例来计算成本和利润；在科学研究中，我们常常需要通过比来描述两个量的关系。
此外，比和比例也是解决许多数学问题的基础，比如在解方程时，我们常常需要通过比例来找到未知数的值。
4.提高比和比例的解题技巧
要提高比和比例的解题技巧，首先我们需要理解比和比例的概念，熟悉它们的基本性质。
其次，我们需要多做一些有关比和比例的练习题，这样可以帮助我们加深对比和比例的理解，提高我们的解题能力。
最后，我们需要学会灵活运用比和比例的知识，比如在解题时，我们可以通过比例来简化方程，这样更容易找到未知数的值。
总的来说，比和比例是数学中非常重要的概念，它们在实际生活中的应用也非常广泛。
(完整版)六年级下册数学第四单元比例知识点
人教版六年级数学下册知识点归纳整理第四单元比例1、比的意义（1)两个数相除又叫做两个数的比。
（2)“：”是比号，读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项.比的前项除以后项所得的商,叫做比值。
（3）同除法比较，比的前项相当于被除数，后项相当于除数，比值相当于商。
(4）比值通常用分数表示，也可以用小数表示，有时也可能是整数。
(5）比的后项不能是零。
（6）根据分数与除法的关系，可知比的前项相当于分子，后项相当于分母，比值相当于分数值.2、比的基本性质：比的前项和后项同时乘上或者除以相同的数（0除外），比值不变,这叫做比的基本性质。
3、求比值和化简比:求比值的方法:用比的前项除以后项，它的结果是一个数值可以是整数,也可以是小数或分数。
根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、后项是互质的数。
4、按比例分配：在农业生产和日常生活中，常常需要把一个数量按照一定的比来进行分配。
这种分配的方法通常叫做按比例分配。
方法：首先求出各部分占总量的几分之几,然后求出总数的几分之几是多少。
5、比例的意义：表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项.6、比例的基本性质：在比例里，两个外项的积等于两个两个内项的积.7、比和比例的区别(1）比表示两个量相除的关系，它有两项（即前、后项）；比例表示两个比相等的式子，它有四项（即两个内项和两个外项）。
（2)比有基本性质，它是化简比的依据；比例有基本性质,它是解比例的依据。
8、解比例：根据比例的基本性质,把比例转化成以前学过的方程,求比例中的未知项，叫做解比例。
9、成正比例的量：两种相关联的量，一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。
用字母表示y/x=k（一定）10、成反比例的量：两种相关联的量,一种量变化,另一种量也随着变化，如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量，他们的关系叫做反比例关系。
(完整版)小学六年级比和比例知识点复习
比和比例知识点1、基本概念（1）两个数相除，又叫做这两个数的比，“∶”是比号，比号前面的数叫做比的前项，比号后面的数叫做比的后项，前项除以后项所得的商叫做比值。
比的后项不能为0。
（2）分数的基本性质∶分数的分子和分母同时乘以或者除以相同的数（0除外）， 分数的大小不变。
乘积是1的两个数互为倒数。
1的倒数是1，0没有倒数。
（3）商不变的规律∶在除法里，被除数和除数同时扩大或者同时缩小相同的倍（0除外），商不变。
（4）比的基本性质∶比的前项和后项同时乘以或者除以相同的数（0除外），它们的比值不变。
（5）小数的性质∶在小数的末尾添上零或者去掉零小数的大小不变。
（6）公因数只有1的两个数叫做互质数。
如（5和7,7和9）最简整数比∶比的前项和后项是互质数。
（7）比的化简∶用商不变的性质、分数的基本性质或比的基本性质来化简。
求比值：比的前项除以比的后项所得的商叫做比值。
（8）比例∶①表示两个比相等的式子叫做比例。
比例有四个项，分别是两个内项和两个外项。
在3∶4=9∶12中，其中3与12叫做比例的外项，4与9叫做比例的内项。
比例的四个数均不能为0。
（9）比例的基本性质∶在一个比例中，两个外项的积等于两个内项的积。
（10）比、比例、比例尺、百分数的后面不能带单位。
（11） “比”进行分配。
基本方法：1. 先求出总份数，先求出每份数，再求每份数分别占各部分的几分之几。
2．然后用总量乘以每份数分别占各部分的几分之几，求出各部分的数量。
2、正比例∶两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。
（1）用字母表示∶xy= k （一定） （2）正比例关系两种相关联的量的变化规律∶同时扩大，同时缩小，比值不变。
3、反比例∶两种相关联的量一种量变化，另种量也随着变化，如果这两种量中，相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做成反比例关系。
六年级下册数学专题-比和比例
知识点一：认识比1、两个数相除又叫两个数的比,任何两个相关数量的比都可以抽象为两个数的比。
知识点二：比、除法、分数的关系2、比、除法、分数之间的联系：知识点三：比值的计算方法3、计算方法：求两个数的比的比值,就是用比的前项除以后项。
4、比和比值的区别：（1）比表示的是两个数的一种关系；比值是一个数值； （2）比可以写成bab a 或:的形式；比值可以是分数、小数或整数。
知识点四：比的基本性质5、比的前项、后项同时乘或除以相同的数（0除外）,比值不变。
这叫做比的基本性质。
知识点五：化简比6、如果比的前项和后项都是整数,化简时可直接把比的前项和后项同时除以它们的最大公因数。
比 前项 比号 后项 比值 除法 被除数 除号 除数 商 分数 分子分数线分母分数值比和比例知识归纳提示：在以后解决问题或计算时,求两个数或几个数的比,如果没有特殊要求,一般要求出最简单的整数比。
知识点六：比例的意义7、比例的意义：表示两个比相等的式子叫做比例。
比例中有两个内项和两个外项。
拓展：比和比例的联系：比例是由比组成的。
比和比例的区别：（1）意义不同,比表示两个数相除的关系；比例表示两个比相等的关系 （2）形式不同,比由两项组成,比例由四项组成。
知识点七：比例的基本性质8、在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
如果用字母表示比例的四个项,d c b a ::=,那么比例的基本性质可以表示成c b d a ⨯=⨯。
拓展：（1）根据比例的基本性质,可以判断两个比能否组成比例。
（2）组成比例的4个数最多可以组成8个不同的比例。
（3）根据比例的基本性质,已知比例中的任意三项,就可以求出第四项。
知识点八：解比例9、根据比例的基本性质,把两个外项和两个内项分别相乘,将比例式改写成c b d a ⨯=⨯的形式,再解方程求出x 的值。
【例1】 比的意义：一辆汽车3小时行驶了150千米,这辆汽车行驶的路程和时间的比是多少？比值是多少？比值表示什么？【练习】甲3小时走15千米,乙4小时走24千米。
六年级数学下册比例讲义
六年级数学下册比例讲义知识点一、比和比例（一）比和比例的意义和基本性质例题1：应用比例的意义判断6.4 : 4和9.6 : 6能否组成比例？因为：6.4 : 4 = 6.4 ÷4 = 1.6 9.6 : 6 = 9.6 ÷ 6 = 1.6所以：6.4 : 4 = 9.6 : 6例题2：运用比例的基本性质判断3．6 ：1．8和0．5 ：0．25能否组成比例？因为 3.6 × 0.25 = 0.9 1.8 × 0.5 = 0.9所以 3．6 ：1．8 = 0．5 ：0．25例题3：从12的因数中任意选出4个数，再组成8个比例式。
因为：12 = 1 × 12 = 2 × 6 = 3 × 4所以从12的因数中任意选出两组4个数并运用比例的基本性质可以组成8个不同的比例。
2 × 6 = 3 ×4（2）︰（3）= （4）︰（6）（3）︰（2）= （6）︰（4）（2）︰（3）= （4）︰（6）（3）︰（2）= （6）︰（4）（6）︰（4）= （3）︰（2）（4）︰（6）= （2）︰（3）（6）︰（4）= （3）︰（2）（4）︰（6）= （2）︰（3）（二）比、除法和分数的关系联 系 区别 比6:3=2 前项 比号 后项 比值 比的基本性质 一种关系 除法6÷3=2 被除数 除号 除数 商 商不变的性质 一种运算 分数6/3=2分子分数线分母分数值分数的基本性质一个数（三）求比值和化简比举例 一般方法结果求比值4:2/5=4÷2/5根据比值的意义，用前项除以后项 是一个商，可以是整数、小数或分数化简比4:2/5=20:2=10:1根据比的基本性质，把比的前项和后项同时乘上或除以相同的数（0除外）是一个最简整数比。
（前项和后项互质）解比例3 : 8 = ⅹ : 40 8x=3×40 8x=120 X=15 根据比例的基本性质，如果已知比例中的任意三项，就可以求出这个比例中的另一个未知项。
(新插图)人教版六年级下册数学 6-1-13 比和比例 求比值、化简比和解比例 知识点梳理课件
(3)龙龙每分钟跳绳120个，聪聪每分钟跳绳96个，龙 龙和聪聪每分钟跳绳个数的最简整数比是( 5:4 )。 龙龙每分钟跳的个数是聪聪的(1.25 )倍。
2．化简比并求比值。
0.18:0.42
3:7
3 7
67:251
1Байду номын сангаас:5
18 5
9 20:0.375
6 6:5 5
1.2 t:450 kg
8:3
8 3
考点2 解比例
3．解比例。
x:0.5＝30:2 x＝7.5
10:x＝92:45 x＝196
0x.5＝09.3 x＝610 x:34＝245:x1＝235
提分必练 提升点1 列比例解决问题
4．某公司按1:50的比给祝融号火星车做了一个模型， 火星车的实际长是3.3 m，宽是3.2 m。模型的长和 宽各是多少厘米？
解：设模型的长是x cm，宽是y cm。 3.3 m＝330 cm 3.2 m＝320 cm x:330＝1:50
x＝ 6.6 y:320＝1:50
y＝ 6.4 答：模型的长是6.6 cm，宽是6.4 cm。
提升点2 根据比例的基本性质解题 5．(易错题)图中阴影部分的面积是甲的13，是乙的14，已
人教版数学六年级下册课件
第13课时 比和比例▶求比值、化简比和 解比例
6 整理和复习
考点必知
考点1 求比值和化简比 1．填一填。 (1)周末，典典骑车郊游，1.5小时骑行了27 km，典典
骑车的路程和时间的比是( 18:1 )，比值是( 18 )， 这个比值表示( 速度 )。 (2)把5 g盐加入到100 g水中，盐和水的比是( 1:20 )， 盐水的浓度是( 4.76)%。
人教版六年级数学下册期末复习专题五《比和比例》课件
x
2.4 = 15∶0.8 解：0.8x = 36
x = 45
某冶炼厂原有锌和铜共84 kg。将锌和铜按1∶2的比熔铸成一种合 金，还需要添加15 kg铜。该冶炼厂原有铜多少千克？[★★★]源自84 152 1 2
=
66（kg）
原有铜：66－15 = 51（kg）
答：该冶炼厂原有铜51千克。
3∶ 9 8 16 ＝2∶3 =2 3
0.25∶1.5 ＝1∶6 =1
6
5∶10 4 11 ＝11∶8 = 11 8
1 kg∶125 g 5 ＝8∶5 =8 5
解比例。[★★★]
x 0.7 9 0.3
解：0.3x = 6.3 x = 21
2.6∶x = 0.13∶0.5 解：0.13x = 1.3
答：六年级参加植树的同学有75人。
水果超市原有苹果与梨的质量比是8∶3，苹果卖了 1 ，梨卖了 5
50 kg后，苹果比梨多220 kg。水果超市原有苹果和梨共多少千
克？[★★★★]
8
1
1 5
=6.4
（220－50）÷（ 6.4－3 ）＝50（kg）
50×（8＋3）＝550（kg）
答：水果超市原有苹果和梨共550kg。
高铁行驶的时间比是（ 4∶3 ），路程比是（ 16∶21 ），
速度比是（ 4∶7 ）。0.8∶0.6
160∶210
（160÷0.8）∶（210÷0.6）
×4
（2） 3 ＝（ 9 ）∶24＝12∶（ 32 ）＝ 0.375 8 ×3
长与宽的和是48÷2=24（m）
（3）一个长方形菜地的周长是48 m，长和宽的比是5∶3，长是
（ 15 ）m，宽是（ 9 ）m，面积是（ 135 ）m2。
六年级下数学第28课-比和比例
不
一定
比值或商
乘积
同
关系式
X ×Y = K（一定）
点 变化图像
基础练习
填空题 （图上距离）：（实际距离 ）＝比例尺
小时：30 分的比值是（9 ）化简比是（9 : 1 ）
比例尺分为（数值比例尺）和（ 线段比例尺 ）
（ 2 ）：8 ＝ 0.25 ＝ ＝20 ÷80（ ）
出粉率一定，面粉重量和小麦重量成（ 正 ）比例。 被除数一定，除数和商成（ 反 ）比例。 总价一定，单价和数量成（ 反 ）比例。 小明每天看8页书，它看书的总页数和看书的天数成（ 正 ）比例。
求比值 化简比
比和比例
比 比、分数和除法的关系
ห้องสมุดไป่ตู้
求比例尺
比例的应用 求图上距离
比的应用 按比分配
求实际距离
比例
比例的意义 反比例意义 正比例意义
比例的基本性质
解比例
正比例意义 比例应用
反比例意义
知识网络图
比例的意义
表示两个比相等
比例的意义 的式子叫做比例
比的意义
两个数相除又 叫两个数的比
比例
比例的基本性质
？（用正、反比例解答） 工作效率×工作时间＝工作总量（一定）
工作总量 = 工作效率（一定）
工作时间
解：设完成任务 需要 x 天。 8 × 30 ＝（36 ÷ 3）x
解：设完成任务需要 x 天
x ＝ 240 ÷ 12
x ＝ 20
答：需要 20 天。
x ＝ 20
答：需要20天。
拓展练习
3 克的蚂蚁能搬动 45 克的物体；3 吨的大象能拉动 4.5 吨的物体，蚂蚁和大 象谁的力气大？（要求：用学过的知识说明你的观点，回答要全面）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
推进新课
（4）用比例知识解题： 大家回忆一下用比例知识解决实际问题的 步骤是什么样的？
①认真审题找出两种相关联的量； ②判断两种量成什么比例； ③设未知数x； ④列出比例式（含有未知数）； ⑤解比例； ⑥检验。
①修一条公路，全长12km，开工3天修了 1.5km。照这样计算，修完这条公路一共 需要多少天？
两种相关联的量是什么？ 路程（工作量）和时间。
两种量成什么比例？ （正比例）
题中的等量关系应该怎样表示？ 全部工作量∶全部时间=3天工作量∶3天
解：设未知数x，解比例。 设修完这条公路一共需要x天
全部工作量∶全部时间=3天工作量∶3天 12∶x=1.5∶3
1.5x=36 x=24
答：修完这条公路一共需要24天
(2)说出下面各比例尺的具体意义。
①比例尺1:3000000表示
②比例尺20:1表示
③比例尺
表示
（3）巩固练习。 ①求比例尺。
一条绿化带长350m，在平面图上用 7cm的线段表示。这幅图纸的比例尺 是多少？
②求实际距离。
在比例尺是1:8000000的地图上，量 得A地到B地的距离是5cm。求AB两 地的实际距离。
第10课时 比和比例（1）
R·六年级下册
新课导入
什么叫做比？举例说明。各部分名称是什么？ 什么叫做比的基本性质？举例说明。 什么叫做比例？举例说明。各部分名称是什么？ 什么叫做比例的基本性质？举例说明。
推进新课
比和分数有什么关系？ 比和除法有什么关系？
5
5
Байду номын сангаас
6
6
化简下面各比并求比值。
复习比例尺。 (1)什么叫做比例尺? 图上距离:实际距离=比例尺
答案：①1∶5000②400km。
课堂小结
新课导入
回忆一下什么叫正比例，什么叫反比例？
正比例：两种相关联的量，其中一种量增加， 另一种量也随着增加，一种量减少，另一种 量也随着减少；两种量的比值一定。 反比例：两种相关联的量中，其中一种量增 加，另一种量反而减少，一种量减少，另一 种量反而增加；两种量的积一定。
a.这里两种量的变化情况。 b.什么量是一定的？ c.这两种量成什么比例？ d.写一个等量关系式。
a.这里两种量的变化情况。 b.什么量是一定的？ c.这两种量成什么比例？ d.写一个等量关系式。
（3）巩固练习： 判断下列各题中两种量是否成比例，若成比例， 请指出成什么比例？ ①速度一定，路程和时间。 ②正方形的边长和它的面积。 ③订《少年报》的数量和所需钱数。 ④小明从家到学校，行走的速度和时间。 ⑤圆的周长和半径。 ⑥圆的面积和半径。 答案：正比例 不成比例 正比例 反比例 正比例 不成比例
课堂小结
与肝胆人共事，无字句处读书。 ——周恩来