14元阵列天线方向图及其MATLAB仿真
基于MATLAB的智能天线及仿真
基于M A T L A B的智能天线及仿真This model paper was revised by the Standardization Office on December 10, 2020摘要随着移动通信技术的发展，与日俱增的移动用户数量和日趋丰富的移动增值服务，使无线通信的业务量迅速增加，无限电波有限的带宽远远满足不了通信业务需求的增长。
另一方面，由于移动通信系统中的同频干扰和多址干扰的影响严重，更影响了无线电波带宽的利用率。
并且无线环境的多变性和复杂性，使信号在无线传输过程中产生多径衰落和损耗。
这些因素严重地限制了移动通信系统的容量和性能。
因此为了适应通信技术的发展，迫切需要新技术的出现来解决这些问题。
这样智能天线技术就应运而生。
智能天线是近年来移动通信领域中的研究热点之一，应用智能天线技术可以很好地解决频率资源匮乏问题，可以有效地提高移动通信系统容量和服务质量。
开展智能天线技术以及其中的一些关键技术研究对于智能天线在移动通信中的应用有着重要的理论和实际意义。
论文的研究工作是在MATLAB软件平台上实现的。
首先介绍了智能天线技术的背景；其次介绍了智能天线的原理和相关概念，并对智能天线实现中的若干问题，包括:实现方式、性能度量准则、智能自适应算法等进行了分析和总结。
着重探讨了基于MATLAB的智能天线的波达方向以及波束形成，阐述了music和capon两种求来波方向估计的方法，并对这两种算法进行了计算机仿真和算法性能分析;关键字:智能天线；移动通信；自适应算法；来波方向； MUSIC算法AbstractWith development of mobile communication technology，mobile users and communication，increment service are increasing，this make wireless services increase so that bandwidth of wireless wave is unfit for development of communication，On the other hand，much serious Co-Channel Interruption and the Multiple Address interruption effect utilize rate of wireless wave’s bandwidth，so the transported signals are declined and wear down，All this has strong bad effect on the capacity andperformance of question and be fit for the development of communication，so smart antenna arise Smart Antenna，which is considered to be a solution to the problem of lacking frequency, becomes a hotspot in the Mobile Communication area．With this technology, Capacity of Mobile Communication system can be increased effectively and the quality of service can be improved at the same time. To study Smart Antenna and its key technologies is important both in theory and in practice。
阵列天线方向图的MATLAB实现
阵列天线方向图的MATLAB 实现课程名称：MATLAB程序设计与应用任课教师：周金柱班级：04091202姓名：黄文平学号：04091158成绩：阵列天线方向图的MATLAB 实现摘要：天线的方向性是指电磁场辐射在空间的分布规律，文章以阵列天线的方向性因子F（θ，φ）为主要研究对象来分析均匀和非均匀直线阵天线的方向性。
讨论了阵列天线方向图中主射方向和主瓣宽度随各参数变化的特点，借助M ATLAB绘制出天线方向性因子的二维和三维方向图，展示天线辐射场在空间的分布规律，表现辐射方向图的特点。
关键词：阵列天线;;方向图；MATLAB前言：天线是发射和接收电磁波的重要的无线电设备，没有天线也就没有无线电通信。
不同用途的天线要求其有不同的方向性，阵列天线以其较强的方向性和较高的增益在工程实际中被广泛应用。
因此，对阵列天线方向性分析在天线理论研究中占有重要地位。
阵列天线方向性主要由方向性因子F（θ，φ）表征，但F（θ，φ）在远区场是一组复杂的函数，如果对它的认识和分析仅停留在公式中各参数的讨论上，很难理解阵列天线辐射场的空间分布规律[ 1 ]。
MATLAB以其卓越的数值计算能力和强大的绘图功能，近年来被广泛应用在天线的分析和设计中。
借助MATLAB可以绘制出阵列天线的二维和三维方向图，直观地从方向图中看出主射方向和主瓣宽度随各参数的变化情况，加深对阵列天线辐射场分布规律的理解。
1 均匀直线阵方向图分析若天线阵中各个单元天线的类型和取向均相同，且以相等的间隔d 排列在一条直线上。
且各单元天线的电流振幅均为I，相位依次滞后同一数值琢，那么，这种天线阵称为均匀直线式天线阵，如图1 所示[ 2 ]:均匀直线阵归一化阵因子为[ 3 ]：Fn（θ，φ）是一个周期函数，所以除§= 0 时是阵因子的主瓣最大值外，§= ±2 mπ（m=1,2,...）都是主瓣最大值，这些重复的主瓣称为栅瓣，在实际应用中，通常希望出现一个主瓣，为避免出现栅瓣，必须把g限制在- 2π＜§＜2π范围内[ 4 ]，其中k=λ/2π，即波数，n 表示阵元数目。
matlab.方向图
概述
天线的远区场分布是一组复杂的函数，分析不同天线的辐射场可从 中得到该天线的 各种重要性能参数。方向性函数F（θ，Φ）是表 征辐射场在不同方向辐射特性的重要关系式，对它的分析和认识如 果仅仅停留在方向性函数以及公式中各参数的讨论上，很难理解天 线辐射场的空间分布以及定向天线集中辐射的概念。表征天线辐射 场空间分布的方向性函数通过二维、三维图形显示，可直观描述、 形象化展示及揭示各参量之间的内在关系，借助matlab的绘图功能 可以加深对天线辐射场空间分布理论的理解和认识，并可得到更有 效更直观的分析结果。我分别用matlab画了六元端和十四元端的方 向图，因为他们的最大辐2*pi); %生成一个等差数列 b=linspace(0,pi); f=sin((cos(a).*sin(b)-1)*(14/2)*pi)./(sin((cos(a).*sin(b)-1)*pi/2)*14); subplot(221); polar(a,f.*sin(b)); %极坐标 title('14元端射式H面，d=波长/2,相位=滞后'); y1=(f.*sin(a))'*cos(b); z1=(f.*sin(a))'*sin(b); x1=(f.*cos(a))'*ones(size(b)); subplot(223); surf(x1,y1,z1);特征匹配算法 axis equal %纵、横坐标采用等长刻度 title('14元端射式三维图'); a=linspace(0,2*pi); b=linspace(0,pi); f=sin((cos(a).*sin(b)+1)*(6/2)*pi)./(sin((cos(a).*sin(b)+1)*pi/2)*6); subplot(222); polar(a,f.*sin(b)); title('6元端射式H面，d=波长/2,相位=超前'); y1=(f.*sin(a))'*cos(b); z1=(f.*sin(a))'*sin(b); x1=(f.*cos(a))'*ones(size(b)); subplot(224); surf(x1,y1,z1); axis equal title('6元端射式三维图');
天线线列阵方向图
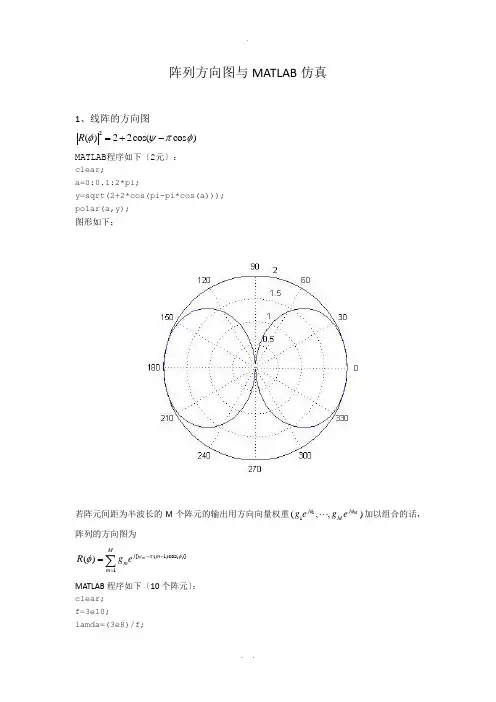
阵列方向图与MATLAB 仿真1、线阵的方向图2()22cos(cos )R φψπφ=+-MATLAB 程序如下〔2元〕：clear;a=0:0.1:2*pi;y=sqrt(2+2*cos(pi-pi*cos(a)));polar(a,y); 图形如下：若阵元间距为半波长的M 个阵元的输出用方向向量权重11(,,)M j j M g eg e φφ⋅⋅⋅加以组合的话，阵列的方向图为 [(1)cos()]1()m Mj m m m R g e ψπφφ--==∑MATLAB 程序如下〔10个阵元〕：clear;f=3e10;lamda=(3e8)/f;beta=2.*pi/lamda;n=10;t=0:0.01:2*pi;d=lamda/4;W=beta.*d.*cos(t);z1=((n/2).*W)-n/2*beta* d;z2=((1/2).*W)-1/2*beta* d;F1=sin(z1)./(n.*sin(z2));iK1=abs(F1) ;polar(t,K1);方向图如下：2、圆阵方向图程序如下：clc;clear all；close all;M = 16; % 行阵元数k = 0.8090; % k = r/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta，俯仰角位fi的波束的权值m = [0 : M-1];w = exp(-j*2*pi*k*cos(2*pi*m'/M-DOA_theta*pi/180)*cos(DOA_fi*pi/180));% w = exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)+sin(2*pi*m'/M)*si n(DOA_fi*pi/180))); % 竖直放置% w = chebwin(M, 20) .* w; % 行加切比雪夫权% 绘制水平面放置的均匀圆阵的方向图theta = linspace(0,180,360);fi = linspace(0,90,180);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)a = exp(-j*2*pi*k*cos(2*pi*m'/M-theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180));%a=exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)+sin(2*pi*m'/ M)*sin(fi(i_fi)*pi/180))); % 竖直放置Y(i_theta,i_fi) = w'*a;endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);% Y = (Y+20) .* ((Y+20)>0) - 20; % 切图Z = Y + 20;Z = Z .* (Z > 0);Y = Z - 20;figure; mesh(fi, theta, Y); view([66, 33]);title('水平放置时的均匀圆阵方向图');% title('竖面放置时的均匀圆阵方向图'); % 竖直放置axis([0 90 0 180 -20 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角/(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下：3、平面阵方向图：clc;clear all；close all;Row_N = 16; % 行阵元数Col_N = 16; % 列阵元数k = 0.5; % k = d/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta，俯仰角位fi的波束的权值Row_n = [0 : Row_N-1]; Col_n = [0 : Col_N-1];W_Row = exp(-j*2*pi*k*Row_n'*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); % W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_fi*pi/180)); % 竖直放置W_Row = chebwin(Row_N, 20) .* W_Row; % 行加切比雪夫权W_Col = chebwin(Col_N, 30) .* W_Col; % 列加切比雪夫权W = kron(W_Row, W_Col); % 合成的权值N*N x 1% 绘制水平面放置的平面阵的方向图theta = linspace(0,180,180);fi = linspace(0,90,90);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)row_temp = exp(-j*2*pi*k*Row_n'*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 行导向矢量N x 1col_temp = exp(-j*2*pi*k*Col_n'*sin(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 列导向矢量N x 1% col_temp = exp(-j*2*pi*k*Col_n'*sin(fi(i_fi)*pi/180)); % 竖直放置Y(i_theta,i_fi) = W'*kron(row_temp, col_temp); % 合成的导向矢量N*N x 1 endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);Y = (Y+60) .* ((Y+60)>0) - 60; % 切图% Z = Y + 60;% Z = Z .* (Z > 0);% Y = Z - 60;figure; mesh(fi, theta, Y); view([66, 33]);title('水平面放置时的面阵方向图');axis([0 90 0 180 -60 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下：4、CAPON方法波束形成MATLAB程序如下〔阵元16，信号源3，快拍数1024〕：clear alli=sqrt(-1);j=i;M=16;%均匀线阵列数目P=3;%信号源数目f0=10;f1=50;f2=100;%信号频率nn=1024;%快拍数angle1=-15;angle2=15;angle3=30;%the signal angleth=[angle1;angle2;angle3]';SN1=10;SN2=10;SN3=10;%信噪比sn=[SN1;SN2;SN3];degrad=pi/180;tt=0:.001:1024;x0=exp(-j*2*pi*f0*tt);%3个信号x0、x1、x2x1=exp(-j*2*pi*f1*tt); %x2=exp(-j*2*pi*f2*tt); %t=1:nn;S=[x0(t);x1(t);x2(t)];nr=randn(M,nn);ni=randn(M,nn);u=nr+j*ni;%复高斯白噪声Ps=S*S'./nn;%信号能量ps=diag(Ps);refp=2*10.^(sn/10);tmp=sqrt(refp./ps);S2=diag(tmp)*S;%加入噪声tmp=-j*pi*sin(th*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A=exp(a2);X=A*S2+.1*u;%接收到的信号Rxx=X*X'./nn;%相关矩阵invRxx=inv(Rxx);%搜寻信号th2=[-90:90]';tmp=-j*pi*sin(th2'*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A2=exp(a2);den=A2'*invRxx*A2;doa=1./den;semilogy(th2,doa,'r');title('spectrum'); xlabel('angle'); ylabel('spectrum'); axis([-90 90 1e1 1e5]); grid;。
MATLAB仿真天线阵代码共8页
天线阵代码http://pudn/downloads164/sourcecode/math/detail750575.html一、clcclear allf=3e9;N1=4;N2=8;N3=12;a=pi/2; %馈电相位差i=1; %天线电流值lambda=(3e8)/f; %lambda=c/f 波长d=lambda/2;beta=2.*pi/lambda;W=-2*pi:0.001:2*pi;y1=sin((N1.*W./2))./(N1.*(sin(W./2))); %归一化阵因子y1=abs(y1);r1=max(y1);y2=sin((N2.*W./2))./(N2.*(sin(W./2))); %归一化阵因子y2=abs(y2);r2=max(y2);y3=sin((N3.*W./2))./(N3.*(sin(W./2))); %归一化阵因子y3=abs(y3);r3=max(y3);%归一化阵因子绘图程序,figure(1)subplot(311);plot(W,y1) ; grid on; %绘出N=4等幅等矩阵列的归一化阵因子xlabel('f=3GHz,N=4,d=1/2波长,a=π/2')subplot(312);plot(W,y2) ; grid on; %绘出N=8等幅等矩阵列的归一化阵因子xlabel('f=3GHz,N=8,d=1/2波长,a=π/2')subplot(313);plot(W,y3) ; grid on; %绘出N=12等幅等矩阵列的归一化阵因子xlabel('f=3GHz,N=12,d=1/2波长,a=π/2')%只有参数N改变的天线方向图t=0:0.01:2*pi;W=a+(beta.*d.*cos(t));z1=(N1/2).*(W);z2=(1/2).*(W);W1=sin(z1)./(N1.*sin(z2)); %非归一化的阵因子K1K1=abs(W1);W=a+(beta.*d.*cos(t));z3=(N2/2).*(W);z4=(1/2).*(W);W2=sin(z3)./(N2.*sin(z4)); %非归一化的阵因子K2K2=abs(W2);W=a+(beta.*d.*cos(t));z5=(N3/2).*(W);z6=(1/2).*(W);W3=sin(z5)./(N3.*sin(z6)); %非归一化的阵因子K3K3=abs(W3);%--------------------绘图函数figure(2)subplot(131);polar(t,K1);xlabel('f=3GHz,N=4,d=1/2波长,a=π/2'); subplot(132);polar(t,K2);xlabel('f=3GHz,N=8,d=1/2波长,a=π/2'); subplot(133);polar(t,K3);xlabel('f=3GHz,N=12,d=1/2波长,a=π/2'); %只有阵列单元方向角a改变的天线方向图N4=10;d1=lambda/4;a1=0;a2=pi/2;a3=pi/2+pi/10;A=a1+(beta.*d1.*cos(t));x1=(N4/2).*(A);x2=(1/2).*(A);A1=sin(x1)./(N4.*sin(x2)); %非归一化的阵因子K4K4=abs(A1);B=a2+(beta.*d1.*cos(t));y_1=(N4/2).*(B);y_2=(1/2).*(B);B1=sin(y_1)./(N4.*sin(y_2)); %非归一化的阵因子K5K5=abs(B1);C=a3+(beta.*d1.*cos(t));v1=(N4/2).*(C);v2=(1/2).*(C);C1=sin(v1)./(N4.*sin(v2)); %非归一化的阵因子K6K6=abs(C1);%--------------------------绘图函数figure(3)subplot(131);polar(t,K4);xlabel('f=3GHz,N=10,d=1/4波长,a=0'); subplot(132);polar(t,K5);xlabel('f=3GHz,N=10,d=1/4波长,a=π/2'); subplot(133);polar(t,K6);xlabel('f=3GHz,N=10,d=1/4波长,a=π/2+π/10');%只有阵列单元间隔d改变的天线方向图N5=20;d2=lambda/4;d3=lambda/2;d4=0.7*lambda;a4=pi/2;D=a4+(beta.*d2.*cos(t));p1=(N5/2).*(D);p2=(1/2).*(D);D1=sin(p1)./(N5.*sin(p2)); %非归一化的阵因子K7K7=abs(D1);E=a4+(beta.*d3.*cos(t));q1=(N5/2).*(E);q2=(1/2).*(E);E1=sin(q1)./(N5.*sin(q2)); %非归一化的阵因子K8K8=abs(E1);F=a4+(beta.*d4.*cos(t));r_1=(N5/2).*(F);r_2=(1/2).*(F);F1=sin(r_1)./(N5.*sin(r_2)); %非归一化的阵因子K9K9=abs(F1);%-----------------------绘图函数figure(4)subplot(131);polar(t,K7);xlabel('f=3GHz,N=20,d=1/4波长,a=π/2'); subplot(132);polar(t,K8);xlabel('f=3GHz,N=20,d=1/2波长,a=π/2'); subplot(133);polar(t,K9);xlabel('f=3GHz,N=20,d=0.7波长,a=π/2');%---------------------------------------3D-天线方向图n_tehta = 130; %-------------------- 采样视角点的仰角n_phi = 130; %--------------------采样点的方向角[tehta,phi]=meshgrid(eps:pi./(n_tehta-1):pi,... %meshgrid函数为矩形区域的设定范围是epf<tehta<π 0<phi<2π0:2*pi./(n_phi-1):2*pi) ;t3=tehta;%-------------只有参数N改变的天线方向3D图M=a+(beta.*d.*cos(t3)); %----N1=4;N2=8;N3=12;z_1=(N1/2).*(M);z_2=(1/2).*(M);M1=sin(z_1)./(N1.*sin(z_2)); %非归一化的阵因子K1K_1=abs(M1);radio_1 =K_1;X1=radio_1.*sin(tehta).*cos(phi);Y1=radio_1.*sin(tehta).*sin(phi);Z1=radio_1.*cos(tehta);M=a+(beta.*d.*cos(t3));z_3=(N2/2).*(M);z_4=(1/2).*(M);M2=sin(z_3)./(N2.*sin(z_4)); %非归一化的阵因子K2K_2=abs(M2);radio_2 =K_2;X2=radio_2.*sin(tehta).*cos(phi);Y2=radio_2.*sin(tehta).*sin(phi);Z2=radio_2.*cos(tehta);M=a+(beta.*d.*cos(t3));z_5=(N3/2).*(M);z_6=(1/2).*(M);M3=sin(z_5)./(N3.*sin(z_6)); %非归一化的阵因子K3K_3=abs(M3);radio_3 =K_3;X3=radio_3.*sin(tehta).*cos(phi);Y3=radio_3.*sin(tehta).*sin(phi);Z3=radio_3.*cos(tehta);%------------------------------------3D绘图函数figure(5)surf(X1,Y1,Z1); %三维绘图函数surf，采用伪彩色表示曲面的高度camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=4,d=1/2波长,a=π/2');figure(6)surf(X2,Y2,Z2);camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=8,d=1/2波长,a=π/2');figure(7)surf(X3,Y3,Z3)camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=12,d=1/2波长,a=π/2');%--------------------只有阵列单元方向角a改变的天线方向图N4=10;d1=lambda/4;a1=0;a2=pi/2;a3=pi/2+pi/10;A_3d=a1+(beta.*d1.*cos(t3));x_1=(N4/2).*(A_3d);x_2=(1/2).*(A_3d);A_1=sin(x_1)./(N4.*sin(x_2)); %非归一化的阵因子K4K_4=abs(A_1);radio_4 =K_4;X4=radio_4.*sin(tehta).*cos(phi);Y4=radio_4.*sin(tehta).*sin(phi);Z4=radio_4.*cos(tehta);B_3d=a2+(beta.*d1.*cos(t3));y_1_3d=(N4/2).*(B_3d);y_2_3d=(1/2).*(B_3d);B_1=sin(y_1_3d)./(N4.*sin(y_2_3d)); %非归一化的阵因子K5K_5=abs(B_1);radio_5 =K_5;X5=radio_5.*sin(tehta).*cos(phi);Y5=radio_5.*sin(tehta).*sin(phi);Z5=radio_5.*cos(tehta);C_3d=a3+(beta.*d1.*cos(t3));v_1=(N4/2).*(C_3d);v_2=(1/2).*(C_3d);C_1=sin(v_1)./(N4.*sin(v_2)); %非归一化的阵因子K6K_6=abs(C_1);radio_6 =K_6;X6=radio_6.*sin(tehta).*cos(phi);Y6=radio_6.*sin(tehta).*sin(phi);Z6=radio_6.*cos(tehta);figure(8)surf(X4,Y4,Z4); %三维绘图函数surf，采用伪彩色表示曲面的高度camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=10,d=1/4波长,a=0');figure(9)surf(X5,Y5,Z5);camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=10,d=1/4波长,a=π/2');figure(10)surf(X6,Y6,Z6)camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=10,d=1/4波长,a=π/2+π/10');%-------------------只有阵列单元间隔d改变的天线方向3D图N5=20;d2=lambda/4;d3=lambda/2;d4=0.7*lambda;a4=pi/2;D_3d=a4+(beta.*d2.*cos(t3));p_1=(N5/2).*(D_3d);p_2=(1/2).*(D_3d);D_1=sin(p_1)./(N5.*sin(p_2)); %非归一化的阵因子K7K_7=abs(D_1);radio_7 =K_7;X7=radio_7.*sin(tehta).*cos(phi);Y7=radio_7.*sin(tehta).*sin(phi);Z7=radio_7.*cos(tehta);E_3d=a4+(beta.*d3.*cos(t3));q_1=(N5/2).*(E_3d);q_2=(1/2).*(E_3d);E_1=sin(q_1)./(N5.*sin(q_2)); %非归一化的阵因子K8K_8=abs(E_1);radio_8 =K_8;X8=radio_8.*sin(tehta).*cos(phi);Y8=radio_8.*sin(tehta).*sin(phi);Z8=radio_8.*cos(tehta);F_3d=a4+(beta.*d4.*cos(t3));r_1_3d=(N5/2).*(F_3d);r_2_3d=(1/2).*(F_3d);F_1=sin(r_1_3d)./(N5.*sin(r_2_3d)); %非归一化的阵因子K9K_9=abs(F_1);radio_9 =K_9;X9=radio_9.*sin(tehta).*cos(phi);Y9=radio_9.*sin(tehta).*sin(phi);Z9=radio_9.*cos(tehta);figure(11)surf(X7,Y7,Z7); %三维绘图函数surf，采用伪彩色表示曲面的高度camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=20,d=1/4波长,a=π/2');figure(12)surf(X8,Y8,Z8);camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=20,d=1/2波长,a=π/2');figure(13)surf(X9,Y9,Z9)camlight rightlightcolorbaraxis imagerotate3D ontitle('f=3GHz,N=20,d=0.7波长,a=π/2');二、%-----------------均匀直线阵列天线的应用之一：边射阵clcclear allf=3e10; %30GHz,厘米波i=1; %天线电流值lambda=(3e8)/f; %lambda=c/f 波长beta=2.*pi/lambda;N=15;t=0:0.01:2*pi;d1=lambda/4; %没有栅瓣效应的边射阵，即间隔d<波长W1=beta.*d1.*cos(t); %定义kdcos(方向角)z1=(N/2).*W1;z2=(1/2).*W1;F1=sin(z1)./(N.*sin(z2));K1=abs(F1);d2=lambda*1.5; %有栅瓣现象的边射阵，即间隔d>波长W2=beta.*d2.*cos(t); %定义kdcos(方向角)z3=(N/2).*W2;z4=(1/2).*W2;F2=sin(z3)./(N.*sin(z4));K2=abs(F2);figure(1)subplot(121);polar(t,K1);title('边射阵 f=30GHz,N=15,d=1/4波长'); subplot(122);polar(t,K2);title('边射阵（有栅瓣） f=30GHz,N=15,d=1.5倍波长');三、%-----------------均匀直线阵列天线的应用之二：普通端射阵clcclear allf=3e10; %30GHz,厘米波i=1; %天线电流值lambda=(3e8)/f; %lambda=c/f 波长beta=2.*pi/lambda;N=15;t=0:0.01:2*pi;d1=lambda/4; %没有栅瓣效应的普通端射阵，即间隔d<1/2波长W1=beta.*d1.*cos(t); %定义kdcos(方向角)z1=((N/2).*W1)+N/2*beta*d1;z2=((1/2).*W1)+1/2*beta*d1;F1=sin(z1)./(N.*sin(z2));K1=abs(F1);d2=lambda*0.7; %有栅瓣现象的普通端射阵，即间隔d>1/2波长W2=beta.*d2.*cos(t); %定义kdcos(方向角)z3=((N/2).*W2)+N/2*beta*d2;z4=((1/2).*W2)+1/2*beta*d2;F2=sin(z3)./(N.*sin(z4));K2=abs(F2);figure(2)subplot(121);polar(t,K1);title('普通端射阵 f=30GHz,N=15,d=1/4波长'); subplot(122);polar(t,K2);title('普通端射阵（有栅瓣） f=30GHz,N=15,d=0.7倍波长');四%-----------------均匀直线阵列天线的应用之三：强方向性端射阵clcclear allf=3e10; %30GHz,厘米波i=1; %天线电流值lambda=(3e8)/f; %lambda=c/f 波长beta=2.*pi/lambda;N=15;t=0:0.01:2*pi;d1=lambda/4; %没有栅瓣效应的强方向性端射阵，即间隔d<(1/2波长)*(1-1/N)W1=beta.*d1.*cos(t); %定义kdcos(方向角)z1=((N/2).*W1)+N/2*(beta*d1+pi/N);z2=((1/2).*W1)+1/2*(beta*d1+pi/N);F1=sin(pi/2/N).*sin(z1)./(sin(z2));K1=abs(F1);d2=lambda*0.5; %有栅瓣现象的强方向性端射阵，即间隔d>1/2波长*(1-1/N) W2=beta.*d2.*cos(t); %定义kdcos(方向角)z3=((N/2).*W2)+N/2*(beta*d2+pi/N);z4=((1/2).*W2)+1/2*(beta*d2+pi/N);F2=sin(pi/2/N).*sin(z3)./(sin(z4));K2=abs(F2);figure(3)subplot(121);polar(t,K1);title('强方向性端射阵 f=30GHz,N=15,d=1/4波长');subplot(122);polar(t,K2);title('强方向性端射阵（有栅瓣）f=30GHz,N=15,d=0.5倍波长');。
MATLAB在天线方向图中的应用与研究
MATLAB在天线方向图中的应用与研究王曼珠1,张民1,崔红跃2(1.北京电子科技学院 通信工程系,北京100070;2.中国民用航空大学,天津300300)ª摘 要:以天线方向图函数为例,分析了对称阵子天线、阵列天线方向图函数F(H,U)随各参量变化的规律以及二维图形的特点,并讨论了直线天线阵(单向端射阵)的最大辐射方向和主瓣宽度随各参量变化的二维、三维图形特点。
借助M AT LAB的绘图功能,对各种天线的方向图函数的二维、三维图形进行研究,可以观察到天线辐射场在不同方向的辐射能量分布,直观清楚地表现出辐射方向图的特点。
关键词:天线;M AT LAB;辐射方向图中图分类号:TN820.1+2;TP391.77 文献标识码:A文章编号:1008-0686(2004)04-0024-04The Application and Study of Antenna Radiation Pattern Based on MATLABWANG Man-zhu1,ZHANG Zhe-min1,C UI Hong-yue2(1.Dep t.of Communication Eng ineer ing B eij ing E le ctronic S cience&T echnology I nstitute,B eij ing100070,China;2.Civ il A viation Unive rsity of China,T ianj ing300300,China)Abstract:This paper takes the antenna radiation pattern as an exam ple,and analy zes the rules of the function F(H,U)varg ing w ith the par am eters for the dipole and antenna ar rays r adiation pattern,as w ell as the characteristic of the tw o-dimensio nal fig ure.In addition,w e discuss the characteristics of the two and thr ee-dimensional fig ure when the max imum radiation and the width o f m ajo r lobe vary s w ith the param eters in the end-fire array.It introduces the w ay of plo tting co mplicated antenna directional r adiation pattern of two and three-dim ensional figure w ith the help of plo tting functions of MAT LAB,the radiating energy distribution of the antenna radiation field in different directions can be observed from r adiation pattern of the antenna,and the characteristic of the radiation pattern can be sho w n clearly.Keywords:antenna;M AT LA B;radiation pattern 天线的远区场分布是一组复杂的函数,分析不同天线的辐射场可从中得到该天线的各种重要性能参数。
MATLAB仿真在通信与电子工程中的应用第9章 天线及智能天线仿真试验
的相位差是［29］：
Ak K
2
d sin cos
第9章 天线及智能天线仿真试验 式中，λ与d分别是入射波的波长和阵元的间距， AK 亦称阵因子。计入阵因子的影响，第K号阵元的输
出是AKxK ，即uK 。为了使天线阵的输出满足需要，在
每个阵元上，用加权因子wK 进行控制。这样第K号阵 元上输出的信号为wKAKxK，即wK wK 。若到达天线阵
′;
Pmusic（n）=（A1a）′*A1a*（inv（（A1a）′*Vn*（Vn） ′*A1a））;%应用MUSIC法估计输出
第9章 天线及智能天线仿真试验 Pcap（n）=inv（（A1a）′*ci*（A1a））; %应用Capon法估计输出 T（n）=q1a（n）; P1=abs（Pmusic）; P2=abs（Pcap）;
的信号是N个，则天线阵的输出是N个信号在M个阵元
上的输出的叠加。将问题简化为xy平面的二维问题 （sinθ=1），并用解析式表达如下：
X(n)=［x1(n),x2(n),…，xN智能天线仿真试验
1 其中，为第1个信号的入射角。
A=［A1,A2,…,AN］ (9-4）
的方向图线。MUSIC法的方向图线的幅度更大。
第9章 天线及智能天线仿真试验
9.3 天线阵的波束形成
我们以等距离圆阵为例来讨论天线阵的波束形成。 图9-10所示是等距离圆线阵的三维图。
第9章 天线及智能天线仿真试验
图9-10 等距离圆线阵的三维图
第9章 天线及智能天线仿真试验 我们把天线阵元顺序定为从OB起顺时针排列为0到 M-1。若有一平面波以θ角入射到阵列上，第K号阵元
Capon 法 亦 称 最 小 方 差 无 畸 变 响 应 MVDR
14元阵列天线方向图及其MATLAB仿真
阵列天线方向图及其MATLAB 仿真1设计目的1.了解阵列天线的波束形成原理写出方向图函数2.运用MATLAB 仿真阵列天线的方向图曲线3.变换各参量观察曲线变化并分析参量间的关系2设计原理阵列天线：阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整，这就使阵列天线具有各种不同的功能，这些功能是单个天线无法实现的。
在本次设计中，讨论的是均匀直线阵天线。
均匀直线阵是等间距，各振源电流幅度相等，而相位依次递增或递减的直线阵。
均匀直线阵的方向图函数依据方向图乘积定理，等于元因子和阵因子的乘积。
二元阵辐射场：式中： 类似二元阵的分析，可以得到N 元均匀直线振的辐射场：令 ，可得到H 平面的归一化方向图函数，即阵因子的方向函数：式中：ζφθψ+=cos sin kd均匀直线阵最大值发生在0=ψ 处。
由此可以得出这里有两种情况最为重要。
1.边射阵，即最大辐射方向垂直于阵轴方向，此时 ，在垂直于阵轴的方向上，])[,(212121ζθθθϕθj jkr jkr m e r e r e F E E E E --+=+=12cos ),(21jkr m e F r E E -=ψϕθθζφθψ+=cos sin kd ∑-=+-=10)cos sin (),(N i kd ji jkr m e e r F E E ζϕθθϕθ2πθ=)2/sin()2/sin(1)(ψψψN N A =kd m ζϕ-=cos 2πϕ±=m各元观察点没有波程差，所以各元电流不需要有相位差。
2.端射振，计最大辐射方向在阵轴方向上，此时0=mϕ或π，也就是说阵的各元电流沿阵轴方向依次超前或滞后kd 。
3设计过程本次设计的天线为14元均匀直线阵天线，天线的参数为：d=λ/2，N=14相位滞后的端射振天线。
微波与天线MATLAB实验二
实验二：N 元阵列天线实验实验目的：1实现数对称振子天线学建模、编程、仿真实现图形可视化。
2通过本实验使学生掌握matlab7.0仿真软件在电磁场编程中的应用。
实验设备：计算机、matlab7.0仿真软件实验内容1 N 元阵列天线方向图二维图形分析N 个均匀天线元中点排成一直线构成均匀直线阵列天线，各天线元在p 点产生的辐射场可表示为10N nn E E -==∑ 。
假定天线元为相同对称阵子，且为等间距n d n d =⨯，等相位差n n δδ=⨯，等幅N 元直线阵，总辐射场为：(1)0060sin()(,)sin()j N u e I N Nu E j f e r N u θϕ-=∙，其中：1(cos sin )2u kd θϕδ=+，),(ϕθe f 为元函数天线阵辐射场大小与方向之间关系的阵函数为：(cos sin +)sin sin 2()(,)(cos sin )sin sin 2a a kd NNu F u F kd N u N θϕδθϕθϕδ===+ （3.3.7）（1）()~a F u u 图形的大波瓣反映了阵函数图的主瓣，其最大值：1)(±==πn u a u F ，就是阵数的最大值，而与m u n π=相对应的m θ即为阵函数的最大辐射方向。
（2）()~a F u u 图形的小波瓣反映了阵函数图的旁瓣，极值等于旁瓣峰值，出现极值的im u 所对应的im θ就是旁瓣峰值所在的方向。
（3）()~a F u u 图形的零值等于阵函数的零值，而出现a F u =的u 值，i0/u i N π=所对应的0i θ就是阵函数图的零辐射方向。
以五元等幅阵为例说明阵函数出现最大值的方向与u 的关系：a. 00δ=时（无电流相位差），090=ϕ，H 面时的阵函数取：1(c o s )c o s2d u k d πθθλ==。
b. kd δ=±时（电流相位差等于波程差），090=ϕ，H 面时的阵函数取(c o s 1)du πθλ=±。
手把手教你天线设计——用MATLAB仿真天线方向图
手把手教你天线设计——用MATLAB仿真天线方向图吴正琳天线是一种变换器，它把传输线上传播的导行波，变换成在无界媒介（通常是自由空间）中传播的电磁波，或者进行相反的变换。
在无线电设备中用来发射或接收电磁波的部件。
无线电通信、广播、电视、雷达、导航、电子对抗、遥感、射电天文等工程系统，凡是利用电磁波来传递信息的，都依靠天线来进行工作。
此外，在用电磁波传送能量方面，非信号的能量辐射也需要天线。
一般天线都具有可逆性，即同一副天线既可用作发射天线，也可用作接收天线。
同一天线作为发射或接收的基本特性参数是相同的。
这就是天线的互易定理。
天线的基本单元就是单元天线。
1、单元天线对称振子是一种经典的、迄今为止使用最广泛的天线，单个半波对称振子可简单地单独立地使用或用作为抛物面天线的馈源，也可采用多个半波对称振子组成天线阵。
两臂长度相等的振子叫做对称振子。
每臂长度为四分之一波长、全长为二分之一波长的振子，称半波对称振子。
对称振子是一种经典的、迄今为止使用最广泛的天线，单个半波对称振子可简单地单独立地使用或用作为抛物面天线的馈源，也可采用多个半波对称振子组成天线阵。
两臂长度相等的振子叫做对称振子。
每臂长度为四分之一波长、全长为二分之一波长的振子，称半波对称振子。
1.1用MATLAB画半波振子天线方向图主要是说明一下以下几点：1、在Matlab中的极坐标画图的方法：polar(theta,rho,LineSpec)；theta：极坐标坐标系0-2*pirho：满足极坐标的方程LineSpec：画出线的颜色2、在方向图的过程中如果rho不用abs(f)，在polar中只能画出正值。
也就是说这时的方向图只剩下一半。
3、半波振子天线方向图归一化方程：Matlab程序：clear alllam=1000;%波长k=2*pi./lam;L=lam/4;%天线臂长theta=0:pi/100:2*pi;f1=1./(1-cos(k*L));f2=(cos(k*L*cos(theta))-cos(k*L))./sin(theta);rho=f1*f2;polar(theta,abs(rho),'b');%极坐标系画图2、线性阵列天线2.1方向图乘积定理阵中第i 个天线单元在远区产生的电场强度为：2(,)ij i i i i ie E K If r πλθϕ-=式中，i K 为第i 个天线单元辐射场强的比例常数，i r 为第i 个天线单元至观察点的距离，(,)i f θϕ为第i 个天线单元的方向图函数，i I 为第i 个天线单元的激励电流，可以表示成为：Bji i i I a e φ-∆=式中，i a 为幅度加权系数，B φ∆为等间距线阵中，相邻单元之间的馈电相位差，亦称阵内相移值。
天线辐射方向图及其matlab仿真
随着现代通信技术的迅猛发展，无线通讯越来越广泛，越来越多的应 用于国防建设，经济建设以及人民的生活等领域。在无线通信系统中，需 要将来自发射机的导波能量转变为无线电波，用来辐射或接受无线电波的 装置称为天线。在通信过程中，特别是点对点的通信，要求天线具有相当 强的方向性，即希望天线能将绝大部分的能量集中向某一预定方向辐射。 阵列天线就是近代天线研究的一种方向，其研究催生了包括相控阵天线， 均匀直线列天线，智能天线等在无线通信，雷达，导航领域中广泛应用的 新型天线。而天线阵列辐射场的研究是其中很重要的一部分。 本文首先介绍天线是如何产生电磁波的，并介绍辐射场的几种情况。 接下来介绍单个天线的基本参数包括主瓣宽度，增益系数，极化特性，方 向性等。然后介绍和分析了边射阵，端射阵和均匀线性阵。阵列天线的方 向相乘性原理，随后使用了 MATLAB 仿真软件分别对二项阵，三角阵和 道尔夫切比雪夫阵模型进行了仿真。在综合对比了阵元的数量，间距，排 列方式后得出天线阵列辐射场的特性。 关键词 元天线；阵列天线；MATLAB 仿真；辐射方向图
- -
I
Research on Radiation Field of Antenna Array Abstract
With the rapid development of modern communication technology, wireless communication is more and more widely, more and more applications on the national defense construction, economic construction and people’s life and other fields. In the wireless communication system, it needs guiding wave energy which will come from the transmitter to the radio .The device which is used to radiation or receiving is known as the Antenna of radio waves. Antenna is an essential part of the wireless communications system. It requests the antenna to have the quite strong directive in the communication, especially in the point-to-point communications. It hopes that the antenna is able to radios in the direction with mainly energy. Single symmetrical antenna cannot satisfy this kind of request forever. Therefore, the array antenna is an important method to realizes this request. This paper first introduces the antenna is how to generate electromagnetic wave, and introduces several cases of radiation field. The basic parameters of next introduces the single antenna comprises a main lobe width, gain, polarization, direction. Then, it introduces and analyzes the direction of multiplicative principle and mathematical model of antenna array of antenna array, then using MATLAB simulation software on simulation Binomial array, Triangular array and Dolph-Tschebyscheff array for a sidelobe through comparison and reasoning factors control antenna array performance method of control parameter, finally embarks from the reality, put forward its own on array antenna and improve some of the views of its radiation performance Keywords - element antenna；array antenna；MATLAB；antenna pattern
阵列天线的三维波束赋形技术及其Matlab实现_赵季红
的角度分辨率明显降低，但可以通过增加阵元的数目提高垂直方向的角度分辨率，实现对特定目标方向有效的三
维波束赋形．
关 键 词： 均匀平面阵； 三维波束赋形； Matlab 仿真
中图分类号： TN929. 53
文献标志码： A
3D-Beamforming of Array Antenna and the Simulation Based on Matlab
其中，
∑ Fx（ θ，φ）
=
M －1 m =0
ejmψx ，ψx
= 2λπΔxsinθcosφ
－ αx
（ 5a）
∑ Fy（ θ，φ）
=
N －1 n =0
ejmψy ，ψy
= 2λπΔysin
θsin
φ － αy
（ 5b）
以上公式说明，矩形网格矩形边界的均匀平面
阵总场方向图函数可以分解为沿 x 和 y 方向排列的
别为
ax（ θ0，φ0）
=［1，e ，…，e ］ － j2λπΔxsin θ0sin φ0
－ j2λπΔx（ N － 1） sin θ0sin φ0 T
（ 2a）
ay（ θ0，φ0）
=［1，e ，…，e ］ － j2λπΔysin θ0sin φ0
－ j2λπΔy（ N － 1） sin θ0sin φ0 T
2014 年 6 月 第 37 卷 第 3 期
北京邮电大学学报 Journal of Beijing University of Posts and Telecommunications
文章编号： 1007-5321（ 2014） 03-0078-05
DOI： 10． 13190 / j． jbupt． 2014． 03． 016
阵列天线方向图及其MATLAB仿真
阵列天线方向图及其MATLAB仿真一．实验目的1.了解阵列天线的波束形成原理写出方向图函数2.运用MATLAB仿真阵列天线的方向图曲线3.变换各参量观察曲线变化并分析参量间的关系二．实验原理1.阵列天线：阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整，这就使阵列天线具有各种不同的功能，这些功能是单个天线无法实现的。
^2.方向图原理：对于单元数很多的天线阵，用解析方法计算阵的总方向图相当繁杂。
假如一个多元天线阵能分解为几个相同的子阵，则可利用方向图相乘原理比较简单地求出天线阵的总方向图。
一个可分解的多元天线阵的方向图，等于子阵的方向图乘上以子阵为单元阵列天线天线阵的方向图。
这就是方向图相乘原理。
一个复杂的天线阵可考虑多次分解，即先分解成大的子阵，这些子阵再分解为较小的子阵，直至得到单元数很少的简单子阵为止，然后再利用方向图相乘原理求得阵的总方向图。
这种情况适应于单元是无方向性的条件，当单元以相同的取向排列并自身具有非均匀辐射的方向图时，则天线阵的总方向图应等于单元的方向图乘以阵的方向图。
三．源程序及相应的仿真图1.方向图随n变化的源程序clear;sita=-pi/2::pi/2;lamda=;]d=lamda/4;n1=20;beta=2*pi*d*sin(sita)/lamda;z11=(n1/2)*beta;z21=(1/2)*beta;f1=sin(z11)./(n1*sin(z21));F1=abs(f1);figure(1);plot(sita,F1,'b');hold on;n2=25;：beta=2*pi*d*sin(sita)/lamda;z12=(n2/2)*beta;z22=(1/2)*beta;f2=sin(z12)./(n2*sin(z22));F2=abs(f2);plot(sita,F2,'r');hold on;n3=30;beta=2*pi*d*sin(sita)/lamda;z13=(n3/2)*beta;z23=(1/2)*beta;>f3=sin(z13)./(n3*sin(z23));F3=abs(f3);plot(sita,F3,'k')hold off;grid on;xlabel('theta/radian');ylabel('amplitude');title('方向图与阵列个数的关系'); legend('n=20','n=25','n=30');·结果分析：随着阵列个数n的增加，方向图衰减越快，效果越好；2.方向图随lamda变化的源程序clear;sita=-pi/2::pi/2;n=20;d=;lamda1=;beta=2*pi*d*sin(sita)/lamda1;z11=(n/2)*beta;z21=(1/2)*beta;f1=sin(z11)./(n*sin(z21));~F1=abs(f1);%·½ÏòͼÇúÏßfigure(1);lamda2=;beta=2*pi*d*sin(sita)/lamda2;z12=(n/2)*beta;z22=(1/2)*beta;f2=sin(z12)./(n*sin(z22));F2=abs(f2);lamda3=;beta=2*pi*d*sin(sita)/lamda3;z13=(n/2)*beta;，z23=(1/2)*beta;f3=sin(z13)./(n*sin(z23));F3=abs(f3)plot(sita,F1,'b',sita,F2,'r',sita,F3,'k');grid on;xlabel('theta/radian');ylabel('amplitude');title('方向图与波长的关系');legend('lamda=','lamda=','lamda=');四．,随着波长lamda的增大，方向图衰减越慢，收敛性越五．结果分析：不是很好；3.方向图随d变化的源程序clear;sita=-pi/2::pi/2;n=20;lamda=;d1=;beta=2*pi*d1*sin(sita)/lamda;z11=(n/2)*beta;z21=(1/2)*beta;【f1=sin(z11)./(n*sin(z21));F1=abs(f1);%·½ÏòͼÇúÏßfigure(1);plot(sita,F1,'b');hold on;d2=;beta=2*pi*d2*sin(sita)/lamda;z12=(n/2)*beta;z22=(1/2)*beta;f2=sin(z12)./(n*sin(z22));F2=abs(f2);-plot(sita,F2,'r');hold on;d3=;beta=2*pi*d3*sin(sita)/lamda;z13=(n/2)*beta;z23=(1/2)*beta;f3=sin(z13)./(n*sin(z23));F3=abs(f3)plot(sita,F3,'k')hold off;grid on;xlabel('theta/radian');ylabel('amplitude');title('·½ÏòͼÓëÌìÏßÕóÁмä¸ôdµÄ¹Øϵ'); legend('d1=','d=','d=');结果分析；随着阵元之间间隔的增加，方向图衰减越快，主次瓣的差距越大，次瓣衰减越快，效果越好。
基于MATLAB的智能天线及仿真
摘要随着移动通信技术的发展，与日俱增的移动用户数量和日趋丰富的移动增值服务，使无线通信的业务量迅速增加，无限电波有限的带宽远远满足不了通信业务需求的增长。
另一方面，由于移动通信系统中的同频干扰和多址干扰的影响严重，更影响了无线电波带宽的利用率。
并且无线环境的多变性和复杂性，使信号在无线传输过程中产生多径衰落和损耗。
这些因素严重地限制了移动通信系统的容量和性能。
因此为了适应通信技术的发展，迫切需要新技术的出现来解决这些问题。
这样智能天线技术就应运而生。
智能天线是近年来移动通信领域中的研究热点之一，应用智能天线技术可以很好地解决频率资源匮乏问题，可以有效地提高移动通信系统容量和服务质量。
开展智能天线技术以及其中的一些关键技术研究对于智能天线在移动通信中的应用有着重要的理论和实际意义。
论文的研究工作是在MATLAB软件平台上实现的。
首先介绍了智能天线技术的背景；其次介绍了智能天线的原理和相关概念，并对智能天线实现中的若干问题，包括:实现方式、性能度量准则、智能自适应算法等进行了分析和总结。
着重探讨了基于MATLAB的智能天线的波达方向以及波束形成，阐述了music和capon两种求来波方向估计的方法，并对这两种算法进行了计算机仿真和算法性能分析;关键字:智能天线；移动通信；自适应算法；来波方向；MUSIC算法AbstractWith development of mobile munication technology，mobile users and munication，increment service are increasing，this make wireless services increase so that bandwidth of wireless wave is unfit for development of munication，On the other hand，much serious Co-Channel Interruption and the Multiple Address interruption effect utilize rate of wireless wave’s bandwidth，so the transported signals are declined and wear down，All this has strong bad effect on the capacity and performance of question and be fit for the development of munication，so smart antenna arise Smart Antenna，which is considered to be a solution to the problem of lacking frequency, bees a hotspot in the Mobile munication area．With this technology, Capacity of Mobile munication system can be increased effectively and the quality of service can be improved at the same time. To study Smart Antenna and its key technologies is important both in theoryand in practice。
14元阵列天线方向图及其MATLAB仿真
阵列天线方向图及其MATLAB 仿真1设计目的1.了解阵列天线的波束形成原理写出方向图函数2.运用MATLAB 仿真阵列天线的方向图曲线3.变换各参量观察曲线变化并分析参量间的关系2设计原理阵列天线：阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整，这就使阵列天线具有各种不同的功能，这些功能是单个天线无法实现的。
在本次设计中，讨论的是均匀直线阵天线。
均匀直线阵是等间距，各振源电流幅度相等，而相位依次递增或递减的直线阵。
均匀直线阵的方向图函数依据方向图乘积定理，等于元因子和阵因子的乘积。
二元阵辐射场：式中： 类似二元阵的分析，可以得到N 元均匀直线振的辐射场：令 ，可得到H 平面的归一化方向图函数，即阵因子的方向函数：式中：ζφθψ+=cos sin kd均匀直线阵最大值发生在0=ψ 处。
由此可以得出])[,(212121ζθθθϕθj jkr jkr m e r e r e F E E E E --+=+=12cos ),(21jkrm e F r E E -=ψϕθθζφθψ+=cos sin kd ∑-=+-=1)cos sin (),(N i kd ji jkrme erF E E ζϕθθϕθ2πθ=)2/sin()2/sin(1)(ψψψN N A =kdm ζϕ-=cos这里有两种情况最为重要。
1.边射阵，即最大辐射方向垂直于阵轴方向，此时 ，在垂直于阵轴的方向上，各元观察点没有波程差，所以各元电流不需要有相位差。
2.端射振，计最大辐射方向在阵轴方向上，此时0=mϕ或π，也就是说阵的各元电流沿阵轴方向依次超前或滞后kd 。
3设计过程本次设计的天线为14元均匀直线阵天线，天线的参数为：d=λ/2，N=14相位滞后的端射振天线。
基于MATLAB 可实现天线阵二维方向图和三维方向图的图形分析。
基于matlab的天线方向图
计算天线均匀直线阵方向性系数的程序clc;clear;global n posai sita d;sita=(0:pi/600:pi);k=2*pi;nn=(2:19/100:20);d=0.25;for jj=1:length(nn);n=nn(jj);beta=0;%beta=k*d;%beta=-k*d-pi/n;posai=beta+k*d*cos(sita);jifen=0;f=zxz(sita);for i=1:length(sita);jifen=jifen+f(i)*pi/600;end;fxxs(jj)=2/jifen;end;plot(nn,fxxs);hold onfunction y=zxz(sita);f1=abs(sin(n*posai/2));eps=2.2204e-016;f2=abs(sin(posai/2));for j=1:length(posai);if f1(j)<eps&f2(j)<eps;f1(j)=abs(n/2*cos(n/2*posai(j)));f2(j)=abs(1/2*cos(posai(j)/2));end;end;y=f1./f2;y=y/max(y);y=y.*y.*sin(sita);演示方向图乘积定理sita=meshgrid(0:pi/90:pi);fai=meshgrid(0:2*pi/90:2*pi)';l=0.25;%对称阵子的长度d=1.25;%二元阵的间隔距离beta=0;%电流初始相位差m=1;%电流的振幅比r1=abs(cos(2*pi*1*cos(sita))-cos(2*pi*1))./abs(sin(sita)+eps); r2=sqrt(1+m*m+2*m*cos(beta+2*pi*d*sin(sita).*sin(fai)));r3=r1.*r2;r1max=max(max(r1));r2max=max(max(r2));r3max=max(max(r3));[x1,y1,z1]=sph2cart(fai,pi/2-sita,r1/r1max);[x2,y2,z2]=sph2cart(fai,pi/2-sita,r2/r2max);[x3,y3,z3]=sph2cart(fai,pi/2-sita,r3/r3max);subplot(2,2,1);surf(x1,y1,z1);axis([-1 1 -1 1 -1 1]);shading interp;subplot(2,2,2);surf(x2,y2,z2);axis([-1 1 -1 1 -1 1]);shading interp;subplot(2,2,2);surf(x3,y3,z3);axis([-1 1 -1 1 -1 1]);shading interp;有两个半波阵子组成一个共线二元阵，其间隔距离d=λ，电流比I m2=I m1。
相控阵天线方向图推导及仿真
相控阵天线方向推导及仿真1、推导线阵天线方向图公式一个接收线阵，由等间距为d 的N 个各向同性单元组成，那么在θ方向，相邻单元接收信号的相位差为Ф=2πdλsinθ，线阵排列情况如图1所示。
图1 线阵排列示意图因为天线辐射方向图可以由天线上各种各样电流源辐射的单独贡献进行矢量叠加而得出，故各单元电压和为：E a =sin (ωt )+sin (ωt +ϕ)+sin (ωt +2ϕ)+⋯+sin[ωt +(N −1)ϕ]将等式两边同时乘以2sin(ϕ2)，根据积化和差、和差化积等相关数学公式，可得到如下公式：2sin (ϕ2)E a =cos (ωt −ϕ2)−cos (ωt +ϕ2)+cos (ωt +ϕ2)−cos (ωt −32ϕ)+⋯+cos (ωt +2N −32ϕ)−cos(ωt +2N −12ϕ)整理得，2sin (ϕ2)E a =cos (ωt −ϕ2)−cos (ωt +2N−12ϕ)=2sin(ωt +N −12ϕ)sin(N2ϕ) 最终得到场强方向图，E a =sin[ωt +(N −1)ϕ2⁄]sin(Nϕ2⁄)sin(ϕ2⁄)平方归一化后，得到辐射方向图（阵列因子）：|G a (θ)|=sin 2[Nπ(dλ)sinθ]N 2sin 2[π(dλ)sinθ]上式中，当(dλ)sinθ=0,±1,±2,···±n 时|G a (θ)|取得相等的最大值，但是我们只期望看到(dλ)sinθ=0的情况，取其他值产生的栅瓣是我们所不想见到的，为避免这种情况，特令d <λ。
前面的公式中认定主瓣指向为0°，当主瓣指向θ0方向时，则各向同性单元线阵的归一化辐射方向图为：G (θ)=sin 2[Nπ(dλ)(sinθ−sinθ0)]N 2sin 2[π(d λ)(sinθ−sinθ0)]此时，由于−2≤sin (θ)−sin (θ0)≤2，故防止产生栅瓣的条件为d <λ2⁄。
阵列天线方向图的MATLAB实现
阵列天线方向图的MATLAB实现
陈天禄;郭燕红
【期刊名称】《西藏大学学报（自然科学版）》
【年(卷),期】2010(025)001
【摘要】天线的方向性是指电磁场辐射在空间的分布规律,文章以阵列天线的方向性因子F(θ,φ)为主要研究对象来分析均匀和非均匀直线阵天线的方向性.讨论了阵列天线方向图中主射方向和主瓣宽度随各参数变化的特点,借助MATLAB绘制出天线方向性因子的二维和三维方向图,展示天线辐射场在空间的分布规律,表现辐射方向图的特点.
【总页数】5页(P103-107)
【作者】陈天禄;郭燕红
【作者单位】西藏大学理学院,西藏拉萨,850000;西藏大学理学院,西藏拉
萨,850000
【正文语种】中文
【中图分类】TN82
【相关文献】
1.基于C++ Builder和Matlab实现天线方向图可视化软件的设计 [J], 王勋志;王玲丽
2.阵列天线方向图的MATLAB实现 [J], 陈天禄;郭燕红
3.基于Matlab的阵列天线方向图仿真 [J], 张承畅;余洒;罗元;徐余;陈银锋
4.基于WCA的阵列天线方向图综合算法研究及实现 [J], 仇亮;王云秀;郑霞;樊琴;
段寅龙;贾瑞林
5.基于WCA的阵列天线方向图综合算法研究及实现 [J], 仇亮;王云秀;郑霞;樊琴;段寅龙;贾瑞林
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
14元阵列天线方向图及其MATLAB仿真
阵列天线方向图及其MATLAB 仿真
1设计目的
1.了解阵列天线的波束形成原理写出方向图函数
2.运用MATLAB 仿真阵列天线的方向图曲线
3.变换各参量观察曲线变化并分析参量间的关系
2设计原理
阵列天线：阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整，这就使阵列天线具有各种不同的功能，这些功能是单个天线无法实现的。
在本次设计中，讨论的是均匀直线阵天线。
均匀直线阵是等间距，各振源电流幅度相等，而相位依次递增或递减的直线阵。
均匀直线阵的方向图函数依据方向图乘积定理，等于元因子和阵因子的乘积。
二元阵辐射场：
式中： 类似二元阵的分析，可以得到N 元均匀直线振的辐射场：
令 ，可得到H 平面的归一化方向图函数，即阵因子的方向函数：
式中：ζφθψ+=cos sin kd
均匀直线阵最大值发生在0=ψ 处。
由此可以得出
])[,(212121ζθθθϕθj jkr jkr m e r e r e F E E E E --+=+=12
cos ),(21jkr m e F r E E -=ψϕθθζ
φθψ+=cos sin kd ∑-=+-=10)cos sin (),(N i kd ji jkr m e e r F E E ζϕθθϕθ2πθ=)2/sin()2/sin(1)(ψψψN N A =kd
m ζϕ-=cos
这里有两种情况最为重要。
1.边射阵，即最大辐射方向垂直于阵轴方向，此时 ，在垂直于阵轴的方向上，各元观察点没有波程差，所以各元电流不需要有相位差。
2.端射振，计最大辐射方向在阵轴方向上，此时0=m ϕ或π，也就是说阵的各元电流沿阵轴方向依次超前或滞后kd 。
3设计过程
本次设计的天线为14元均匀直线阵天线，天线的参数为：d=λ/2，N=14相位滞后的端射振天线。
基于MATLAB 可实现天线阵二维方向图和三维方向图的图形分析。
14元端射振天线H 面方向图的源程序为：
a=linspace(0,2*pi);
b=linspace(0,pi);
f=sin((cos(a).*sin(b)-1)*(14/2)*pi)./(sin((cos(a).*sin(b)-1)*pi/2)*14);
polar(a,f.*sin(b));
title('14元端射振的H 面方向图 ，d=/2,相位=滞后');
得到的仿真结果如图所示：
14元端射振天线三维方向图的源程序为：
y1=(f.*sin(a))'*cos(b);
z1=(f.*sin(a))'*sin(b);
x1=(f.*cos(a))'*ones(size(b)); surf(x1,y1,z1);
2
πϕ±=m
得到的方向图和相位之间的关系图如图所示：
当天线各个阵元之间的间隔d=0.001m时，波长和方向图之间有一定的关系，其中程序代码如下：
clear;
sita=-pi/2:0.01:pi/2;
n=14;
d=0.001;
lamda1=0.002;
beta=2*pi*d*sin(sita)/lamda1;
z11=(n/2)*beta;
z21=(1/2)*beta;
f1=sin(z11)./(n*sin(z21));
F1=abs(f1);
figure(1);
lamda2=0.005;
beta=2*pi*d*sin(sita)/lamda2;
z12=(n/2)*beta;
z22=(1/2)*beta;
f2=sin(z12)./(n*sin(z22));
F2=abs(f2);
lamda3=0.01;
beta=2*pi*d*sin(sita)/lamda3;
z13=(n/2)*beta;
z23=(1/2)*beta;
f3=sin(z13)./(n*sin(z23));
F3=abs(f3)
plot(sita,F1,'b',sita,F2,'r',sita,F3,'k');
grid on;
xlabel('theta/radian');
ylabel('amplitude');
title('方向图与波长的关系');
legend('lamda=0.002','lamda=0.005','lamda=0.01');
得到的方向图和波长的关系如图所示；
从图中可以得到：随着波长lamda的增大，方向图衰减越慢，收敛性越不是很好。