弹簧刚度计算器
常用圆柱弹簧计算器-压缩与拉伸弹簧Excel计算表

有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - 3*d) / n
= 0.75
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 未平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - d) / n
= 0.775
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = L / n
= 0.8
mm
压并高度, H = d * (N + 1)
常用圆柱弹簧计算器
圆柱弹簧 - 圆线
压缩与拉伸弹簧强度计算
输入
试验载荷, P = 24.00
N
线径, d = 0.188
mm
弹簧中径, D = 2.000
mm
有效圈数, n = 10
-
材料的切变模量, G = 10,000,000
Mpa
输出
弹簧刚度系数, R = G*d^4 / (8*n*D^3)
= 19.52
= 3.125
mm
圆柱弹簧 - 方线
压缩与拉伸弹簧计算
试验载荷, 线截面厚, 线截面高, 弹簧中径, 有效圈数, 材料的切变模量,
弹簧刚度计算

8030 kgf/mm2
C=D2/d
弹簧中
径:
拉、压弹
1.1232
D2钢丝直
26.75
mm
簧: K
50
计 径:有效圈d 数:弹簧刚n
2.2
mm
20.25
材料: 65Mnτ
拼圈高度
度允:许极限
0.0607 kgf/mm 0.5949
N/mm
(参考)
负荷:
6.99
kgf 68.6
N
验
极限负荷 弹簧总变
簧: K
钢丝直
50
簧 径:有效圈d 数:弹簧刚n
0.7
mm
4
材料: 65Mnτ
拼圈高度
度允:许极限
0.2923 kgf/mm 2.8661
N/mm
负荷:
(参考)
P极3限负荷
0.97
kgf 9.5
N
设 66.6
弹簧总变
11.65217
材料剪切弹 性系数:
mm 3.3
mm
拉伸(压缩)弹簧计算 (方旋案绕比五:)
。
b≤3 b≤3
0.93 0.34
钢丝直径 弹簧中径
工作圈数
最小工作
负荷下变
n1
4.36
形量
最大工作
负荷下变
P1
26.60 kgf 形量
极限负荷
P2
34.70 kgf 下变形量
F1
7.00 mm 总圈数
最小工作
F2
9.00 mm 负荷
最大工作
F3
8.83 mm 负荷
最小工作
负荷下高
P3
35.77 kgf (长)度
弹簧刚度计算大全
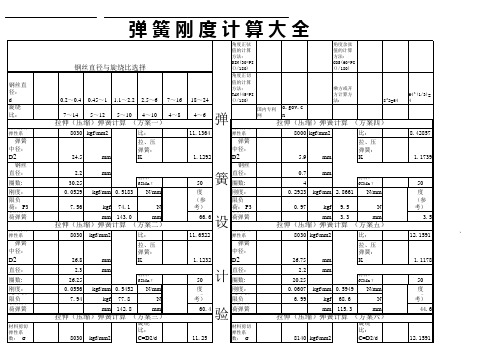
YII型 H
48.41 mm
C 5.7500
L型(不 加钩环 尺寸) H
24.00 mm
弹
簧
刚
度 :
P
`
0.0432 kgf/mm 0.4240 N/mm
允
许
极
限
负 荷
:
P
3
10.47 kgf 102.7
N
极
限 负
荷
弹
簧
总
变 形
量
:
f
3
242.2
mm
拼圈高 度
(参 考)
62.2
曲度系 数
K 1.2649
弹簧刚度计算大全
角度正弦 值的计算
角度余弦 值的计算
钢丝直径与旋绕比选择
方法: SIN(30*PI ()/180)
方法: COS(60*PI ()/180)
钢丝直 径:
d
0.2~0.4 0.45~1 1.1~2.2 2.5~6 7~16 18~24
角度正切 值的计算 方法: TAN(45*PI ()/180)
N
极
限
负
荷
弹 簧
总
变
形
量
:
f
3
4.2
mm
75
5
拼圈高 度
(参 考)
0
0
20
40
60
5.3
``
www.sip
乘方或开 方计算方 法:
8^2=64
64^(1/3)= 4
旋绕 比:
材料剪切 弹性系
7~14 5~12 5~10 4~10 4~8
拉伸(压缩)弹簧计算 (方旋绕案一)
8030 kgf/mm2
弹簧设计计算软件
L=n*l+钩 mm 316.44 环展开尺
寸
计算
公式
661.5 N/mm2
78500 N/mm2 203000 N/mm2
备注
2.16 mm
Mn'>Mn
合理
8
n)/(3667* Mn*D)= φn/Ψn=
23 工作极限扭矩 Mj
N.mm
787.5
Mj=(d^3* [σ BP])/(10* K)
24 最小工作扭矩 M1 25 工作极限扭矩下扭转角 φj
N.mm (°)
295
M1=φ 1/(Ψ'*n)
88 φj=Ψ '*n*Mj
步骤 原始条件
选材
系数选取
序号 1 2 3 4 5 6 7 8
9 10 11 12 13
14
15 16
17
18
19
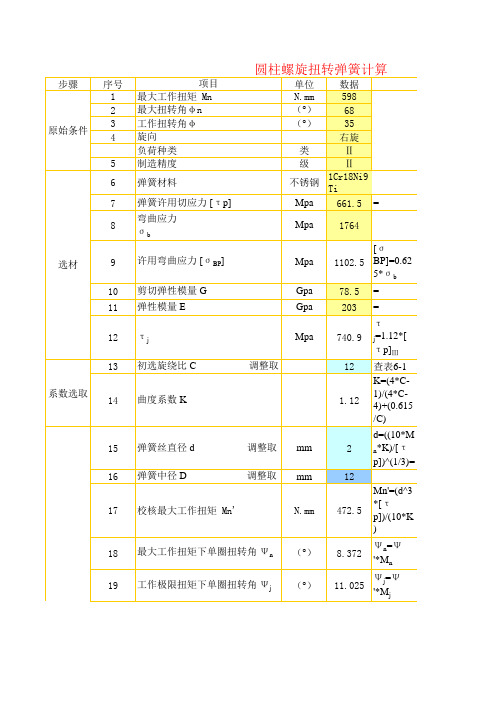
项目 最大工作扭矩 Mn 最大扭转角φn 工作扭转角φ 旋向 负荷种类 制造精度
弹簧材料
弹簧许用切应力 [τp] 弯曲应力 σb
许用弯曲应力 [σBP]
剪切弹性模量 G 弹性模量 E
圆柱螺旋扭转弹簧计算
(°) (°)
8.372 11.025
Ψn=Ψ '*Mn
Ψj=Ψ '*Mj
公式
Ψ
'=(3667*
20 在1N.mm扭矩作用下单圈扭转角Ψ' (°) 0.014 D)/(E*d^ 4)=Ψ
n/Mn l=((π
21 弹簧单圈展开长度 l
mm
37.68
*D)^2*t^ 2)^(1/2)
≈π*D
参数计算 22 有效圈数 n
26 最小工作扭矩下扭转角 φ1
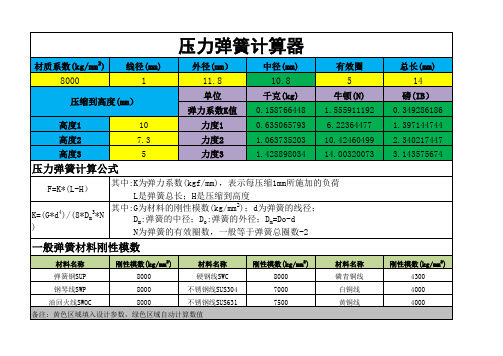
(完整版)压力弹簧力度计算器及计算公式
高度3
5
力度3
1.428898034 14.00320073
压力弹簧计算公式
F=K*(L-H)
其中:K为弹力系数(kgf/mm),表示每压缩1mm所施加的负荷 L是弹簧总长;H是压缩到高度
ቤተ መጻሕፍቲ ባይዱ
K=(G*d4)/(8*Dm3*N )
其中:G为材料的刚性模数(kg/mm2);d为弹簧的线径; Dm:弹簧的中径;Do:弹簧的外径;Dm=Do-d N为弹簧的有效圈数,一般等于弹簧总圈数-2
压力弹簧计算器
材质系数(kg/mm2) 线径(mm)
外径(mm)
中径(mm)
有效圈
8000
1
11.8
10.8
5
压缩到高度(mm)
单位 弹力系数K值
千克(kg) 0.158766448
牛顿(N) 1.555911192
高度1
10
力度1
0.635065793 6.22364477
高度2
7.3
力度2
1.063735203 10.42460499
总长(mm) 14
磅(IB) 0.349286186 1.397144744 2.340217447 3.143575674
刚性模数(kg/mm2) 4300 4000 4000
一般弹簧材料刚性模数
材料名称
刚性模数(kg/mm2)
材料名称
弹簧钢SUP
8000
硬钢线SWC
钢琴线SWP
8000
不锈钢线SUS304
油回火线SWOC
8000
不锈钢线SUS631
备注: 黄色区域填入设计参数,绿色区域自动计算数值
刚性模数(kg/mm2) 8000 7000 7500
压力弹簧刚度计算

压力弹簧刚度计算压力弹簧是一种常见的弹性元件,可以用于各种场合,例如汽车悬挂系统、机械设备、电子产品等。
计算压力弹簧的刚度是衡量其性能的重要指标之一,也是设计过程中必须考虑的参数之一压力弹簧的刚度可以用以下公式来计算:K=(Gd^4)/(8ND^3)其中,K是压力弹簧的刚度(N/mm),G是弹性模量(N/mm^2),d是线径(mm),N是圈数,D是直径(mm)。
在计算压力弹簧的刚度时,首先需要获得弹簧材料的弹性模量。
弹性模量是材料的重要力学特性之一,表示了材料在受力时的变形能力和恢复能力。
不同的材料具有不同的弹性模量,常见的弹簧材料有钢、铜、合金等。
在得到弹性模量后,可以开始计算压力弹簧的刚度了。
首先,需要测量弹簧的线径和直径。
线径是弹簧丝线的直径,直径是弹簧的外径。
在测量线径和直径时,需要使用准确的测量工具,例如游标卡尺、微量卡尺等,确保测量结果的准确性。
接下来,需要测量压力弹簧的圈数。
圈数是指弹簧的螺旋圈数,可以通过数圈的方式进行测量。
可以使用标尺或线尺量取弹簧两端之间的距离,然后除以弹簧的线径,得到圈数。
将测得的线径、直径和圈数代入上述的刚度计算公式中,就可以计算得到压力弹簧的刚度值。
刚度值的单位是N/mm,表示单位弹性变形时所受到的力大小。
在实际的工程应用中,压力弹簧的刚度是设计中的重要参数之一、根据实际需求和设计要求,可以通过调整材料、线径、直径等参数,来改变压力弹簧的刚度,从而满足不同的应用需求。
需要注意的是,压力弹簧的刚度计算是一个理论计算,并且只考虑了弹簧的几何尺寸和材料等因素。
实际应用中,考虑到各种实际因素的影响,例如弯曲、扭转、疲劳等,需要进行更为复杂的分析和计算。
因此,在实际工程中,常常需要进行试验和验证,以确保设计的可靠性和合理性。
总结起来,压力弹簧的刚度计算是压力弹簧设计中的关键步骤之一、通过计算,可以得到弹簧的刚度值,从而为设计和应用提供参考依据。
需要注意的是,在实际应用中,需要综合考虑各种因素的影响,并进行试验和验证,以确保设计的合理性和可靠性。
弹簧刚度计算以及校核

. 弹簧各刚度段的压并情况 F1 F2 F3 F4 F5 弹簧多级刚度 K1 K2 K3 59.86876 167.6475 #DIV/0!
第一拐点 99.16176 49 5936.692
弹簧拐点位置 第二拐点 第三拐点 153.1845 70 80 14993.47 #DIV/0!
弹簧设计校核
项目 设计核算 余隙t 1.25 旋绕比C 5.6 曲度系数K 1.272864907 螺旋升角α=arctan(t/πd) 高比径b 4.629285714 压并长度Lb 175 标准范围 >0.1d 4~8 <1.35 5~度计算 k1 k2 圆柱弹簧刚度计算 k1' K2' k3' 弹簧总长计算L 弹簧总长计算L 有效圈n 节距t 3 28 刚度 322.4401945 #DIV/0! 刚度 93.12458242 349.2171841 #DIV/0! G 78500 78500 G 78500 78500 78500 d 12.5 12.5 d 12.5 12.5 12.5 D2小中 55 0 D1大中 70 70 D1大中 70 70 70
选最大Pn
<1200
n有 3 0 n有 7.5 2 0 12.5 圆柱部分 0 0 力值(N) 14993.46905 #DIV/0! 5936.692129 13549.62674 #DIV/0! P拐点 (t1-d)*n1*k1*k2/(k2-k1) ### ###
4330.293083
K4 0
钢丝直径
324.05 圆锥部分 0 0
7.5 21
圆柱部分 2 31.9
弹簧一级刚度结论 两端圆锥不含圆柱 #DIV/0! 两端圆锥单级距圆柱 #DIV/0! 两端圆锥双级距圆柱 #DIV/0! 两端圆锥三级距圆柱 #DIV/0! 322.4401945 单圆锥不含圆柱 72.25614426 单圆锥单级距圆柱 59.86876401 单圆锥双级距圆柱 #DIV/0! 单圆锥三级距圆柱 圆柱等级距 93.12458242 圆柱双级距 73.51940718 圆柱三级距 #DIV/0! 弹簧理论重量计算 材料密度ρ(Kg/mm3) 0.0000078 截面积S(mm2) 122.7184609 钢丝长度L(mm) 3118.030656 理论重量(Kg) 理论重量(Kg) 2.985 按公斤价(元/Kg) 11.5 价格上浮 0% 单件计算价格( 34. 单件计算价格(元) ¥34.32
弹簧刚度计算

·压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;
拉力弹簧
拉力弹簧的k值与压力弹簧的计算公式相同
·拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。
拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不平均的现象。
所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。
·初张力=P-(k×F1)=最大负荷-(弹簧常数×拉伸长度)
·拉力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;
·弹簧常数:以k表示,当弹簧被拉伸时,每增加1mm距离的负荷(kgf/mm);
·弹簧常数公式(单位:kgf/mm):
G=线材的钢性模数:碳钢丝G=79300 ;不锈钢丝G=697300 ,磷青铜线G=4500 ,黄铜线G=350 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
扭力弹簧
·弹簧常数:以k 表示,当弹簧被扭转时,每增加1°扭转角的负荷(kgf/mm).
·弹簧常数公式(单位:kgf/mm):
E=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
R=负荷作用的力臂
p=3.1416。
