如何证明正多面体只有正四面体 正六面体 正十二面体 和正二十面体
什么是多面体有哪些常见类型

什么是多面体有哪些常见类型在我们的日常生活和数学世界中,多面体是一个常见而又有趣的概念。
那到底什么是多面体呢?简单来说,多面体是由多个平面多边形所围成的立体图形。
多面体的每个平面多边形都被称为多面体的面,两个面的公共边叫做多面体的棱,多条棱的公共顶点叫做多面体的顶点。
多面体有着各种各样的类型,下面我们就来介绍一些常见的多面体。
首先,我们来认识一下棱柱。
棱柱是一个相当常见的多面体类型。
它有两个互相平行且全等的底面,侧面都是平行四边形。
如果棱柱的底面是三角形,那就叫做三棱柱;底面是四边形,那就是四棱柱,以此类推。
比如,我们常见的长方体就是一种四棱柱,它的六个面都是矩形。
接下来是棱锥。
棱锥有一个多边形的底面,其余各面都是有一个公共顶点的三角形。
如果底面是三角形,那就是三棱锥,也叫四面体,因为它有四个面。
如果底面是四边形,那就是四棱锥。
棱锥的顶点到底面的距离叫做棱锥的高。
还有棱台,棱台可以看作是用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分就是棱台。
棱台的上下底面是相似的多边形。
再说说正多面体。
正多面体是指各个面都是全等的正多边形,并且各个多面角都是全等的多面角。
正多面体只有五种,分别是正四面体、正六面体(也就是正方体)、正八面体、正十二面体和正二十面体。
正四面体的四个面都是等边三角形,它是最简单也是最对称的正多面体。
正方体大家就更熟悉了,六个面都是正方形,十二条棱长度相等,八个顶点。
正八面体是由八个等边三角形围成的,它有六个顶点。
正十二面体有十二个正五边形的面,二十个顶点。
正二十面体则由二十个等边三角形组成,有十二个顶点。
多面体在我们的生活中有着广泛的应用。
在建筑设计中,许多建筑物的外形都可以看作是由不同的多面体组合而成。
比如,一些现代的体育馆、展览馆,其独特的造型往往包含了各种多面体的元素。
在包装设计中,多面体的结构也经常被运用,以达到节省材料、增加稳定性等目的。
在数学研究中,多面体的性质和相关定理也是一个重要的领域。
正多面体只有5种的又一证法

vt
= 2e ,即
v
=
2e t
.
正多面体每个面由 h 条边围成 ,则 f h =
2e ,即
f
=
2e h
.
把
v
=
2e t
,
f
=
2 e代入
h
(1)
式得
2e t
-
e
+
2e h
=
2
,
∴e
=
2
h
-
2 ht ht
+
2
t
(2)由Biblioteka (2) 得 2 h - ht + 2 t > 0 ,
32
数 学 通 讯 2003 年第 1 期
正多面体只有 5 种的又一证法
周素芬
(集美中学 ,福建 361021)
中图分类号 :O123. 3 文献标识码 :A 文章编号 :0488 - 7395 (2003) 01 - 0032 - 01
瑞士数学家欧拉在 1752 年发现各种正
多面体均有的关系 :
v - e + f = 2
(1)
其中 v , e , f 分别表示凸多面体的顶点数 、棱
数及面数. (1) 式后人称为欧拉公式 , 它在空
间图形及图论中有许多重要应用.
所谓正多面体是指多面体的各个面均是
全等正多边形 , 每个正多面体的各边的长和 顶角的交角均相等. 那么空间有多少种不同 正多面体 ? 本文对此问题给出了一种新的简 便论证方法.
正四面体 正八面体 正六面体
正十二面体 正二十面体 图 1 正多面体
参考文献 :
正多面体证明

正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。
证明
顶点数V,面数F,棱数E
设正多面体的每个面是正n边形,每个顶点有m条棱。
棱数E应是面数F与n的积的一半(每两面共用一条棱),即
nF=2E--------------①
同时,E应是顶点数V与m的积的一半,即
mV=2E--------------②
由①、②,得
F=2E/n,V=2E/m,
代入欧拉公式V+F-E=2,
有
2E/m+2E/n-E=2
整理后,得1/m+1/n=1/2+1/E.
由于E是正整数,所以1/E>0。
因此
1/m+1/n>1/2--------------③
说明m,n不能同时大于3,否则③不成立。
另一方面,由于m和n的意义(正多面体一个顶点处的棱数与多边形的边数)知,m≥3且n≥3。
因此m和n至少有一个等于3当m=3时,因为1/n>1/2-1/3=1/6,n又是正整数,所以n只能是3,4,5
同理n=3,m也只能是3,4,5
所以有以下几种情况:
n m类型
33正四面体
43正六面体
34正八面体
53正十二面体
35正二十面体
由于上述5种多面体确实可以用几何方法作出,而不可能有其他种类的正多面体所以正多面体只有5种。
立体几何——正多面体专题

立体几何——正多面体专题
一、引言
立体几何研究了空间中的各种几何形状及其性质。
正多面体是指拥有相等大小的正多边形作为面的多面体。
本文将深入探讨正多面体的定义、分类及特性。
二、定义
正多面体是由相等的正多边形完全围成的几何体。
它们具有以下特点:
- 每个面都是相等的正多边形。
- 每个顶点都相连于相等数量的边。
- 每个边都与相等数量的面相接。
三、分类
根据面的数量,正多面体可以分为以下几类:
1.三个面:三角形棱柱和三角形棱锥。
2.四个面:四面体和正四面体。
3.八个面:八面体和正八面体。
4.二十个面:二十面体和正二十面体。
四、特性
正多面体具有一些独特的特性:
1.对称性:正多面体在各个面和顶点上具有对称性,这使其在空间中呈现出美感。
2.空间效率:正多面体在空间中填充效率高,因此在建筑、工程和科学领域具有广泛的应用。
3.共面性:正多面体的面都可以完全位于同一个平面内。
五、结论
正多面体作为立体几何中的重要概念,不仅具有美学价值,还有着实际应用。
通过了解正多面体的定义、分类及特性,我们可以更好地理解空间中的几何形状,并将其运用到实际场景中。
参考文献:
[1] 张三。
李四。
王五。
空间几何学导论[M]。
北京:科学出版社。
2010.
[2] 陈六。
赵七。
欧几里得几何学基础[M]。
上海:___。
2008.。
正多面体-高中数学知识点讲解
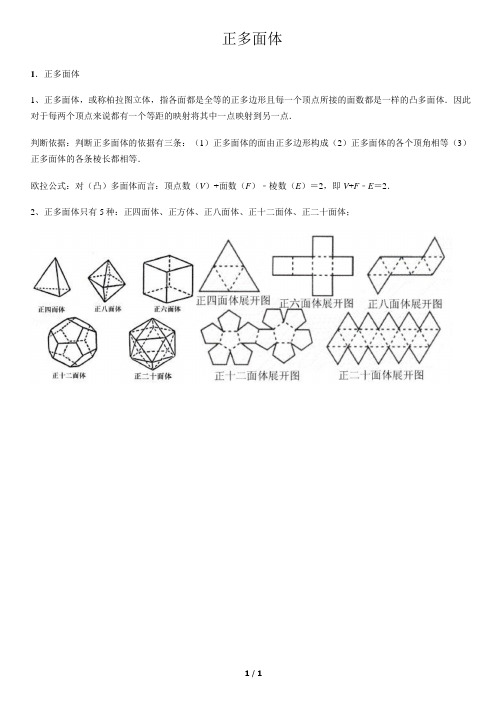
正多面体
1.正多面体
1、正多面体,或称柏拉图立体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体.因此对于每两个顶点来说都有一个等距的映射将其中一点映射到另一点.
判断依据:判断正多面体的依据有三条:(1)正多面体的面由正多边形构成(2)正多面体的各个顶角相等(3)正多面体的各条棱长都相等.
欧拉公式:对(凸)多面体而言:顶点数(V)+面数(F)﹣棱数(E)=2,即V+F﹣E=2.
2、正多面体只有 5 种:正四面体、正方体、正八面体、正十二面体、正二十面体;
1/ 1。
常见正多面体总结-六面体八面体十二面体和二十面体
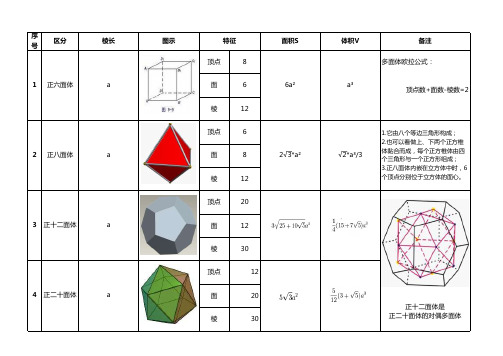
序号
区分
棱长
图示 顶点
特征ቤተ መጻሕፍቲ ባይዱ8 6 12 6 8 12 20 12 30 12 20 30
面积S
体积V
备注 多面体欧拉公式:
1
正六面体
a
面 棱 顶点
6a²
a³
顶点数+面数-棱数=2
2
正八面体
a
面 棱 顶点
2√3*a²
√2*a³/3
1.它由八个等边三角形构成; 2.也可以看做上、下两个正方椎 体黏合而成,每个正方椎体由四 个三角形与一个正方形组成; 3.正八面体内嵌在立方体中时,6 个顶点分别位于立方体的面心。
3
正十二面体
a
面 棱 顶点
4
正二十面体
a
面 棱
正十二面体是 正二十面体的对偶多面体
多面体欧拉定理的发现 (1)2

多面体欧拉定理的发现我们知道,平面多边形由它的边围成,它的顶点数与边数相等,按边数可以对多边形进行分类,同类的多边形具有某些相同的性质。
多面体是由它的面围成立体图形,这些面的交线形成棱,棱与棱相交形成顶点。
在研究多面体的分类等问题中,人们逐步发现它的顶点数,面数和棱数之间有特定的关系。
以下我们将体验这种关系的发现及证明过程。
探索研究问题1:下列共有五个正多面体,分别数出它们的顶点数V、面数F和棱数E,并填表1观察表中填出的数据,请找出顶点数V、面数F及棱数E之间的规律。
教师巡视指导,如正十二面体,先定面数E=12;再定棱数,每个面有5条棱,共有12×5=60条,由于每条棱都是两个面的公共边,所以上面的计算每条棱被算过两次,于是棱数E=60/2=30;最后算顶点数,每个顶点处连有三条棱,所以它共有3V条棱,又因为每条棱连着两个顶点,所以上面的计算每条棱被算过两次,因此实际上只有3V/2条棱,即E=3V/2,所以V=20。
表1中多面体的面数F都随顶点数目V的增大而增大吗?(不一定).请举例说明.(如八面体和立方体的顶点数由6增大到8,而面数由8减小到6).此时棱的数目呢?(棱数都是一样的).所以我们得到:棱的数目也并不随顶点数目的增大而增大.大家从表中还发现了其他的什么规律,请积极观察,勇于发言.(当多面体的棱数增加时,它的顶点与面数的变化也有一定规律).上面的归纳引导去猜想,棱数与顶点数+面数即E与V+F是否有某种关系,请大家按这个方向考察表中的数据,发现并归纳出它们都满足的关系.(积极验证,得出)V+F-E=2以上同学们得到的V+F-E=2这个关系式是由表1中的五种多面体得到,那么这个关系式对于其他的多面体是否也成立吗?请大家尽可能的画出多个其他多面体去验证.(许多同学可能举出前面学过的图形)四棱锥、五棱锥、六棱柱等.(教师应启发学生展开想象,举出更多的例子)一个三棱锥截去含3条棱的一个顶得到的图形、一个立方体截去一个角所得的图形等.好,同学们现在想象,例如:n棱锥在它的n边形面上增加一个“屋顶”或截去含n条棱的一个顶后,刚才的猜想是否成立?能证明吗?所得的多面体的棱数E为3n条,顶点数V为2n个,面数V为2+n 个,因2n +(2+n )-3n =2,故满足V +F -E =2这个关系式.请继续来观察下面的图形,填表2,并验证得出的公式工V +F -E =2_A(学生观察,数它们的顶点数V、面数F、棱数E,并填入表2,可能有些同学出错,教师在巡视时要及时给予指导,帮助学生填完)观察你们的数据,请验证这些图形是否符合前面找出的规律吗?其中哪些图形符合?一起来设想问题1和问题2中的图形.在某个橡皮膜上,当橡皮膜变形后,有的地方伸长、有的地方压缩,但不能破裂或折叠,橡皮膜上的图形的形状也跟着改变,这种图形的变化过程我们称之为连续变形.那么请大家试想这些图形中的哪些在连续变形中最后其表面可变为一个球面?问题1中的(1)~(5)和问题2中的(1)个图形表面经过连续变形能变为一个球面.请同学们继续设想问题2中⑴~⑻在连续变形中,其表面最后将变成什么图形?问题2中第⑻个图形;表面经过连续变形能变为环面像以上那些在连续变形中,表面能变为一个球面的多面体叫简单多面体.请大家判断我们前面所学的图哪些是简单多面体?棱柱、棱锥、正多面体、凸多面体是简单多面体.简单多面体的顶点数V、面数F的和与棱数E之间存在规律V+F -E=2.我们将它叫做欧拉公式,以上3个问题的解决让我们体会到了数学家欧拉发现V+F-E=2的过程.那么如何证明欧拉公式呢?请大家打开课本P65的欧拉公式证明方法中的一种,认真体会它的证明思路和其间用到的数学思想.(学生自学、教师查看,发现问题,收集问题下节课处理)在欧拉公式中,令f(p)=V+F-E。
正多面体证明范文

正多面体证明范文正多面体是指所有的面都是正多边形的立体形状。
在数学中,有五种常见的正多面体,分别是四面体、六面体(或立方体)、八面体、十二面体和二十面体。
下面将分别对这些正多面体进行证明。
首先来证明四面体是正多面体。
四面体由四个三角形组成,每个三角形都是正三角形,因此四面体的每个面都是正多边形。
此外,四面体的每个顶点处有三个面相交,且每个面都能通过相邻两个面沿边构建正角,满足正多面体的性质。
因此,四面体是正多面体。
接下来证明六面体(或立方体)是正多面体。
六面体由六个正方形组成,每个面都是正方形,因此满足正多面体的定义。
此外,六面体的每个顶点处有三个面相交,且每个面都能通过相邻两个面沿边构建正角,满足正多面体的性质。
因此,六面体是正多面体。
再来证明八面体是正多面体。
八面体由八个正三角形组成,每个面都是正三角形,满足正多面体的定义。
此外,八面体的每个顶点处有四个面相交,且每个面都能通过相邻三个面沿边构建正角,满足正多面体的性质。
因此,八面体是正多面体。
继续证明十二面体是正多面体。
十二面体由十二个正五边形组成,每个面都是正五边形,满足正多面体的定义。
此外,十二面体的每个顶点处有五个面相交,且每个面都能通过相邻四个面沿边构建正角,满足正多面体的性质。
因此,十二面体是正多面体。
最后证明二十面体是正多面体。
二十面体由二十个正三角形组成,每个面都是正三角形,满足正多面体的定义。
此外,二十面体的每个顶点处有五个面相交,且每个面都能通过相邻三个面沿边构建正角,满足正多面体的性质。
因此,二十面体是正多面体。
综上所述,四面体、六面体、八面体、十二面体和二十面体都是正多面体。
每个正多面体都有对应的面数、边数和顶点数,可以通过欧拉公式进行验证。
欧拉公式表达为:V+F-E=2,其中V代表顶点数,F代表面数,E代表边数。
对于正多面体,欧拉公式可以写为V+F-E=2、根据每个正多面体的顶点数、面数和边数计算,都能满足欧拉公式。
