第三章 稳恒电流
稳恒电流与电场

J E
dU dI ds dl
dI 1 dU ds dl
电导率
电流密度与电场强度点点对应关系 四、焦耳楞次定律的微分形式: 我们熟悉的焦耳楞次定率 其微分形式是
2 2
2 U p I 2R R 2
we E
2
dl p I R j ds小 J dI 1、电流密度矢量: ds 2、电流场: 电流线:曲线的切线方向和该点 的电流密度方向一致
I
三、欧姆定律的微分形式: J E
欧姆定律
电阻
s
J ds
s
J cosds
dU dI R
dl
dI
dU
dl R ds
ds
R
r2
r1
r2 dr ln 2ra 2a r1
r2
r1
单位长度漏电阻
r2 R ln 2 r1
'
7
解、设径向漏电流为I,两导体间任意点的电流密度
I J 2ra
而
J E
I E 2ra
内外导体之间的电位差
U
r2
r1
r2 I Edr ln 2a r1
r2 U R ln I 2a r1
r2 R ln 2 r1
'
8
稳恒电流 与电场
1
稳恒电流与电场
一、稳恒电流与稳恒电场形成电流的条件:
1、电流:电荷有规则移动形成电流 2、形成电流的条件:有可以自由移动的电荷; 存在电场。 3、电流强度: 电流的方向:本身是标量, 规定正电荷流动的方向为正 电流强度的大小: I 单位:安培
dq dt
第三章 静电场和稳恒磁场1

y
r′
q′
r
q x
( x, y , z ) x = 0 = 0
(1)
ε
z
q
2
O v n 1 2 ε
q
4πε ( x a ) + y 2 + z 2 4πε r 由对称性:a, 0, 0 ) , q ( a, 0, 0 ) , q′ = q : (
r = 3ε 0 E 0 c o s θ
r=a
由真空中电偶极矩 v 在真空中产生的电势
P
v v P r = 4π ε 0 r 3
P P cos θ = 4π ε 0 r 2
v P = 4π ε 0 E 0 a 3
例2.
P75
解:电势是球对称,则 b1 1 = a1 + (R > R3 ) R b2 2 = a2 + ( R 2 > R > R1 ) R 条件:
v δ (x) = 0
v
∫ δ ( x )dV = 1
v x≠0 v x = 0 ∈V
v v x δ x x′ 表示 ( ) v 与 x = 0 的 δ 函数定义相较,则有
v v δ ( x x′) = 0
v v
v 处于 x′点上的单位点电荷密度用函数
∫ δ ( x x′)dV = 1
v v x ≠ x′ v x′ ∈V
1) 2 3) σ ∴
R = R1
R3
2
R2 R1 1
= 1
R→ ∞
= 0, 2 ) 2 ,σ
R = R3 2
R = R2
= 1
R = R3
1
= ε0
1 R
= ε0
2 R
大物电磁学课后答案3经典.ppt
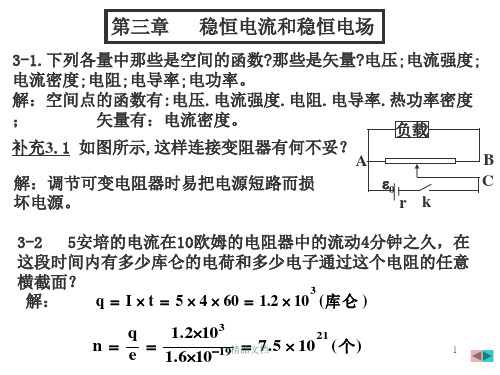
(1)电流强度在10秒内均匀的有零增加到3安培; (2)电流强度从18安培起,每过0.01秒减少一半,直到零。
解:(1)I 3 t 10
q
I dt
010
t 10
dt
15(库 仑)
(2)q I0k
1 2
I
0k
1 4
I0k
I0k(1 1 / 2 1 / 4 ) 180.011/(11/ 2)0.36(库 仑)
安培起,每过0.01秒减少一半,直到零。求导线产生的热量。
解:
3
2
(1) I 10 t dQ I rdt
| Q
t
(
3
t)2 Rdt
3
Rt3
10
180(焦)
0 10
10 0
2
2
2
(2) Q Q1 Q 2 Q 3 I1 Rt I 2Rt I 3Rt
Rt[I02
(
I0
/
2)2
电势差为4.25伏特,当该电池放电时,通过的电流为4安培两极
间的电势差为3.90伏特,求该电池的电动势和电阻。
解:
I1r 4.25 I 2r 3.90
精品文档
r
0.05(欧 4.10(伏
姆) 特)
6
3-10 设在图中所示的电路中,三个电容开始时均不带电,求将 它们与A、B、C点联结后,各极板上的电量。
7
补 Rr;3(2==充330)..3a06.,欧欧4d一姆姆两电,,点R路4求电=如1:势.(图01差欧),通其;姆(过中4,)每bb1点,=个c6接.电两0地伏阻点,,的电rR1电1势==01流差.04.;(00(5欧欧2))a姆姆每,b,,个,c2R电=,28d=源.各20.的伏点5欧端特电姆电势,压。
稳恒电流

B
A B
电源
1. 电源:提供(产生)非静电力 Fk (非静电场 Ek Fk q )的装置(器件) (电源的正极、负极;电源内电路;电 源外电路)
2. (电源)电动势 :定量反映电源中 非静电场作功能力大小的物理量
Ek dl Ek dl B 或 Ek dl ( Ek dl 0) 外
解:由欧姆定律
I R r
i i
0
A
i
r
B
VA VB 0
r
在恒定电流的电路中,电路中电流 为零,电路两端电势差可以不为零; 电路中电流不为零,电路两端电势差 可以为零!
三.基耳霍夫定理的应用
1.电势差计 A. 当开关与标准电池接通时: (1)任选回路的 绕向方向和假设各 支路的电流方向
I R r
i i
i
2. 一段电路两端电势差(电压)
U AB VA VB i IRi Iri
(一段电路两端电势差等于电路上 各电势降落的代数和)
正负号选定规则
第二节.基尔霍夫定理 一.基尔霍夫第一定理: 节点:三条或三条以上的通电导线的会合点。 支路:两节点间的一段电路。
(3):符号规定用一句话可表示为:在绕行方向 上,电压降低则为负,电压升高则为正.
例题一:一复杂的电路中, 计算一段电路两端电势差
U AB
1 I1R1 I1r1 2 I 2 R2 I 2 r2
UCD 3 I 3 R3 I 3r3
例题二:图示 1 2 r 和 R , 求电路中电流及 U AB U A U B
0.4( A)
高等电磁理论第三章答案3

第三章 稳恒电流场的边值问题3-1 在电导率为σ的均匀半空间表面布以相距2L 的电极A 和B ,并分别以I +和I -向媒质中供电。
试根据电场的叠加原理,求出A 和B 两个点电流源在表面上M 点形成的电位。
解:易知点电流源A 在介质中任意一点产生的电位为2A I RΦπσ=,同理可得点电流源B 在介质中任意一点产生的电位为2B IRΦπσ=-,则叠加后介质中任意一点的总电位为22A BI IR R Φπσπσ=-对于表面上一点M (设其坐标为(0)x ,)而言,||A R x L =+,||B R x L =-,则有22||||2||2||2||I I I x L x L x L x L x L Φπσπσπσ--+=-=+--3-2 当地表水平、地下为均匀各向同性岩石时,在地层表面布以相距2L 的电极A 和B ,并分别以电流强度I +和I -向地下供电,在地下建立稳定电流场。
试解答如下问题:(1)求A 和B 连线中垂线上h 处电流密度h j 的表达式;(2)计算并绘图说明深度为h 处的电流密度h j 随AB 的变化规律;(3)确定使h j 为最大时,供电电极距AB 与h 的关系式。
解:(1)易知点电流源A 在介质中任意一点产生的电位为2A IRΦπσ=,则31()()()=22A I I E R RσσΦσπσπ==⋅-∇=⋅-⋅∇Rj 同理可得点电流源B 在介质中任意一点产生的电流密度为32B I Rπ=-Rj ,叠加后得介质中任意一点的电流密度为3322A BA BI I R R ππ=-R R j 在A 、B 连线的中垂线上,A B R =R ,A B =2L ρ-R R e ,则有3322222()I I L L R L h ρρππ=⋅=⋅+j e e (2)(3)设3222()()f L L L h -=⋅+,对其求导可得35'2222222()()3()f L L h L L h --=+-+令其等于0,得22230L h L +-=,解得L = 故h j 为最大时电极距AB 与h 的关系为22AB L ===3-3 在习题3-2中,电极距AB 时,均匀各向同性半空间中h 深度处的电流密度最大。
《电磁学》赵凯华陈熙谋No3chapter答案

第三章 稳 恒 电 流§3.1 电流的稳恒条件和导电规律思考题:1、 电流是电荷的流动,在电流密度j ≠0的地方,电荷的体密度ρ是否可能等于0? 答:可能。
在导体中,电流密度j ≠0的地方虽然有电荷流动,但只要能保证该处单位体积内的正、负电荷数值相等(即无净余电荷),就保证了电荷的体密度ρ=0。
在稳恒电流情况下,可以做到这一点,条件是导体要均匀,即电导率为一恒量。
2、 关系式U=IR 是否适用于非线性电阻?答:对于非线性电阻,当加在它两端的电位差U改变时,它的电阻R要随着U的改变而变化,不是一个常量,其U-I曲线不是直线,欧姆定律不适用。
但是仍可以定义导体的电阻为R=U/I。
由此,对非线性电阻来说,仍可得到U=IR的关系,这里R不是常量,所以它不是欧姆定律表达式的形式的变换。
对于非线性电阻,U、I、R三个量是瞬时对应关系。
3、 焦耳定律可写成P=I 2R 和P=U 2/R 两种形式,从前者看热功率P 正比于R ,从后式看热功率反比于R ,究竟哪种说法对?答:两种说法都对,只是各自的条件不同。
前式是在I一定的条件下成立,如串联电路中各电阻上的热功率与阻值R成正比;后式是在电压U一定的条件下成立,如并联电路中各电阻上的热功率与R成反比。
因此两式并不矛盾。
4、 两个电炉,其标称功率分别为W 1、W 2,已知W 1>W 2,哪个电炉的电阻大? 答:设电炉的额定电压相同,在U一定时,W与R成反比。
已知W 1>W 2,所以R1<R 2,5、 电流从铜球顶上一点流进去,从相对的一点流出来,铜球各部分产生的焦耳热的情况是否相同?答:沿电流方向,铜球的截面积不同,因此铜球内电流分布是不均匀的。
各点的热功率密度p=j 2/σ不相等。
6、 在电学实验室中为了避免通过某仪器的电流过大,常在电路中串接一个限流的保护电阻。
附图中保护电阻的接法是否正确?是否应把仪器和保护电阻的位置对调? 答:可以用图示的方法联接。
稳恒电流知识介绍

非静电力场强 二.电动势
EK
FK q
把单位正电荷经电源内部由负极移向正极
过程中 非静电力所作的功
EK dl EK dl
L
第三章 稳恒电流 steady current(自学)
从场的角度认识 内容要点 §1 电流和电流密度 一.电流强度 大小:单位时间内通过导体某一横截面的电量
I dq dt
方向:正电荷运动的方向 单位:安培
二.电流密度 current density
1.电流密度 J dI dS
dI
ds
ds
导体中某点的电流密度,数值上等于和该点正电荷定 性移动方向垂直的单位面积上的电流强度。
稳恒电场对运动电荷作功 稳恒电场的存在 总伴随着能量的转移
§3 欧姆定律的微分形式
导体中任一点电流密度的方向(正电荷运动的
方向)和该点场强方向相同
有关系式
J E
§4 电动势 electromotive force (emf)
一.电源及电源的作用 source of emf
非静电力 non-electrostatic force
对于稳恒电路 导体内存在电场 稳恒电场 由不随时间改变的电荷分布产生
2.和静电场比较
相同之处
电场不随时间改变
满足高斯定理 满足环路定理 是保守场
可引入电势概念
LE dl 0
回路电压定律(基尔霍夫第二定律)
在稳恒电路中 沿任何闭合回路一周的电势 降落的代数和等于零
不同之处
产生稳恒电流的电荷是运动的电荷 电荷 分布不随时间改变
方向:该点正电荷定向移动的方向。
2.电流密度和电流强度的关系
I SJ ds
dI Jds J ds
稳恒电流的闭合性及导电规律

第三章 稳恒电流前几章(真空、导体与电介质)为静电学,涉及静止电荷的电现象;本章论述有关运动电荷知识。
带电粒子运动伴有电量迁移而形成电流,若电流不随t 而改变,则称为稳恒电流,即直流(DC)。
研究方法:路论,重点以金属导体为例研究规律及计算。
§1 稳恒电流的闭合性及导电规律一、电流电荷的定向移动形成电流。
1、产生电流的条件产生电流需要两方面的条件:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧.;);(.;);(,机械作用等化学作用本章以此为主电场作用的某种作用有迫使电荷作定向运动对半导体中:电子、空穴离子、电子流电解液、气体中:正负本章以此为主金属中:自由电子即载流子荷存在可以自由移动的电 2、电流方向惯例规定:正电荷流动的方向。
多数情况下导电由负电荷引起,而正电荷沿某方向定向运动与负电荷沿反方向运动产生相同效果(注:有例外,如霍耳效应)。
二、电流强度和电流密度矢量1、电流强度I金属中自由电子作无规则热运动,即使在K T 0=,仍s m u 610≈热,但0=热u 。
故无宏观净电量迁移。
定向运动形成宏观净电荷迁移,此定向运动为漂移运动v需由电场提供力作用来完成,漂v 虽小,约为104-sm 量级,但却形成宏观电流。
电流强弱用电流强度I 描述,定义如下:dtdq I =即导体中单位时间通过的某一给定截面的电量为通过该面的电流强度。
(不涉及导体截面粗细和截面上电流详细分布)。
[说明](1) I 为标量,单位为:安培(A )—— SI 制中基本单位之一。
秒库安11=, A mA A μ6310101==(2) 仅粗略描述单位时间内通过某一曲面(可大可小、可任意形状)的总电量,不够点点详细,如图4-1所示。
(a) I 相同,但分布有别 (b) 高频趋肤(c) 电阻法探矿 (d) 用电流场模拟静电场图4-1下面引入电流密度矢量J详细描述电流场分布。
2、电流密度矢量J),,(z y x J J=是空间坐标的矢函数,其定义为:⎪⎪⎩⎪⎪⎨⎧⋅=⊥,即电流方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r e r 自由电子加速度: a = − m E
r 其平均值称为漂移速度,形成宏观电流,设为 u
加外电场: 电子速度 = 原来的速度 + 附加定向速度
T1
T2
T2
∫σ
B
(T )d T
T2
T1
应用
温差电偶(热电偶), 用于测温。测量范围广, 灵敏 度、准确度高,敏感面和热容量小 温差电堆(热电堆),可用作电源 20 半导体制冷
例题2: 平行板电容器极间充满两层均匀电介质,其厚
度为d 1和d 2,电导率为σ1和σ2,介电常数为ε1和ε2 。 设极间电压为V, 忽略边缘效应, 计算: ⑴ 通过电容器的电流密度
k =1 n
电流管
3
r 二. 电流密度矢量 j
1.
r dI r n 定义: j = dS ⊥ 单位垂直面积通过的电流强度 ⎧ 大小: r ⎨ ⎩ 方向: n 电流的方向
r r dI = jdS ⊥= j cos θdS = j ⋅ dS
电流强度是电流密度的通量: I = ∫∫
r r 2. 电流连续方程: j ⋅ dS = − d q ∫∫ dt S
(电荷守恒)
S
r r j ⋅ dS
r ∂ρ ∇⋅ j + =0 ∂t
4
r r 3. 电流稳恒条件: ∫∫ j ⋅ dS = 0
S
r ∇⋅ j = 0
三. 欧姆定律
r r 稳恒电场与静电场相似,有 ∫ E ⋅ d l = 0
L
1. 欧姆定律
U I= R
1 G I = GU, = R
——可引入 “电压”
即:汇于节点的各支路的电流的代数和为零. 对于具有n个节点的多回路电路,有n-1个独立的 节点电流方程.
约定:
1. 对已知电流,从节点流出者为正,流入节点者为负 2. 对未知电流,按标定方向,流出冠以“+”,流入冠 以“-”;(解出的结果,正者与标定方向相同,负者与 标定方向相反)
23
二. 基尔霍夫第二定律 (回路电压方程):
路端电压: U =ε − Ir
r K
r j
r E
( ,r) ε
ε = Ir + IR (能量守恒) ε I = I 2r + I 2 R
R
r K
r j
3. 电源充电情况
充电:电流从正极经电源内流向负极 + dl ε = − Ir + U (推导过程?) r = ∫− (内)σS 路端电压: U =ε + Ir IU =ε I + I 2 r (能量守恒)
d1
ε1
σ1
d2 ⑵ 两极间电场强度的分布 ⑶ 两介质分界面上的束缚电荷面密度 ⑷ 两介质分界面上的自由电荷面密度
ε2 σ 2
V
答:
j=
σ 1σ 2 V σ 2 d1 + σ 1d 2
σ 2V E1 = σ 2d1 + σ1d2
σ 1V E2 = σ 2 d1 + σ 1d 2
(ε − ε )σ − (ε 2 − ε 0 )σ 1 ′= 1 0 2 σ V σ 2 d1 + σ 1d 2
(ε 2σ 1 − ε 1σ 2 ) σ= V σ 2 d1 + σ 1d 2
21
§3 基尔霍夫定律
节点:三条及三条以上导线的连接点 支路:两相邻节点间,由电阻、电源串联而成的不 含其它节点的电流通路 回路:由几条支路构成的闭合电路 独立回路:回路中至少有一条支路是其它回路中 所没有的回路
22
一.基尔霍夫第一定律 (节点电流方程): ∑I = 0
§2 电源与电动势
一. 非静电力和电源电动势 1.非静电力
电源外:在电场力作用下,电荷运动;
L
r K
A
I r E
B
电源内:电场力阻止正电荷自电源负极移至正极;必 须靠非静电力克服电场力做功,使正电荷自负极移至 正极,以维持电荷分布不变,保持稳恒态。
K:作用在单位正电荷上的非静电力.(非静电场) r r r 欧姆定律(电源内部): j = σ ( K + E ) 11
2. 电动势
定义:电源内部非静电力把单位正电荷经电源内 部从电源负极推到电源正极所做的功。
ε= ∫
+
−
r r K ⋅ dl
r K
(电源内)
r r 推广: ε = K ⋅dl ∫
( L)
r E
12
二. 含源电路的讨论 欧姆定律:
r r r j = σ (K + E) r r j = σE
(电源内部)
四. 化学电源与温差电现象
不同类型的电源,产生非静电力的机制不同。常用 的电源有化学电源、温差电源、光电源、核能电源、 发电机等。
化学电源——非静电力为溶液中离子与极板的化学亲和力 温差电源——非静电力是与温度梯度和电子浓度梯度相关的扩 散作用 光电源——非静电力为光电效应使金属表面发射电子所引起 核能电源——非静电力为核力 发电机——非静电力是由电磁感应引起
24
三. 独立方程的个数
1. 若整个电路可以化为平面电路,所有的节点和支路都 在一平面上而不存在支路相互跨越的情形——可以把 电路看成一张网络, 网孔数目就是独立回路的数目. 2. 若整个电路不能化为平面网络,网孔的概念不再适 用, 独立回路个数的判据要依据图论中树图来建立.
结论:对于一个有n个节点、l 条支路的电路, 共有 m 个独立回路,其中:m = l - (n-1)
ΔS Δl
I
一段电流管
j = neu
r r ne2 λ r r E 考虑方向 j = − ne u 或 j = 2m υ r r ne2λ 比较 j = σE 得 σ = 2mυ
Q v ∝ T ∴ ρ ∝ T , 但大多数金属 ρ ∝ T
(ρ —电阻率,T—温度,这一矛盾待用量子论解释) 8
例题1:
(电源外部)
路端电压: 1. 开路情况
U = U+ −U−
r K
U+ U−
r r r j = σ (K + E) = 0 r r ⇒ K = −E r r − r + r ⇒ U = ∫ E ⋅ dl = ∫ K ⋅ dl =ε
+ −
r E
( ,r) ε
13
(内)
(内)
2. 电源放电情况
放电:电流从负极经电源内流向正极 + dl ε = Ir + U (推导过程?) r = ∫− (内)σS
第三章 稳恒电流
§1 电流的稳恒条件和导电规律 §2 电源与电动势 §3 基尔霍夫定律
1
§1 电流的稳恒条件和导电规律
电荷的定向运动形成电流。传导电流的产 生条件: 存在可移动电荷(自由电荷) 存在电场,即ΔU≠0,或 E≠0 ,或某种 非静电力
注:超导体除外
2
一. 电流强度 I
1. 电流强度:MKSA基本量之一 大小:I =Δq/Δt 或 I = dq/dt 方向:正电荷运动方向(电场方向); 单位:A 2. 稳恒电流:I 不随时间变化 必要条件:导体中任意两点间电势差 ΔU=const , r 或导体中任意一点处的场强 E = 恒矢量. 3. 稳恒电流的连续性 电流管:I入= I出 反证法:若 I入≠ I出 ,必有电荷堆积, r 则导致 E 变化,破坏稳恒条件. n 个支路: ∑ I 入 = ∑ I 出 , ∑ I k = 0
16
1. 化学电源
非静电力:溶液中离子与极板的化学亲和力
丹聂耳电池
电势分布
17
2. 温差电现象 汤姆孙效应
(J.Thomson) I
T+ΔT
(自由电子气,热扩散)
I
I
T+ΔT
I
r K
放电吸热
T
r K
充电放热
T
汤姆孙电动势:
ε
r r T + ∆T (T , T + ∆ T ) = ∫ K ⋅ d l = ∫ σ (T ) d T
I2
I3
r2
r1 R1
L1 L2
R3 R2
ε2
R4
(a)
26
四. 叠加原理
有多个电源的电路中,通过任一支路的电流等于各 电源单独存在时(其它电源电动势置零)在同一支路 产生的电流的代数和。
利用图 (a)、(b) 和 (c) 来说明叠加原理,即
I1 = I1′ + I1′′ ′ ′ I 2 = I 2 + I 2′
铜中电流密度 自由电子数密度 则漂移速度 j = 2.4A/mm2 = 2.4×106A/m2 n = 8.4×1028m-3
2.4×106 j u= = = 1 .8 × 10 − 4 m ⋅ s − 1 ne 8.4×1028 ×1.6×10−19
(
)
热运动平均速率
v≈
2kT ≈ 105 m ⋅ s −1 m
r E
( ,r) ε
14
三. 稳恒电路中的电荷分布和静电场的调节作用
1. 稳恒时,电力线和电流线必须与导体表面平行 2. 稳恒时,静电场与非静电场共同使电流闭合,静电 场起着能量的中转作用 3. 在外电路中,静电场决定了电流的分布
电源的电场
电荷分布示意图
接通电路瞬间,电荷重新分布,使导线内电场平行 导线表面,电荷分布在导体表面及导体内不均匀处. 15
(L) T
对于同一种金属,汤姆孙电动势只与两端温度有关. 单一汤姆孙效应,在回路中并不能形成稳恒电流. 18
