第五章 稳恒磁场1节
大学物理稳恒磁场解读

2018/9/27
24
r the displacement from
I dl
I
Idl toward P.
dB
the contribution of Idl to the magnetic induction at point P.
r
P
B
the magnetic field of I at point P.
I
S
2018/9/27 5
I
Magnetic field lines surrounding a long and straight wires
2018/9/27
6
I
Magnetic field lines for a tightly wound solenoid of finite length carrying a steady current.
Gauss’ theorem
B dS 0
Ampere’s circulation theorem (Ampere’s Law) L B d l 0 Ii
i
11
2018/9/27
Affect of magnetic field force on currents
right hand rule
26
Superposition Principle of Magnetic Induction
B d B
L
B Bi
u Idl r B d B= 4 r
L
0
L
3
2018/9/27
27
DISCUSSION
大学物理稳恒磁场

1.通电密绕长直螺线管内部的磁感强度
设总匝数为N、总长为L 通过稳恒电流电流强度为I 分析对称性,知内部场沿轴向,
l B
B外 0
I
方向与电流成右手螺旋关系
螺线管均匀密绕无漏磁 B外 0
B外 0 I B d l B d l B d l B d l B d l 外 内
沿半径方向引到很远的电源上,求:环中心处 o 点的 磁感应强度。
E
解:如图所示的电流系统在 o 点激发的 B 为 5 段电流 所产生的 B 矢量的迭加。 o 点在直电流 IAE 与 IFB 所 在延长线上。
A
c
o
I1
R
I2 D
B
F
B AE B FB 0
又O点离IEF很远,此电流的磁场可不计。
(C) L3 B dl 0 I
(D) L4 B dl 0 I
2 I
L1
L3
I
L2
[ D ]
L4
二、安培环路定理在解场方面的应用 对于一些对称分布的电流 可以通过取合适的环路L 利用磁场的环路定理比较方便地求解场量 (类似于电场强度的高斯定理的解题) 以例题说明解题过程
R1 的阴影部分均匀带正电荷,面电荷密度为 + ,其余部分均匀带负电荷,面电荷密度为 – , 当圆盘以角速度 旋转时,测得圆盘中心点 o 的磁感应强度为零, 问 R1 与 R2 满足什么关系?
解:当带电圆盘转动时,可 看作无数个圆电流的磁场 在 o 点的迭加,
R1 R2
o
半径为 r ,宽为 dr 的圆电流 dI= 2rdr / 2 = rdr 磁场 dB = 0dI/2r =0dr/2
《大学物理》稳恒磁场

第四节 安培环路定理
Bdl L
0 (I1 I2 )
(0 I1
I
)
2
I1
I2 I3
I1
L
I1
问(1)B 是否与回路 L 外电流有关?
(2)若
LB d l 0 ,是否回路 L 上各处
B
0
?
是否回路 L 内无电流穿过?
43
第四节 安培环路定理
安培环路定理的应用
例题 无限长载流圆柱体的磁场
33
第三节 磁通量 磁场的高斯定理
例题 如图载流长直导线的电流为 I, 试求通过矩形面积的磁通量.
B
I
l
d1 d2
o
x
解
B 0I
2π x
dΦm
BdS
0I
2πx
ldx
Φm
B dS 0Il
S
2π
d2 dx x d1
Φm
0 Il
2π
ln
d2 d1
34
第三节 磁通量 磁场的高斯定理 磁场的高斯定理
d
I
B1
r1
dl1
B2 dl2
r2
l
B1
0I ,
2 π r1
B2
0 I
2 π r2
B1
dl1
B2
dl2
0 I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
40
第四节 安培环路定理
多电流情况
I1
I2
I3
l
B B1 B2 B3
Bdl
l
0(I2 I3)
推广:
➢ 安培环路定理
第13章
第五章 稳恒磁场典型例题

第五章 稳恒磁场设0x <的半空间充满磁导率为μ的均匀介质,0x >的半空间为真空,今有线电流沿z 轴方向流动,求磁感应强度和磁化电流分布。
解:如图所示令 110A I H e r = 220A IH e r= 由稳恒磁场的边界条件知,12t t H H = 12n n B B = 又 B μ= 且 n H H =所以 1122H H μμ= (1) 再根据安培环路定律H dl I ⋅=⎰得 12IH H rπ+= (2) 联立(1),(2)两式便解得,21120I I H r rμμμμπμμπ=⋅=⋅++012120I I H r rμμμμπμμπ=⋅=⋅++ 故, 01110IB H e r θμμμμμπ==⋅+ 02220IB H e rθμμμμμπ==⋅+ 212()M a n M M n M =⨯-=⨯ 220()B n H μ=⨯-00()0In e rθμμμμπ-=⋅⋅⨯=+ 222()M M M J M H H χχ=∇⨯=∇⨯=∇⨯0000(0,0,)zJ Ie z μμμμδμμμμ--=⋅=⋅++ 半径为a 的无限长圆柱导体上有恒定电流J 均匀分布于截面上,试解矢势A 的微分方程,设导体的磁导率为0μ,导体外的磁导率为μ。
?解: 由电流分布的对称性可知,导体内矢势1A 和导体外矢势2A 均只有z e 分量,而与φ,z 无关。
由2A ∇的柱坐标系中的表达式可知,只有一个分量,即 210A J μ∇=- 220A ∇= 此即101()A r J r r r μ∂∂=-∂∂21()0A r r r r∂∂=∂∂ 通解为 21121ln 4A Jr b r b μ=-++212ln A c r c =+ 当0r =时,1A 有限,有10b =由于无限长圆柱导体上有恒定电流J 均匀分布于截面上,设r a =时, 120A A ==,得202121ln 04Ja b c a c μ-+=+=)又r a =时,12011e A e A ρρμμ⨯∇⨯=⨯∇⨯,得 112c Ja a μ-=所以 2221220111,,224c Ja c Ja b Ja μμμ=-=-=所以, 22101()4A J r a μ=--221ln 2a A Ja rμ=写成矢量形式为 22101()4A J r a μ=--221ln 2a A Ja rμ=设无限长圆柱体内电流分布,0()z J a rJ r a =-≤求矢量磁位A 和磁感应B 。
电磁场理论课件 第五章 第1节 电磁场的矢势和标势

但将
E
t
A
t
t
t
t
中的与此融合也作相应的变换,则仍
可使 E 保持不变
t
A ( ) ( A )
t
t t
( ) A ( )
t
t t
A E
t
即设任意的标量函数 (x,t),作下述变换式:
A A A
t
于是我们得到了一组新的 A. ,满足
可以引入势的概念。但是,由于电场的旋度不为
零,这里引入的矢势、标势(时间的函数)与静
电场(与时间无关)情况有很大的不同。
D
E
B t
B 0
H
J
D
t
? B A
三.辐射问题的本质也是边值问题
变化电荷、电流分布激发电磁场,电磁场又 反过来影响电荷、电流分布。空间电磁场的分布 就是在这一对矛盾相互制约下形成的。变化的电 荷电流分布一般具有边界,因此在求解时要考虑 它们的边界条件和边值关系。但是,一般情况下 这种的边界很复杂,使得电荷、电流分布无法确 定,因此使得求解问题无法进行。在本章我们仅 讨论电荷、电流分布为已知的辐射问题。
种独立偏振。
洛仑兹规范的优点是:它的标势
和矢势
A
构成的势方程具有对称性。它的矢势 A 的纵向部
分和标势 的选择还可以有任意性,即存在多余
的自由度。尽管如此,它在相对论中显示出协变
性。因此,本书以后都采用洛仑兹规范。
总结本次课的内容
1. 用势描述电磁场
B A
E
A t
2. 两种规范
1.库仑规范 A 0
potential)。
c) 在时变场中,磁场和电场是相互作用着的整体,必须把
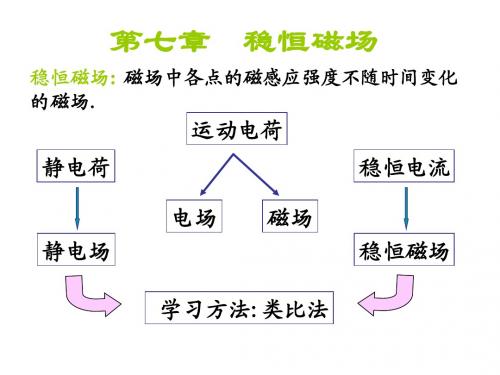
第五章稳恒磁场.

第五章稳恒磁场第一节磁场运动电荷的磁场1. 磁场磁现象的发现要比电现象早得多,公元前300 多年我国就发现了磁石吸铁现象,东汉时期就有了“司南”。
从1820 年开始,科学家逐步发现了磁和电的紧密关系:①磁铁有磁性,即有吸引铁、钻、镍等磁性物质的性质;②磁铁有磁极(磁性最强处),且恒有N 极和S极,磁极间有相互作用力,同性相斥,异性相吸;③运动电荷和电流对磁针有作用;④磁铁对运动电荷和电流也有作用;⑤运动电荷和电流与运动电荷和电流之间都有相互作用等。
由此而得,磁铁周围有磁场,运动电荷和电流周围也有磁场,它们之间的相互作用是通过磁场进行的,而非超距作用,安培磁性起源假设表明:一切磁现象的根源都是运动电荷(电流).2. 磁感应强度为了表征磁场的强弱及分布,引入物理量磁感应强度,用 B 表示,单位是特斯拉(T) , 1T= 1N-A-1•m-1。
关于B的定义有各种不同的方法,有的用电流在磁场中受的力来定义,有的用通电线圈在磁场中受的力矩来定义,为了更好地反映磁场的本质,且与电场强度E的定义相对应,我们定义:磁感应强度B为单位运动正电荷qv 在磁场中受到的最大力 F ,即F=q(v x B)实验证明磁场像电场一样,也满足叠加原理B 二刀B 或B = /dB第二节 电流的磁场 毕-萨定律1.电流的磁场电流周围有磁场,稳恒电流的磁场是稳恒磁场。
由于稳恒电 流总是闭合的,且形状各异,所以要想求得总磁场分布,必须先 研究一小段电流的磁场。
沿电流方向取一小段电流 I dl,称作电流元。
得出电流元产生磁场的规律:2d B =卩 o ldl x r/4 n r称作毕奥-萨伐尔定律,它表明一小段电流元产生的磁感应强度 dB 的大小,与电流元I dl 成正比,与电流元到场点距离r 的平方 成反比,且与I dl 和r 夹角的正弦成正比,其方向由右手螺旋法 则确定。
毕-萨定律可以从运动电荷的磁场公式中推得,而它也是一 个实验定律,虽然电流元不可能单独存在,但大量间接的实验都 证明了它的正确性。
大学物理稳恒磁场 ppt课件

NI R
B2
0 NI R2
2(R2 x2 )32
R
O1
O2
x
(1) 电流方向相同:
B B1 B2
0 NI
2R
[1
(R2
R3
x2
3
)2
]
8.51105 T
(2) 电流方向相反:
B B1 B2
0 NI
2R
[1 pp(t课R件2
R3
x
2
)
3 2
]
4.06 105 T
R 2 Indx R2 x2 3/2
B
dB 0nI
2
x2 x1
R2dx μ0nI ( R2 x2 3/2 2
x2 R2 x22
x1 ) R2 x12
B
0nI
2
cos2
ppt课件
cos1
27
讨论
B
0nI
2
cos2
cos1
I
在弧长为 dl 的线元内 流过的电流元为:
dI
dI I dl
真空的磁导率ppt课件
13
O
r P
Idl
dB
dB
Idl
P r
dB
I
电流元的磁感应线在垂直于电流元的平面内 是圆心在电流元轴线上的一系列同心圆。
磁感应线绕向与电流流向成右手螺旋关系
磁场叠加原理: B dB
oIdl rˆ
ppt课L件
L 4r 2
dB
μ0 4π
稳恒磁场
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 稳恒磁场引言:电流通过导体有热效应,通过电解液有化学效应。
本章讨论电流的磁效应:电流在其周围空间激发磁场,磁场对电流有磁力作用。
本章重点介绍真空中静磁学知识,建立稳恒磁场之基本方程式。
研究方法仍为场论方法,注意与静电场比较和区别。
§1 磁的基本现象和规律一、磁作用电与磁常相伴随、相互转化,相互作用综述为图5-1所示几种情况。
图5-1 图5-21、磁铁间的相互作用 结合实物演示说明:(1)同种磁极相互排斥、异种磁极相互吸引,参见图5-2; (2)将一磁棒分为两段,N 、S 极并不能相互分离,不存在磁单极; (3)地球本身是一大磁体,其磁性N 极在地理南极,磁性S 极在地理北极。
自由悬挂的条形磁棒或长磁针始终指南北,即是上规律的体现——指南针及应用。
2、电流对磁铁的作用图5-3NS NSSNN S N S电流磁铁磁铁电流③ ②② ③①④I SNNI NSSINN SSS通电导线周围产生磁场,通电螺线管相当于条形磁铁,参见图5-3。
3、磁铁对电流的作用电流是运动电荷形成,表明磁极对运动电荷也有磁力作用,参见图5-4。
图5-4 右手定则判受力4、电流对电流的作用 参见图5-5说明。
同向电流:吸引 反向电流:排斥图5-5以上均称为磁相互作用,是基本的磁现象。
二、磁场1、物质磁性的基本来源螺线管通电后的磁性与磁棒的相似性,启发人们:磁铁与电流是否在本源上一致?(19世纪,法国)安培分子电流假说:组成磁铁的最小单元——磁分子就是环形电流。
若这些分子电流定向排列,宏观上即显示N 、S 极。
●磁分子的“分子电流”等效成图5-6●分子环流形成的微观解释:原子、分子内电子的绕核旋转和自转。
综上可见:一切磁效应均来源于电流;一切磁作用都是电流与电流之间的相互作用,或说成运动电荷之间的相互作用。
I NSFN SF图5-62、磁场在静电学中,电的作用是近距作用,同样磁作用也是近距的:即磁作用是通过磁场传递。
电流(或N 、S 极)在空间激发磁场,而磁场对置于其中另外的电流(或磁极)施力作用,这一观点与电场近距观点一致。
即:电流 ———— ————电流无论电荷静止与否均存在库仑作用,但只有运动电荷之间才存在磁作用! 三、安培定律既然一切磁作用均归于电流之间的相互作用,本节当研究电流之间的相互作用规律—— A mpere’s Law 。
1、电流元的概念电学中:研究带电体间相互作用时,先引入点电荷理想模型,研究点电荷间的作用满足库仑定律; 再椐叠加原理,把任带电体视作点电荷之集合把整个问题求出。
磁学中:研究电流之间相互作用时,仿上——把载流回路看作大量无穷小载流线元之集合。
这些载流线元称为电流元(与点电荷位置相当),用l Id表示,只要知道任一对电流元之间相互作用规律,即可据叠加原理计算整体回路间的相互作用。
需要指出——稳恒电流只能存在于闭合回路中,孤立电流元是不存在的,如磁场mi s磁矩s i m内部消磁棒断面 相当于螺线管5-7(a),无法由实验直接验证,只能由此假设导出的结论间接验证。
(a) (b)图5-72、安培定律通过对各种载流回路间相互作用分析、概括。
安培认为:载流回路上任一电流元对另一载流回路上任一电流元之作用力,如图5-7(b),即电流元1:11l d I电流元2:22l d I作用力为21212112212)(r r l d I l d I k F d式中k 为比例系数,与单位的选取有关。
在SI 制中,电流强度为安培,比例系数k 取为40k (2A N )式中0 为真空磁导率,实验测得为 70104 (2A N )故安培力公式成为212121122012)(4r r l d I l d I F d[讨论]I 回路lIdL 2I 1L 1I 211l d I22l d I12rL 1、L 2两载流回路(1) 12F d 的大小—12F d: 与(221l d I l d I )成正比;与212r 成反比(平方反比律);与两电流元的取向有关。
(2) 12F d的方向。
如图5-8,设11l d I 与12r 组成的平面为1S 平面,它们之间的夹角为1 ;22l d I 与1211r l d I组成的平面为2S 平面,对应夹角为2 。
则:2S 平面垂直于1S 平面(22l d I在2S 平面内); (1211r l d I)垂直于1S 平面(即在1S 面之法向)。
可见:12F d 在1S 平面内,且与22l d I 、(1211r l d I )均垂直,即12F d既垂直于22l d I (受力者)、又垂直于(1211r l d I)(施力者)所决定的平面。
图5-8有了方向分析,便可写出其大小表式212212211012sin sin 4r dl I dl I dF 在其中,当仅仅改变.1 、2 时,只改变了12F d 的大小,而不影响12F d的方向。
分析如下:若11l d I 在1S 面内仅方向发生变化,即改变1 时,但不改变1211r l d I之方向,即12F d 的方向不变。
当1 =0 时,即11l d I //12r 时,12F d =0;当21时,即垂直时,12F d达最大。
1 θ1 S 1S 22θ2 I 11l d22l d II 1121r l dd 12F12r若22l d I 在2S 面内仅改变方向时,即2 变化时,则12F d方向不变。
当02 时,即22l d I 在(1211r l d I )方向时,12F d=0,-----此方向有特殊意义(见后);当22时,即22l d I ⊥(1211r l d I ),则12F d最大,------此最大值很有用(见后)。
(注:它们分别定义了B的方向、大小)(3) 同理,1122l d I l d I的作用力仍有类似形式:221212211021)(4r r l d I l d I F d(4) 电流元之间的作用力一般不满足牛顿第三定律。
举一反例进行说明如下:如图5-9放置的两电流元,则 0)(4212121122012 r r l d I l d I F d,(∵1 =0,故括号内因子为零) 0)90sin (90sin 4221022011012 r dl I dl I F d 但可以证明(见作业):两闭合回路1L 、2L 间的合作用力满足牛顿第三定律。
图5-9 图5-10(5)若电流不是线分布,则需考虑细节。
因稳恒电流线闭合,可取电流管元作为电流元,然后积分之。
此时替代关系为:dv j l Id,参见图5-10予以理解。
3、安培力的叠加原理(1) 回路1L 对电流元22l d I的合作用如图5-11,只考虑22l d I 受1L 作用时,可对1L 上各电流元对22l d I的作用进行dSjd ι电流元21F d 11l d I22l d I 2112r r矢量叠加2212l d I L F d F d =)(412121211220 L r r l d I l d I式中积分只与空间取定点的场点P 有关,由1L 而定,而与22l d I的情况无关。
图5-11(2)回路1L 对回路2L 的合作用上述2F d是22l d I 所受1L 之合作用,2L 上有许多电流元,2L 所受1L 的合作用则为221212L L L F d F F122121211220)(4L L r r l d I l d I可证:两闭合回路间的相互作用满足牛顿第二定律(见练习)。
四、磁感应强度矢量B1、B的定义仿照电学中定义电场:0q FE,变形成E q F 0 。
磁学中稍复杂:电流在其周围空间激发磁场,仍从置于场中的试探电流元00l d I 受安培力角度定义描述磁场的物理量B----磁感应强度(历史用名)。
电流元00l d I受回路L 的作用力为(见上述):L 1 I 111dl I变12rP 22l d I)4(2000 L r r l Id l d I F d式中r为L 上电流元l Id 指向00l d I 的位置矢,如图5-12(a)。
对于确定的载流回路L ,式中积分值与00l d I的大小、方向无关,但与其所在位置P 有关(因为涉及r)。
若用B 表示此积分结果,即L r r l d I B 204则B反映了00l d I 所在处P 点磁场的强弱,它完全由回路L 所确定,是计算电流回路(L )激发磁场的计算公式。
以后会发现此B表式特别有用,另有研究,称毕奥—萨伐尔定律。
需要说明:这样的分解与E q F0 形式上一致。
(a) (b)图5-12 引入B的表示之后,则回路对00l d I 的作用力可写为B l d I F d 00此公式称为安培公式,是B 的定义式。
值得指出:上式中B可不只局限于回路L激发的,应理解成除00l d I 之外的空间存在的总磁场,F d则为此场中对00l d I 之作用,故F d的大小、方向可列于下sin 00B dl I dF ,式中 为B l d与0的夹角,如图5-12(b),最大值为F dθ 00dl IBI l IdL 场源rP 00l d I场点dF Bdl I dF 00max(c) (d)图5-12定义空间某点磁场B:分别地就大小、方向进行定义 大小----B 0000max dl I dF dl I dF,对应于:图5-12(c)。
方向---00l d I不受力的方向(即 ,0 )。
对应于:图5-12(d)。
最后,再根据B l d I F d 00即可唯一地确定B。
这样定义的B的方向,与中学内容有关磁针北极受力方向即磁场方向相一致。
2、B的单位在SI 制中,据00dl I dF B 知B 的单位为:1T m A N1 (特斯拉)。
文献中常沿用实用制单位GS (高斯): GS T 4101 。
3、磁感应线----B线引入B 线形象化地描述磁场矢量场,象电力线描述电场一样。
B线的切向代表该点磁场方向,疏密表示磁场的强弱,磁感应线在实验上可显示。
综上,比较静电与静磁静电:r r q q F221041, E q F 0, r r dq E2041;B0l d I 00l d I 00l d I BB静磁:212121122012)(4r r l d I l d I F d,B l d I F d 00, L r r l d I B 204。
两个常数:21201085.8mN C,270104A N。
