关于在某时间段约会相遇的概率计算的问题
几何概型约会型问题

例1.小明家的晚报在下午5:30~6:30 之间的任何一个时间随机地被送到,小 明一家在下午6:00~7:00之间的任何 一个时间随机地开始晚餐 . 那么晚报在 晚餐开始之前被送到的概率是多少?
分析: 该题题意明确,但如何转化为数学模型 需要从实际问题中分析出存在的两个变量. 由于晚报送到和晚饭开始都是随机的,设 然后 晚报送到和晚饭开始的时间分别为 x、 y , 把这两个变量所满足的条件写成集合的形式, 把问题转化为线性规划问题进行求解.
1 1 1 7 S ABCD 1 1 1, S阴 影 1 2 2 2 8 7 S阴 影 7 8 P 所以所求概率为: S ABCD 1 8
故晚报在晚餐开始之前被送到 7 的概率是 8 .
.
反思:此类问题常会涉及两个随机变量的相互关 系,其求解的步骤为: (1)找设变量.从问题中找出两个随机变量,设为 x , y ; (2)集合表示.用( x, y )表示每次试验结果, 则可用相应的集合分别表示出全部结果 和事件 A 所包含的试验结果.一般来说,两个集合都是几个 二元一次不等式的交集. (3)作出区域.把上面的集合所表示的平面区域作 出,并求出集合 , A 对应的区域的面积. (4)计算求解.由几何概型公式求出概率.
2 2 当且仅当- ≤x-y≤ , 3 3
因此转化成面积问题,利用几何概型求解.
解:设两人分别于x时和y时到达约见地 点,要使两人能在约定时间范围内相 见,当且仅当 2 ≤ x y ≤ 2 .
3 3
两人到达约见地点所有时刻(x,y)的各 种可能结果可用图中的单位正方形内(包括 边界)的点来表示,两人能在约定的时间范 围内相见的所有时刻(x,y)的各种可能结果 可用图中的阴影部分(包括边界)来表示. 因此阴影部分与单位正方形的面积比 就反映了两人在约定时间范围内相遇的可 能性的大小,因此所求的概率为
几何概型复习约会型概率的求解

例1 假设你家订了一份报纸,送报人可能在早
上6:30—7:30之间把报纸送到你家,你父亲 离开家去工作的时间在早上7:00—8:00之间, 问你父亲在离开家前能得到报纸(称为事件A) 的概率是多少?
解: 以横坐标X表示报纸送到时间,以纵坐标 Y表示父亲离家时间建立平面直角坐标 系,假设随机试验落在方形区域内任何一 点是等可能的,所以符合几何概型的条件. 根据题意,只要点落到阴影部 分,就表示父亲在离开家前能 得到报纸,即时间A发生,所以
应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三
班车到站的时刻在图形中画出,则甲乙两人要想同乘一班车,
必须满足 7 ≤ x ≤ 7 1 ,7 ≤ y ≤ 7 1 ;
3
3
7
1
≤
x
≤7
2 ,7
1
≤
y
≤7
2 ;
3
33
3
7 2 ≤ x ≤ 8, 7 2 ≤ y ≤ 8.
3
3
即(x,y)必须落在图形中的三个带阴影的小正方形内, 所以由几何概型的计算公式得,P= 即甲、乙同乘一车的概率为
P( A)
12
1 2 12
1 2
1 2
7. 8
例2:两人约定在12∶00到1∶00之间相见, 并且先到者必须等迟到者40分钟方可离去, 如果两人出发是各自独立的,在12∶00至 1∶00各时刻相见的可能性是相等的,求两 人在约定时间内相见的概率.
2
两人不论谁先到都要等迟到者40分钟,即
小时,
3
设两人分别于x时和y时到达约见地点,要使两人在约
时刻相差不超过2秒的概率___3_/_4
3、甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的 码头,它们在一昼夜内任何时刻到达是等可能的 1)如果甲和乙的停泊时间都是4小时,它们中的任 何一条船不需要等待码头空出的概率是__2_5_/36 2)如果甲的停泊时间为4小时,乙的停泊时间为2小 时,它们中的任何一条船不需要等待码头空出的概 率是__2_2_1_/288
会面问题 利用概率论及MATLAB来求解
会面问题甲乙两人相约某天9:00-10:00在某地会面商谈生意,双方约定先到者必须等候另一人20分钟,过时如果另一人仍未到则可离去,试求两人能够会面的概率。
1用所学概率论知识建模并求解;2用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
解:用所学概率论知识建模并求解将9点到10点看成是0到60分钟,则甲乙两人到达的时间概率分布可看做是分布,此时不妨设甲到达的时间为t1,乙到达的时间为t2,(0<=t1,t2<=60) 当t1,t2满足|t1-t2|<=20时,两人则可碰面。
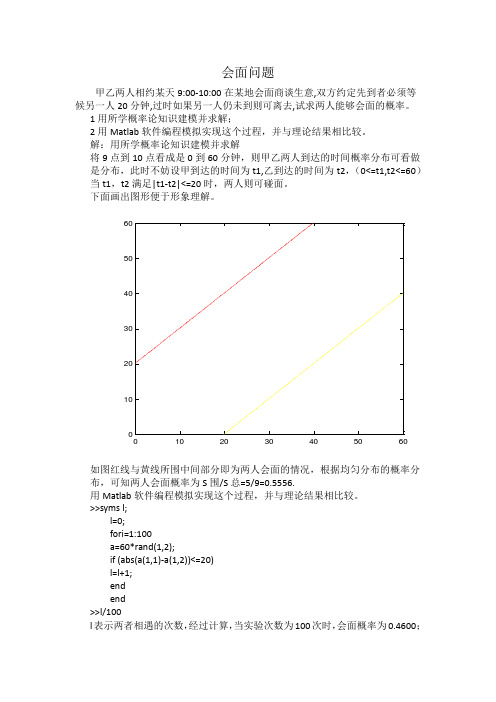
下面画出图形便于形象理解。
如图红线与黄线所围中间部分即为两人会面的情况,根据均匀分布的概率分布,可知两人会面概率为S 围/S 总=5/9=0.5556.用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
>>syms l;l=0;fori=1:100a=60*rand(1,2);if (abs(a(1,1)-a(1,2))<=20)l=l+1;endend>>l/100l 表示两者相遇的次数,经过计算,当实验次数为100次时,会面概率为0.4600; 01020304050600102030405060下面我们增大实验次数,实验次数为1000时,会面概率为0.5590;实验次数为10000时,会面概率为0.5525;实验次数为100000时,会面概率为0.5546;实验次数为1000000时,会面概率为0.5552;…从随机实验可以发现,当实验次数越来越大时,随机事件发生的概率就越来越稳定于一个值,而这个值与我们理论计算出来的值是一致的,因此从实验角度证明了概率论概率计算理论的正确性。
相遇问题的计算公式

相遇问题的计算公式一、相遇问题的基本公式1. 一般相遇问题- 路程和 = 速度和×相遇时间- 速度和 = 路程和÷相遇时间- 相遇时间 = 路程和÷速度和二、题目解析1. 例1:- 题目:甲、乙两人分别从A、B两地同时出发相向而行,甲的速度是5米/秒,乙的速度是3米/秒,经过10秒两人相遇,求A、B两地的距离。
- 解析:- 已知甲的速度v_甲 = 5米/秒,乙的速度v_乙=3米/秒,相遇时间t = 10秒。
- 根据路程和 = 速度和×相遇时间,速度和v = v_甲+v_乙=5 + 3=8米/秒。
- 则A、B两地的距离(路程和)s=v× t = 8×10 = 80米。
2. 例2:- 题目:A、B两地相距120千米,甲、乙两车分别从A、B两地同时出发相向而行,经过2小时相遇,已知甲车的速度是35千米/小时,求乙车的速度。
- 解析:- 已知路程和s = 120千米,相遇时间t = 2小时,甲车速度v_甲=35千米/小时。
- 根据速度和 = 路程和÷相遇时间,速度和v=(s)/(t)=(120)/(2)=60千米/小时。
- 乙车速度v_乙=v - v_甲=60 - 35 = 25千米/小时。
3. 例3:- 题目:甲、乙两人从相距200米的两地同时出发相向而行,甲的速度为12米/分钟,乙的速度为8米/分钟,他们多长时间能相遇?- 解析:- 已知路程和s = 200米,甲的速度v_甲 = 12米/分钟,乙的速度v_乙 = 8米/分钟。
- 根据相遇时间 = 路程和÷速度和,速度和v=v_甲 + v_乙=12+8 = 20米/分钟。
- 相遇时间t=(s)/(v)=(200)/(20)=10分钟。
初中五年级相遇问题应用题

初中五年级相遇问题应用题
题目描述
小红和小明在初中五年级认识了,他们是同桌,也是一个学校的。
某天,小明到一个陌生城市游玩,恰好在街上遇到了他在五年级时的同桌小红,两人非常惊讶。
假设两人都没有提前约定,在这个城市的可能性很小,假设这个城市的学生有10万人,问:"小红和小明在这个城市相遇的概率是多少?"
题目分析
小红和小明相遇的条件是在同一个城市,所以可以先求出两人在同一个城市的概率。
由于该城市的学生有10万人,那么小明来到这个城市的概率为1/10万,小红同理。
故两人在同一个城市的概率为 1/(10万*10万)=1/10亿。
而此时两人仅仅在同一个城市,在街上相遇还需要假设小红和小明在不同的地方,那么小红和小明在不同的地方的概率为1,因为他们两个肯定不可能在同一个地方。
所以两人相遇的概率就是在同一个城市的概率乘以在不同的地方的概率,即为 1/10亿。
结论
小红和小明在该城市相遇的概率为1/10亿,也就是说,两人重逢的几率十分渺小,是一件非常巧合的事情。
概率之见面的问题

见面的问题1、甲乙两人相约见面,并约定第一人到达后,等15分钟不见第二人就可以离去,假设他们都在10点到10点半的任何一时间来到见面地点,则两人见面的概率是多少?解:设甲、乙到达时间为x,y。
则一般0<=x<=30,0<=y<=30符合条件为|x-y|<=15,可解得p=1-1/4=3/4=75%建立直角坐标系。
x轴代表甲到达的时刻,y轴代表乙到达的时刻。
以10点为原点,则在边长为30的正方形中,任意一点的值都可代表甲乙到达的时刻(这里以边长3的正方形)。
两人在15分钟内见面的点如下阴影:则见面的概率即用阴影面积除以整个面积,即得0.75。
2、在(0,1)间随机选择两个数,这两个数对应的点把(0,1)之间的线段分成了三段,试求这三条线段能构成三角形的概率。
解:设这两个数为x,y,并且0<x<y<1,则这三个线段分别为:x,y-x,1-y,由三角形边长性质,有:x+(y-x)>1-yx+(1-y)>y-x(y-x)+(1-y)>x得:y-x<1/2,x<1/2,y>1/2,画得可行域面积为1/8,而总面积为1,所以概率为1/83、甲乙两人约定在6时到7时之间在某处会面,并约定先到者等候另一方15分钟,过时即可离去,求两个人会面的概率,解1:能见面的概率是这个区域和总区域比值见面的区域面积为:正方形面积-两个三角形面积=60*60-2*1/2*45*45=3600-2025=1575所以见面的概率为1575/3600=43.75%解2:设甲到的时间为X,乙到的时间为Y,则满足6<=X<=7,6<=Y<=7,作图,满足|X-Y|<=0.25的面积占总面积的多少则是概率,是7/16。
数学中的约会问题

数学中的约会问题数学中的约会问题在数学中,约会问题是一个经典的问题,它涉及到时间、日期和计算等多个方面。
该问题的解决需要一定的数学知识和技巧。
下面是一些与约会问题相关的子问题以及相应的解释说明。
1. 阶乘的运算阶乘是指从1乘积到某个给定的正整数的连续整数的乘积,通常以n!表示,其中n是一个正整数。
阶乘的运算在约会问题中经常用到,特别是在计算可能的排列组合数量时。
2. 排列和组合排列是指从一组元素中取出一部分进行组合,得到不同的顺序。
组合是指从一组元素中取出一部分进行组合,不考虑顺序。
在约会问题中,排列和组合的概念常常用于计算可能的安排和选择方式。
3. 时间和日期的表示在约会问题中,时间和日期的正确表示和计算非常重要。
在数学中,通常采用24小时制和日期格式(年-月-日)进行表示。
而对于约会问题,还需考虑到星期几、季节等因素,以便更全面地解决问题。
4. 方程的求解约会问题中,有时需要通过解方程来得到正确的答案。
方程求解是数学中的基本概念,其涉及到代数、解析几何等多个领域的知识和技巧。
通过解方程,可以求得满足约束条件的变量值,从而解决约会问题。
5. 概率和统计概率和统计在约会问题中也有一定的应用。
通过统计和概率分析,可以得到一些可能的情况和结果的概率,从而为问题的解决提供参考。
概率和统计的概念和计算方法对于确定约会的时间和结果非常有帮助。
6. 优化问题约会问题有时也可以看作是一个优化问题,即找到最佳解决方案。
优化问题涉及到目标函数和约束条件的确定,以及对可能解的搜索和比较。
通过应用优化方法,可以最大程度地满足约会者的需求和要求。
7. 约会问题的变种除了常见的约会问题,还存在一些约会问题的变种,例如考虑多人约会、不同地点的约会等。
这些变种问题可能需要更加复杂的数学模型和计算方法,但基本的解决思路和技巧仍然适用。
以上是数学中的约会问题及其相关子问题的列举和解释说明。
通过运用数学知识和技巧,可以有效地解决约会问题,提高约会的效率和成功率。
多次相遇问题原理及解题方法

多次相遇问题原理及解题方法多次相遇问题指的是在一定条件下,两个或多个人或物体在某一时刻相遇,然后经过一段时间后再次相遇。
这种问题可以应用于很多场景,如两个人在同一地点同时出发,同时以不同的速度前往另一个地点,问他们何时再次相遇。
解决多次相遇问题可以使用最小公倍数的概念。
最小公倍数是指能被两个或多个整数整除的最小正整数。
对于多次相遇问题,我们需要找到两个或多个物体在相遇之间所需的时间间隔,然后将这些时间间隔的最小公倍数作为解。
假设有两个人A和B,在同一地点同时出发,A的速度是a,B的速度是b。
设t是他们再次相遇的时间,那么在这段时间内,A走了a*t的距离,B走了b*t的距离。
因为他们再次相遇时,走过的距离是相同的,所以可以得到以下等式:a*t =b*t。
从中解出t的值,就可以得到他们再次相遇的时间。
而在解决多次相遇问题时,我们需要找到一个最小的t的值,也就是他们多次相遇的最小时间间隔。
这个最小的t值就是两个速度a和b的最小公倍数。
解题方法可以总结如下:1. 确定问题中的已知条件,如两个物体的速度,或者多个物体的速度等。
2. 根据已知条件,列出方程或等式。
根据两个物体再次相遇时走过的距离相等的原则,可以得到相应的方程。
3. 求解方程,得到两个物体再次相遇的时间。
4. 如果问题要求多次相遇的最小时间间隔,找到所有时间的最小公倍数,即为解。
继续以上面的问题为例,假设A和B两人同时出发,A的速度是3m/s,B的速度是5m/s。
我们想知道他们何时再次相遇。
根据以上的解题方法,我们可以列出方程:3t = 5t,其中t为他们再次相遇的时间。
解这个方程可以得到t=0,但这显然不符合实际情况,因为他们必须要有一段时间才能相遇。
我们知道,t的最小值就是他们再次相遇的时间,但我们想要求的是他们多次相遇的最小时间间隔。
为了求得最小时间间隔,我们需要求解出两个物体相遇的周期。
两个物体再次相遇的周期是两个物体速度的最小公倍数。
