同步奥数培优四年级
苏教版四年级下册同步奥数培优 第二讲 认识多位数(排列组合一)

苏教版四年级下册同步奥数培优第二讲认识多位数(排列组合一)【知识概述】:生活中常有这样的情况,就是在做一件事时,有几类不同的方法,而每一类方法中,又有几种可能的做法,那么考虑完成这件事所有可能的做法,就要用加法原理的知识去解决。
同样的,日常生活中常常会遇到这样一些间题:就是做一件事情时,要分几步才能完成,而在完成每一步时,又有儿种不同的方法,要知道完成这件事一共有多少种方法,就要用到乘法原理的知识去解决。
把两种方法灵活地运用,考虑顺序关系,称为排列问题,只考虑选出来,不需要按一定的排列顺序去思考,称为组合,今天我们就来研究相关知识。
例1:从1到99的所有自然数中,不含有数字4的自然数有多少个?练习一:1.1~100的自然数中,一共有多少个数字0?2.从1到99的所有自然数中,含有数字5的自然数有多少个?3.从1到99的所有自然数中,不含有数字2的自然数有多少个?例2:由数字0,1,2,3组成三位数,问:可组成多少个没有重复数字的三位数。
练习二:1.用0,3,4,6可组成多少个没有重复数字的三位数?2.用1,3,5,2可组成多少个没有重复数字的三位数?3.用1,2,3,4可组成多少个没有重复数字的三位数并且是双数?例3:用1,2,3,4,5可组成多少个没有重复数字的三位数?练习三:1.用数字3,4,5,6,7可组成多少个没有重复数字的三位数?2.用数字2,3,4,7,6可组成多少个个位上数字是6的没有重复数字的三位数?3.从黄、红、绿、蓝、紫、橙色这6种不同颜色的小信号旗中,每次取3种不同颜色作为一种信号,共有多少种不同的信号?例4:从1,3,4,6,8,9这六个数中,任意选取两个数作乘积,可以得到多少种不同的结果?练习四:1.从1,2,4,5,6,7这六个数中,任意选取两个数作乘积,可以得到多少种不同的结果?2.数字和是6的两位数总共有多少个?3.在两位整数中,十位数字小于个位数字的共有多少个?练习卷一、填空题。
四年级奥数培优专题第四章 数与计算(二)

四年级奥数培优专题第四章数与计算(二)第一讲定义新运算【专题导引】我们学过常用的运算有加、减、乘、除等。
如6+2=8,6×2=12等。
都是2和6,为什么运算结果不同呢?主要是运算方式不同,实质上是对应法则不同。
由此可见,一种运算实际就是两个数与一个数的一种对应方法。
对应法则不同就是不同的运算。
当然,这个对应法则应该是对任意两个数。
通过这个法则都有一个惟一确定的数与它们对应。
这一周,我们将定义一些新的运算形式,它们与我们常用的加、减、乘、除运算是不相同的。
【典型例题】【例1】有a、b两个数,规定a◎b=a+(b-2)。
那么5◎2= ?【试一试】1、有a、b两个数,规定a※b=a+2-b。
那么2※3= ?2、有a、b两个数,规定a#b=a+2-b+9。
那么6#8= ?【例2】如果规定a◎b=a-b×2 ,那么a=8、b=3时,求8◎3= ?【试一试】1、如果规定a△b=a×3+b ,那么a=3、b=10时,求3△10= ?2、如果规定a△b=(a+b)÷4 ,那么a=1、b=7时,求1△7= ?【例3】设a、b都表示数,规定是a△b表示a的3倍减去b的2倍,a△b=a×3-b×2。
试计算:①5△6,②6△5。
【试一试】1、设a、b都表示数,规定a○b=6×a-2×b。
试计算3○4。
2、设a、b都表示数,规定a*b=3×a+2×b。
试计算①(5*6)*7,②5*(6*7)。
【例4】对于两个数a与b,规定a※b= a×b + a+b。
试计算6※2。
【试一试】1、对于两个数a与b,规定a※b=a×b-(a+b)。
试计算3※5。
2、对于两个数A与B,规定A※B=A×B÷2。
试计算6※4。
【例5】如果2△3=2+3+4,5△4=5+6+7+8,按此规律计算:3△5。
【试一试】1、如果5◎2=5×6,2◎3=2×3×4,按此规律计算:3◎4= ?2、如果2◎4=24÷(2+4),3◎6=36÷(3+6),按此规律计算:8◎4= ?【※例6】对于两个数a与b,规定a□b=a+(a+1)+(a +2)+……(a+b -1)。
苏教版四年级上册同步奥数培优 第十讲 统计与可能性(游戏与对策)

苏教版四年级上册奥数培优第十讲统计与可能性(游戏与对策)【知识概述】我国古代有一个“田忌赛马”的故事;齐王经常要求将军田忌和他赛马。
规定各从自己的马中选上等马、中等马和下等马各一匹,进行三场比赛,每场各出一匹马,每胜一场可得一千金。
田忌的朋友孙膑给他出了个主意,叫田忌用下等马对齐王的上等马,上等马对齐王的中等马,中等马对齐王的下等马。
结果田忌先负一场然后连胜两场,反而赢了一千金。
这个故事是对策的一个典型例子。
它告诉我们:在竞争时,要认真分析研究、寻求并制定尽可能好的方案,利用它取得尽可能大的胜利,或在胜利无望时,也不至于输得太惨。
这种思想在20世纪形成了对策这门新兴科学。
例1:有一堆棋子共53颗,甲、乙两人轮流从中拿走1颗或2颗棋子。
规定谁拿走最后1颗棋子,谁获胜。
如果甲先拿,那么他有没有获胜的策略?练习一:1.有287个球,甲、乙两人用这些球进行取球比赛,比赛规则是:甲、乙两人轮流取,每人每次取1个或2个,取最后一个球的人为失败者。
甲想取胜,他应该如何安排?2.有388个球,甲、乙两人用这些球进行取球比赛。
比赛的规则是:甲、乙轮流取球,每人每次取1个、2个或3个,取最后一个球的人为失败者。
如果甲先取,甲为了取胜,他应该采取怎样的策略?3.有197粒棋子,甲、乙两人分别轮流取棋子,每次至少取1粒,至多取3粒,不能不取,取到最后一粒的为胜者,现在两人通过抽签决定谁先取。
你认为先取的获胜,还是后取的获胜?例2:有两堆火柴,一堆16根,一堆11根。
甲、乙两人轮流从中拿走1根或几根甚至一堆,但每次只能在某一堆中拿火柴,谁拿走最后一根算谁胜,问甲如何才能获胜?练习二:1.有两个箱子分别装有63,108个球。
甲、乙两人轮流在任一箱中任意取球,规定取得最后一个球的为胜。
甲先取,他应如何取才能获胜?2.取两堆石子,游戏双方轮流从其中的任意一堆拿走一粒或几粒石子(甚至可以把这堆石子一次拿走),但每次至少拿一粒,不准同时在两堆中拿,谁拿走最后一粒或几粒石子,谁就获胜,如何取胜?3.下面是个圆形,两人轮流在圆形中画规定了大小的□,每人每次画一个□,所画的□不能与已画的相交或重叠,圆形总有被画满的时候,谁画最后一个□,谁就获胜。
四年级奥数培优讲义上下册

目录第一章趣题与智巧(一)····························································第一讲找规律(一)··························································第二讲找规律(二)··························································第二章数与计算(一)······························································第一讲巧妙求和(一)························································第二讲变化规律(一)························································第三讲变化规律(二)························································第三章空间与图形·································································第一讲图形问题·····························································第二讲数数图形(一)························································第三讲数数图形(二)························································第四章实践与应用·································································第一讲应用题(一)··························································第二讲和倍问题·····························································第三讲植树问题·····························································第五章数与计算(二)······························································第一讲错中求解·····························································第二讲巧妙求和·····························································第六章趣题与智巧(二)····························································第一讲算式迷(一)··························································第二讲算式迷(二)··························································第七章组合与推理·································································第一讲简单推理·····························································第二讲最优化问题···························································第三讲简单列举·····························································第一章趣题与智巧(一)第一讲找规律(一)【一】找规律填数:2,4,6,8,,12练习1、1,3,5,7,,112、0,5,10,,20,25【二】找规律填数:18,15,,9,6,练习1、100,98,,,92,902、120,110,,,80,70【三】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
苏教版四年级上册同步奥数培优 第九讲 混合运算(一般的盈亏问题)

苏教版四年级上册奥数培优第九讲混合运算(一般的盈亏问题)【知识概述】日常生活中,我们常常要分配东西,一般有两种分配方法,按一种方法分配,东西有余(称作“盈”);而按另一种方法分配,东西不足(称作“亏”),求参加分配的份数及被分配的总量,我们称这样的应用题为盈亏问题。
盈亏问题的基本解法是:(盈十亏)÷两次分配数的差=份数每份个数×份数十盈数=物品总数或每份个数×份数一亏数=物品总数例1:幼儿园老师给每个小朋友分糖果,每个小朋友分5个糖果,就多出22个糖果;每个小朋友分7个糖果,就少18个糖果。
有多少个小朋友和多少个糖果?练习一:1.学校买来一些足球,若每个班借4个则多3个;若每个班借6个则少7个。
那么学校买来足球多少个?2.幼儿园买来一些苹果,若每个班分20个苹果,还多17个;若每班分25个苹果,就少18个。
那么幼儿园有多少个班?买来的苹果一共有多少个?3.一个植树小组植树,如果每人栽5棵,还剩14棵;如果每人栽7棵,就缺4棵。
这个植树小组有多少人?一共有多少棵树?例2:学校春游,租了几条船让学生们划,每条船坐3人,则有20人没船划;如果每条船坐5人,恰恰安排好,间共有学生多少人?共租了多少条船?练习二:1.小朋友分糖果,若每人分8粒,则剩下25粒,若每人分9粒,正好分完。
问:有多少个小朋友?多少粒糖果?2.在一次大扫除中,老师分配若干人擦玻璃,如果每人擦5块,则余20块;如果每人擦7块,正好擦完。
求擦玻璃的人数和玻璃的块数.3.学校分配宿舍,每个房间住3人,则多出20人;每个房间住5人,恰好安排完。
有多少房间?有多少人?例3:学校安排学生宿舍,如果每间安排4人,就有20人没床位;如果每间安排6人,就多4个空床位。
问有多少间宿舍?有多少名学生?练习三:1.有一批书分给阅读小组的同学,如果每人分7本书,就会剩6本书;如果每人分9本书,就缺8本书。
这批书一共有多少本?2.旅游团带游客到旅馆住宿,如果每个房间住5人,就有14名旅客没有床位;如果每个房间住7人,就会有4张床位空着。
同步奥数培优(四年级)

同步奥数培优(小学生四年级)用假设法解题【知识概述】同学们,假设是一种常用的重要的数学思想方法,当遇到较难的题或较复杂的题目时,用假设法常会使难题迎刃而解。
假设法是解应用题常用的一种思维方法,在一些应用题中,要求两个或两个以上的未知量,思考时可以假设要求的两个或几个未知量相等,或者先假设两种要求的未知量是同一种量,然后按题目中的已知条件进行推算,并对照已知条件,把数量上出现的矛盾加以调整,最后找到答案。
例题精学例1鸡兔同笼,共有头34个,脚118只,鸡兔各有几只?【思路分析】假设一:假设笼里装的全部是兔子,由于每只兔子有4只脚,那么,34只兔子共有4×34=136(只)脚,比实际的118只脚多了18只,因为每只兔子比每只鸡多2只脚,就可以算出鸡的只数。
假设二:笼里装的全部是鸡,由于每只鸡有2只脚。
那么,34只鸡共有2×34=68(只),比实际的118只脚少了50只脚,因为每只鸡比每只兔少2只,就可以求出兔子的只数。
假设三:假设鸡兔各17只,17×2=34(只),17×4=68(只),34+68=82(只),比实际的118只少了吗,所以接着假设,鸡16只,兔18只,计算脚的只数,以此类推,直到找到最终结果。
方法四:(吹哨法)假设这是一群训练有素的鸡和兔,我现在吹一次口哨它们就各抬起一只脚,两次过后,34×2=68(只),就剩下了50只脚,剩下的都是兔子的脚,每只兔现在剩下2只脚,50÷2=25(只)兔,那么鸡就是9只。
方法五:方程(了解)同步精练1.笼子里的鸡和兔共有100个头,共有284只脚,那么鸡有多少只?兔有多少只?2.全班46人去划船,共乘12只船,其中大船每只坐5人,小船每只坐3人,求大船和小船各有多少只?3. 停车场上停了35辆小轿车和两轮摩托车,地面上数一上共有10个轮子,请问小轿车和摩托车各有多少辆?。
数学培优班题典(四年级)

数学培优班题典(四年级)专题一速算与巧算知识对对碰在乘法、加法和以此类推混合运算中,常常利用发生改变运算顺序展开巧算,其中存有利用两数优势互补关系展开凑整巧算、借数二奶巧算、挑选最合适的数做为基数巧算等,还可以利用乘法的交换律和结合律展开巧算。
整数秦九韶法的速算与巧算,一条最基本的原则就是“凑整”。
必须达至“凑整”的目的,就要对一些数水解、变形,再运用乘法的交换律、结合律、分配律以及四则运算中的一些规则,把某些数女团至一起,并使繁杂的排序过程形式化。
1.同学们要记住一些速算结果,如2×5=10,25×4=100,125×8=1000,625×8=5000,625×16=10000等,这样,在计算时才能迅速而准确。
2.有效率地运用“头同尾念诵”和“尾同头念诵”的赖草算法算草。
“头同尾合十”的巧算方法是:用十位上的数字乘十位上的数字加1的积,再乘100,最后加上个位上两个数字的乘积。
如23×27=2×(2+l)×100+3×7=621.“尾同头合十”的巧算方法是:十位数字的乘积加上个位数字的和,再乘100,最后加上个位上的数字的积。
例如:如72×32=(7×3+2)×100+2×2=2304。
3.两数之和乘这两数之差的只等于这两个数的平方差。
4.另外存有一些常用方法。
(??5)(a?5)?a2?b2(1)乘数兎整法乘数凑整法是利用特殊数的乘积特性进行速算,如:5×2=10,25×4=100,125×8=1000,?运算时可以将涵盖这几个因子的乘数水解然后明确提出这几个因子,同时实现速算。
比如:32×625=4×8×125×5。
(2)乘法分配律、结合律该方法利用谋几个乘积之和时具有共同乘数的特点,轻易利用乘法结合律,先议和再算草。
苏教版四年级上册同步奥数培优 第八讲 垂线和平行线(最优化问题)
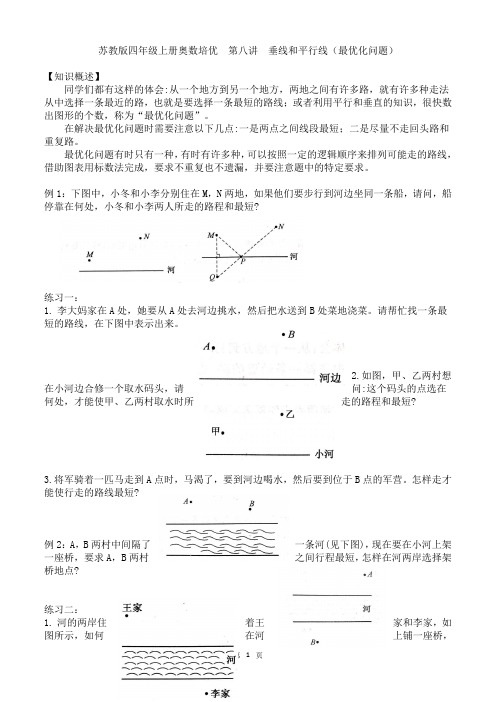
苏教版四年级上册奥数培优第八讲垂线和平行线(最优化问题)【知识概述】同学们都有这样的体会:从一个地方到另一个地方,两地之间有许多路,就有许多种走法从中选择一条最近的路,也就是要选择一条最短的路线;或者利用平行和垂直的知识,很快数出图形的个数,称为“最优化问题”。
在解决最优化问题时需要注意以下几点:一是两点之间线段最短;二是尽量不走回头路和重复路。
最优化问题有时只有一种,有时有许多种,可以按照一定的逻辑顺序来排列可能走的路线,借助图表用标数法完成,要求不重复也不遗漏,并要注意题中的特定要求。
例1:下图中,小冬和小李分别住在M,N两地,如果他们要步行到河边坐同一条船,请问,船停靠在何处,小冬和小李两人所走的路程和最短?练习一:1.李大妈家在A处,她要从A处去河边挑水,然后把水送到B处菜地浇菜。
请帮忙找一条最短的路线,在下图中表示出来。
2.如图,甲、乙两村想在小河边合修一个取水码头,请问:这个码头的点选在何处,才能使甲、乙两村取水时所走的路程和最短?3.将军骑着一匹马走到A点时,马渴了,要到河边喝水,然后要到位于B点的军营。
怎样走才能使行走的路线最短?例2:A,B两村中间隔了一条河(见下图),现在要在小河上架一座桥,要求A,B两村之间行程最短,怎样在河两岸选择架桥地点?练习二:1.河的两岸住着王家和李家,如图所示,如何在河上铺一座桥,使两家串门方便,走的路程最短?2.A,B两村位于河的两岸,要在河上垂直于河岸建一座桥,桥应修在什么地方,才能使从A 经过桥到B的路最近?(河的宽度不变)3.如图甲、乙两人分别在公路的两侧,两人约好在公路上的某一处见面,要使两人到公路上的距离和最短,那么,他们应约在公路上的哪一处见面?例3:下图(1)中的线段表示的是某人从A 到B所能经过的路,某人从A到B共有多少条最短路线?练习三:1.小华从家上学,所经过的街道平面示意图如下,从家到学校所走的最近的路线有多少条?2.下面是一个小区的平面图,某人从A到B(只能从北到南及从西向东),共有多少种不同的走法?3.小明假日要到奶奶家,A处正在修花坛,不能通过,那么,小明到奶奶家的最短路线有几条?例4:数出下面有多少个平行四边形?练习四:数出下面各图中分别有多少个平行四边形?练习卷1.如图,A,B两村分别在小河两侧,现在要在A,B两村之间找一条最短的路线,使两村人来往时走的路程最少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同步奥数培优四年级标准化管理部编码-[99968T-6889628-J68568-1689N]
同步奥数培优(小学生四年级)
用假设法解题
【知识概述】
同学们,假设是一种常用的重要的数学思想方法,当遇到较难的题或较复杂的题目时,用假设法常会使难题迎刃而解。
假设法是解应用题常用的一种思维方法,在一些应用题中,要求两个或两个以上的未知量,思考时可以假设要求的两个或几个未知量相等,或者先假设两种要求的未知量是同一种量,然后按题目中的已知条件进行推算,并对照已知条件,把数量上出现的矛盾加以调整,最后找到答案。
例题精学
例1鸡兔同笼,共有头34个,脚118只,鸡兔各有几只
【思路分析】
假设一:
假设笼里装的全部是兔子,由于每只兔子有4只脚,那么,34只兔子共有4×34=136(只)脚,比实际的118只脚多了18只,因为每只兔子比每只鸡多2只脚,就可以算出鸡的只数。
假设二:
笼里装的全部是鸡,由于每只鸡有2只脚。
那么,34只鸡共有2×34=68(只),比实际的118只脚少了50只脚,因为每只鸡比每只兔少2只,就可以求出兔子的只数。
假设三:
假设鸡兔各17只,17×2=34(只),17×4=68(只),34+68=82(只),比实际的118只少了吗,所以接着假设,鸡16只,兔18只,计算脚的只数,以此类推,直到找到最终结果。
方法四:(吹哨法)假设这是一群训练有素的鸡和兔,我现在吹一次口哨它们就各抬起一只脚,两次过后,34×2=68(只),就剩下了50只脚,剩下的都是兔子的脚,每只兔现在剩下2只脚,50÷2=25(只)兔,那么鸡就是9只。
方法五:方程(了解)
同步精练
1.笼子里的鸡和兔共有100个头,共有284只脚,那么鸡有多少只兔有多少只
2.全班46人去划船,共乘12只船,其中大船每只坐5人,小船每只坐3人,
求大船和小船各有多少只
3.?停车场上停了35辆小轿车和两轮摩托车,地面上数一上共有10个轮子,请问小轿车和摩托车各有多少辆。
