三校生高考数学模拟试卷
三校生数学模拟试卷十
三校生数学模拟试卷十标题：三校生数学模拟试卷十及其解析一、试卷概述本次三校生数学模拟试卷十是一份全真模拟试题，旨在帮助同学们在备战高考的同时，全面提升数学应用能力。
试卷整体难度适中，但在某些题目的解答上需要一定的思维深度和知识储备。
试卷包含选择题、填空题和解答题等各类题型，考察范围涵盖了高中数学的主要知识点。
二、试题解析1.选择题第1题：考察实数的概念和运算，正确答案为C。
解题关键在于理解并掌握实数的定义和基本运算规则。
2.选择题第5题：考察三角函数的应用，正确答案为D。
解题关键在于熟练掌握三角函数的性质和图像，并能够灵活运用。
3.填空题第10题：考察平面几何的知识，正确答案为根号3。
解题关键在于理解并掌握勾股定理的应用。
4.解答题第20题：考察二重积分的计算，正确答案为2π。
解题关键在于掌握二重积分的计算方法，并能够准确计算。
三、解题技巧1.对于选择题，可以采用排除法、逆推法等技巧，以节约解题时间。
2.对于填空题，要注重计算的准确性和规范性，避免因为粗心大意而失分。
3.对于解答题，要注意步骤的完整性和条理性，不要跳步或漏步，以免在评分中失分。
四、总结通过本次模拟试卷的练习，同学们可以对自己的数学应用能力进行全面的评估和提升。
同时，也要注意针对自己的薄弱环节进行针对性的强化训练，以备战即将到来的高考。
在解题过程中，要注重思路的开阔和方法的灵活运用，不断提高自己的数学思维能力和解决问题的能力。
五、启示与反思通过完成这份模拟试卷，我们应该得到以下启示与反思：1.夯实基础，巩固知识体系：高中数学的知识点繁多，我们需要在对各个知识点充分理解的基础上，构建起完整的知识框架。
只有打好基础，才能在解题时灵活运用，游刃有余。
2.提高计算能力和解题速度：在考试中，不仅要求我们能够正确解题，还需要我们有足够的计算速度。
在平时的训练中，我们要注重练习计算的准确性和速度。
3.掌握解题方法与技巧：高中数学中存在许多特定的解题方法和技巧，如排除法、逆推法等。
中职三校生高考数学试卷
一、选择题（每题5分，共50分）1. 下列各数中，无理数是（）A. √4B. √9C. √16D. √252. 已知等差数列{an}的首项a1=3，公差d=2，则第10项an=（）A. 21B. 22C. 23D. 243. 函数f(x) = x^2 - 4x + 4的图像是（）A. 抛物线开口向上B. 抛物线开口向下C. 直线D. 没有图像4. 在三角形ABC中，角A、B、C的对边分别为a、b、c，若a=5，b=7，c=8，则角C的大小为（）A. 45°B. 60°C. 90°D. 120°5. 下列方程中，无解的是（）A. x + 2 = 0B. x^2 - 4 = 0C. x^2 + 4 = 0D. x^2 - 3x + 2 = 06. 已知函数f(x) = 2x + 1，则f(-1)的值为（）A. -1B. 0C. 1D. 27. 在直角坐标系中，点P(2,3)关于y轴的对称点为（）A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)8. 已知数列{an}的前n项和为Sn，若a1=2，a2=4，且an+1 = 2an，则S5的值为（）A. 62B. 64C. 66D. 689. 下列不等式中，正确的是（）A. 2x + 3 > 5B. 2x - 3 < 5C. 2x + 3 < 5D. 2x - 3 > 510. 已知等比数列{an}的首项a1=1，公比q=2，则第n项an=（）A. 2nB. 2n-1C. 2n+1D. 2n-2二、填空题（每题5分，共50分）11. 若等差数列{an}的首项a1=1，公差d=2，则第n项an=________。
12. 函数f(x) = x^2 - 4x + 4的顶点坐标为________。
13. 在三角形ABC中，若a=6，b=8，c=10，则三角形ABC的面积S=________。
人教版三校生高考数学试卷
一、选择题（本大题共20小题，每小题3分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
）1. 若集合A={x|-1≤x≤2}，集合B={x|x≤-1或x≥2}，则A∩B=（）A. {x|-1≤x≤2}B. {x|x≤-1或x≥2}C. {x|x=-1或x=2}D. 空集2. 函数f(x)=2x+1在定义域内的单调性为（）A. 单调递增B. 单调递减C. 既有单调递增又有单调递减D. 无单调性3. 若log2x+log2(x+1)=2，则x的值为（）A. 1B. 2C. 3D. 44. 已知等差数列{an}中，a1=3，d=2，则a10=（）A. 21B. 22C. 23D. 245. 下列命题中，正确的是（）A. 如果a>b，则a^2>b^2B. 如果a>b，则a-c>b-cC. 如果a>b，则ac>bcD. 如果a>b，则a+c>b+c6. 已知圆的方程为x^2+y^2-2x-4y+5=0，则圆心坐标为（）A. (1,2)B. (2,1)C. (1,-2)D. (-2,1)7. 已知向量a=(2,3)，向量b=(4,-1)，则a·b=（）A. 11B. 10C. 9D. 88. 若sinA=1/2，cosB=-1/2，则sin(A+B)=（）A. √3/2B. -√3/2C. 1/2D. -1/29. 已知等比数列{an}中，a1=2，q=3，则a5=（）A. 54B. 162C. 486D. 145810. 下列函数中，有最大值的是（）A. f(x)=x^2B. f(x)=x^3C. f(x)=x^4D. f(x)=x^511. 已知函数f(x)=ax^2+bx+c的图象开口向上，且对称轴为x=1，则a、b、c的关系为（）A. a>0，b=0，c=0B. a>0，b=0，c≠0C. a>0，b≠0，c=0D. a>0，b≠0，c≠012. 已知等差数列{an}中，a1=5，d=-3，则an≤0的项数为（）A. 3B. 4C. 5D. 613. 下列命题中，正确的是（）A. 如果a>b，则a-c>b-cB. 如果a>b，则ac>bcC. 如果a>b，则a+c>b+cD. 如果a>b，则a^2>b^214. 已知圆的方程为x^2+y^2-4x-6y+9=0，则圆心到原点的距离为（）A. 2B. 3C. 4D. 515. 已知向量a=(2,3)，向量b=(4,-1)，则|a-b|=（）A. 5B. 6C. 7D. 816. 若sinA=√3/2，cosB=√3/2，则sin(A+B)=（）A. 1B. 0C. -1D. 217. 已知等比数列{an}中，a1=3，q=1/3，则a5=（）A. 1/243B. 1/81C. 1/27D. 1/918. 下列函数中，有最小值的是（）A. f(x)=x^2B. f(x)=x^3C. f(x)=x^4D. f(x)=x^519. 已知函数f(x)=ax^2+bx+c的图象开口向下，且对称轴为x=2，则a、b、c的关系为（）A. a<0，b=0，c=0B. a<0，b=0，c≠0C. a<0，b≠0，c=0D. a<0，b≠0，c≠020. 已知等差数列{an}中，a1=5，d=-3，则an≤0的项数为（）A. 3B. 4C. 5D. 6二、填空题（本大题共10小题，每小题3分，共30分。
上海数学三校生高考模拟卷-3
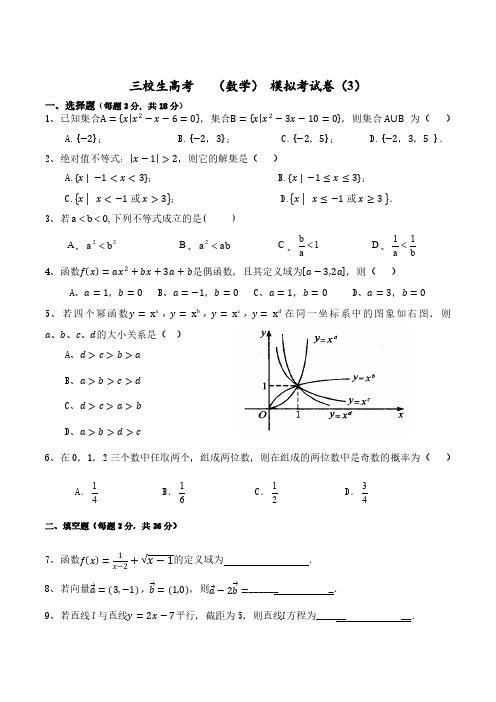
三校生高考 （数学） 模拟考试卷（3）一、选择题（每题3分, 共18分）1、已知集合A =*x |x 2−x −6=0+，集合B =*x |x 2−3x −10=0+，则集合 A⋃B 为（ ）A.{−2}；B.{−2，3}；C.{−2，5}；D.{−2，3，5 }．2、绝对值不等式：|x −1|>2，则它的解集是（ ）A.*x | −1<x <3+；B.*x | −1≤x ≤3+；C.{x | x <−1或 x >3}；D.{x | x ≤−1或 x ≥3 }．3、若,0<<b a 下列不等式成立的是( )A 、22b a <B 、ab a <2C 、1<a bD 、b a 11<4、函数f (x )=ax 2+bx +3a +b 是偶函数，且其定义域为,a −3,2a -，则（ ）A 、a =1，b =0B 、a =−1，b =0C 、a =1，b =0D 、a =3，b =05、若四个幂函数y =a x ，y =b x ，y =c x ，y =d x 在同一坐标系中的图象如右图，则a 、b 、c 、d 的大小关系是（ ）A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c6、在0，1，2三个数中任取两个，组成两位数，则在组成的两位数中是奇数的概率为（） A ．14 B ．16 C ．12 D ．34二、填空题（每题3分，共36分）7、函数f (x )=1x−2+√x −1的定义域为 ．8、若向量a ⃗=(3,−1)，b ⃗⃗=(1,0)，则a ⃗−2b ⃗⃗=______ _．9、若直线 与直线y =2x −7平行，截距为5，则直线 方程为______ __．10、不等式(x+2)(x−7)<0的解集为．11、等差数列*a+中，若a=2，a2+a=13，则数列公差d= ___ __．12、有6名男生，4名女生，现选3名参加比赛，要求至少一男一女，则有种不同选法.13、在∆ABC中，已知sinA：sinB：sinC=3：5：7，且最大边长为14，则∆ABC的面积是 .14、已知角 α 终边上一点 P(−3,4),则 sinα+cosα=。
三校生高考模拟数学试卷
一、选择题（本大题共20小题，每小题5分，共100分）1. 下列函数中，在实数域内单调递增的是（）A. y = -x^2 + 2xB. y = 2^xC. y = log2xD. y = √x2. 已知等差数列{an}的前n项和为Sn，若S10 = 100，S20 = 300，则第15项a15的值为（）A. 10B. 15C. 20D. 253. 若复数z满足|z - 1| = |z + 1|，则复数z的实部是（）A. 0B. 1C. -1D. 无法确定4. 下列命题中，正确的是（）A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0，则a^2 > b^2D. 函数y = log2x在（0，+∞）上单调递减5. 已知函数f(x) = x^3 - 3x^2 + 2，则f(x)的极小值为（）A. -1B. 0C. 1D. 26. 下列方程组中，无解的是（）A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 107. 已知等比数列{an}的首项a1 = 2，公比q = 3，则第10项a10的值为（）A. 18B. 54C. 162D. 4868. 下列函数中，在区间（0，+∞）上为减函数的是（）A. y = x^2B. y = 2^xC. y = log2xD. y = √x9. 若复数z满足|z - 1| = |z + 1|，则复数z的虚部是（）A. 0B. 1C. -1D. 无法确定10. 下列命题中，正确的是（）A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0，则a^2 > b^2D. 函数y = log2x在（0，+∞）上单调递减11. 已知函数f(x) = x^3 - 3x^2 + 2，则f(x)的极大值为（）A. -1B. 0C. 1D. 212. 下列方程组中，有唯一解的是（）A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1013. 已知等比数列{an}的首项a1 = 2，公比q = 3，则第10项a10的值为（）A. 18B. 54C. 162D. 48614. 下列函数中，在区间（0，+∞）上为增函数的是（）A. y = x^2B. y = 2^xC. y = log2xD. y = √x15. 若复数z满足|z - 1| = |z + 1|，则复数z的虚部是（）A. 0B. 1C. -1D. 无法确定16. 下列命题中，正确的是（）A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0，则a^2 > b^2D. 函数y = log2x在（0，+∞）上单调递减17. 已知函数f(x) = x^3 - 3x^2 + 2，则f(x)的极大值为（）A. -1B. 0C. 1D. 218. 下列方程组中，无解的是（）A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1019. 已知等比数列{an}的首项a1 = 2，公比q = 3，则第10项a10的值为（）A. 18B. 54C. 162D. 48620. 下列函数中，在区间（0，+∞）上为减函数的是（）A. y = x^2B. y = 2^xC. y = log2xD. y = √x二、填空题（本大题共10小题，每小题5分，共50分）21. 已知等差数列{an}的前n项和为Sn，若S10 = 100，S20 = 300，则第15项a15的值为______。
三校生高考数学模拟试卷
数学试卷 一、 单项选择题（每小题3分，共2×12=24分）1．集合{}{}13,15A x x B x x =-<≤=<<则A B ⋃=（ ）A ．{}15x x -<< B.{}35x x << C. {}11x x -<< D. {}13x x <≤2.不等式24210x x --+≥的解集是（ ）A ．(,7][3,)-∞-⋃+∞B ．[7,3]-C ．(,3][7,)-∞-⋃+∞D ．[3,7]-3．下列函数既是奇函数又是增函数的是（ ）A ．3y x =B ．1y x =C ．22y x =D ．13y x =- 4．已知3log 2=则x=( )A ．3B ．9C ．27D ．815．已知{}n a 是等比数列，252,6a a ==则8a =（ ）A ． 12B ．18C ． 24D ．366．已知两点坐标A （-1，2），B （1，-2），则下列各式正确的是（ ）A ．5OA OB →→∙= B ．OA BO →→=C ．(2,4)AB →=-D ．10AB →=7．一个袋子中有7个球，其中3个绿球，4个红球，问从中摸出一个球是红球的概率是（ ）A ．14B ．13C ．112D ．478．如右图，O 为正六边形对角线的交点，则与OA →共线的向量有（ ）个A ．2B ．3C ．7D ．99．已知直线2310x y +-=，则斜率和在y 轴上的截距是（） A ．21,33- B ．21,33- C ．21,33 D ．21,33-- 10．已知球的大圆周长为6π，求该球的表面积和体积（ ） A ．9,18ππ B ．9,36ππ C ．18,36ππD ．36,36ππ11．甘肃省3家省属单位被安排某县4个材开展“联村联户，为民富民”活动，要求每家单位至少对口帮助其中1个村且每村只受1家单位帮扶，则不同的安排方法总数是 （ ）A ．7B ．12C ．36D ．7212．如图为1500辆汽车通过某路段 AO40 50 60 70 80时的速度频率分布直方图，在速度为[60，70]的车辆约有（ ）辆A ．450B ．600C ．800D ．1000二、填空题（每小题3分，共12分）12、已知3cos 5θ=，且θ在第四象限，则sin θ= 13、过点()3,1-且垂直于直线032=+-y x 的直线方程为14、在等差数列}{n a 中，已知42=a ，84=a 则该数列的前10项之和等于15、函数lg(4)3x y x -=-的定义域是 ____________________________.三、解答题（共14分，17、18每题4分，19题6分）16．（6分）解不等式358x -<.17．(6分)已知等差数列{}n a 中，3915,9a a ==-求1a 和20S 的值.18．（7分）求经过点M （3，2），圆心在直线2y x = .。
三校生高考数学模拟试卷
三校生高考数学模拟试卷一、选择题（本大题共10小题，每小题3分，共30分。
在每小题给出的四个选项中，只有一项是符合题目要求的）1. 设集合A = {xx^2 - 3x + 2 = 0}，B={1, 2}，则A与B的关系是（）A. A⊂neqq BB. A = BC. A⊃neqq BD. A∩ B=varnothing2. 函数y=√(x - 1)的定义域是（）A. (-∞,1]B. [1,+∞)C. (-∞, 0]D. [0,+∞)3. 若sinα=(3)/(5)，且α是第二象限角，则cosα的值为（）A. (4)/(5)B. -(4)/(5)C. (3)/(4)D. -(3)/(4)4. 过点(1,2)且斜率为3的直线方程为（）A. y - 2 = 3(x - 1)B. y+2=3(x + 1)C. y - 2=-3(x - 1)D. y+2=-3(x + 1)5. 二次函数y = x^2+2x - 3的对称轴为（）A. x = - 1B. x = 1C. x = 2D. x=-26. 已知向量→a=(1,2)，→b=(3,-1)，则→a·→b等于（）A. 1B. -1C. 5D. -57. 在等差数列{a_n}中，若a_1=1，d = 2，则a_5的值为（）A. 9B. 10C. 11D. 128. 若x>0，则函数y = x+(1)/(x)的最小值是（）A. 1B. 2C. 3D. 49. 从5名男生和3名女生中选3人参加某项活动，要求既有男生又有女生，则不同的选法有（）种。
A. 45B. 30C. 15D. 1010. 若f(x)是定义在R上的奇函数，当x>0时，f(x)=x^2+1，则f(-1)的值为（）A. -2B. 2C. -1D. 1二、填空题（本大题共5小题，每小题4分，共20分）11. 计算log_28=_。
12. 椭圆frac{x^2}{16}+frac{y^2}{9}=1的长半轴长a = _。
最新三校生数学高考模拟试卷
三校生数学高考模拟试卷一、是非选择题。
（对的选A ，错的选Ｂ。
每小题3分，共30分）1．如果A=｛0.1.2.3｝，B=｛1｝，则B ∈A …………………………………………（ ） 2．已知直线上两点A （－3,3）,B （3,－1），则直线AB 的倾斜角为65π（ ） 3．lg 2+lg5=lg7………………………………………………………………………（ ） 4．函数f(x)=245x x -+的定义域是【－1，5】…………………………（ ）5．sin750·sin3750=41-……………………………………………………………（ ）6．在等比数列｛a n ｝中，a 1=31，a 4=89，则数列的公比为23…………………（ ）7．若向量32=+，则∥……………………………………（ ）8．双曲线13422=-y x 的渐近线方程为x y 23±=，焦距为2………………（ ） 9．直线l ⊥平面α，直线m ∥平面β，若l ∥m ，则α⊥β………………（ ）10．二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………（ ）二、选择题（每小题5分，共40分） 11．函数f(x)=lg(x-3)的定义域是 ( )A.RB.（－3，3）C.（－∞,－3）∪（3，＋∞）D.【0，＋∞） D.112．以点M （－2，3）为圆心且与x 轴相切的圆的方程（ ）A.（x ＋2）2＋（y －3）2=4 B . （x －2）2＋（y ＋3）2=4C.（x ＋2）2＋（y －3）2=9 D . （x －2）2＋（y ＋3）2=913．10件产品中，3件次品，甲、乙两人依次各取一件产品，按取后放回，求恰有一件次品的概率为（ ） A.10021 B. 241 C. 4521 D. 502114．若函数f(x)在定义域R 上是奇函数，且当x ﹥0时，f(x)=2410x x -,则f(－2)=（ ）.A. －104B.104C. 1D.10-1215．a=2是直线（a 2－2）x ＋y=0和直线2x ＋y ＋1=0互相平行的（ ）.A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16．设数列｛a n ｝的前n 项和为2n s n=,则a 8=（）A.64B.49C.16D.1517．在直角坐标系中，设A （－2，3），B （－3，－3）,现沿x 轴把直角坐标系折成直二面角，则AB 的长为（ ）A.6B.5C.19D.118．a =（1，2），b =（x ，5）,且b a⊥2，则x= ( )A .10B .－10 C.25 D.25-三、填空题（每题5分，共30分）19.已知x ∈（ππ,-）,已知sinx=21， 则x= _ 已知tanx=－1，则x= _20.已知正方形ABCD 的边长为2，AP ⊥平面ABCD ，且AP=4，则点P 到BD 的距离 21.过圆3622=+y x 上一点（4，52）的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排，其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级： 姓名： 座号：四、解答题（第25、26、题，每小题10分，第27.28题，每小题15分，共50分）255=8=，<b a ,> =32π,求()()b a b a -∙+2。
三校生高三复习数学试卷
一、选择题（每题5分，共50分）1. 若函数f(x) = 2x - 3在区间[1, 4]上单调递增，则f(3)的值介于下列哪个区间内？A. [1, 2]B. [2, 3]C. [3, 4]D. [4, 5]2. 下列哪个数是方程x^2 - 4x + 3 = 0的根？A. 1B. 2C. 3D. 43. 已知等差数列{an}的前三项分别为a1, a2, a3，若a1 + a2 + a3 = 12，且a2 = 4，则该等差数列的公差为：A. 1B. 2C. 3D. 44. 若函数f(x) = x^3 - 3x^2 + 2x在区间[0, 2]上单调递增，则f(1)的值介于下列哪个区间内？A. [0, 1]B. [1, 2]C. [2, 3]D. [3, 4]5. 已知等比数列{bn}的前三项分别为b1, b2, b3，若b1 = 2，b2 = 4，则该等比数列的公比为：A. 1B. 2C. 4D. 86. 若函数f(x) = ax^2 + bx + c在区间[-1, 2]上单调递增，则下列哪个条件是错误的？A. a > 0B. b > 0C. c > 0D. a + b + c > 07. 已知等差数列{an}的前n项和为Sn，若S10 = 55，S20 = 200，则该等差数列的首项a1为：A. 1B. 2C. 3D. 48. 若函数f(x) = 2x + 1在区间[0, 3]上单调递减，则f(2)的值介于下列哪个区间内？A. [0, 1]B. [1, 2]C. [2, 3]D. [3, 4]的首项b1为：A. 1B. 2C. 3D. 410. 若函数f(x) = ax^2 + bx + c在区间[-1, 2]上单调递增，则下列哪个条件是正确的？A. a > 0B. b > 0C. c > 0D. a + b + c > 0二、填空题（每题5分，共25分）11. 若函数f(x) = 3x^2 - 2x + 1在区间[-1, 2]上单调递增，则f(1)的值为______。
三校生高考数学模拟试卷.pptx
四、解答题：本大题共 6 小题，25-28 小题每小题 8 分，29-30 小题每小题 9 分，共 50 分. 25. (本小题满分 8 分)
已知向量a (1,2)，b (1,m),若a b，求实数m的值
学海无 涯 已知C的方程是: x2 y2 2x 4 y 5 m 0(m 0).
(1)求圆心C的坐标; (2)若圆C与直线l : 3x 4 y 9 0相切，求实数m的值.
26（.本 小 题 满 分 8分 )
已知函数f (x) 1 1 cos x
(1)求函数f (x)的定义域； (2)判断函数f (x)的奇偶性.
29. (本小题满分 9 分)
已知函数f (x) x2 ax b(a,b R)在区间(,1]上单调递增，在区间(1,)上 单调递增. (1)求实数a的值. (2)若f (x)在x [1,0]上的最小值为2，求实数b的值.
3 6. lg 25 lg 4 2
(A B) (A B) (A B)
7. 函数 y sin x 的最小周期是 2
8. 若点 A,B 到平面a 的距离都等于 1，则直线 AB // a. 9 . 当 (2x 3)3的展开式中x的系数是6
(A B) (A B) (A B)
10,等差数列1,3,5 的通项公式为a n 2n 1(n N * ).
(A B)
A. -1
B. 0 C. 2 D. 3
15. 三个数cos(- )，cos ，cos 3 的大小关系是（
8
5
5
3
A. cos( ) cos( ) cos( )
8
5
5
）
B.cos(3 ) cos() cos
5
5 8
B.C.
2023-2024学年云南省高考数学三联考模拟试题(一模)含答案
2023-2024学年云南省高考数学三校联考模拟试题（一模）一、单选题1．已知1z ，2z 是方程2220x x +=-的两个复根，则2212z z -=（）A ．2B ．4C ．2iD ．4i【正确答案】B【分析】利用求根公式求出两个复根，然后利用复数的运算法则及模的公式直接计算即可.【详解】已知1z ，2z 是方程2220x x +=-的两个复根，所以222i1i 22z ±===±，则设11i z =+，21i z =-，所以()()2212121222i 4i 4z z z z z z -=+-=⨯==，故选：B.2．已知集合{}1,0,1A =-，{}2,32B a a a =-+，若{}0A B ⋂=，则=a （）A ．0或1B ．1或2C ．0或2D ．0或1或2【正确答案】C【分析】根据集合的并集的结果分类讨论求参数.【详解】由于{}0A B ⋂=，则0B ∈.若0a =，则2322a a -+=，此时{}0,2B =符合题意.若2320a a -+=，则1a =或2,1a =时，{}0,1B =，此时{}0,1A B = 不合题意；2a =时，{}0,2B =符合题意，因此0a =或2，故选:C.3．有7个人排成前后两排照相，前排站3人后排站4人，其中甲同学站在前排，乙同学站在后排的概率为（）A ．142B ．114C ．221D ．27【正确答案】D【分析】总事件数看成7人站一排,考虑符合题意的情况，从余下5人中选2人与甲站在前排,根据古典概型的计算公式求解即可.【详解】先计算总事件数，可以看成7人站一排有77A 种.现在考虑符合题意的情况，从余下5人中选2人与甲站在前排，乙站在后排有234534C A A 种，概率为23453477C A A 2A 7P ==.故选:D.4．平面向量a 与b 的夹角为2π3，已知()6,8a =- ，10b = ，则向量b 在向量a 上的投影向量的坐标为（）A ．()3,4-B ．()4,3-C ．()4,3-D ．()3,4-【正确答案】D【分析】利用投影向量的定义结合向量的坐标运算可求得结果.【详解】向量b 在向量a 上的投影向量的坐标为()()250cos ,6,83,4100a b b a b a a a a ⋅-⋅=⋅=⋅-=-，故选：D.5．已知椭圆E ：()222210x y a b a b +=>>的左、右焦点分别为1F ，2F （如图），过2F 的直线交E 于P ，Q 两点，且1PF x ⊥轴，229PF F Q =，则E 的离心率为（）AB ．12CD【正确答案】A【分析】根据题意利用向量可求得点Q 的坐标，结合椭圆方程运算求解.【详解】设椭圆E 的半焦距为()000,,c Q x y >，由题意可得：()22,,,0b P c F c a ⎛⎫- ⎪⎝⎭，则()222002,,,b PF c F Q x c y a ⎛⎫=-=- ⎪⎝⎭uuu r uuu r，因为229PF F Q =uuu r uuu r ，则()020299c x c b y a ⎧=-⎪⎨-=⎪⎩，解得0201199x c b y a ⎧=⎪⎪⎨⎪=-⎪⎩，即211,99b Q c a ⎛⎫- ⎝⎭，且点Q 在椭圆E 上，则4222212181811b c a a b+=，整理得()221211118181e e +-=，解得223e =，即e =.故选：A.6．已知正四棱锥的高为h ，其顶点都在同一球面上，若该球的体积为36π，且3922h ≤≤，则当该正四棱锥体积最大时，高h 的值为（）A ．2B ．32C ．4D ．92【正确答案】C【分析】根据题意列出体积与高之间的函数关系式，利用导数讨论单调性和最值求解.【详解】如图，设高为h ，底边长为a ，则()222R h R =-+，又34π36π3V R ==球，∴3R =，又39,22h ⎡⎤∈⎢⎣⎦，()()2232111()1823212333V h a h h h h h =⋅=--=-+⎡⎤⎣⎦，()21()6242(4)3V h h h h h '=-+=--,所以当3,42h ⎡⎫∈⎪⎢⎣⎭时，()0V h '>，当94,2h ⎛⎤∈ ⎥⎝⎦时，()0V h '<，所以函数()321()2123V h h h =-+在3,42⎡⎫⎪⎢⎣⎭单调递增，94,2⎛⎤ ⎥⎝⎦单调递减，故max 464|3h V V ===，故选:C.7．定义方程()()f x f x '=的实数根x 叫做函数()f x 的“奋斗点”.若函数()ln g x x =，()32h x x =-的“奋斗点”分别为m ，n ，则m ，n 的大小关系为（）A ．m n ≥B ．m n>C ．m n≤D ．m n<【正确答案】D【分析】求导，根据“奋斗点”的定义可得1ln m m=，3223n n -=，构造函数，利用导数及零点存在定理求出m 的范围，由223n n =+求出n 的范围，从而可比较大小.【详解】函数()ln g x x =，得()1g x x'=，由题意可得，()()g m g m '=，即1ln m m=.设()1ln H x x x=-，()211H x x x '=--，因为0x >，所以()0H x '<，易得()H x 在()0,∞+上单调递减且()110H =>，()12ln202H =-=<，故12m <<.由()32h x x =-，()23h x x '=，由题意得：3223n n -=，易知0n ≠，所以2233n n =+>，因为12m <<，所以m n <.故选:D.8．若,x y ∈R ）A ．2B C ．12D ．e【正确答案】A【分析】设点(),e x P x x 是函数()e xf x x =图象上的点，点(),1Q y y -是直线:1l y x =-上的点，则PQ =，设函数()e xf x x =在点()00,M x y 处的切线1l 与直线l 平行，求出函数的导函数，即可得到()()0001e 1x f x x '=+=，再令()()e 11xg x x =+-，利用导数说明函数的单调性，求出函数的零点，即可求出M 点坐标，从而求出min PQ ，从而得解.【详解】设点(),e x P x x 是函数()e xf x x =图象上的点，点(),1Q y y -是直线:1l y x =-上的点，可以转化为P ，Q 两点之间的距离，PQ =，因为()()1e x f x x '=+，设函数()e xf x x =在点()00,M x y 处的切线1l 与直线l 平行，则直线1l 的斜率为1，可得()()0001e 1xf x x '=+=，整理得()00e 110x x +-=，令()()e 11x g x x =+-，则()()e 2xg x x '=+，当<2x -时()0g x '<，当2x >-时()0g x '>，所以()g x 在(),2-∞-上单调递减，在()2,-+∞上单调递增，且当x →-∞时()1g x →-，()00g =，()22e 10g --=--<，当x →+∞时()g x ∞→+，所以()g x 有且仅有一个零点0，∴方程()00e 110xx +-=有且仅有一个解00x =，则()0,0M ，故PQ 的最小值为点()0,0M 到直线:1l y x =-的距离d ==的最小值为2.故选：A.二、多选题9．已知()f x ，()g x 都是定义在R 上且不恒为0的函数，则（）A ．()()y f x f x =⋅-为偶函数B ．()()y g x g x =+-为奇函数C ．若()g x 为奇函数，()f x 为偶函数，则()()y f g x =为奇函数D ．若()f x 为奇函数，()g x 为偶函数，则()()y f x g x =-为非奇非偶函数【正确答案】AD【分析】根据奇函数和偶函数的定义判断即可.【详解】选项A ：设()()()h x f x f x =⋅-，因为()f x 是定义在R 上的函数，所以()h x 的定义域为R ，()()()()h x f x f x h x -=-⋅=，所以()h x 为偶函数，故A 正确；选项B ：()()()t x g x g x =+-，因为()g x 是定义在R 上的函数，所以()t x 的定义域为R ，()()()()t x g x g x t x -=-+=，所以()t x 为偶函数，故B 错误；选项C ：设()()()m x f g x =，因为()f x ，()g x 都是定义在R 上的函数，所以()m x 的定义域为R ，因为()g x 为奇函数，()f x 为偶函数，所以()()()()()()()()m x f g x f g x f g x m x -=-=-==，所以()m x 为偶函数，故C 错误；选项D ：设()()()n x f x g x =-，因为()f x ，()g x 都是定义在R 上的函数，所以()n x 的定义域为R ，()()()()()()()()()()()2n x n x f x g x f x g x f x g x f x g x g x +-=-+---=---=-，因为()g x 是不恒为0的函数，所以()()0n x n x +-=不恒成立，所以()n x 不是奇函数，()()()()()()()()()()()2n x n x f x g x f x g x f x g x f x g x f x --=-----=-++=⎡⎤⎣⎦，因为()f x 是不恒为0的函数，所以()()n x n x =-不恒成立，所以()n x 不是偶函数，所以()n x 是非奇非偶函数，故D 正确，故选：AD.10．已知α，β是两个不同的平面，m ，n ，l 是三条不同的直线，则下列命题正确的是（）A ．若m α⊥，n α⊥，则//m nB ．若//m α，//n α，则//m nC ．若αβ⊥，l αβ= ，m α⊂，m l ⊥，则m β⊥D ．若l αβ= ，//m α，//m β，则//m l【正确答案】ACD【分析】根据空间中线、面位置关系逐项分析判断.【详解】对于选项A ：因为m α⊥，n α⊥，所以由线面垂直的性质可得m n ∥，故A 正确；对于选项B ：若m α∥，n α∥，则m 与n 可能异面或相交或平行，故B 错误；对于选项C ：因为αβ⊥，l αβ= ，m α⊂，m l ⊥，由面面垂直的性质定理知，m β⊥，故C 正确；对于选项D ：设a αδ= ，且m δ⊂，因为m α∥，则m a ，设b βγ= ，且m γ⊂，因为m β∥，则m b ∥，可得a b ∥，又因为b β⊂，a β⊄，则a β∥，且a α⊂，l αβ= ，则a l ∥，可得m l ∥，故D 正确；故选：ACD.11．在如图所示的平面直角坐标系中，锐角α，β的终边分别与单位圆交于A ，B 两点.则（）A ．若A 点的横坐标为1213，B 点的纵坐标为45，则()16cos 65αβ+=B ．()sin sin sin αβαβ+<+C ．()sin sin sin ααββ>++D ．以sin α，sin β，()sin αβ+为三边构成的三角形的外接圆的面积为π3【正确答案】AB【分析】根据三角函数定义结合两角和的余弦公式可判断A ；利用两角和的正弦公式结合正余弦函数的性质可判断B ，C ；判断sin α，sin β，()sin αβ+可构成三角形，并结合正余弦定理求得三角形外接圆面积可判断D.【详解】对于A ，由已知得，12cos 13α=，4sin 5β=，α，β为锐角，则5sin 13α=，3cos 5β=，则()1235416cos cos cos sin sin 13513565αβαβαβ+=-=⨯-⨯=，故A 正确；对于B ，∵π,0,2αβ⎛⎫∈ ⎪⎝⎭，()0,παβ+∈，∴()cos 0,1∈α，()cos 0,1β∈，∴()sin cos cos sin si i s n n s n i αβαβαβαβ=+<++，故B 正确；对于C ，∵()()cos 1,1αβ+∈-，∴()()()()sin sin sin cos cos sin sin sin ααββαββαββαββ=+-=+-+<++⎡⎤⎣⎦，故C 错误；对于D ，同理()()()()sin sin sin cos cos sin sin sin βαβααβααβααβα=+-=+-+<++⎡⎤⎣⎦，结合B 、C 可知sin α，sin β，()sin αβ+，可以作为三角形的三边；设该三角形为A B C ''' ，角A '，B '，C '所对的边长分别为sin α，sin β，()sin αβ+，由余弦定理可得，()()222222sin sin sin sin sin sin cos cos sin cos 2sin sin 2sin sin C αβαβαβαβαβαβαβ+-++-+'=222222sin sin sin cos cos sin 2sin cos cos sin 2sin sin αβαβαβαβαβαβ+---=()()2222sin 1cos sin 1cos cos cos 2sin sin αββααβαβ-+-=-222222sin sin sin sin 2sin sin cos cos cos cos 2sin sin 2sin sin αββααβαβαβαβαβ+=-=-()sin sin cos cos cos αβαβαβ=-=-+，∴()sin sin C αβ'==+，设外接圆半径为R ，则由正弦定理可得()()sin 21sin sin A B R C αβαβ+''==='+，∴12R =，∴π4S =，故D 错误，故选：AB.12．已知长方体1111ABCD A B C D -中，2AB BC ==，1AA =，点P 是四边形1111D C B A 内（包含边界）的一动点，设二面角P AD B --的大小为α，直线PB 与平面ABCD 所成的角为β，若αβ=，则（）A ．点P 的轨迹为一条抛物线B ．线段PB 长的最小值为3C ．直线1PA 与直线CD 所成角的最大值为π4D ．三棱锥11P A BC -体积的最大值为3【正确答案】BCD【分析】作PO ⊥平面ABCD ，OH AD ⊥，根据二面角平面角定义和线面角定义可得PHO PBO ∠=∠，由此可得OH OB =，根据抛物线定义可知O 点轨迹为抛物线的一部分，对应的P点轨迹也为抛物线的一部分，知A 错误；若PB 取得最小值，则OB 最小，根据抛物线性质可知当O 为AB 中点时，OB 最小，由此可求得PB 最小值，知B 正确；将问题转化为求解OA 与AB 所成角OAB ∠的最大值，建立平面直角坐标系，可知当OA 与抛物线相切时，OAB ∠最大，利用抛物线切线的求法可求得该最大值，知C 正确；由体积桥1111P A BC B PA C V V --=可确定当点O 到AC 的距离最大时，所求体积最大，结合抛物线图形可知当O 为AB 中点时距离最大，由此可求得D 正确.【详解】过点P 作PO ⊥平面ABCD ，垂足为O ，作OH AD ⊥，垂足为H ，对于A ，PO ⊥ 平面ABCD ，AD ⊂平面ABCD ，AD PO ∴⊥，又OH AD ⊥，PO OH O ⋂=，,PO OH ⊂平面POH ，AD ∴⊥平面POH ，PH ⊂ 平面POH ，AD PH ∴⊥，PHO ∴∠即为二面角P AD B --的平面角，即PHO α∠=，又PBO β∠=，PHO PBO ∴∠=∠，OH OB ∴=，O ∴点轨迹为以B 为焦点，AD 为准线的抛物线在四边形ABCD 内（含边界）的部分，则P 点轨迹为以1B 为焦点，11A D 为准线的抛物线在四边形1111D C B A 内（含边界）的部分，A 错误；对于B ，由抛物线性质知：当O 为AB 中点时，min 1OB =，min 3PB ∴=，B 正确；对于C ，1PA 与CD 所成角即为OA 与AB 所成角OAB ∠，在平面ABCD 中，以AB 中点M 为坐标原点，可建立如图所示平面直角坐标系，则当OA 与抛物线相切时，OAB ∠取得最大值；由题意知：抛物线方程为：24y x =，()1,0A -，设切线方程为：1x ty =-，则由214x ty y x=-⎧⎨=⎩得：2440y ty -+=，216160t ∴∆=-=，解得：1t =±，O 在四边形ABCD 内（含边界），结合图形可知：1t =，此时π4OAB Ð=，∴直线1PA 与CD 所成角的最大值为π4，C 正确；对于D ，1111111111233P A BC B PA C PA C PA C V V S BB S --==⋅= ，1122AC =∴若三棱锥11P A BC -的体积最大，则点P 到11A C 的距离最大，即点O 到AC 的距离最大；由C 中图象可知：当O 为AB 中点时，点O 到AC 的距离最大，最大值为1242BD =即点P 到11A C 距离的最大值为22，()11max21222223223P A BC V -∴=⨯=，D 正确.故选：BCD.关键点点睛：本题考查立体几何中的轨迹相关问题的求解，解题关键是能够作出二面角的平面角，结合线面角定义确定动点满足到定点的距离等于到定直线的距离，从而确定动点轨迹为抛物线的一部分，进而结合直线与抛物线的知识来进行求解.三、填空题13．在621x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是____________.（用数字作答）【正确答案】15【分析】由题意利用二项展开式的通项公式，求得展开式中常数项【详解】二项式621x x ⎛⎫+ ⎪⎝⎭的展开式的通项公式为()62361661C C rrr r r r T x x x --+⎛⎫== ⎪⎝⎭，令360r -=，即2r =，∴常数项为2615C =.故15.14．假设云南省40万学生数学模拟考试的成绩X 近似服从正态分布()98,100N ，已知某学生成绩排名进入全省前9100名，那么该生的数学成绩不会低于____________分.（参考数据：()0.6827P X μσμσ-<<+=，()220.9545P X μσμσ-<<+=）【正确答案】118【分析】求出从40万名学生任取1名，成绩排名在前9100名的概率，再利用正态分布的对称性求出对应分数作答.【详解】从40万名学生任取1名，成绩排名在前9100名的概率为91000.022********=，因为成绩X 近似服从正态分布()98,100N ，则98μ=，10σ=，()()22781180.9545P X P X μσμσ-<<+=<<=，显然()()1180.510.95450.02275P X ≥=⨯-=，从而数学成绩大于等于118分的人数恰好为9100，所以要进入前9100名，成绩不会低于118分.故11815．已知抛物线C ：28x y =，在直线4y =-上任取一点P ，过点P 作抛物线C 的两条切线，切点分别为A ，B ，则原点到直线AB 距离的最大值为____________.【正确答案】4【分析】先根据切线方程得到直线AB 的方程，根据其过定点()0,4可得直线AB 距离的最大值为4.【详解】设()11,A x y ，()22,B x y ，则2118x y =，2228x y =，由28x y =得28x y =，284x x y '==，在A 处的切线方程为()1114x y y x x -=-，即114xy x y =-在B 处的切线方程为()2224x y y x x -=-，即224xy x y =-设(),4P t -，则1144x t y -=-，2244xt y -=-，则直线AB 方程为：44x t y -=-，即44ty x =+，直线AB 恒过定点()0,4，所以原点到直线AB 的距离的最大值为4.故4四、双空题16．定义x 表示与实数x 的距离最近的整数（当x 为两相邻整数的算术平均值时，x 取较大整数），如413=，523=，22=，2.53=，令函数()K x x =，数列{}n a 的通项公式为n a =其前n 项和为n S ，则6S =______；2025S =______.【正确答案】489【分析】空1：根据数列新定义求出前6项，求和即可；空2：根据数列新定义，数列{}n a 重新分组可得()11111111111111,1,(,,),(,,,,,),,(,,,)2222333333n n n，且满足第n 组有2n 个数，且每组中所有数之和为122n n⨯=，根据规律求和即可.【详解】空1：因为()1111a K ==，21a ==，312a ==，()41122a K ==，512a ==，612a ==，所以6111442S =++⨯=；空2：根据()K x x =，当12n ≤≤时，1 1.5≤<，则1K=，1n a==，当36n ≤≤时，1.5 2.5<，则2K=，12n a ==，当712n ≤≤时，2.5 3.5<<，则3K=，13n a =，当1320n ≤≤时，3.5 4.5<<，则4K=，14n a =，以此类推，将n a =()11111111111111,1,,,,,,,,,,,,,,,2222333333n nn ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，第n 组有2n 个数，且每组中所有数之和为122n n⨯=，设2025a =1n +组中，则(22)20252n n+≤，可得(1)2025n n +≤，解得4445n <<，故2025a 在第45组，前面共有44组，共1980项，所以20251244458945S =⨯+⨯=.故4；89.关键点睛：涉及数列新定义问题，关键是理解新定义，利用新定义合理推导，结合数列通项和求和知识解答.五、解答题17．如图，正ABC 是圆柱底面圆O 的内接三角形，其边长为a .AD 是圆O 的直径，PA 是圆柱的母线，E 是AD 与BC 的交点，圆柱的轴截面是正方形.(1)记圆柱的体积为1V ，三棱锥-P ABC 的体积为2V ，求12V V ；(2)设F 是线段PE 上一点，且12FE PF =，求二面角A FC O --的余弦值.【正确答案】(1)π3【分析】（1）利用正弦定理求解圆柱底面圆的半径r 与正ABC 的边长为a 的关系，从而得圆柱的高h 与a 的关系，分别计算体积即可得比值；（2）建立空间直角坐标系，分别求解平面AFC 与平面FCO 的法向量，根据空间向量的坐标运算求解二面角A FC O --的余弦值即可.【详解】（1）已知正ABC 的边长为a ，由正弦定理，2sin 60ar =︒（r 为圆柱底面圆的半径），从而r OA ==，由题意，圆柱高2h r a =，所以231πV r h a ==，232111sin 60326V a h a =⨯︒⨯=，因此12π3V V =.（2）如图，过A 作Ax ⊥平面PAD ，易知Ax ，AD ，AP 两两垂直，以A 为原点建立如图所示的空间直角坐标系A xyz -，设2AD =，则2AP =，1AO =.由于O 为正ABC 的中心，则23AO AE =，于是32AE =，由（1）知正ABC的边长a =，从而BC =.则()0,0,0A ，()0,1,0O ，30,,02E ⎛⎫⎪⎝⎭，3,,022C ⎫⎪⎪⎝⎭，()002P ,,，由题意，F 为线段PE 上靠近E 的三等分点，则113120,,20,,33223EF EP ⎛⎫⎛⎫==-=- ⎪ ⎪⎝⎭⎝⎭，于是20,1,3F ⎛⎫ ⎪⎝⎭，20,1,3AF ⎛⎫= ⎪⎝⎭，12,23FC ⎫=-⎪⎪⎝⎭，1,02CO ⎛⎫=- ⎪ ⎪⎝⎭ ，设平面AFC 的法向量为()1111,,n x y z =，所以111111111112*********n AF y z y n FC y z y z ⎧⎧⋅=+==⎪⎪⎪⎪⇒⎨⎨⎪⎪⋅+-==-⎪⎪⎩⎩，取11x =-，则1n ⎛=-- ⎝⎭ ，设平面FCO 的法向量为()2222,,n x y z =所以22222222221020120223n CO x y y z n FC x y z ⎧⋅=-=⎪⎧=⎪⎪⇒⎨⎨=⎪⎩⎪⋅=+-=⎪⎩，取21x =-，则()2n =- ，所以121212cos ,6n n n n n n ⋅= 由图可知二面角A FC O --的夹角为锐角，所以二面角A FC O --的夹角的余弦值为5.18．已知函数()4sin sin 6f x x x πωω⎛⎫=+ ⎪⎝⎭2π.(1)求函数()f x 在区间3,34ππ⎡⎤⎢⎥⎣⎦上的值域；(2)在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且()f A ==，c =，求ABC 的面积.【正确答案】(1)[]1,2-(2)3【分析】（1）对函数进行化简，用辅助角公式合为一个三角函数，相邻两条对称轴之间的距离为2π即为半周期，可求出1ω=；（2）由()f A =3A π=，由正弦定理求解即可.【详解】（1）()14sin sin 4sin sin cos 622f x x x x x x πωωωωω⎫⎛⎫=+=+⎪ ⎪⎪⎝⎭⎝⎭)22sin cos 1cos 2sin 2x x x x x ωωωωω=+=-+sin 222sin 23x x x πωωω⎛⎫==- ⎪⎝⎭，∵22T T ππ=⇒=，1ω=，()2sin 23f x x π⎛⎫=- ⎪⎝⎭，∵334x ππ≤≤，72336x πππ≤-≤，∴当7236x ππ-=时，()min 1f x =-，当232x ππ-=时，()max 2f x =，即()f x 的值域为[]1,2-.（2）由()f A =0,2A π⎛⎫∈ ⎪⎝⎭，可得3A π=，A B ⇒=，0,2B π⎛⎫∈ ⎪⎝⎭，∴4B π=，∴()sin sin 4C A B =+=，由sin sin a c a A C =⇒=∴1sin 32ABC S ac B ==+△19．已知数列{}n a 的前n 项和为n S ，11a =，1122n n n S S ++=+，*n ∈N .(1)求数列{}n a 的通项公式；(2)设3n n n b S =，{}n b 的前n 项和为n T ，若对任意的正整数n ，不等式2727n m m T -+>恒成立，求实数m 的取值范围.【正确答案】(1)()21,1,212,2n n n a n n -=⎧=⎨+⋅≥⎩(2)()1,2-【分析】（1）根据等差数列的定义以及,n n a S 的关系求解；（2）利用错位相减法可求得n T ，在根据题意得()2min 727n m m T -+<即可求解.【详解】（1）由1122n n n S S ++=+，得11122n n n n S S ++=+，又111222S a ==，所以数列2n n S ⎧⎫⎨⎬⎩⎭是以12为首项，公差为1的等差数列，∴()1211222n n S n n -=+-=，即()1212n n S n -=-⋅，∴当2n ≥时，()()()1221212232212n n n n n n a S S n n n ----=-=-⋅--⋅=+⋅，又11a =不满足上式，所以()21,1,212,2n n n a n n -=⎧=⎨+⋅≥⎩.（2）由（1）知()1212n n S n -=-⋅，∴()121212323nn nnn b n --⋅⎛⎫⎛⎫==-⋅⎪ ⎪⎝⎭⎝⎭，∴12123212232323nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，①23121232123232323n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，②①−②得：23111222123333323nn n T n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+--⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，整理得()25253nn T n ⎛⎫=-+ ⎪⎝⎭，又因为对任意的正整数n ，2727n m m T -+>恒成立，所以()2min 727n m m T -+<，∵()()11222212527033333nn nn n T T n n n ++⎛⎫⎛⎫⎛⎫⎛⎫-=+-+=+> ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，∴n T 在()0,∞+上单调递增，()1min 13n T T ==，由271273m m -+<，可得12m -<<，所以实数m 的取值范围是()1,2-.20．“学习强国”学台是由中宣部主管，以深入学习宣传为主要内容，立足全体党员，面向全社会的优质平台，现日益成为老百姓了解国家动态，紧跟时代脉搏的热门app .为了了解全民对于“学习强国”使用的情况，现从某单位全体员工中随机抽取3人做问卷调查.已知某单位有N 名员工，其中25是男性，35是女性.(1)当20N =时，求抽出3人中男性员工人数X 的分布列和数学期望；(2)我们知道，当总量N 足够大而抽出的个体足够小时，超几何分布近似为二项分布.现在全市范围内考虑.从N 名员工（男女比例不变）中随机抽取3人，在超几何分布中男性员工恰有2人的概率记作1P ；在二项分布中（即男性员工的人数2~3,5X B ⎛⎫ ⎪⎝⎭）男性员工恰有2人的概率记作2P .那么当N 至少为多少时，我们可以在误差不超过0.001（即120.001P P -≤）的前提下认为超几何分布近似为二项分布.24.04≈）【正确答案】(1)分布列见解析，数学期望为65(2)N 至少为145时，我们可以在误差不超过0.001（即120.001P P -≤）的前提下认为超几何分布近似为二项分布【分析】（1）利用超几何分布概率模型求出概率，即可列出分布列和求数学期望；（2）利用二项分布概率模型和超几何分布概率模型即可求解.【详解】（1）当20N =时，男性员工有8人，女性员工有12人.X 服从超几何分布，0,1,2,3X =，()312320C 220110C 114057P X ====，()12812320C C 528441C 114095P X ====，()21812320C C 336282C 114095P X ====，()38320C 56143C 1140285P X ====，∴X 的分布列为X0123P11574495289514285数学期望为()11442814601235795952855E X =⨯+⨯+⨯+⨯=.（2）()()()()212355131232C C 111855551C 2512126NNNN N N N N P N N N N N ⎛⎫⎛⎫-⨯- ⎪ ⎪⎝⎭⎝⎭===⋅----，22232336C 0.28855125P ⎛⎫=⋅== ⎪⎝⎭，由于120.001P P -≤，则()()211850.2880.0012512N N N N ⎛⎫- ⎪⎝⎭⋅-≤--，即()()211828950.28925121000N N N N ⎛⎫- ⎪⎝⎭⋅≤=--，即()()2128925289512100018720N N N N ⎛⎫- ⎪⎝⎭≤⨯=--，由题意易知()()120N N -->，从而()()27201289125N N N N ⎛⎫-≤-- ⎪⎝⎭，化简得21475780N N -+≥，又0N >，于是578147N N+≥.由于函数578y x x=+在24.04x =≈处有极小值，从而578y N N=+当25N ≥时单调递增，又578142146.07147142+≈<，578143147.04147143+≈>.因此当143N ≥时符合题意，而又考虑到25N 和35N 都是整数，则N 一定是5的整数倍，于是145N =.即N 至少为145时，我们可以在误差不超过0.001（即120.001P P -≤）的前提下认为超几何分布近似为二项分布.21．已知圆C ：(224x y ++=，定点)D，如图所示，圆C 上某一点1D 恰好与点D 关于直线PQ 对称，设直线PQ 与直线1D C 的交点为T .(1)求证：TC TD -为定值，并求出点T 的轨迹E 方程；(2)设()1,0A -，M 为曲线E 上一点，N 为圆221x y +=上一点（M ，N 均不在x 轴上）.直线AM ，AN 的斜率分别记为1k ，2k ，且124k k =-.求证：直线MN 过定点，并求出此定点的坐标.【正确答案】(1)证明见解析，2214y x -=(2)证明见解析，定点坐标为()1,0【分析】（1）根据对称性求得TC TD -为定值，结合双曲线定义求得轨迹E 方程；（2）解一：根据M A ，在双曲线上，用点差法得1111141y x x y -=⋅+，222211y x x y -=-+，代入124k k =-可得122121x y x y y y =--，将MN 方程()y k x m =+代入求得直线MN 恒过定点.解二：分别联立直线与双曲线、圆，求出M N ，的坐标，设定点(),0T t ，由三点共线得1t =，得直线MN 恒过定点.【详解】（1）证明：由图，由点1D 与D 关于PQ 对称，则1TD TD =，所以112TC TD TC TD CD -=-==，故为定值.由2TC TD CD -=<=，由双曲线定义知，点T的轨迹为以()C，)D 为焦点，实轴长为2的双曲线，设双曲线E 方程为()222210,0x y a b a b-=>>，所以1a =，c =2224b c a =-=，所以双曲线E 的方程为2214y x -=.（2）解一：因为()1,0A -，如图，令()11,M x y ，()22,N x y ，()2211221,4101,y x ⎧-=⎪⎨⎪--=⎩两式相减得：1111141y x x y -=⋅+，同理，()2222221,101,x y ⎧+=⎪⎨-+=⎪⎩两式相减得：222211y x x y -=-+，124k k =-，即2121122121211111444x x k k x y x y y y y y ⎛⎫--=-⇒-=-⋅⋅⇒-=- ⎪⎝⎭，由题知直线MN 斜率一定存在，设直线MN 方程()y k x m =+，则()()()()211122k x m k x m k x m k x m x x +++-=+-，整理得()1212m x x x x =--，所以1m =，故直线MN 恒过定点()1,0.解二：由已知得AM l ：()11y k x =+，AN l ：()21y k x =+，联立直线方程与双曲线方程()1221,1,4y k x y x ⎧=+⎪⎨-=⎪⎩消去y 整理得()22221114240k x k x k ----=，由韦达定理得212144A M k x x k --=-，所以212144M k x k +=-，即()1121814M M k y k x k =+=-.所以211221148,44k k M k k ⎛⎫+ ⎪--⎝⎭.联立直线方程与圆的方程()2221,1,y k x x y ⎧=+⎨+=⎩消去y 整理得()22222221210k x k x k +++-=，由韦达定理得222211A N k x x k -=+，所以222211N k x k -+=+，即()22222211N N k y k x k =+=+，因为14AN AM k k =-，即2114k k =-，所以2112211168,1616k k N k k ⎛⎫-+- ⎪++⎝⎭，若直线MN 过定点，则由对称性得定点在x 轴上，设定点(),0T t .由三点共线得MT NT k k =，即()()1122222211111122112211884164416161416416k k k k k k t k k t t k k t t k k --+=⇒++-=-++⇒=+-+---+，所以直线MN 过定点()1,0T .方法点睛：圆锥曲线中直线过定点问题通法，是先设出直线方程y kx m =+，通过韦达定理和已知条件若能求出m 为定值可得直线恒过定点，若得到k 和m 的一次函数关系式，代入直线方程即可得到直线恒过定点.此题中由于两点分别是直线与双曲线、圆的交点，故只能求出两交点的坐标，用两点坐标结合直线方程得到直线恒过定点.22．已知函数()()ln 22f x x x =+-+，()e ln x g x a x a =-+.(1)求函数()f x 的极值；(2)请在下列①②中选择一个作答（注意：若选两个分别作答则按选①给分）.①若()()f x g x ≤恒成立，求实数a 的取值范围；②若关于x 的方程()()f x g x =有两个实根，求实数a 的取值范围.【正确答案】(1)极大值为3，无极小值(2)选①，[)e,a ∈+∞；选②，a 的取值范围为()0,e 【分析】（1）先求导函数，再根据单调性求解极值即可；（2）把恒成立式子整理化简后，构造函数求导函数结合单调性求解.【详解】（1）函数()f x 的定义域为{}2x x >-，()111022x f x x x --'=-==++，解得=1x -，当2<<1x --时，()0f x ¢>，()f x 单调递增；当1x >-时，()()0,f x f x '<单调递减；所以()()13f x f =-=极大值，无极小值.（2）若选①：由()()f x g x ≤恒成立，即()e ln 2ln 20x a x a -++-≥恒成立，整理得：()ln e ln ln 22x a a x x x ++≥++++，即()()ln 2ln e ln ln 2e x x a a x x ++≥++++，设函数()e x h x x =+，则上式为()()()ln ln 2h x a h x +≥+，因为()e 10x h x '=+>恒成立，所以()h x 单调递增，所以()ln ln 2x a x +≥+，即()ln ln 2a x x ≥+-，令()()ln 2m x x x =+-，()2,x ∈-+∞，则()11122x m x x x +'=-=-++，当()2,1x ∈--时，()0m x '>；当()1,x ∈-+∞时，()0m x '<；所以()m x 在=1x -处取得极大值，()m x 的最大值为()11m -=，故ln 1a ≥，即e a ≥.故当[)e,a ∈+∞时，()()f x g x ≤恒成立.若选择②：由关于x 的方程()()f x g x =有两个实根，得()e ln 2ln 20x a x a -++-=有两个实根，整理得()ln eln ln 22x a a x x x ++=++++，即()()ln 2ln e ln ln 2e x x a a x x ++=++++，设函数()e x h x x =+，则上式为()()()ln ln 2h x a h x +=+，因为()e 10x h x '=+>恒成立，所以()h x 单调递增，所以()ln ln 2x a x +=+，即()ln ln 2a x x =+-，令()()ln 2m x x x =+-，()2,x ∈-+∞，则()11122x m x x x +'=-=-++，当()2,1x ∈--时，()0m x '>；当()1,x ∈-+∞时，()0m x '<；所以()m x 在=1x -处取得极大值，()m x 的最大值为()11m -=，又因为()(),,2,,x m x x m x →+∞→-∞→-→-∞所以要想()ln ln 2a x =+有两个根，只需要ln 1a <，即0e a <<，所以a 的取值范围为()0,e .。
最新三校生数学高考模拟试卷教学内容
三校生数学高考模拟试卷一、是非选择题。
（对的选A ，错的选Ｂ。
每小题3分，共30分）1．如果A=｛0.1.2.3｝，B=｛1｝，则B ∈A …………………………………………（ ） 2．已知直线上两点A （－3,3）,B （3,－1），则直线AB 的倾斜角为65π（ ） 3．lg 2+lg5=lg7………………………………………………………………………（ ） 4．函数f(x)=245x x -+的定义域是【－1，5】…………………………（ ）5．sin750·sin3750=41-……………………………………………………………（ ）6．在等比数列｛a n ｝中，a 1=31，a 4=89，则数列的公比为23…………………（ ）7．若向量32=+，则∥……………………………………（ ）8．双曲线13422=-y x 的渐近线方程为x y 23±=，焦距为2………………（ ） 9．直线l ⊥平面α，直线m ∥平面β，若l ∥m ，则α⊥β………………（ ）10．二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………（ ）二、选择题（每小题5分，共40分） 11．函数f(x)=lg(x-3)的定义域是 ( )A.RB.（－3，3）C.（－∞,－3）∪（3，＋∞）D.【0，＋∞） D.112．以点M （－2，3）为圆心且与x 轴相切的圆的方程（ ）A.（x ＋2）2＋（y －3）2=4 B . （x －2）2＋（y ＋3）2=4C.（x ＋2）2＋（y －3）2=9 D . （x －2）2＋（y ＋3）2=913．10件产品中，3件次品，甲、乙两人依次各取一件产品，按取后放回，求恰有一件次品的概率为（ ） A.10021 B. 241 C. 4521 D. 502114．若函数f(x)在定义域R 上是奇函数，且当x ﹥0时，f(x)=2410x x -,则f(－2)=（ ）.A. －104B.104C. 1D.10-1215．a=2是直线（a 2－2）x ＋y=0和直线2x ＋y ＋1=0互相平行的（ ）.A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16．设数列｛a n ｝的前n 项和为2n s n=,则a 8=（）A.64B.49C.16D.1517．在直角坐标系中，设A （－2，3），B （－3，－3）,现沿x 轴把直角坐标系折成直二面角，则AB 的长为（ ）A.6B.5C.19D.118．a =（1，2），b =（x ，5）,且b a⊥2，则x= ( )A .10B .－10 C.25 D.25-三、填空题（每题5分，共30分）19.已知x ∈（ππ,-）,已知sinx=21， 则x= _ 已知tanx=－1，则x= _20.已知正方形ABCD 的边长为2，AP ⊥平面ABCD ，且AP=4，则点P 到BD 的距离 21.过圆3622=+y x 上一点（4，52）的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排，其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级： 姓名： 座号：四、解答题（第25、26、题，每小题10分，第27.28题，每小题15分，共50分） 255=8=，<b a ,> =32π,求()()b a b a -•+2。
数学试卷三校生高考
一、选择题（每题4分，共40分）1. 已知函数f(x) = x^2 - 2x + 1，那么f(2)的值为（）A. 1B. 3C. 0D. -12. 下列函数中，是奇函数的是（）A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^43. 已知等差数列{an}的公差为d，若a1 + a2 + a3 = 9，a1 + a2 + a3 + a4 = 18，则d的值为（）A. 2B. 3C. 4D. 54. 在△ABC中，角A、B、C的对边分别为a、b、c，若a^2 + b^2 = c^2，则△ABC是（）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形5. 下列方程中，有唯一解的是（）A. x^2 + x + 1 = 0B. x^2 - 2x + 1 = 0C. x^2 + 2x + 1 = 0D. x^2 - 4x + 3 = 06. 已知等比数列{an}的公比为q，若a1 + a2 + a3 = 12，a1 a2 a3 = 27，则q的值为（）A. 3B. 2C. 1D. -17. 下列函数中，在定义域内单调递增的是（）A. f(x) = x^2B. f(x) = 2^xC. f(x) = log2xD. f(x) = x^38. 已知函数f(x) = x^2 - 3x + 2，那么f(-1)的值为（）A. 0B. 1C. 2D. -19. 在△ABC中，角A、B、C的对边分别为a、b、c，若a = 3，b = 4，c = 5，则△ABC的面积为（）A. 6B. 8C. 10D. 1210. 下列方程中，有无数解的是（）A. x^2 + y^2 = 1B. x^2 + y^2 = 4C. x^2 + y^2 = 9D. x^2 + y^2 = 16二、填空题（每题4分，共40分）1. 已知等差数列{an}的首项为a1，公差为d，那么第n项an = _______。
三校生数学模拟试卷一
26.已知 A 0, 4, B x | x2 px q 0 ，若 A B A ，求 p 、 q 的值。
27.设 a (x 1)2 ,b 2x2 2x 1 ，比较 a 与 b 的大小。
A.2, 5
B.2
C.5
14.设全集U x | 4 x 10, x N, A 4, 6,8,10，则 U A =
A.5
B.5, 7
C.7, 9
D.
D.5, 7, 9
15.下列各题中正确的是
A. 若 a b c b ，则 a c C. 若 ab bc ，则 a c
B. 若
a b
30.设U R, A
x | x2 16 0
,
B
x
|
x3 x 1
CU A ， CU B 。
学号
21.不等式 2x 3 4 的整数解的解集是
班级
…………………………………………………………………………………………………………
姓名
………………………………………………密…………封…………线………………………………………………
22.已知 A x | x 3, B x | 2 x 7，则 A B
9. p (x 2)(x 3), q x(x 1) ，则 p q …………………………………………( A B )
10.空集是任意集合的真子集 ……………………………………………………………( A B )
二、单项选择题：本大题共 8 题，每小题 5 分，共计 40 分。
11.已知集合 A 1,3,5,7, B 2,3, 4,5,6 ，则 A B
三校生数学考试题及答案
三校生数学考试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是方程2x+3=7的解？A. x=1B. x=2C. x=3D. x=4答案：B2. 函数y=x^2-4x+4的最小值是多少？A. 0B. 1C. 4D. 7答案：A3. 已知一个等差数列的首项为3，公差为2，那么它的第五项是多少？A. 11B. 13C. 15D. 17答案：C4. 一个圆的半径为5厘米，那么它的面积是多少平方厘米？A. 25πB. 50πC. 75πD. 100π答案：C5. 以下哪个函数是奇函数？A. y=x^2B. y=x^3C. y=x^4D. y=x^5答案：B6. 计算下列极限：\[\lim_{x \to 0} \frac{\sin(x)}{x}\]A. 0B. 1C. πD. 2答案：B7. 一个三角形的两边长分别为3和4，且这两边的夹角为60度，那么这个三角形的面积是多少？A. 3√3B. 4√3C. 6√3D. 8√3答案：A8. 以下哪个不等式是正确的？A. |x| > xB. |x| ≥ xC. |x| < xD. |x| ≤ x答案：B9. 计算下列定积分：\[\int_0^1 x^2 dx\]A. 1/3B. 1/2C. 2/3D. 1答案：A10. 以下哪个选项是不等式x^2 - 4x + 4 ≤ 0的解集？A. (-∞, 2]B. [2, ∞)C. (-∞, 2) ∪ (2, ∞)D. {2}答案：D二、填空题（每题4分，共20分）11. 计算等比数列的前三项和，首项为2，公比为3，和为______。
答案：1412. 已知函数f(x) = 2x - 1，求f(3)的值，结果为______。
答案：513. 一个直角三角形的两直角边长分别为6和8，那么斜边的长度为______。
答案：1014. 计算下列极限：\[\lim_{x \to \infty} \frac{1}{x}\]结果为______。
三校生的高考数学试卷
考试时间：120分钟满分：150分一、选择题（每小题5分，共50分）1. 下列各数中，绝对值最小的是（）A. -3B. 0C. 1.5D. -2.12. 已知函数f(x) = 2x - 3，那么f(2)的值是（）A. 1B. 3C. 5D. 73. 如果a < b，那么下列不等式中一定成立的是（）A. a - 1 < b - 1B. a + 1 < b + 1C. a / 2 < b / 2D. a 2 < b 24. 在直角坐标系中，点P(3, 4)关于y轴的对称点坐标是（）A. (-3, 4)B. (3, -4)C. (-3, -4)D. (3, 4)5. 下列哪个图形的面积可以用勾股定理来计算？（）A. 矩形B. 圆C. 三角形D. 梯形6. 若a, b, c是等差数列的连续三项，且a + b + c = 18，则a的值是（）A. 6B. 4C. 2D. 87. 下列哪个函数是奇函数？（）A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = 1/x8. 如果一个等腰三角形的底边长为6cm，腰长为8cm，那么这个三角形的面积是（）A. 24cm²B. 28cm²C. 32cm²D. 36cm²9. 下列哪个数是实数集R中的无理数？（）A. √4B. √9C. √16D. √2510. 下列哪个方程的解是x = 2？（）A. 2x + 3 = 7B. 3x - 1 = 5C. 4x + 2 = 9D. 5x - 3 = 11二、填空题（每小题5分，共50分）11. 若x = 2，则x^2 - 3x + 2的值为______。
12. 下列函数中，f(0)的值最小的是f(x) = x^2 + 2x + 1。
13. 在直角坐标系中，点A(1, 2)和点B(-3, 4)之间的距离是______。
上海数学三校生高考模拟卷-5
三校生高考模拟考试卷（5）一、选择题1、已知集合A=,−1,2),B=Z，则A∩B=（）A.*−1,0,1+B.*0,1,2+C.*0,1+D.*1+2、若角α=5π4，则 α 是（）A. 第一象限角B.第二象限角C. 第三象限角D. 第四象限角3、幂函数y=x k,k∈{−1,12,1,2,3},在这5个幂函数中，奇函数有（）个A.1B.2C.3D. 44、函数y=sinπx3的最小正周期为（）A. 4B. 6C.4πD. 6π5、在平面直角坐标系中，角 α 的顶点是坐标原点，始边与 x 轴正半轴重合，若角 α 的终边经过点P(−3,4)，则sinα=（）A. 35B.45C. −35D.−456、为了检测学生的身体素质指标，从游泳类1项，球类3项，田径类4项，共8项项目中抽取四项进行检测，则每一类都被抽到的概率为（）A. 17B.27C.37D.47二、填空题7、函数f(x)=√x+2x−1的定义域是．8、若向量a⃗=(3,−2)，b⃗⃗=(1,−1)，则a⃗+2b⃗⃗=．9、若直线 l 与直线y=3x−1垂直，则直线 l 的斜率为．10、不等式(x+2)(x−7)>0的解集．11、若实数 a满足：log2a=4，则a=．12、底面边长为8，侧棱长为5的正四棱锥侧面积为．13、在∆ABC中，∠ABC=60°，∠BAC=45°，AC=√3，则BC=．14、某水果店部分商品价格如下表：则该水果店水果的售价用列矩阵表示是．15、流程框图计算，则S=．16、设数列*a n+是等差数列.若a2和a2022是方程4x2−8x+1=0的两根，则数列*a n+中的a1012=．17、学校在“职业体验日”中开设了智能制造和信息技术两大专业类的体验活动，其中智能制造类包含5个项目，信息技术类包含4个项目，若参加活动的同学想在两大专业中各选2个项目进行体验，则不同的选法共有种。
18、单位为鼓励员工爱岗敬业，在分配方案中规定：年度考核合格的员工，从下一年一月份开始在上一年平均月工资收入基础上增加7%作为新一年的月工资收入，员工老魏自2005年一月以来在该单位供职，历年考核都为合格，且同一年内月工资收入相同，2005年的月工资收入为5000.00元，则2022年一月该员工的月工资收入为元。
三校生高考数学模拟试卷.pdf
(A B)
A. -1
B. 0 C. 2 D. 3
15. 三个数cos(- )，cos ，cos 3 的大小关系是 （ ）
8
5
5
A. cos(− ) cos( ) cos(3 )
8
5
5
B. cos(3 ) cos( ) cos−
5
5 8
B.C. cos(3 ) cos(− ) cos
21. 若双曲线 x2 − x2 = 1右支上一点 p到右焦点的距离为 3，则点p到右焦点的距离为 9 16
22. 已知一个圆柱的底面半径为 1，高为 2，则该圆柱的全面积为
23. 已知向量 a = (−1,1),b = (2,−1), 则a + b =
24.甲乙两人投掷飞镖，他们的成绩（环数）如下面的频数条形统计图所示，用甲、乙训练
5
8
5
D. cos(− ) cos(3 ) cos
8
5
5
16. 不等式 若是直线与平面所成的角，则的取值范围是( )
A.0, )
B. (0, ) C. [0, )
2
2
17. 如果a b,那么下列说法正确的是( )
D.[0, ] 2
A. a 1 b
B. a2 b2 C. 1 1 D. a3 b3 ab
学海无涯
三校生高考数学模拟试卷
14. 不等式函数y = −x2 + 3, x −1,2的最小值为 （ ）
班级
姓名
学号
得分
第 I 卷（选择题 70 分）
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
答案
（请将是非选择题、单项选择题答案写到表格中） 一、是非选择题：本大题共 10 小题，每小题 3 分，共 30 分.对每小题的命题作出选择，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三校生高考数学模拟试卷
班级 姓名 学号 得分
（请将是非选择题、单项选
择题答案写到表格中）
一、是非选择题：本大题共10小题，每小题3分，共30分.对每小题的命题作出选择，
的选A,错的选B. 1. 实数0与集合A={0,1}的关系是.0A ∈
(A B) 2. 点M(1,1)在圆.1)1(2
2
上=+-y x
(A B)
3. 若非零向量.0,//,=•b a b a b a 则满足
(A B)
4. }.10{02
<<<+x x x x 的解集是不等式
(A B) 5. 3
4
2tan ,2tan ==θθ则若
(A B) 6. 24lg 25lg =+
(A B)
7. 函数x y πsin = 的最小周期是2
(A B)
8. 若点A,B 到平面a 的距离都等于1，则直线
.//a AB
(A B)
9. 当6)32(3
的系数是的展开式中x x +
(A B) 10,
等
差数列
).(125,3,1*N n n a n ∈-=的通项公式为
(A B)
共40分.
11. 的离心率为椭圆125
92
2=+y x （ ）
A.
5
3 B.
5
4 C.
） A.{}
0≤y y
B. {}
0≥y y
C. {}
0>y y
D. {}
R y y ∈
13. 已知[]()=⋂==B A B A 则集合,5,2,3,0（ ）
A. (]3,2
B. [)5,0
C.
()3,2
D. []3,2
14.
不
等
式
[]的最小值为函数2,1,32-∈+-=x x y （ ）
A. -1
B. 0
C. 2
D. 3
15. 的大小关系是，，三个数5
3cos 5cos )8-(cos π
ππ
（ ）
A.)5
3cos()5cos()8cos(πππ
<<-
B.⎪⎭
⎫
⎝⎛-<<8cos )5cos()53cos(
πππ B.C.⎪⎭
⎫ ⎝⎛<-<5cos )8cos()53cos(πππ
D
.
⎪⎭
⎫
⎝⎛<<-5cos )53cos()8cos(πππ
16.
不
等
式
的取值范围是
，则是直线与平面所成的角若θθ( )
A.[)π,0
B. )2
,
0(
C.
)2
,0[π
D.]2
,
0[π
17.
那么下列说法正确的是如果,b a >( )
A.
1>b
a
B. 2
2b a >
C.
b
a 1
1< D. 33b a > 18. 从1,2,3,4,5,6中任取两个数，则这两个数之和为9的概率是（ ）
A.
154 B.
51 C. 15
2
D. 15
1
第I 卷（非选择题 80分）
三、填空题：本大题共6小题，每小题5分，共30分.
19.在直角坐标系中，过点(0,1)和(1,0)的直线l 的
方程是 20. 在=
==∠=∠∆AC BC B A ABC ，则，，中，44530 21. 到右焦点的距离为
，则点到右焦点的距离为右支上一点若双曲线p p x
x 3116
92
2=-
22. 已知一个圆柱的底面半径为1，高为2，则该圆柱的全面积为
23. 已知向量),1,2(),1,1(-=-=b a =+b a 则
24.甲乙两人投掷飞镖，他们的成绩（环数）如下面的频数条形统计图所示，用甲、乙训练 的成绩的方差大小关系是，乙甲2
2s s
四、解答题：本大题共6小题，25-28小题每小题8分，29-30小题每小题9分，共50分.
的值
，求实数若，已知向量m b a m b a ⊥=-=),,1()2,1(
.
)()2()()1(cos 11
)()8.26的奇偶性判断函数的定义域；求函数已知函数分（本小题满分x f x f x x f +=
27. (本小题满分8分) }{21的前项和，若是递增等比数列已知n n a a a S =
28. 已(本小题满分8分)
已知
).
0(0542:22>=-+--+m m y x y x C 的方程是
.
0943:)2(;
)1(的值相切，求实数与直线若圆的坐标求圆心m y x l C C =++
29. (本小题满分9分)
.
),1(]1,(),()(2单调递增上上单调递增，在区间在区间已知函数+∞-∞∈++=R b a b ax x x f .
2]0,1[)()2(.
)1(的值，求实数上的最小值为在若的值求实数b x x f a -∈
30. (本小题满分9分)
.
1111-AA BC AB C B A ABC ==形，的底面是等腰直角三角如图，已知直三棱柱
(1)求异面直线所成的角与11CC AB .
若M 为线段AC 的中点，N 为线段
1
111//:BMC N AB C A 平面平面的中点，求证 饱食终日，无所用心，难矣
哉。
——《论语•阳货》 (2)。