火车行程问题
第九讲 火车行程问题

第九讲火车行程问题1、基本关系及基本现象同向行驶(1)追上(头尾齐)——超过(A长+B长)÷(A速-B速)=时间(2)头相齐——超过A长÷(A速-B速)=时间(3)尾相齐——超过B长÷(A速-B速)=时间相向行驶:(1)相遇——错过(A长+B长)÷(A速+B速)=时间(2)头相齐——尾相齐A长÷(A速+B速)=时间(3)头尾齐——尾头齐(A长-B长)÷(A速+B速)=时间(4)尾头齐——两尾齐B长÷(A速+B速)=时间2、解决问题例:慢车车身长125米,车速每秒17米,快车车身长140米,车速每秒22米,慢车在前,快车在后面从追上到完全超过需要多少秒?据关系(1)可知:(125+140)÷(22-17)=53(秒)答:快车从追上到超过慢车需要53秒。
练:长150米的的火车以每秒18米的速度穿越一条长300米的隧道,问:火车穿越这条隧道(从入隧道开始到完全离开)需要多少秒?(150+300)÷18=25秒答:火车穿越这条隧道需要25秒。
例:一列火车通过一座长1260米的桥(车头上桥到车尾离开)用了60秒,它穿越长2010米的隧道,用了90秒,问:这列火车的车速和车身长各是多少?(2010-1260)÷(90-60)=25米路程差时间差车速或25×60-1260=240米,25×9-2010=240米答:车速为每秒25米,车身长240米。
讲与练:两列火车相向而行,甲车每小时行36米,乙车每小时行54米,两车错车时,甲车上一乘客发现:从乙车车头经过他的车窗时开始到乙车车尾离开他的车窗时共用了14秒,求:乙车的车长?此题可以理解为:乘客以每小时36千米的速度与乙车以每小时54千米的速度,从同一起点同时作反向运动,因此,可用相遇问题的基本关系式解。
36000÷3600=10(米)……甲每秒速54000÷3600=15(米)……乙车速(10+15)×14=350(米)……乙车身长答:乙车车身长350米。
火车行程问题

⽕车⾏程问题第⼀讲⽕车型⾏程问题通常,在⾏程中所涉及的运动物体(如⼈或车)是不考虑本⾝长度的。
但⽕车(或⼀⽀队伍)的长度较长,不能忽略不计。
从“追上”到“超过”,就是⼀个追及过程。
在此过程中,⼆者的路程之差为A车长+B车长从“相遇”到“错过”,这是⼀个相遇过程。
在此过程中,⼆者的路程之和为A车长+B车长理解了这两个隐藏条件,我们再做这类似题时,就可以把它当作⼀般⾏程问题来做了。
例1、长150⽶的⽕车以每秒18⽶的速度穿越⼀条长300⽶的隧道,问:⽕车穿越隧道(从进⼊到完全离开)要⽤多少时间?同类题型练习:1、长130的列车,以每秒16⽶的速度⾏驶,通过⼀条隧道⽤了48秒,问:这条隧道长多少⽶?例2、慢车车长125⽶,车速为每秒17⽶;快车车长140⽶,车速为每秒22⽶。
慢车在前⾯⾏驶,快车从后⾯追上到完全超过慢车需要多少时间?同类题型练习:1.甲⽕车长250⽶,车速每秒16⽶;⼄车长140⽶,车速每秒21⽶。
⼄车从后⾯追上到完全超越甲车需要多少秒?例3、⼀列⽕车通过⼀座长1260⽶的桥(车头上桥⾄车尾完全离桥)⽤了60秒,它以相同速度穿越长2010⽶的隧道⽤了90秒。
问:这列⽕车的车速和车⾝长各是多少?同类题型练习:1.⼀列⽕车通过长为450⽶的⼤桥⽤了23秒,从车头到车尾经过⼀位铁路边的扳道⼯⼈⽤了8秒(⼯⼈的⾝宽忽略不计)。
这列⽕车的速度和车⾝长度各是多少?例4、两列⽕车相向⽽⾏。
甲车每⼩时⾏36千⽶,⼄车每⼩时⾏54千⽶。
两车错车时,甲车上⼀乘客发现:从⼄车车头经过他的车窗时开始到⼄车车尾经过他车窗时共⽤14秒。
求⼄车的车长。
同类题型练习:1、快车每秒⾏18⽶,慢车每秒⾏10⽶。
现两列⽕车同时同⽅向齐头⾏进,经过10秒后,快车超过慢车;如果两车车尾相齐⾏进,则7秒后,快车超过慢车。
求两列⽕车的车⾝长度各是多少⽶?例5、某⼩学528⼈排成4路纵队去看电影,队伍的速度是每分钟25⽶,前后两⼈都相距1⽶。
火车行程问题

一:火车过桥、过隧道问题公式:路程=速度×时间基本数量关系是:火车长+桥长=火车速度×过桥时间火车速度=(火车长+桥长)÷过桥时间过桥时间=(火车长+桥长)÷火车速度一般的火车过桥所求的分为:求过桥时间;求桥长;求火车长;求火车的速度。
下面我们分别研究这些问题。
经典例题:例1:一列火车长180米,每秒行25米。
全车通过一条120米的大桥,需要多长时间?解:如图过桥时间=(火车长+桥长)÷火车速度(180+120)÷25=300÷25=12(秒)答:需要12秒。
课堂训练:(1)一列火车长200米,它以每秒10米的速度穿过200米长的隧道,从车头进入隧道到车尾离开隧道共需要多少秒?(2)一列火车长250米,每秒行驶50米,全车通过一座长2750米的隧道,一共需要多少时间?(3)一列火车长150米,每秒行驶16米,全车通过一座长330米的大桥。
一共需要多少时间?(4)一列火车长210米,每秒钟行驶25米,全车通过一个190米的山洞需要多少时间?例2:一列火车长160米,全车通过一座桥需要30秒钟,这列火车每秒行20米,求这座桥的长度.解:由公式:火车长+桥长=火车速度×过桥时间变形可得:桥长=火车速度×过桥时间-火车长20×30-160=600-160=440(米)答:这座桥长440米。
课堂训练:(5)一列350米长的火车以每秒25米的速度穿过一座桥花了20秒,问:大桥的长度是多少?(6)一列长240米的火车以每秒30米的速度过一座桥,从车头上桥到车尾离桥用了1分钟,求这座桥长多少米?(7)一列火车长200米,以每秒8米的速度通过一条隧道,从车头进洞到车尾离洞,一共用了40秒。
这条隧道长多少米?(8)一座大桥长590米,一列火车以每秒15米的速度通过大桥,从车头上桥到车尾离开桥共用时间50秒,求这列火车长多少米?(9)一座大桥长2100米。
四年级奥数--- 火车行程问题初步

第7次火车行程问题初步1、有快、慢两列火车,相向而行。
慢车车身长120米,车速为每秒22米,快车车5长140米,车速为每秒30米。
快、慢两车从相遇到离开,需要多少秒?2、有甲、乙两列火车,甲车长105米,每秒行38米;乙车长123米,每秒行35米甲、乙两车同向而行,从甲车追上乙车到两车离开需要多少秒?3、一列长280米的火车匀速通过一座桥,每小时行120千米,从车头上桥到车尾离开桥所用的时间是30秒,求桥长多少米?4、一座大桥长2400米。
一列火车以每分1800米的速度通过大桥,从车头上桥到车尾离开桥共需要1分30秒。
这列火车长多少米?5、一列长250米火车通过一长1150米的大桥,从车上桥车尾离开桥共用56秒,求这列火车平均每秒行驶多少米。
6、一列火车长288 米,每秒行驶14 米,它通过一个山洞需42秒。
求这个山洞长多少米?7、一列火车匀速通过540米长的桥需23秒,以同样的速度穿过360米长的山洞需17秒。
求这列火车的速度和车长。
8、一列火车经过南京长江大桥,大桥长约6700米,这列火车长125米,每秒行35米,这列火车通过南京长江大桥需要多少秒?9、一列火车匀速通过一座480米长的铁桥用了26秒,以同样的速度经过一位站在路边的扳道工人用了10秒。
此列火车的速度和车长各是多少?10、列货运火车共60节,每节车厢长15米,相邻两节车厢间隔1.5米,这列火车平均每秒行驶30米,要穿1711.5米的山洞,需要多少秒?11、438名少先队员排成两个纵队去参观科技展览。
队伍行进的速度是每分钟22米,前后两人都相距0.5米,现在要走过一座长441米的桥,问整个队伍从上到离桥共需几分钟?。
第十三讲 火车行程问题

第十三讲火车行程问题同学们肯定对行程问题已经不陌生了,前面我们已经接触过两讲的行程问题,那么有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题,也是一种行程问题。
和前面所学的行程问题不同的是:在考虑速度、时间和路程三种数量关系时,必须考虑到火车本身的长度。
例题精析:例1、甲火车长210米,每秒行18米,乙火车长140米,每秒行13米。
乙火车在前,两火车在双轨车道上行驶。
求甲火车从后面追上到完全超过乙火车要用多少秒?例2、一列火车长180米,每秒钟行25米。
全车通过一条120米的山洞,需要多少时间?例3、有两列火车,一车长130米,每秒行23米,另一车长250米,每秒行15米,现在两车相向而行,问从相遇到离开需要几秒钟?例4、一列火车通过2400米的大桥需要3分钟,用同样的速度从路边的一根电线杆旁边通过,只用了1分钟。
求这列火车的速度。
例5、甲列车每秒行20米,乙列车每秒行14米,若两列车齐头并进,则甲车行40秒超过乙车,若两列车齐尾并进,则甲车行30秒超过乙,求甲列车和乙列车各长多少米?方法技巧:疯狂操练:①、一列快车长150米,每秒行22米,一列慢车长100米,每秒行14米。
快车从后面追上慢车到超过慢车,共需几秒钟?②、一列火车长360米,每秒行18米。
全车通过一座长90米的大桥,需要多少时间?③、有两列火车,一列长360米,每秒行18米,另一列长216米,每秒行30米。
现两列列车相向而行,从相遇到相离一共需要几秒钟?④、一列火车从小明身旁通过用了15秒,用同样的速度通过一座长100米的桥用了20秒。
这列火车的速度是多少?⑤、一列快车长200米,每秒行22米,一列慢车长160米,每秒行17米,两列车齐头并进,快车超过慢车要多少秒?若齐尾并进,快车超过慢车要多少秒?趣味板块:小叮当有两包糖果,一包有48粒,另一包有12粒,他每次从多的一包里取出3粒,放到少的一包里去,经过()次,才能使两包糖果的粒数相等。
【小高数学知识点】火车行程问题
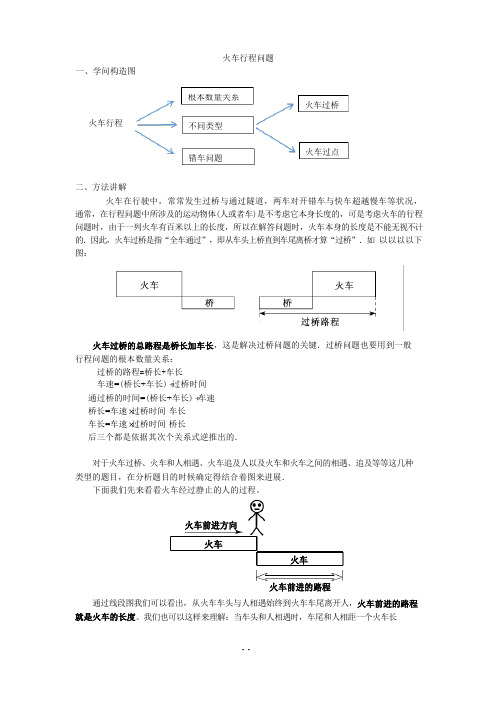
火车过桥 火车过点火车前进方向火车火车行程问题一、学问构造图火车行程二、方法讲解火车在行驶中,常常发生过桥与通过隧道,两车对开错车与快车超越慢车等状况, 通常,在行程问题中所涉及的运动物体(人或者车)是不考虑它本身长度的,可是考虑火车的行程问题时,由于一列火车有百米以上的长度,所以在解答问题时,火车本身的长度是不能无视不计的.因此,火车过桥是指“全车通过”,即从车头上桥直到车尾离桥才算“过桥”.如 以以以以下图:火车过桥的总路程是桥长加车长,这是解决过桥问题的关键.过桥问题也要用到一般行程问题的根本数量关系:过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长后三个都是依据其次个关系式逆推出的.对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候确定得结合着图来进展.下面我们先来看看火车经过静止的人的过程。
火车前进的路程通过线段图我们可以看出,从火车车头与人相遇始终到火车车尾离开人,火车前进的路程就是火车的长度。
我们也可以这样来理解:当车头和人相遇时,车尾和人相距一个火车长火车根本数量关系不同类型错车问题度,所以整个过程就是车尾和人的相遇问题。
以上是人不动状况下的火车行程问题,下面我们来介绍一下行人和火车的相遇和追及问题,如以以以以下图所示:火车前进方向车尾离开行人车头遇到行人 火车行人的路程火车前进的路程火车的长度我们可以将火车看成一个点:开头的时候行人和车尾的距离为一个车长,完毕的时候行人和车尾相遇了。
也就是说,从火车与行人的相遇到错开,这个过程可以看成是行人与车尾相遇了。
也就是说,从火车与行人的相遇到错开,这个过程可以看成是行人与车尾的相遇问题,火车和行人经过的路程和等于火车的长度。
类似的,对于火车追行人的过程,从追上到离开,火车和行人的路程差等于火车的长 度。
第十讲:火车行程问题

第十讲:火车行程问题知识要点:通常,在行程问题中所涉及的运动物体是不考虑本身的长度的,课时当考虑火车的行程问题时,火车的长度是不能忽略不计的,今天我们就来学习火车的行程问题。
基本公式:1、错车问题:两个车身长之和÷速度和=错车时间2、超车问题:头对尾:两个车身长之和÷速度差=超车时间头对齐:快车车长÷速度差=超车时间尾对齐:慢车车长÷速度差=超车时间基本概念:错车:从两车车头相遇到车尾相离超车:头对尾超车:从快车头追上慢车尾(追上),到快车尾离开慢车头(超过)头对齐超车:开始两车头对齐,同时,同向行驶,到快车尾对慢车头尾对齐超车:开始两车尾对齐,同时,同向行驶,到快车尾对慢车头例题精讲:例1:长150米的火车以每秒15米的速度穿越一条300米的隧道,问火车穿越对到(从进入隧道直至完全离开)要用多长时间模仿练习:长130米的列车,以每秒16米的速度行驶,通过一条隧道用了48秒,问这条隧道长多少米?例2:甲乙两列火车相向而行,甲车长400米,每秒行驶20米,乙车长300米,每秒行15米。
两车在平行的轨道上错车,从车头相遇到车尾相离需要多少时间?模仿练习:在平行的轨道上,两列火车相对开来,一列火车长182米,每秒行18米,另一列火车每秒行17米,两列火车错车而过用了10秒钟,求另一列火车长多少米?例3:甲乙两城之间的双轨铁路上,一列长145米,慢车以每秒钟15米的速度从甲城向乙城开去;另一列长185米的特快列车以每秒20米的速度从后面追来,那么这列快车从追上慢车开始到完全超过慢车需几秒?模仿练习:一列快车长150米,每秒行22米;一列慢车长100米,每秒行17米。
快车从后面追上慢车道超过慢车,共需几秒钟?例4:铁路旁的一条与铁路平行的小路上,有一行人与骑车人同时向南行进,行人速度是3.6千米/时,骑车人的速度是10.8千米/时,这时有一列火车从他们背后开过来,火车通过行人用22秒,通过骑车人用26秒,这列火车的车身总长是多少?模仿练习:铁路旁的一条与铁路平行的小路上,有一行人与骑车人同时向南行进,行人速度是1.2米/秒,骑车人的速度是4米/秒,这时有一列火车从他们背后开过来,火车通过行人用15秒,通过骑车人用18秒,这列火车的车身总长是多少?例5:模仿练习:1、一列火车长360米,每秒行18米。
火车行程问题

130
250
380
练一练
有两列火车,一列长360米,每秒行 18米,另一列长216米,每秒行30米。 现两列车相向而行,从相遇到相离一 共需要几秒钟?
(360+216)÷(18+30) =576÷48 =12(秒)
难题
一列火车通过2400米得大桥需 要3分钟,用同样的速度从路边 的一根电线杆旁边通过,只用了 1分钟。求这列火车的速度。
3.有两列火车,一车长130米,每秒 行23米,另一车长250米,每秒行15 米,现在两车相向而行,问从相遇到 离开需要几秒钟?
解析:相(2遇50+—13—0)甲÷火(23车+15头)=&10乙(S)火车头 离开——甲火车尾&乙火车尾
两火车尾从相距两个火车长度的距离到相遇过程
(130+250)÷(23+15)=10(秒)
2.甲火车长210米,每秒行18米,乙 火车长140米,每秒行13米。乙火车 在前,两火车在双轨车道上行驶。求 甲火车从后面追上到完全超过乙火车 要多少秒?
甲 乙
210
140
350
2.甲火车长210米,每秒行18米,乙 火车长140米,每秒行13米。乙火车 在前,两火车在双轨车道上行驶。求 甲火车从后面追上到完全超过乙火车 要多少秒?
有两列火车,一列长220米,每秒行22米, 另一列长200米迎面开来,两车从相遇到 离开共用了10秒钟,求另一列火车的速度?
一列火车从小明身旁通过用了15秒,用同 样的速度通过一座长100米得桥用了20秒。 这列火车的速度是多少?
解析:追上——甲火车头&乙火车尾 完全超过——甲火车尾&乙火车头
(210+140)÷(18-13)=70(秒)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(24-4) ÷2=10(米) 答:快车速度是每秒14米,
慢车速度是每秒10米。
=252 ÷15
=16.8(秒)
答:快车从追上到完全超过慢车要16.8秒。
1.有两列火车在双轨道上相向行驶,一列长360 米,车速是每秒18米,另一列长216米,车速 是每秒30米,两列火车从车头相遇到车尾相离 (360+216)÷(18+30) 用了多少秒?
=576÷48 =12(秒)
2.从南京到上海的铁路上,一列慢车车身长150米, 每秒行驶28米;一列快车车身长120米,每秒行 驶34米。慢车在前面行驶,快车从追上到完全超 过慢车需要多少秒?
=250 ÷5-22
=50-22
=28(米)
答:乙车的速度是每秒28米。
一列快车长280米,一列慢车长200米, 在平行的轨道上相向而行。从两车相遇到相 离经过20秒。若两车同向行驶,慢车在前, 快车在后,从两车相遇到相离经过2分钟。 求各车的速度? 2分=120秒
速度和:(280+200)÷20=24(米) 速度差:(280+200) ÷120=4 (米) (24+4) ÷2=14(米)
一列长150米的火车穿越了3810米的 隧道用了2分钟,这列火车的速度是 每秒多少米?
火车速度=(火车长度+桥的长度)÷过桥时间 (3810+150)÷(60×2) =3960÷120
=33(米)
答:这列火车的速度是每秒33米。
一列火车长200米,每秒行驶11米,要通过2000 米的大桥,从车头上桥到车尾离桥共需多少秒?
火车过桥
1.会分析简单的火车过桥问题中速度、时间和 路程的数量关系,提高学生解决实际应用问题 的能力。(教学重点) 2.在与他人合作、交流的基础上进行反思,总 结出火车过桥问题解决方法的基本策略,培养 学生创造性思维。(教学难点)
3.进一步体验奥数与日常生活的密切关系,培 养学生学习奥数的兴趣。(情感目标)
=4(秒)
答:两列火车从车头相遇到车尾相离用了4秒。
有两列火车相向行驶,一列长130米,每秒行23 米;另一列长250米,每秒行15米,两列火车从车头 相遇到车尾相离,共需要多少时间? 错车时间=(甲车身长+乙车身长)÷(甲车速+乙车速)
(130+250)÷(23+15) =380 ÷38 =10(秒) 答:共需要10秒钟。
错车时间=(甲车身长+乙车身长)÷(甲车速+乙车速)
?
例1:两列火车在双轨道上相向行驶,甲车身长 130米,车速是每秒30米,乙车身长150米,车速 是每秒40米,两列火车从车头相遇到车尾相离用 了多少秒? 错车时间=(甲车身长+乙车身长)÷(甲车速+乙车速)
(150+130) ÷(40+30) =280÷70
超车时间=(快车身长+慢车身长)÷(快车速-慢车速)
?
例2:一列慢车车身长120米,车速是每秒15米; 一列快车车身长132米,车速是每秒30米。慢车 在前面行驶,快车与它同向行驶,从后面追上 到完全超过需要多少秒? 超车时间=(快车身长+慢车身长)÷(快车速-慢车速)
(132+120)÷(30-15)
火车的追及问题一般研究快车车头与慢车车 尾相遇,到快车车尾离开慢车车头相离的有 关问题,一般又叫超车问题。
两列火车同向而行,慢车在前,快车在后,从快车车头追上慢车 车尾到快车车尾离开慢车车头,要追及的路程就是两车车身 之长的和, 追及的速度就是两车的速度差, 追及时间就是指快 车从遇到慢车到超出慢车所需的时间,又叫超车时间。
时间=路程÷速度
火车的相遇问题一般研究两列火车相向运行,从 车头相遇到车尾相离的有关问题,就是错车问题。
两车车长之和
两列火车相向而行,从两车车头相遇到两车车尾相离, 这段时间共行的路程就是两车车身长的和。 相向而行的速度就是两车的速度和。 这里的相遇时间 就是指两车从相遇到相离的时间,又叫错车时间。
南京长江大桥全长6700米,一列长140米的 从车头上桥到车尾离桥 火车,从车头上桥到车尾离桥共用 342秒,这 列火车的速度? 火车过桥:就是指火车车头上桥到车尾离桥。 速度=路程÷时间
342秒→桥长670 Nhomakorabea米火车速度=(火车长度+桥的长度)÷过桥时间
(6700+140)÷342
=6840 ÷342 =20(米)答:这列火车的速度是每秒20米。
火车过桥
火车速度=(火车长度+桥的长度)÷过桥时间 过桥时间=(火车长度+桥的长度)÷火车速度 火车长度=过桥时间×火车速度-桥的长度 桥的长度=过桥时间×火车速度-火车长度
例1:两列火车在双轨道上相向行驶,甲车身长 130米,车速是每秒30米,乙车身长150米,车速 是每秒40米,两列火车从车头相遇到车尾相离用 了多少秒?
(150+120)÷(34-28) =270 ÷6 =45(秒) 答:快车从追上到完全超过慢车需要45秒。
答:两列火车从车头相遇到车尾相离用了12秒.
两列火车相向而行,甲车长130米,乙车长120 米,两车从相遇到相离,经过5秒钟。已知甲车每 秒行22米,求乙车的速度?
乙车速度=(甲车身长+乙车身长)÷错车时间-甲车速 (130+120)÷(5+22)
