信号与系统123章习题课
信号与系统课后习题与解答第三章
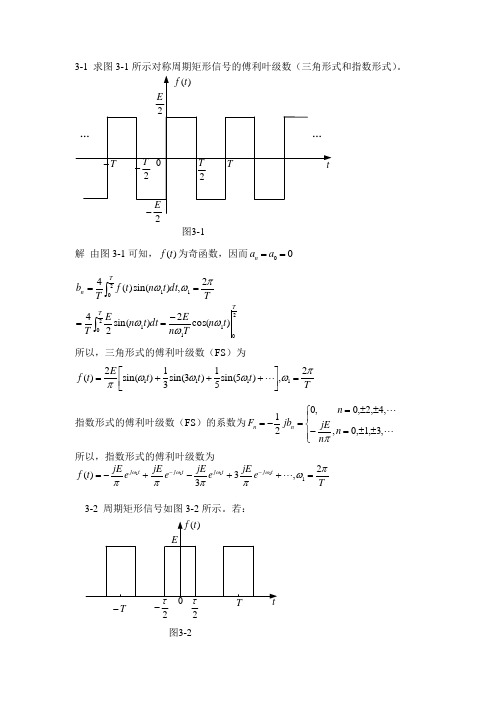
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。
图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统123章习题课
十、信号f1(t)，f2(t)的波形如图(a)、(b)所示，设f(t)= f1(t)*f2(t)，求f(t)分别在t=4，6，8时的数值。
f 1(t) 2 1 2 f 2(t)
0
2
4
6
t
0
1
3
t
十一、某LTI连续系统，初始状态一定，已知当输入f1(t) = (t)时，系统的全响应y1(t)= –e – t(t)；当输入f2(t)= (t) 时，系统的全响应y2(t)= (1–5e – t)(t)； 求当输入f3(t) = t(t)时，系统的全响应y3(t)。
六、（2）一LTI连续系统，当输入f1(t)时的零状态响应 yzs1(t)如图(a)所示，求输入f2(t)[如图(b)所示]时系统的 零状态响应yzs2(t)(写出表达式或画出图形均可）。
yzs1(t) f1(t) 1 0 2 t 0 (a) 1 2 t -1 0 2 2 1 1 (b) 2 t f2(t)
求系统的单位序列响应h(k)。
十七、线性时不变系统输入f(t)与零状态响应y(t)之间 的关系为： t y(t ) e (t ) f ( 2) d
（1）求系统的单位冲激响应h(t)； （2）求当f(t)=(t+1)–(t–2)时的零状态响应。
-1 f1(k) 2 1 -2 0 1 (a) 2 3 k -1 0 -1 (b) 1 2 3 k 1 f2(k)
十四、已知某LTI离散系统，当输入为(k–1)时，系统的 零状态响应为 1 k
(k 1) 2
试计算输入为f(k)=2(k)+(k)时，系统的零状态响应y(k)。
七、一连续LTI系统的输入、输出方程为 2y'(t) + 3y(t) = f'(t) 已知 f(t)=ε(t) ，y(0-) =1，则y(0+)=_______________。 八、(1)试求图示系统的冲激响应h(t)。
信号与系统(习题课)
∴ y(t) = e-3t + t e-3t = (1+ t) e-3t
by wky
习题 3-6 (1)
已知系统的微分方程为 y’’(t) +5 y’(t) + 4 y(t) =2 f ’(t) + 5f(t), t >0; 初始状态y(0-) =1，y’(0-) =5， 求系统的零输入响应yx(t)。 解：系统特征方程为 s2+5s+4=0 , 解得特征根 s1=-1, s2=-4
特解 （强迫响应）
比较：完全响应=零输入响应 + 零状态响应 = e－t + (1 - 1/2e－t -1/2e－3t)
by wky
习题 3-4
已知微分方程为 y’(t) + 3 y (t) = f(t)，t >0; y(0) =1，
求系统的固有响应(齐次解) yh(t)、强迫响应 (特解) yp(t)和完全响应(全解) y(t) 解：系统特征方程为 s+3=0,
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
2 f(t+2)
f(-3t)
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t by wky
2-10 已知信号波形, 绘出下列信号波形
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
信号与系统 陈后金 第二版 课后习题答案(完整版)
（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与线性系统分析习题答案
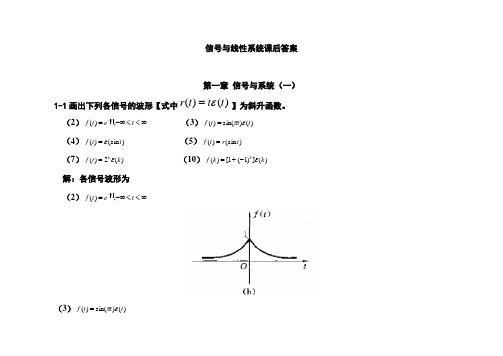
信号与线性系统课后答案第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)tf=r(sin)(t（7）)tf kε(k=(2)（10）)f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
《信号与系统》课后习题参考答案
《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。
又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值 又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。
信号与系统习题课（傅里叶变换
才有
F
(ω
)
=
(
1 jω
)2
F
⎡ d2
⎢ ⎣
dt
2
f
( t ) ⎤⎥
⎦
Signals and Systems, Tsinghua University
7
强调
由
F
⎡d ⎢⎣ dt
f
( t )⎤⎥⎦
= Φ(ω)
得到
F
⎡⎣
f
(t )⎤⎦
=
1 jω
Φ (ω )
实际上是引用了FT的积分性质.
因此要考虑 f (−∞) = 0
法二，频移
F(ω) = F0(ω +ω0)+ F(ω −ω0)
求出f0(t)后,
1 F0(ω)
ω
−ω1 0 ω1
[ ] f (t) = f0(t) ejωt +e−jωt =2f0(t)cosω0t
如何求f0S(igt)na?ls
and
定义、对称性、查表。
Systems, Tsinghua University
−2
−1
1
( ) ejω −e−jω ejω +e−jω − ej2ω +e−j2ω
=2
+
jω
ω2
= ......
（1）计算量大；（2）一些函数积分不收敛。
Signals and Systems, Tsinghua University
法二，利用FT的微积分性质
4 1 f(t)
思路：
f
(t
)
d
⎯⎯dt→δ
Φ(0) = 0
Signals and Systems, Tsinghua University
陈后金《信号与系统》(第2版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)
图2-2
3．有一离散时间信号
（1）画出
（2）求序列 学]
使之满足
解：（1）
又 比较上述两式可得： 故如图2-3所示。
[电子科技大
图2-3
4．已知 如图2-4（a），画出
和
的波形。[北
京理工大学]
解：将 反转得 如图2-4（b）所示，将它们相加、减得 ，波形如图2-4（c）、（d）所示。
图2-4 5．已知f（t）的波形如图2-5所示，令r（t）＝tu（t）。
大学]
图1-2 解：因为：
故：
y2（t）的波形如图1-3所示。
图1-3 3．将如图1-4（a）、（b）所示的连续信号展成如下形式：
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解：（a）该信号可分为两段：
和
可化简为
故
，即：
（b）该信号可分为三段： 可化简为 故
，即
4．求
的值。[北京航空航天大学2006研]
，应该与齐次解有关，即系统的特征根为－1和－3，故特征方程应为 ，即a0＝4，a1＝3。
（2）设系统对激励 rzs（t），则
的零输入响应和零状态响应分别为rzi（t）和
由于
，则由线性时不变系统的微分特性可知
同时，设系统的单位冲激响应为h（t），则由线性时不变系统的叠加性 可知
由式（1）、式（2），并设
陈后金《信号与系统》（第2版）配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1．方程 天大学2007研] A．线性时不变 B．非线性时不变 C．线性时变 D．非线性时变 E．都不对 【答案】B
描述的系统是（ ）。[北京航空航
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
123习题课
一、计算下列积分或和：
t 4 （1） (t 2)( )dt ______________ 2
2
（ 2）
k
t
δ(t)+ε(t) (1 x)( x)dx ______________
1 2ε(t) （3） 2t (1 2 ) d _____________
(k 1) 2
试计算输入为f(k)=2(k)+(k)时，系统的零状态响应y(k)。
第0-11页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
十五、某LTI离散系统的单位脉冲响应 h(k)= (k) –2 (k –1) +3 (k –2) ，系统的输入 f(k)= 3(k) +2 (k –1) – (k –2) ,求yzs(k)，并画图形。
1 , k 0 f (k ) 4 , k 1,2 0 , 其余 0 , k 0 时，其零状态响应 y(k ) 9 , k 0
十六、若已知某LTI系统的输入为
求系统的单位序列响应h(k)。
第0-12页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 十七、线性时不变系统输入f(t)与零状态响应y(t)之间 的关系为： t y(t ) e (t ) f ( 2) d
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
三、（1）已知f(t)的波形如图所示， 画出 d f (1 2t ) 的波形。
dt
f(t) 4 2
-2
0
2
t
（2）已知f(–2t+1)波形如图所示，试画出f(t)的波形。
f(-2t+1) 1 0 -1 (2)
-0.5
0.5
1
t
第0-3页
(b) f2(t)
2
t
(a) f1(t)及其零状态响应
第0-6页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 七、一连续LTI系统的输入、输出方程为 2y'(t) + 3y(t) = f '(t) 已知 f(t)=ε(t) ，y(0–) =1，则y(0+)=_______________。 八、(1)试求图示系统的冲激响应h(t)。
第0-9页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 十二、描述某LTI离散系统的差分方程为 y(k) + 3y(k –1)+ 2y(k –2) = 2f(k) +3f(k –1) 求该系统的单位脉冲响应h(k)。 十三、离散序列f1(k)和f2(k)如题图(a)、(b)所示。设 y(k) = f1(k)﹡f2(k)，则y(2)等于
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 四、用下列微分方程描述的系统为线性时变系统是 (A) y"(t) + 2y'(t) y(t) = 2 f (t) (B) y"(t) + 2y'(t)+ y(t) = 2 f (1 – t) (C) y"(t) + 2 y'(t)+ 5y(t) = 2 f 2(2t) (D) y"(t) + 2y'(t)+ y(t) = 2 f (t –1) 五、某离散系统的全响应为
2
f(t)
∑
1
∫
∑
y (t)
第0-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 八、(2)某线性时不变系统的输入输出方程为 y〃(t) + 2y'(t) + 2y(t) = f '(t)+3f(t) (a) 求该系统的冲激响应h(t)。 (b) 若f(t)=ε(t)，y(0+)=1，y'(0+)=3，求系统的零输入响 应yzi(t)。 九、（1）已知f(t)=e2t(–t)，h(t)=(t–3)，计算卷积 y(t)=f(t)﹡h(t)，并绘出y(t)的波形。 （2）一线性时不变连续系统的阶跃响应 g(t)=(1.5 – t – 1.5e –2t)ε(t) 输入信号f(t) = et，–∞<t<∞，求系统的零状态响应yzs(t)。
(A) -1 (C) 1 (B) 0 (D) 3
-1 f1(k) 2 1 -2 0 1 2 3 k -1 0 -1 1 2 3 k 1 f2(k)
第0-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 十四、已知某LTI离散系统，当输入为(k–1)时，系统的 零状态响应为 1 k
信号与系统 电子教案 二、试确定下列信号周期： （1）f(t)=3cos (4t+ ） 3 (A) 2 (B) (C) /2 (D) 2/
（2）f(k)=2cos ( k)+sin ( k)+sin ( k) 8 4 2
(A) 8 (B) 16 (C) 2 (D) 4
第0-2页
第0-5页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 六、（2）一LTI连续系统，当输入为f1(t)时的零状态响 应yzs1(t)如图(a)所示，求输入为f2(t)[如图(b)所示]时系统 的零状态响应yzs2(t)(写出表达式或画出图形均可）。
f1(t) 1 0 2 t 0 1 2 t -1 0 yzs1(t) 2 2 f2(t) 1 1
第0-8页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
十、信号f1(t)，f2(t)的波形如图所示，设f(t)= f1(t)﹡f2(t)， 求f(t)分别在t=4，6，8时的数值。
f 1(t) 2 1 2 f 2(t)
0
2
4
6
t
0
1
3
t
十一、某LTI连续系统，初始状态一定，已知当输入f1(t) = (t)时，系统的全响应y1(t)= –e – t(t)；当输入f2(t)= (t) 时，系统的全响应y2(t)= (1–5e – t)(t)； 求当输入f3(t) = t(t)时，系统的全响应y3(t)。
6
（ 4） （ 5） （ 6）
第0-1页
n
(2 n) k Βιβλιοθήκη ε( k–2) _______
2 ( k 2 4k 5)(k 1) _____
1
3
e [(t ) (1 0.5t )]d t
2t
2 _______
复合
■
©西安电子科技大学电路与系统教研中心
（1）求系统的单位冲激响应h(t)； （2）求当f(t)= (t+1) – (t–2)时的零状态响应。
第0-13页
■
©西安电子科技大学电路与系统教研中心
y(k ) a k x(0) b f (k )
，k≥0
式中，a,b为常数，x(0)为初始状态，在k=0时接入激 励f(k)；试分析该系统是否是线性系统？是否是时不 变系统？（写出分析过程。）
第0-4页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
六、（1）某LTI因果连续系统，起始状态为x(0–)，输入、 输出分别为f(t)、y(t)。已知当x(0–) = 1，输入因果信号f1(t) 时，全响应y1(t) = e–t + cos t，t≥0；当x(0–) = 2，输入信号 为f2(t)=3f1(t)时，全响应y2(t) = –2e–t + 3cos t，t≥0；求当 x(0–) = 3，输入f3(t)=5f1(t –1)时，系统的全响应y3(t)，t≥0。