中考反比例函数的常见模型以及例习题--含答案
反比例函数常见几何模型归纳(七大模型)(解析版)-初中数学
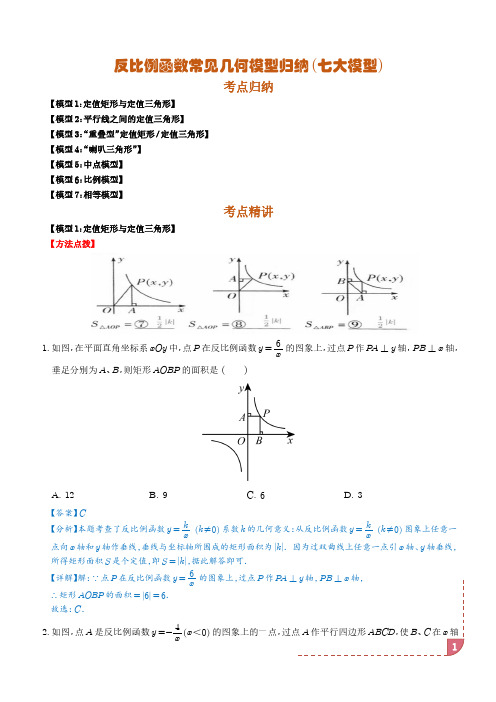
反比例函数常见几何模型归纳(七大模型)考点归纳【模型1:定值矩形与定值三角形】【模型2:平行线之间的定值三角形】【模型3:“重叠型”定值矩形/定值三角形】【模型4:“喇叭三角形”】【模型5:中点模型】【模型6:比例模型】【模型7:相等模型】考点精讲【模型1:定值矩形与定值三角形】【方法点拨】1.如图,在平面直角坐标系xOy 中,点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,垂足分别为A 、B ,则矩形AOBP 的面积是()A.12B.9C.6D.3【答案】C【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .因为过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积S 是个定值,即S =k ,据此解答即可.【详解】解:∵点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,∴矩形AOBP 的面积=6 =6.故选:C .2.如图,点A 是反比例函数y =-4x <0 的图象上的一点,过点A 作平行四边形ABCD ,使B 、C 在x 轴上,点D 在y 轴上,则平行四边形ABCD 的面积为()A.2B.4C.6D.8【答案】B【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .作AH ⊥OB 于H ,根据平行四边形的性质得AD ∥OB ,则S 平行四边形ABCD =S 矩形AHOD ,再根据反比例函数y =kxk ≠0 系数k 的几何意义得到S 矩形AHOD =-4 =4,所以有S 平行四边形ABCD =4.【详解】解:作AH ⊥OB 于H ,如图,∵四边形ABCD 是平行四边形,∴AD ∥OB ,∴S 平行四边形ABCD =S 矩形AHOD ,∵点A 是反比例函数y =-4xx <0 的图象上的一点,∴S 矩形AHOD =-4 =4,∴S 平行四边形ABCD =4.故选:B .3.如图,A 、B 是反比例函数y =kx(k ≠0)的图象上两点,点C 、D 、E 、F 分别在坐标轴上,若正方形OCAD 的面积为6,则矩形OEBF 的面积为.【答案】6【分析】本题主要考查反比例函数中比例系数k 的几何意义和函数图象的对称性,难易程度适中,是中考较常见的考查点.根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的四边形的面积S 的关系即S =k ,进行解答即可.【详解】解:∵S 正方形OCAD =OD ⋅OC =x A ⋅y A =k =6,∴S 长方形OCAD =OE ⋅OF =x B ⋅y B =k =6.故答案为:6.4.如图是反比例函数y =-4x在第二象限内的图象,则图中矩形BCOA 的面积为.【答案】4【分析】根据矩形的面积公式S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,再根据反比例函数的性质解答即可.本题考查了矩形的面积公式,反比例函数的性质,熟练运用反比例函数的性质是解题的关键.【详解】解:设点B a ,b ,∵四边形BCOA 是矩形,∴AB =a ,BC =b ,∴S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,∵点B 在反比例函数y =-4x在图象上,∴a ⋅b =-4,∴a ⋅b =4,∴S 矩形BCOA =ab =4;故答案为4.【模型2:平行线之间的定值三角形】【方法点拨】5.如图,是反比例函数y =5x 和y =-9x在x 轴上方的图象,x 轴的平行线AB 分别与这两个函数图象相交于点A ,B ,则△AOB 的面积是()A.7B.14C.18D.28【答案】A【分析】本题考查了反比例函数k 的几何意义,利用反比例函数的比例系数的几何意义直接写出答案即可.【详解】解:∵x 轴的平行线AB 分别与这两个函数图象相交于点A .B ,∴AB ⊥y 轴,∵点A 、B 在反比例函数y =5x 和y =-9x 的x 轴上方的图象上,∴S △AOB =S △COB +S △AOC =12(5+9)=7,故选:A .6.已知反比例函数y =-6x x <0 与y =2xx >0 的图象如图所示,过y 轴正半轴上的任意一点P 作x 轴的平行线,分别与这两个函数的图象交于M ,N 两点.若点A 是x 轴上的任意一点,连接MA ,NA ,则S △AMN 等于.【答案】4【分析】本题考查了反比例函数k 的几何意义,连接MO ,NO ,根据MN ∥x 轴可得,S △AMN =S △OMN ,进而即可求解.【详解】解:如图所示,连接MO ,NO ,∵MN ∥x 轴∴S △AMN =S △OMN =S △POM +S △PON =-62+22=4故答案为:4.7.如图,在函数y =2x x >0 的图象上任取一点A ,过点A 作y 轴的垂线交函数y =-8xx <0 的图象于点B ,连接OA 、OB ,则△AOB 的面积是.【答案】5【分析】根据反比例函数系数k 的几何意义进行计算即可.理解反比例函数系数k 的几何意义是正确解答的关键.【详解】解:如图,∵点A 在函数y =2xx >0 的图象上,∴S △AOC =12×2=1,又∵点B 在反比例函数y =-8xx <0 的图象上,∴S △BOC =12×8=4,∴S △AOB =S △AOC +S △BOC =1+4=5,故答案为:5.8.如图,B 、C 两点分别在函数y =5x (x >0)和y =-1x(x <0)的图象上,线段BC ⊥y 轴,点A 在x 轴上,则△ABC 的面积为.【答案】3【分析】设B m ,n ,则mn =5,结合BC ⊥y 轴,得到C -1n ,n ,计算BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为1BC ·y B =1m +1×n 计算即可.本题考查了反比例函数的性质,平行线间距离处处相等,熟练掌握反比例函数的性质是解题的关键.【详解】设B m ,n ,根据题意,得mn =5,∵BC ⊥y 轴,∴C -1n ,n ,∴BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为12BC ·y B =12m +1n ×n =12mn +1 =3,故答案为:3.【模型3:“重叠型”定值矩形/定值三角形】【方法点拨】9.如图,点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,且AB ∥x 轴,点C .D 在x 轴上,若四边形ABCD 为长方形,则它的面积为.【答案】2【分析】此题考查了反比例函数的系数k 的几何意义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.首先延长BA 交y 轴于点E ,易得四边形ADOE 与四边形BCOE 是矩形,又由点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,即可得S 矩形ADOE =1,S 矩形BCOE =3,继而求得答案.【详解】解:延长BA 交y 轴于点E ,∵四边形ABCD 为矩形,且AB ∥x 轴,点C 、D 在x 轴上,∴AE ⊥y 轴,∴四边形ADOE 与四边形BCOE 是矩形,∵点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,∴S 矩形ADOE =1,S 矩形BCOE =3,∴S 矩形ABCD =S 矩形BCOE -S 矩形ADOE =3-1=2.故答案为:2.10.如图,点A 、B 分别是反比例函数y =3xx >0 的图象上两点,分别过点A 、B 向坐标轴作垂线,四边形ACEG 的面积记作S 1,四边形BFDG 的面积记作S 2,则S 1S 2(填>、<或=).【答案】=【分析】本题考查了反比例系数k 的几何意义,在反比例函数y =kx图像中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值k ,在反比例函数的图像上任意一点作坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12k ,且保持不变.根据反比例函数解析式中k 的几何意义可知S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,得出S 1=3-m ,S 2=3-m ,即可得出答案.【详解】解:∵A ,B 两点在反比例函数y =3xx >0 的图像上,∴S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,∴S 1=3-m ,S 2=3-m ,∴S 1=S 2.故答案为:=.11.如图,平行于x 轴的直线l 与函数y =6x (x >0)和y =2x(x >0)的图象分别相交于A ,B 两点,分别连接AO 、BO ,则△ABO 的面积为.【答案】2【分析】本题考查反比例函数图象上点的坐标特征,k 的几何意义,设l 交y 轴于点M ,根据反比例函数k 的几何意义,得出S △ABO =S △AOM -S △BOM =2,即可求解.【详解】解:如图,设l 交y 轴于点M ,∵S △AOM =3,S △BOM =1,则S △ABO =S △AOM -S △BOM =2,故答案为:2.12.如图,点A 在双曲线y =1x 上,点B 在双曲线y =3x上,且AB ∥x 轴,则△ABO 的面积是.【答案】1【分析】本题主要考查了反比例函数比例系数的几何意义,延长BA 交y 轴于C ,则AB ⊥y 轴,根据反比例函数比例系数的几何意义可得S △AOC =12,S △BOC =32,则S △AOB =S △BOC -S △AOC =1.【详解】解:如图所示,延长BA 交y 轴于C ,∵AB ∥x 轴,∴AB ⊥y 轴,∵点A 在双曲线y =1x 上,点B 在双曲线y =3x上,∴S △AOC =12,S △BOC =32,∴S △AOB =S △BOC -S △AOC =1,故答案为:1.【模型4:“喇叭三角形”】【方法点拨】13.如图,点A ,B ,在反比例函数y =4x的图象上,连接OA ,OB ,分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,图中两块阴影部分面积分别为S 1、S 2;若S 1=1,则AMBN=.【答案】2【分析】本题考查的是反比例函数系数k 的几何意义,熟知在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积为12|k |是解答此题的关键.利用k 的几何意义求出△OAM 、△OBN 的面积,然后求出△OCM 的面积,利用相似三角形的性质得到S △OCM S △OBN =OM ON 2即可求解.【详解】解:设OB 交AM 于点C ,∵分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,∴S △OAM =S △OBN =2,∴S △OCM =S △OAM -S 1=2-1=1,又∵AM ∥BN ,∴△OCM ∽△OBN ,∴S △OCM S △OBN =OM ON2=12,∴OM ON=22,又∵OM ⋅AM =ON ⋅BN ,∴AM BN =ON OM =2.故答案为:214.如图是一个反比例函数(x >0)的图象,点A (2,4)在图象上,AC ⊥x 轴于C ,当点A 运动到图象上的点B (4,2)处,BD ⊥x 轴于D ,△AOC 与△BOD 重叠部分的面积为()A.1B.2C.34D.13【答案】A【解答】解:如图所示:∵点A (2,4),点B (4,2),AC ⊥x 轴于C ,BD ⊥x 轴于D ,∴点C 的坐标为(2,0),点D 的坐标为(4,0),AC ∥BD ,∴△OCE ∽△ODB ,∴OC OD =CE DB ,即24=CE 2解得CE =1,∴S △OCE OC ⋅CE 2=2×12=1,即△AOC 与△BOD 重叠部分的面积为1.故选:A .15.如图,过反比例函数y =9x(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得()A.S 1>S 2B.S 1=S 2C.S 1<S 2D.大小关系不能确定【答案】B 【解答】解:由于A 、B 均在反比例函数y =9x 的图象上,且AC ⊥x 轴,BD ⊥x 轴,则S 1=92;S 2=92.故S 1=S 2.故选:B .16.如图,在第一象限内,点P (2,3),M (a ,2)是双曲线y =k x (k ≠0)上的两点,P A ⊥x 轴于点A ,MB ⊥x 轴于点B ,P A 与OM 交于点C ,则△OAC 的面积为()A.32B.43C.2D.83【答案】B 【解答】解:把P (2,3),M (a ,2)代入y =k x得k =2×3=2a ,解得k =6,a =3,设直线OM 的解析式为y =mx ,把M (3,2)代入得3m =2,解得m =23,所以直线OM 的解析式为y =23x ,当x =2时,y =23×2=43,所以C 点坐标为(2,43),所以△OAC 的面积=12×2×43=43.故选:B .【方法点拨】条件:A /B 两点分别位y =k x上不同两点,延长AB 交x 轴与点F ,B 位AF 的中点结论:①▲ACF ~▲BDF ,且相似比为BF AF =12。
反比例函数几何模型求k值(经典)

反比例函数常见几何模型汇总近年来,反比例函数作为中考压轴小题,出现的次数一直居高不下,仔细研读中考真题,不难发现一些常见几何模型,基于此,本文重点介绍常用的几种与反比例结合的几何模型,帮助读者梳理解题思路,部分模型结论可以记忆,在考试小题中直接套用即可!【模型一】定值矩形与定值三角形k【例1】如图,点 P 是反比例函数图象上的一点,过 P 向 x 轴作垂线,若阴影面积为 2,则这个反比例函数的关系式是______________。
【答案】xy 4-= 【模块二】平行线之间的定值三角形条件:A 是x k y 1=上一点,B 是xk y 2=上一点,AB∥x 轴, 结论:)(2121k k S S ABP ABO +==∆∆【例2】如图,A 是反比例函数xk y =图象上的一点,过点 A 作 AB ⊥y 轴于点 B,点 P 在 x 轴上,△ABP 的面积为 2,则 k 的值为_______。
【答案】4【模块三】“重叠型”定值矩形、定值三角形条件:A 是x k y 1=上一点,D 是xk y 2=上一点,AB ⊥x 轴,AM ⊥y 轴, 结论:21k k S ABCD -=矩形。
【例3】如图,A 是x y 1=上一点,B 是xy 3=上一点,且AB ∥x 轴,C 、D 两点在x 轴上,则矩形ABCD 的面积为________。
【答案】2【模块四】“喇叭三角形”条件:A 、B 两点分别为xk y =上不同两点,且AC ⊥x 轴,BD ⊥x 轴。
②EBDC AOE S S 四边形=∆;【例4】如图,反比例函数xk y =经过A(2,2)和B(4,m),则△AOB 的面积为______。
【答案】3.【模块五】中点模型②C 、D 为线段OF 的三等分点,即DF CD OC ==;④1:3:2::=∆∆BDF ACDB OAC S S S 四边形。
【例5】如图,平行四边形AOBC 中,对角线AB 和OC 交于点E ,反比例函数xk y =经过A 、E 两点,若18=AOBC S ,则。
专题1 反比例函数K的几何意义——初中几何与代数必考模型+例题+变式

8.如图,A,B两点在双曲线y= 上,分别经过A,B两点向轴作垂线段,已知阴影小矩形的面积为1,则空白两小矩形面积的和S1+S2=______.
【答案】4
【解析】
【分析】欲求S1+S2,只要求出过A、B两点向x轴、y轴作垂线段求出与坐标轴所形成的矩形的面积即可,而矩形面积为双曲线y= 的系数k,由此即可求出S1+S2.
【详解】解:作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD//x轴,∴四边形ADOE为矩形,
∴ ,而 =|−k|,
∴|−k|=6,而−k<0,即k>0,∴k=6.
故选C.
【点睛】本题考查了反比例函数 (k≠0)系数k的几何意义:从反比例函数 (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
【解析】
【分析】根据反比例函数的性质对A、B、D进行判断;根据反比例函数系数k的几何意义对C进行判断.
【详解】解:A、反比例函数图象分布在第二、四象限,则k<0,所以A选项错误;
B、在每一象限,y随x的增大而增大,所以B选项错误;
C、矩形OABC面积为2,则|k|=2,而k<0,所以k=﹣2,所以C选项正确;
A.1B.3C.6D.-6
【答案】C
【解析】
【分析】作AE⊥BC于E,由四边形ABCD为平行四边形得AD//x轴,则可判断四边形ADOE为矩形,所以平行四边形ABCD的面积=矩形ADOE的面积,根据反比例函数k的几何意义得到矩形ADOE的面积=|−k|,则|−k|=6,利用反比例函数图象得到−k<0,即k>0,于是有k=6.
【点睛】考查了反比例函数的图象的知识,解题的关键是了解系数k的几何意义.
部编版初中九年级数学反比例函数(含中考真题解析答案)

部编版初中九年级数学反比例函数(含中考真题解析答案)反比例函数(含答案)?解读考点知识点 1.反比例函数概念反比例函数概2.反比例函数图象念、图象和性3.反比例函数的性质质 4.一次函数的解析式确定名师点晴会判断一个函数是否为反比例函数。
知道反比例函数的图象是双曲线,。
会分象限利用增减性。
能用待定系数法确定函数解析式。
会用数形结合思想解决此类问题.反比例函5.反比例函数中比例系数的几何能根据图象信息,解决相应的实际问题.数的应用意义能解决与三角形、四边形等几何图形相关的计算和证明。
?2年中考【2021年题组】y?1.(2021崇左)若反比例函数kx的图象经过点(2,-6),则k的值为()A.-12 B.12 C.-3 D.3【答案】A.【解析】y?试题分析:∵反比例函数kx的图象经过点(2,��6),∴k?2?(?6)??12,解得k=��12.故选A.考点:反比例函数图象上点的坐标特征. 2.(2021苏州)若点A(a,b)在反比例函数A.0 B.��2 C.2 D.��6 【答案】B.【解析】y?y?2x的图象上,则代数式ab��4的值为()试题分析:∵点(a,b)反比例函数22b?x上,∴a,即ab=2,∴原式=2��4=��2.故选B.考点:反比例函数图象上点的坐标特征. 3.(2021来宾)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是()- 1 -A. B. C.D.【答案】C.考点:1.反比例函数的应用;2.反比例函数的图象.4.(2021河池)反比例函数y1?mx(x?0)的图象与一次函数y2??x?b的图象交于A,B两点,其中A(1,2),当y2?y1时,x的取值范围是()A.x<1 B.1<x<2 C.x>2 D.x<1或x>2 【答案】B.【解析】试题分析:根据双曲线关于直线y=x对称易求B(2,1).依题意得:如图所示,当1<x<2时,y2?y1.故选B.考点:反比例函数与一次函数的交点问题.- 2 -5.(2021贺州)已知k1?0?k2,则函数y?k1x和y?k2x?1的图象大致是()A.【答案】C.B.C. D.考点:1.反比例函数的图象;2.一次函数的图象. 6.(2021宿迁)在平面直角坐标系中,点A,B的坐标分别为(��3,0),(3,0),点P在y?反比例函数2x的图象上,若△PAB为直角三角形,则满足条件的点P的个数为()A.2个 B.4个 C.5个 D.6个【答案】D.【解析】y?试题分析:①当∠PAB=90°时,P点的横坐标为��3,把x=��3代入此时P点有1个;22y??x得3,所以2222222(x?3)?()(x?3)?()22x,PB=x,AB2 ②当∠APB=90°,设P(x,x),PA=222222(x?3)?()?(x?3)?()222(3?3)xxPA?PB?AB==36,因为,所以=36,整理得2x4?9x2?4?0,所以x2?9?659?65x2?22,或,所以此时P点有4个;y?22y?x得3,所以此时P点有1个;③当∠PBA=90°时,P点的横坐标为3,把x=3代入综上所述,满足条件的P点有6个.故选D.考点:1.反比例函数图象上点的坐标特征;2.圆周角定理;3.分类讨论;4.综合题.7.(2021自贡)若点(的点,并且x1,y1),(x2,y2),(x3,y3y??),都是反比例函数1x图象上y1?0?y2?y3,则下列各式中正确的是()- 3 -A.D.x1?x2?x3 B.x1?x3?x2 C.x2?x1?x3x2?x3?x1【答案】D.【解析】试题分析:由题意得,点(的点,且(x1,y1)xy,xy,(2,2)(3,3)都是反比例函数y??1x上y1?0?y2?y3,xy,xy位于第三象限,x?x3,则(2,2)(3,3)y随x的增大而增大,2 x1,y1)位于第一象限,x1最大,故x1、x2、x3的大小关系是x2?x3?x1.故选D.考点:反比例函数图象上点的坐标特征.8.(2021凉山州)以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面y?直角坐标系,双曲线3x经过点D,则正方形ABCD的面积是()A.10 B.11 C.12 D.13 【答案】C.考点:反比例函数系数k的几何意义.y?9.(2021眉山)如图,A、B是双曲线kx上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()48A.3 B.3 C.3 D.4- 4 -【答案】B.考点:1.反比例函数系数k的几何意义;2.相似三角形的判定与性质. 10.(2021内江)如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点Ay?的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线有公共点,则k的取值范围为()kx与正方形ABCDA.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16 【答案】C.【解析】试题分析:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则Ay?的坐标是(1,1),∵AB=BC=3,∴C点的坐标是(4,4),∴当双曲线kx经过点(1,1)时,k=1;当双曲线kx经过点(4,4)时,k=16,因而1≤k≤16.故选C.考点:1.反比例函数与一次函数的交点问题;2.综合题.- 5 -11.(2021孝感)如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函y?数1ky?x的图象上.若点B在反比例函数x的图象上,则k的值为()A.��4 B.4 C.��2 D.2【答案】A.考点:1.反比例函数图象上点的坐标特征;2.相似三角形的判定与性质;3.综合题.41012.(2021宜昌)如图,市煤气公司计划在地下修建一个容积为m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是()- 6 -【答案】A.B. C. D.考点:1.反比例函数的应用;2.反比例函数的图象.y?13.(2021三明)如图,已知点A是双曲线2x在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为()A.n??2m B.【答案】B.【解析】n??24n??m C.n??4m D.m2试题分析:∵点C的坐标为(m,n),∴点A的纵坐标是n,横坐标是:n,∴点A 的坐22标为(n,n),∵点C的坐标为(m,n),∴点B的横坐标是m,纵坐标是:m,∴点B2nm?2222mmn??mn,∴m2n2?4,又∵m<0,n>0,∴的坐标为(m,m),又∵n,∴- 7 -mn??2,∴n??2m,故选B.考点:反比例函数图象上点的坐标特征.y?14.(2021株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数图象上的概率是()12x1111A.2 B.3 C.4 D.6【答案】D.考点:1.列表法与树状图法;2.反比例函数图象上点的坐标特征.OA3?OB4.15.(2021乌鲁木齐)如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,∠y?AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数kx的图象2过点C.当以CD为边的正方形的面积为7时,k的值是()- 8 -A.2 B.3 C.5 D.7 【答案】D.考点:1.反比例函数综合题;2.综合题;3.压轴题. 16.(2021重庆市)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴y?平行,A,B两点的纵坐标分别为3,1.反比例函数ABCD的面积为()3x的图象经过A,B两点,则菱形A.2 B.4 C.22 D.42 【答案】D.【解析】y?试题分析:过点A作x轴的垂线,与CB的延长线交于点E,∵A,B两点在反比例函数3x的图象上且纵坐标分别为3,1,∴A,B横坐标分别为1,3,∴AE=2,BE=2,∴AB=22,S菱形ABCD=底×高=22×2=42,故选D.- 9 -考点:1.菱形的性质;2.反比例函数图象上点的坐标特征;3.综合题.17.(2021临沂)在平面直角坐标系中,直线y??x?2与反比例函数1y?x的图象有2个公共点,则b的取值范围是公共点,若直线y??x?b与反比例函数()y?1x的图象有唯一A.b>2 B.��2<b<2 C.b>2或b<��2 D.b<��2 【答案】C.考点:反比例函数与一次函数的交点问题. 18.(2021滨州)如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA12y??y?x、x的图象交于B、A两点,则∠OAB的大小的变化趋势为的两边分别与函数()- 10 -A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变【答案】D.考点:1.相似三角形的判定与性质;2.反比例函数图象上点的坐标特征;3.综合题. 19.(2021扬州)已知一个正比例函数的图象与一个反比例函数的一个交点坐标为(1,3),则另一个交点坐标是.【答案】(��1,��3).【解析】试题分析:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点的坐标与点(1,3)关于原点对称,∴该点的坐标为(��1,��3).故答案为:(��1,��3).考点:反比例函数图象的对称性.20.(2021泰州)点(a��1,1)、(a+1,2)在反比例函数yyy?k?k?0?x的图象上,若y1?y2,- 11 -则a的范围是.【答案】��1<a<1.考点:1.反比例函数图象上点的坐标特征;2.分类讨论.y?21.(2021南宁)如图,点A在双曲线23ky?x(x?0)上,x(x?0)点B在双曲线上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k= .【答案】63.【解析】y?试题分析:因为点A在双曲线2323x(x?0)上,设A点坐标为(a,a),因为四23边形OABC是菱形,且∠AOC=60°,所以OA=2a,可得B点坐标为(3a,a),可得:3a?k=23a=63,故答案为:63.考点:1.菱形的性质;2.反比例函数图象上点的坐标特征;3.综合题. 22.(2021桂林)如图,以?ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直y?角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数交BC于D,连接AD,则四边形AOCD的面积是.kx的图象- 12 -【答案】9.考点:1.平行四边形的性质;2.反比例函数系数k的几何意义;3.综合题;4.压轴题. 23.(2021贵港)如图,已知点A1,A2,…,An均在直线y?x?1上,点B1,B2,…,y??Bn均在双曲线1x上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若则a2021= .a1??1,【答案】2.- 13 -考点:1.反比例函数图象上点的坐标特征;2.一次函数图象上点的坐标特征;3.规律型;4.综合题.24.(2021南京)如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1?1x,则y2与x的函数表达式是.【答案】【解析】y2?4x.试题分析:过A作AC⊥x轴于C,过B作BD⊥x轴于D,∵点A在反比例函数y1?1x上,11∴设A(a,a),∴OC=a,AC=a,∵AC⊥x轴,BD⊥x轴,∴AC∥BD,∴△OAC∽△ACOCOAACOCOA12?????OBD,∴BDODOB,∵A为OB的中点,∴BDODOB2,∴BD=2AC=a,- 14 -2k2y2?2a??4yx,∴k=aOD=2OC=2a,∴B(2a,a),设,∴2与x的函数表达式是:y2?44y2?x.故答案为:x.考点:1.反比例函数与一次函数的交点问题;2.综合题;3.压轴题.y?25.(2021攀枝花)如图,若双曲线kx(k?0)与边长为3的等边△AOB(O为坐标原点)的边OA、AB分别交于C、D两点,且OC=2BD,则k的值为.363【答案】25.- 15 -考点:1.反比例函数图象上点的坐标特征;2.等边三角形的性质;3.综合题.93(x>0)y?x26.(2021荆门)如图,点A1,A2依次在的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为.【答案】(62,0).- 16 -考点:1.反比例函数图象上点的坐标特征;2.等边三角形的性质;3.综合题;4.压轴题. 27.(2021南平)如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OCy?是△OAB的中线,点B,C在反比例函数于.3x(x?0)的图象上,则△OAB的面积等9【答案】2.考点:1.反比例函数系数k的几何意义;2.综合题. 28.(2021烟台)如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比y?例函数kx(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为.- 17 -15【答案】4.考点:1.反比例函数系数k的几何意义;2.反比例函数综合题;3.综合题. 29.(2021玉林防城港)已知:一次函数y??2x?10的图象与反比例函数y?kx(k?0)的图象相交于A,B两点(A在B的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)当A(a,��2a+10),B(b,��2b+10)时,直线OA与此反比例函数图象的另一支交BC5?BD2,求△ABC的面积.于另一点C,连接BC交y轴于点D.若y?【答案】(1)81?x,B(1,8);(2)(��4,��2)、(��16,2);(3)10.- 18 -【解析】y?试题分析:(1)把点A的坐标代入kx,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;(2)①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=��2x+10,当y=0时,��2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5��4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴AHMH2MH??EHAH,∴12,∴MH=4,∴M(0,0),可设直线AP的解析式为y?mx,1?y?x??2??x?4811?y??y?xy?2?x,2,则有4m?2,解得m=2,∴直线AP的解析式为解方程组?得:??x??4?y??2,∴点P的坐标为(��4,��2)或?.1②若∠ABP=90°,同理可得:点P的坐标为(��16,2).?- 19 -1综上所述:符合条件的点P的坐标为(��4,��2)、(��16,2);?(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,则有BS∥CT,CDCTBC5CTCD3????BD2.∵A(a,��2a+10)∴△CTD∽△BSD,∴BDBS.∵BD2,∴BS,B(b,��2b+10),∴C(��a,2a��考点:1.反比例函数综合题;2.待定系数法求一次函数解析式;3.反比例函数与一次函数的交点问题;4.相似三角形的判定与性质;5.压轴题.【2021年题组】1. (2021年湖南湘潭)如图,A、B两点在双曲线线段,已知S阴影=1,则S1+S2=()y?4x上,分别经过A、B两点向轴作垂- 20 -④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是(把所有正确的结论的序号都填上).【答案】①④.考点:1.反比例函数综合题;2. 反比例函数的图象和k的几何意义;3.平行四边形、矩形的性质和菱形的性质.- 26 -9. (2021年湖北荆州)如图,已知点A是双曲线y?2x在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线是.y?kx(k<0)上运动,则k的值【答案】��6.考点:1.单动点问题;2.曲线上点的坐标与方程的关系;3. 等边三角形的性质;4.相似三角形的判定和性质;5.锐角三角函数定义;6.特殊角的三角函数值.- 27 -10. (2021年江苏淮安)如图,点A(1,6)和点M(m,n)都在反比例函数y?kx(x>0)的图象上,(1)k的值为;(2)当m=3,求直线AM的解析式;(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.【答案】(1)6;(2)y=��2x+8;(3)直线BP与直线AM的位置关系为平行,.- 28 -考点:1.反比例函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.相似三角形的判定和性质;5.平行的判定.?考点归纳归纳 1:反比例函数的概念基础知识归纳:一般地,函数(k是常数,k0)叫做反比例函数。
中考反比例函数的常见模型以及例习题

反比例函数的常见模型解决反比例函数的问题,除了掌握反比例函数的图像及性质以及反比例函数常见的面积模型之外,还要熟练掌握以下几个经典模型:【模型1】正比例函数图像被反比例函数图像所截得的线段相等【模型2】一次函数图像被坐标系和反比例函数图像所截得的相等线段【模型3】同一象限内反比例函数图像上两点连线的平行线【模型4】反比例函数与矩形(1)【模型5】反比例函数与矩形(2)【模型6】反比例函数与最值【模型7】反比例函数与黄金分割让我们一起领略反比例函数的神奇一、个人对反比例函数的几点困惑与感悟1.为何正比例函数的比例系数是比,而反比例函数的比例系数却不是比?2.为何我市中考的反比例函数问题总不像其它函数那么深入?只探究一些皮毛问题!至多探究一下的几何意义(面积),例如2016年台州市中考考查的也是“函数的研究通法”,并非专门深入研究反比例函数.3.过去我们遇到稍难一点的反比例函数问题,就只有“暴力设元”这一途径,总无法避开多元方程、分式方程、高次方程.4.个人认为作为老师,不应该只应付中考,而应该研究更纯粹的数学,站在更高的位置来了解数学本质!做到居高临下、解有依据!5.实际上,反比例函数中也存在很多的“比”,斜比、直比(纵比、横比、纵横比)、面积比,可以说“比比皆是”!现在就让我们一起来比出精彩、比出神奇.二、一道曾经困惑我多时的中考题某年宁波市中考的填空压轴题:如图,的顶点(,),双曲线经过点、,当以、、为顶点的三角形与的相似时,则.1.常规性解法:通过设元,例如设(,),则(,),再根据条件列方程:(1)利用、、或列方程;(2)利用列方程;(3)利用“一线三等角”模型、和列方程.实际上,在上述常规处理方法中,已经透着一点智慧、一点灵性了,具体操作方法中也具备了一定的技巧性.但我本人对此,却一直难言满意,耿耿于怀!2.挖掘隐含性质,巧解此题(1)实际上,此图中含有一些很重要的性质:过点作轴于,连接,直线分别交坐标轴于点、.则有①∥;②,;③,.基于以上这些性质,有如下解法.(2)我的第一种解法(整体思想):由,可得,,即,于是,,……(3)我一个同事的解法(斜边转直比):由,可得,,转为横比,,因此,……(4)我一个学生的解法(斜等转直等):由得,则,……(5)我的第二种解法(平行导角度):由∥得,,于是,……(6)下面我们要着重解决两件事:①上述性质是否永远成立?如何证明?②解题技巧除上述方法:整体思想、斜边转直比、斜等转直等、平行导角度外,还有斜长转直长、面积比与边比互转、纯面积转化等等,后面将一、一介绍.三、探究性质1.如图,双曲线与矩形边交于点、,直线交坐标轴于点、.①如图1,若,则;②如图2,若,则;③如图3,若,则,直线与的位置关系是,与的大小关系.图1图2图32.①如图1,双曲线与直线交于点、,轴于点,轴于点,请探究直线与的位置关系,线段与的大小关系.②如图2,双曲线与直线交于点、,轴于,轴于,轴于,轴于,请探究直线与、的位置关系,以及线段与的大小关系.图1图2四、最常见思想方法(斜转直):斜边转直比、斜等转直等、斜长转直长1.如图,直线反比例函数()图象交直线于点、,且,则的值为.(1)常规方法(斜长转直长):,则,可设(,),则(,),列方程解决;(2)口算巧解(斜边转直比):由,得,,转为横比得,,则,,……2.同类变式题:如图,直线交坐标轴于点、,双曲线交直线于点、.若,则的值为;3.难题展示(中国数学教育名师讲堂481230254,每日一题第8题,2017/3/29)如图,点(,),,在双曲线上,,分别交,轴于,,分别交,轴于,.(1)求的面积;(2)求证:.4.原创清新小题和近年的中考题:(1)如图1,,的面积为,则的值为.(2)如图2,点,在双曲线上运动,轴,.①在运动过程中,的面积是不是定值?答:;②若,且是正三角形,则点的坐标为.(3)如图3,□中,,,双曲线经过点和中点,则该双曲线的解析式为.(4)如图4,直线与分别与双曲线交于点、,,则的值为.图1图2图3图4(5)(十堰)如图5,正的边长为,双曲线经过点、,且,则的值为.(6)如图6,双曲线与直线交于点、.①(原创、铺垫②)若、,且,则;②(常州模拟·改编)若,且,则;③(杭州模拟·改编)若,且,则.(7)(据上题改编)如图7,为双曲线上的动点,过点作矩形,直线的解析式为,交矩形边于,,则.图5图6图7五、面积比、边比互转1.①(原创、铺垫)如图1①,直线与双曲线交于点,为双曲线上一点,射线交轴于点,若的面积为,则点坐标为;②(成都)如图1②,直线与双曲线交于点、,为双曲线上一点,射线交轴于点,若的面积为,则点坐标为.2.(无锡)如图2,轴,∥轴,双曲线过点、,且,已知的面积为,则的值为.图1①图1②图33.(宁波)如图3,正的顶点在双曲线上,双曲线与边交于点,连接,则的面积为.4.(丽水)如图4,双曲线与直线交于点、,轴,设点的横坐标为.①用含的式子表示;②若与四边形的面积和为,则.5.如图5,双曲线与直线交于点、.①(常州模拟)若,且,则;②(改编自①)若、,且,则.图3图4图56.如图6,轴,为中点,延长到,延长到,若双曲线恰好经过点,,且,则.7.如图7,双曲线过点,,过点,,若,均与轴平行,,,且它们之间的距离长为,则.8.如图8,直线交双曲线于点,,若,则.图6图7图89.如图,点在双曲线上,轴,,延长线交轴于,若的面积为,则的值为.10.如图,点、在双曲线上,轴,轴,垂足、分别在轴的正半轴和负半轴上,,,是的中点,若面积是的倍,则的值为.六、反比例函数图象中的“一线三等角”构造,初探黄金比例1.如图1,中,,,双曲线经过点、,且点的纵坐标为,则的值为.(1)剖析:对于坐标系中的一个直角,若两条边均“倾斜”,我们经常构造“”形全等或相似,即“一线三等角”模型,或叫“矩形大法”,见图2,得. (2)后感:我们可以发现,矩形恰好是一个“黄金矩形”,这到底是一种偶然的巧合,还是一种必然的存在呢?这有待于我们进一步探究…(3)探究(2016临沭模拟):如图3,双曲线与矩形的边交于点,,若设点的坐标为(,),且有,,则.图1图2图32.类似题:①(2015临海模拟·填空压轴题)如图,,,双曲线经过点,双曲线经过点,已知点的纵坐标为,则,点的坐标为.②(个人原创)如图2,中,,,双曲线经过点,双曲线经过点,且点的纵坐标为,则的值为.3.难题展示(常州·于新华老师原创题)(1)如图1,点(,),均在双曲线上,过点作轴垂线,过点作轴垂线,两垂线交于点,垂足分别为,,将沿翻折,点恰好落在轴上的点处.求点的坐标.(2)如图2,点(,),均在双曲线上,过点作轴垂线,过点作轴垂线,两垂线交于点,垂足分别为,,将沿翻折,点恰好落在轴上的点处.求点的坐标.图1图24.如图,矩形的边的解析式为,顶点,在双曲线上.①若,则点的坐标为;②连接,,若是等边三角形,则.后感:若能发现,本题将更简单!拓展:如图,正方形的顶点、在双曲线上,、在双曲线上,则正方形的面积为.5.(2013湖州模拟)如图1,矩形的顶点、在双曲线上,若点(,),则点的坐标为.6.如图2,矩形中,,点(,),点,在双曲线上,若为中点,则的值为.图1图27.①如图1,点,在双曲线上运动,以为底边作等腰直角,则点也在一条双曲线上运动,则该双曲线的解析式为;②如图2,点,在双曲线上运动,以为底边作等腰,则点也在一条双曲线上运动,若,则该双曲线解析式为;③如图3,点,在双曲线上运动,以为底作等腰,点在另一双曲线上运动,若,请用,表示.图1图2图3七、平行导角度,角度导比例1.如图,点,在双曲线上,经过原点,过点作∥轴,连接并延长,交双曲线于点.①求证:;②求的值.根据本题的发现,改编了一个清新小题:如图,点,在双曲线上,经过原点,过点的直线交该双曲线于点,分别交轴,轴于点,,若,.求的值.2.如图,直线交在双曲线于点、,经过原点,过作交轴于点,连接并延长,交双曲线于点.求的值.3.如图,双曲线与过原点的直线交于点、,点在双曲线上,直线、分别交轴于点、.若设,,则.4.如图,,双曲线经过点、、,求证:.八、纯面积推导1.如图,点(,),,在双曲线上,,分别交,轴于,,分别交,轴于,.求证:.(此方法感谢江苏·于新华老师的指导!)2.(2016菏泽)如图,,均是等腰直角三角形,双曲线经过点,交线段与点,求与的面积之差.后感:①题中条件“,均是等腰直角三角形”可如何改变?②写出,,的关系:.3.(十堰)如图5,正的边长为,双曲线经过点、,且,则的值为.4.(常州)如图1,,双曲线经过点、,且,求的值;5.如图2,,双曲线经过点、、,求证:.图1图2。
专题64 反比例函数k的八种几何模型及解法(解析版)-中考数学解题大招复习讲义

模型介绍考点1一点一垂线模型【模型讲解】反比例函数图象上一点关于坐标轴的垂线、另一坐标轴上一点(含原点)围成的三角形面积等于12|k|.【示例】拓展:【例1】.如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=(x >0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会()A.越来越小B.越来越大C.不变D.先变大后变小解:如图,过点B作BC⊥PA于点C,则BC=OA,设点P(x,),=PA•BC=••x=3,则S△P AB当点A的横坐标逐渐增大时,△PAB的面积将会不变,始终等于3,故选:C.变式训练【变1-1】.如图,点A、B的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是4,则k的值为﹣.解:设OM=a,则OM=MN=NC=a,∵点A、B在反比例函数y=的图象上,AM⊥OC、BN⊥OC,∴AM=,BN=,=S△AOM+S四边形AMNB+S△BNC,∵S△AOC∴﹣×3a×=﹣k+4﹣×a×,解得k=﹣,故答案为:﹣.【变1-2】.如图,在第一象限内,点P(2,3),M(a,2)是双曲线y=(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为()A.B.C.2D.解:把P(2,3),M(a,2)代入y=得k=2×3=2a,解得k=6,a=3,设直线OM的解析式为y=mx,把M(3,2)代入得3m=2,解得m=,所以直线OM的解析式为y=x,当x=2时,y=×2=,所以C点坐标为(2,),所以△OAC的面积=×2×=.故选:B.考点2一点两垂线模型【模型讲解】反比例函数图象上一点与坐标轴的两条垂线所围成的矩形面积等于|k |.【示例】ABCD S k【例2】.双曲线与在第一象限内的图象如图所示,作一条平行于y 轴的直线分别交双曲线于A 、B 两点,连接OA 、OB ,则△AOB 的面积为()A .1B .2C .3D .4解:设直线AB 与x 轴交于点C .∵AB ∥y 轴,∴AC ⊥x 轴,BC ⊥x 轴.∵点A 在双曲线y =的图象上,∴△AOC 的面积=×10=5.∵点B 在双曲线y =的图象上,∴△COB的面积=×6=3.∴△AOB的面积=△AOC的面积﹣△COB的面积=5﹣3=2.故选:B.变式训练【变2-1】.如图,函数y=(x>0)和(x>0)的图象分别是l1和l2.设点P在l2上,PA∥y轴交l1于点A,PB∥x轴交l1于点B,△PAB的面积为.解:设点P(x,),则点B(,),A(x,),∴BP=x﹣=,AP=﹣=,==,∴S△ABP故答案为:.【变2-2】.如图,直线AB∥x轴,分别交反比例函数y=图象于A、B两点,若S△AOB=2,则k2﹣k1的值为4.解:设A(a,b),B(c,d),代入得:k1=ab,k2=cd,=2,∵S△AOB∴cd﹣ab=2,∴cd﹣ab=4,∴k2﹣k1=4,故答案为:4.【变2-3】.如图,在平面直角坐标系中,M为y轴正半轴上一点,过点M的直线l∥x轴,l分别与反比例函数y=和y=的图象交于A、B两点,若S△AOB=3,则k的值为﹣2.解:∵直线l∥x轴,∴AM⊥y轴,BM⊥y轴,=|k|,S△BOM=×4=2,∴S△AOM=3,∵S△AOB=1,∴S△AOM∴|k|=2,∵k<0,∴k=﹣2,故答案为:﹣2.考点3两曲一平行模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例3】.如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为()A.﹣8B.﹣12C.﹣24D.﹣36解:设A(x,0).∵正方形ADEF的面积为16,∴ADEF的边长为4,∴E(x﹣4,4),∵BF=2AF,∴BF=2×4=8,∴B(x,12).∵点B、E在反比例函数y=(k为常数,k≠0)的图象上,∴4(x﹣4)=12x,解得x=﹣2,∴B(﹣2,12),∴k=﹣2×12=﹣24,故选:C.变式训练【变3-1】.若正方形OABC的顶点B和正方形ADEF的顶点E都在函数的图象上.若正方形OABC的面积为1,则k的值为1;点E的坐标为(+,﹣).解:∵正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上,且正方形OABC的边长为1.∴B点坐标为:(1,1),设反比例函数的解析式为y=;∴xy=k=1,设正方形ADEF的边长为a,则E(1+a,a),代入反比例函数y=(x>0)得:1=(1+a)a,又a>0,解得:a=﹣.∴点E的坐标为:(+,﹣).【变3-2】.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S=1.7,则S1+S2等于 4.6.阴影解:如图,∵A、B两点在双曲线y=上,=4,S四边形BDOC=4,∴S四边形AEOF∴S1+S2=S四边形AEOF+S四边形BDOC﹣2×S阴影,∴S1+S2=8﹣3.4=4.6故答案为:4.6.【变3-3】.如图,在反比例函数(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为1,2,3,4,….分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,则S1+S2+S3+…+S n=.(用n的代数式表示,n为正整数)解:当x=1时,P1的纵坐标为2,当x=2时,P2的纵坐标1,当x=3时,P3的纵坐标,当x=4时,P4的纵坐标,当x=5时,P5的纵坐标,…则S1=1×(2﹣1)=2﹣1;S2=1×(1﹣)=1﹣;S3=1×(﹣)=﹣;S4=1×(﹣)=﹣;…S n=﹣;S1+S2+S3+…+S n=2﹣1+1﹣+﹣+﹣+…+﹣=2﹣=.故答案为:.考点4两点一垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作垂线围成的三角形面积等于|k|,反比例函数与一次函数图象的交点及坐标轴上任一点构成三角形的面积,等于坐标轴所分的两个三角形面积之和.【示例】【例4】.如图,正比例函数y=kx与反比例函数y=﹣相交于A,C两点,点A的横坐标为﹣4,过点A作x轴的垂线交x轴于B点,连接BC,下列结论:①k=﹣;②不等式kx<﹣的解集为﹣4<x<0或x>4;③△ABC的面积等于16.其中正确的结论个数为()A.0B.1C.2D.3解:将x=﹣4代入y=﹣得y=﹣=2,∴点A坐标为(﹣4,2),将(﹣4,2)代入y=kx得2=﹣4k,解得k=﹣,∴①正确.由反比例函数及正比例函数的对称性可得点C坐标为(4,﹣2),∴当﹣4<x<0或x>4时,kx<﹣,∴②正确.=S△AOB+S△BOC=OB•y A+OB•(﹣y C)=BO(y A﹣y C)=×(2+2)∵S△AOC=8,∴③错误.故选:C.变式训练【变4-1】.如图所示,一次函数y=kx(k<0)的图象与反比例函数y=﹣的图象交于A,B两点,过点B作BC⊥y轴于点C,连接AC,则△ABC的面积为4.解:∵BC⊥y轴于点C,=|﹣4|=2,∴S△COB∵正比例函数y=kx(k>0)与反比例函数y=﹣的图象均关于原点对称,∴OA=OB,=S△COB=2,∴S△AOC=S△AOB+S△BOC=2+2=4,∴S△ABC故答案为:4.【变4-2】.如图,过点O的直线与反比例函数y=的图象交于A、B两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为.解:∵点A反比例函数y=的图象上,过点A作AC⊥x轴于点C,=|k|=,∴S△AOC∵过点O的直线与反比例函数y=的图象交于A、B两点,∴OA=OB,=S△AOC=∴S△BOC=2S△ACO=,∴S△ABC故答案为:.【变4-3】.如图,函数y=x与y=的图象交于A、B两点,过点A作AC垂直于y轴,垂=3,则k=3.足为C,连接BC,若S△ABC解:设A(a,a)(a>0),∵函数y=x与y=的图象的中心对称性,∴B(﹣a,﹣a),=•a•2a=a2=3,∴S△ABC∴a=,∴A(,),把A(,)代入y=得k==3.故答案为:3.考点5两点两垂线模型【模型讲解】反比例函数与正比例函数图象的交点及由交点向坐标轴所作两条垂线围成的图形面积等于2|k|.【示例】【例5】.如图,正比例函数y=kx与反比例函数y=﹣的图象交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为4.解:∵点A在反比例函数y=﹣上,且AB⊥x轴,∴=2,∵A,C是反比例函数与正比例函数的交点,且CD⊥x轴,∴O是BD的中点,=2S△ABO=4.∴S△ABD故答案为:4.变式训练【变5-1】.如图,一次函数y=kx与反比例函数上的图象交于A,C两点,AB∥y轴,BC∥x轴,若△ABC的面积为4,则k=﹣2.解:设AB交x轴于点D,的面积为,由反比例函数系数的几何意义可得S△ADO由函数的对称性可得点O为AC中点,即DO为△ABC中位线,∴=,=4S△ADO=2|k|=4,∴S△ABC∵k<0,∴k=﹣2.故答案为:﹣2.【变5-2】.如图,正比例函数y=kx(k>0)与反比例函数y=的图象交于A,C两点,过点A作x轴的垂线,交x轴于点B,过点C作x轴的垂线,交x轴于点D,连接AD,BC,则四边形ABCD的面积为2.解:∵A、C是两函数图象的交点,∴A、C关于原点对称,∵CD⊥x轴,AB⊥x轴,∴OA=OC,OB=OD,=S△BOC=S△DOC=S△AOD,∴S△AOB又∵A点在反比例函数y=的图象上,=S△BOC=S△DOC=S△AOD×1=,∴S△AOB=4S△AOB=4×=2,∴S四边形ABCD故答案为:2.【变5-3】.如图,直线分别与反比例函数y=﹣和y=的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x轴交于点D,则四边形ABCD的面积是5.解:过点A作AF⊥y轴,垂足于点F;过点B作BE⊥y轴,垂足为点E.∵点P是AB中点.∴PA=PB.又∵∠APF=∠BPE,∠AFP=∠BEP=90°,∴△APF≌△BPE.=S△BPE.∴S△APF=S四边形ACOF+S四边形EODB=|﹣2|+|3|=5.∴S四边形ABCD故答案为:5.考点6反比例函数上两点和外一点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点在同一分支上,用减法.【示例】方法一:S △AOB =S △COD -S △AOC -S △BOD .方法二:作AE ⊥x 轴于点E ,交OB 于点M ,BF ⊥x 轴于点F ,则S △OAM =S 四边形MEFB (划归到模型一),则S △AOB =S 直角梯形AEFB .【拓展】方法一:当BE CE 或BFFA=m 时,则S 四边形OFBE =m |k |.方法二:作EM ⊥x 轴于M ,则S △OEF =S 直角梯形EMAF (划归到上一个模型示例).【例6】.如图,一次函数y =ax +b 的图象与反比例函数y =的图象交于A ,B 两点,则S△AOB=()A.B.C.D.6解:把A(﹣4,1)代入y=的得:k=﹣4,∴反比例函数的解析式是y=﹣,∵B(1,m)代入反比例函数y=﹣得:m=﹣4,∴B的坐标是(1,﹣4),把A、B的坐标代入一次函数y=ax+b得:,解得:a=﹣1,b=﹣3,∴一次函数的解析式是y=﹣x﹣3;把x=0代入一次函数的解析式是y=﹣x﹣3得:y=﹣3,∴D(0,﹣3),=S AOD+S△BOD=×3×(1+4)=.∴S△AOB故选:A.变式训练【变6-1】.如图,直线AB经过原点O,且交反比例函数的图象于点B,A,点C在x=12,则k的值为()轴上,且.若S△BCAA.12B.﹣12C.﹣6D.6解:作AD⊥x轴于D,BE⊥x轴于E,∵点A、B在反比例函数的图象上,直线AB经过原点,∴OA=OB=AB,=12,∵,S△BCA=S△BCA=6,∴OB=BC,S△BCO∵BE⊥OC,∴OE=CE,=S△BCO=3,∴S△OBE∵BE⊥x轴于E,=|k|,∴S△OBE∴|k|=6,∵k<0,∴k=﹣6.故选:C.【变6-2】.如图,在平面直角坐标系中,反比例函数y=与直线y=交于A,B,x轴的正半轴上有一点C 使得∠ACB =90°,若△OCD 的面积为25,则k 的值为48.解:设点A 坐标为(3a ,4a ),由反比例函数图象与正比例函数图象的对称性可得点B 坐标为(﹣3a ,﹣4a ),∴OA =OB ==5a ,∵∠ACB =90°,O 为AB 中点,∴OC =OA =OB =5a ,设直线BC 解析式为y =kx +b ,将(﹣3a ,﹣4a ),(5a ,0)代入y =kx +b 得,解得,∴y =x ﹣a ,∴点D 坐标为(0,﹣a ),∴S △OCD =OC •OD =5a ×a =25,解得a =2或a =﹣2(舍),∴点A 坐标为(6,8),∴k =6×8=48.故答案为:48.【变6-3】.如图,正比例函数y =﹣x 与反比例函数y =的图象交于A ,B 两点,点C 在x 轴上,连接AC ,BC .若∠ACB =90°,△ABC 的面积为10,则该反比例函数的解析式是y =﹣.解:设点A 为(a ,﹣a ),则OA ==﹣a ,∵点C 为x 轴上一点,∠ACB =90°,且△ACB 的面积为20,∴OA =OB =OC =﹣a ,∴S △ACB =×OC ×(y A +|y B |)=×(﹣a )×(﹣a )=10,解得,a =±(舍弃正值),∴点A 为(﹣,2),∴k =﹣×2=﹣6,∴反比例函数的解析式是y =﹣,故答案为:y =﹣.考点7反比例函数上两点和原点模型【模型讲解】反比例函数与一次函数图象的交点和原点所围成的三角形面积,若两交点分别在两个分支上,用加法.【示例】方法一:S △AOB =12OD ·|x B -x A |=12OC ·|y A -y B |.方法二:S △AOB =S △AOC +S △OCD +S △OBD .方法三:作AE ⊥y 轴于点E ,BF ⊥x 轴于点F ,延长AE 与BF 相交于点N ,则S △AOB =S △ABN -S △AOE -S △OBF -S 矩形OENF .【例7】.如图,直线AB 交双曲线于A 、B ,交x 轴于点C ,B 为线段AC 的中点,过=12.则k的值为8.点B作BM⊥x轴于M,连接OA.若OM=2MC,S△OAC解:过A作AN⊥OC于N,∵BM⊥OC∴AN∥BM,∵,B为AC中点,∴MN=MC,∵OM=2MC,∴ON=MN=CM,设A的坐标是(a,b),则B(2a,b),=12.∵S△OAC∴•3a•b=12,∴ab=8,∴k=ab=8,故答案为:8.变式训练【变7-1】.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且四边形ODBE的面积为21,则k=7.解:设D点的横坐标为x,则其纵坐标为,∵BD=3AD,∴点B点的坐标为(4x,),点C的坐标为(4x,0)=21,∵S四边形ODBE﹣S△OCE﹣S△OAD=21,∴S矩形ABCD即:4x•﹣﹣=21解得:k=7.故答案为:7.【变7-2】.如图,点是直线AB与反比例函数图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.(1)求反比例函数和直线AB的解析式;(2)△ABC和△ABD的面积分别为S1,S2,求S2﹣S1.解:(1)由点A(,4)在反比例函数y=(x>0)图象上,∴n=×4=6,∴反比例函数的解析式为y=(x>0),将点B(3,m)代入y=(x>0)并解得m=2,∴B(3,2),设直线AB的表达式为y=kx+b,∴,解得,∴直线AB的表达式为y=﹣x+6;(2)由点A坐标得AC=4,则点B到AC的距离为3﹣=,∴S1==3,设AB与y轴的交点为E,则点E(0,6),如图:∴DE=6﹣1=5,由点A(,4),B(3,2)知,点A,B到DE的距离分别为,3,∴S2=S△BDE﹣S△AED=﹣=,∴S2﹣S1=﹣3=.考点8两双曲线k值符号不同模型【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.类型1两条双曲线的k值符号相同【示例】【例8】.如图,在平面直角坐标系中,函数y=kx与的图象交于A、B两点,过A作y轴的垂线,交函数的图象于点C,连接BC,则△ABC的面积为()A.2B.3C.5D.6解:∵正比例函数y=kx与反比例函数y=﹣的图象交点关于原点对称,∴设A点坐标为(x,﹣),则B点坐标为(﹣x,),C(﹣2x,﹣),=×(﹣2x﹣x)•(﹣﹣)=×(﹣3x)•(﹣)=6.∴S△ABC故选:D.变式训练【变8-1】.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=(x>0)和y=﹣(x>0)的图象交于B、A两点.若点C是y轴上任意一点,则△ABC的面积为()A.3B.6C.9D.解:设P(a,0),a>0,则A和B的横坐标都为a,将x=a代入反比例函数y=﹣中得:y=﹣,故A(a,﹣);将x=a代入反比例函数y=中得:y=,故B(a,),∴AB=AP+BP=+=,=AB•x P的横坐标=××a=,则S△ABC故选:D.【变8-2】.如图,点A和点B分别是反比例函数y=(x>0)和y=(x>0)的图象上=2,则m﹣n的值为4.的点,AB⊥x轴,点C为y轴上一点,若S△ABC解:连接AO.CO,∵AB⊥x轴,点C为y轴上一点,∴AB∥y轴,=S△ABO=2,∴S△ABC∴=2.∴=2,即m﹣n=4.故答案为:4.1.如图,Rt△ABC的顶点A在双曲线y=的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是()A.4B.﹣4C.2D.﹣2解:∵∠ACB=30°,∠AOB=60°,∴∠OAC=∠AOB﹣∠ACB=30°,∴∠OAC=∠ACO,∴OA=OC=4,在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,∴∠OAB=30°,∴OB=OA=2,∴AB=OB=2,∴A点坐标为(﹣2,2),把A(﹣2,2)代入y=得k=﹣2×2=﹣4.故选:B.2.如图,平行四边形OABC的顶点B,C在第一象限,点A的坐标为(3,0),点D为边AB的中点,反比例函数y=(x>0)的图象经过C,D两点,若∠COA=α,则k的值等于()A.8sin2αB.8cos2αC.4tanαD.2tanα解:方法一:过点C作CE⊥OA于点E,过点D作DF⊥OA交OA的延长线于点F,设C点横坐标为:a,则:CE=a•tanα,∴C点坐标为:(a,a•tanα),∵平行四边形OABC中,点D为边AB的中点,∴D点纵坐标为:a•tanα,设D点横坐标为x,∵C,D都在反比例函数图象上,∴a×a•tanα=x×a•tanα,解得:x=2a,则FO=2a,∴FE=a,∵∠COE=∠DAF,∠CEO=∠DFA,∴△COE∽△DAF,∴==2,∴AF=,∴AO=OF﹣AF=a,∵点A的坐标为(3,0),∴AO=3,∴a=3,解得:a=2,∴k=a×a•tanα=2×2tanα=4tanα.方法二:∵C(a,a tanα),A(3,0),∴B(a+3,a tanα),∵D是线段AB中点,∴D(,a tanα),即D(,a tanα).∵反比例函数过C,D两点,∴k=a•a tanα=(a+6)•a tanα,解得a=2,∴k=4tanα.故选:C.3.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,=.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是()A.2B.3C.5D.7解:设OA=3a,则OB=4a,∴A(3a,0),B(0,4a).设直线AB的解析式是y=kx+b,则根据题意得:,解得:,则直线AB的解析式是y=﹣x+4a,直线CD是∠AOB的平分线,则OD的解析式是y=x.根据题意得:,解得:则D的坐标是(,),OA的中垂线的解析式是x=,则C的坐标是(,),将C点坐标代入反比例函数y=,则k=.设OA的垂直平分线交x轴于点F,过点D作DE⊥x轴于点E,如图,则OF=CF=,OE=DE=a,∵∠DOA=45°,∴△COF和△DOE为等腰直角三角形,∴OC=OF=a,OD=OE=a,∴CD=OD﹣OC=()=(﹣)=a.∵以CD为边的正方形的面积为,∴=,则a2=,∴k=×=7.故选:D.4.如图,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,且OA⊥OB,cos A=,则k的值为()A.﹣3B.﹣4C.﹣D.﹣2解:过A作AE⊥x轴,过B作BF⊥x轴,∵OA⊥OB,∴∠AOB=90°,∴∠BOF+∠EOA=90°,∵∠BOF+∠FBO=90°,∴∠EOA=∠FBO,∵∠BFO=∠OEA=90°,∴△BFO∽△OEA,在Rt△AOB中,cos∠BAO==,设AB=,则OA=1,根据勾股定理得:BO=,∴OB:OA=:1,:S△OEA=2:1,∴S△BFO∵A在反比例函数y=上,=1,∴S△OEA=2,∴S△BFO则k=﹣4.故选:B.5.如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是()A.B.C.D.解:如图,∵点A坐标为(﹣1,1),∴k=﹣1×1=﹣1,∴反比例函数解析式为y=﹣,∵OB=AB=1,∴△OAB为等腰直角三角形,∴∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,∵点B和点B′关于直线l对称,∴PB=PB′,BB′⊥PQ,∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,∴B′P⊥y轴,∴点B′的坐标为(﹣,t),∵PB=PB′,∴t﹣1=|﹣|=,整理得t2﹣t﹣1=0,解得t1=,t2=(不符合题意,舍去),∴t的值为.故选:A.6.如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(﹣3,2),若反比例函数y=(x>0)的图象经过点A,则k的值为()A.﹣6B.﹣3C.3D.6解:∵A与C关于OB对称,∴A的坐标是(3,2).把(3,2)代入y=得:2=,解得:k=6.故选:D.7.如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为()A.3B.6C.D.解:∵将直线y=向上平移4个单位长度后,与y轴交于点C,∴平移后直线的解析式为y=x+4,分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,x),∵OA=3BC,BC∥OA,CF∥x轴,∴△BCF∽△AOD,∴CF=OD,∵点B在直线y=x+4上,∴B(x,x+4),∵点A、B在双曲线y=上,∴3x•x=x•(x+4),解得x=1,∴k=3×1××1=.故选:D.8.如图,已知四边形ABCD是平行四边形,BC=2AB.A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y=(k<0)的图象上,则k等于﹣12.解:设点C坐标为(a,),(k<0),点D的坐标为(x,y),∵四边形ABCD是平行四边形,∴AC与BD的中点坐标相同,∴(,)=(,),则x=a﹣1,y=,代入y=,可得:k=2a﹣2a2①;在Rt△AOB中,AB==,∴BC=2AB=2,故BC2=(0﹣a)2+(﹣2)=(2)2,整理得:a4+k2﹣4ka=16a2,将①k=2a﹣2a2,代入后化简可得:a2=4,∵a<0,∴a=﹣2,∴k=﹣4﹣8=﹣12.故答案为:﹣12.方法二:因为ABCD是平行四边形,所以点C、D是点B、A分别向左平移a,向上平移b得到的.故设点C坐标是(﹣a,2+b),点D坐标是(﹣1﹣a,b),(a>0,b>0),∴﹣a(2+b)=b(﹣1﹣a),整理得2a+ab=b+ab,解得b=2a.过点D作x轴垂线,交x轴于H点,在直角三角形ADH中,由已知易得AD=2,AH=a,DH=b=2a.AD2=AH2+DH2,即20=a2+4a2,得a=2.所以D坐标是(﹣3,4)所以k=﹣12.9.如图,点E,F在函数y=(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是2,△OEF的面积是(用含m的式子表示)解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,∵△OEP的面积为1,∴|k|=1,而k>0,∴k=2,∴反比例函数解析式为y=,∵EP⊥y轴,FH⊥y轴,∴EP∥FH,∴△BPE∽△BHF,∴==,即HF=mPE,设E点坐标为(t,),则F点的坐标为(tm,),+S△OFD=S△OEC+S梯形ECDF,∵S△OEF=S△OEC=1,而S△OFD=S梯形ECDF=(+)(tm﹣t)∴S△OEF=(+1)(m﹣1)=.故答案为:2,.10.如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k=.解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.则有PD⊥OA,PE⊥AB.设⊙P的半径为r,∵AB=5,AC=1,=AB•PE=r,S△APC=AC•PD=r.∴S△APB∵∠AOB=90°,OA=4,AB=5,∴OB=3.=AC•OB=×1×3=.∴S△ABC=S△APB+S△APC,∵S△ABC∴=r+r.∴r=.∴PD=.∵PD⊥OA,∠AOB=90°,∴∠PDC=∠BOC=90°.∴PD∥BO.∴△PDC∽△BOC.∴=.∴PD•OC=CD•BO.∴×(4﹣1)=3CD.∴CD=.∴OD=OC﹣CD=3﹣=∴点P的坐标为(,).∵反比例函数y=(k≠0)的图象经过圆心P,∴k=×=.故答案为:.11.如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=;②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是①④(把所有正确的结论的序号都填上).解:作AE⊥y轴于E,CF⊥y轴于F,如图,∵四边形OABC是平行四边形,∴S△AOB=S△COB,∴AE=CF,∴OM=ON,∵S△AOM=|k1|=OM•AM,S△CON=|k2|=ON•CN,∴=,故①正确;∵S△AOM=|k1|,S△CON=|k2|,∴S阴影部分=S△AOM+S△CON=(|k1|+|k2|),而k1>0,k2<0,∴S阴影部分=(k1﹣k2),故②错误;当∠AOC=90°,∴四边形OABC是矩形,∴不能确定OA与OC相等,而OM=ON,∴不能判断△AOM≌△CNO,∴不能判断AM=CN,∴不能确定|k1|=|k2|,故③错误;若OABC是菱形,则OA=OC,而OM=ON,∴Rt△AOM≌Rt△CNO,∴AM=CN,∴|k1|=|k2|,∴k1=﹣k2,∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.故答案为:①④.12.如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,A n,…记点A n的横坐标为a n,若a1=2,则a2=﹣,a2013=﹣;若要将上述操作无限次地进行下去,则a1不可能取的值是0、﹣1.解:当a1=2时,B1的纵坐标为,B1的纵坐标和A2的纵坐标相同,则A2的横坐标为a2=﹣,A2的横坐标和B2的横坐标相同,则B2的纵坐标为b2=﹣,B2的纵坐标和A3的纵坐标相同,则A3的横坐标为a3=﹣,A3的横坐标和B3的横坐标相同,则B3的纵坐标为b3=﹣3,B3的纵坐标和A4的纵坐标相同,则A4的横坐标为a4=2,A4的横坐标和B4的横坐标相同,则B4的纵坐标为b4=,即当a1=2时,a2=﹣,a3=﹣,a4=2,a5=﹣,b1=,b2=﹣,b3=﹣3,b4=,b5=﹣,∵=671,∴a2013=a3=﹣;点A1不能在y轴上(此时找不到B1),即x≠0,点A1不能在x轴上(此时A2,在y轴上,找不到B2),即y=﹣x﹣1≠0,解得:x≠﹣1;综上可得a1不可取0、﹣1.故答案为:﹣;﹣;0、﹣1.13.如图,一次函数y=x+1的图象与反比例函数y=(x>0)的图象交于点A(a,3),与y轴交于点B.(1)求a,k的值;(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.解:(1)把x=a,y=3代入y=x+1得,,∴a=4,把x=4,y=3代入y=得,3=,∴k=12;(2)∵点A(4,3),D点的纵坐标是0,AD=AC,∴点C的纵坐标是3×2﹣0=6,把y=6代入y=得x=2,∴C(2,6),①如图1,作CF⊥x轴于F,交AB于E,当x=2时,y==2,∴E(2,2),∵C(2,6),∴CE=6﹣2=4,∴x A==8;②如图2,当AB是对角线时,即:四边形APBQ是平行四边形,∵A(4,3),B(0,1),点Q的纵坐标为0,∴y P=1+3﹣0=4,当y=4时,4=,∴x=3,∴P(3,4),当AB为边时,即:四边形ABQP是平行四边形(图中的▱ABQ′P′),﹣y B=y P′﹣y A得,由y Q′0﹣1=y P′﹣3,=2,∴y P′当y=2时,x==6,∴P′(6,2),综上所述:P(3,4)或(6,2).14.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数y2=的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,∴,解得.∴一次函数的解析式为:y1=﹣x+.∵△OAP的面积为,∴•OA•y P=,∴y P=,∵点P在一次函数图象上,∴令﹣x+=.解得x=4,∴P(4,).∵点P在反比例函数y2=的图象上,∴k2=4×=2.∴一次函数的解析式为:y1=﹣x+.反比例函数的解析式为:y2=.(2)令﹣x+=,解得x=1或x=4,∴K(1,2),由图象可知,当y2>y1时,x的取值范围为:0<x<1或x>4.(3)如图,作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,∵P(4,).∴P′(4,﹣).∴PP′=1,∴直线KP′的解析式为:y=﹣x+.令y=0,解得x=.∴C(,0).=•(x C﹣x K)•PP′∴S△PKC=×(﹣1)×1=.∴当PC+KC最小时,△PKC的面积为.15.如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.(1)求这个反比例函数的表达式;(2)求△AOB的面积;(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x+1经过点A(m,2),∴m+1=2,∴m=1,∴A(1,2),∵反比例函数y=经过点(1,2),∴k=2,∴反比例函数的解析式为y=;(2)由题意,得,解得或,∴B(﹣2,﹣1),∵C(0,1),=S△AOC+S△BOC=×1×2+×1×1=1.5;∴S△AOB(3)有三种情形,如图所示,满足条件的点P的坐标为(﹣3,﹣3)或(﹣1,1)或(3,3).16.已知A(3,0)、B(0,4)是平面直角坐标系中两点,连接AB.(1)如图①,点P在线段AB上,以点P为圆心的圆与两条坐标轴都相切,求过点P 的反比例函数表达式;(2)如图②,点N是线段OB上一点,连接AN,将△AON沿AN翻折,使得点O与线段AB上的点M重合,求经过A、N两点的一次函数表达式.解:(1)作PC⊥x轴于C,PD⊥y轴于D,则四边形OCPD是矩形,∵以点P为圆心的圆与两条坐标轴都相切,∴PC=PD,∴矩形OCPD是正方形,设PD=PC=x,∵A(3,0)、B(0,4),∴OA=3,OB=4,∴BD=4﹣x,∵PD∥OA,∴△PDB∽△AOB,∴,∴,解得x=,∴P(,),设过点P的函数表达式为y=,∴k=xy==,∴y=;(2)方法一:∵将△AON沿AN翻折,使得点O与线段AB上的点M重合,∴ON=NM,MN⊥AB,由勾股定理得,AB=5,=S△AON+S△ABN,∴S△AOB∴=+,解得,ON=,∴N(0,),设直线AN的函数解析式为y=mx+,则3m+=0,∴m=﹣,∴直线AN的函数解析式为y=﹣x+.方法二:利用△BMN∽△BOA,求出BN的长度,从而得出ON的长度,。
《反比例函数》专项练习和中考真题(含答案解析及点睛)

三角形的面积的性质求得△BOD 的面积,依据反比例函数的比例系数 k 的几何意义即可求解.
OA 1 【解析】解:如图作 AC⊥x 轴于点 C,作 BD⊥x 轴于点 D.∵ OB 3OA∴ =
OB 3
1
1
∵点 A 是双曲线 y (x 0) 上∴S△OAC= ∵∠AOB=90°,∴∠AOC+∠BOD=90°,
22
4
1 ﹣S△AOD=S 梯形 ADCE,得到
mm
1
( + )•(m﹣
m)= 3 ,即可求得 k= m2
=2.
2 42
2
2
4
mm
【解析】解:根据题意设 B(m,m),则 A(m,0),∵点 C 为斜边 OB 的中点,∴C( , ),
22
∵反比例函数 y= k (k>0,x>0)的图象过点 C,∴k= m m = m2 ,
(3)设 B'(2m 5, 4) , C'(2m 8,1) 在直线 y k (k 0) 上, x
有 (2m 5) 4 (2m 8) 1, m 2 , B' (1, 4) , C' (4,1) ,代入方程后有 k=-4;
综上所述,k=-6 或 k=-4;故答案为:-6 或-4. 【点睛】本题考查轴对称图形的坐标关系以及反比例函数解析式,其中明确轴对称图形纵坐标相等,横坐标之和为 对称轴横坐标的 2 倍是解题的关键.
x
22 4
∵∠OAB=90°,∴D 的横坐标为 m,
k
m
∵反比例函数 y= (k>0,x>0)的图象过点 D,∴D 的纵坐标为 ,作 CE⊥x 轴于 E,
x
4
3
∵S△COD=S△COE+S 梯形 ADCE﹣S△AOD=S 梯形 ADCE,S△OCD= ,
中考专题反比例函数常见模型

模型九:等角2——对称型
结论:正比例函数图象与双曲线交于Q、R两点,
则∠1=∠2,∠3=∠4
证明:作P点关于点O对称点S,
连SR,SP,SQ
易证四边形PQSQ为平行四边形
由模型八可知∠2=∠5,
又∵PR∥QS,∴∠5=∠1,
∴∠1=∠2
∵∠2+∠4=90°,∠3+∠1=90°
∴∠3=∠4
|k|等于双曲线上任意一点作x轴、y轴的垂线的矩形的面积。
二、反比例函数的基本模型
模型一、对称性
结论:
∵正比例、反比例函数的图象都是关于原点成中心对称图形,
∴①OA=OB,OC=OD;
②四边形ACBD是平行四边形;
模型二:双曲矩形
结论:1、不论P在双曲线上何处,
2、当OA在x轴上平移时,
同理:当OB在y轴上平移时,
等底同高可证,证明略
模型三:双曲三角形
结论:
1、不论P在双曲线上何处,
2、不论O'在y轴上何处,
同底等高可证,证明略
模型四:等分面积
结论:
3、若Q为AB中点,则P也必为BC中点。
由2可得,证明略
模型五:三角转梯形
结论:
模型六:斜向平行线
结论:过双曲线上任意两点P、Q分别作PC⊥y轴于C,QA⊥x轴于A,连结AC,则PQ∥AC
由模型七得
∵ABQP为平行四边形
∴PQ∥AB,AP∥BQ,PQ=AB,AP=BQ
∴∠2=∠6=∠EPA
∵∠PEA=∠BCQ=90°
∴பைடு நூலகம்PEA≌△BCQ(AAS)∴PE=BC=a,
∵OM=a+b,OC=b,∴CM=OM-OC=a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数的常见模型解决反比例函数的问题,除了掌握反比例函数的图像及性质以及反比例函数常见的面积模型之外,还要熟练掌握以下几个经典模型:【模型1】正比例函数图像被反比例函数图像所截得的线段相等【模型2】一次函数图像被坐标系和反比例函数图像所截得的相等线段【模型3】同一象限内反比例函数图像上两点连线的平行线【模型4】反比例函数与矩形(1)【模型5】反比例函数与矩形(2)【模型6】反比例函数与最值【模型7】反比例函数与黄金分割让我们一起领略反比例函数的神奇一、个人对反比例函数的几点困惑与感悟 1.为何正比例函数的比例系数是比xyk =,而反比例函数的比例系数却不是比xy k =? 2.为何我市中考的反比例函数问题总不像其它函数那么深入?只探究一些皮毛问题!至 多探究一下k 的几何意义(面积),例如2016年台州市中考考查的也是“函数的研究 通法”,并非专门深入研究反比例函数.3.过去我们遇到稍难一点的反比例函数问题,就只有“暴力设元”这一途径,总无法避开 多元方程、分式方程、高次方程.4.个人认为作为老师,不应该只应付中考,而应该研究更纯粹的数学,站在更高的位置来 了解数学本质!做到居高临下、解有依据!5.实际上,反比例函数中也存在很多的“比”,斜比、直比(纵比、横比、纵横比)、面积 比,可以说“比比皆是”!现在就让我们一起来比出精彩、比出神奇. 二、一道曾经困惑我多时的中考题某年宁波市中考的填空压轴题: 如图,AOB Rt Δ的顶点B (2,4),双曲线xky =经过 点C 、D ,当以B 、C 、D 为顶点的三角形与AOB Δ的相似时,则=k .1.常规性解法:通过设元,例如设C (m ,m 2),则D (2,2m ),再根据条件列方程: (1)利用CD BC 2=、224=CD BC 、CD BD 5=或225=CD BD 列方程;(2)利用)(D C C D y y x x -2=-列方程;(3)利用“一线三等角”模型、和D D C C y x y x ⋅=⋅列方程.实际上,在上述常规处理方法中,已经透着一点智慧、一点灵性了,具体操作方法中也具 备了一定的技巧性. 但我本人对此,却一直难言满意,耿耿于怀!2.挖掘隐含性质,巧解此题(1)实际上,此图中含有一些很重要的性质:过点C 作y CP ⊥轴于P ,连接PA ,直线CD 分别交坐标轴于点M 、N . 则有①PA ∥CD ;②AN PC =,AD PM =; ③DN MC =,CN MD =. 基于以上这些性质,有如下解法. (2)我的第一种解法(整体思想):由OM ON 2=,PM AD AN 2=2=可得,)(PM OM AN ON -2=-,即OP OA 2=,于是1=21=OA OP ,21=21=OP PC ,…… (3)我一个同事的解法(斜边转直比):由421=::::CN OC MC ,DN MC =可得,131=::::DN CD MC ,转为横比,131=--::)(:)(:D N C D C x x x x x ,因此21=41=OA x C ,…… (4)我一个学生的解法(斜等转直等): 由CN MD =得2==-OA x x C N ,则1=-21=)(C N C x x y ,…… (5)我的第二种解法(平行导角度):由PA ∥CD 得,B MNO PAO ∠=∠=∠,于是1=21=OA OP ,…… (6)下面我们要着重解决两件事: ①上述性质是否永远成立?如何证明?②解题技巧除上述方法:整体思想、斜边转直比、斜等转直等、平行导角度外,还有斜长转直长、面积比与边比互转、纯面积转化等等,后面将一、一介绍.三、探究性质 1.如图,双曲线xky =与矩形OABC 边交于点M 、N ,直线MN 交坐标轴于点D 、E . ①如图1,若21=::AB AM ,则=CB CN : ; ②如图2,若41=::AB AM ,则=CB CN : ; ③如图3,若n AB AM ::1=,则=CB CN : ,直线MN 与AC 的位置关系是 ,EN 与MD 的大小关系 .图1 图2 图3 2.①如图1,双曲线xky =与直线DE 交于点M 、N ,y MA ⊥轴于点A ,x NC ⊥轴于 点C ,请探究直线MN 与AC 的位置关系,线段EN 与MD 的大小关系. ②如图2,双曲线xky =与直线EF 交于点M 、N ,y MA ⊥轴于A ,x MC ⊥轴于C , y ND ⊥轴于D ,x NB ⊥轴于B ,请探究直线MN 与AB 、CD 的位置关系,以及线段ME 与FN 的大小关系.图1 图2四、最常见思想方法(斜转直):斜边转直比、斜等转直等、斜长转直长 1.如图,直线4+-=x y 反比例函数xky =(0>x )图象交直线AB 于点C 、D ,且CD AB 2=, 则k 的值为 . (1)常规方法(斜长转直长):22=21=AB CD ,则2=22=-CD x x C D , 可设C (m ,m -4),则D (2+m ,m -2),列方程解决; (2)口算巧解(斜边转直比):由DB AC =,CD AB 2=得,121=::::DB CD AC ,转为横比得,121=--::)(:)(:D B C D C x x x x x ,则1=C x ,3=1-4=C y ,……2.同类变式题:如图,直线2+-=x y 交坐标轴于点A 、B , 双曲线xky =交直线AB 于点C 、D . 若AB CD 2=,则k 的值为 ;3.难题展示(中国数学教育名师讲堂481230254,每日一题第8题,2017/3/29)如图,点A (2,2),B ,C 在双曲线上,o BAC 45=∠,AB 分别交x ,y 轴于D ,F , AC 分别交x ,y 轴于D ,E . (1)求DOE Δ的面积; (2)求证:DBCE ADE S S 四边形=Δ.4.原创清新小题和近年的中考题:(1)如图1,BC AB =,AOB Δ的面积为3,则k 的值为 . (2)如图2,点A ,B 在双曲线xky =上运动,x AB ⊥轴,BC AC =. ①在运动过程中,ABC Δ的面积是不是定值?答: ; ②若32=k ,且ABC Δ是正三角形,则点A 的坐标为 .(3)如图3,□OABC 中,o B 60=∠,3=OA ,双曲线经过点C 和AB 中点D ,则该双曲线的解析式为 . (4)如图4,直线x y 21=与3+21=x y 分别与双曲线xky =交于点A 、B ,BC OA 2=,则k 的值为 .图1 图2 图3 图4(5)(十堰)如图5,正AOB Δ的边长为5,双曲线xky =经过点C 、D ,且OB CD ⊥, 则k 的值为 . (6)如图6,双曲线xky =与直线b mx y +=交于点C 、D . ①(原创、铺垫②)若3-=m 、6=b ,且CD AB 3=,则=k ;②(常州模拟·改编)若6=b ,且CD AB 3=,则=⋅m k ;③(杭州模拟·改编)若3-=m ,且8=⋅AD AC ,则=k . (7)(据上题改编)如图7,P 为双曲线xy 2-=上的动点,过点P 作矩形PAOB ,直线 CD 的解析式为b x y +2=,交矩形边于M ,N ,则=⋅DN CM .图5 图6 图7五、面积比、边比互转1.①(原创、铺垫)如图1①,直线x y 23=与双曲线xy 6=交于点A ,C 为双曲线上一点, 射线CA 交y 轴于点D ,若COD Δ的面积为9,则点C 坐标为 ; ②(成都)如图1②,直线x y 23=与双曲线xy 6=交于点A 、B ,C 为双曲线上一点, 射线CA 交y 轴于点D ,若BCD Δ的面积为20,则点C 坐标为 . 2.(无锡)如图2,x AB ⊥轴,BC ∥x 轴,双曲线过点C 、D ,且21=::DB OD , 已知OBC Δ的面积为3,则k 的值为 .图1① 图1② 图33.(宁波)如图3,正AOB Δ的顶点A 在双曲线xy 9=上,双曲线x y 1=与边OA 交于点C ,连接BC ,则ABC Δ的面积为 . 4.(丽水)如图4,双曲线xy 4=与直线b x y +-=交于点A 、B ,⊥AE x 轴,设点A 的 横坐标为m .①用含m 的式子表示=b ;②若AOF Δ与四边形BCEF 的面积和为4,则=m . 5.如图5,双曲线xky =与直线b mx y +=交于点C 、D . ①(常州模拟)若6=b ,且COD AOB S S ΔΔ3=,则=⋅m k ;②(改编自①)若6=k 、3-=m ,且CD AB 2=,则=COD S Δ .图3 图4 图56.如图6,⊥AB x 轴,C 为AB 中点,延长OC 到E ,延长OA 到D ,若双曲线xk y =恰 好经过点D ,E ,且CE OC =,则=OD OA : . 7.如图7,双曲线x k y 1=过点A ,B ,xky 2=过点C ,D ,若AC ,BD 均与x 轴平行, 6=AC ,4=BD ,且它们之间的距离EF 长为5,则=-21k k . 8.如图8,直线AB 交双曲线xy 5=于点C ,D ,若8=AOB S Δ,则=BOC S Δ .图6 图7 图89.如图,点A 在双曲线xky =上,x AB ⊥轴,CD AD 2=,DB 延长线交y 轴于E ,若 BCE Δ的面积为4,则k 的值为 . 10.如图,点A 、B 在双曲线xky =上,x AC ⊥轴,x BD ⊥轴,垂足C 、D 分别在x 轴的 正半轴和负半轴上,k CD =,AC AB 25=,E 是AB 的中点,若BCE Δ面积是ADE Δ的2倍,则k 的值为 .六、反比例函数图象中的“一线三等角”构造,初探黄金比例 1.如图1,ABC Δ中,BA OB =,o OBA 90=∠,双曲线xky =经过点A 、B ,且点B 的 纵坐标为2,则k 的值为 .(1)剖析:对于坐标系中的一个直角,若两条边均“倾斜”,我们经常构造“K ”形全等或相似,即“一线三等角”模型,或叫“矩形大法”,见图2,得1-5=m .(2)后感:我们可以发现,矩形ODCE 恰好是一个“黄金矩形”,这到底是一种偶然的巧 合,还是一种必然的存在呢?这有待于我们进一步探究… (3)探究(2016临沭模拟):如图3,双曲线xky =与矩形ODCE 的边交于点A ,B ,若 设点B 的坐标为(a ,b ),且有AB OB =,AB OB ⊥,则=b a : .图1 图2 图32.类似题:①(2015临海模拟·填空压轴题)如图, AB OA =,oOAB 90=∠,双曲线xky =经过 点A ,双曲线xk y -=经过点B ,已知点A 的纵坐标为2-,则=k ,点B 的坐标为 . ②(个人原创)如图2,ABC Δ中,BA OB =,o OBA 90=∠,双曲线x k y =经过点B ,双曲线xk y 1+=经过点A ,且 点B 的纵坐标为2,则k 的值为 .3.难题展示(常州·于新华老师原创题) (1)如图1,点A (3,4),B 均在双曲线xky =上,过点A 作y 轴垂线,过点B 作x 轴 垂线,两垂线交于点P ,垂足分别为E ,F ,将PAB Δ沿AB 翻折,点P 恰好落在x 轴上的点Q 处. 求点B 的坐标.(2)如图2,点A (3,4),B 均在双曲线xky =上,过点A 作y 轴垂线,过点B 作x 轴 垂线,两垂线交于点P ,垂足分别为E ,F ,将PAB Δ沿AB 翻折,点P 恰好落在x 轴上的点Q 处. 求点B 的坐标.图1 图24.如图,矩形ABCD 的边AB 的解析式为2+=kx y ,顶点C ,D 在双曲线xmy =上. ①若2=∠ADB tan ,则点D 的坐标为 ; ②连接OC ,OD ,若COD Δ是等边三角形,则=∠ADB tan .后感:若能发现OB OA =,本题将更简单!拓展:如图,正方形ABCD 的顶点A 、B 在双曲线x y 3=上,C 、D 在双曲线xy 7=上, 则正方形ABCD 的面积为 .5.(2013湖州模拟) 如图1,矩形OABC 的顶点A 、B 在 双曲线xky =上,若点A (1,2),则点B 的坐标为 . 6.如图2,矩形ABCD 中,AD AB 2=,点A (0,1),点C ,D 在双曲线xky =上,若E 为 AB 中点,则k 的值为 .图1 图27.①如图1,点A ,B 在双曲线xy 2=上运动,以AB 为底边作等腰直角ABC Δ,则点 C 也在一条双曲线上运动,则该双曲线的解析式为 ;②如图2,点A ,B 在双曲线xy 2=上运动,以AB 为底边作等腰ABC Δ,则点C 也 在一条双曲线上运动,若2=∠CAB tan ,则该双曲线解析式为 ; ③如图3,点A ,B 在双曲线xky =上运动,以AB 为底作等腰ABC Δ,点C 在另一 双曲线xk y '=上运动,若m CAB =∠tan ,请用m ,k 表示='k .图1 图2 图3七、平行导角度,角度导比例 1.如图,点A ,B 在双曲线xky =上,AB 经过原点O ,过点A 作AC ∥x 轴,连接BC 并延长,交双曲线于点D . ①求证:CD AD =; ②求BD AD :的值.根据本题的发现,改编了一个清新小题: 如图,点A ,B 在双曲线xky =上,AB 经过原点O ,过点A 的直线b x y +3=交该 双曲线于点C ,分别交x 轴,y 轴于点D ,E ,若4=BC ,8=AC . 求k 的值.2.如图,直线x y 3=交在双曲线xky =于点A 、B ,AB 经过原点O ,过A 作AB AC ⊥ 交y 轴于点C ,连接BC 并延长,交双曲线于点D .求BD AD :的值.3.如图,双曲线xky =与过原点的直线l 交于点A 、B ,点M 在双曲线上,直线AM 、 BM 分别交y 轴于点P 、Q .若设PM m AM ⋅=,QM n BM ⋅=,则=-n m .4.如图,AB OA =,双曲线经过点C 、D 、E ,求证:AE AC AD ⋅=2.八、纯面积推导1. 如图,点A (2,2),B ,C 在双曲线上,o BAC 45=∠,AB 分别交x ,y 轴于D ,F , AC 分别交x ,y 轴于D ,E . 求证:DBCE ADE S S 四边形=Δ.(此方法感谢江苏·于新华老师的指导!)2.(2016菏泽)如图,AOC Δ,ABD Δ均是等腰直角三角形,双曲线xy 6=经过点B ,交线 段OA 与点E ,求AOC Δ与ABD Δ的面积之差.后感:①题中条件“AOC Δ,ABD Δ均是等腰直角三角形”可如何改变? ②写出2OA ,2OE ,2AB 的关系: . 3.(十堰)如图5,正AOB Δ的边长为5,双曲线xky =经过点C 、D ,且OB CD ⊥, 则k 的值为 .4.(常州)如图1,AB OA =,双曲线经过点C 、D ,且a b OC BD =,求ADAC的值; 5.如图2,AB OA =,双曲线经过点C 、D 、E ,求证:AE AC AD ⋅=2.图1 图2。
