反比例函数中的模型.docx
反比例函数常见几何模型

反比例函数常见模型一、知识点回忆1..反比例函数的图像是双曲线,故也称双曲线y=kx〔k≠0〕.其解析式有三种表示方法:①xk y =〔0≠k 〕;②1-=kx y 〔0≠k 〕;③k xy = 2.反比例函数y=kx〔k≠0〕的性质〔1〕当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.〔2〕当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.〔3〕在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).〔4〕假设双曲线y=kx图像上一点〔a ,b 〕满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.〔5〕由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要表达出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,那么有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,〔1〕求m 的值 〔2〕求ABC ∆的面积变式题1、如下列图,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影局部的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,假设四边形ABCD 为矩形,那么它的面积为.模型二:如图:点A 、B 是双曲线)0(≠=k xky 任意不重合的两点,直线AB 交x 轴于M 点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,那么有:AB DF ||且BM =ANDFAB DF MN xy O例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有以下四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是.〔把你认为正确结论的序号都填上〕例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD .〔1〕假设点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. 〔2〕假设点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,那么AN 与BM 还相等吗?试证明你的结论.y x DC A B O F E模型三:如图,反比例函数ky x=〔k ≠0,x>0〕上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,那么OPC PADC S S ∆=梯形.图1图2例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,那么△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x =的图象交于A 〔1,4〕、B 〔3,m 〕两点,那么△AOB 的面积是______.例6:如图1,直线12y x =与双曲线(0)ky k x=>交于A 、B 两点,且点A 的横坐标为4. 〔1〕求k 的值;〔2〕如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点〔点C 在第一象限且在点A 的左边〕,当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如下列图的平面直角坐标系.F 是BC 上的一个动点〔不与B 、C 重合〕,过F 点的反比例函数(0)ky x x=>的图象与AC 边交于点E ,那么CE aCF b=.xBF C EAOy例7:两个反比例函数k y x =和1y x =在第一象限内的图象如下列图,点P 在k y x=的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的选项是_________〔把你认为正确结论的序号都填上〕.课堂练习: 一、选择题1、m<0,那么函数mx y =1与xmy -=2的图像如图,大致是〔 〕A. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,那么ABC ∆的周长为〔 〕 A.72 B.5C.74D.22 3、如图,双曲线xky =〔k>0〕经过矩形OABC 的边BC 的中点E ,交AB 于点D ,假设梯形ODBC 的面积为3,那么双曲线的解析式为〔 〕 A.x y 1=B.x y 2=C.x y 3=D.xy 6=题3 题4 题5 4、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,那么S 〔 〕A.S=2B.S=4C.2<S<4D.S>45、如下列图,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,假设双曲线y=k x〔k≠0〕与△ABC 有交点,那么k 的取值范围是〔 〕A .1<k<2B .1≤k≤3C.1≤k≤4 D.1≤k<4二、填空题1、如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,假设四边形ABCD为矩形,那么它的面积为.DBAyxOC2、如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA上,那么四边形OABC 的面积是.3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B 〔2,0〕,∠AOB =60°,点A在第一象限,过点A 的双曲线为y = kx,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. 〔1〕当点O ′与点A 重合时,点P 的坐标是.〔2〕设P 〔t ,0〕,当O ′B ′与双曲线有交点时,t 的取值范围是.4、如图,双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .假设点A 的坐标为〔6-,4〕,那么△AOC 的面积为.5、双曲线1y 、2y 在第一象限的图像如图,14y x=,过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,假设1AOB S ∆=,那么2y 的解析式是.课后习练一、填空题1、如图,直线y=kx 〔k>0〕与双曲线y=4x交于A 〔x 1,y 1〕,B 〔x 2,y 2〕两点,那么2x 1y 2-7x 2y 1的值等于_______.2、反比例函数y=kx的图像上有一点P 〔a ,b 〕,且a ,b 是方程t 2-4t -2=0的两个根,那么k=_______;点P 到原点的距离OP=_______.3、双曲线xy=1与直线y=-x+b 无交点,那么b 的取值范围是______.4、反比例函数y=kx的图像经过点P 〔a ,b 〕,其中a ,b 是一元二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______. 5、如图,双曲线)0k (xky >=经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .假设△OBC 的面积为3,那么k =___.第5题图 第6题图6、如图,点A 是一次函数y=x 的图像与反比例函数y=2x的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为〔 〕 A .2 B .22C .2D .22 ABCD E yxO. . jz* 7、P 为函数y=2x的图像上一点,且PP 点数为〔〕 A .0个 B .2个 C .4个 D .无数个。
反比例函数图象中的等角模型及其在中考题中的应用
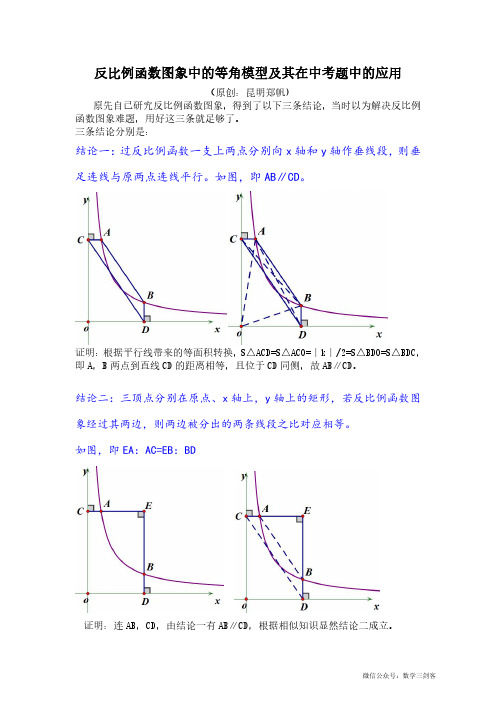
反比例函数图象中的等角模型及其在中考题中的应用(原创:昆明郑帆)原先自己研究反比例函数图象,得到了以下三条结论,当时以为解决反比例函数图象难题,用好这三条就足够了。
三条结论分别是:结论一:过反比例函数一支上两点分别向x轴和y轴作垂线段,则垂足连线与原两点连线平行。
如图,即AB∥CD。
证明:根据平行线带来的等面积转换,S△ACD=S△ACO=∣k∣/2=S△BDO=S△BDC,即A,B两点到直线CD的距离相等,且位于CD同侧,故AB∥CD。
结论二:三顶点分别在原点、x轴上,y轴上的矩形,若反比例函数图象经过其两边,则两边被分出的两条线段之比对应相等。
如图,即EA:AC=EB:BD证明:连AB,CD,由结论一有AB∥CD,根据相似知识显然结论二成立。
结论三:过双曲线一支上两点作直线与坐标轴相交,则每点与其相邻坐标轴交点构成的线段长相等。
如图,即AE=BF证明:过A作y轴垂线段垂足为C,过B作x轴垂线段垂足为D。
连接CD,由结论一有AB∥CD,则四边形ACDF与BDCE均为平行四边形,得到AC=DF,CE=DB,再通过全等得到△ACE≌△FDB,AE=BF。
另外,这三个结论还有另外一个证明体系,先用面积思想证明结论二,再依次证明结论一和结论三。
现给出结论二的证明:S△CEO=S△DEO(矩形性质),S△CAO=S△BDO(反比例函数图象性质),则S△AEO=S△BEO(等量代换),则S△AEO:S△ACO=S△BEO:S△BDO,即EA:AC=EB:BD至于设点坐标用代数证,一来略超纲,二来繁琐,最重要是没有美感,反正我没有这个习惯。
这三个结论还有一些小的变形,比如一支上的两点变两支上的两点,作垂线的顺序改变等,基本都是结论相同,证明类似,且这些不是今天要讲的重点内容而只是铺垫,因此不再赘述只是给出几张图。
今天要讲的内容:后来才发现,反比例函数图象还有一些模型和结论,不能由前三个结论直接解决,但可以以前三个结论为基础推出结果间接解决。
反比例函数的模型及应用 第一讲

反比例函数模型及应用 第一讲一、反比例函数的四个模型:(证明略)模型一:(1)=ABOC S k 矩形;(2)=2ACO ABO ACN OBM kS S S S ∆∆∆∆===模型二:=ABO AMNB S S ∆梯形;模型三:AM BN =模型四:AB N //M注:以上四个模型中点A 、B 都是反比例函数上的任一点.二、模型的应用例1:如图,一次函数y ax b =+的图象与x 轴、y 轴交于A ,B 两点,与反比例函数ky x=的图象交于C ,D 两点,过C ,D 两点 分别作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列 四个结论:①△DEF 与△CEF 的面积相等; ②△AOB ∽△FOE ; ③△DCE ≌△CDF ; ④AC=BD . 其中正确的结论是____________(填写序号).例2:已知反比例函数(0)ky k x=>的图象与一次函数y=-x+6 相交与第一象限的A 、B 两点,如图所示,过A 、B 两点分别做 x 、y 轴的垂线,线段AC 、BD 相交与P ,给出以下结论:① OA=OB ;②△OAM ∽△OBN ;③若△ABP 的面积是8,则k=5;④ P 点一定在直线y=x 上;其中正确的结论是____________(填 写序号).例3:(2014遵义)如图,反比例函数(0)ky k x=>的图象与矩 形ABCO 的两边相交于E 、F 两点,若E 是AB 的中点,2BEF S ∆=,则k 得值为____________ .例4:(2013•重庆)如图,在直角坐标系中,正方形OABC 的顶 点O 与原点重合,顶点A 、C 分别在x 轴、y 轴上,反比例函数(0)ky k x=>的图象与正方形的两边AB 、BC 分别交于点M 、N , ND ⊥x 轴,垂足为D ,连接OM 、ON 、MN .下列结论:①△OCN ≌ △OAM ;②四边形DAMN 与△MON 面积相等;③若∠MON=45°, MN=2,则点C的坐标为1).其中正确的结论是____________(填写序号).一、反比例函数与几何图形的综合(重庆中考12题) 1. 如图,已知四边形ABCD 是平行四边形,BC=2AB ,A ,B 两点 的坐标分别是(-1,0),(0,2),C ,D 两点在反比例函k y x =(0x <)的图象上,则k 的值为______________.第1题图 第2题图2. 如图,已知第一象限内的点A 在反比例函数2y x=的图象 上,第二象限内的点B 在反比例函数ky x =的图象上,且OA ⊥OB ,,则k 的值为______________.3. 如图,在函数11k y x =(0x <)和22ky x =(0x >)的图象上,分别有A ,B 两点,若AB ∥x 轴,交y 轴于点C ,且OA ⊥OB ,12AOC S =△,92BOC S =△,则线段AB 的长度为__________.第3题图 第4题图4. 如图,等腰直角三角形ABC 的顶点A ,C 在x 轴上,∠ACB= 90°,22AC BC ==3y x=(0x >)的图象分别与AB ,BC 交于点D ,E .连接DE ,当△BDE ∽△BCA 时,点E 的坐标为______________. 5. 如图,已知直线12y x =与双曲线ky x=(0k >)交于A ,B 两点,点B 的坐标为(-4,-2),C 为第一象限内双曲线ky x=(0k >)上一点.若△AOC 的面积为6,则点C 的坐标为______________.第5题图 第6题图6. 如图,直线12y x =与双曲线ky x=(0k >,0x >)交于点 A ,将直线12y x =向上平移4个单位长度后,与y 轴交于点C ,与双曲线ky x=(0k >,0x >)交于点B .若OA=3BC ,则k 的值为____________.7. 如图,在平面直角坐标系xOy 中,□ABOC 的对角线OA ,BC交于点E ,双曲线ky x =(0k <)经过C ,E 两点.若□ABOC 的面积为10,则k 的值为________________.第7题图第8题图8.如图,正方形ABCD的边BC在x轴上,E是对角线AC,BD的交点.若反比例函数2yx=(0x>)的图象经过A,E两点,则点E的坐标为________________.。
反比例函数19种模型

反比例函数19种模型反比例函数是数学中常见的函数类型之一,用来表示两个变量之间的反比关系。
以下是反比例函数的一些常见模型:1.直线模型:y = k/x,其中k为常数。
2.比例关系模型:y = (kx)/(ax + b),其中k、a、b为常数。
3.反比例关系模型:y = (k/x) + a,其中k、a为常数。
4.工作时间模型:y = k/t,其中k为常数,t表示时间。
5.人口密度模型:y = k/A,其中k为常数,A表示面积。
6.速度和时间模型:y = k/t,其中k为常数,t表示时间。
7.飞行时间和飞行距离模型:y = k/(x^2),其中k为常数,x表示距离。
8.投资收益模型:y = k/(x+a),其中k和a为常数,x表示投资金额。
9.流量与管道直径模型:y = k/(x^2),其中k为常数,x表示管道直径。
10.压力和体积模型:y = k/x,其中k为常数,x表示体积。
11.购买力和价格模型:y = k/x,其中k为常数,x表示价格。
12.照明强度和距离模型:y = k/(x^2),其中k为常数,x表示距离。
13.土地价格和面积模型:y = k/A,其中k为常数,A表示面积。
14.音量和距离模型:y = k/(x^2),其中k为常数,x表示距离。
15.饼干消耗和人数模型:y = k/n,其中k为常数,n表示人数。
16.温度和容器大小模型:y = k/V,其中k为常数,V表示容器大小。
17.实验结果和样本数量模型:y = k/n,其中k为常数,n表示样本数量。
18.电阻和电流模型:y = k/I,其中k为常数,I表示电流。
19.体积和浓度模型:y = k/C,其中k为常数,C表示浓度。
这些模型仅是反比例函数在不同应用领域中的一些示例。
实际上,反比例函数可以描述的反比关系很多,取决于具体应用的背景和需求。
对于不同的问题和场景,可以选择适合的反比例模型来建模和分析。
反比例函数常见几何模型(完整资料).doc

【最新整理,下载后即可编辑】反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=k x(k≠0).其解析式有三种表示方法:①xk y = (0≠k );②1-=kx y (0≠k );③k xy =2.反比例函数y=k x(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=k x 中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=k x图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-. (5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=m 在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x=上,点B 在双曲线3y x=上,且AB∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB交x 轴于M 点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数kyx=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEFS S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE≌△CDF ;④A CB D =其中正确的结论是 .(把你认为正确结论的序号都填上)y xDC A BOFEDFABDF MN xy O例3:一次函数y ax b=+的图象分别与x轴、y轴交于点,M N,与反比例函数kyx=的图象相交于点,A B.过点A分别作AC x⊥轴,AE y⊥轴,垂足分别为,C E;过点B分别作BF x⊥轴,BD y⊥轴,垂足分别为F D,,AC与BD交于点K,连接CD.(1)若点A B,在反比例函数kyx=的图象的同一分支上,如图1,试证明:①AEDK CFBKS S=四边形四边形;②AN BM=.(2)若点A B,分别在反比例函数kyx=的图象的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论.模型三:如图,已知反比例函数kyx=(k≠0,x>0)上任意两点P、C,过P做PA⊥x轴,交x轴于点A,过C做CD⊥x轴,交x轴于点D,则OPC PADCS S∆=梯形.图1 图2例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)k y k x=>交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)k y k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)k y x x=>的图象与AC 边交于点E ,则CEaCFb=.例7:两个反比例函数k y x=和1y x=在第一象限内的图象如图所示,点P 在k y x=的图象上,PC ⊥x 轴于点C ,交1y x=的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在k y x=的图象上运动时,以下结论: ①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发xBFC EAOy生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )A. B. C. D2、如图,点A 在双曲线xy 6=上,且OA=4,过点A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC于B,则ABC ∆的周长为( )A.72B.5C.74D.223、如图,双曲线xk y =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( )A.xy 1= B.xy 2=C.xy 3=D.x y 6=题 3 题 4 题54、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,则S ( )A.S=2B.S=4C.2<S<4D.S>45、如图所示,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,若双曲线y=k x(k≠0)与△ABC 有交点,则k 的取值范围是( )A .1<k<2B .1≤k≤3C .1≤k≤4 D.1≤k<4二、填空题1、如图,点A 在双曲线1y x=上,点B 在双曲线3y x=上,且AB∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .2、如图,双曲线)0(2 x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 . 3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′.(1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 .4、如图,已知双曲线(0)k y k x=<经过直角三角形OAB 斜边OA 的DBAyxOC中点D,且与直角边AB相交于点C.若点A的坐标为(6-,4),则△AOC的面积为.5、双曲线1y、2y在第一象限的图像如图,14yx=,过1y上的任意一点A,作x轴的平行线交2y于B,交y轴于C,若1AOBS∆=,则2y的解析式是.课后习练一、填空题1、如图,直线y=kx(k>0)与双曲线y=4x交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1的值等于_______.2、反比例函数y=kx的图像上有一点P(a,b),且a,b是方程t2-4t-2=0的两个根,则k=_______;点P到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b无交点,则b的取值范围是______.4、反比例函数y=kx的图像经过点P(a,b),其中a,b是一元学习靠自觉,进步靠努力,每天比别人多付出一点点,将来比别人收获多许多!!! 【最新整理,下载后即可编辑】 二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______.5、如图,已知双曲线)0k (xk y > 经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图6、如图,已知点A 是一次函数y=x 的图像与反比例函数y=2x 的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( )A .2B .22C .2D .22 7、已知P 为函数y=2x 的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( ) A .0个 B .2个C .4个D .无数个AB CD E y x O。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kx(k≠0).其解析式有三种表示方法:①xk y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=kx图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:||=||,2k S k S ∆=矩形xyO已知 点P 是反比例函数 在第一象限内图象上的一动点.如图,若 轴于点B , 轴于点N ,连接PM ,PN ,则矩形MONP 的面积为|K|yxMO PNyxMO PNyxMO PNyxMOPN已知 点P 是反比例函数 在第一象限内图象上的一动点.如图,若点B 为y 轴(不同于O )的任意一点,连接 ,则△PAB 的面积为|K|/2.y x AO PByxA O PByxA O P ByxA O P(B )已知 点P 是反比例函数 在第一象限内图象上的一动点.如图,若 轴于点M ,N 为 轴上任意一点,连接MN ,PN ,则△PMN 的面积为_________yx MO P(N )yx MOPNyx MOPNyxMOPN例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN如图,直线 与反比例函数 相交于A 、B 两点,分别过点A 、B 作AE ⊥y 轴、BF ⊥x 轴,求证: ①AC=BD ,AE=BF ②AB ∥EF③△ACE ≌△BDFy x EC D FOBAy x EC D F O BAyxP EC D FOB ADFAB DF MN xy O例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD .(1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.y x DC A B O F E图1图2模型三:如图,A 、B 是反比例函数 在第一象限内图象上的一两个不重合的动点,AC ⊥x 轴于点C , BD ⊥x 轴于点D ,求证:S △OAB=S 梯ACDB .yx DC OAByxS 2S 1DC OAB例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)ky x x =>的图象与AC 边交于点E ,则CE a CF b=.A 、B 是反比例函数 在第一象限内图象上的一两个不重合的动点, AC ⊥y 轴于点C , BD ⊥x 轴于点D ,AC 与BD 相交于点E ,求证:A EB EA CB D=y xCE DO AByxS 1S 2CE DOABxB FC E A O y例7:两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x=的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形P AOB 的面积不会发生变化;③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).【结论1】一次函数y= - x+b(b >0)与反比例函数xy=k(k >0)的图像交于点A ,B ,一次函数图像与y 轴和x 轴分别交于点C 、D 。
反比例函数八大解题模型(模型+例题+练习题)

3、特征
[象限]经过一三象限或二四象限 [坐标轴]双曲线与x轴或y轴无限接近, 但永不相交 [变化趋势]在一三象限,图象呈下降趋势, 在二四象限,图象呈上升趋势
模型一: 模型一:判断是否为反比例函数
(1)给出解析式判断是否为反比例函数(y 是 x 的函数) 例 1、下列函数中,是反比例函数的是( ) A y = x +1 B y=
2、下列函数中 y 是 x 的反比例函数的是( ) (A 级) A y=
y=
2 x +1
D y=
1 −1 x
(2)给出文字先列解析式再判断是否为反比例函数 例 2:当路程 s 一定时。速度 v 与时间 t 之间的函数是( A 正比例函数 B 反比例函数 C 一次函数 对象:路程 s 角度:速度 v、时间 t 分析与解:路程=速度 × 时间 即 s = vt → v = ) (A 级) D 二次函数
第 2 页 共 8 页
是:________________;药物燃烧后 y 关于 x 的函数关系式为:___________________. (2)研究表明,当空气中每立方米的含药量低于 1.6 毫克时学生方可进教室,那么从消毒开始,至少需要经 过_______分钟后,学生才能回到教室; (3)研究表明,当空气中每立方米的含药量不低于 3 毫克且持续时间不低于 10 分钟时,才能有效杀灭空 气中的病菌,那么此次消毒是否有效?为什么?
反比例函数八大 反比例函数八大解题模型 八大解题模型( 解题模型(模型+例题+练习题) 练习题)
基本知识点 1、定义:反比例函数的图像是经过 A(1,k)和 B(k,1)的双曲线 对应解析式 y = 2、举例说明: y =
k k ← 经过(x, (k 是常数,k≠0) ) x x
反比例函数6个模型证明

反比例函数6个模型证明
反比例函数是一种数学模型,可以用来描述两个变量之间的关系。
反比例函数的一般形式是 y = k/x,其中 k 是常数,表示两个变量之间的比例因子。
1. 水缸填水速度和填充时间:当水缸填水速度增加时,填充时间减少。
填充时间与填水速度成反比例关系,可以用反比例函数模型来描述。
2. 人口密度和土地面积:人口密度是指单位面积内的人口数量。
当土地面积固定时,人口密度与土地面积成反比例关系。
可以用反比例函数模型来描述不同土地面积下的人口密度。
3. 电阻值和电流强度:根据欧姆定律,电阻值与电流强度成反比例关系。
当电流强度增加时,电阻值减小。
可以用反比例函数模型来描述电阻值与电流强度之间的关系。
4. 速度和旅行时间:当旅行时间固定时,速度与旅行距离成反比例关系。
旅行速度越快,旅行距离相应地减小,可以使用反比例函数模型来描述这种关系。
5. 工人数量和任务完成时间:假设一项任务需要完成固定的工作量,当工人数量增加时,任务完成时间减少。
工人数量与任务完成时间成反比例关系,可以用反比例函数模型来描述。
6. 阻尼力和物体振幅:在振动系统中,阻尼力与振幅成反比例关系。
阻尼力越大,振幅相应减小。
可以使用反比例函数模型来描述阻尼力与物体振幅之间的关系。
总之,反比例函数可以用来描述许多现实生活中的关系,并且在数学建模和解决实际问题中起到了重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数中的模型(讲义)一、知识点睛
与反比例函数相关的几个结论,在解题时可以考虑调用.
①y
y=
C B k
x
y
y=
D
k
x
C
O A x A x
O B
结论:S矩形2S | k | 结论:S OCD S ABCD
△梯形
ABCO ABO
△
y
y
②
A
A
B
k
O y=
C
x
D D x
B
C
x
O
结论:AB=CD
③y y= k
x
y
B
A
C
D
A
P
D B
O x
E
x
O C
结论:B D∥CE
二、精讲精练
1. 如图,已知点A,B在双曲线y k
x
(x>0)的图象上,AC⊥x 轴于点C,BD⊥y 轴于点D,AC 与
BD相交于点P,且P是AC的中点.若△ABP的面积为3,则k=________.
2. 如图,A,B是双曲线y k
x
(k>0)上的点,且A,B两点的横坐标分别为a,2a,线段AB的延
长线交x 轴于点C.若S△AOC=6,则k=________.
y
y
A
A
B
B
O
C
x
O
C
x
第 2 题图
第 3 题图
3. 如图,直线
4 y x 与双曲线 3 y k x
(x>0)交于点 A .将直线 4 y x 向右平移 3
9 2
个单位后,与双曲
线 y
k x AO (x> 0)交于点 B ,与 x 轴交于点 C ,若
2
BC
,则 k=________.
4. 如图,平行四边形 AOBC 中,对角线交于点 E ,双曲线 形 AOBC 的面积为 18,
y
k x (k>0)经过 A ,E 两点.若平行四边
则k=________.
y
y
y A E C
A O
B C
D
x B C
A D O
x
x
O
B 第 4 题图
第 5 题图
5. 如图,已知函数 y x 1的图象与 x 轴、y 轴分别交于 C ,B 两点,与双曲线
点.若 AB+CD=B ,C 则 k 的值为________.
y
k x 交于 A ,D 两
6. 已知:如图,直线 3
y x 6与双曲线 4
y k x
(x<0)相交于 A ,B 两点,与 x 轴、y 轴分别交于 D ,
C 两点,若 AB=5,则 k=_________.
3
7. 如图,直线 y
x b
3
AB AC 4, 与 y 轴交于点 A ,与双曲线
k y
在第一象限交于 B ,C 两点,且 x
则k=_______
y
y
A B
A B
B'
C
C
x
O
x
O
8. 双曲线y11
x
, 2
y
3
x
在第一象限内的图象如图所示,过y2 上的任意一点 A 作x 轴的平行线,交
y 于点B,交y 轴于点C,过点 A 作x轴的垂线,交1 y 于点D,交x 轴于点E,连接BD,CE,则
1
BD
CE
=________.
y y
N
A
B
B A
C
D
y2
y1
x O E
O M x
第9 题图第10 题图
9. 如图,双曲线y 2
x
(x> 0)经过四边形OABC的顶点A,C,∠ABC=90°,OC平分OA与x轴正半
轴的夹角,AB∥x 轴.将△ABC沿AC翻折后得△A B′C,且点B′恰好落在OA上,则四边形OABC 的面积为__________.
10. 如图,双曲线y k
x
经过Rt△OMN斜边上的点A,与直角边MN 相交于点B,已知OA=2AN,△OAB
的面积为5,则k 的值是__________.
11. 如图,在平面直角坐标系xOy中,直线AB与x 轴、y 轴分别交于点A,B,与反比例函数k
y
( k
x 为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y 轴于M,过点F 作FN⊥x 轴于N,直线EM 与FN 交于点C.若BE:BF=1:m(m 为大于1 的常数).记△CEF的面积为S1,△OEF 的面积为S2,则S1:S2=__________.(用含m 的代数式表示)
y
y
B M E C
A
B
C F
x O N A x O
12. 如图,一次函数y k1x b 的图象过点A(0,3),且与反比例函数y k
2
x
(x>0)的图象相交于B,
C两点.(1)若B(1,2),求k1 k2 的值.
(2)若A B=B C,则k1 k2 的值是否为定值若是,请求出该定值;若不是,请说明理由.解:(1)将A(0,3),B(1,2)
代入y k x b ,
1
得b 3
,___________
解得k1 ____
b ____
.
k
将B( 1,2)代入 2
y
x
,
得k2=______,
∴k1 k2 =______.
(2)_____定值,k k =____.理由:
1 2
过点B作BG⊥y 轴于点G,
过点C作C H⊥y 轴于点H,
则BG∥CH.
又∵AB=BC,
∴AG=____,CH=___BG.
k 设B(m, 2
m ),则C(_____,_____ ),
∴AG=_______,GH=_______,
k
∴3 2
m
=______,
∴m=_____,
∴B( ,).
把B( ,)代入y=k1x+3,得____________,
∴k1 k2 =________.。
