信号检测实验报告
信号检测论_实验报告

一、实验目的1. 理解信号检测论的基本原理和概念。
2. 掌握信号检测论实验方法,包括实验设计、数据收集和分析。
3. 分析信号检测论在心理学研究中的应用,探讨其在不同领域中的价值。
二、实验背景信号检测论(Signal Detection Theory,简称SDT)是心理学中一种重要的理论和方法,主要研究个体在感知和判断过程中的心理机制。
该理论认为,人们在感知外界刺激时,总是受到噪声的干扰,而信号检测论旨在研究个体在噪声中如何识别和判断信号。
三、实验方法1. 实验设计实验采用2(刺激类型:信号与噪音)× 2(判断标准:接受信号、拒绝信号)的混合设计。
2. 实验材料实验材料包括信号、噪音、判断标准等。
3. 实验程序(1)被试随机分为两组,每组10人。
(2)实验开始前,主试向被试讲解实验目的、实验流程及注意事项。
(3)被试依次进行信号和噪音的判断,主试记录被试的判断结果。
(4)实验结束后,主试向被试表示感谢。
四、实验结果1. 数据收集根据实验记录,统计被试对信号和噪音的判断次数。
2. 数据分析(1)计算被试的辨别力指数(d'):d' = Z(SN) - Z(N),其中Z(SN)为信号判断的Z得分,Z(N)为噪音判断的Z得分。
(2)计算被试的判断标准(C):C = Z(SN) - Z(N),其中Z(SN)为信号判断的Z 得分,Z(N)为噪音判断的Z得分。
五、讨论1. 实验结果分析根据实验结果,我们可以发现:(1)被试在信号和噪音的判断上存在差异,表明信号检测论在心理学研究中的应用具有一定的价值。
(2)被试的辨别力指数和判断标准在不同刺激类型和判断标准下存在差异,表明信号检测论可以揭示个体在感知和判断过程中的心理机制。
2. 信号检测论的应用信号检测论在心理学研究中具有广泛的应用,例如:(1)认知心理学:研究个体在感知、记忆、思维等认知过程中的心理机制。
(2)临床心理学:评估个体的认知功能,为心理疾病的诊断和治疗提供依据。
序列信号检测实验报告

一、实验目的1. 理解序列信号检测的基本原理。
2. 掌握序列信号检测的方法和步骤。
3. 通过实验验证序列信号检测的准确性。
4. 分析实验结果,探讨影响序列信号检测准确性的因素。
二、实验原理序列信号检测是数字信号处理中的一个重要领域,主要研究如何从含有噪声的信号中检测出特定的序列信号。
本实验采用模拟信号检测的方法,通过设计序列信号发生器和检测器,实现对特定序列信号的检测。
三、实验器材1. 信号发生器2. 数据采集器3. 计算机及软件(如MATLAB等)4. 信号分析仪四、实验步骤1. 设计序列信号发生器:- 根据实验要求,设计特定的序列信号,如“1101”。
- 使用信号发生器产生该序列信号。
2. 设计序列信号检测器:- 设计一个检测器,用于检测序列信号。
- 检测器可以采用状态机或有限状态机(FSM)实现。
3. 实验设置:- 将信号发生器产生的序列信号输入到数据采集器。
- 将数据采集器采集到的信号输入到计算机进行后续处理。
4. 信号处理:- 使用MATLAB等软件对采集到的信号进行预处理,如滤波、去噪等。
- 对预处理后的信号进行序列信号检测。
5. 结果分析:- 分析实验结果,比较检测器检测到的序列信号与原始序列信号是否一致。
- 分析影响序列信号检测准确性的因素,如噪声水平、信号带宽等。
五、实验结果与分析1. 实验结果:- 通过实验,成功检测到了设计的序列信号“1101”。
- 检测到的序列信号与原始序列信号基本一致。
2. 结果分析:- 实验结果表明,所设计的序列信号检测器能够有效地检测出特定序列信号。
- 影响序列信号检测准确性的因素主要包括:- 噪声水平:噪声水平越高,检测难度越大。
- 信号带宽:信号带宽越窄,检测难度越大。
- 序列长度:序列长度越长,检测难度越大。
六、实验结论1. 序列信号检测实验验证了序列信号检测的基本原理和方法。
2. 通过实验,掌握了序列信号检测的步骤和技巧。
3. 实验结果表明,所设计的序列信号检测器能够有效地检测出特定序列信号。
信号检验论实验报告(3篇)

第1篇一、实验背景信号检测论(Signal Detection Theory,SDT)是心理学中用于研究个体在噪声环境中对信号的识别和判断的理论。
该理论强调个体在感知和决策过程中的主观因素,并通过对信号和噪声的辨别能力进行量化分析,揭示个体在感知过程中的心理机制。
本次实验旨在探讨信号检测论在心理学研究中的应用,通过模拟信号和噪声环境,考察被试在不同条件下的信号识别能力和决策倾向。
二、实验目的1. 了解信号检测论的基本原理和实验方法。
2. 探讨信号和噪声对被试识别能力的影响。
3. 分析被试在不同先验概率下的决策倾向。
三、实验方法1. 实验设计本实验采用2(信号与噪声)× 2(先验概率)的混合实验设计,即信号与噪声两个因素各分为两个水平,先验概率因素也分为两个水平。
实验流程如下:(1)向被试介绍实验目的和规则;(2)展示信号和噪声样本,并要求被试判断样本是否为信号;(3)记录被试的判断结果,包括击中、虚报、漏报和正确否定。
2. 实验材料(1)信号样本:随机生成的具有一定频率和振幅的正弦波;(2)噪声样本:随机生成的白噪声;(3)先验概率:信号出现的概率和噪声出现的概率。
3. 被试招募20名年龄在18-25岁之间的志愿者,男女比例均衡。
四、实验结果1. 信号检测指标(1)击中率(Hit Rate):被试正确识别信号的概率;(2)虚报率(False Alarm Rate):被试错误地将噪声识别为信号的概率;(3)漏报率(Miss Rate):被试错误地将信号识别为噪声的概率;(4)正确否定率(Correct Rejection Rate):被试正确否定噪声的概率;(5)似然比(Likelihood Ratio):信号与噪声的似然比,用于衡量被试对信号的识别能力。
2. 先验概率对信号检测指标的影响结果表明,先验概率对被试的信号检测指标有显著影响。
当信号先验概率较高时,被试的击中率和正确否定率显著提高,虚报率和漏报率显著降低;当信号先验概率较低时,被试的击中率和正确否定率显著降低,虚报率和漏报率显著提高。
心理学“信号检测论”实验报告
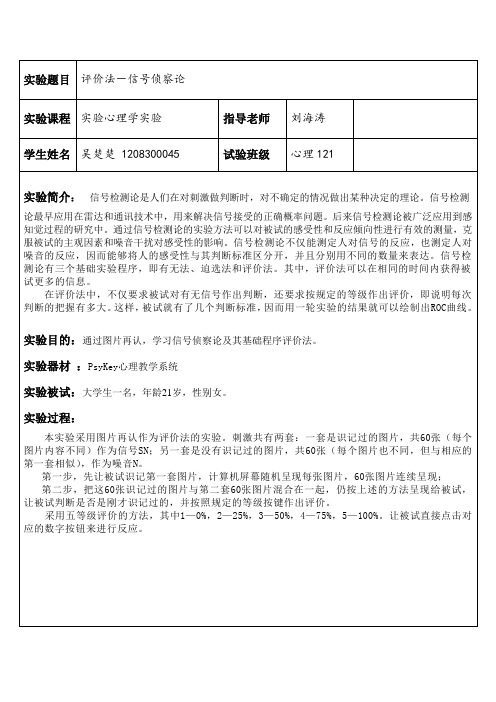
实验题目评价法-信号侦察论实验课程实验心理学实验指导老师刘海涛学生姓名吴楚楚1208300045 试验班级心理121实验简介:信号检测论是人们在对刺激做判断时,对不确定的情况做出某种决定的理论。
信号检测论最早应用在雷达和通讯技术中,用来解决信号接受的正确概率问题。
后来信号检测论被广泛应用到感知觉过程的研究中。
通过信号检测论的实验方法可以对被试的感受性和反应倾向性进行有效的测量,克服被试的主观因素和噪音干扰对感受性的影响。
信号检测论不仅能测定人对信号的反应,也测定人对噪音的反应,因而能够将人的感受性与其判断标准区分开,并且分别用不同的数量来表达。
信号检测论有三个基础实验程序,即有无法、迫选法和评价法。
其中,评价法可以在相同的时间内获得被试更多的信息。
在评价法中,不仅要求被试对有无信号作出判断,还要求按规定的等级作出评价,即说明每次判断的把握有多大。
这样,被试就有了几个判断标准,因而用一轮实验的结果就可以绘制出ROC曲线。
实验目的:通过图片再认,学习信号侦察论及其基础程序评价法。
实验器材:PsyKey心理教学系统实验被试:大学生一名,年龄21岁,性别女。
实验过程:本实验采用图片再认作为评价法的实验。
刺激共有两套:一套是识记过的图片,共60张(每个图片内容不同)作为信号SN;另一套是没有识记过的图片,共60张(每个图片也不同,但与相应的第一套相似),作为噪音N。
第一步,先让被试识记第一套图片,计算机屏幕随机呈现每张图片,60张图片连续呈现;第二步,把这60张识记过的图片与第二套60张图片混合在一起,仍按上述的方法呈现给被试,让被试判断是否是刚才识记过的,并按照规定的等级按键作出评价。
采用五等级评价的方法,其中1—0%,2—25%,3—50%,4—75%,5—100%。
让被试直接点击对应的数字按钮来进行反应。
实验结果:=====结果分数=====----------------------------------类型12345合计----------------------------------信号 3 1 9 10 37 60噪音24 6 16 6 8 60----------------------------------计算各标准下的击中率,虚报率,以及d和β判断标准C4 C3 C2 C1P(y/N) 0.61 0.78 0.93 0.94P(y/N) 0.13 0.23 0.50 0.60Z/SN -1.530 -0.261 0.858 0.933Z/N -0.614 -0.352 0.352 0.6140.124 0.386 0.276 0.259击中率的纵坐标0.331 0.375 0.375 0.331虚报率的纵坐标d 0.916 0.095 0.506 0.319β0.37 1.03 0.74 0.78 可对此表进一步处理,画出ROC曲线.实验结果分析:1.由数据可知,被试的感受性d值约为0.46。
信号检测论实验报告

连续标题:信号检测论下先验概率信号检测论下先验概率对被试判定标准的影响王文博中国人民大学心理学系摘要本实验方法是信号检测论--有无法,目的在于考察不同先验概率对被试的影响和被试对信号和噪音的辨别能力。
实验被试为中国人民大学心理学系本科二年级学生一名,实验要求被试在不同先验概率下进行重量类型信号噪音的判别,信号出现的先验概率次序依次为50%、20%、80%,并计算被试在不同情况下辨别力指标d’和判定标准β,绘制ROC曲线,通过ROC 曲线测出被试对信号和噪音的辨别能力。
结果显示,信号(SN)的先验概率越大,被试的判断标准β也越随之变松;同时被试辨别力d’也受到先验概率的影响。
信号检测论下先验概率对被试判定标准的影响信号检测论(Signal detection theory,SDT)是现代心理物理学最重要的内容之一,它的出现彻底改变了以往人们对阈限的理解,将个体客观的感受性和主观的动机、反应偏好等加以区分,从而解决了传统心理物理学所无法解决的问题。
先验概率(Prior probability)是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现,在本实验中即为给定的信号出现概率。
实验用两个不同重量的刺激作为“信号”和“噪声”随机呈现。
根据被试的击中率和虚报率计算辨别力d’和判定标准β并绘制操被试操作特性曲线即ROC曲线。
研究假设被试的判断标准和辨别力会受到先验概率的影响,先验概率越大,判断标准越松。
方法被试中国人民大学心理学系大二本科生一名,对重量有清楚的感受,辨别能力正常。
仪器JGW—E型心理试验台,重量阈标称物,记录纸。
流程准备:主试了解操作流程之后,在JGW—E型心理试验台中进入实验目录界面首页,由键盘输入“29”,选中信号检测法实验图标进入实验参数选择界面。
把104克、108克和112克的重量分别和100克的重量比较10次,选出一个10次比较重7次或8次觉得比100克重的重量作为信号刺激,100克重量作为噪音。
信号检测法实验报告

信号检测法—有无法的实验报告摘要:本实验采用了信号检测论的有无法,考察了一名心理系本科生在文本材料和图片材料下的辨别力和判定标准的大小。
实验发现:被试在文本材料上的学习优于图片材料上的学习。
关键字:信号检测论有无法辨别力d’判定标准1.前言信号检测论是现代心理物理学的重要组成部分,它假设人们对刺激进行感知时,干扰也总是存在的,即人作为一个接受者对刺激的辨别问题可等效于在噪音中检测信号的问题。
信号检测论的研究对象是信息传播系统中信号接收问题,在心理学中它是借助数学的形式描述”接收者”在某一观察时间内将掺有噪音的信号从噪音中辨别出来.信号检测论应用于心理学中的基本原理:将人的感官、中枢分析综合过程看做是信息处理系统,应用信号检测理论中的一些概念、原理进行分析。
在心理学领域中,信号检测论所指的信号可以理解为刺激。
在信号检测论中,噪音就是对信号检测其干扰作用的所有背景,对信号起干扰作用的因素都可以当成噪音。
信号检测论把刺激的判断看成对信号的检查,并做出决策的过程。
感觉过程是神经系统对信号或噪音的客观反应,它仅取决于外在刺激的性质,即信号和噪音之间的客观区别;而决策过程受到主观因素的影响.信号检测论认为:被试觉察信号有一个中枢神经效应,这种效应随着每次刺激呈现,时刻都在变化。
信号总是在噪音的背景上产生,信号的影响和噪音的影响都被假定为正态分布,这两种分布由于信号比噪音微弱或增强,故有一定的重叠,而使信号和噪音都可能引起同一程度的感觉。
人类觉察是建立在统计决策论的基础上,就是说被试选择一个标准,当给定的刺激超过这个标准时,被试就反应“有”,否则说“无”.信号检测论的实验方法有三种:有无法、迫选法和评价法。
有--无法实验是信号检测实验的基本形式。
信号检测论(signal detection theory)属于信息论的一个分支,研究对象是信号传输系统中的信号接收部分。
它借助于数学形式,分析信号接收者如何把信号从噪声中提取出来。
信号检测论实验报告

信号检测论实验报告信号检测论实验报告引言信号检测论是一门研究如何在噪声背景下准确地检测和判断信号存在与否的学科。
在实际应用中,如雷达、通信系统等领域,信号检测论的研究具有重要的理论和实践意义。
本实验旨在通过实际操作,探究信号检测论的基本原理和方法。
实验目的1. 了解信号检测论的基本概念和理论框架;2. 掌握信号检测论中的常用指标和性能度量;3. 进行实际信号检测实验,验证理论与实践的一致性。
实验装置与方法实验中我们使用了一套基于噪声的信号检测系统。
该系统由信号发生器、噪声源、放大器、滤波器和信号检测器等组成。
我们首先设置信号发生器产生一定频率和幅度的信号,然后将信号与噪声源混合,经过放大和滤波后送入信号检测器。
信号检测器会根据预设的判决准则,判断信号是否存在。
实验过程1. 实验前,我们先了解了信号检测论中的基本概念,如信号和噪声的概率密度函数、信号和噪声的假设等。
2. 在实验中,我们选择了两种常用的判决准则:最大似然准则和最小平均错误概率准则。
我们通过调节信号发生器的频率和幅度,以及噪声源的强度,来模拟不同的信号和噪声场景。
3. 针对每一种场景,我们记录了实验结果,包括判决准确性和性能度量指标,如误报概率和漏报概率等。
4. 在实验过程中,我们还对比了不同判决准则的性能差异,并对实验结果进行了分析和总结。
实验结果与讨论通过实验,我们得到了一系列的实验结果。
在不同的信号和噪声场景下,最大似然准则和最小平均错误概率准则的性能表现有所差异。
在某些场景下,最大似然准则的误报概率较低,但漏报概率较高;而最小平均错误概率准则则相反。
这说明在不同的应用场景中,选择合适的判决准则至关重要。
此外,我们还发现信号和噪声的强度对判决准确性有着重要影响。
当信号强度较弱或噪声强度较大时,判决的准确性会下降。
因此,在实际应用中,我们需要根据实际情况,合理调节信号和噪声的参数,以保证准确判断信号的存在与否。
结论通过本次实验,我们深入了解了信号检测论的基本概念、理论框架和实验方法。
信号检测实验报告

一、实验目的1. 理解信号检测论的基本原理和概念。
2. 掌握信号检测实验的方法和步骤。
3. 分析信号检测实验结果,了解信号检测论在心理学研究中的应用。
二、实验背景信号检测论(Signal Detection Theory,简称SDT)是现代心理物理学的重要组成部分,起源于20世纪50年代。
它主要研究人类在感知和判断过程中,如何从含噪声的信号中提取有效信息。
信号检测论的核心观点是:人们在感知信号时,不仅受到信号本身的制约,还受到噪声和个体主观因素的影响。
三、实验方法1. 实验对象:选取10名身心健康、年龄在18-25岁之间的志愿者作为实验对象。
2. 实验材料:JGWB心理实验台操作箱、100克、104克、108克、112克的重量各一个。
3. 实验步骤:(1)准备工作:将实验器材准备好,确保实验环境安静、光线适宜。
(2)实验过程:实验者随机抽取四个重量(100克、104克、108克、112克)进行判断。
每个重量呈现3次,共计12次。
实验者需要判断每个重量的重量大小,并报告是否为“重”。
(3)数据记录:实验者对每个重量的判断结果进行记录,包括“重”和“轻”两种情况。
4. 实验数据分析:运用信号检测论的相关指标,对实验数据进行统计分析。
四、实验结果1. 辨别力(d'):辨别力是反映个体对信号与噪声差异敏感程度的指标。
在本实验中,10名志愿者的辨别力平均值约为2.3。
2. 判断标准(C):判断标准是反映个体在判断过程中所采用决策规则的指标。
在本实验中,10名志愿者的判断标准平均值约为0.7。
3. 先验概率:先验概率是指实验者在判断前对信号出现的概率估计。
在本实验中,设定信号出现的概率为0.5。
五、实验分析1. 辨别力分析:实验结果显示,志愿者的辨别力平均值约为2.3,说明志愿者在判断过程中能够较好地识别信号与噪声的差异。
2. 判断标准分析:实验结果显示,志愿者的判断标准平均值约为0.7,说明志愿者在判断过程中倾向于宽松的决策规则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Harbin Institute of Technology匹配滤波器实验报告课程名称:信号检测理论院系:电子与信息工程学院姓名:高亚豪学号:14SD05003授课教师:郑薇哈尔滨工业大学1. 实验目的通过Matlab 编程实现对白噪声条件下的匹配滤波器的仿真,从而加深对匹配滤波器及其实现过程的理解。
通过观察输入输出信号波形及频谱图,对匹配处理有一个更加直观的理解,同时验证匹配滤波器具有时间上的适应性。
2. 实验原理对于一个观测信号()r t ,已知它或是干扰与噪声之和,或是单纯的干扰,即0()()()()a u t n t r t n t +⎧=⎨⎩这里()r t ,()u t ,()n t 都是复包络,其中0a 是信号的复幅度,()u t 是确知的归一化信号的复包络,它们满足如下条件。
2|()|d 1u t t +∞-∞=⎰201||2a E = 其中E 为信号的能量。
()n t 是干扰的均值为0,方差为0N 的白噪声干扰。
使该信号通过一个线性滤波系统,有效地滤除干扰,使输出信号的信噪比在某一时刻0t 达到最大,以便判断信号的有无。
该线性系统即为匹配滤波器。
以()h t 代表系统的脉冲响应,则在信号存在的条件下,滤波器的输出为00()()()d ()()d ()()d y t r t h a u t h n t h τττττττττ+∞+∞+∞=-=-+-⎰⎰⎰右边的第一项和第二项分别为滤波器输出的信号成分和噪声成分,即00()()()d x t a u t h τττ+∞=-⎰()()()d t n t h ϕτττ+∞=-⎰则输出噪声成分的平均功率(统计平均)为220E[|()|]=E[|()()d |]t n t h ϕτττ+∞-⎰**00*00200=E[()(')]()(')d d '=2()(')(')d d '2|()|d n t n t h h N h h N h ττττττδττττττττ+∞+∞+∞+∞+∞---=⎰⎰⎰⎰⎰而信号成分在0t 时刻的峰值功率为2220000|()||||()()d |x t a u t h τττ+∞=-⎰输出信号在0t 时刻的总功率为22000E[|()|]E[|()()|]y t x t t ϕ=+22**0000002200E[|()||()|()()()()]|()|E[|()|]x t t x t t t x t x t t ϕϕϕϕ=+++=+上式中输出噪声成分的期望值为0,即0E[()]0t ϕ=,因此输出信号的功率成分中只包含信号功率和噪声功率。
则该滤波器的输出信噪比为222000022000|||()()d ||()|E[|()|]2|()|d a u t h x t t N h τττρϕττ+∞+∞-==⎰⎰根据Schwartz 不等式有222000|()()d ||()|d |()|d u t h u t h τττττττ+∞+∞+∞-≤-⎰⎰⎰当且仅当*0()()h cu t ττ=-时等号成立,其中c 为任意非零复常数。
此时获得最大信噪比,即22000|||()|d 2m a u t N ττρ+∞-=⎰对该式进行0t t τ=-的变量置换,得到220|()|d |()|d t u t u t t ττ+∞-∞-=⎰⎰因此,()u t 只有在0t t =时刻之前结束,才能使信噪比达到最大值。
即观察时刻0t 需设置在输入信号结束之后,此时022|()|d |()|d 1t u t t u t t +∞-∞-∞==⎰⎰。
则最大信噪比为2000||2m a EN N ρ==综上所述,匹配滤波器的单位冲激响应为*0()()m h cu t ττ=-,对其进行傅里叶变换得到它的频率响应为0j2*()()e ft m H f cU f π-=,其中()U f 输入信号()u t 傅里叶变换。
从匹配滤波器的频率响应可以看出,滤波处理不仅对信号的幅度进行了匹配,使输入信号较强的频率成分得到较大的加权,而且将输入信号的非线性相位补偿掉,使输出信号具有线性相位。
3. 实验步骤(1)设定采样频率、噪声功率等仿真参数,产生输入信号的波形()u t 。
(2)根据()u t 得到匹配滤波器的单位冲激响应()h t 。
u t及其延迟叠加构成,即输入信号中存在两个回(3)生成输入信号,它有()波。
(4)对输入信号和单位脉冲响应分别进行N点FFT,其中N不小于输入信号和冲激响应的点数之和,将它们的结果相乘,在进行FFT的逆变换,得到滤波器的输出信号。
(5)生成输出信号的波形图即频谱图。
检测输出信号的两个峰值,将它们出现的时间与理论值比较,验证滤波器在时间上的适应性。
4.实验结果与分析本实验中采用的仿真参数如下:采样频率为100KHz,载波频率为2KHz,信号脉冲宽度为0.015s,第二个回波信号延迟为0.025s。
首先,在无噪声干扰的条件下,将有限时间的正弦信号及其延迟输入匹配滤波器,得到各部分仿真波形如下所示:τ=,与仿真设定值相等。
计算得到的延迟结果为0.025s从图像中可以看出,匹配滤波器的输出有两个峰值,分别对应两个输入信号结束的时刻,且它们之间的时间间隔等于输入信号的延迟时间,验证了匹配滤波器具有时间上的适应性。
即当信号存在延迟时,不需要改变滤波器的形式,只需将观察时刻延迟相应的时间即可。
输出信号的幅度谱与输入信号相比,有了更强的对比度,即在较大的频率分量上得到了较大加权,并且输出信号具有线性相位,验证了匹配处理对输入信号进行了幅度匹配和相位匹配。
在有噪声干扰的条件下,仿真得到的结果如下所示,其中噪声平均功率为0.3:τ=。
其中滤波器的频率响应与上面的相同,计算得到的延迟结果为0.025s在此不再列出。
以上结果说明在该噪声环境下仍能够实现信号的匹配滤波。
只是输出信号的相位不再是线性的,这是由于滤波器无法对噪声的相位进行补偿。
仍在该噪声条件下,将输入信号改为线性调频信号,得到的仿真结果为:其它条件不变,只将输入信号改为m序列的二相编码,其码元速率为2Kb/s,伪码周期为31,得到如下结果:可见,当改变信号波形时,进行相应的匹配滤波可以得到相似的结果,与理论推导结果一致,从而验证了匹配滤波器的幅度和相位匹配特性,以及时间适应性。
5.实验仿真程序clear all;close all;clc;%仿真参数设定fs = 1e5; %采样频率100kHzA = 0.3; %设置噪声平均功率fo = 2e3; %载波频率2kHzTo = 0.015; %调制脉冲长度0.015sts = 1 / fs; %采样周期td = 0.01; %第二个回波的延时%df = 1e4; %线性调频信号频率变化率%rb = 2e3; %二相编码的码元速率tu = 0 : ts : (To - ts);% mseq = m_sequence([0, 0, 1, 0, 1], 1);% [u, tu] = wave(mseq, fs, rb); %m序列二相编码%u = cos(2 * pi * (fo + df * tu) .* tu); %线性调频信号u = cos(2 * pi * fo * tu); %回波信号为正弦信号h = fliplr(u); %匹配滤波器单位脉冲响应x = [u, zeros(1, fix(td / ts)), u] + A * randn(1, 2 * size(u, 2) + fix(td / ts)); N1 = size(x, 2);N2 = size(h, 2);M = N1 + N2 - 1; %傅里叶变换的点数X = fft(x, M);H = fft(h, M);Y = X .* H;y = ifft(Y, M);[C, I1] = max(y);y1 = y;y1(I1 - 10 : I1 + 10) = 0;[C, I2] = max(y1);tao = ts * abs(I1 - I2)%仿真图像t = 0 : ts : ts * (M - 1);figure(1);tx = 0 : ts : ts * (N1 - 1);plot(tx, x);axis([0, 0.045, -2, 2]);title('匹配滤波器输入信号波形(两个回波)');xlabel('时间/s');ylabel('幅度/V');figure(2);fd = fs / M;f = 0 : fd : (fs - fd);subplot(2, 1, 1);plot(f, abs(H));title('匹配滤波器幅频响应');xlabel('频率/Hz');ylabel('幅度');subplot(2, 1, 2);plot(f, angle(H));title('匹配滤波器相频响应');xlabel('频率/Hz');ylabel('角度/rad');figure(3);plot(t, y);title('匹配滤波器输出');xlabel('时间/s');ylabel('幅度/V');figure(4);subplot(2, 1, 1);plot(f, abs(X));title('输入信号与输出信号的幅频特性比较');xlabel('频率/Hz');ylabel('幅度');subplot(2, 1, 2);plot(f, abs(Y));xlabel('频率/Hz');ylabel('幅度');figure(5);subplot(2, 1, 1);plot(f, angle(X));title('输入信号与输出信号的相频特性比较');xlabel('频率/Hz');ylabel('角度/rad');subplot(2, 1, 2);plot(f, angle(Y));xlabel('频率/Hz');ylabel('角度/rad');%产生m序列function mseq = m_sequence(fbconnection, period)n = length(fbconnection);N = 2^n - 1; %m序列的长度for k = 1 : periodregister = [zeros(1,n - 1) 1]; %定义移位寄存器的初始状态mseq(1 + N * (k - 1)) = register(n); %m序列的第一个输出码元for i = 2 + (N * (k - 1)) : (N * k)newregister(1) = mod(sum(fbconnection.*register),2);for j = 2 : nnewregister(j) = register(j-1);end;register = newregister; %移位后的寄存器mseq(i) = register(n); %新的寄存器输出endend%对m序列进行二相编码function [y, t] = wave(code, fs, rb)T = fs / rb;N = length(code);for i = 1 : N;if code(i) == 1;for j = 1 : T;y(T * (i - 1) + j) = 1;endendif code(i) == 0;for j = 1 : T;y(T * (i - 1) + j) = -1;endendendy = [y, y(T * N)];t = 0 : (1 / fs) : (N / rb);。
